Improved Stereophotogrammetric and Multi-View Shape-from-Shading DTMs of Occator Crater and Its Interior Cryovolcanism-Related Bright Spots
Abstract
:1. Introduction
2. Background
2.1. Dawn Mission Overview
| Orbit Phase | ID | Orbit | Start | Orbit Radii (km) | Height (km) | GSD (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Mdn. | Max. | Min. | Mdn. | Max. | Min. | Mdn. | Max. | ||||
| Vesta–Ceres Cruise | VCC | 2012/09/10 | ||||||||||
| Ceres Science Approach | CSA | 2015/01/13 | ||||||||||
| Ceres Science RC3 | CSR | 2015/04/25 | 13,963 | 14,012 | 14,104 | 13,493 | 13,568 | 13,996 | 1258.7 | 1265.6 | 1305.0 | |
| Ceres Transfer to Survey | CTS | 2015/05/16 | 5545 | 5575 | 7771 | 5079 | 5126 | 7310 | 473.8 | 478.4 | 681.9 | |
| Ceres Science Survey | CSS | 2015/06/05 | 4854 | 4863 | 4870 | 4379 | 4402 | 4575 | 407.7 | 410.6 | 426.7 | |
| Ceres Transfer To HAMO | CTH | 2015/07/01 | ||||||||||
| Ceres Science HAMO | CSH | 2015/08/18 | 1932 | 1940 | 1945 | 1456 | 1480 | 1602 | 135.6 | 138.0 | 149.5 | |
| Ceres Transfer to LAMO | CTL | 2015/10/23 | ||||||||||
| Ceres Science LAMO | CSL | 2015/12/16 | 839 | 848 | 861 | 388 | 386.9 | 615 | 33.0 | 36.1 | 57.4 | |
| End of Dawn’s primary mission at Ceres | ||||||||||||
| Ceres Extended LAMO | CXL | XMO1 | 2016/06/19 | 836 | 849 | 861 | 357 | 392 | 693 | 33.3 | 36.5 | 64.7 |
| Ceres Transfer to Juling | CTJ | 2016/09/02 | ||||||||||
| Ceres Extended Juling | CXJ | XMO2 | 2016/10/17 | 1930 | 1961 | 1965 | 1476 | 1489 | 1734 | 137.4 | 138.9 | 161.7 |
| Ceres Transfer of GRaND | CTG | 2016/11/03 | ||||||||||
| Ceres Extended GRaND | CXG | XMO3 | 2017/01/27 | 8014 | 8024 | 8197 | 7580 | 7653 | 7812 | 705.7 | 713.7 | 729.9 |
| Ceres Transfer to Opposition | CTO | 2017/02/23 | ||||||||||
| Ceres Extended Opposition | CXO | XMO4 | 2017/03/28 | 19,267 | 20,457 | 48,876 | 18,837 | 19,998 | 48,629 | 1757.2 | 1865.6 | 4536.4 |
| End of Dawn’s first extended mission (XM1) at Ceres | ||||||||||||
| Extended Mission Orbit 5 | XMO5 | 2017/07/01 | ||||||||||
| Transfer to Extended Mission Orbit 6 | 2018/04/16 | |||||||||||
| Extended Mission Orbit 6 | XMO6 | 2018/05/16 | 911 | 982 | 3508 | 451 | 537 | 3059 | 41.9 | 50.1 | 285.4 | |
| Transfer to Extended Mission Orbit 7 | 2018/05/31 | |||||||||||
| Extended Mission Orbit 7 | XMO7 | 2018/06/09 | 503 | 529 | 4458 | 29 | 57 | 4297 | 2.7 | 5.3 | 400.9 | |
2.2. The Dawn Framing Camera (FC)
2.3. Currently Published and Archived DTMs
| Method | Data | Dataset ID | Data Extent | GSD | |||
|---|---|---|---|---|---|---|---|
| lonmin | latmin | lonmax | latmax | ||||
| (°) | (°) | (°) | (°) | (m) | |||
| SPG | HAMO | CE_HAMO_G_00N_180E_EQU_DTM | 0 | −90 | 360 | 90 | 136.72 |
| SPG | LAMO | CE_LAMO_L_AHUNAMONS_EQU_DTM | 308 | −17 | 322 | −3 | 32.04 |
| SPG | LAMO | CE_LAMO_L_ERNUTET_EQU_DTM | 30 | 35 | 60 | 70 | 32.04 |
| SPG | LAMO | CE_LAMO_L_HAULANI_EQU_DTM | 0 | −3 | 20 | 17 | 32.04 |
| SPG | LAMO | CE_LAMO_L_IKAPATI_EQU_DTM | 32 | 22 | 54 | 44 | 32.04 |
| SPG | LAMO | CE_LAMO_L_KUPALO_EQU_DTM | 164 | −50 | 184 | −30 | 32.04 |
| SPG | LAMO | CE_LAMO_L_OCCATOR_EQU_DTM | 223 | 3 | 256 | 36 | 32.04 |
| SPG | LAMO | CE_LAMO_L_YALODE_EQU_DTM | 266 | −72 | 322 | −16 | 32.04 |
| SPC | SURVEY | DAWN-A-FC2-5-CERESSHAPESPC-V1.0 | 0 | −90 | 360 | 90 | 100.00 |
| HAMO | |||||||
| LAMO | |||||||
| SPG | HAMO | CSH_CXJ_OCCATOR_EQU_SPG_DTM | 213.5 | 2.0 | 263.5 | 36.2 | 135.99 |
| SfS | HAMO | CSH_CXJ_OCCATOR_EQU_SFS_DTM | 213.5 | 2.0 | 263.5 | 36.2 | 67.99 |
| SPG | LAMO | CSL_CXL_OCCATOR_EQU_SPG_DTM | 220.3 | 8.8 | 256.7 | 31.7 | 33.99 |
| SfS | LAMO | CSL_CXL_OCCATOR_EQU_SFS_DTM | 232.7 | 13.3 | 245.5 | 26.1 | 16.99 |
| SfS | LAMO | CSL_CXL_FRESHCR_EQU_SFS_DTM | 206.8 | 12.8 | 230.1 | 15.9 | 16.99 |
2.4. Topography Reconstruction Methods (Laser Altimeter, SPG, SfS)
3. Data
3.1. Cartographic Information
3.2. CSH/CXJ SPG DTM
3.3. CSH/CXJ SfS DTM
3.4. CSL/CXL SPG DTM
3.5. CSL/CXL/XMO7 SfS DTM
4. Methods
4.1. Bad/Warm Pixel Removal
4.2. Image Registration
4.3. Photometric Models
4.4. Pre-Processing
4.4.1. dawnfc2isis
4.4.2. spiceinit
4.4.3. campt, qtie, and jigsaw (Co-Registration and Bundle Adjustment)
4.4.4. fx (Noise Removal)
4.4.5. cam2map
4.4.6. phocube + fx (Photometric Correction)
4.4.7. specpix + cropspecial (HIS Pixel Removal)
4.5. SPG Processing
4.5.1. Disparity Map Initialization
4.5.2. Sub-Pixel Refinement and Outlier Rejection
4.5.3. Triangulation and DTM Generation
4.6. SfS Processing
5. Results
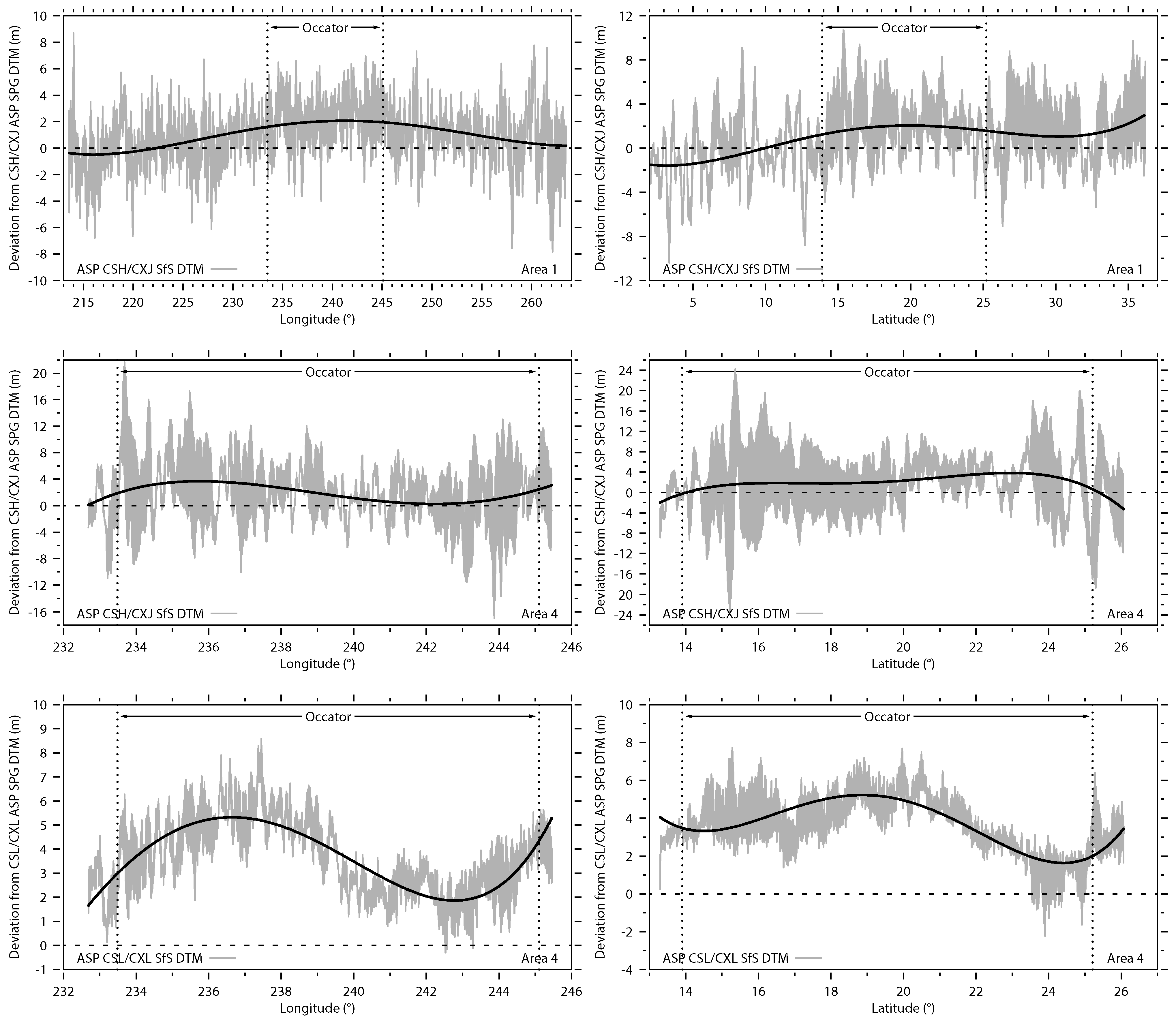
5.1. SPG vs. SfS
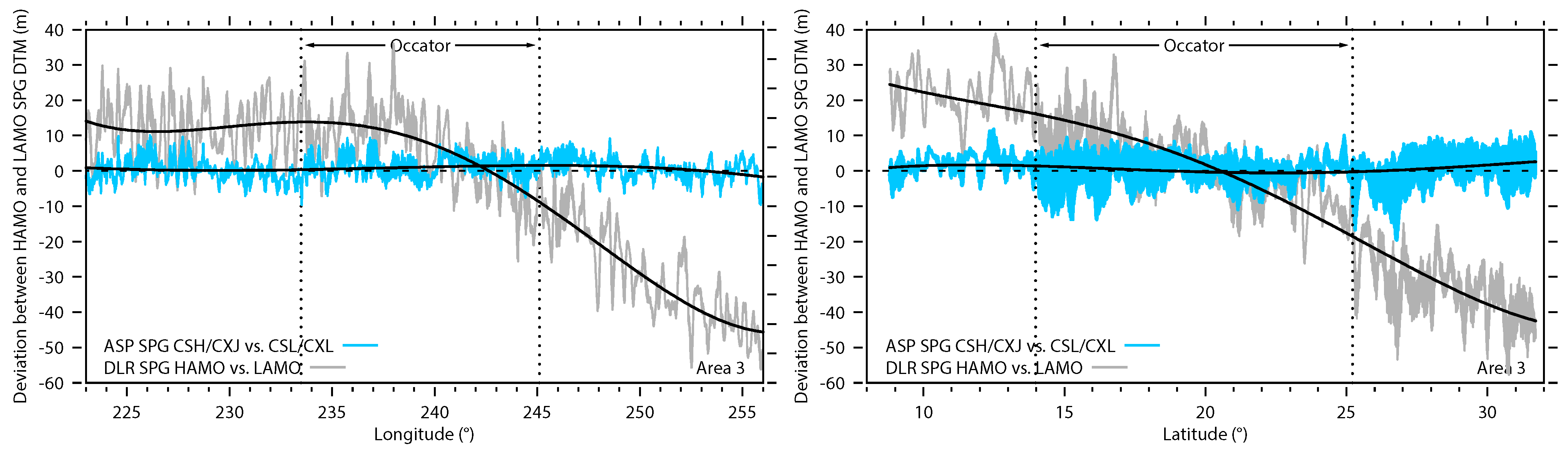
5.2. HAMO SPG vs. LAMO SPG
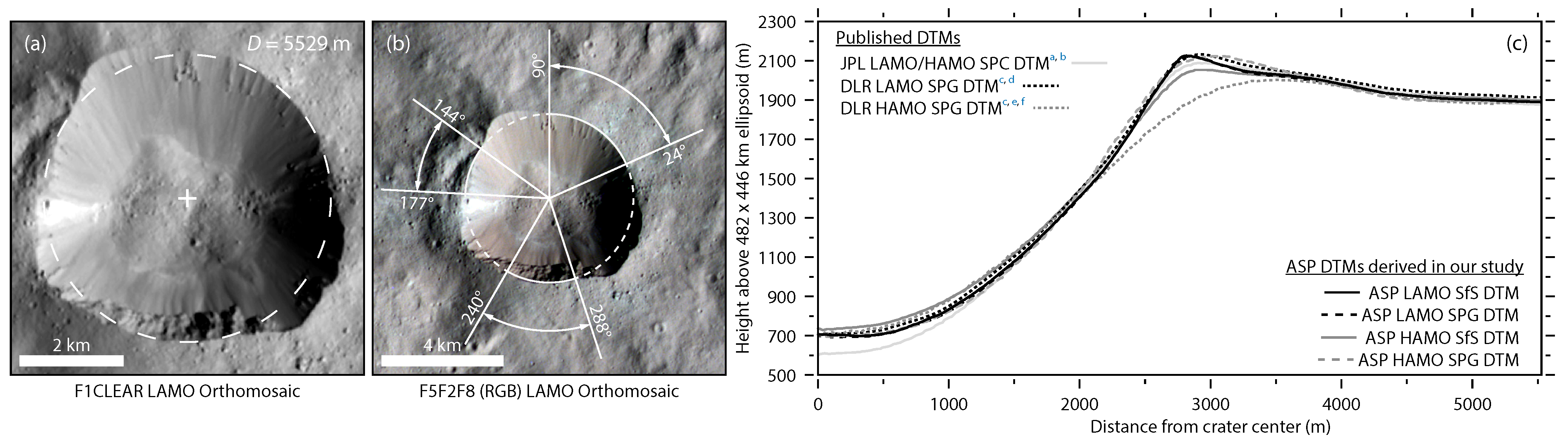
5.3. Comparison of DLR, JPL, and ASP 2.7 DTMs
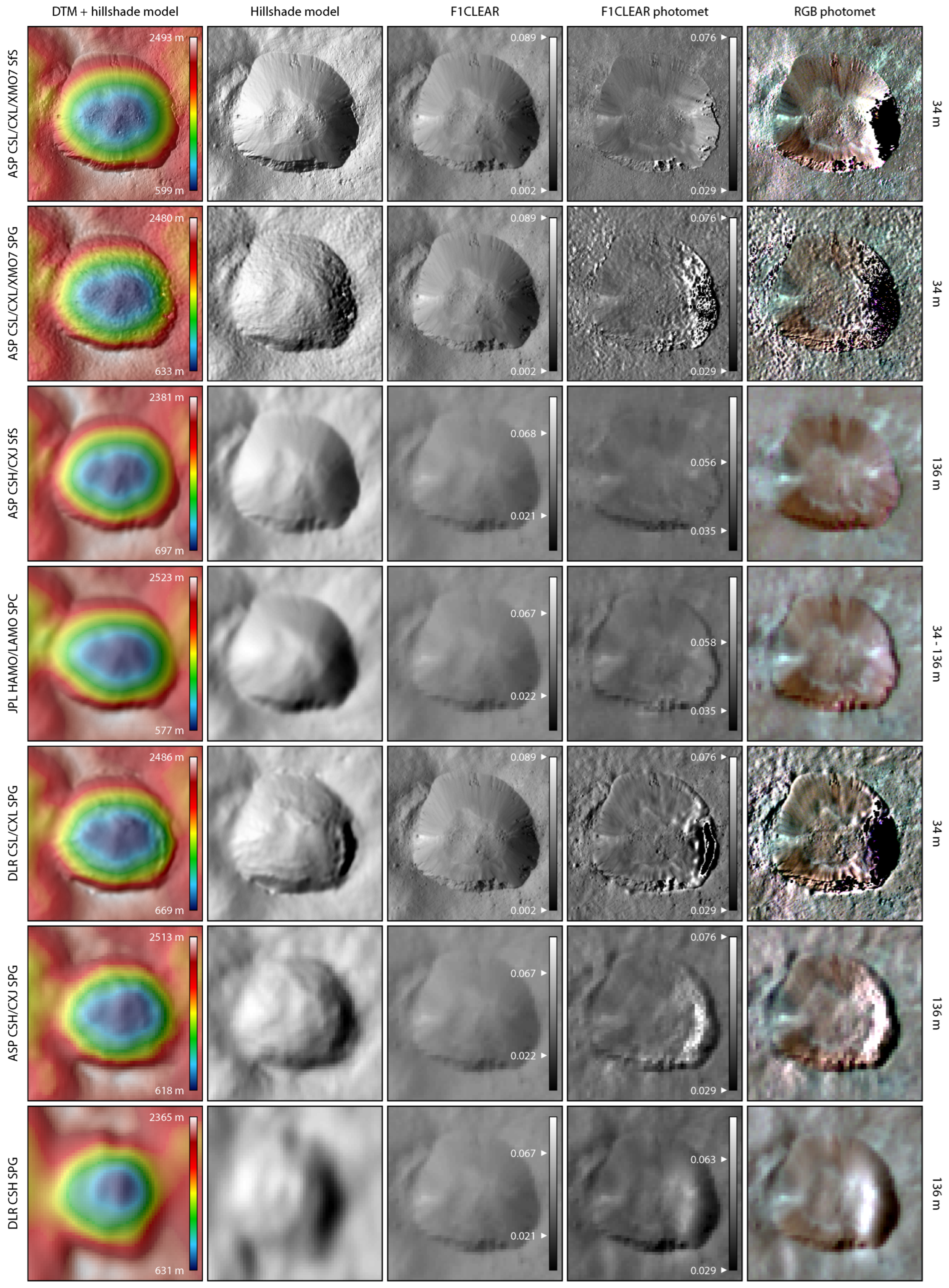
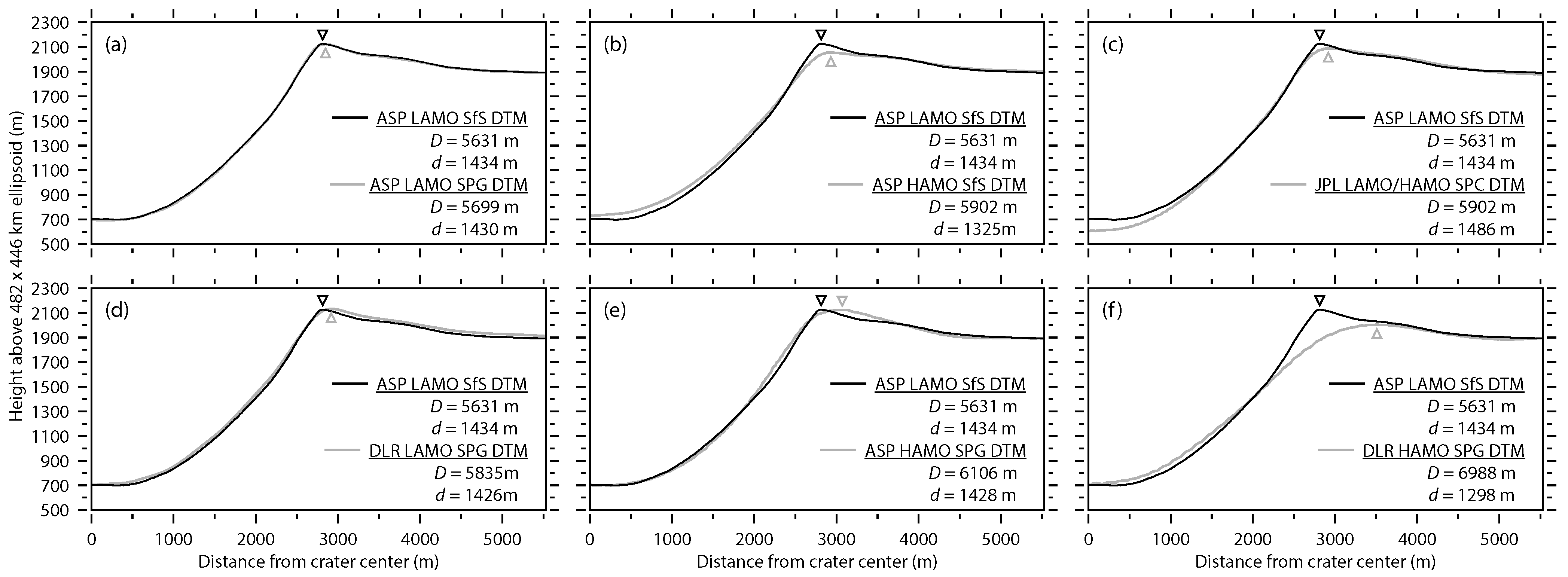
5.4. Qualitative Comparison
5.4.1. Fresh Crater
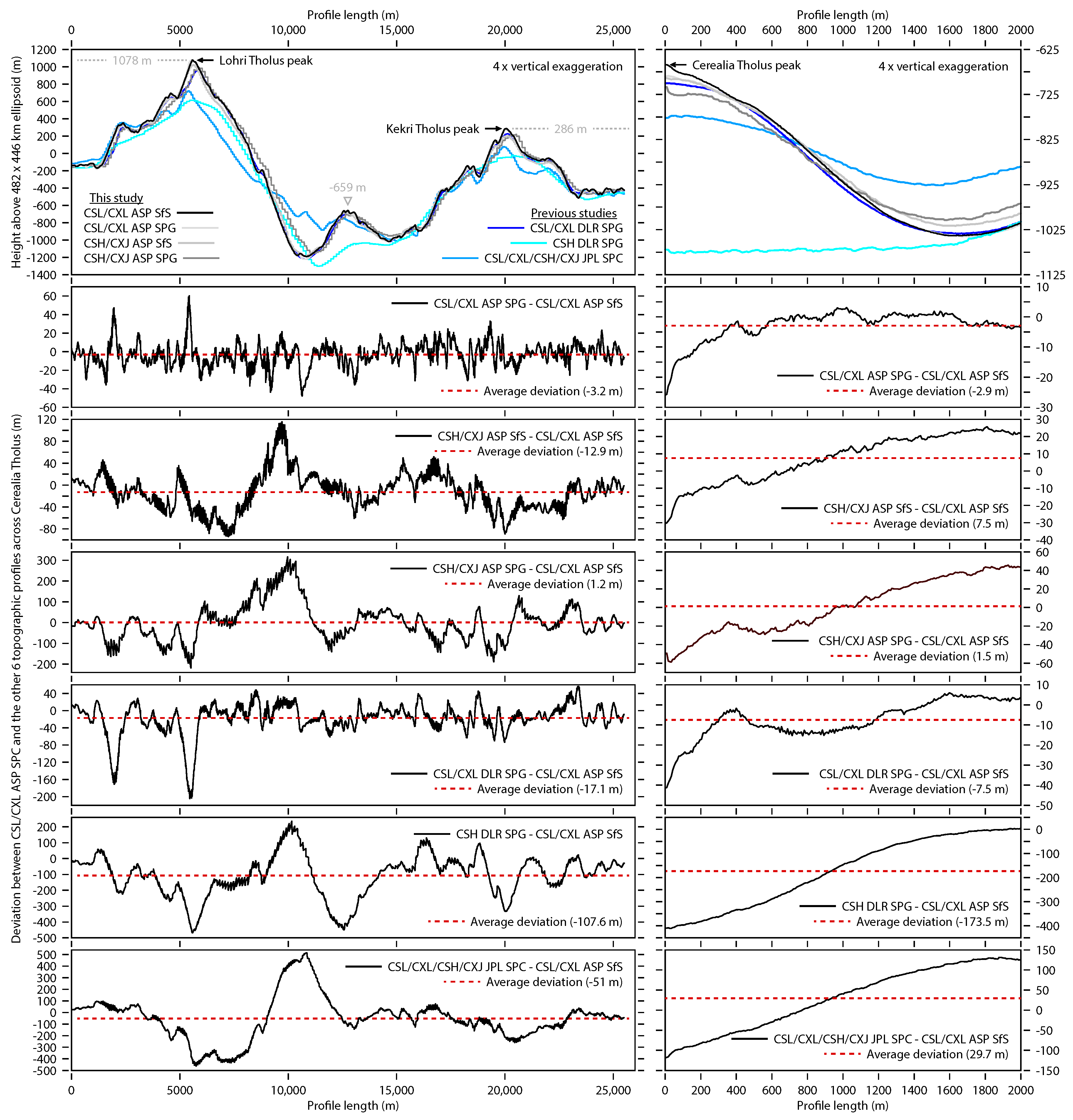
5.4.2. Cerealia Tholus

6. Discussion
6.1. Representational Quality and Generalizability of Our Two Test Sites
6.2. Errors Between Different DTMs
6.3. Influence of Photometric Models on SfS and SPC
6.4. Influence of Faculae on SfS and SPC DTMs (ASP 2.7 and JPL)
7. Conclusions
- Improved Co-Registration and Data Alignment: Our manual, iterative co-registration multi-mission process aligns Dawn’s imaging data accurately, minimizing offsets that could hinder the model’s precision. While we observed offsets of up to 2–3 pixels between the DLR and JPL data products in the Occator crater region, our HAMO- and LAMO-based DTMs and orthomosaics are precisely aligned, with an average offset of approximately 0.5 pixels. This step is critical for SPG, SfS, and SPC approaches, ensuring the alignment of multi-temporal and multi-angle datasets. The new DTMs also improve the orthorectification quality and thus further minimize the offsets between overlapping images, specifically those acquired at high emission angles.
- Resolution and Grid Spacing: Our new DTMs offer significantly enhanced grid spacing and resolution, down to 17 m and 34 m/px compared to the LAMO-based SPG DTM from the DLR (32 m) and the HAMO/LAMO-based SPC DTM from the JPL (100 m). More important than the GSD, however, is the effective resolution. Compared to our CSL/CXL ASP SPC DTM, which has a GSD and resolution of 17 m and 34 m/px, the LAMO-based SPG DTM from the DLR, which was processed to an almost identical GSD of 32 m, appears to be oversampled by a factor of about 4–5. As we have shown at our two example sites, the finer resolution of our DTMs allows for a more detailed view of geomorphologic features, enabling more precise analyses of terrain features (e.g., through surface slope and roughness analyses) for landing site selection.
- Enhanced Detail and Reduction in Artefacts: Using a combination of SPG and SfS, the new DTMs provide a more detailed surface reconstruction and reduce the artifacts that appear in prior models. This combination approach allows the new DTMs to capture fine topographic details in smooth regions and high-contrast zones, which were previously difficult to model accurately. The resulting DTMs feature clearer delineations of Occator’s cryovolcanic structures, such as the fractured dome of the Cerealia Tholus and the thinner dispersed Vinalia Faculae deposits.
- Topographic Accuracy in High-Albedo Regions: Previous DTMs struggled with accuracy in high-albedo areas like the Cerealia Facula and Vinalia Faculae due to their reflective properties, which created challenges in traditional photometric topography reconstruction. The new DTMs developed in this study integrate custom photometric corrections that mitigate the effects of a high brightness contrast, capturing these regions with improved clarity and topographic fidelity. Despite the exceptionally high albedo variations observed in the study area, the DTMs show a consistently high quality and suggest that multi-view shape-from-shading with albedo modeling has the potential to produce convincing results for other planetary bodies as well.
- Impact on Photometric Correction: The SfS DTMs created in this study have a significantly positive impact on the quality of the photometric correction. On the one hand, the improved co-registration combined with more accurate orthorectification already reduces the offsets at topographically exposed areas (e.g., sharply defined crater rims). These offsets, when using lower resolution DTMs for orthorectification, previously resulted in false color seamlines in RGB composites. Photometric correction is always only as accurate as the underlying DTM. Since our SfS DTMs match the resolution of the image data, they meet the requirements for achieving photometric correction with minimal artifacts.
- Replicability: Both DLR and JPL use proprietary in-house software for data processing and DTM generation, which can make it challenging for external researchers to trace individual processing steps and reproduce their results. In contrast, our work relies exclusively on free and open-source software commonly used in the planetary science community, specifically the ISIS 3 and the ASP 2.7. This approach ensures the accessible reproducibility of our data products, although it is computation- and time-intensive and requires suitable resources. We have provided a detailed description of our methodology for using these tools to aid future researchers who may apply them in other contexts.
8. Foresight
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASP 2.7 | Ames Stereo Pipeline |
| CK | C-matrix Kernel |
| CSH | Ceres Science HAMO |
| CSL | Ceres Science LAMO |
| CXJ | Ceres Science Juling |
| CXL | Ceres Science LAMO |
| DLR | Deutsches Zentrum für Luft- und Raumfahrt (German Aerospace Center) |
| FC | Framing Camera |
| GRaND | Gamma Ray and Neutron Detector |
| GSD | Ground Sample Distance |
| HAMO | High-Altitude Mapping Orbit |
| ISIS 3 | Integrated Software for Imagers and Spectrometers |
| JPL | Jet Propulsion Laboratory |
| LAMO | Low-Altitude Mapping Orbit |
| PC | Photoclinometry |
| SfS | Shape-from-Shading |
| SPG | Stereophotogrammetry/-grammetric |
| SPICE | Spacecraft Planetary Instrument C-matrix Events |
| SPK | Spacecraft and Planet Kernel |
| SPC | Stereophotoclinometry/-clinometric |
| VIR | Visual and Infrared Spectrometer |
Appendix A
Appendix A.1
| Image ID | Emission (°) | Incidence (°) | SubSolGrAzi (°) | Resolution (m/px) | Exposure (ms) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | ||
| CSH/CXJ (F1CLEAR) | |||||||||||||
| FC21B0040736_15235021136F1G | 0.0 | 9.2 | 19.6 | 25.6 | 34.8 | 44.0 | 105.8 | 124.5 | 146.2 | 136.5 | 137.1 | 138.3 | 17 |
| FC21B0040752_15235022645F1G | 0.0 | 9.3 | 19.7 | 23.2 | 32.3 | 41.5 | 96.7 | 116.8 | 138.6 | 136.3 | 136.8 | 138.2 | 17 |
| FC21B0042108_15243003612F1E | 19.7 | 35.4 | 50.2 | 28.9 | 42.9 | 56.7 | 90.2 | 105.6 | 122.2 | 137.5 | 142.1 | 148.0 | 17 |
| FC21B0042110_15243005112F1E | 18.3 | 34.5 | 51.6 | 26.7 | 40.3 | 53.2 | 84.3 | 101.1 | 117.8 | 137.4 | 141.8 | 148.2 | 17 |
| FC21B0042152_15243190004F1E | 18.8 | 37.1 | 54.6 | 32.9 | 47.6 | 62.3 | 101.1 | 116.0 | 134.8 | 137.6 | 142.8 | 150.4 | 17 |
| FC21B0043026_15264224605F1E | 18.8 | 40.4 | 65.1 | 31.3 | 44.2 | 56.2 | 82.9 | 103.0 | 120.1 | 139.2 | 145.8 | 157.0 | 24 |
| FC21B0043028_15264230106F1E | 15.9 | 35.6 | 57.6 | 32.2 | 44.9 | 56.8 | 84.8 | 102.3 | 117.8 | 138.4 | 143.7 | 152.6 | 22 |
| FC21B0043072_15265170904F1E | 17.1 | 36.0 | 57.9 | 39.6 | 50.6 | 61.5 | 96.4 | 112.9 | 127.3 | 139.5 | 144.9 | 154.0 | 24 |
| Image ID | Emission (°) | Incidence (°) | SubSolGrAzi (°) | Resolution (m/px) | Exposure (ms) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | ||
| CSL/CXL (RGB) | |||||||||||||
| FC21B0060467_16085151005F5C | 2.9 | 9.9 | 16.3 | 41.9 | 44.2 | 46.6 | 105.3 | 108.5 | 112.0 | 33.7 | 34.1 | 34.6 | 190 |
| FC21B0060470_16085151026F8C | 3.0 | 10.0 | 16.4 | 41.8 | 44.1 | 46.5 | 104.9 | 108.1 | 111.6 | 33.6 | 34.0 | 34.0 | 190 |
| FC21B0060472_16085151040F2C | 3.0 | 9.9 | 16.3 | 41.7 | 44.0 | 46.4 | 104.7 | 107.8 | 111.3 | 33.7 | 34.0 | 34.6 | 190 |
| FC21B0060475_16085151225F5C | 3.2 | 9.9 | 16.2 | 41.1 | 43.4 | 45.7 | 102.7 | 105.7 | 109.0 | 33.6 | 33.9 | 34.3 | 190 |
| FC21B0060478_16085151251F8C | 3.3 | 10.0 | 16.3 | 40.9 | 43.2 | 45.5 | 102.2 | 105.2 | 108.5 | 33.5 | 33.8 | 34.3 | 190 |
| FC21B0060480_16085151307F2C | 3.3 | 9.9 | 16.2 | 40.8 | 43.1 | 45.5 | 101.9 | 104.8 | 108.2 | 33.5 | 33.9 | 34.3 | 190 |
| FC21B0060592_16086182742F5C | 2.5 | 9.8 | 16.2 | 43.3 | 45.7 | 48.1 | 108.2 | 111.4 | 115.1 | 33.8 | 34.1 | 34.6 | 190 |
| FC21B0060595_16086182808F8C | 2.6 | 9.9 | 16.3 | 43.1 | 45.5 | 47.9 | 107.7 | 111.0 | 114.6 | 33.8 | 34.1 | 34.5 | 190 |
| FC21B0060597_16086182821F2C | 2.6 | 9.9 | 16.3 | 43.0 | 45.4 | 47.8 | 107.5 | 110.7 | 114.3 | 33.9 | 34.1 | 34.6 | 190 |
| FC21B0060600_16086183004F5C | 2.4 | 9.7 | 16.1 | 42.3 | 44.6 | 47.0 | 105.6 | 108.8 | 112.2 | 33.9 | 34.1 | 34.4 | 190 |
| FC21B0060603_16086183025F8C | 2.5 | 9.8 | 16.1 | 42.1 | 44.5 | 46.9 | 105.2 | 108.4 | 111.8 | 33.8 | 34.1 | 34.4 | 190 |
| FC21B0060605_16086183039F2C | 2.4 | 9.7 | 16.1 | 42.0 | 44.4 | 46.8 | 105.0 | 108.1 | 111.5 | 33.8 | 34.1 | 34.5 | 190 |
| FC21B0060608_16086183222F5C | 2.6 | 9.6 | 16.0 | 41.4 | 43.7 | 46.1 | 103.0 | 106.1 | 109.5 | 33.7 | 34.0 | 34.5 | 190 |
| FC21B0060611_16086183245F8C | 2.6 | 9.6 | 16.0 | 41.3 | 43.6 | 45.9 | 102.6 | 105.6 | 109.0 | 33.6 | 34.0 | 34.5 | 190 |
| FC21B0060613_16086183301F2C | 2.6 | 9.5 | 15.9 | 41.2 | 43.5 | 45.8 | 102.3 | 105.3 | 108.6 | 33.6 | 34.0 | 34.5 | 190 |
| FC21B0070444_16168012919F8C | 15.5 | 23.1 | 30.2 | 51.7 | 54.6 | 57.5 | 100.6 | 103.2 | 106.0 | 34.0 | 35.1 | 36.3 | 190 |
| FC21B0070447_16168012941F5C | 15.4 | 23.0 | 30.2 | 51.5 | 54.4 | 57.4 | 100.3 | 102.9 | 105.7 | 34.1 | 35.1 | 36.4 | 190 |
| FC21B0070450_16168013002F2C | 15.3 | 23.0 | 30.1 | 51.4 | 54.3 | 57.3 | 100.1 | 102.6 | 105.4 | 34.0 | 35.1 | 36.4 | 190 |
| FC21B0070453_16168013135F8C | 15.2 | 22.8 | 30.0 | 50.9 | 53.8 | 56.7 | 98.9 | 101.4 | 104.1 | 33.9 | 35.0 | 36.2 | 190 |
| FC21B0070456_16168013158F5C | 15.1 | 22.7 | 29.9 | 50.7 | 53.6 | 56.6 | 98.6 | 101.1 | 103.7 | 34.0 | 35.1 | 36.3 | 190 |
| FC21B0070459_16168013223F2C | 15.1 | 22.6 | 29.8 | 50.6 | 53.5 | 56.5 | 98.3 | 100.7 | 103.4 | 34.0 | 35.0 | 36.3 | 190 |
| FC21B0070806_16169044524F8C | 15.6 | 23.2 | 30.4 | 52.2 | 55.1 | 58.0 | 101.4 | 104.1 | 106.9 | 34.2 | 35.3 | 36.4 | 190 |
| FC21B0070809_16169044550F5C | 15.6 | 23.2 | 30.4 | 52.0 | 54.9 | 57.9 | 101.1 | 103.7 | 106.6 | 34.2 | 35.3 | 36.5 | 190 |
| FC21B0070812_16169044613F2C | 15.5 | 23.2 | 30.3 | 51.9 | 54.8 | 57.7 | 100.9 | 103.5 | 106.3 | 34.3 | 35.4 | 36.5 | 190 |
| FC21B0070815_16169044747F8C | 15.4 | 23.0 | 30.1 | 51.3 | 54.2 | 57.1 | 99.7 | 102.3 | 105.0 | 34.3 | 35.3 | 36.3 | 190 |
| FC21B0070818_16169044808F5C | 15.3 | 22.9 | 30.0 | 51.2 | 54.1 | 57.0 | 99.4 | 102.0 | 104.7 | 34.3 | 35.3 | 36.4 | 190 |
| FC21B0070821_16169044833F2C | 15.2 | 22.8 | 30.0 | 51.0 | 53.9 | 56.8 | 99.1 | 101.6 | 104.4 | 34.1 | 35.3 | 36.4 | 190 |
| FC21B0070824_16169045004F8C | 15.1 | 22.6 | 29.8 | 50.5 | 53.4 | 56.4 | 97.9 | 100.4 | 103.1 | 34.0 | 35.1 | 36.3 | 190 |
| FC21B0070827_16169045025F5C | 15.0 | 22.6 | 29.7 | 50.4 | 53.3 | 56.3 | 97.7 | 100.1 | 102.8 | 34.0 | 35.1 | 36.3 | 190 |
| FC21B0070830_16169045047F2C | 15.0 | 22.6 | 29.7 | 50.3 | 53.2 | 56.1 | 97.4 | 99.8 | 102.5 | 34.1 | 35.1 | 36.3 | 190 |
| FC21B0079017_16214225823F2I | 12.2 | 18.9 | 25.5 | 51.8 | 54.4 | 57.1 | 98.2 | 100.1 | 102.3 | 35.2 | 35.9 | 36.6 | 190 |
| FC21B0079020_16214225844F5I | 12.1 | 18.9 | 25.4 | 51.7 | 54.3 | 57.0 | 97.9 | 99.8 | 102.0 | 35.2 | 35.9 | 36.6 | 190 |
| FC21B0079023_16214225912F8I | 12.1 | 18.9 | 25.4 | 51.6 | 54.2 | 56.9 | 97.6 | 99.4 | 101.6 | 35.1 | 35.8 | 36.5 | 190 |
| FC21B0079376_16216021551F2I | 12.0 | 18.6 | 25.1 | 52.8 | 55.4 | 58.1 | 100.2 | 102.3 | 104.7 | 35.7 | 36.3 | 36.9 | 190 |
| FC21B0079379_16216021617F5I | 12.0 | 18.6 | 25.2 | 52.7 | 55.3 | 58.0 | 99.9 | 102.0 | 104.3 | 35.6 | 36.2 | 36.9 | 190 |
| FC21B0079382_16216021638F8I | 12.0 | 18.6 | 25.0 | 52.6 | 55.2 | 57.8 | 99.7 | 101.8 | 104.0 | 35.6 | 36.2 | 36.8 | 190 |
| FC21B0079384_16216021811F2I | 12.1 | 18.8 | 25.4 | 52.1 | 54.7 | 57.4 | 98.6 | 100.7 | 102.8 | 35.6 | 36.1 | 36.9 | 190 |
| FC21B0079387_16216021834F5I | 12.1 | 18.8 | 25.4 | 52.0 | 54.6 | 57.3 | 98.4 | 100.4 | 102.5 | 35.6 | 36.0 | 36.9 | 190 |
| FC21B0079390_16216021856F8I | 12.2 | 18.9 | 25.5 | 51.9 | 54.5 | 57.2 | 98.1 | 100.1 | 102.2 | 35.5 | 35.9 | 36.8 | 190 |
| Image ID | Cycle | Observation Type | Exposure | CF | VF | Emission |
|---|---|---|---|---|---|---|
| (ms) | (°) | |||||
| FC21B0056964_16047193154F1C | 3 | FC2_CSL_C3S4Occator_002 | 21 | - | v | 0.1 |
| FC21B0056966_16047193414F1C | 3 | FC2_CSL_C3S4Occator_002 | 21 | - | v | 0.0 |
| FC21B0056968_16047193633F1C | 3 | FC2_CSL_C3S4Occator_002 | 21 | v | - | 0.0 |
| FC21B0057271_16048225126F1C | 3 | FC2_CSL_C3S4Occator_007 | 21 | - | v | 1.0 |
| FC21B0057273_16048225349F1C | 3 | FC2_CSL_C3S4Occator_007 | 21 | v | - | 0.6 |
| FC21B0057275_16048225606F1C | 3 | FC2_CSL_C3S4Occator_007 | 21 | v | - | 0.3 |
| FC21B0060479_16085151257F1C | 5 | FC2_CSL_C5S2OccatorColor_006 | 21 | v | - | 3.3 |
| FC21B0060596_16086182814F1C | 5 | FC2_CSL_C5S2OccatorColor_011 | 21 | v | - | 2.5 |
| FC21B0060604_16086183033F1C | 5 | FC2_CSL_C5S2OccatorColor_011 | 21 | v | v | 2.4 |
| FC21B0060612_16086183254F1C | 5 | FC2_CSL_C5S2OccatorColor_011 | 21 | v | - | 2.6 |
| FC21B0062605_16110051118F1B | 6 | FC2_CSL_C6S2Occator_013 | 75 | - | v | 14.5 |
| FC21B0062606_16110051123F1B | 6 | FC2_CSL_C6S2Occator_013 | 21 | - | v | 14.5 |
| FC21B0062607_16110051338F1B | 6 | FC2_CSL_C6S2Occator_013 | 75 | - | v | 14.1 |
| FC21B0062608_16110051343F1B | 6 | FC2_CSL_C6S2Occator_013 | 21 | - | v | 14.0 |
| FC21B0062609_16110051558F1B | 6 | FC2_CSL_C6S2Occator_013 | 75 | v | - | 13.6 |
| FC21B0062610_16110051604F1B | 6 | FC2_CSL_C6S2Occator_013 | 21 | v | - | 13.5 |
| FC21B0062760_16112114850F1B | 6 | FC2_CSL_C6S3Occator_003 | 75 | v | - | 13.2 |
| FC21B0062761_16112114858F1B | 6 | FC2_CSL_C6S3Occator_003 | 21 | v | - | 13.2 |
| FC21B0062762_16112115108F1B | 6 | FC2_CSL_C6S3Occator_003 | 75 | v | - | 12.7 |
| FC21B0062763_16112115113F1B | 6 | FC2_CSL_C6S3Occator_003 | 21 | v | - | 12.7 |
| FC21B0064939_16131092832F1B | 7 | FC2_CSL_C7S2Occator_005 | 75 | - | v | 13.2 |
| FC21B0064940_16131092838F1B | 7 | FC2_CSL_C7S2Occator_005 | 21 | - | v | 13.2 |
| FC21B0064941_16131093053F1B | 7 | FC2_CSL_C7S2Occator_005 | 75 | x | v | 12.9 |
| FC21B0064942_16131093059F1B | 7 | FC2_CSL_C7S2Occator_005 | 21 | v | v | 12.8 |
| FC21B0064943_16131093312F1B | 7 | FC2_CSL_C7S2Occator_005 | 75 | x | v | 12.4 |
| FC21B0064944_16131093316F1B | 7 | FC2_CSL_C7S2Occator_005 | 21 | v | v | 12.4 |
| FC21B0065221_16132124813F1B | 7 | FC2_CSL_C7S2Occator_010 | 75 | - | v | 13.3 |
| FC21B0065222_16132124818F1B | 7 | FC2_CSL_C7S2Occator_010 | 21 | - | v | 13.3 |
| FC21B0065223_16132125034F1B | 7 | FC2_CSL_C7S2Occator_010 | 75 | x | - | 12.9 |
| FC21B0065224_16132125038F1B | 7 | FC2_CSL_C7S2Occator_010 | 21 | v | - | 12.9 |
| FC21B0070442_16168012903F1C | 8 | FC2_CSL_C8S5OccatorColor_006 | 21 | - | v | 15.5 |
| FC21B0070443_16168012908F1C | 8 | FC2_CSL_C8S5OccatorColor_006 | 75 | - | v | 15.5 |
| FC21B0070451_16168013123F1C | 8 | FC2_CSL_C8S5OccatorColor_006 | 21 | - | v | 15.2 |
| FC21B0070452_16168013128F1C | 8 | FC2_CSL_C8S5OccatorColor_006 | 75 | - | v | 15.2 |
| FC21B0070804_16169044512F1C | 8 | FC2_CSL_C8S5OccatorColor_011 | 21 | - | v | 15.7 |
| FC21B0070805_16169044516F1C | 8 | FC2_CSL_C8S5OccatorColor_011 | 75 | - | v | 15.6 |
| FC21B0070813_16169044732F1C | 8 | FC2_CSL_C8S5OccatorColor_011 | 21 | v | v | 15.4 |
| FC21B0070814_16169044738F1C | 8 | FC2_CSL_C8S5OccatorColor_011 | 75 | x | v | 15.4 |
| FC21B0071249_16172143505F1E | 9 | FC2_CSL_C9S1Occator_004 | 75 | - | v | 0.0 |
| FC21B0071250_16172143509F1E | 9 | FC2_CSL_C9S1Occator_004 | 21 | - | v | 0.0 |
| FC21B0071251_16172143725F1E | 9 | FC2_CSL_C9S1Occator_004 | 75 | - | v | 0.0 |
| FC21B0071252_16172143730F1E | 9 | FC2_CSL_C9S1Occator_004 | 21 | - | v | 0.0 |
| FC21B0074624_16190085724F1E | 9 | FC2_CSL_C9S5Occator_003 | 75 | - | v | 16.6 |
| FC21B0074625_16190085729F1E | 9 | FC2_CSL_C9S5Occator_003 | 21 | - | v | 16.6 |
| FC21B0074626_16190085944F1E | 9 | FC2_CSL_C9S5Occator_003 | 75 | - | v | 16.1 |
| FC21B0074627_16190085949F1E | 9 | FC2_CSL_C9S5Occator_003 | 21 | - | v | 16.0 |
| FC21B0074993_16191121351F1E | 9 | FC2_CSL_C9S5Occator_008 | 75 | - | v | 16.0 |
| FC21B0074994_16191121355F1E | 9 | FC2_CSL_C9S5Occator_008 | 21 | - | v | 16.0 |
| FC21B0074995_16191121611F1E | 9 | FC2_CSL_C9S5Occator_008 | 75 | x | v | 15.8 |
| FC21B0074996_16191121617F1E | 9 | FC2_CSL_C9S5Occator_008 | 21 | v | v | 15.7 |
| FC21B0074997_16191121832F1E | 9 | FC2_CSL_C9S5Occator_008 | 75 | x | v | 15.5 |
| FC21B0074998_16191121836F1E | 9 | FC2_CSL_C9S5Occator_008 | 21 | v | v | 15.5 |
| Image ID | Cycle | Observation Type | Exposure | CF | VF | Emission |
|---|---|---|---|---|---|---|
| (ms) | (°) | |||||
| FC21B0079012_16214225336F1I | 10 | FC2_CSL_C10S5Occator_005 | 75 | - | v | 11.9 |
| FC21B0079013_16214225342F1I | 10 | FC2_CSL_C10S5Occator_005 | 21 | - | v | 12.0 |
| FC21B0079014_16214225556F1I | 10 | FC2_CSL_C10S5Occator_005 | 75 | - | v | 12.1 |
| FC21B0079015_16214225601F1I | 10 | FC2_CSL_C10S5Occator_005 | 21 | - | v | 12.1 |
| FC21B0079374_16216021319F1I | 10 | FC2_CSL_C10S5Occator_010 | 75 | x | v | 11.9 |
| FC21B0079375_16216021539F1I | 10 | FC2_CSL_C10S5Occator_010 | 75 | x | v | 12.0 |
| FC21B0082204_16229074738F1F | 11 | FC2_CXL_C11S2OffNadirEq_007 | 75 | - | v | 5.0 |
| FC21B0082205_16229074958F1F | 11 | FC2_CXL_C11S2OffNadirEq_007 | 75 | - | v | 4.9 |
| FC21B0082593_16230110845F1F | 11 | FC2_CXL_C11S2OffNadirEq_012 | 75 | x | v | 5.8 |
| FC21B0082594_16230110852F1F | 11 | FC2_CXL_C11S2OffNadirEq_012 | 21 | v | v | 5.8 |
| FC21B0082595_16230111105F1F | 11 | FC2_CXL_C11S2OffNadirEq_012 | 75 | x | v | 5.9 |
| FC21B0082596_16230111111F1F | 11 | FC2_CXL_C11S2OffNadirEq_012 | 21 | v | v | 5.9 |
| Image ID | Emission (°) | Incidence (°) | SubSolGrAzi (°) | Resolution (m/px) | Exposure (ms) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | ||
| CSH/CXJ (F1CLEAR) | |||||||||||||
| FC21B0040499_15234081518F1G | 13.0 | 14.0 | 14.9 | 33.3 | 33.9 | 34.5 | 100.6 | 101.5 | 102.5 | 136.9 | 137.0 | 137.1 | 118 |
| FC21B0040514_15234081719F1G | 12.6 | 13.5 | 14.5 | 32.1 | 32.7 | 33.3 | 101.3 | 102.2 | 103.3 | 136.8 | 136.9 | 137.0 | 17 |
| FC21B0040752_15235022645F1G | 9.9 | 10.7 | 11.4 | 31.9 | 32.5 | 33.1 | 101.7 | 102.5 | 103.4 | 136.8 | 136.9 | 137.0 | 17 |
| FC21B0040753_15235023924F1G | 3.3 | 4.2 | 5.2 | 24.1 | 24.8 | 25.4 | 106.8 | 108.2 | 109.7 | 136.3 | 136.3 | 136.4 | 118 |
| FC21B0040768_15235024138F1G | 4.6 | 5.4 | 6.2 | 22.8 | 23.5 | 24.1 | 108.0 | 109.6 | 111.1 | 136.3 | 136.4 | 136.5 | 17 |
| FC21B0045847_15283025550F1D | 4.6 | 5.5 | 6.4 | 37.9 | 38.5 | 39.1 | 98.7 | 99.5 | 100.3 | 135.6 | 135.7 | 135.8 | 118 |
| FC21B0085225_16292023334F1H | 7.5 | 8.4 | 9.3 | 57.7 | 58.3 | 58.8 | 97.0 | 97.4 | 97.8 | 138.1 | 138.2 | 138.3 | 170 |
| FC21B0085233_16292024837F1H | 14.9 | 15.5 | 16.0 | 48.2 | 48.7 | 49.2 | 100.1 | 100.4 | 100.7 | 138.9 | 139.0 | 139.1 | 170 |
| FC21B0087643_16301131406F1E | 12.9 | 13.6 | 14.3 | 66.4 | 66.9 | 67.4 | 94.8 | 95.1 | 95.5 | 138.8 | 138.9 | 139.0 | 170 |
| FC21B0087651_16301132907F1E | 4.9 | 5.7 | 6.4 | 56.8 | 57.4 | 57.9 | 97.4 | 97.8 | 98.3 | 138.0 | 138.1 | 138.2 | 170 |
| FC21B0087659_16301134406F1E | 15.8 | 16.8 | 17.7 | 47.4 | 47.9 | 48.5 | 100.6 | 101.2 | 101.8 | 139.2 | 139.4 | 139.5 | 170 |
| FC21B0087809_16302080203F1E | 18.8 | 19.6 | 20.3 | 41.9 | 42.5 | 32.1 | 102.9 | 103.7 | 104.4 | 139.9 | 140.0 | 140.2 | 170 |
| CSH/CXJ (RGB) | |||||||||||||
| FC21B0040500_15234081525F2G | 13.0 | 13.9 | 14.9 | 33.2 | 33.8 | 34.5 | 100.6 | 101.6 | 102.5 | 136.8 | 137.0 | 137.1 | 710 |
| FC21B0040503_15234081550F5G | 12.9 | 13.8 | 14.7 | 33.0 | 33.6 | 34.2 | 100.8 | 101.7 | 102.7 | 136.8 | 136.9 | 137.0 | 980 |
| FC21B0040506_15234081617F8G | 12.8 | 13.7 | 14.7 | 32.7 | 33.3 | 33.9 | 100.9 | 101.9 | 102.9 | 136.6 | 136.7 | 136.8 | 980 |
| FC21B0040507_15234081623F8G | 12.8 | 13.7 | 14.7 | 32.6 | 33.3 | 33.9 | 100.9 | 101.9 | 102.9 | 136.5 | 136.7 | 136.8 | 980 |
| FC21B0040510_15234081647F5G | 12.7 | 13.6 | 14.5 | 32.4 | 33.0 | 33.6 | 101.1 | 102.1 | 103.1 | 136.7 | 136.9 | 137.0 | 550 |
| FC21B0040513_15234081711F2G | 12.6 | 13.5 | 14.4 | 32.3 | 32.8 | 33.4 | 101.2 | 102.2 | 103.2 | 136.8 | 136.9 | 137.0 | 190 |
| FC21B0040754_15235023932F2G | 3.3 | 4.2 | 5.2 | 24.1 | 24.7 | 25.4 | 106.8 | 108.3 | 109.7 | 136.2 | 136.3 | 136.4 | 710 |
| FC21B0040757_15235023956F5G | 3.5 | 4.4 | 5.3 | 23.8 | 24.5 | 25.1 | 107.1 | 108.5 | 110.0 | 136.2 | 136.3 | 136.4 | 980 |
| FC21B0040760_15235024021F8G | 3.7 | 4.6 | 5.5 | 23.6 | 24.2 | 24.9 | 107.3 | 108.8 | 110.3 | 136.0 | 136.1 | 136.2 | 980 |
| FC21B0040761_15235024030F8G | 3.8 | 4.7 | 5.6 | 23.5 | 24.2 | 24.8 | 107.4 | 108.9 | 110.4 | 136.0 | 136.1 | 136.2 | 980 |
| FC21B0040764_15235024105F5G | 4.3 | 5.2 | 6.0 | 23.1 | 23.8 | 24.5 | 107.7 | 109.2 | 110.8 | 136.2 | 136.3 | 136.4 | 550 |
| FC21B0040767_15235024131F2G | 4.5 | 5.4 | 6.2 | 22.9 | 23.6 | 24.2 | 108.0 | 109.5 | 111.1 | 136.2 | 136.3 | 136.4 | 190 |
| CSL/CXL (F1CLEAR) | |||||||||||||
| FC21B0054225_16030011610F1E | 2.8 | 3.6 | 4.6 | 43.7 | 44.1 | 44.5 | 97.6 | 98.2 | 98.9 | 35.0 | 35.1 | 35.2 | 150 |
| FC21B0057277_16048225827F1C | 3.3 | 3.9 | 5.3 | 47.0 | 47.3 | 47.8 | 97.6 | 97.7 | 97.8 | 33.4 | 33.4 | 33.4 | 21 |
| FC21B0057278_16048230042F1C | 4.2 | 5.5 | 6.9 | 45.4 | 46.0 | 46.6 | 97.1 | 97.7 | 98.4 | 33.3 | 33.4 | 33.5 | 150 |
| FC21B0057279_16048230047F1C | 4.4 | 5.7 | 7.1 | 45.4 | 45.9 | 46.5 | 97.1 | 97.7 | 98.4 | 33.3 | 33.4 | 33.5 | 21 |
| FC21B0059297_16067204631F1B | 5.7 | 7.2 | 8.7 | 46.7 | 47.2 | 47.7 | 96.9 | 97.5 | 98.1 | 35.0 | 35.1 | 35.2 | 150 |
| FC21B0059298_16067204638F1B | 6.0 | 7.5 | 9.0 | 46.6 | 47.2 | 47.7 | 96.9 | 97.5 | 98.1 | 35.0 | 35.1 | 35.3 | 21 |
| FC21B0062767_16112115555F1B | 15.6 | 16.6 | 17.6 | 39.6 | 40.1 | 40.6 | 101.2 | 101.5 | 101.9 | 35.4 | 35.4 | 35.6 | 21 |
| FC21B0082599_16230111545F1F | 14.5 | 15.1 | 15.9 | 53.9 | 54.2 | 54.5 | 97.2 | 97.6 | 98.0 | 34.9 | 35.0 | 35.1 | 75 |
| FC21B0082600_16230111550F1F | 14.3 | 15.0 | 15.8 | 53.8 | 54.2 | 54.5 | 97.2 | 97.6 | 98.1 | 34.9 | 35.0 | 35.1 | 21 |
| FC21B0082601_16230111805F1F | 12.0 | 13.5 | 15.0 | 52.4 | 53.0 | 53.5 | 97.5 | 98.0 | 98.5 | 34.6 | 34.8 | 34.9 | 75 |
| CSL/CXL (RGB) | |||||||||||||
| FC21B0079392_16216022028F2I | 23.4 | 24.2 | 25.0 | 55.2 | 55.6 | 56.2 | 97.1 | 97.2 | 97.4 | 36.5 | 36.6 | 36.8 | 190 |
| FC21B0079395_16216022049F5I | 22.6 | 23.8 | 24.9 | 54.9 | 55.4 | 56.0 | 96.8 | 97.1 | 97.5 | 36.4 | 36.6 | 36.8 | 190 |
| FC21B0079398_16216022110F8I | 21.7 | 23.2 | 24.7 | 54.7 | 55.2 | 55.8 | 96.6 | 97.1 | 97.5 | 36.2 | 36.4 | 36.6 | 190 |
| FC21B0079400_16216022249F2I | 17.6 | 19.1 | 20.6 | 53.6 | 54.2 | 54.8 | 96.9 | 97.4 | 97.9 | 35.8 | 35.9 | 36.1 | 190 |
| FC21B0079403_16216022310F5I | 16.7 | 18.3 | 19.8 | 53.4 | 54.0 | 54.5 | 97.0 | 97.5 | 98.0 | 35.7 | 35.8 | 36.0 | 190 |
| FC21B0079406_16216022332F8I | 15.9 | 17.4 | 18.9 | 53.2 | 53.7 | 54.3 | 97.0 | 97.5 | 98.0 | 35.5 | 35.7 | 35.8 | 190 |
| Image ID | Emission (°) | Incidence (°) | SubSolGrAzi (°) | Resolution (m/px) | Exposure (ms) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | ||
| CSH/CXJ (F1CLEAR) | |||||||||||||
| FC21B0040752_15235022645F1G | 1.9 | 2.9 | 4.0 | 29.7 | 30.6 | 31.6 | 117.5 | 119.2 | 121.1 | 136.5 | 136.6 | 136.7 | 17 |
| CSH/CXJ (RGB) | |||||||||||||
| FC21B0040745_15235022547F8G | 1.5 | 2.5 | 3.6 | 30.2 | 31.1 | 32.0 | 116.8 | 118.5 | 120.3 | 136.3 | 136.4 | 136.4 | 980 |
| FC21B0040748_15235022612F5G | 1.7 | 2.7 | 3.7 | 30.0 | 30.1 | 31.8 | 117.1 | 118.8 | 120.6 | 136.5 | 136.6 | 136.6 | 550 |
| FC21B0040751_15235022636F2G | 1.9 | 2.9 | 3.9 | 29.8 | 30.7 | 31.6 | 117.3 | 119.1 | 121.0 | 136.5 | 136.6 | 136.6 | 190 |
| CSL/CXL (F1CLEAR) | |||||||||||||
| FC21B0056968_16047193633F1C | 9.9 | 10.5 | 11.3 | 47.8 | 48.5 | 49.0 | 103.2 | 103.7 | 104.1 | 33.9 | 34.0 | 34.1 | 21 |
| FC21B0057273_16048225349F1C | 3.9 | 5.9 | 7.9 | 45.7 | 46.5 | 47.4 | 104.5 | 105.5 | 106.5 | 33.7 | 33.9 | 33.9 | 21 |
| FC21B0059290_16067203716F1B | 2.3 | 4.1 | 6.0 | 48.3 | 49.1 | 50.0 | 103.3 | 104.1 | 105.0 | 35.4 | 35.5 | 35.6 | 21 |
| FC21B0059292_16067203937F1B | 5.5 | 7.1 | 8.8 | 46.9 | 47.8 | 48.6 | 103.9 | 104.9 | 105.9 | 35.4 | 35.5 | 35.6 | 21 |
| FC21B0060604_16086183033F1C | 2.8 | 4.9 | 6.7 | 45.2 | 45.9 | 46.4 | 105.4 | 106.4 | 107.4 | 33.9 | 34.0 | 34.0 | 21 |
| FC21B0060612_16086183254F1C | 9.2 | 10.9 | 12.4 | 43.8 | 44.6 | 45.4 | 106.2 | 107.0 | 107.7 | 34.0 | 34.1 | 34.2 | 21 |
| FC21B0064942_16131093059F1B | 14.7 | 16.6 | 18.5 | 43.8 | 44.5 | 45.1 | 107.2 | 108.1 | 109.1 | 34.3 | 34.5 | 34.7 | 21 |
| FC21B0064944_16131093316F1B | 21.0 | 22.5 | 24.0 | 42.5 | 43.4 | 44.1 | 107.9 | 108.8 | 109.6 | 34.9 | 35.2 | 35.3 | 21 |
| FC21B0065224_16132125038F1B | 19.0 | 20.9 | 22.8 | 40.8 | 41.5 | 42.2 | 109.5 | 110.7 | 111.9 | 34.9 | 35.2 | 35.4 | 21 |
| FC21B0070813_16169044732F1C | 23.9 | 25.7 | 27.6 | 55.3 | 56.0 | 56.7 | 101.0 | 101.7 | 102.4 | 35.5 | 35.8 | 36.0 | 21 |
| FC21B0074996_16191121617F1E | 22.1 | 24.1 | 26.2 | 55.5 | 56.3 | 57.1 | 101.1 | 101.9 | 102.7 | 36.0 | 36.3 | 36.5 | 21 |
| FC21B0074998_16191121836F1E | 24.2 | 26.1 | 28.0 | 54.1 | 54.9 | 55.7 | 101.8 | 102.6 | 103.3 | 36.1 | 36.4 | 36.7 | 21 |
| FC21B0082594_16230110852F1F | 10.0 | 11.5 | 13.1 | 53.9 | 54.7 | 55.6 | 102.7 | 103.4 | 104.2 | 35.1 | 35.3 | 35.4 | 21 |
| FC21B0082596_16230111111F1F | 8.4 | 10.5 | 12.6 | 52.6 | 53.4 | 54.2 | 103.3 | 104.2 | 105.0 | 34.9 | 35.1 | 35.2 | 21 |
| CSL/CXL (RGB) | |||||||||||||
| FC21B0060600_16086183004F5C | 2.4 | 4.0 | 5.4 | 45.5 | 46.1 | 46.5 | 105.6 | 106.3 | 107.2 | 33.9 | 33.9 | 34.0 | 190 |
| FC21B0060603_16086183025F8C | 2.7 | 4.7 | 6.5 | 45.3 | 45.9 | 46.4 | 105.4 | 106.4 | 107.3 | 33.8 | 33.9 | 33.9 | 190 |
| FC21B0060605_16086183039F2C | 3.1 | 5.2 | 7.0 | 45.1 | 45.8 | 46.4 | 105.4 | 106.4 | 107.4 | 33.9 | 34.0 | 34.0 | 190 |
| FC21B0060608_16086183222F5C | 7.7 | 9.9 | 12.0 | 44.2 | 45.0 | 45.9 | 106.0 | 107.1 | 108.1 | 33.9 | 34.1 | 34.2 | 190 |
| FC21B0060611_16086183245F8C | 8.8 | 10.6 | 12.2 | 43.9 | 44.8 | 45.6 | 106.1 | 107.0 | 107.8 | 33.9 | 34.0 | 34.1 | 190 |
| FC21B0060613_16086183301F2C | 9.5 | 11.0 | 12.4 | 43.8 | 44.6 | 45.3 | 106.3 | 107.0 | 107.6 | 34.0 | 34.1 | 34.2 | 190 |
| FC21B0070815_16169044747F8C | 24.1 | 26.0 | 28.0 | 55.1 | 55.9 | 56.7 | 101.0 | 101.8 | 102.5 | 35.4 | 35.7 | 36.0 | 190 |
| FC21B0070818_16169044808F5C | 24.4 | 26.4 | 28.4 | 54.9 | 55.7 | 56.5 | 101.1 | 101.8 | 102.6 | 35.5 | 35.8 | 36.1 | 190 |
| FC21B0070821_16169044833F2C | 24.7 | 26.7 | 28.8 | 54.7 | 55.5 | 56.3 | 101.2 | 102.0 | 102.8 | 35.6 | 35.9 | 36.1 | 190 |
| FC21B0079376_16216021551F2I | 13.7 | 15.8 | 17.8 | 53.7 | 54.5 | 55.3 | 102.5 | 103.3 | 104.1 | 35.8 | 36.0 | 36.2 | 190 |
| FC21B0079379_16216021617F5I | 12.7 | 14.7 | 16.7 | 53.5 | 54.3 | 55.1 | 102.6 | 103.4 | 104.2 | 35.7 | 35.9 | 36.0 | 190 |
| FC21B0079382_16216021638F8I | 12.5 | 14.0 | 15.8 | 53.2 | 54.1 | 54.9 | 102.7 | 103.4 | 103.9 | 35.6 | 35.8 | 35.9 | 190 |
| Group = Kernels | |||
| LeapSecond | lsk | naif0012.tls | |
| TargetAttitudeShape | pck | pck00009.tpc | |
| dawn_ceres_v05.tpc | |||
| dawn_ceres_v00.tf | |||
| TargetPosition | tspk | de421.bsp | |
| sb_ceres_140724.bsp | |||
| InstrumentPointing | ck | dawn_sc_161024_161030.bc | |
| fk | dawn_v15.tf | ||
| fk | dawn_fc_v3.bc | ||
| Instrument | dawn_fc_v10.ti | ||
| SpacecraftClock | sclk | DAWN_203_SCLKSCET.00091.tsc | |
| InstrumentPosition | spk | dawn_rec_160902-161104_170124_v1.bsp | |
| InstrumentAddendum | iak | dawnfcAddendum002.ti | |
| Shapemodel | CE_HAMO_G_00N_180E_EQU_DTM.cub | ||
| InstrumentPositionQuality | Reconstructed | ||
| InstrumentPointingQuality | Reconstructed | ||
| Extra | dawn_ceres_SPG20160107.tpc | ||
| Pre-processing/stereo_pprc | ||
|---|---|---|
| Pre-alignment method | ||
| -Alignment-method none (recommended for anything map-projected) | ||
| Intensity normalization | ||
| -force-use-entire-range | ||
| Pre-processing filter | ||
| -prefilter-mode 2 (Laplacian of Gaussian) | ||
| Kernel size (1-sigma) for pre-processing | ||
| -prefilter-kernel-width 1.4 (recommended for Laplacian of Gaussian) | ||
| Integer Correlation/stereo_corr | ||
| Cost function to use for initialization | ||
| -cost-mode 2 (normalized cross-correlation) | ||
| Initialization step: correlation kernel size | ||
| -corr kernel 17 17 | ||
| Initialization step: correlation search range | ||
| -‘uncommented’ (value will be chosen by ASP 2.7 automatically) | ||
| Subpixel Refinement/stereo_rfne | ||
| Subpixel step: subpixel modes | ||
| -Subpixel-mode 2 (affine-adaptive window, Bayes EM weighting) | ||
| Subpixel step: correlation kernel size | ||
| -Subpixel -kernel 9 9 | ||
| Post Filtering/stereo_fltr | ||
| Automatic “erode” for low-confidence pixels | ||
| -Rm-half-kernel 5 5 | ||
| -Rm-min-matches 60 | ||
| -Rm-threshold 3 | ||
| -Rm-cleanup passes 1 | ||
References
- Anderson, J.D.; Schubert, G.; Jacobson, R.A.; Lau, E.L.; Moore, W.B.; Sjogren, W.L. Europa’s Differentiated Internal Structure: Inferences from Four Galileo Encounters. Science 1998, 281, 2019–2022. [Google Scholar] [CrossRef] [PubMed]
- Carr, M.H.; Belton, M.J.S.; Chapman, C.R.; Davies, M.E.; Geissler, P.; Greenberg, R.; McEwen, A.S.; Tufts, B.R.; Greeley, R.; Sullivan, R.; et al. Evidence for a subsurface ocean on Europa. Nature 1998, 391, 363–365. [Google Scholar] [CrossRef] [PubMed]
- Khurana, K.K.; Kivelson, M.G.; Stevenson, D.J.; Schubert, G.; Russell, C.T.; Walker, R.J.; Polanskey, C. Induced magnetic fields as evidence for subsurface oceans in Europa and Callisto. Nature 1998, 395, 777–780. [Google Scholar] [CrossRef] [PubMed]
- Kivelson, M.G.; Khurana, K.K.; Stevenson, D.J.; Benett, L.; Joy, S.; Russell, C.T.; Walker, R.J.; Zimmer, C.; Polanskey, C. Europa and Callisto: Induced or intrinsic fields in a periodically varying plasma environment. J. Geophys. Res. 1999, 104, 4609–4625. [Google Scholar]
- Zimmer, C.; Khurana, K.K.; Kivelson, M.G. Subsurface Oceans on Europa and Callisto: Constraints from Galileo Magnetometer Observations. Icarus 2000, 147, 329–347. [Google Scholar] [CrossRef]
- Khurana, K.K.; Kivelson, M.G.; Hand, K.P.; Russell, C.T. Europa; Space Science Series; University of Arizona Press: Tucson, AZ, USA, 2009; Chapter Electromagnetic Induction from Europa’s Ocean and the Deep Interior; pp. 571–588. [Google Scholar]
- Schubert, G.; Sohl, F.; Hussmann, H. Europa; Space Science Series; University of Arizona Press: Tucson, AZ, USA, 2009; Chapter Interior of Europa; pp. 353–368. [Google Scholar]
- Postberg, F.; Kempf, S.; Schmidt, J.; Brilliantov, N.; Beinsen, A.; Abel, B.; Buck, U.; Srama, R. Sodium salts in E-ring ice grains from an ocean below the surface of Enceladus. Nature 2009, 459, 1098–1101. [Google Scholar] [CrossRef]
- Iess, L.; Stevenson, D.J.; Parisi, M.; Hemingway, D.; Jacobson, R.A.; Lunine, J.I.; Nimmo, F.; Armstrong, J.W.; Asmar, S.W.; Ducci, M.; et al. The Gravity Field and Interior Structure of Enceladus. Science 2014, 34, 78–80. [Google Scholar] [CrossRef]
- Beuthe, M.; Rivoldini, A.; Trinh, A. Enceladus’s and Dione’s floating ice shells supported by minimum stress isostasy. Geophys. Res. Lett. 2016, 43, 10088–10096. [Google Scholar] [CrossRef]
- Čadek, O.; Tobie, G.; van Hoolst, T.; Massé, M.; Choblet, G.; Lefèvre, A.; Mitri, G.; Baland, R.M.; Běhounková, M.; Bourgeois, O.; et al. Enceladus’s internal ocean and ice shell constrained from Cassini gravity, shape, and libration data. Geophys. Res. Lett. 2016, 43, 5653–5660. [Google Scholar] [CrossRef]
- Thomas, P.; Tajeddine, R.; Tiscareno, M.S.; Burns, J.A.; Joseph, J.; Loredo, T.J.; Helfenstein, P.; Porco, C. Enceladus’s measured physical libration requires a global subsurface ocean. Icarus 2016, 264, 37–47. [Google Scholar] [CrossRef]
- Hemingway, D.; Iess, L.; Tajeddine, R.; Tobie, G. Enceladus and the Icy Moons of Saturn; Arizona of University Press: Tucson, AZ, USA, 2018; Chapter The Interior of Enceladus; pp. 57–77. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Stiles, B.W.; Kirk, R.L.; Allison, M.D.; Del Marmo, P.P.; Iess, L.; Lunine, J.I.; Ostro, S.J.; Hensley, S. Titan’s Rotation Reveals an Internal Ocean and Changing Zonal Winds. Science 2008, 319, 1649–1651. [Google Scholar] [CrossRef] [PubMed]
- Iess, L.; Jacobson, R.A.; Ducci, M.; Stevenson, D.J.; Lunine, J.I.; Armstrong, J.W.; Asmar, S.W.; Racioppa, P.; Rappaport, N.J.; Tortora, P. The Tides of Titan. Science 2012, 337, 457–459. [Google Scholar] [CrossRef]
- Mitri, G.; Meriggiola, R.; Hayes, A.; Lefevre, A.; Tobie, G.; GEnova, A.; Lunine, J.I.; Zebker, H. Shape, topography, gravity anomalies and tidal deformation of Titan. Icarus 2014, 236, 169–177. [Google Scholar] [CrossRef]
- Saur, J.; Duling, S.; Roth, L.; Jia, X.; Strobel, D.F.; Feldman, P.D.; Christensen, U.R.; Retherford, K.D.; McGrath, M.A.; Musacchio, F.; et al. The search for a subsurface ocean in Ganymede with Hubble Space Telescope observations of its auroral ovals. J. Geophys. Res. Space Phys. 2015, 120, 1715–1737. [Google Scholar] [CrossRef]
- Hendrix, A.R.; Hurford, T.A.; Barge, L.M.; Bland, M.T.; Bowman, J.S.; Brinckerhoff, W.; Buratti, B.J.; Cable, M.L.; Castillo-Rogez, J.; Collins, G.C.; et al. The NASA Roadmap to Ocean Worlds. Astrobiology 2019, 19, 1–27. [Google Scholar] [CrossRef]
- Nimmo, F.; Spencer, J.R. Powering Triton’s recent geological activity by obliquity tides: Implications for Pluto geology. Icarus 2015, 246, 2–10. [Google Scholar] [CrossRef]
- Bierson, C.J.; Nimmo, F.; Stern, S.A. Evidence for a hot start and early ocean formation on Pluto. Nat. Geosci. 2020, 13, 468–472. [Google Scholar] [CrossRef]
- Denton, C.A.; Johnson, B.C.; Wakita, S.; Freed, A.M.; Melosh, H.J.; Stern, S.A. Pluto’s Antipodal Terrains Imply a Thick Subsurface Ocean and Hydrated Core. Geophys. Res. Lett. 2021, 48, e2020GL091596. [Google Scholar] [CrossRef]
- Fu, R.R.; Ermakov, A.I.; Marchi, S.; Castillo-Rogez, J.C.; Raymond, C.A.; Hager, B.H.; Zuber, M.T.; King, S.D.; Bland, M.T.; De Sanctis, M.C.; et al. The Interior Structure of Ceres as Revealed by Surface Topography. Earth Planet. Sci. Lett. 2017, 476, 153–164. [Google Scholar] [CrossRef]
- Russell, C.T.; Raymond, C.A. The Dawn Mission to Vesta and Ceres. Space Sci. Rev. 2011, 163, 3–23. [Google Scholar] [CrossRef]
- De Sanctis, M.C.; Ammannito, E.; Raponi, A.; Frigeri, A.; Ferrari, M.; Carrozzo, F.G.; Ciarniello, M.; Formisano, M.; Rousseau, B.; Tosi, F.; et al. Fresh emplacement of hydrated sodium chloride on Ceres from ascending salty fluids. Nat. Astron. 2020, 4, 786–793. [Google Scholar] [CrossRef]
- De Sanctis, M.C.; Mitri, G.; Castillo-Rogez, J.; House, C.H.; Marchi, S.; Raymond, C.A.; Sekine, Y. Relict Ocean Worlds: Ceres. Space Sci. Rev. 2020, 216, 60. [Google Scholar] [CrossRef]
- Nathues, A.; Schmedemann, N.; Thangjam, G.; Pascker, J.H.; Mengel, K.; Castillo-Rogez, J.C.; Cloutis, E.A.; Hiesinger, H.; Hoffmann, M.; Le Corre, L.; et al. Recent cryovolcanic activity at Occator crater on Ceres. Nat. Astron. 2020, 4, 794–801. [Google Scholar] [CrossRef]
- Park, R.S.; Konopliv, A.S.; Ermakov, A.I.; CastilloRogez, J.C.; Fu, R.R.; Hughson, K.H.G.; Prettyman, T.H.; Raymond, C.A.; Scully, J.E.C.; Sizemore, H.G.; et al. Evidence of non-uniform crust of Ceres from Dawn’s high-resolution gravity data. Nat. Astron. 2020, 4, 748–755. [Google Scholar] [CrossRef]
- Raymond, C.A.; Ermakov, A.I.; Castillo-Rogez, J.C.; Marchi, S.; Johnson, B.C.; Hesse, M.A.; Scully, J.E.C.; Buczkowski, D.L.; Sizemore, H.G.; Schenk, P.M.; et al. Impact-driven mobilization of deep crustal brines on dwarf planet Ceres. Nat. Astron. 2020, 4, 741–747. [Google Scholar] [CrossRef]
- Schenk, P.; Scully, J.; Buczkowski, D.; Sizemore, H.; Schmidt, B.; Pieters, C.; Neesemann, A.; O’Brien, D.; Marchi, S.; Williams, D.; et al. Impact heat driven volatile redistribution at Occator crater on Ceres as a comparative planetary process. Nat. Commun. 2020, 11, 3679. [Google Scholar] [CrossRef]
- Schmidt, B.E.; Sizemore, H.G.; Hughson, K.H.G.; Duarte, K.D.; Romero, V.N.; Scully, J.E.C.; Schenk, P.M.; Buczkowski, D.L.; Williams, D.A.; Nathues, A.; et al. Post-impact cryo-hydrologic formation of small mounds and hills in Ceres’s Occator crater. Nat. Geosci. 2020, 13, 605–610. [Google Scholar] [CrossRef]
- Scully, J.E.C.; Schenk, P.M.; Castillo-Rogez, J.C.; Buczkowski, D.L.; Williams, D.A.; Pasckert, J.H.; Duarte, K.D.; Romero, V.N.; Quick, L.C.; Sori, M.M.; et al. The varied sources of faculae-forming brines in Ceres’ Occator crater emplaced via hydrothermal brine effusion. Nat. Commun. 2020, 11, 3680. [Google Scholar] [CrossRef]
- Castillo-Rogez, J.; Neveu, M.; McSween, H.Y.; Fu, R.R.; Toplis, M.J.; Prettyman, T. Insights into Ceres’s evolution from surface composition. Meteorit. Planet. Sci. 2018, 53, 1820–1843. [Google Scholar] [CrossRef]
- Park, R.S.; Konopliv, A.S.; Bills, B.G.; Rambaux, N.; Castillo-Rogez, J.C.; Raymond, C.A.; Vaughn, A.T.; Ermakov, A.I.; Zuber, M.T.; Fu, R.R.; et al. A partially differentiated interior for (1) Ceres deduced from its gravity field and shape. Nature 2016, 537, 515–517. [Google Scholar] [CrossRef]
- Ermakov, A.I.; Fu, R.R.; Castillo-Rogez, J.C.; Raymond, C.A.; Park, R.S.; Preusker, F.; Russell, C.T.; Smith, D.E.; Zuber, M.T. Constraints on Ceres’ Internal Structure and EvolutionFrom Its Shape and Gravity Measuredby the Dawn Spacecraft. J. Geophys. Res. 2017, 122, 2267–2293. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Park, R.S.; Vaughn, A.T.; Bills, B.G.; Asmar, S.W.; Ermakov, A.I.; Rambaux, N.; Raymond, C.A.; Castillo-Rogez, J.C.; Russell, C.T.; et al. The Ceres gravity field, spin pole, rotation period and orbit from the Dawn radiometric tracking and optical data. Icarus 2018, 299, 411–429. [Google Scholar] [CrossRef]
- Prettyman, T.H.; Yamashita, N.; Toplis, M.J.; McSween, H.Y.; Schörghofer, N.; Marchi, S.; Feldman, W.C.; Castillo-Rogez, J.; Forni, O.; Lawrence, D.J.; et al. Extensive water ice within Ceres’ aqueously altered regolith: Evidence from nuclear spectroscopy. Science 2017, 355, 55–59. [Google Scholar] [CrossRef] [PubMed]
- Prettyman, T.H.; Yamashita, N.; Landis, M.E.; Castillo-Rogez, J.C.; Schörghofer, N.; Pieters, C.M.; Sizemore, H.G.; Hiesinger, H.; Marchi, S.; McSween, H.Y.; et al. Replenishment of Near-Surface Water Ice by Impacts Into Ceres’ Volatile-Rich Crust: Observations by Dawn’s Gamma Ray and Neutron Detector. Geophys. Res. Lett. 2021, 48, e2021GL094223. [Google Scholar] [CrossRef]
- Ruesch, O.; Platz, T.; Schenk, P.; McFadden, L.A.; Castillo-Rogez, J.C.; Quick, L.C.; Byrne, S.; Preusker, F.; O’Brien, D.P.; Schmedemann, N.; et al. Cryovolcanism on Ceres. Science 2016, 353, aaf4286. [Google Scholar] [CrossRef]
- De Sanctis, M.C.; Raponi, A.; Amannito, A.; Ciarniello, M.; Toplis, M.J.; McSween, H.Y.; Castillo-Rogez, J.C.; Ehlmann, B.L.; Carrozzo, F.G.; Marchi, S.; et al. Bright carbonate deposits as evidence of aqueous alteration on (1) Ceres. Nature 2016, 536, 54–57. [Google Scholar] [CrossRef]
- Ruesch, O.; Quick, L.C.; Landis, M.E.; Sori, M.M.; Čadek, O.; Brož, P.; Otto, K.A.; Bland, M.T.; Byrne, S.; Castillo-Rogez, J.C.; et al. Bright Carbonate Surfaces on Ceres as Remnants of Salt-Rich Water Fountains. Icarus 2019, 320, 39–48. [Google Scholar] [CrossRef]
- Scully, J.E.; Baker, S.R.; Castillo-Rogez, J.C.; Buczkowski, D.L. The In Situ Exploration of a Relict Ocean World: An Assessment of Potential Landingand Sampling Sites for a Future Mission to the Surface of Ceres. Planet. Sci. J. 2021, 2, 94. [Google Scholar] [CrossRef]
- Gassot, O.; Panicucci, P.; Acciarini, G.; Bates, H.; Caballero, M.; Cambianica, P.; Dziewiecki, M.; Dionnet, Z.; Enengl, F.; Gerig, S.B.; et al. Calathus: A sample-return mission to Ceres. Acta Astronaut. 2021, 181, 112–129. [Google Scholar] [CrossRef]
- Castillo-Rogez, J.; Brophy, J.; Miller, K.; Sori, M.; Scully, J.; Quick, L.; Grimm, R.; Zolensky, M.; Bland, M.; Buczkowski, D.; et al. Concepts for the Future Exploration of Dwarf Planet Ceres’ Habitability. Planet. Sci. J. 2022, 3, 41. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Origins, Worlds, and Life. A Decadal Strategy for Planetary Science and Astrobiology 2023–2032; The National Academies Press: Cambridge, MA, USA, 2023. [Google Scholar] [CrossRef]
- Castillo-Rogez, J. Future exploration of Ceres as an ocean world. Nat. Astron. 2020, 4, 732–734. [Google Scholar] [CrossRef]
- Kirk, R.; Howington-Kraus, E.; Rosiek, M.; Anderson, J.; Archinal, B.; Becker, K.; Cook, D.; Galuszka, D.; Geissler, P.; Hare, T.; et al. Ultrahigh resolution topographic mapping of Mars with MROHiRISE stereo images: Meter-scale slopes of candidate Phoenixlanding sites. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Sierks, H.; Keller, H.U.; Jaumann, R.; Michalik, H.; Behnke, T.; Bubenhagen, F.; Büttner, I.; Carsenty, U.; Christensen, U.; Enge, R.; et al. The Dawn Framing Camera. Space Sci. Rev. 2011, 163, 263–327. [Google Scholar] [CrossRef]
- Beyer, R.A.; Alexandrov, O.; McMichael, S. The Ames Stereo Pipeline: NASA’s Open Source Software for Deriving and Processing Terrain Data. Earth Space Sci. 2018, 5, 537–548. [Google Scholar] [CrossRef]
- Alexandrov, O.; Beyer, R.A. Multiview Shape-From-Shading for Planetary Images. Earth Space Sci. 2018, 5, 652–666. [Google Scholar] [CrossRef]
- Thomas, V.C.; Makowski, J.M.; Brown, G.M.; McCarthy, J.F.; Bruno, D.; Cardoso, J.C.; Chiville, W.M.; Meyer, T.F.; Nelson, K.E.; Pavri, B.E.; et al. The Dawn Spacecraft. Space Sci. Rev. 2011, 163, 175–249. [Google Scholar] [CrossRef]
- De Sanctis, M.; Coradini, A.; Ammannito, E.; Filacchione, G.; Capria, M.; Fonte, S.; Magni, G.; Barbis, A.; Bini, A.; Dami, M.; et al. The VIR Spectrometer. Space Sci. Rev. 2011, 163, 329–369. [Google Scholar] [CrossRef]
- Prettyman, T.H.; Feldman, W.C.; McSween, H.Y., Jr.; Dingler, R.D.; Enemark, D.C.; Patrick, D.E.; Storms, S.A.; Hendricks, J.S.; Morgenthaler, H.P.; Pitman, K.M.; et al. Dawn’s Gamma Ray and Neutron Detector. Space Sci. Rev. 2011, 163, 371–459. [Google Scholar] [CrossRef]
- Konopliv, A.; Asmar, S.; Bills, B.; Mastrodemos, N.; Park, R.; Raymond, C.; Smith, D.; Zuber, M. The Dawn Mission to Minor Planets 4 Vesta and 1 Ceres; Springer: New York, NY, USA, 2011; Chapter The Dawn Gravity Investigation at Vesta and Ceres. [Google Scholar] [CrossRef]
- Polanskey, C.; Joy, S.; Raymond, C. Dawn Science Planning Operations and Archiving. Space Sci. Rev. 2011, 163, 511–543. [Google Scholar] [CrossRef]
- Roatsch, T.; Kersten, E.; Matz, K.D.; Preusker, F.; SCholten, F.; Elgner, S.; Schroeder, S.; Jaumann, R.; Raymond, C.; Russell, C. DAWN FC2 DERIVED CERES HAMO DTM SPG V1.0, DAWN-A-FC2-5-CERESHAMODTMSPG-V1.0; NASA Planetary Data System: Tucson, AZ, USA, 2016. [Google Scholar]
- Preusker, F.; Scholten, F.; Matz, K.D.; Elgner, S.; Jaumann, R.; Roatsch, T.; Joy, S.P.; Polanskey, C.A.; Raymond, C.A.; Russell, C.T. Dawn at Ceres—Shape Model and Rotational State. Lunar Planet. Sci. Conf. 2016, 47, 1954. [Google Scholar]
- Jaumann, R.; Preusker, F.; Krohn, K.; von der Gathen, I.; Stephan, K.; Matz, K.D.; Elgner, S.; Otto, K.; Schmedemann, N.; Neesemann, A.; et al. Topography and Geomorphology of the Interior of Occator Crater on Ceres. In Proceedings of the Lunar and Planetary Science Conference, The Woodlands, TX, USA, 20–24 March 2017. [Google Scholar]
- Park, R.; Buccino, D. Ceres SPC Shape Model Dataset V1.0 DAWN-A-FC2-5-CERESSHAPESPC-V1.0. NASA Planetary Data System. 2018. Available online: https://sbn.psi.edu/pds/resource/dawn/dwncfcshape.html (accessed on 23 December 2024).
- Park, R.S.; Vaughan, A.T.; Konopliv, A.S.; Ermakov, A.I.; Mastrodemos, N.; Castillo-Rogez, J.C.; Joy, S.P.; Nathues, A.; Polanskey, C.A.; Rayman, M.D.; et al. High-resolution shape model of Ceres from stereophotoclinometry using Dawn Imaging Data. Icarus 2019, 319, 812–827. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Jackson, G.B.; Cavanaugh, J.F.; Neumann, G.A.; Riris, H.; Sun, X.; Zellar, R.S.; Coltharp, C.; Connelly, J.; et al. The Lunar Orbiter Laser Altimeter Investigation on the Lunar Reconnaissance Orbiter Mission. Space Sci. Rev. 2010, 150, 209–241. [Google Scholar] [CrossRef]
- Zuber, M.T.; Smith, D.E.; Lemoine, F.G.; Neumann, G.A. The Shape and Internal Structure of the Moon from the Clementine Mission. Science 1994, 266, 1839–1843. [Google Scholar] [CrossRef] [PubMed]
- Zuber, M.T.; Smith, D.E. Topographic mapping of the Moon. Int. Arch. Photogramm. Remote Sens. 1996, XXXI, 1011–1015. [Google Scholar]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G. Topography of the Moon from the Clementine lidar. J. Geophys. Res. Planets 1997, 102, 1591–1611. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head II, J.W.; Duxbury, T.H.; et al. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA). Geophys. Res. Lett. 2010, 37, L18204. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E.; Lemoine, F.G.; Head III, J.W.; Lucey, P.G.; Aharonson, O.; Robinson, M.S.; Sun, X.; et al. Summary of the results from the lunar orbiter laser altimeter after seven years in lunar orbit. Icarus 2017, 283, 70–91. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Solomon, S.C.; Phillips, R.J.; Head, J.W.; Garvin, J.B.; Banerdt, W.B.; Muhleman, D.O.; Pettengill, G.H.; Neumann, G.A.; et al. The Global Topography of Mars and Implications for Surface Evolution. Science 1999, 284, 1495–1503. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Herbert, V.F.; Garvin, H.B.; Head, J.W.; Muhleman, D.O.; Pettengill, G.H.; Phillips, R.J.; Solomon, S.C.; Zwally, H.J.; et al. Mars Orbiter Laser Altimeter: Experiment Summary after the first year of global mapping of Mars. J. Geophys. Res. 2001, 106, 23689–23722. [Google Scholar] [CrossRef]
- Smith, D.; Zuber, M.T.; Neumann, G.A.; Jester, P. Mars Global Laser Altimeter Precision Experiment Data Record (MGS-M-MOLA-3-PEDR-L1A-V1.0); Techreport; NASA Planetary Data System: Basel, Switzerland, 2003. [Google Scholar] [CrossRef]
- Raymond, C.; Jaumann, R.; Nathues, A.; Sierks, H.; Roatsch, T.; Preusker, F.; Scholten, F.; Gaskell, R.; Jorda, L.; Keller, H.U.; et al. The Dawn Topography Investigation. Space Sci. Rev. 2011, 163, 487–510. [Google Scholar] [CrossRef]
- Jaumann, R.; Neukum, G.; Behnke, T.; Duxbury, T.; Eichentopf, K.; Flohrer, J.; van Gasselt, S.; Giese, B.; Gwinner, K.; Hauber, E.; et al. The high-resolution stereo camera (HRSC) experiment on Mars Express: Instrument aspects and experiment conduct from interplanetary cruise through the nominal mission. Planet. Space Sci. 2007, 55, 928–952. [Google Scholar] [CrossRef]
- Thomas, N.; Cremonese, G.; Ziethe, R.; Gerber, M.; Brändli, M.; Bruno, G.; Erismann, M.; Gambicorti, L.; Gerber, T.; Ghose, K.; et al. The Colour and Stereo Surface Imaging System (CaSSIS) for the ExoMars Trace Gas Orbiter. Space Sci. Rev. 2017, 212, 1897–1944. [Google Scholar] [CrossRef]
- Kirk, R.L.; Mayer, D.P.; Fergason, R.L.; Redding, B.L.; Galuszka, D.M.; Hare, T.M.; Gwinner, K. Evaluating Stereo Digital Terrain Model Quality at Mars Rover Landing Sites with HRSC, CTX, and HiRISE Images. Remote Sens. 2021, 13, 3511. [Google Scholar] [CrossRef]
- Kirk, R.; Mayer, D.; Dundas, C.; Wheeler, B.; Beyer, R.; Alexandrov, O. Comparison of Digital Terrain Models from Two Photoclinometry Methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLIII-B3-2022, 1059–1067. [Google Scholar] [CrossRef]
- Malin, M.C.; Bell, J.F., III; Cantor, B.A.; Caplinger, M.A.; Calvin, W.M.; Clancy, R.T.; Edgett, K.S.; Edwards, L.; Haberle, R.M.; James, P.B.; et al. Context Camera Investigation on board the Mars Reconnaissance Orbiter. J. Geophys. Res. Planets 2007, 112, E05S04. [Google Scholar] [CrossRef]
- McEwen, A.S.; Eliason, E.M.; Bergstrom, J.W.; Bridges, N.T.; Hansen, J.; Delamere, W.A.; Grant, J.A.; Gulick, V.C.; Herkenhoff, K.E.; Keszthelyi, L.; et al. Mars Reconnaissance Orbiter’s High Resolution Imaging Science Experiment (HiRISE). J. Geophys. Res. Planets 2007, 112, E05S02. [Google Scholar] [CrossRef]
- Robinson, M.; Brylow, S.; Tschimmel, M.; Humm, D.; Lawrence, S.; Thomsa, P.; Denevi, B.; Bowman-Cisneros, E.; Zerr, J.; Ravine, M.; et al. Lunar Reconnaissance Ortbiter Camera (LROC) Instrument Overview. Space Sci. Rev. 2010, 150, 81–124. [Google Scholar] [CrossRef]
- Nathues, A.; Hoffmann, M.; Schaefer, M.; Le Corre, L.; Reddy, V.; Platz, T.; Cloutis, E.A.; Christensen, U.; Kneissl, T.; Li, J.Y.; et al. Sublimation in bright spots on (1) Ceres. Nature 2015, 528, 237–240. [Google Scholar] [CrossRef]
- Schäfer, T.; Nathues, A.; Mengel, K.; Izawa, M.R.M.; Cloutis, E.A.; Schäfer, M.; Hoffmann, M. Spectral parameters for Dawn FC color data: Carbonaceous chondrites and aqueous alteration products as potential cerean analog materials. Icarus 2016, 265, 149–160. [Google Scholar] [CrossRef]
- Gaskell, R.; Barnoin-Jha, O.; Scheeres, D.; Konopliv, A.; Mukai, S.; Abe, S.; Saito, J.; Ishiguro, M.; Kubota, T.; Hashimoto, T.; et al. Characterizing and Navigating Small Bodies with Imaging Data. Meteorit. Planet. Sci. 2008, 43, 1049–1061. [Google Scholar] [CrossRef]
- Palmer, E.E.; Gaskell, R.; Daly, M.G.; Barnouin, O.; Adam, C.; Lauretta, D. Practical Stereophotoclinometry for Modeling Shape and Topography on Planetary Missions. Planet. Sci. J. 2022, 3, 102. [Google Scholar] [CrossRef]
- Grumpe, A.; Wöhler, C. Recovery of elevation from estimated gradient fields constrained by digital elevation maps of lower lateral resolution. ISPRS J. Photogramm. Remote Sens. 2014, 94, 37–54. [Google Scholar] [CrossRef]
- Grumpe, A.; Belkhir, F.; Wöhler, C. Construction of lunar DEMs based on reflectance modelling. Adv. Space Res. 2014, 53, 1735–1767. [Google Scholar] [CrossRef]
- Wu, B.; Liu, W.C.; Grumpe, A.; Wöhler, C. Construction of pixel-level resolution DEMs from monocular images by shape and albedo from shading constrained with low-resolution DEM. ISPRS J. Photogramm. Remote Sens. 2018, 140, 3–19. [Google Scholar] [CrossRef]
- Jiang, C.; Douté, S.; Lou, B.; Zhang, L. Fusion of photogrammetric and photoclinometric information for high-resolution DEMs from Mars in-orbit imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 418–430. [Google Scholar] [CrossRef]
- Tenthoff, M.; Wohlfarth, K.; Wöhler, C. High Resolution Digital Terrain Models of Mercury. Remote Sens. 2020, 12, 3989. [Google Scholar] [CrossRef]
- Russell, C.; Raymond, C.; Ammannito, E.; Buczkowski, D.; De Sanctis, M.; Hiesinger, H.; Jaumann, R.; Konopliv, A.; McSween, H.; Nathues, A.; et al. Dawn Arrives at Ceres: Exploration of a Small, Volatile-Rich World. Science 2016, 353, 1008–1010. [Google Scholar] [CrossRef]
- Schröder, S.E.; Gutiérrez-Marqués, P. DAWN—Framing Camera Calibration Pipeline; Techreport DA-FC-MPAE-RP-272; Max Planck Institute for Solar System Research: Göttingen, Germany, 2013. [Google Scholar]
- Stein, N.T.; Ehlmann, B.L.; Palomba, E.; De Sanctis, M.C.; Nathues, A.; Hiesinger, H.; Ammannito, E.; Raymond, C.A.; Jaumann, R.; Longobardo, A.; et al. The Formation and Evolution of Bright Spots on Ceres. Icarus 2019, 320, 188–201. [Google Scholar] [CrossRef]
- Acton, C.H. Ancillary data services of NASA’s Navigation and Ancillary Information Facility. Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Shkuratov, Y.; Kaydash, V.; Korokhin, V.; Velikodsky, Y.; Opanasenko, N.; Videen, G. Optical measurements of the Moon as a tool to study its surface. Planet. Space Sci. 2011, 59, 1326–1371. [Google Scholar] [CrossRef]
- Schröder, S.E.; Mottola, S.; Carsenty, U.; Ciarniello, M.; Jaumann, R.; Li, J.Y.; Longobardo, A.; Palmer, E.; Pieters, C.; Preusker, F.; et al. Resolved Spectrophotometric Properties of the Ceres Surface from Dawn Feaming Camera Images. Icarus 2017, 288, 201–225. [Google Scholar] [CrossRef]
- Li, J.Y.; Helfenstein, P.; Buratti, B.J.; Takir, D.; Clark, B.E. Asteroids IV; Space Science Series; University of Arizona Press: Tucson, AZ, USA, 2015; Chapter 2.2 Asteroid Composition and Physical Properties; pp. 129–150. [Google Scholar]
- Hapke, B. Bidirectional reflectance spectroscopy: 1. Theory. J. Geophys. Res. Solid Earth 1981, 86, 3039–3054. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 3. Correction for macroscopic roughness. Icarus 1984, 59, 41–59. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 4. The extinction coefficient and the opposition effect. Icarus 1986, 67, 264–280. [Google Scholar] [CrossRef]
- Lohse, V.; Heipke, C.; Kirk, R.L. Derivation of planetary topography using multi-imageshape-from-shading. Planet. Space Sci. 2006, 54, 661–674. [Google Scholar] [CrossRef]
- Hapke, B.W.; Nelson, R.M.; Smythe, W.D. The Opposition Effect of the Moon: The Contribution of Coherent Backscatter. Science 1993, 260, 509–511. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 6. Effects of porosity. Icarus 2008, 195, 918–926. [Google Scholar] [CrossRef]
- Li, J.Y.; Schröder, S.; Mottola, S.; Nathues, A.; Castillo-Rogez, J.C.; Schorghofer, N.; Williams, D.A.; Ciarniello, M.; Longobardo, A.; Raymond, C.A.; et al. Spectroscopic Modeling and Mapping of Ceres. Icarus 2019, 322, 144–167. [Google Scholar] [CrossRef]
- Edmundson, K.L.; Cook, D.A.; Thomas, O.H.; Archinal, B.A.; Kirk, R.L. Jigsaw: The ISIS3 bundle adjustment for extraterrestrial photogrammetry. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 203–208. [Google Scholar] [CrossRef]
- Menard, C. Robust Stereo and Adaptive Matching in Correlation Scale-Space. Ph.D. Thesis, Institute of Automation, Vienna Institute of Technology, Wien, Austria, 1997. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the DARPA Image Understanding Workshop, Vancouver, BC, Canada, 24–28 August 1981; pp. 121–130. [Google Scholar]
- Baker, S.; Matthews, I. Lucas-Kanade 20 Years on: A Unifying Framework. Int. J. Comput. Vis. 2004, 56, 221–255. [Google Scholar] [CrossRef]
- Roatsch, T.; Kersten, E.; Matz, K.D.; Preusker, F.; SCholten, F.; Elgner, S.; Schroeder, S.; Jaumann, R.; Raymond, C.; Russell, C. DAWN FC2 DERIVED CERES HAMO DTM SPG V1.0, DAWN-A-FC2-5-CERESLAMODTMSPG-V1.0; NASA Planetary Data System: Tucson, AZ, USA, 2019. [Google Scholar]
- Neesemann, A.; van Gasselt, S.; Schmedemann, N.; Marchi, S.; Walter, S.H.G.; Preusker, F.; Michael, G.G.; Kneissl, T.; Hiesinger, H.; Jaumann, R.; et al. The Various Ages of Occator Crater, Ceres: Results of a Comprehensive Synthesis Approach. Icarus 2019, 320, 60–82. [Google Scholar] [CrossRef]
- Preusker, F.; Oberst, J.; Head, J.W.; Watters, T.R.; Robinson, M.S.; Zuber, M.T.; Solomon, S.C. Stereo topographic models of Mercury after three MESSENGER flybys. Planet. Space Sci. 2011, 59, 1910–1917. [Google Scholar] [CrossRef]
- Roatsch, T.; Kersten, E.; Matz, K.D.; Preusker, F.; Scholten, F.; Jaumann, R.; Raymond, C.A.; Russell, C.T. High-resolution Ceres High Altitude Mapping Orbit atlas derived from Dawn Framing Camera images. Planet. Space Sci. 2016, 129, 103–107. [Google Scholar] [CrossRef]









| FC Filter | C0 | C1 | C2 | C3 |
|---|---|---|---|---|
| F1 | 0.0731 | |||
| F2 | 0.0813 | |||
| F5 | 0.0713 | |||
| F7 | 0.0790 | |||
| F8 | 0.0769 |
| Area 1 | Area 2 | Area 3 | Area 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | Min | Max | Mean | |
| CSH/CXJ ASP SPG | −1397.5 | 17,104.0 | 9400.0 | 1265.8 | 14,994.3 | 9162.5 | 1265.8 | 14,994.3 | 9105.6 | 5225.2 | 13,992.1 | 9060.7 |
| CSH/CXJ ASP SfS | −1417.2 | 17,137.1 | 9400.9 | 1272.1 | 15,014.2 | 9162.6 | 1272.1 | 15,014.2 | 9105.8 | 5210.0 | 13,938.5 | 9062.6 |
| CSL/CXL ASP SPG | - | - | - | 1241.0 | 15,025.3 | 9164.0 | 1241.0 | 15,025.3 | 9106.2 | 5214.6 | 14,011.1 | 9060.7 |
| CSL/CXL ASP SfS | - | - | - | - | - | - | - | - | - | 5198.6 | 14,013.1 | 9064.4 |
| HAMO DLR SPG | −1406.0 | 17,057.0 | 9496.0 | 1339.0 | 14,980.0 | 9149.4 | 1339.0 | 14,980.0 | 9091.6 | 5147.0 | 13,966.0 | 9042.2 |
| LAMO DLR SPG | - | - | - | - | - | - | 1213.0 | 15,042.0 | 9087.9 | 5218.0 | 13,972.0 | 9054.8 |
| HAMO/LAMO JPL SPC | −1615.6 | 17,030.9 | 9359.9 | 1131.2 | 15,059.8 | 9121.5 | 1131.2 | 15,059.8 | 9064.2 | 5160.2 | 13753.4 | 9024.8 |
| Mean | SD | Min | Max | ||
|---|---|---|---|---|---|
| ASP SPG vs. ASP SfS | |||||
| Area 1 | CSH/CXJ ASP SPG vs. CSH/CXJ ASP SfS | 0.95 | 28.82 | −313.05 | 248.47 |
| Area 4 | CSH/CXJ ASP SPG vs. CSH/CXJ ASP SfS | 1.89 | 30.49 | −306.00 | 236.54 |
| Area 4 | CSL/CXL ASP SPG vs. CSL/CXL ASP SfS | 3.64 | 10.48 | −535.83 | 173.37 |
| HAMO vs. LAMO | |||||
| Area 3 | HAMO DLR SPG vs. LAMO DLR SPG | −3.65 | 78.84 | −779.00 | 692.00 |
| Area 3 | CSH/CXJ ASP SPG vs. CSL/CXL ASP SPG | 0.65 | 31.69 | −356.24 | 509.45 |
| DLR HAMO SPG vs. … | |||||
| Area 1 | DLR HAMO SPG vs. CSH/CXJ ASP SPG | 9.97 | 69.51 | −668.81 | 600.73 |
| Area 1 | DLR HAMO SPG vs. CSH/CXJ ASP SfS | 10.92 | 69.59 | −725.05 | 676.06 |
| Area 1 | DLR HAMO SPG vs. JPL HAMO/LAMO SPC | −30.07 | 90.64 | −910.31 | 656.70 |
| Area 4 | DLR HAMO SPG vs. CSL/CXL ASP SPG | 18.51 | 68.67 | −668.81 | 605.31 |
| Area 4 | DLR HAMO SPG vs. CSL/CXL ASP SfS | 20.40 | 70.31 | −728.61 | 727.95 |
| Area 4 | DLR HAMO SPG vs. JPL HAMO/LAMO SPC | −17.40 | 90.74 | −910.31 | 661.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neesemann, A.; van Gasselt, S.; Jaumann, R.; Castillo-Rogez, J.C.; Raymond, C.A.; Walter, S.H.G.; Postberg, F. Improved Stereophotogrammetric and Multi-View Shape-from-Shading DTMs of Occator Crater and Its Interior Cryovolcanism-Related Bright Spots. Remote Sens. 2025, 17, 437. https://doi.org/10.3390/rs17030437
Neesemann A, van Gasselt S, Jaumann R, Castillo-Rogez JC, Raymond CA, Walter SHG, Postberg F. Improved Stereophotogrammetric and Multi-View Shape-from-Shading DTMs of Occator Crater and Its Interior Cryovolcanism-Related Bright Spots. Remote Sensing. 2025; 17(3):437. https://doi.org/10.3390/rs17030437
Chicago/Turabian StyleNeesemann, Alicia, Stephan van Gasselt, Ralf Jaumann, Julie C. Castillo-Rogez, Carol A. Raymond, Sebastian H. G. Walter, and Frank Postberg. 2025. "Improved Stereophotogrammetric and Multi-View Shape-from-Shading DTMs of Occator Crater and Its Interior Cryovolcanism-Related Bright Spots" Remote Sensing 17, no. 3: 437. https://doi.org/10.3390/rs17030437
APA StyleNeesemann, A., van Gasselt, S., Jaumann, R., Castillo-Rogez, J. C., Raymond, C. A., Walter, S. H. G., & Postberg, F. (2025). Improved Stereophotogrammetric and Multi-View Shape-from-Shading DTMs of Occator Crater and Its Interior Cryovolcanism-Related Bright Spots. Remote Sensing, 17(3), 437. https://doi.org/10.3390/rs17030437







