Exploring the Advantages of Multi-GNSS Ionosphere-Weighted Single-Frequency Precise Point Positioning in Regional Ionospheric VTEC Modeling
Abstract
:1. Introduction
2. Methodology
2.1. General Model of the GNSS Single-Frequency PPP
2.2. Extraction of STEC Observables from the Multi-GNSS Ionosphere-Weighted Single-Frequency PPP
2.3. Algorithm of the Regional Ionospheric VTEC Model
3. Experimental Data and Processing Strategies
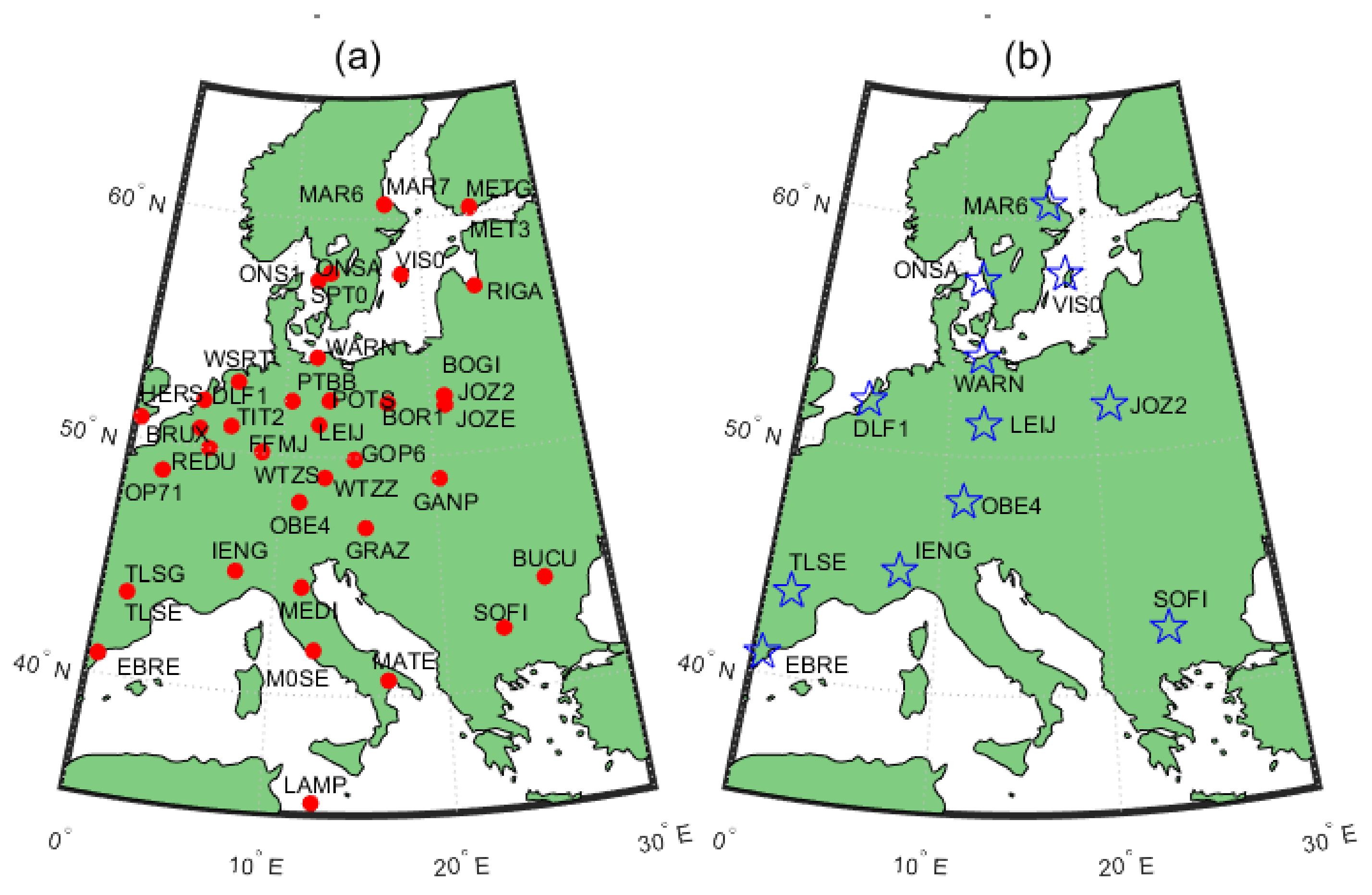
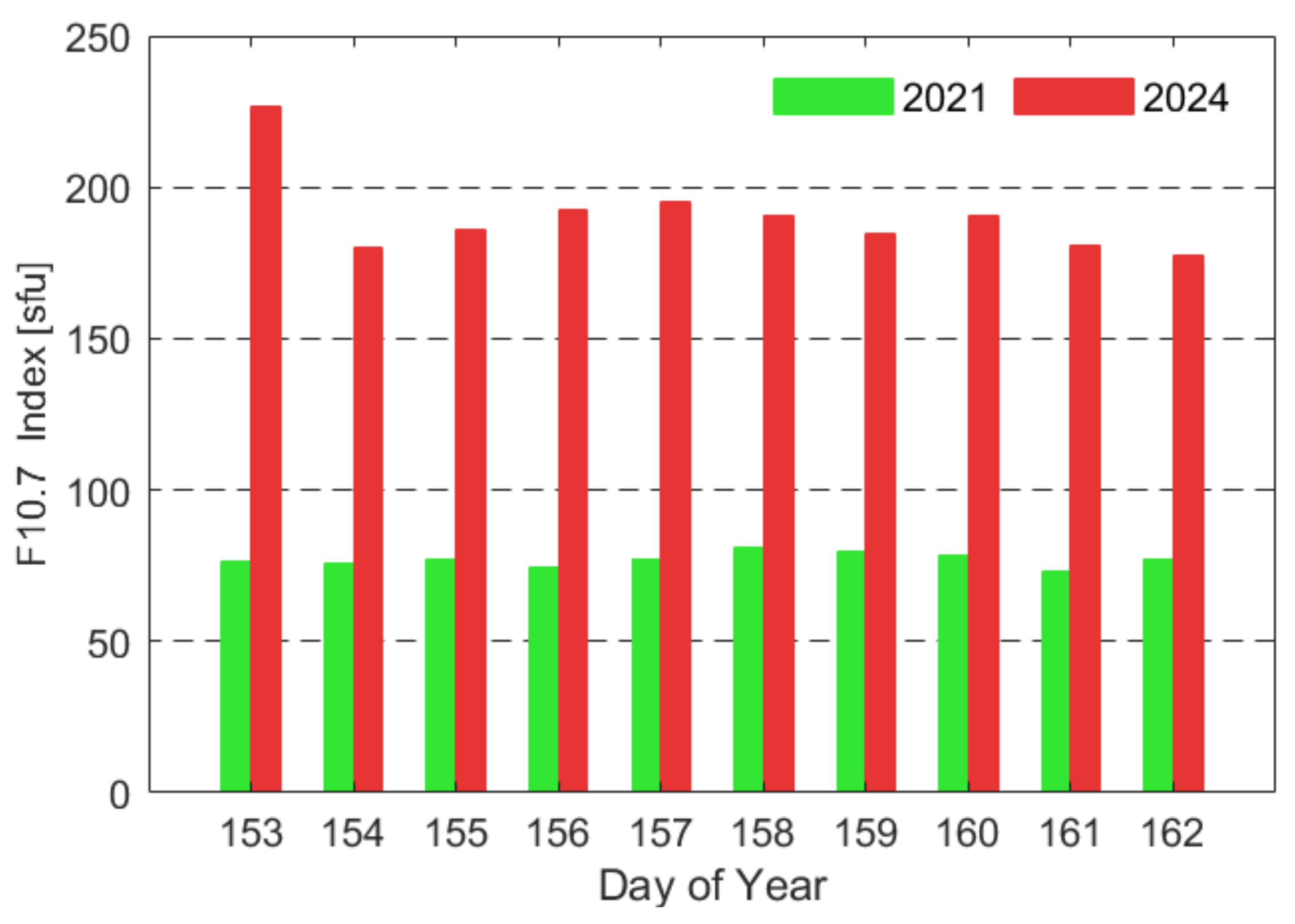
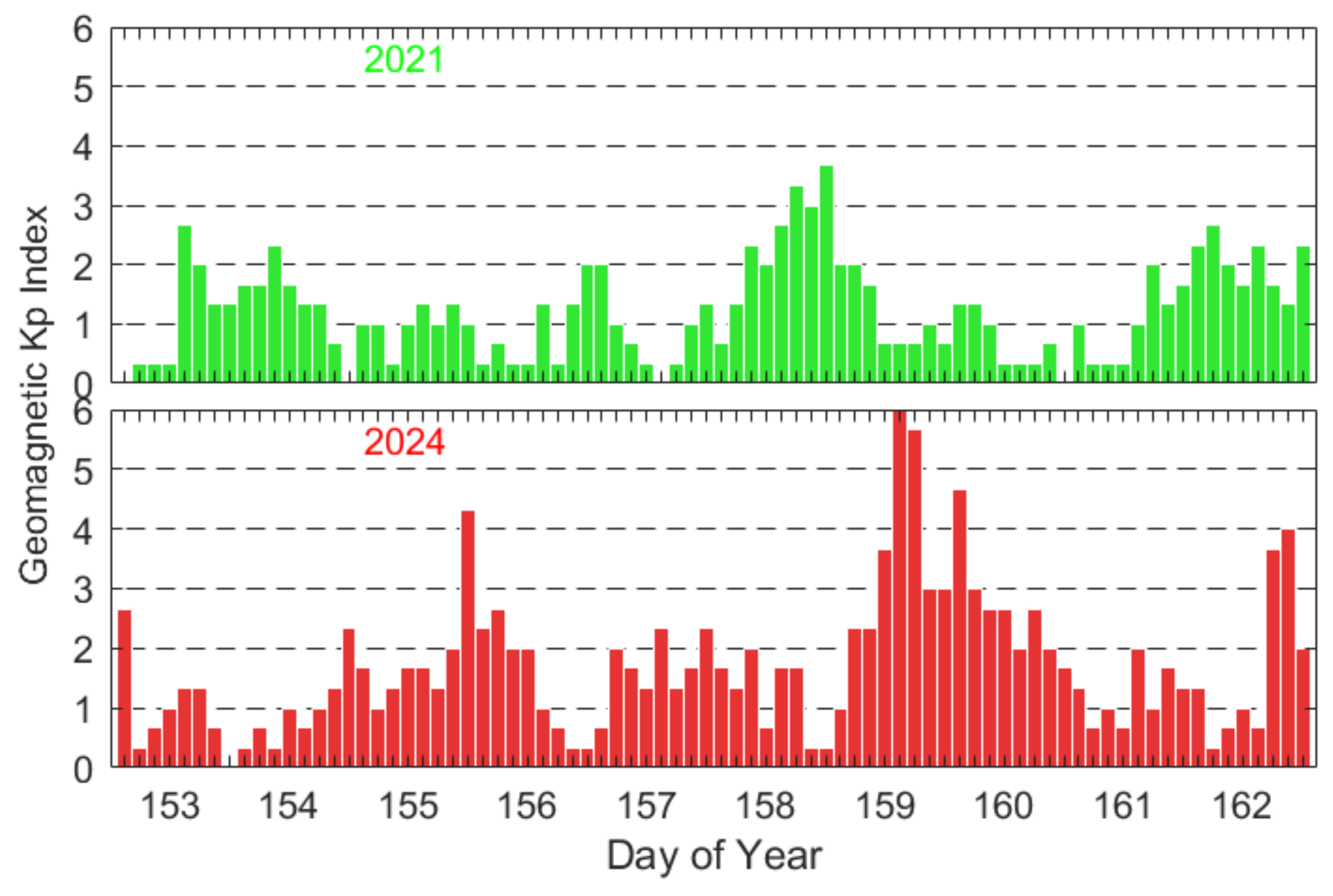
3.1. Experimental Data
3.2. Processing Strategies
4. Results and Discussion
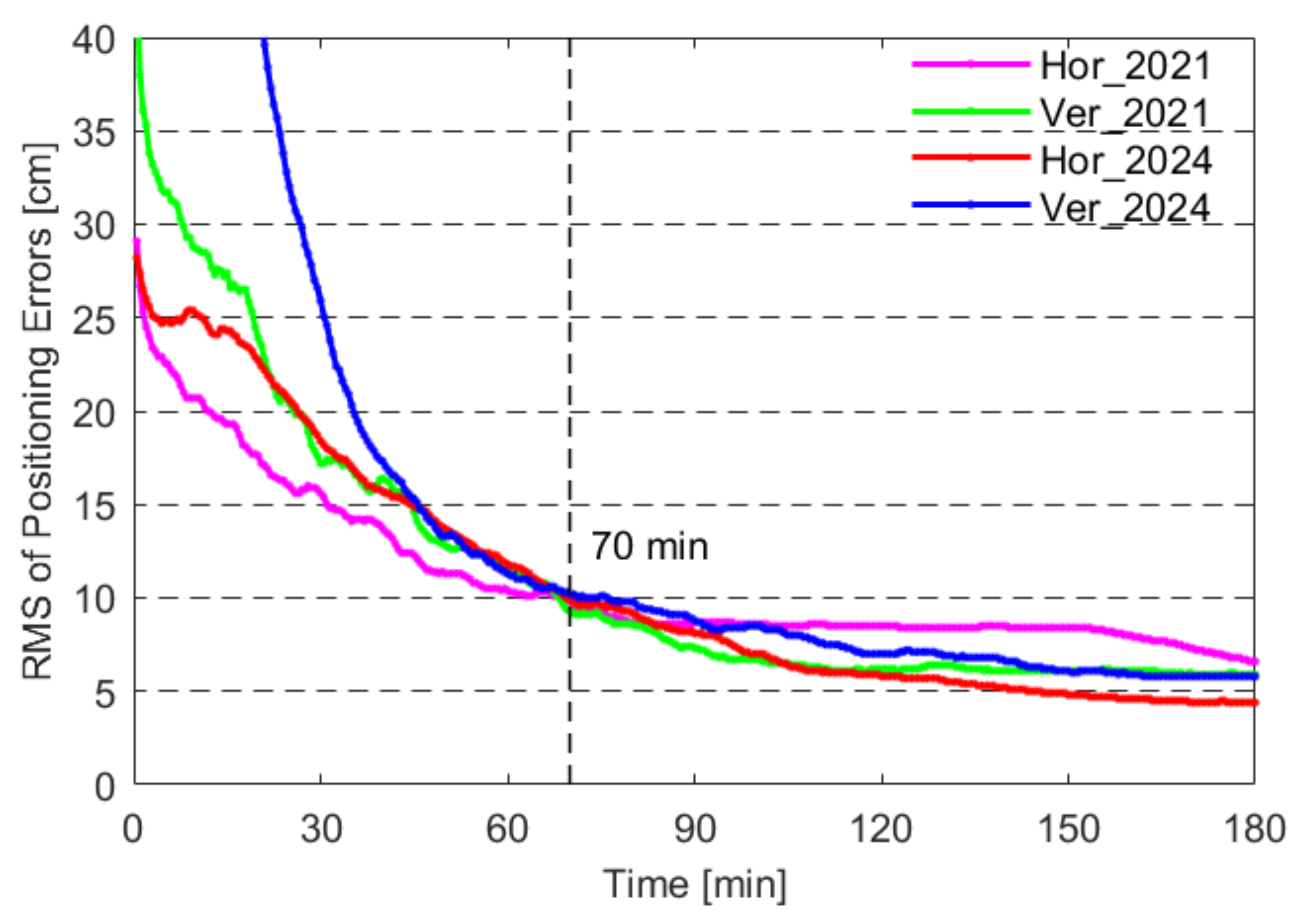
4.1. Performance of the Multi-GNSS Ionosphere-Weighted Single-Frequency PPP
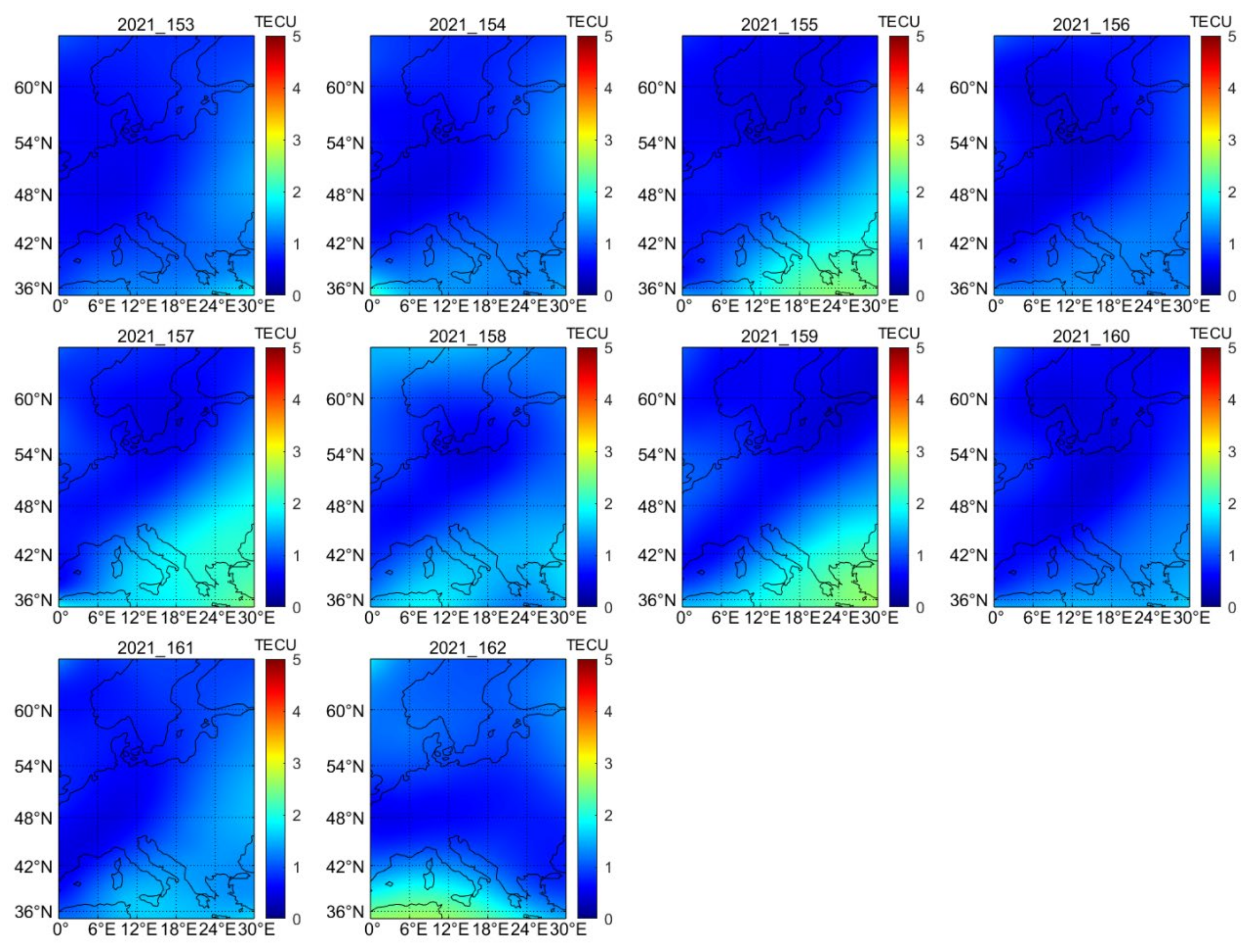
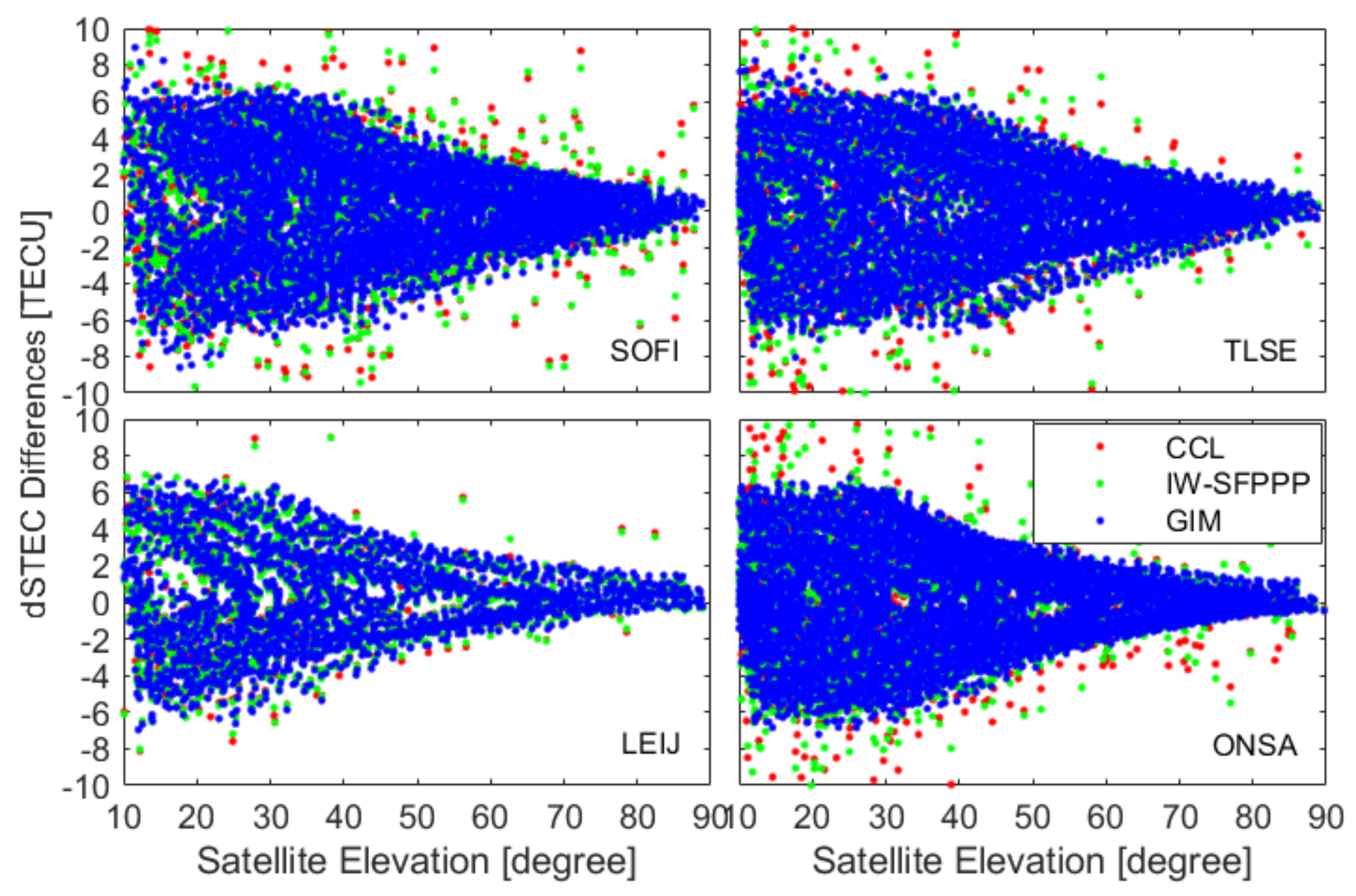
4.2. Quality Assessment of the Regional Ionospheric VTEC Model in Comparison with GIM
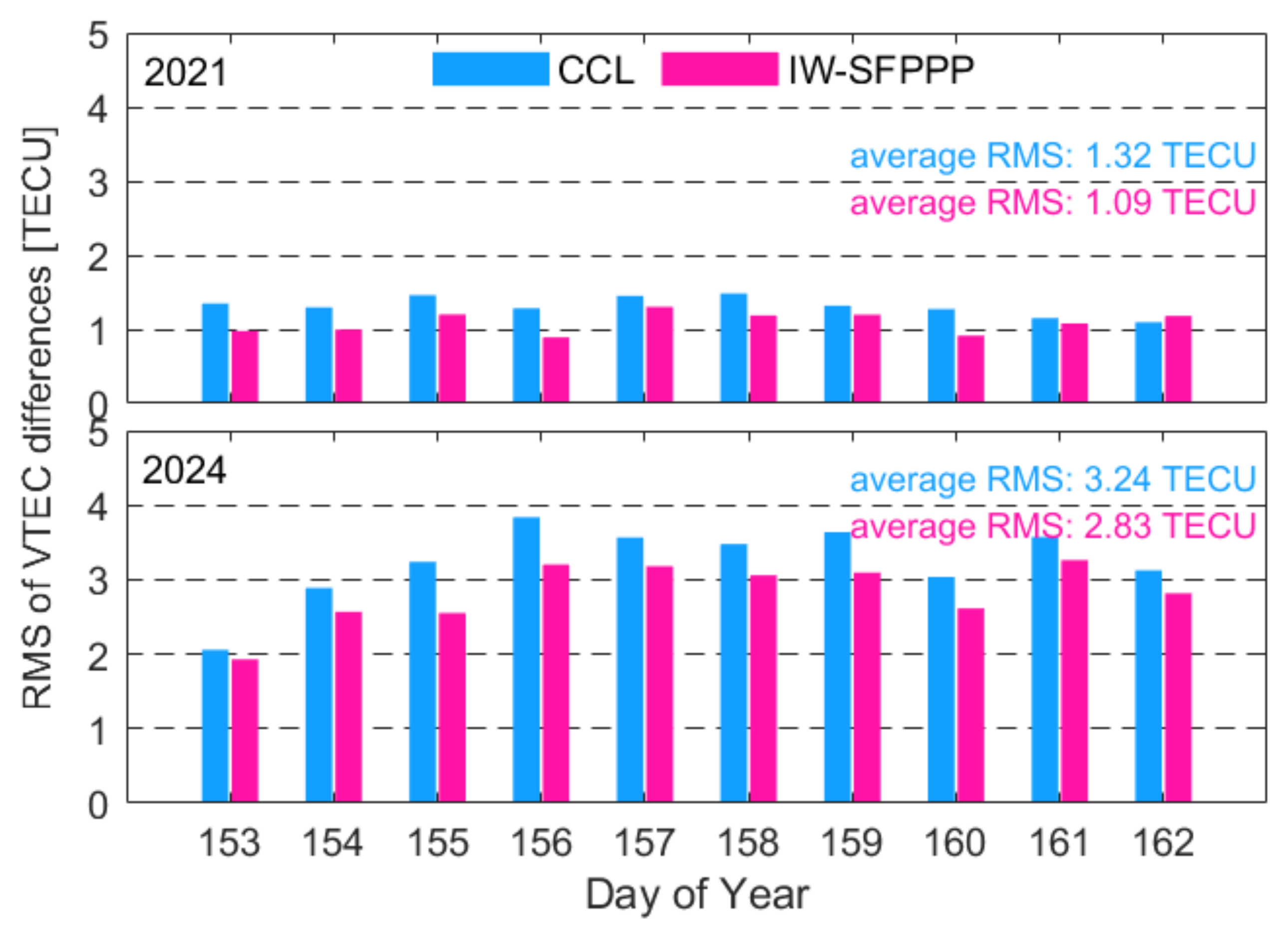
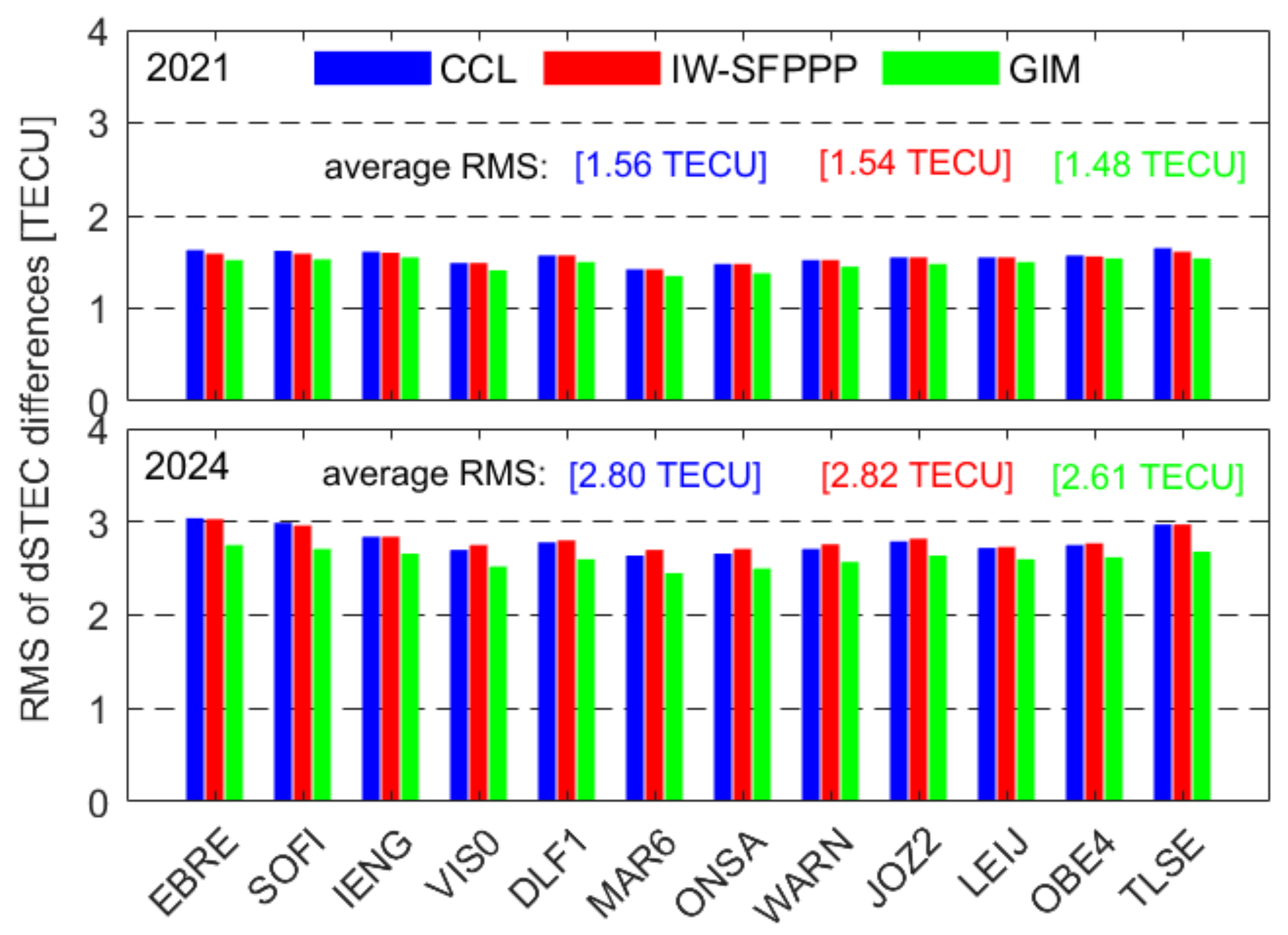
4.3. Evaluation of External Accord Accuracy for Regional Ionospheric VTEC Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feltens, J. The activities of the ionosphere working group of the International GPS Service (IGS). GPS Solut. 2003, 7, 41–46. [Google Scholar] [CrossRef]
- Hernandez-Pajares, M.; Juan, J.M.; Sanz, J.; Aragon-Angel, A.; Garcia-Rigo, A.; Salazar, D.; Escudero, M. The ionosphere: Effects, GPS modeling and the benefits for space geodetic techniques. J. Geod. 2011, 85, 887–907. [Google Scholar] [CrossRef]
- de Bakker, P.F.; Tiberius, C.C.J.M. Real-time multi-GNSS single-frequency precise point positioning. GPS Solut. 2017, 21, 1791–1803. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. An assessment of smartphone and low-cost multi-GNSS single-frequency RTK positioning for low, medium and high ionospheric disturbance periods. J. Geod. 2018, 93, 701–722. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Y.; Chen, J.; Wang, H.; Yuan, D.; Jiang, J.; Zhang, Z. Investigating the contribution of BDS-3 observations to multi-GNSS single-frequency precise point positioning with different ionospheric models. Adv. Space Res. 2024, 73, 553–570. [Google Scholar] [CrossRef]
- Cahuasquí, J.A.; Hoque, M.M.; Jakowski, N. Positioning performance of the Neustrelitz total electron content model driven by Galileo Az coefficients. GPS Solut. 2022, 26, 93. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Z. Anomalies in broadcast ionospheric coefficients recorded by GPS receivers over the past two solar cycles (1992–2013). GPS Solut. 2016, 20, 23–37. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, 23, 325–331. [Google Scholar] [CrossRef]
- Montenbruck, O.; González Rodríguez, B. NeQuick-G performance assessment for space applications. GPS Solut. 2019, 24, 13. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Wang, A.; Chen, J.; Zhang, Y.; Meng, L.; Wang, B.; Wang, J. Evaluating the impact of CNES real-time ionospheric products on multi-GNSS single-frequency positioning using the IGS real-time service. Adv. Space Res. 2020, 66, 2516–2527. [Google Scholar] [CrossRef]
- Liu, H.; Ren, X.; Xu, G. Investigating the performance of IGS real-time global ionospheric maps under different solar conditions. Remote Sens. 2023, 15, 4661. [Google Scholar] [CrossRef]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C.; et al. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2018, 92, 691–706. [Google Scholar] [CrossRef]
- Rovira-Garcia, A.; Juan, J.; Sanz, J.; Gonzalez-Casado, G.; Ibanez, D. Accuracy of ionospheric models used in GNSS and SBAS: Methodology and analysis. J. Geod. 2016, 90, 229–240. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, M. Real-time precise point positioning (RTPPP) with raw observations and its application in real-time regional ionospheric VTEC modeling. J. Geod. 2018, 92, 1267–1283. [Google Scholar] [CrossRef]
- Huo, X.; Long, Y.; Liu, H.; Yuan, Y.; Liu, Q.; Li, Y.; Liu, M.; Liu, Y.; Sun, W. A novel ionospheric TEC mapping function with azimuth parameters and its application to the Chinese region. J. Geod. 2024, 98, 13. [Google Scholar] [CrossRef]
- Ciraolo, L.; Azpilicueta, F.; Brunini, C.; Meza, A.; Radicella, S. Calibration errors on experimental slant total electron content (TEC) determined with GPS. J. Geod. 2007, 81, 111–120. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X. Multi-GNSS contributions to differential code biases determination and regional ionospheric modeling in China. Adv. Space Res. 2020, 65, 221–234. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Zhou, P.; Yang, Y.; Zhang, Q.; Gao, Y. Advantages of uncombined precise point positioning with fixed ambiguity resolution for slant total electron content (STEC) and differential code bias (DCB) estimation. Remote Sens. 2020, 12, 304. [Google Scholar] [CrossRef]
- Zhang, B.; Ou, J.; Yuan, Y.; Li, Z. Extraction of line-of-sight ionospheric observables from GPS data using precise point positioning. Sci. China Earth Sci. 2012, 55, 1919–1928. [Google Scholar] [CrossRef]
- Xiang, Y.; Gao, Y.; Shi, J.; Xu, C. Consistency and analysis of ionospheric observables obtained from three precise point positioning models. J. Geod. 2019, 93, 1161–1170. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X. Ionospheric total electron content estimation using GNSS carrier phase observations based on zero-difference integer ambiguity: Methodology and assessment. IEEE Trans. Geosci. Remote Sens. 2020, 59, 817–830. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Y.; Chen, J.; Liu, X.; Wang, H. Regional real-time between-satellite single-differenced ionospheric model establishing by multi-GNSS single-frequency observations: Performance evaluation and PPP augmentation. Remote Sens. 2024, 16, 1511. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. A novel GNSS single-frequency PPP approach to estimate the ionospheric TEC and satellite pseudorange observable-specific signal bias. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5801712. [Google Scholar] [CrossRef]
- Zhao, C.; Yuan, Y.; Zhang, B.; Li, M. Ionosphere sensing with a low-cost, single-frequency, multi-GNSS receiver. IEEE Trans. Geosci. Remote Sens. 2019, 57, 881–892. [Google Scholar] [CrossRef]
- Li, B.; Zang, N.; Ge, H.; Shen, Y. Single-frequency PPP models: Analytical and numerical comparison. J. Geod. 2019, 93, 2499–2514. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Wilgan, K.; Hadas, T.; Hordyniec, P.; Bosy, J. Real-time precise point positioning augmented with high-resolution numerical weather prediction model. GPS Solut. 2017, 21, 1341–1353. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Yu, C.; Wang, A.; Song, Z.; Zhou, J. Models and performance of SBAS and PPP of BDS. Satell. Navig. 2022, 3, 4. [Google Scholar] [CrossRef]
- Hernandez-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, L.; Li, B.; Balz, T. M_GIM: A MATLAB-based software for multi-system global and regional ionospheric modeling. GPS Solut. 2023, 27, 42. [Google Scholar] [CrossRef]
- Sanz, J.; Miguel, J.J.; Rovira-Garcia, A.; Gonzalez-Casado, G. GPS differential code biases determination: Methodology and analysis. GPS Solut. 2017, 21, 1549–1561. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Gong, X.; Chen, Q. The update of BDS-2 TGD and its impact on positioning. Adv. Space Res. 2020, 65, 2645–2661. [Google Scholar] [CrossRef]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Manuscr. Geod. 1993, 18, 91–98. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions; IERS Technical 2010 Note 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Boehm, J.; Moller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Y.; Chen, J.; Wang, H. Improving the (re-)convergence of multi-GNSS real-time precise point positioning through regional between-satellite single-differenced ionospheric augmentation. GPS Solut. 2022, 26, 39. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, H.; Li, B.; Li, J.; Xu, A.; Zhang, M. Analysis of characteristics for inter-system bias on multi-GNSS undifferenced and uncombined precise point positioning. Remote Sens. 2023, 15, 2252. [Google Scholar] [CrossRef]
- Feltens, J.; Angling, M.; Jackson-Booth, N.; Jakowski, N.; Hoque, M.; Hernández-Pajares, M.; Aragón-Àngel, A.; Orús, R.; Zandbergen, R. Comparative testing of four ionospheric models driven with GPS measurements. Radio Sci. 2011, 46, 6. [Google Scholar] [CrossRef]
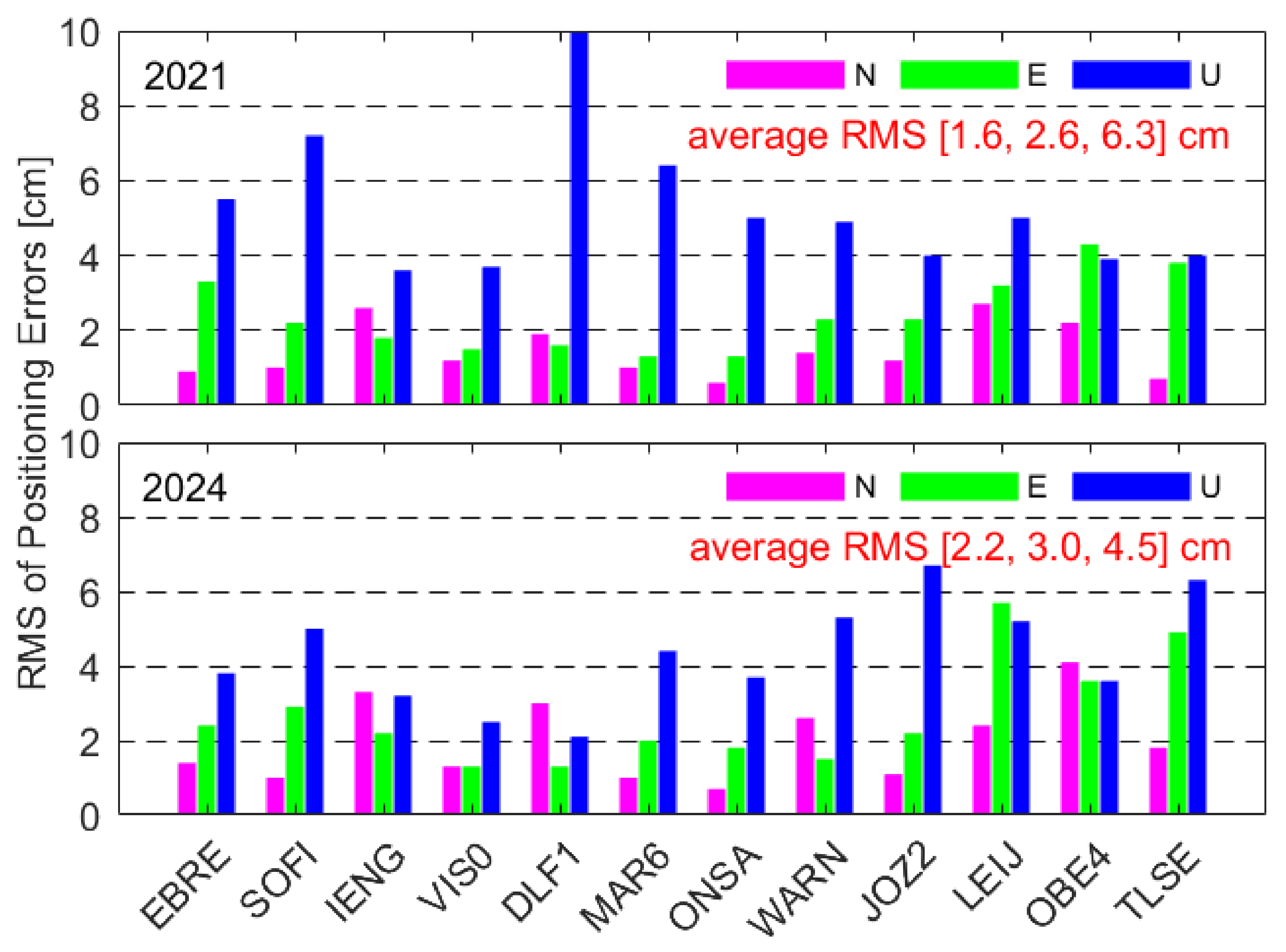
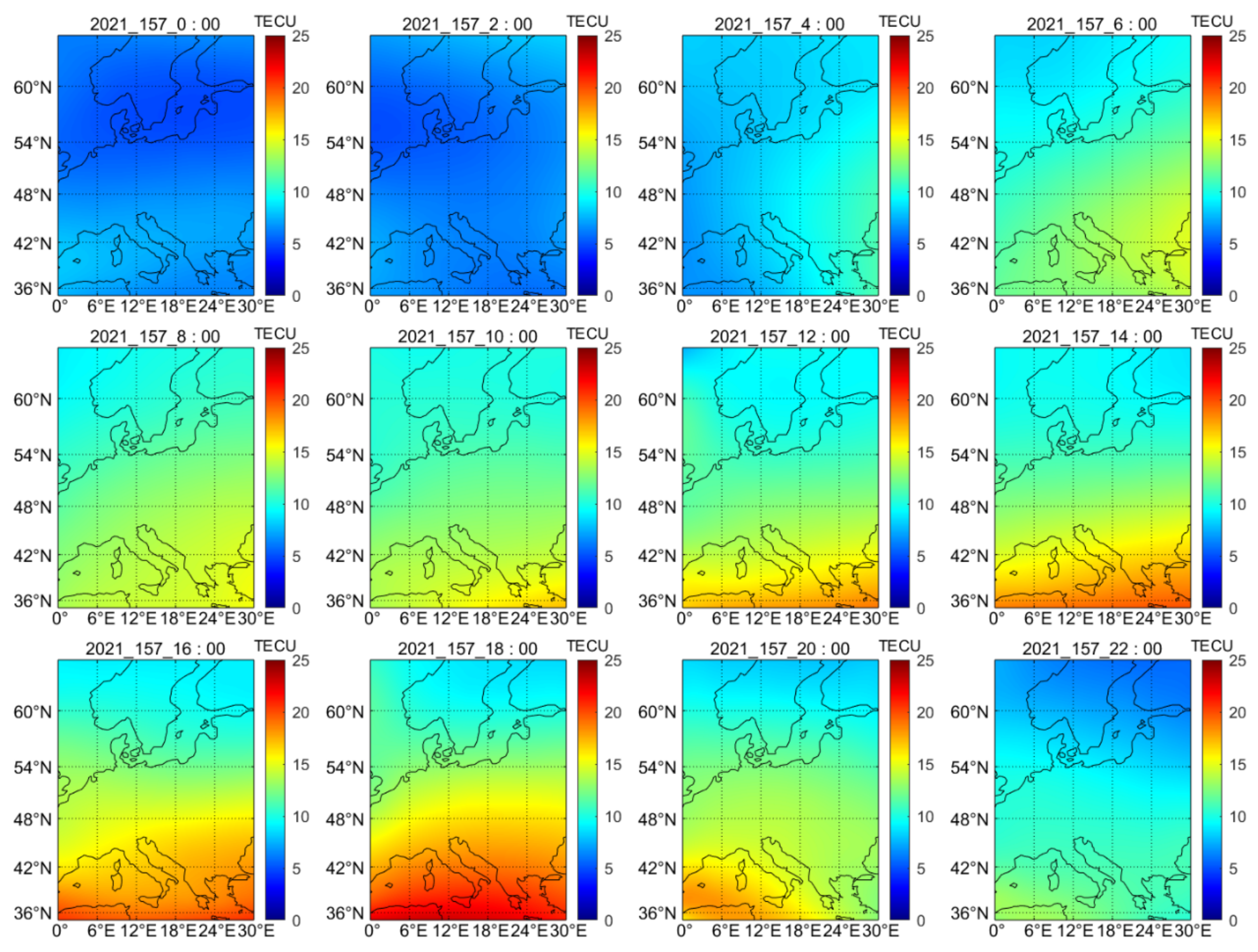
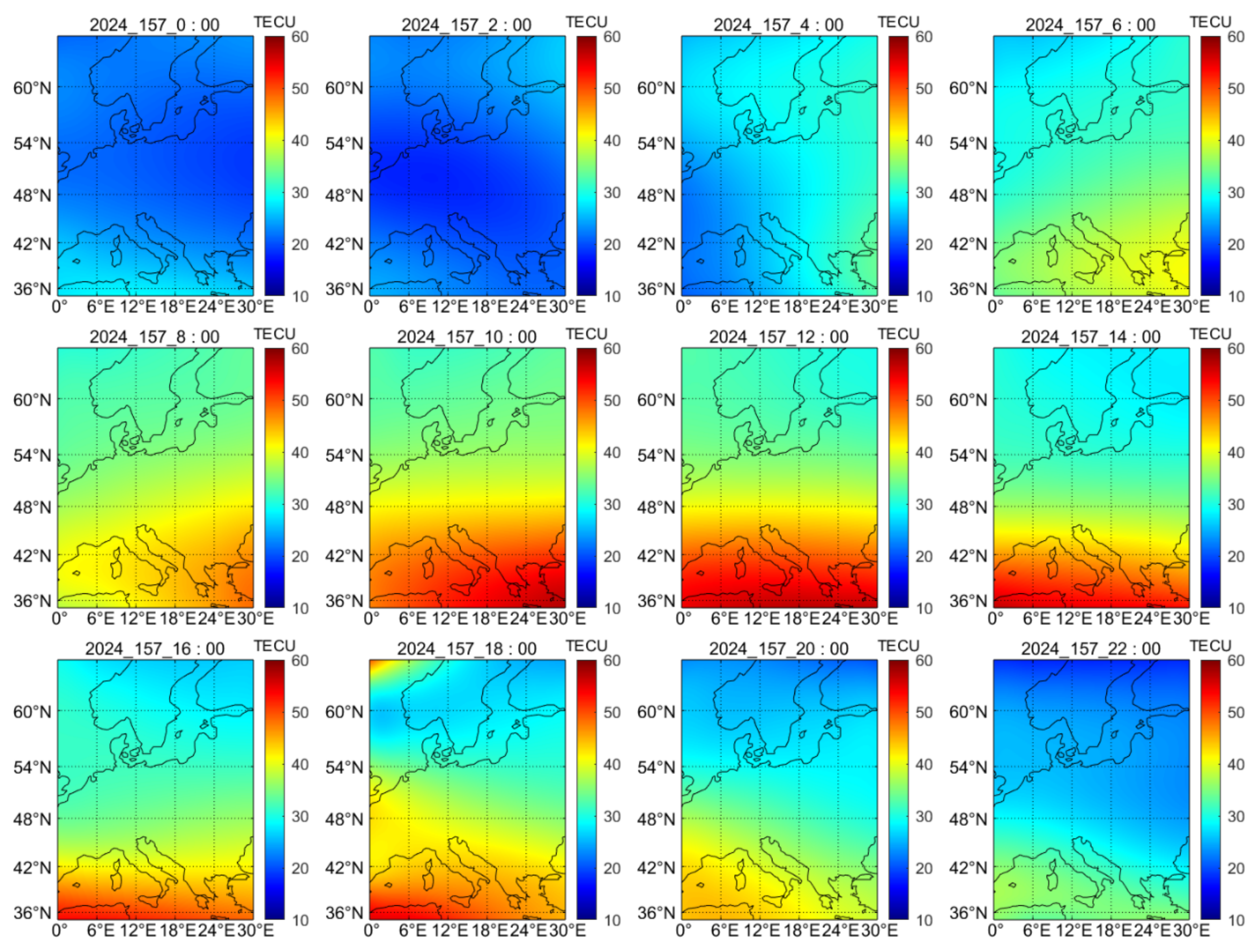
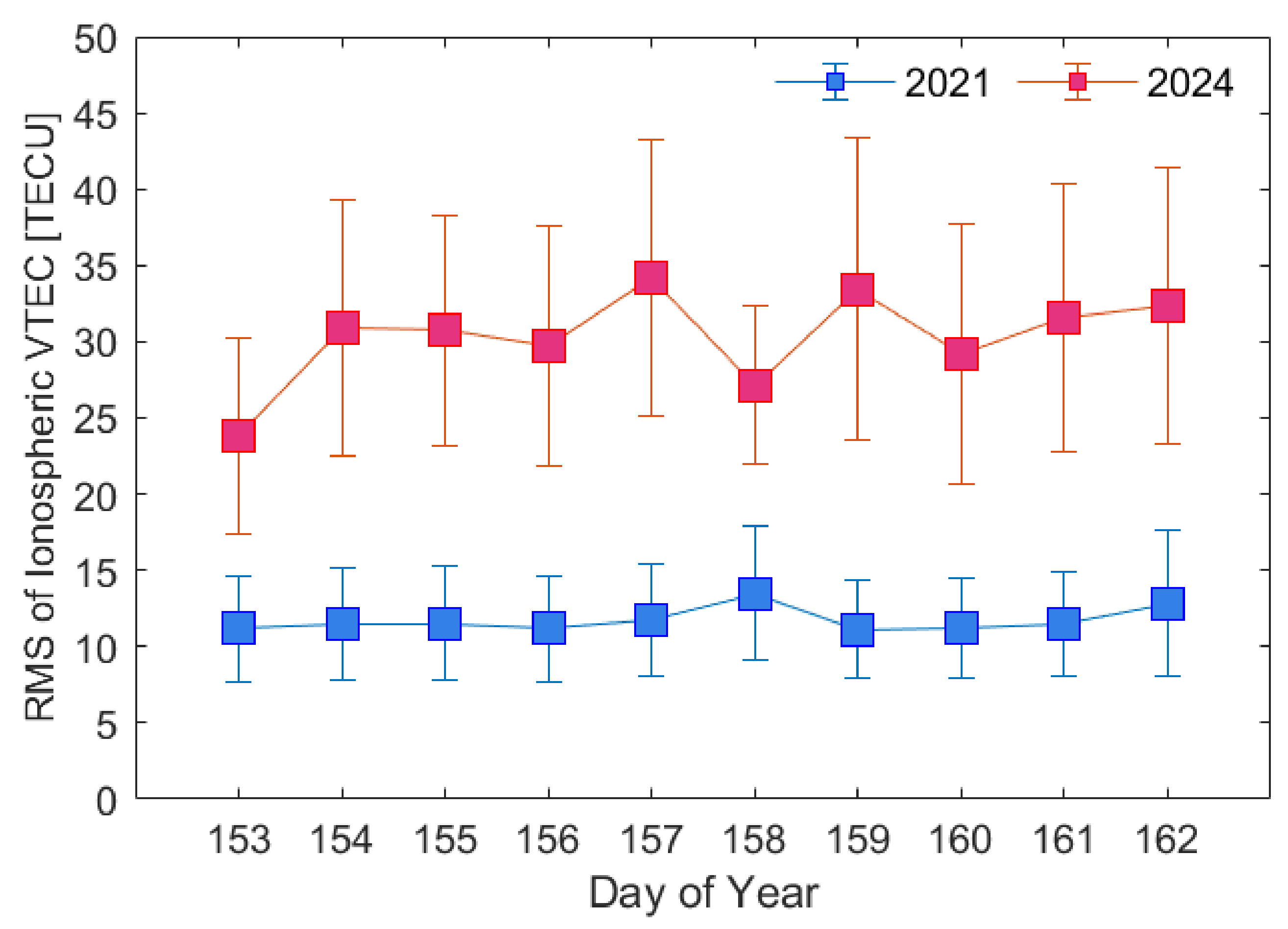





| Items | Strategies |
|---|---|
| I: IW SFPPP processing | |
| Estimator | Kalman filter |
| Satellite/receiver antenna center offsets and variations | Corrected with igs20_2317.atx products |
| Satellite DCB | Corrected with CAS daily BSX products |
| Tropospheric delay | Dry delay: corrected with GPT2w+SAAS+VMF models Wet delay: estimated as random-walk process [36] |
| Ionospheric delay | Estimated as random-walk process [37] |
| Receiver clock | Estimated as white noise |
| Galileo and BDS-3 ISB | Estimated as random-walk process [38] |
| Phase ambiguity | Estimated as float solution |
| II: Regional ionospheric VTEC modeling | |
| Estimator | Sequential least-squares adjustment |
| VTEC modeling algorithm | Polynomial function (6 orders × 4 degrees, 2 h interval) |
| Receiver DCB | Estimated as constant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.; Zhang, Y.; Chen, J.; Wang, H.; Liu, X.; Xu, Y.; Li, J.; Yan, Y. Exploring the Advantages of Multi-GNSS Ionosphere-Weighted Single-Frequency Precise Point Positioning in Regional Ionospheric VTEC Modeling. Remote Sens. 2025, 17, 1104. https://doi.org/10.3390/rs17061104
Wang A, Zhang Y, Chen J, Wang H, Liu X, Xu Y, Li J, Yan Y. Exploring the Advantages of Multi-GNSS Ionosphere-Weighted Single-Frequency Precise Point Positioning in Regional Ionospheric VTEC Modeling. Remote Sensing. 2025; 17(6):1104. https://doi.org/10.3390/rs17061104
Chicago/Turabian StyleWang, Ahao, Yize Zhang, Junping Chen, Hu Wang, Xuexi Liu, Yihang Xu, Jing Li, and Yuyan Yan. 2025. "Exploring the Advantages of Multi-GNSS Ionosphere-Weighted Single-Frequency Precise Point Positioning in Regional Ionospheric VTEC Modeling" Remote Sensing 17, no. 6: 1104. https://doi.org/10.3390/rs17061104
APA StyleWang, A., Zhang, Y., Chen, J., Wang, H., Liu, X., Xu, Y., Li, J., & Yan, Y. (2025). Exploring the Advantages of Multi-GNSS Ionosphere-Weighted Single-Frequency Precise Point Positioning in Regional Ionospheric VTEC Modeling. Remote Sensing, 17(6), 1104. https://doi.org/10.3390/rs17061104









