Efficient Aero-Optical Degraded Image Restoration via Adaptive Frequency Selection

Abstract

During high-speed flight, the aircraft causes rapid compression of the surrounding air, creating a complex turbulent flow field. This high-speed flow field interferes with the optical transmission of optical imaging systems, resulting in high-frequency random displacement, blurring, intensity attenuation, or saturation of the target scene. Aero-optical effects severely degrade imaging quality and target recognition capabilities. Based on the spectral characteristics of aero-optical degraded images and the deep learning approach, this paper proposes an adaptive frequency selection network (AFS-NET) for correction. To learn multi-scale and accurate features, we develop cascaded global and local attention mechanism modules to capture long-distance dependency and extensive contextual information. To deeply excavate the frequency component, an adaptive frequency separation and fusion strategy is proposed to guide the image restoration. Integrating both spatial and frequency domain processing and learning the residual representation between the observed data and the underlying ideal data, the proposed method assists in restoring aero-optical degraded images and significantly improves the quality and efficiency of image reconstruction.

1. Introduction

With the development of aviation technology, aircraft are continuously surpassing the previous altitude and speed limits. During high-speed flight, the optical window is subjected to notable aero-optical effects due to spatial variations in the airflow density field near the aircraft. The inhomogeneity in air density induces high-frequency, random fluctuations in the local refractive index, resulting in distortion or optical aberration as the target scene traverses the fluctuating medium [1,2,3]. Consequently, aero-optical effects can adversely affect high-speed imaging performance and, in extreme cases, cause a complete loss of imaging and detection system functionality.

In recent years, substantial progress has been made in the accurate quantification and mitigation of aero-optical effects, largely fueled by significant advances in numerical simulation and imaging technologies. As detailed in [4,5], the aero-optical effects can be effectively addressed through the application of three primary methods: (1) turbulent flow control; (2) Adaptive Optics-Electronic Correction; (3) Digital Image Restoration. Firstly, turbulent flow control systems often struggle to keep up with the rapid variations in the aerodynamic flow field, resulting in unstable or delayed control. Consequently, the system cannot obtain real-time clear images when the imaging becomes blurred or severely distorted. Secondly, the quality of detection and imaging during high-speed flight usually fail to reach the desired levels, owing to the complexity of control technology and the prohibitively high cost of adaptive optics (AO). Consequently, the quality of detection and imaging during high-speed flight usually fails to reach the desired levels, owing to the complexity of turbulent flow control technology and the prohibitively high cost of AO. However, digital image restoration is both component-free and economically feasible, providing an effective approach for correcting aero-optical degradation. These methods can generally be divided into two categories: optimization-based methods and learning-based methods. Some optimization methods restore the degraded image based on constraints of the Point Spread Function (PSF) through iterative refinement between the spatial and frequency domains, for example, blind iterative restoration [6], Wiener filtering [7], and the Richardson-Lucy algorithm [8]. However, these earlier deblurring algorithms are sensitive to noise and fluctuations in PSF, and noise amplification and ringing effects may occur during restoration. It is difficult to ensure the effective estimation of PSF in the high-speed dynamic imaging scenarios. So other optimization methods leverage image prior constraints, such as dark channel [9] and gradient distribution [10], to construct optimization models for restoring degraded aero-optical images. These methods avoid explicit estimation of the PSF but rely heavily on the hand-crafted features parameter selection (e.g., sparser lp gradient regularization weights). Extensive experiments demonstrated that these methods can effectively enhance the degraded image quality without significant noise amplification, but the sharp edge of the restored image cannot be maintained and the ringing effect is still a problem [11,12]. In addition, optimization-based methods are time-consuming in high-speed dynamic imaging.

In view of the powerful representation ability of deep learning and the availability of large image datasets, an increasing number of attempts have been made to address turbulence degradations with network models. In 2019, Su et al. [13] proposed a single-frame recovery algorithm based on a generative adversarial network (GAN) to deal with image deformation and blurring caused by aero-transmission effect and aero-heat radiation effect. In 2022, Gao et al. [14] adopted the mean filter to remove additive noise from the image, then employed a GAN based on MobileNet-v2 to restore blurred images with aero-optical effects. These GANs adopt conventional Convolutional Neural Networks to generate image details. However, Li [15] has indicated that using Convolutional Neural Networks to counteract turbulence degradation leads to over-smoothing and loss of detail. Besides, the lack of physical constraints makes reliable results difficult. Ref. [16] used the modified Transformer block as baseline and proposed that increasing the network depth to restore high-quality images provides a possible solution to the problem of aero-optical image restoration. All these approaches purely operate in the spatial domain, and fail to consider the variations in low-frequency and high-frequency caused by aero-optical effects. Actually, we observe that different aero-optical distortions may affect the image content in different frequency subbands, as illustrated in Figure 1. On the one hand, images in Figure 1a,b are dominated by low-frequency degradation, while on the other hand, more high-frequency discrepancies arise in Figure 1c,d. This indicates the need to treat each restored image on its specific characteristics.

In this paper, we introduce a deep-learning approach inspired by the Fourier Transform to mitigate the aero-optical effects on degradation images [17]. Drawing on the aero-optical imaging model and deep learning principle, we propose the AFS-NET for learning alterations in both spatial and frequency domains. Specifically, unlike the optimization algorithms those require prior information regarding the corruption present in the input images, a learnable mask block is generated in our model to separate the low-frequency and high-frequency components according to the residual spectral weight distribution. Then the most informative frequency information will be selectively extracted and emphasized in the subsequent fusion process. Besides, by analyzing the architectures of advanced methods and extracting their fundamental components, we establish a baseline with lower system complexity. An Efficient Channel Attention (ECA) module with negligible additional cost is also introduced to further enhance model performance [18]. These specifically designed modules make our method achieve state-of-the-art aero-optical degraded image restoration performance while maintaining computational efficiency. The main contributions include:

(1)

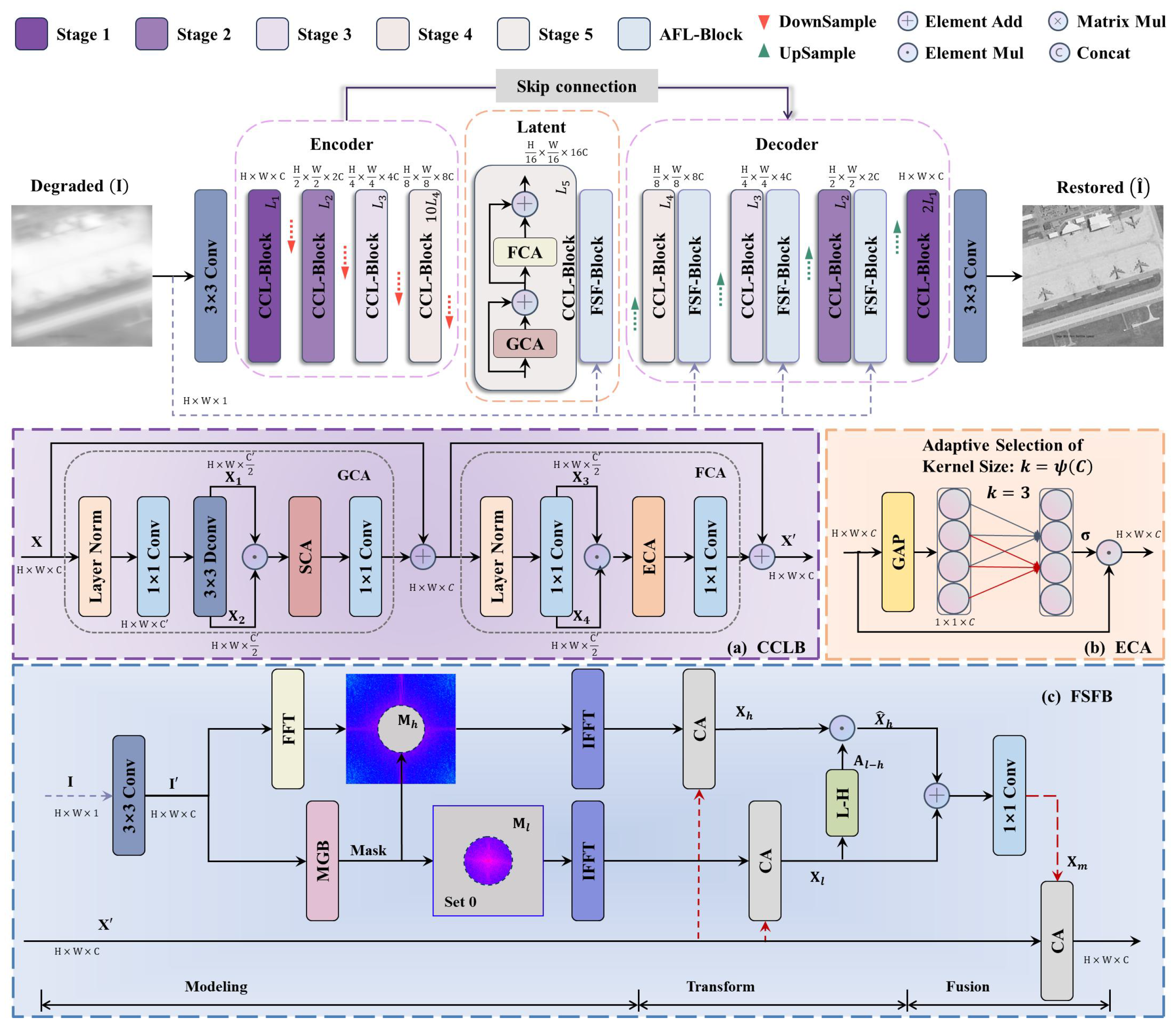
We propose the Composite Channel Learning Block (CCL-Block) as the baseline to minimize information loss during feature mapping in the network transfer process, which employs cascaded global and local attention mechanism modules to enhance the network’s focus on multi-scale features within the channels.

(2)

We design a Frequency Separation and Fusion Block (FSF-Block) by analyzing the residual spectral characteristics of degraded and clear images. This block adaptively adjusts the feature weights of degraded images across different frequency subbands, which enhances the high-frequency restoration performance in aero-optical degraded images.

(3)

Experiments show that the proposed method outperforms the comparison algorithms on the simulated dataset, while also shortening the network running time.

2. Materials and Methods

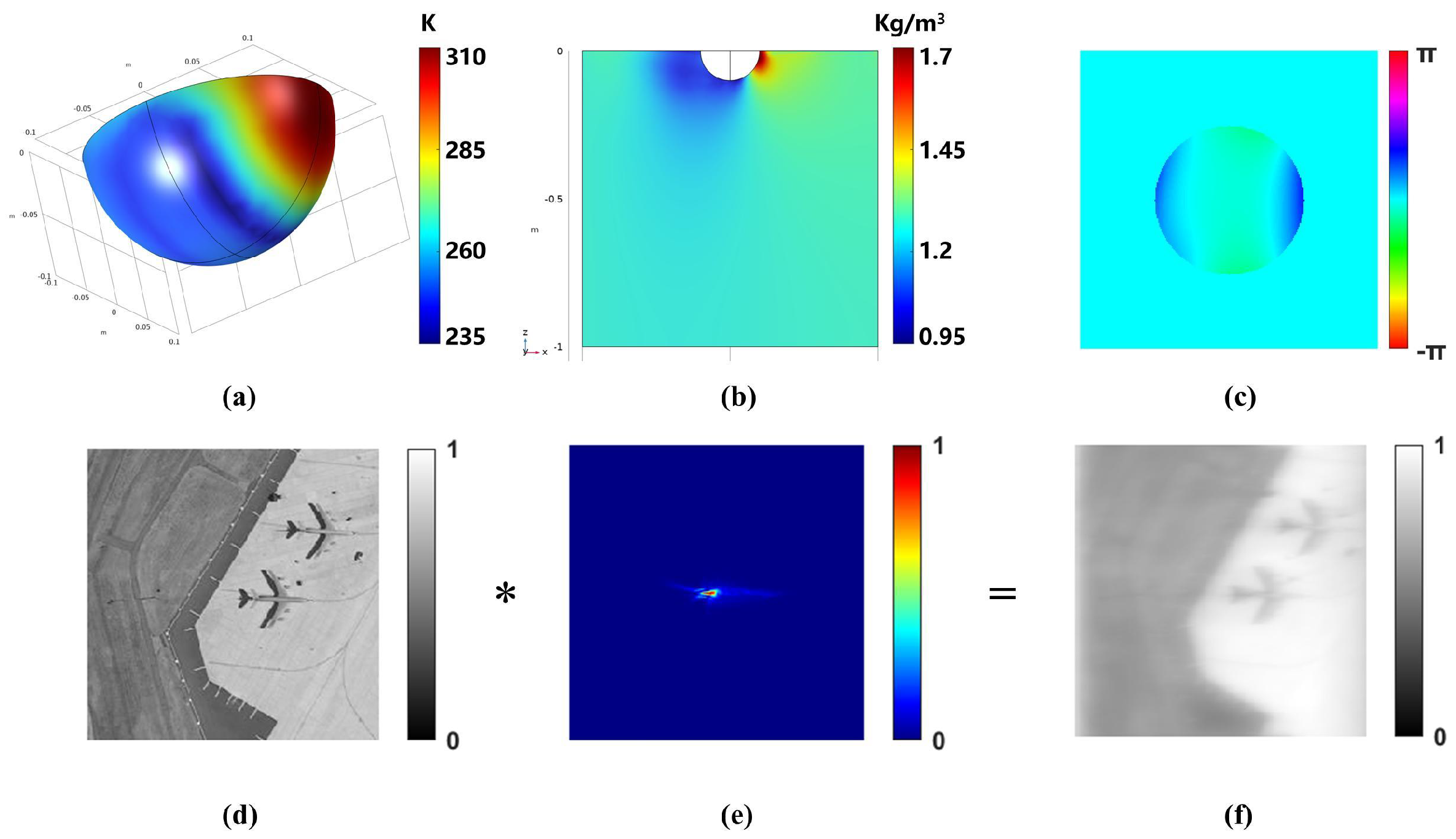
2.1. Degradation Model

In order to quantify aero-optical effects, one needs to use the ray-tracing method to evaluate the aerodynamic fluctuations around the aircraft inducing time-varying wavefront aberration in the exit pupil of the optical system. The computed Optical Path Length ($\mathit{OPL}$) directly reflects the air’s unsteady density field in the flow, as the air’s refractive index n is directly influenced by fluctuating density according to the Gladstone-Dale relationship [19],

$$OPL=\sum _i{n}_i{z}_i=\sum _i\left[1+K_{GD}\left(\lambda \right){\rho }_i)\right]z_i$$

(1)

where $n_i$, $z_i$, ${\rho }_i$ represent the indexes of refraction, the distance, and the density in the ith step on the ray respectively.

The Gladstone-Dale coefficient $K_{GD}\left(\lambda \right)$ is only dependent on the wavelength $\lambda$, and can be approximately acquired by:

$$K_{GD}\left(\lambda \right)=2.22\times {10}^{-4}\times \left(1+{\left(6.71\times {10}^{-8}/\lambda \right)}^2\right)$$

(2)

Indeed, the variation in OPL, referred to as the Optical Path Difference (OPD), is more significant for assessing the intensity of aero-optical effects. The OPD is given by [19]:

$$OP{D}_k=OP{L}_k-\overline{OPL}$$

(3)

where the overline represents the spatially averaged component, and corresponding aberrations are defined as $\phi =2\pi \times OPD/\lambda$. To investigate the impact of high-speed incoming flow on the performance of a hemispherical optical cover and its internal imaging optical window, COMSOL Multiphysics 6.2 is used to build the simulation model, as shown in Figure 2. The model includes a hemispherical optical cover mounted on the underside of the aircraft, with a 100 mm diameter imaging optical window installed inside. The external flow conditions are set to a subsonic flow at Mach 0.8 and 0 angle of attack. To minimize the influence of the computational boundaries on the flow field, the computational domain is designed as a 1 m × 1 m × 1 m rectangular region, consisting of 400,000 mesh elements. Then, the surface temperature distribution and density distribution on the optical window are obtained through simulation to calculate the wavefront distribution. The wavefront aberration is expressed as a series of orthogonal Zernike polynomials to facilitate the subsequent simulation of the imaging system [20,21,22]:

$$\phi (x,y)=\sum _{k=1}^{\infty }{a}_k·z_k(x,y)$$

(4)

where $a_k$ is the weighting coefficient corresponding to the Zernike polynomial $z_k$. Then, the point spread function (PSF) caused by the wavefront aberration is computed by:

$$PSF(x,y)={\left|\mathcal{F}\left\{P(x,y)exp\left[i\phi (x,y)\right]\right\}\right|}^2$$

(5)

where $\mathcal{F}\{*\}$ represents the Fourier transform, $P(x,y)$ represents the optical pupil function of the system. Thus, the degradation model can be mathematically formulated as:

$$g(x,y)=f(x,y)\ast PSF(x,y)+n(x,y)$$

(6)

where $g(x,y)$ is the degraded image, $f(x,y)$ is the sharp image, $n(x,y)$ is the additive noise. We aim to obtain a sharp image $f(x,y)$ from the degraded image $g(x,y)$.

2.2. Restoration Model

Here, we will propose our AFS-NET to restore the aero-optical degraded image, which is illustrated in Figure 3. AFS-NET consists of two key sub-blocks: Composite Channel Learning Block (CCL-Block) and Frequency Separation and Fusion Block (FSF-Block): (1) A basic CCL-Block consists of two residual modules, each integrated with Global channel attention ($GCA$) and Focal channel attention ($FCA$), respectively. The local residual learning allows the less important information such as low-frequency to be bypassed through multiple local residual connections, let the learning process focus on more efficient feature propagation. Furthermore, the propagated features are refined through channel attention mechanisms, enhancing the CCL-Block’s ability to capture essential details. (2) A novel FSF-Block integrates context modeling, feature transformation, and feature fusion. Context modeling is first applied to separately extract the high- and low-frequency information from the image. Feature transformation then processes these frequency components independently, reducing noise interference while preserving fine details. Feature fusion is finally employed to gradually reconstruct the image by integrating the refined features. By treating different frequency components and feature representations unequally, FSF-Block provides additional flexibility in dealing with complex types of aero-optical degraded images, expanding the representational ability of CNNs.

Figure 2. (a) Simulated aerodynamic flow field model. (b) Density field distribution near the optical window. (c) Aero-optical degraded wavefront. (d) Original image. (e) Aero-optical degraded PSF. (f) Degraded image. * denotes convolution operation.

Figure 2. (a) Simulated aerodynamic flow field model. (b) Density field distribution near the optical window. (c) Aero-optical degraded wavefront. (d) Original image. (e) Aero-optical degraded PSF. (f) Degraded image. * denotes convolution operation.

Main Backbone. AFS-NET employs a simple U-Net architecture as the backbone. We design the CCL-Block as our building block. As shown in Figure 3, we input more building blocks to lower encoder stage-4 for efficiency, i.e., from encoder to decoder, the number of CCL-Blocks is respectively set as [1, 1, 1, 10] and [1, 1, 1, 2]. The latent level contains one CCL-Block. A single CCL-Block incurring a small computational overhead of 0.030 M parameters and 1.69 G MACs (we evaluate Params and MACs with the stage 1 input tensor). Then, we insert FSF-Block after CCL-Block to progressively reconstruct high-resolution clean output from latent stage-5 to decoder stage-2, i.e., the architecture of AFS-NET uses a single FSF-Block in latent and the number of FSF-Blocks in each sub-decoder is [1, 1, 1, 0]. A single FSF-Block introduces a modest computational overhead, with 0.234M parameters and 14.72 G MACs (we evaluate with a stage-2 input tensor). Depending on the task complexity, we adjust the default network width by setting the number of channels C to 64 for deblurring.

2.2.1. CCL-Block Introduction

Recently, the channel attention mechanism has exhibited substantial potential for improving the performance of deep learning networks [23,24]. Motivated by this, we propose the CCL-Block that incorporates two residual modules which are combined with $GCA$ and $FCA$, respectively. $GCA$ is responsible for processing the Global channel information. $FCA$, on the other hand, focuses on modeling local inter-channel dependencies. When the intermediate feature X is input, the whole process is formulated as:

$$\begin{array}{c}X=GCA\left(X\right)+X\\ X=FCA\left(X\right)+X\end{array}$$

(7)

Global channel attention ($GCA$) unit: This unit is introduced by NAFNET [13], and its details are shown in Figure 3a. Overall, given the input $X\in {\mathbb{R}}^{H\times W\times C}$, $GCA$ is computed as:

$$\begin{array}{c}X=f_{3\times 3}^{dwc}\left(f_{1\times 1}^c\left(LN\left(X\right)\right)\right),[X_1,X_2]=X\\ GCA\left(X\right)=f_{1\times 1}^c\left(SCA(X_1\odot X_2)\right)\end{array}$$

(8)

where $f_{3\times 3}^{dwc}(·)$ is the learnable parameters of the depth-wise convolution, $f_{1\times 1}^c(·)$ represent linear projection, and $LN(·)$ is the layer-norm layer. Both $X_1$ and $X_2$ are in $X\in {\mathbb{R}}^{H\times W\times {\displaystyle \frac{C^{\prime }}{2}}}$ space, where $C^{\prime }$ denotes the hidden dimension in $GCA$. ⊙ denotes the element-wise multiplication. $SCA$ denotes the simplified channel attention, which is introduced into $GCA$ to capture global information. It extracts the global features of each channel through global average pooling and then uses a $1\times 1$ convolution to directly transform the channel features, thus, suppressing less useful features and only allowing more informative ones to pass further. However, it does not capture dependencies between channels. Formally, $SCA$ is defined as:

$$SCA\left(X\right)=X·f_{1\times 1}^{\mathrm{c}}\left(GAP\left(X\right)\right)$$

(9)

where $GAP$ denotes the adaptive average pooling operation, which extracts a scale factor of each channel, and · represents the channel-wise product operation.

Focal cross-channel attention (FCA) unit: Previous studies [25,26] usually introduce single-scale depth-wise convolutions into the regular feed-forward network (FFN) to improve locality. However, the redundant information in channels hinders feature expression competence (an ablation study is provided in the experiments section). The motivation for this part is to build a more efficient and effective FFN mechanism. Here, a novel $FCA$ module is proposed. As illustrated by Figure 3a, the $FCA$ first performs a convolution operation, followed by element-wise multiplication. Second, the channel-wise attention vector is obtained by using the Efficient Channel Attention ($ECA$) module to extract the attention of the feature map at different scales. Finally, another convolution operation is applied to refine the features. The overall process of $FCA$ is summarized as:

$$\begin{array}{c}X=f_{1\times 1}^{\mathrm{c}}\left(LN\left(X\right)\right),[X_3,X_4]=X\\ FCA\left(X\right)=f_{1\times 1}^{\mathrm{c}}\left(ECA(X_3\odot X_4)\right)\end{array}$$

(10)

Note that $ECA$ guarantees both efficiency by appropriately capturing focal cross-channel interactions. The calculation is presented as follows:

$$ECA\left(X\right)=X·\sigma \left(f_{1\times 1}^k\left(GAP\left(X\right)\right)\right)$$

(11)

where $\sigma (·)$ denotes the sigmoid function. $f_{1\times 1}^k(·)$ indicates 1-D convolution, which only involves k parameters. The kernel size k represents the extent of local cross-channel interaction, i.e., how many neighbors participate in attention prediction of one channel. The calculation for parameter k is as follows:

$$\begin{gathered} \begin{array}{c}t=\mathrm{int}\left(\mathrm{abs}\left(log(C,2)+b\right)/\mathrm{gamma}\right)\end{array} \\ k=t\mathrm{if}t\%2=0\mathrm{else}t+1 \end{gathered}$$

(12)

where C is channel inputs, gamma and b are empirically set to 2 and 1 as in [15], respectively. Finally, our $FCA$ can capture more precise channel information and mitigate the redundancy of channel features in the FFN layers. Moreover, the proposed AFS-NET inherits the advantages of the CCL-block, and thus it has strong multi-scale representation capabilities and can adaptively recalibrate the cross-dimension channel-wise weight.

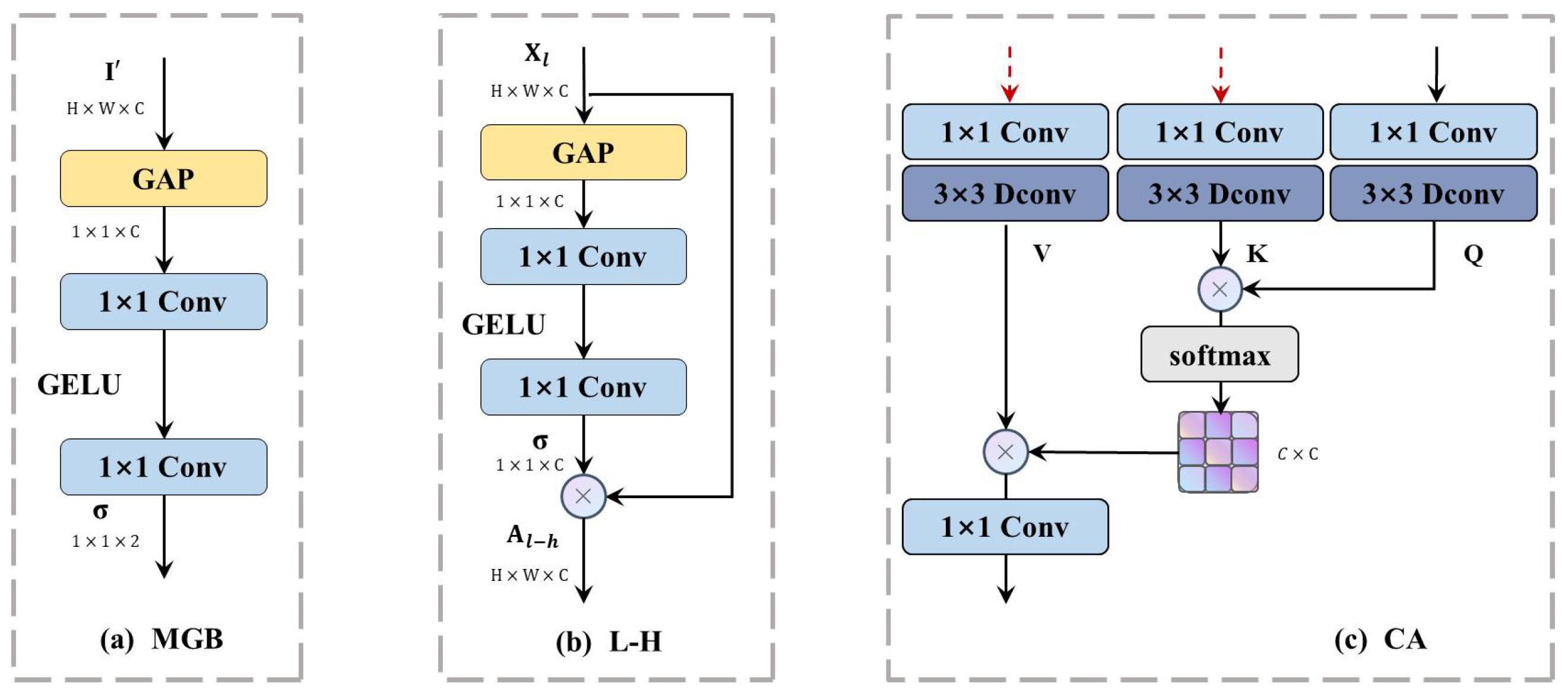
2.2.2. FSF-Block Introduction

Since complex aero-optical degradations affect image content across diverse frequency subbands (as shown in Figure 1), we specifically design the FSF-Block to extract both low- and high-frequency components from the input features and then modulate them to emphasize the corresponding subbands for each aero-optical degraded image. As shown in Figure 3c, given as input both the degraded image $I\in {\mathbb{R}}^{H\times W\times 1}$ and the CCL-Block output features $X^{\prime }\in {\mathbb{R}}^{H\times W\times C}$, FSF-Block adaptively segregates the degradation content from the input image content in the frequency domain, and subsequently assists in refining the intermediate features $X^{\prime }\in {\mathbb{R}}^{H\times W\times C}$ in the spatial domain for effective image restoration. FSF-Block mainly refers to frequency process that is realized in three parts: Context modeling, feature transform, and feature fusion.

Context modeling: For the adaptive extraction of different frequency bands from the adjusted degraded image $I\in {\mathbb{R}}^{H\times W\times 1}$, a Mask Generation Block (MGB) is used to generate a mask M that serves as the boundary for frequency separation. This boundary is adjusted according to the frequency distribution of each degraded image I. Notably, a convolutional layer is applied to the degraded input image $3\times 3$ in the FSF-Block, aiming to align with the feature channel dimensions $I\in {\mathbb{R}}^{H\times W\times 1}$ of each stage of CCL-Block. As shown in Figure 4a, the input feature map $I^{\prime }\in {\mathbb{R}}^{H\times W\times C}$ is processed by a $GAP$, two $1\times 1$ convolution layers, and a GELU activation function, thus the factors ranging from 0 to 1 are produced to define the width and height of the mask. The process is formally expressed as follows:

$$[\alpha ,\beta ]=\sigma \left(f_{1\times 1}^{\mathrm{c}}\left(\mathrm{GELU}\left(f_{1\times 1}^{\mathrm{c}}\left(GAP\left(X\right)\right)\right)\right)\right)$$

(13)

where the reduction ratio of $f_{1\times 1}^{\mathrm{c}}(·)$ are $r_1$ and ${\displaystyle \frac{C}{2r_1}}$, respectively, progressively down-sampling the channel dimensions to 2. Subsequently, the binary mask $M_l\in {\{0,1\}}^{H\times W}$ is generated by checking whether the normalized distance is less than or equal to 1:

$$M_l(x,y)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}D(x,y)\le 1\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(14)

where the distance from each pixel to the center $D(H,W)=\sqrt{{\left({\displaystyle \frac{H-H_{\mathrm{center}}}{k_h}}\right)}^2-{\left({\displaystyle \frac{W-W_{\mathrm{center}}}{k_w}}\right)}^2}$, the coordinates of the center point $[H_{\mathrm{center}},W_{\mathrm{center}}]=\left[{\displaystyle \frac{H}{2}},{\displaystyle \frac{W}{2}}\right]$, $[k_h,k_w]=\left[\alpha {\displaystyle \frac{H}{n}},\beta {\displaystyle \frac{W}{n}}\right]$, where n is set to a small value of 128, as the curve junction in Figure 1 is relatively minor. Accordingly, the mask for high-frequency $M_h$ can be obtained by $M_h=1-M_l$. Next, we can obtain the adaptively decoupled features by applying the learned masks to the spectra via element-wise multiplication and using the inverse Fourier transform.

Feature transform: To capture the inter-channel dependencies, we pass the descriptor and through the multi-deconv head transposed cross attention, resulting in new attention features (as displayed in Figure 4c). The feature transform process is defined as:

$$X_{*}=\mathrm{SOFTMAX}\left(Q{K}^T/\gamma \right)V$$

(15)

where we generate query, key, and value tensors (denoted as Q, K, and V, respectively), $Q=f_{3\times 3}^{\mathrm{c}}\left(f_{1\times 1}^{\mathrm{c}}\left(\mathrm{IFFT}\left(\mathrm{FFT}\left(M_{*}\right)\right)\right)\right)$, $K=f_{3\times 3}^{\mathrm{c}}\left(f_{1\times 1}^{\mathrm{c}}\left(X\right)\right)$, $V=f_{3\times 3}^{\mathrm{c}}\left(f_{1\times 1}^{\mathrm{c}}\left(X\right)\right)$. $[\ast ]\in \{l,h\}$ is a set for low/high frequency, $\gamma$ is a learnable scale factor. Aero-optical blur essentially attenuates or even eliminates high-frequency information (such as edges and sharp transitions). To address this, we leverage low-frequency information $X_l\in {\mathbb{R}}^{H\times W\times C}$ to enrich high-frequency $X_h$, which lets AFS-NET pay more attention to effective information such as high-frequency textures and details via an ultra-lightweight unit (L-H).

$${\widehat{X}}_h=X_h\odot A_{l\to h}$$

(16)

where $A_{l\to h}=\sigma \left(f_{1\times 1}^{\mathrm{c}}\left(\mathrm{GELU}\left(f_{1\times 1}^{\mathrm{c}}\left(GAP\left(X\right)\right)\right)\right)\right)$, $A_{l\to h}\in {\mathbb{R}}^{H\times W\times C}$.

Feature fusion: low-frequency features $X_l$ and reconstructed high-frequency features $X_h$ are combined and processed via a $1\times 1$ convolution. Cross attention is then used to aggregate contextual features $X_m$ to each position of the intermediate features X, following the process defined in Equation (15), where Q is produced from X, while K and V are generated from $X_m$.

The proposed FSF-Block boasts several advantages. Primarily, it effectively analyzes degradation information present in the degraded input images, thereby enhancing feature representation during subsequent up-sampling in the encoder and promoting more stable model training. Moreover, the FSF-Block adaptively modulates both low- and high-frequency contents of the input features, ensuring the fusion of the most useful information, and thereby enhancing aggregation features for more efficient high-quality image reconstruction.

3. Results

In this section, we describe the details of image datasets, loss function and network implementation. Then, we provide a comprehensive evaluation of the results produced by our AFS-NET and compare it with the state-of-the-art methods.

3.1. Image Datasets

The simulation is implemented on an aero-imaging system with a 1-m aperture imaging window mounted on an aircraft. The aircraft flies at a speed of 0.8 Mach at an altitude of 10 km. The simulated data acquired over 5 s is then added to the clear images in the MAR20 [27] dataset, which is one of the largest remote sensing image datasets for aircraft recognition, resulting in degraded images. Each image pair consists of a clear image and its corresponding degraded image. The first 3420 image pairs are used for training and the last 380 pairs for testing.

For scene generalization testing, we extensively evaluate the network on multiple individual scenes from the NWPU-RESISC45 [28] dataset and the AID [29] dataset. The sample images from these two datasets exhibit high scene diversity and stylistic. Considering typical terrestrial features found in human-inhabited environments, we construct ten scene image test sets with aero-optical degradation. Specifically, four scene image test sets are constructed from the NWPU dataset, including harbors, storage facilities, runways, and overpasses. Each data set contains 700 image pairs. Additionally, six scene test sets are constructed from the AID dataset. Following the settings in [29], the numbers of test image pairs for Playground, School, Square, Center, Church, and Stadium are 370, 300, 330, 260, 240, and 290, respectively.

For robustness testing under different scenarios and noise conditions, we assess the network on the single-scene MAR20 test set and the multi-scene NWPU test set. The MAR20 test set contains 380 image pairs, while the NWPU test set consists of 2800 image pairs across four scene categories. Different levels of Gaussian noise are then added to both datasets with aero-optical degradation.

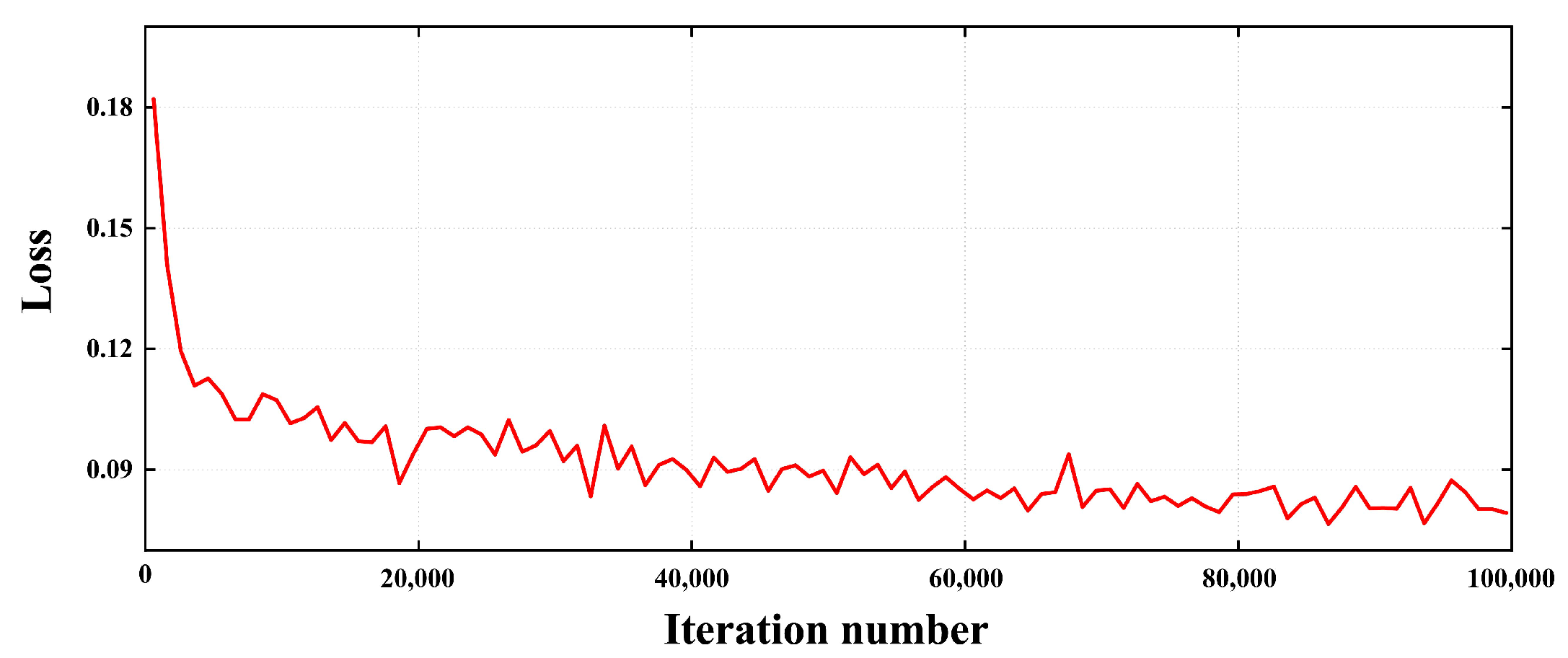
3.2. Loss Function

In order to train AFS-NET, three kinds of loss functions are adopted:

1. Frequency Reconstruction loss [30]. As shown in Figure 1, the degraded image experiences severe blurring due to the impact of aero-optical effects, with a significant loss of detail information. Since the purpose of mitigating these effects is mainly to restore the lost high-frequency components, it is crucial to minimize the difference between the restored image and the sharp image in the frequency domain. To this end, we employ Frequency Reconstruction loss ${\ell }_{\mathrm{fft}}$ as follows:

$${\ell }_{\mathrm{fft}}={∥\mathcal{F}\left({\tilde{S}}_k\right)-\mathcal{F}\left(S_k\right)∥}_1$$

(17)

where $\mathcal{F}$ represents the FFT operation.

2. Charbonnier loss [24]. Similar to other deblurring networks, we adopt the Charbonnier loss ${\ell }_{\mathrm{char}}$ [24,31], where we found that ${\ell }_{\mathrm{char}}$ produces better results than L1 loss for our network. The ${\ell }_{\mathrm{char}}$ is formulated as follows:

$${\ell }_{\mathrm{char}}=\sqrt{{∥{\tilde{S}}_k-S_k∥}^2+{ϵ}^2}$$

(18)

3. Edge loss [24]. Recent studies suggest the auxiliary loss terms in addition to the Charbonnier loss for the performance improvement [31,32]. Consequently, we present the additional Edge loss ${\ell }_{\mathrm{edge}}$ to constrain the high-frequency components between the sharp image and the restored image, defined as:

$${\ell }_{\mathrm{edge}}=\sqrt{{∥\mathrm{\Delta }\left({\tilde{S}}_k\right)-\mathrm{\Delta }\left(S_k\right)∥}^2+{ϵ}^2}$$

(19)

where $\mathrm{\Delta }$ denotes the Laplacian operator. Overall, the total loss function for AFS-NET is: ${\ell }_{\mathrm{total}}={\ell }_{\mathrm{fft}}+{\ell }_{\mathrm{char}}+\lambda {\ell }_{\mathrm{edge}}$, where $\lambda$ is the tradeoff-parameter set to 0.1. This loss function ensures that the network emphasizes detailed features from both frequency and spatial domains, thereby restoring a sharper image.

3.3. Implementation Details

The proposed architecture is end-to-end trainable and requires no pre-training of any sub-modules. The training parameters, consistent across all experiments, are as follows. Our framework is implemented on two NVIDIA GeForce RTX 3090 GPUs. AFS-NET is trained with Adam optimizer for 100,000 iterations, with an initial learning rate of $1\times {10}^{-3}$, which is steadily reduced to $1\times {10}^{-6}$ using a cosine annealing strategy. The batch size is set to 8 and, for data augmentation, we perform horizontal and vertical flips, along with rotation. All images are resized to $256\times 256$ to ensure consistency and compatibility with the network architecture. Figure 5 illustrates the loss curve over 100,000 iterations. The loss drops sharply at the start and stabilizes around 0.09, indicating effective convergence of the model.

3.3.1. The Test of Image Restoration

To evaluate the feasibility of our proposed method for clear imaging in aero-optical turbulent flow, we conduct a comparative analysis with representative iteration-based methods, such as IBD [7], and several recent deep learning-based image restoration algorithms. This comparison includes turbulence removal algorithms like CGAN [12] and DETURNET [14], as well as low-level vision methods such as the Spatial Domain Operations-based NAFNET [15] and Improved Restormer [33], and the Frequency Domain Operations-based DEEPRFT [31] and LoFormer [34]. As presented in

Table 1. Average restoration results of different methods on 380 test images (best are highlighted in Bold and second-best are Underlined). MACs and inference times are computed on an input tensor shape of (1, 256, 256).

	PSNR	SSIM	MACs (G)	Times (s)
Degraded	13.66	0.5317	-	-
IBD	13.68	0.5448	-	15.05
CGAN	22.82	0.6951	78.30	0.077
DeturNET	25.14	0.8348	88.70	0.033
Improved Restormer	25.88	0.8033	64.46	0.097
DEEPRFT	26.22	0.8488	63.46	0.089
LoFormer-B	26.32	0.8375	73.04	0.132
NAFNET-64	26.62	0.8423	63.21	0.044
Ours	27.42	0.8504	50.16	0.026

, the traditional IBD algorithm performs negligibly due to severe blur from aero-optical degradation. In contrast, our approach achieves the best performance on the same dataset, with a PSNR of 27.42 dB and an SSIM of 0.8504. Specifically, our method outperforms the second-ranked NAFNET by 0.80 dB in PSNR on aero-optical degraded images while incurring 13.05 G lower MACs, demonstrating the high efficiency of our frequency separation and fusion unit. Additionally, AFS-NET processes each image in just 0.026 s, which significantly outperforms other methods in inference speed and makes it superior for real-time applications.

The visual comparisons on the aero-optical degraded images dataset are illustrated in Figure 6. The IBD and CGAN methods consistently exhibit significant residual aero-optical blur and substantial detail loss, thereby failing to delineate a coherent target outline. DeturNET, Improved Restormer and DEEPRFT lack fine details, showing slight blurring and artifacts around the target. While LoFormer and NAFNET perform well in aero-optical restoration, but do not effectively present sharp edges in the results. In contrast, AFS-NET significantly reduces aero-optical residuals and the corrected images exhibit sharper edges, higher image contrast, and clearer targets. These results demonstrate that our method is more effective in reconstructing high-quality aero-optical restoration images than other competitors.

3.3.2. Scene Generalization Testing of AFS-NET

To extensively evaluate the generalization performance of our network, we train AFS-NET on the single-scene MAR20 training set and assess it on ten scene image testing sets from the NWPU and AID datasets. Each class represents a unique environment with varying structural features, object density, and texture complexity, which challenge the ability of the model to accurately restore scene content. Initially, we analyzed the four scene image datasets constructed by NWPU. As shown in Figure 7, in the enlarged details of storage and runway scenes, key elements such as storage tanks and runway markings are successfully reconstructed, and the restored images of complex scenes like overpasses and harbors retain the approximate shapes of their features, which demonstrates that our proposed method can restore the target image well in unknown scenarios. Furthermore, we also present the restoration results for six scene image datasets constructed by AID. As depicted in Figure 8, while some minor detail loss is observed in scenes like School, Square, Church, and Stadium, the overall contours of each scene image are well restored. These observations highlight the strong generalization capability of our network across diverse scenes.

From a quantitative analysis perspective, our method significantly improves both PSNR and SSIM values across all tested scenes as shown in

Table 2. Comparison of the ten scene data sets.

		Scene Test		Restoration
	Sets	PSNR	SSIM	PSNR	SSIM
NWPU	Storage	13.90	0.3526	24.81	0.8096
	Runway	12.22	0.5710	24.52	0.8549
	Overpass	10.27	0.3305	23.56	0.7938
	Harbor	11.51	0.3615	23.51	0.8106
AID	Playground	12.74	0.4767	25.70	0.8272
	School	12.10	0.2650	24.47	0.7997
	Square	12.72	0.3280	24.10	0.7986
	Center	15.08	0.3724	24.07	0.7866
	Church	12.00	0.2608	23.68	0.7618
	Stadium	14.77	0.3933	23.53	0.8050

. In the four scene testing sets from the NWPU dataset, significant gains are observed in image quality assessment metrics. In the harbor scene, PSNR increased by 12 dB and SSIM by 0.4491. The storage scene saw a PSNR increase of 10.91 dB and an SSIM improvement of 0.4570. The runway scene experienced a PSNR improvement of 12.30 dB and an SSIM increase of 0.2839. For the overpass scene, PSNR rose by 13.29 dB and SSIM enhanced by 0.4633. For the AID dataset, the results across the six scene test sets also show notable improvements. As shown in Table 2, the Playground, School, Square, Center, Church, and Stadium sets achieved PSNR improvements of 12.96 dB, 12.37 dB, 11.38 dB, 8.99 dB, 11.68 dB, and 8.76 dB, respectively. Meanwhile, SSIM increased by 0.3505, 0.5347, 0.4706, 0.4142, 0.5010, and 0.4117, respectively. These substantial improvements highlight that our method consistently elevates image quality, and the overall reconstruction effectiveness remains robust across different scene datasets. These substantial improvements demonstrate that our method consistently elevates image quality, and the overall reconstruction effectiveness remains robust.

3.3.3. The Robustness of AFS-NET on Different Noises

To further assess the effectiveness of aero-optical restoration, we evaluated the single-scene degraded MAR20 test set and the multi-scene degraded NWPU test set by adding Gaussian noise with a mean of 0 and variances of 0.01, 0.03, 0.05, 0.08, and 0.10. The restoration results on the MAR20 test set, shown in Figure 9, indicate that higher Gaussian noise variances progressively reduce image clarity. The aircraft details remain distinguishable at lower noise levels (variances 0.01, 0.03, and 0.05), which preserves key features essential for accurate recognition. However, at higher noise variances (0.08 and 0.10), some targets in the image become smoothly blurred, which results in a slight loss of fine details while maintaining the overall image structure. The results on the multi-scene NWPU test set, shown in Figure 10, further demonstrate the robustness of our network. At lower noise levels (0.01, 0.03, and 0.05), the lines within the scene images are restored, preserving the overall structural clarity. As the noise variance increases, particularly at higher levels (0.08 and 0.10), the key target contours are still retained. Overall, AFS-NET maintains high restoration quality even under different scenarios and noise conditions, which demonstrates its potential applicability in real-world environments.

Table 3. Comparison of the MAR20 and NWPU datasets under the same experimental settings for noise robustness testing.

		Noise Test		Restoration
		PSNR	SSIM	PSNR	SSIM
MAR20	Var = 0.01	13.65	0.4804	24.13	0.7200
	Var = 0.03	13.61	0.4144	24.04	0.7003
	Var = 0.05	13.58	0.3707	23.83	0.6880
	Var = 0.08	13.53	0.3254	23.54	0.6746
	Var = 0.10	13.50	0.3027	23.37	0.6665
		PSNR	SSIM	PSNR	SSIM
NWPU	Var = 0.01	11.96	0.3650	20.97	0.6604
	Var = 0.03	11.93	0.3135	20.64	0.6388
	Var = 0.05	11.90	0.2790	20.40	0.6243
	Var = 0.08	11.85	0.2428	20.14	0.6078
	Var = 0.10	11.82	0.2248	20.02	0.5988

reports denoising results on different datasets with five distinct noise variances. As the noise variance increases, PSNR and SSIM values for restorations gradually decrease. Nevertheless, our method consistently maintains favorable performance across all noise levels.

3.3.4. Ablation Studies

We conduct ablation experiments on the MAR20 dataset with aero-optical degradation to verify the effectiveness of each module in AFS-NET. All ablation experiments follow the experimental setup of the previous section. First, we investigate different choices for the FSF-Block. As shown in

Table 4. Different configurations of FSF-Block components in AFS-NET. The ✔ symbol indicates that the corresponding component is included in the FSF-Block configuration.

Net	L-H	Rect Mask	Ellip Mask	PSNR	SSIM
a	✔	✔		27.19	0.8493
b			✔	27.31	0.8487
c	✔		✔	27.42	0.8504

, the rectangular mask achieves only 27.19 dB PSNR, which is 0.23 dB lower than our proposed elliptical mask. To further illustrate this improvement, we analyze the residual frequency spectra of the restored images under different masks, as depicted in Figure 11. In contrast to the rectangular mask, the elliptical mask yields a more naturally distributed frequency restoration and reduces directional bias near segmentation boundaries, thus minimizing prominent residual components. Furthermore, the L-H unit brings a gain of 0.11 dB PSNR over using only the elliptical mask, resulting in the highest performance as presented in Table 4. Second, we quantitatively evaluate AFS-NET without ECA and/or FSF-Block in

Table 5. Ablation studies on the impact of ECA and / or FSF-Block in AFS-NET. The ✔ symbol indicates that the corresponding component is included in the network configuration.

Net	ECA	FSF-Block	PSNR	SSIM	Parms (M)	FLOPs (G)
a			26.85	0.8495	34.50	35.69
b	✔		26.99	0.8556	34.50	35.74
c		✔	27.25	0.8466	53.80	50.11
d	✔	✔	27.42	0.8504	53.80	50.16

. FSF-Block significantly boosts PSNR by 0.74 dB, using only the FSF-Block in AFS-NET leads to SSIM performance drop. ECA improves the results by 0.08 dB, without introducing more parameters or runtime in inference. Finally, we experimentally verify the effectiveness of our total loss function. The results are shown in

Table 6. Design choices for loss functions in AFS-NET.

Loss Method	PSNR	SSIM
${\ell }_{\mathrm{char}}$	26.42	0.8308
${\ell }_{\mathrm{char}}+0.1{\ell }_{\mathrm{fft}}$	27.24	0.8493
${\ell }_{\mathrm{char}}+{\ell }_{\mathrm{fft}}$	27.32	0.8494
${\ell }_{\mathrm{char}}+{\ell }_{\mathrm{fft}}+0.1{\ell }_{\mathrm{edge}}$	27.42	0.8504

. We can see that combining the frequency loss function and perceptual loss function with a weight ratio of $1:1$ achieves a PSNR of 27.32 dB and an SSIM of 0.8494. When an additional edge loss function with a weight of 0.1 is included, the PSNR improves to 27.42 dB, and the SSIM increases to 0.8504, which is higher than other versions. These results demonstrate the effectiveness of our design.

4. Discussion

The proposed Adaptive Frequency Selection Network (AFS-NET) introduces an innovative approach for restoring aero-optical degraded images by integrating spatial and frequency domain processing. Through extensive experimentation, we have demonstrated that AFS-NET effectively mitigates aero-optical degradation, outperforming both traditional optimization-based methods and contemporary deep learning-based solutions.

As the basic building block of AFS-Net, the CCL-Block incorporates global and focal channel attention mechanisms to significantly enhance feature extraction efficiency. This design enables the network to capture multi-scale contextual information, ultimately improving the clarity and sharpness of the restored images.

Moreover, a key strength of AFS-NET lies in its ability to adaptively separate and fuse frequency components. Unlike conventional spatial-domain methods that primarily focus on pixel-wise restoration, our approach explicitly model the frequency characteristics of degraded images. By leveraging the FSF-Block, our method selectively enhances high-frequency details while preserving the overall structural integrity, ensuring superior reconstruction quality.

The generalization capability of AFS-NET is another notable advantage. Our evaluation across multiple simulated datasets of aero-optical degraded images, confirms that AFS-NET performs robustly across a wide range of typical terrestrial features commonly found in human-inhabited environments. The ability to maintain high PSNR and SSIM scores across various scenarios highlights the model’s adaptability to diverse and unseen environments. Additionally, AFS-NET exhibits strong resilience to noise on both single-scene and multi-scene datasets. Under varying levels of Gaussian noise, the model consistently achieves effective reconstruction with notable improvements, demonstrating its robustness in noisy scene.

Despite its promising results, there are still potential areas for improvement. First, while our method achieves high-quality performance, the computational cost of frequency-domain processing remains a consideration for real-time applications. Future work could explore lighter-weight architectures or hardware-accelerated implementations to further reduce inference time. Second, our approach primarily addresses blur and intensity distortions, but additional adversarial learning strategies could be integrated to enhance fine-grained texture restoration, particularly in extreme turbulence conditions.

5. Conclusions

Aero-optical effects are a major cause of the degradation of the image quality of aircraft with optical imaging systems under high-speed flight. In this paper, we have introduced the Efficient aero-optical degraded image restoration via adaptive frequency selection method (AFS-NET). This method reflects that the negative impact of aero-optical effects on the propagation of target information in turbulence can be mitigated through learning from highly productive digit imaging processing approach. The main CCL-Block utilizes channel attention mechanisms to focus on preserving precise spatial details, and the supplementary FSF-Block integrates spectral information to enhance the context feature representation. The Frequency loss, Charbonnier loss and Edge loss have been combined to enhance the performance of the network. The simulation results show that the AFS-NET has the ability to restore complex textures and achieve more competitive restoration results compared with other state-of-the-art networks, which provides a new direction for mitigating the impact of aero-optical effects. Additionally, the accomplishments of this study in high-quality and efficient reconstruction lay a foundation for subsequent wind tunnel experimental research.