Detection and Spatiotemporal Distribution Analysis of Vertically Developing Convective Clouds over the Tibetan Plateau and East Asia Using GEO-KOMPSAT-2A Observations
Abstract
:1. Introduction
2. Study Area and Datasets
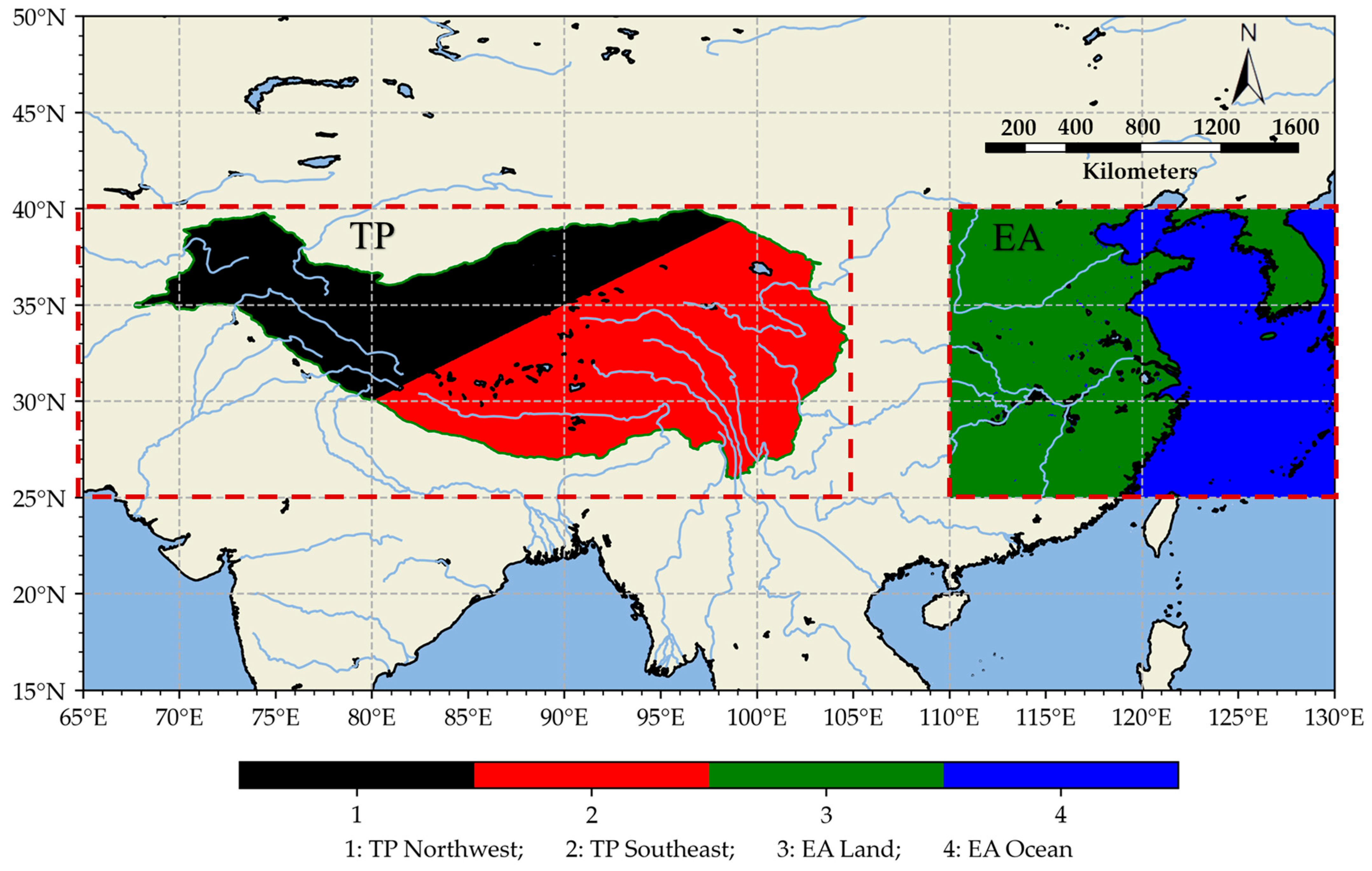
2.1. Study Area
2.2. GEO-KOMPSAT-2A Data
2.3. CALIPSO Level 2 Lidar Vertical Feature Mask
2.4. Precipitation Data from Global Precipitation Measurement
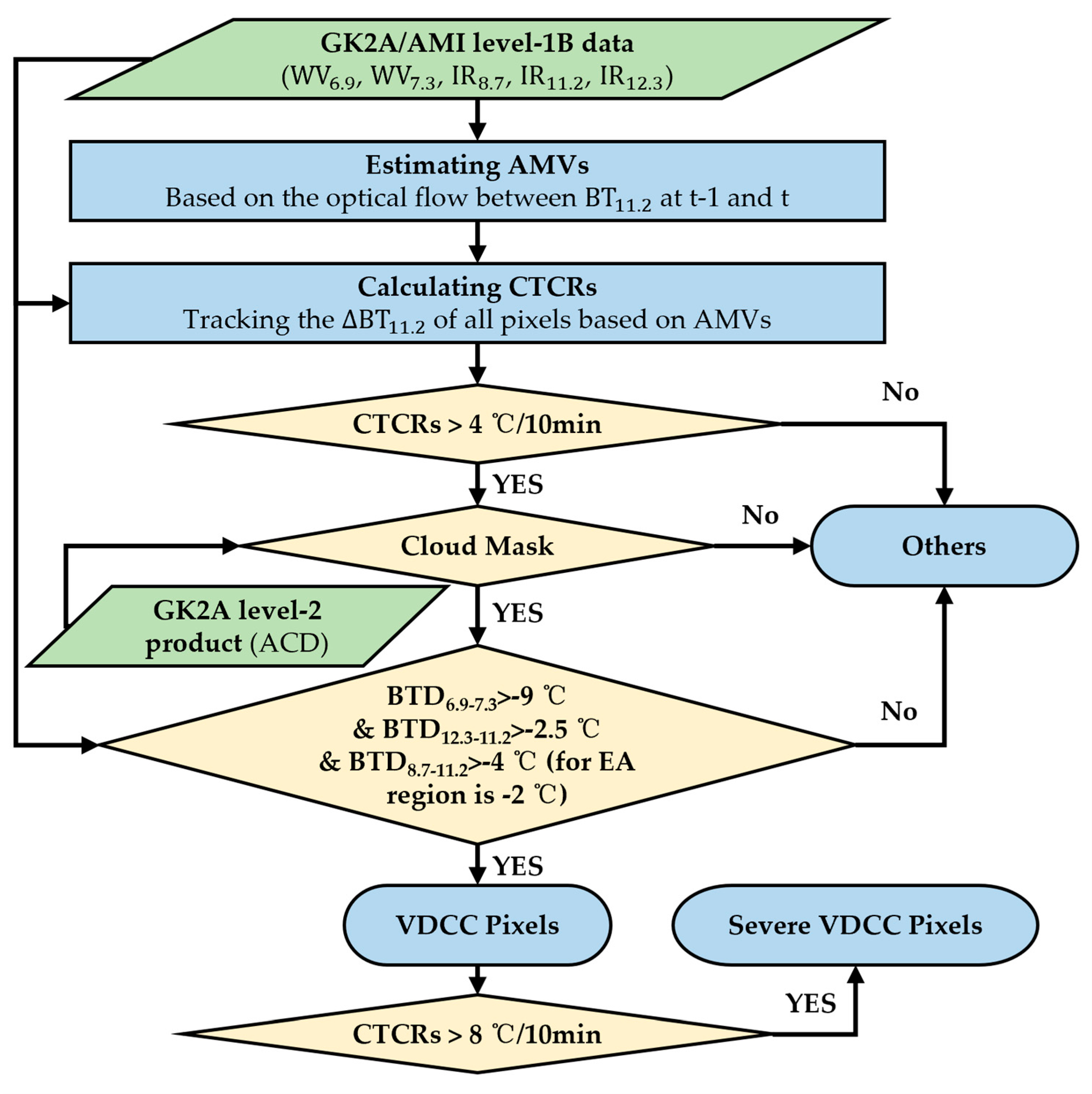
3. Detection of VDCCs
- Tracking all pixels using dense optical flow and calculating the corresponding unfiltered CTCRs.
- Filtering out non-cloud pixels using cloud masks from the ACD product, followed by excluding non-convective cloud pixels through region-specific refined BT and BTD thresholds. These thresholds were determined by matching VFM data with AMI infrared observations, tailored to the TP and EA regions.
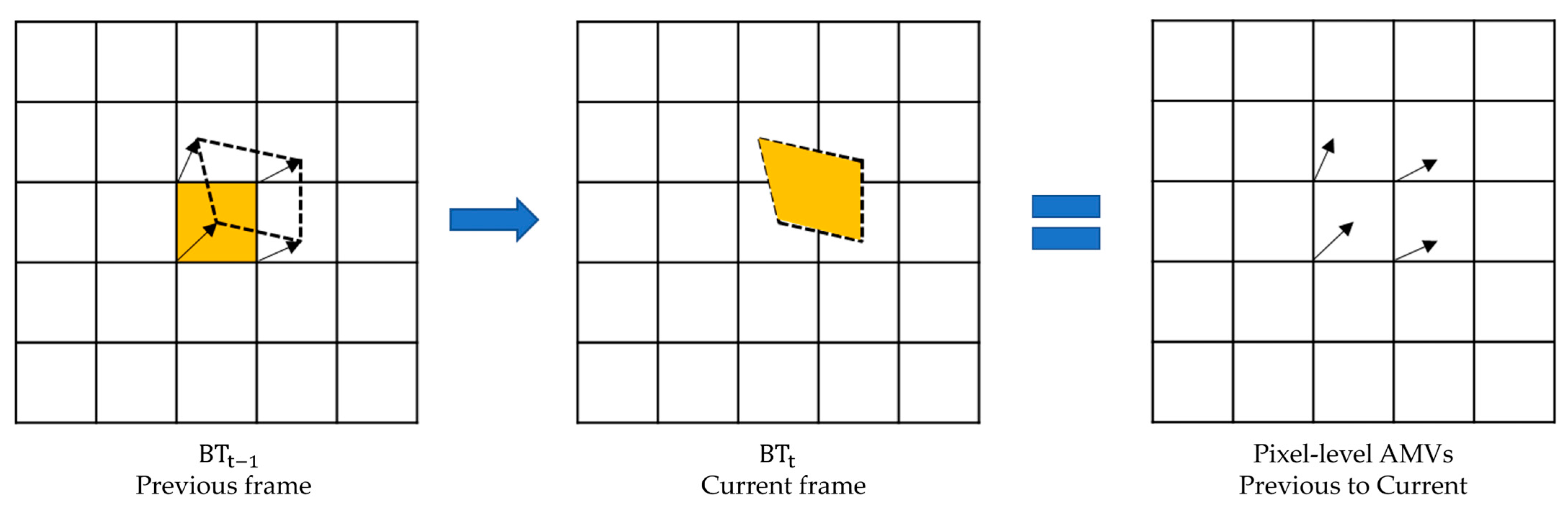
3.1. Pixel-Level Tracking Based on Dense Optical Flow
- Processing: Normalize the from AMI at the current time (t) and the previous time (t − 1) (10 min interval) to a range of 0~255, and use these as the input brightness images.
- Estimating AMVs: Estimate the pixel-level AMVs from time t − 1 to time t using dense optical flow.
- Tracking pixels: Use the AMVs as the displacement vectors of pixels to calculate the location of all pixels at time t − 1 based on their positions at time t.
- Calculating unfiltered CTCRs: Calculate the cooling rate of all pixels at time t based on tracking, and apply mean filtering to reduce the effect of noise and outliers.
3.2. Eliminating Non-Convective Cloud Pixels
- BTD6.9−7.3 (BTD between 6.9 and 7.3 μm channels) is derived from adjacent water vapor channels [63,64]. The 6.9 μm channel is strongly absorbed by moisture and primarily responds to upper-layer water vapor. Due to lower water-vapor absorption, the 7.3 μm channel can partially penetrate through upper-level moisture and respond to lower layers. Therefore, the 7.3 μm channel is typically warmer than the 6.9 μm channel, leading to a negative BTD6.9−7.3 [63]. For rapidly growing convective clouds, upward moisture transport increases upper-level humidity and optical thickness. This simultaneously enhances the absorption of two channels, resulting in a smaller absolute value of their difference and larger BTD6.9-7.3 values [60].
- BTD12.3−11.2 (BTD between 12.3 and 11.2 μm channels) is derived from adjacent atmospheric window channels. In clear-sky conditions, this BTD typically shows negative values (below −2 °C) due to the weak water vapor absorption in the 12.3 μm channel (dirty window), and the negative signature becomes more pronounced (below −4 °C) for semi-transparent clouds [63,65]. But for convective clouds, the absolute BTD value progressively approaches 0 K as the cloud-top height increases, the optical thickness grows, and the overlying water vapor decreases [63,66]. Moreover, this BTD can be positive for overshooting and extremely intensive convective clouds that penetrate the tropopause [63]. These numerical variations enable effective discrimination between convective and semi-transparent clouds.
- BTD8.7−11.2 (BTD between 8.7 and 11.2 μm channels) is related to the phase state of the cloud-top particles [60]. While water and ice exhibit comparable imaginary refractive indices at 8.7 μm, significant divergence occurs at 11.2 μm [60]. This spectral contrast enhances ice cloud absorption relative to water clouds of equivalent water content at 11.2 μm, resulting in negative BTD8.7−11.2 values for water cloud tops [67]. In contrast, for rapidly growing convective clouds, the glaciation process at the cloud tops will lead to larger BTD8.7−11.2 values [3].
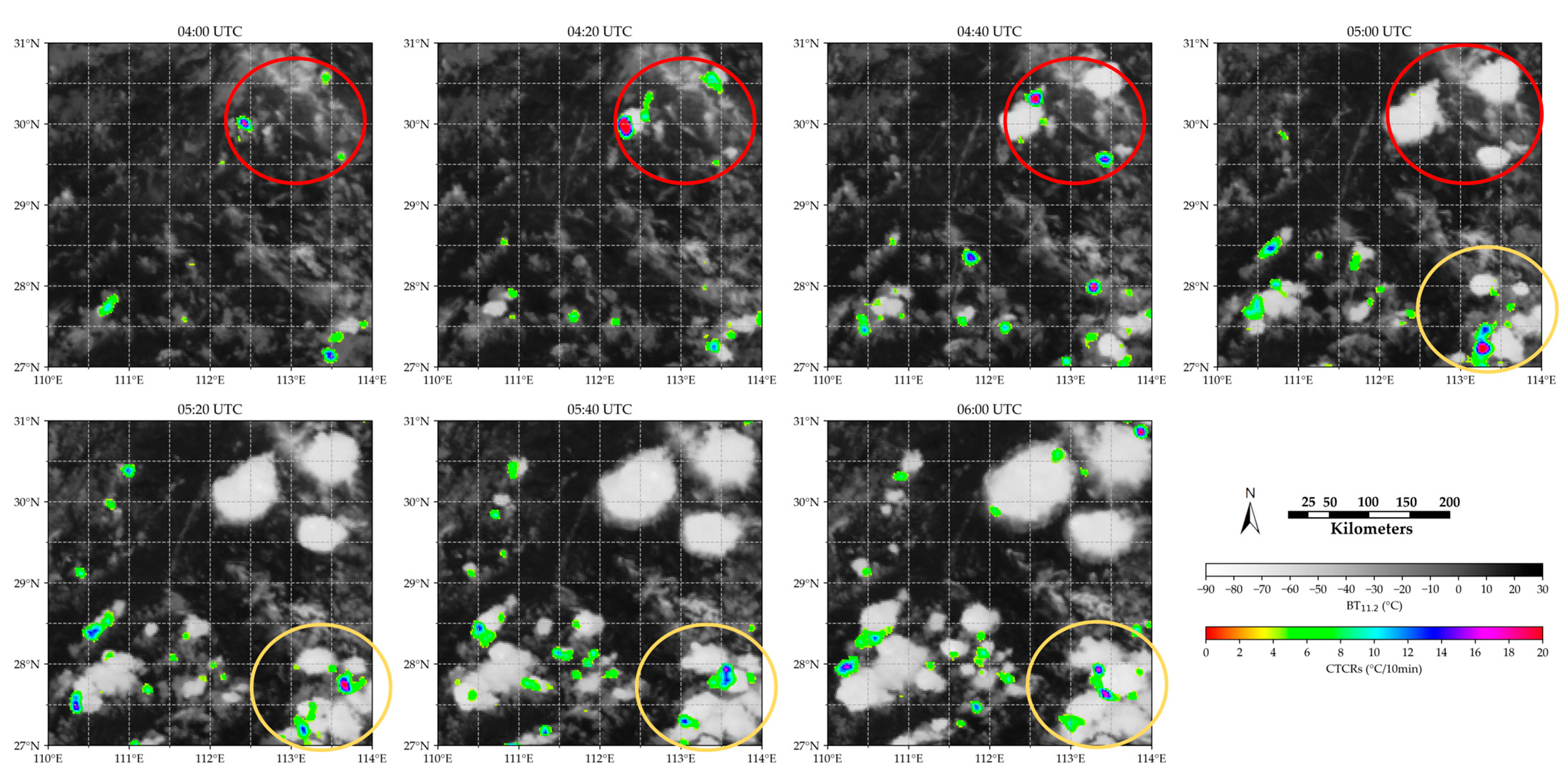
3.3. Detection Results of VDCCs
4. Statistical Analysis of VDCCs
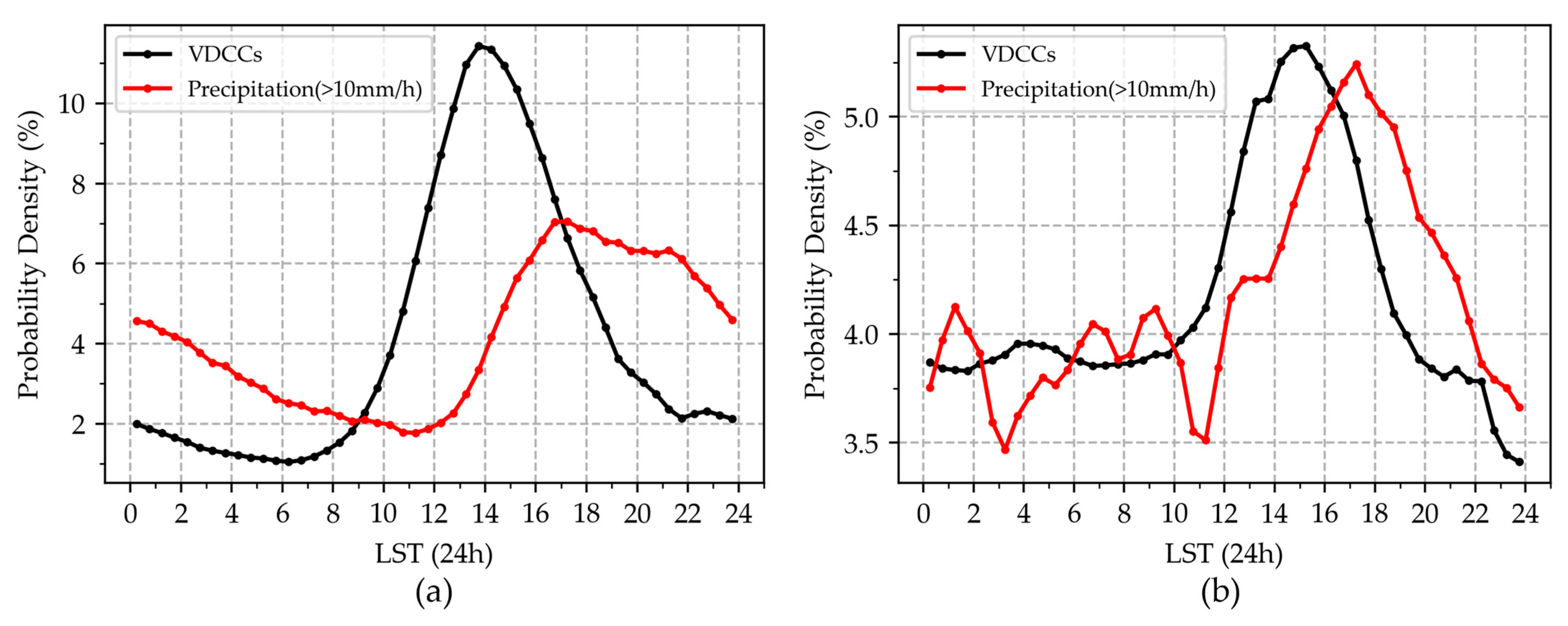
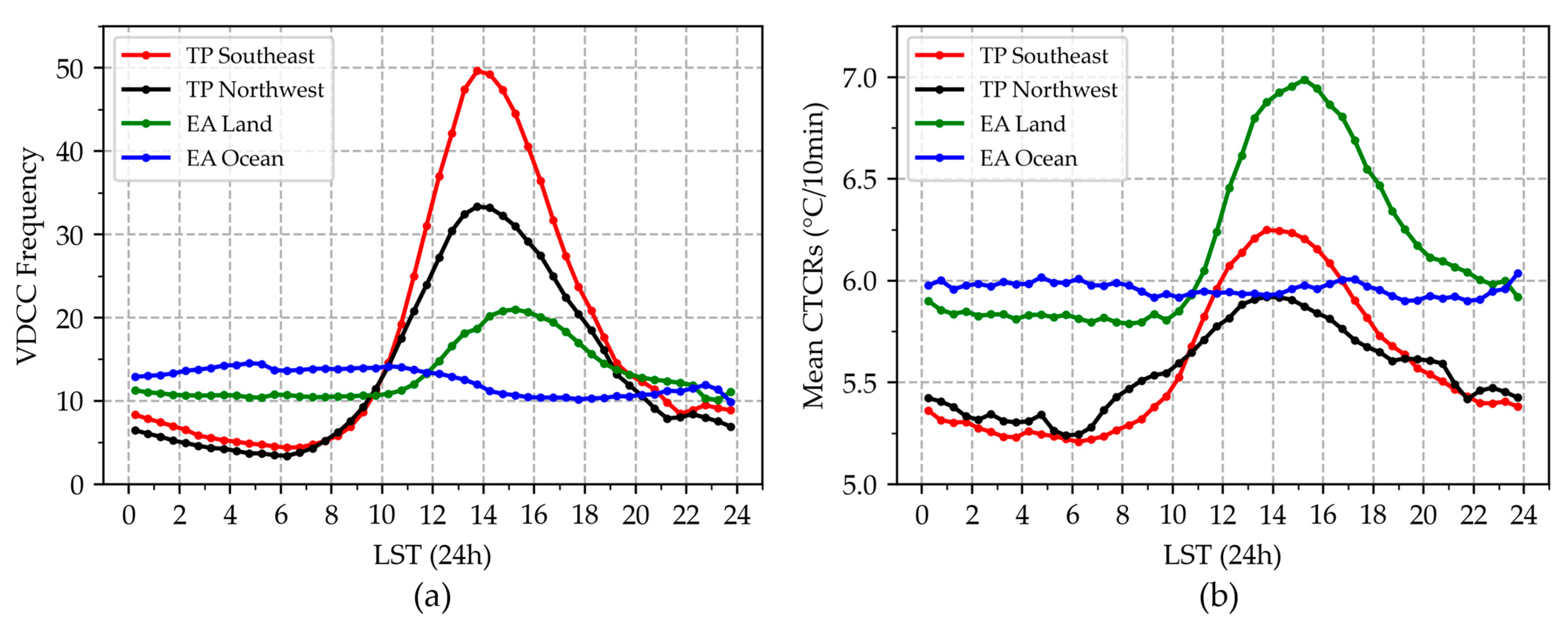
4.1. Diurnal Variation of VDCCs
4.2. Horizontal Distributions of VDCCs
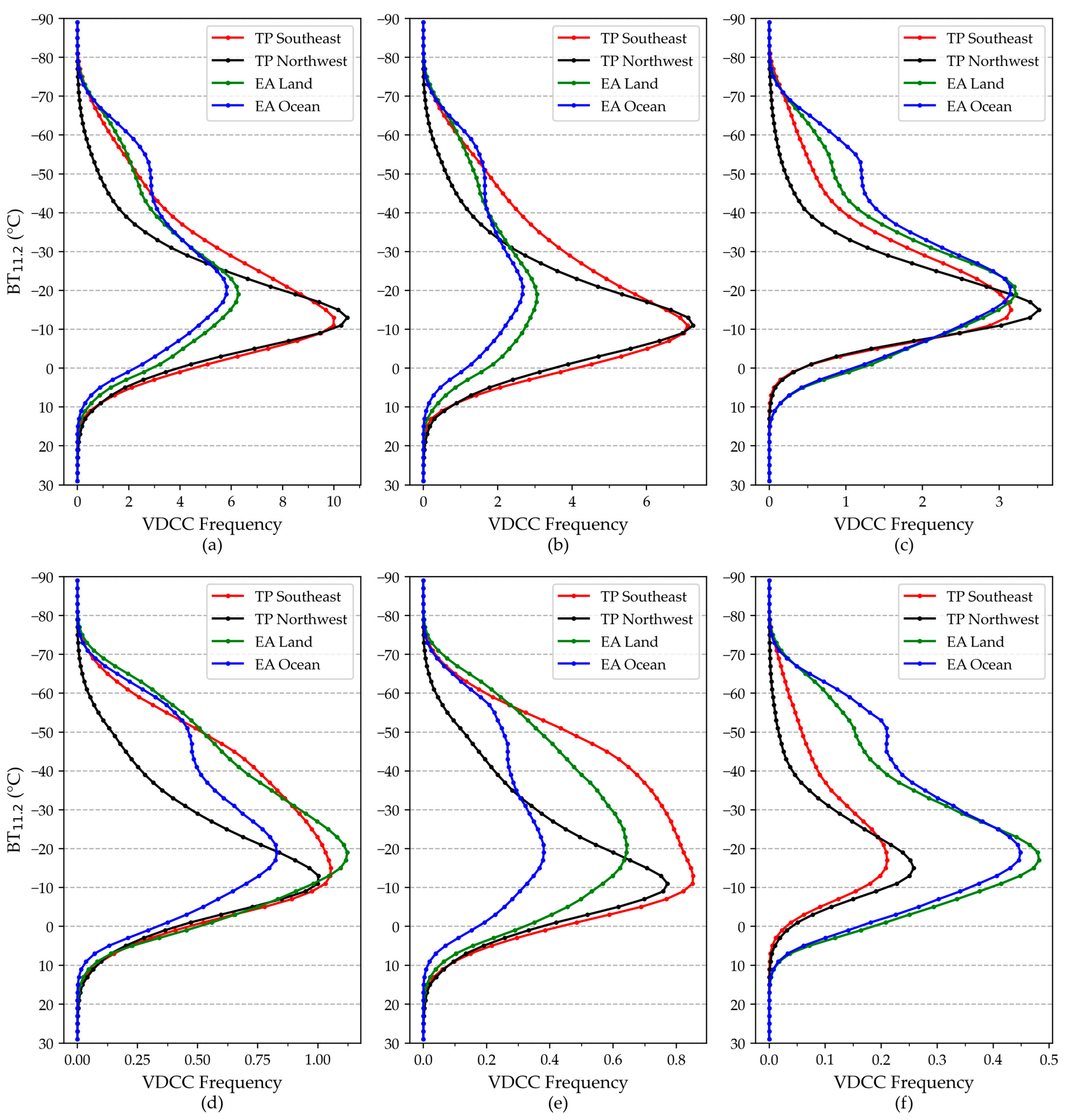
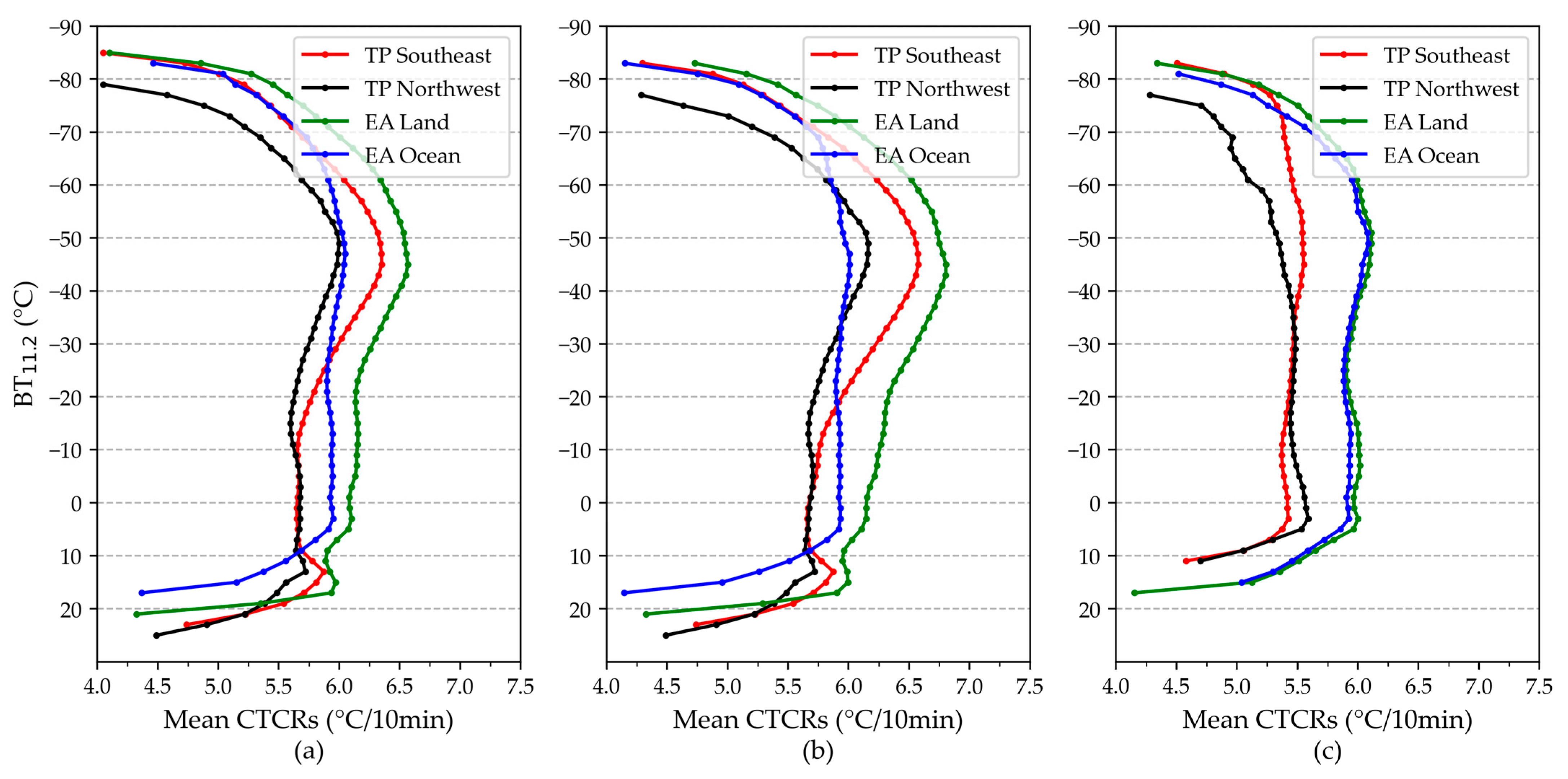
4.3. Vertical Distribution of VDCCs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Li, P.; Moseley, C.; Prein, A.F.; Chen, H.; Li, J.; Furtado, K.; Zhou, T. Mesoscale Convective System Precipitation Characteristics over East Asia. Part I: Regional Differences and Seasonal Variations. J. Clim. 2020, 33, 9271–9286. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, C.; Sun, Y.; Chi, Y.; Fan, H. Convective Cloud Detection and Tracking Using the New-Generation Geostationary Satellite Over South China. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4103912. [Google Scholar] [CrossRef]
- Senf, F.; Deneke, H. Satellite-Based Characterization of Convective Growth and Glaciation and Its Relationship to Precipitation Formation over Central Europe. J. Appl. Meteorol. Climatol. 2017, 56, 1827–1845. [Google Scholar] [CrossRef]
- Adler, R.F.; Fenn, D.D. Thunderstorm Vertical Velocities Estimated from Satellite Data. J. Atmos. Sci. 1979, 36, 1747–1754. [Google Scholar] [CrossRef]
- Sieglaff, J.M.; Cronce, L.M.; Feltz, W.F.; Bedka, K.M.; Pavolonis, M.J.; Heidinger, A.K. Nowcasting Convective Storm Initiation Using Satellite-Based Box-Averaged Cloud-Top Cooling and Cloud-Type Trends. J. Appl. Meteorol. Climatol. 2011, 50, 110–126. [Google Scholar] [CrossRef]
- Hartung, D.C.; Sieglaff, J.M.; Cronce, L.M.; Feltz, W.F. An Intercomparison of UW Cloud-Top Cooling Rates with WSR-88D Radar Data. Weather. Forecast. 2013, 28, 463–480. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Jewett, C.P.; Apke, J.M.; Carey, L.D. Analysis of Cumulus Cloud Updrafts as Observed with 1-Min Resolution Super Rapid Scan GOES Imagery. Mon. Weather. Rev. 2016, 144, 811–830. [Google Scholar] [CrossRef]
- Luo, Z.J.; Jeyaratnam, J.; Iwasaki, S.; Takahashi, H.; Anderson, R. Convective Vertical Velocity and Cloud Internal Vertical Structure: An A-Train Perspective. Geophys. Res. Lett. 2014, 41, 723–729. [Google Scholar] [CrossRef]
- Adler, R.F.; Markus, M.J.; Fenn, D.D. Detection of Severe Midwest Thunderstorms Using Geosynchronous Satellite Data. Mon. Weather. Rev. 1985, 113, 769–781. [Google Scholar] [CrossRef]
- Roberts, R.D.; Rutledge, S. Nowcasting Storm Initiation and Growth Using GOES-8 and WSR-88D Data. Weather. Forecast. 2003, 18, 562–584. [Google Scholar] [CrossRef]
- Sieglaff, J.M.; Hartung, D.C.; Feltz, W.F.; Cronce, L.M.; Lakshmanan, V. A Satellite-Based Convective Cloud Object Tracking and Multipurpose Data Fusion Tool with Application to Developing Convection. J. Atmos. Ocean. Technol. 2013, 30, 510–525. [Google Scholar] [CrossRef]
- Sieglaff, J.M.; Cronce, L.M.; Feltz, W.F. Improving Satellite-Based Convective Cloud Growth Monitoring with Visible Optical Depth Retrievals. J. Appl. Meteorol. Climatol. 2014, 53, 506–520. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Bedka, K.M. Forecasting Convective Initiation by Monitoring the Evolution of Moving Cumulus in Daytime GOES Imagery. Mon. Weather. Rev. 2006, 134, 49–78. [Google Scholar] [CrossRef]
- Siewert, C.W.; Koenig, M.; Mecikalski, J.R. Application of Meteosat Second Generation Data towards Improving the Nowcasting of Convective Initiation. Meteorol. Appl. 2010, 17, 442–451. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; MacKenzie, W.M.; Koenig, M.; Muller, S. Cloud-Top Properties of Growing Cumulus Prior to Convective Initiation as Measured by Meteosat Second Generation. Part I: Infrared Fields. J. Appl. Meteorol. Climatol. 2010, 49, 521–534. [Google Scholar] [CrossRef]
- Walker, J.R.; MacKenzie, W.M.; Mecikalski, J.R.; Jewett, C.P. An Enhanced Geostationary Satellite–Based Convective Initiation Algorithm for 0–2-h Nowcasting with Object Tracking. J. Appl. Meteorol. Climatol. 2012, 51, 1931–1949. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Williams, J.K.; Jewett, C.P.; Ahijevych, D.; LeRoy, A.; Walker, J.R. Probabilistic 0–1-h Convective Initiation Nowcasts That Combine Geostationary Satellite Observations and Numerical Weather Prediction Model Data. J. Appl. Meteorol. Climatol. 2015, 54, 1039–1059. [Google Scholar] [CrossRef]
- Vandal, T.J.; Duffy, K.; McCarty, W.; Sewnath, A.; Nemani, R. Dense Feature Tracking of Atmospheric Winds with Deep Optical Flow. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; ACM: New York, NY, USA, 2022; pp. 1807–1815. [Google Scholar]
- Posselt, D.J.; Wu, L.; Mueller, K.; Huang, L.; Irion, F.W.; Brown, S.; Su, H.; Santek, D.; Velden, C.S. Quantitative Assessment of State-Dependent Atmospheric Motion Vector Uncertainties. J. Appl. Meteorol. Climatol. 2019, 58, 2479–2495. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, H.-Q.; Lin, Y.-J.; Zhuang, Y.-Z.; Zhang, Y. Deriving AMVs from Geostationary Satellite Images Using Optical Flow Algorithm Based on Polynomial Expansion. J. Atmos. Ocean. Technol. 2016, 33, 1727–1747. [Google Scholar] [CrossRef]
- Bedka, K.M.; Wang, C.; Rogers, R.; Carey, L.D.; Feltz, W.; Kanak, J. Examining Deep Convective Cloud Evolution Using Total Lightning, WSR-88D, and GOES-14 Super Rapid Scan Datasets. Weather. Forecast. 2015, 30, 571–590. [Google Scholar] [CrossRef]
- Zheng, D.; Zhang, Y.; Zhang, Y.; Yao, W.; Wang, F.; Lyu, W.; Meng, Q.; Fan, X.; Ma, Y.; Yang, J. Lightning and Deep Convective Activities over the Tibetan Plateau. Natl. Sci. Rev. 2020, 7, 487–488. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yue, Z.; Lu, C.; Chen, J.; Wu, X.; Xu, X.; Luo, S.; Zhu, L.; Wu, S.; Wang, F.; et al. Convective Entrainment Rate over the Tibetan Plateau and Its Adjacent Regions in the Boreal Summer Using SNPP-VIIRS. Remote Sens. 2022, 14, 2073. [Google Scholar] [CrossRef]
- Li, J.; Lu, C.; Chen, J.; Zhou, X.; Yang, K.; Li, J.; Wu, X.; Xu, X.; Wu, S.; Hu, R.; et al. The Influence of Complex Terrain on Cloud and Precipitation on the Foot and Slope of the Southeastern Tibetan Plateau. Clim. Dyn. 2024, 62, 3143–3163. [Google Scholar] [CrossRef]
- Fu, Y.; Ma, Y.; Zhong, L.; Yang, Y.; Guo, X.; Wang, C.; Xu, X.; Yang, K.; Xu, X.; Liu, L.; et al. Land-Surface Processes and Summer-Cloud-Precipitation Characteristics in the Tibetan Plateau and Their Effects on Downstream Weather: A Review and Perspective. Natl. Sci. Rev. 2020, 7, 500–515. [Google Scholar] [CrossRef]
- Zhang, G.; Mao, J.; Liu, Y.; Wu, G. PV Perspective of Impacts on Downstream Extreme Rainfall Event of a Tibetan Plateau Vortex Collaborating with a Southwest China Vortex. Adv. Atmos. Sci. 2021, 38, 1835–1851. [Google Scholar] [CrossRef]
- Chen, L.; Reiter, E.R.; Feng, Z. The Atmospheric Heat Source over the Tibetan Plateau: May–August 1979. Mon. Weather. Rev. 1985, 113, 1771–1790. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, Y. Tibetan Plateau Forcing and the Timing of the Monsoon Onset over South Asia and the South China Sea. Mon. Weather. Rev. 1998, 126, 913–927. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, X.; Liu, L.; Zhang, R.; Xu, H.; Wang, Y.; Li, J. Effects of Convection over the Tibetan Plateau on Rainstorms Downstream of the Yangtze River Basin. Atmos. Res. 2019, 219, 24–35. [Google Scholar] [CrossRef]
- Kukulies, J.; Chen, D.; Wang, M. Temporal and Spatial Variations of Convection, Clouds and Precipitation over the Tibetan Plateau from Recent Satellite Observations. Part II: Precipitation Climatology Derived from Global Precipitation Measurement Mission. Int. J. Climatol. 2020, 40, 4858–4875. [Google Scholar] [CrossRef]
- Li, D.; Yang, K.; Tang, W.; Li, X.; Zhou, X.; Guo, D. Characterizing Precipitation in High Altitudes of the Western Tibetan Plateau with a Focus on Major Glacier Areas. Int. J. Climatol. 2020, 40, 5114–5127. [Google Scholar] [CrossRef]
- Xu, X.; Heng, Z.; Li, Y.; Wang, S.; Li, J.; Wang, Y.; Chen, J.; Zhang, P.; Lu, C. Improvement of Cloud Microphysical Parameterization and Its Advantages in Simulating Precipitation along the Sichuan-Xizang Railway. Sci. China Earth Sci. 2024, 67, 856–873. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, B.; Liu, L.; Zheng, D. Redetermine the Region and Boundaries of Tibetan Plateau. Geogr. Res. 2021, 40, 1543–1553. [Google Scholar] [CrossRef]
- Zhang, Y. Integration Dataset of Tibet Plateau Boundary. National Tibetan Plateau/Third Pole Environment Data Center. Available online: https://data.tpdc.ac.cn/en/data/61701a2b-31e5-41bf-b0a3-607c2a9bd3b3/ (accessed on 10 April 2025).
- Kim, D.; Gu, M.; Oh, T.-H.; Kim, E.-K.; Yang, H.-J. Introduction of the Advanced Meteorological Imager of Geo-Kompsat-2a: In-Orbit Tests and Performance Validation. Remote Sens. 2021, 13, 1303. [Google Scholar] [CrossRef]
- Chen, D.; Guo, J.; Wang, H.; Li, J.; Min, M.; Zhao, W.; Yao, D. The Cloud Top Distribution and Diurnal Variation of Clouds Over East Asia: Preliminary Results from Advanced Himawari Imager. J. Geophys. Res. Atmos. 2018, 123, 3724–3739. [Google Scholar] [CrossRef]
- Lee, S.; Choi, J. Daytime Cloud Detection Algorithm Based on a Multitemporal Dataset for GK-2A Imagery. Remote Sens. 2021, 13, 3215. [Google Scholar] [CrossRef]
- Jang, J.-C.; Lee, S.; Sohn, E.-H.; Noh, Y.-J.; Miller, S.D. Combined Dust Detection Algorithm for Asian Dust Events Over East Asia Using GK2A/AMI: A Case Study in October 2019. Asia Pac. J. Atmos. Sci. 2022, 58, 45–64. [Google Scholar] [CrossRef]
- Chung, S.-R.; Ahn, M.-H.; Han, K.-S.; Lee, K.-T.; Shin, D.-B. Meteorological Products of Geo-KOMPSAT 2A (GK2A) Satellite. Asia Pac. J. Atmos. Sci. 2020, 56, 185. [Google Scholar] [CrossRef]
- Liu, Z.; Vaughan, M.; Winker, D.; Kittaka, C.; Getzewich, B.; Kuehn, R.; Omar, A.; Powell, K.; Trepte, C.; Hostetler, C. The CALIPSO Lidar Cloud and Aerosol Discrimination: Version 2 Algorithm and Initial Assessment of Performance. J. Atmos. Ocean. Technol. 2009, 26, 1198–1213. [Google Scholar] [CrossRef]
- Vaughan, M.A.; Powell, K.A.; Winker, D.M.; Hostetler, C.A.; Kuehn, R.E.; Hunt, W.H.; Getzewich, B.J.; Young, S.A.; Liu, Z.; McGill, M.J. Fully Automated Detection of Cloud and Aerosol Layers in the CALIPSO Lidar Measurements. J. Atmos. Ocean. Technol. 2009, 26, 2034–2050. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Hagihara, Y.; Okamoto, H.; Yoshida, R. Development of a Combined CloudSat-CALIPSO Cloud Mask to Show Global Cloud Distribution. J. Geophys. Res. Atmos. 2010, 115, D00H33. [Google Scholar] [CrossRef]
- Delanoë, J.; Hogan, R.J. Combined CloudSat-CALIPSO-MODIS Retrievals of the Properties of Ice Clouds. J. Geophys. Res. Atmos. 2010, 115, D00H29. [Google Scholar] [CrossRef]
- NASA/LARC/SD/ASDC. CALIPSO Lidar Level 2 Vertical Feature Mask (VFM), V4-51. NASA Langley Atmospheric Science Data Center DAAC. Available online: https://asdc.larc.nasa.gov/project/CALIPSO/CAL_LID_L2_VFM-Standard-V4-51_V4-51 (accessed on 10 April 2025).
- Wang, Y.; Li, Z.; Gao, L.; Zhong, Y.; Peng, X. Comparison of GPM IMERG Version 06 Final Run Products and Its Latest Version 07 Precipitation Products across Scales: Similarities, Differences and Improvements. Remote Sens. 2023, 15, 5622. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kulie, M.; Milani, L.; Munchak, S.J.; Wood, N.B.; Levizzani, V. Satellite Estimation of Falling Snow: A Global Precipitation Measurement (GPM) Core Observatory Perspective. J. Appl. Meteorol. Climatol. 2019, 58, 1429–1448. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kirschbaum, D.; Petersen, W.; Huffman, G.; Kidd, C.; Stocker, E.; Kakar, R. The Global Precipitation Measurement (GPM) Mission’s Scientific Achievements and Societal Contributions: Reviewing Four Years of Advanced Rain and Snow Observations. Q. J. R. Meteorol. Soc. 2018, 144, 27–48. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Vollmer, B.; Deshong, B.; Macritchie, K.; Greene, M.; Kempler, S. Global Precipitation Measurement Mission Products and Services at the NASA GES DISC. Bull. Am. Meteorol. Soc. 2017, 98, 437–444. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Jackson, T. GPM IMERG Final Precipitation L3 Half Hourly 0.1 Degree x 0.1 Degree V07, Greenbelt, MD, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGHH_07/summary (accessed on 10 April 2025).
- Velden, C.; Daniels, J.; Stettner, D.; Santek, D.; Key, J.; Dunion, J.; Holmlund, K.; Dengel, G.; Bresky, W.; Menzel, P. Recent Innovations in Deriving Tropospheric Winds from Meteorological Satellites. Bull. Am. Meteorol. Soc. 2005, 86, 205–224. [Google Scholar] [CrossRef]
- Apke, J.M.; Hilburn, K.A.; Miller, S.D.; Peterson, D.A. Towards Objective Identification and Tracking of Convective Outflow Boundaries in Next-Generation Geostationary Satellite Imagery. Atmos. Meas. Tech. 2020, 13, 1593–1608. [Google Scholar] [CrossRef]
- Jones, W.K.; Christensen, M.W.; Stier, P. A Semi-Lagrangian Method for Detecting and Tracking Deep Convective Clouds in Geostationary Satellite Observations. Atmos. Meas. Tech. 2023, 16, 1043–1059. [Google Scholar] [CrossRef]
- Yanovsky, I.; Posselt, D.J.; Wu, L.; Hristova-Veleva, S. Quantifying Uncertainty in Atmospheric Winds Retrieved from Optical Flow: Dependence on Weather Regime. J. Appl. Meteorol. Climatol. 2024, 63, 1113–1135. [Google Scholar] [CrossRef]
- Farneback, G. Very High Accuracy Velocity Estimation Using Orientation Tensors, Parametric Motion, and Simultaneous Segmentation of the Motion Field. In Proceedings of the Eighth IEEE International Conference on Computer Vision, ICCV 2001, Vancouver, BC, Canada, 7–14 July 2001; pp. 171–177. [Google Scholar]
- Farnebäck, G. Two-Frame Motion Estimation Based on Polynomial Expansion. In Proceedings of the 13th Scandinavian Conference, SCIA 2003, Halmstad, Sweden, 29 June–2 July 2003; pp. 363–370. [Google Scholar]
- Adelson, E.H.; Burt, P.J.; Anderson, C.H.; Ogden, J.M.; Bergen, J.R. Pyramid methods in image processing. RCA Eng. 1984, 29, 33–41. [Google Scholar]
- Ranjan, A.; Black, M.J. Optical Flow Estimation Using a Spatial Pyramid Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Zinner, T.; Mannstein, H.; Tafferner, A. Cb-TRAM: Tracking and Monitoring Severe Convection from Onset over Rapid Development to Mature Phase Using Multi-Channel Meteosat-8 SEVIRI Data. Meteorol. Atmos. Phys. 2008, 101, 191–210. [Google Scholar] [CrossRef]
- Matthee, R.; Mecikalski, J.R. Geostationary Infrared Methods for Detecting Lightning-producing Cumulonimbus Clouds. J. Geophys. Res. Atmos. 2013, 118, 6580–6592. [Google Scholar] [CrossRef]
- Wang, C.; Luo, Z.J.; Huang, X. Parallax Correction in Collocating CloudSat and Moderate Resolution Imaging Spectroradiometer (MODIS) Observations: Method and Application to Convection Study. J. Geophys. Res. Atmos. 2011, 116, 17201. [Google Scholar] [CrossRef]
- Wang, G.; Wang, H.; Zhuang, Y.; Wu, Q.; Chen, S.; Kang, H. Tropical Overshooting Cloud-Top Height Retrieval from Himawari-8 Imagery Based on Random Forest Model. Atmosphere 2021, 12, 173. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, H.-Q.; Zhuang, Y.-Z.; Lin, Y.-J.; Zhang, Y.; Ding, S.-S. Correlations of Multispectral Infrared Indicators and Applications in the Analysis of Developing Convective Clouds. J. Appl. Meteorol. Climatol. 2016, 55, 945–960. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, Z.; Li, J.; Li, W.; Bai, L.; Zhang, M.; Wang, X. Distribution and Variability of Satellite-Derived Signals of Isolated Convection Initiation Events Over Central Eastern China. J. Geophys. Res. Atmos. 2017, 122, 11,357–11,373. [Google Scholar] [CrossRef]
- Setvák, M.; Rabin, R.M.; Wang, P.K. Contribution of the MODIS Instrument to Observations of Deep Convective Storms and Stratospheric Moisture Detection in GOES and MSG Imagery. Atmos. Res. 2007, 83, 505–518. [Google Scholar] [CrossRef]
- Wang, P.K. Moisture Plumes above Thunderstorm Anvils and Their Contributions to Cross-tropopause Transport of Water Vapor in Midlatitudes. J. Geophys. Res. Atmos. 2003, 108, 4194. [Google Scholar] [CrossRef]
- Baum, B.A.; Frey, R.A.; Mace, G.G.; Harkey, M.K.; Yang, P. Nighttime Multilayered Cloud Detection Using MODIS and ARM Data. J. Appl. Meteorol. 2003, 42, 905–919. [Google Scholar] [CrossRef]
- Xiangde, X.; Tianliang, Z.; Xiaohui, S.; Chungu, L.; Xiangde, X.; Tianliang, Z.; Xiaohui, S.; Chungu, L. A Study of the Role of the Tibetan Plateau’s Thermal Forcing in Modulating Rainband and Moisture Transport in Eastern China. Acta Meteorol. Sin. 2015, 1, 20–35. [Google Scholar] [CrossRef]
- Lee, T.-Y.; Shin, U.; Park, S.-H. Atmospheric Structure for Convective Development in the Events of Cloud Clusters over the Korean Peninsula. Asia Pac. J. Atmos. Sci. 2021, 57, 511–531. [Google Scholar] [CrossRef]
- Johnson, R.H.; Rickenbach, T.M.; Rutledge, S.A.; Ciesielski, P.E.; Schubert, W.H. Trimodal Characteristics of Tropical Convection. J. Clim. 1999, 12, 2397–2418. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, G.Y.; Stephens, G.L.; Johnson, R.H. Terminal versus Transient Cumulus Congestus: A CloudSat Perspective. Geophys. Res. Lett. 2009, 36, L05808. [Google Scholar] [CrossRef]

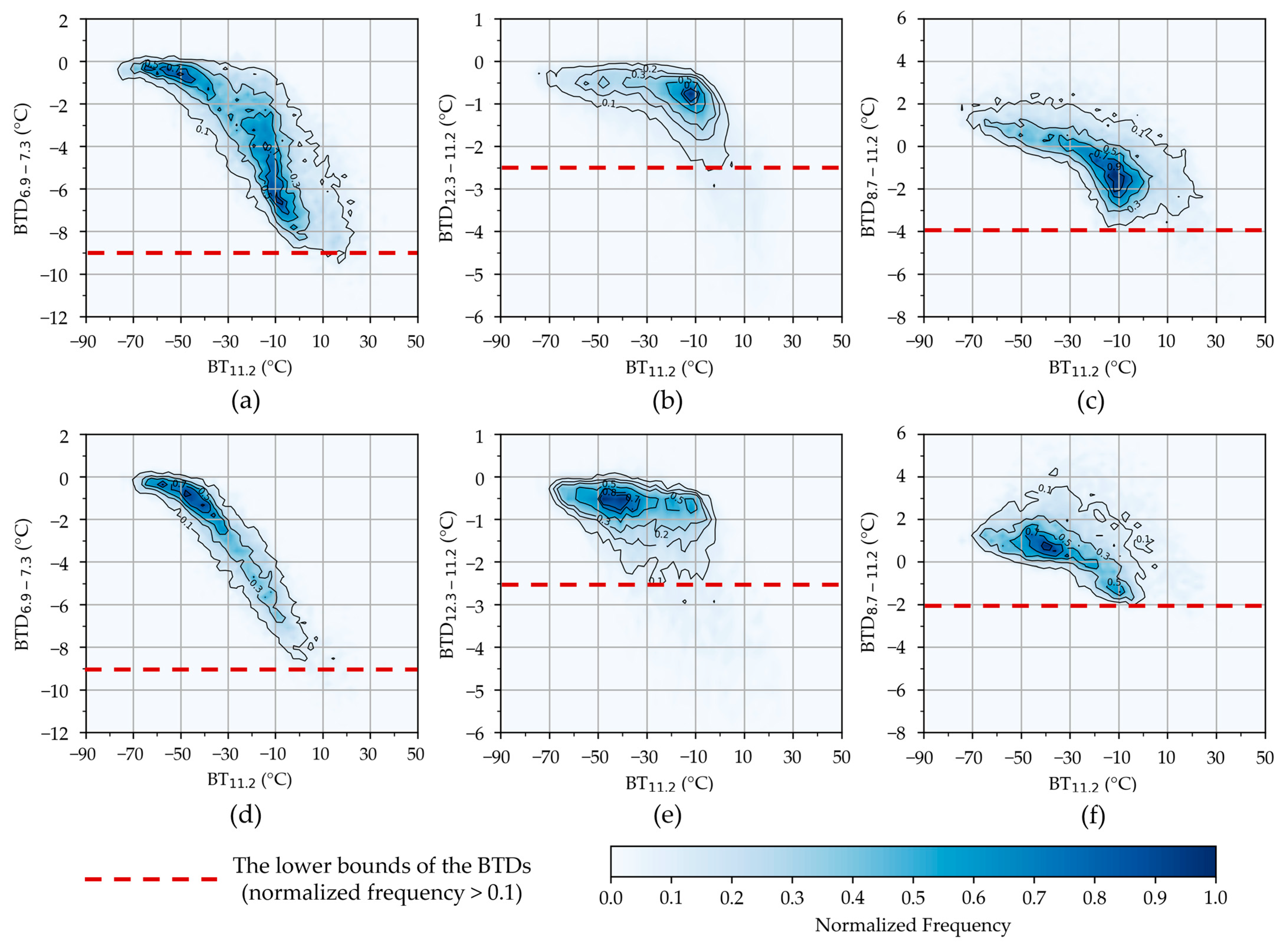

| Region | BTD6.9−7.3 (°C) | BTD12.3−11.2 (°C) | BTD8.7−11.2 (°C) |
|---|---|---|---|
| TP | >−9 | >−2.5 | >−4 |
| EA | >−9 | >−2.5 | >−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H.; Wang, H.; Wu, Q.; Zhang, Y. Detection and Spatiotemporal Distribution Analysis of Vertically Developing Convective Clouds over the Tibetan Plateau and East Asia Using GEO-KOMPSAT-2A Observations. Remote Sens. 2025, 17, 1427. https://doi.org/10.3390/rs17081427
Kang H, Wang H, Wu Q, Zhang Y. Detection and Spatiotemporal Distribution Analysis of Vertically Developing Convective Clouds over the Tibetan Plateau and East Asia Using GEO-KOMPSAT-2A Observations. Remote Sensing. 2025; 17(8):1427. https://doi.org/10.3390/rs17081427
Chicago/Turabian StyleKang, Haokai, Hongqing Wang, Qiong Wu, and Yan Zhang. 2025. "Detection and Spatiotemporal Distribution Analysis of Vertically Developing Convective Clouds over the Tibetan Plateau and East Asia Using GEO-KOMPSAT-2A Observations" Remote Sensing 17, no. 8: 1427. https://doi.org/10.3390/rs17081427
APA StyleKang, H., Wang, H., Wu, Q., & Zhang, Y. (2025). Detection and Spatiotemporal Distribution Analysis of Vertically Developing Convective Clouds over the Tibetan Plateau and East Asia Using GEO-KOMPSAT-2A Observations. Remote Sensing, 17(8), 1427. https://doi.org/10.3390/rs17081427






