LEO Satellite Navigation Signal Multi-Dimensional Interference Optimisation Method Based on Hybrid Game Theory
Abstract
1. Introduction
- In this study, a distributed and collaborative LEO satellite jamming architecture with jammers is established to meet the fast, time-varying demand for LEO satellite signal jamming.
- In this study, we propose a multi-dimensional adaptive optimisation method based on a hybrid game in the air–temporal–frequency–energy domain to achieve the optimal relative jammer allocation strategy under the Nash equilibrium for millisecond-level interference optimisation.
- In this study, an LEO satellite interference verification system based on full-sky star fitting is constructed in a large microwave darkroom, and the verification of an LEO satellite multi-dimensional interference optimisation method based on hybrid game theory is completed. Compared with the existing interference optimisation methods, it has shown improvements in the BER and real-time response speed.
2. Related Work
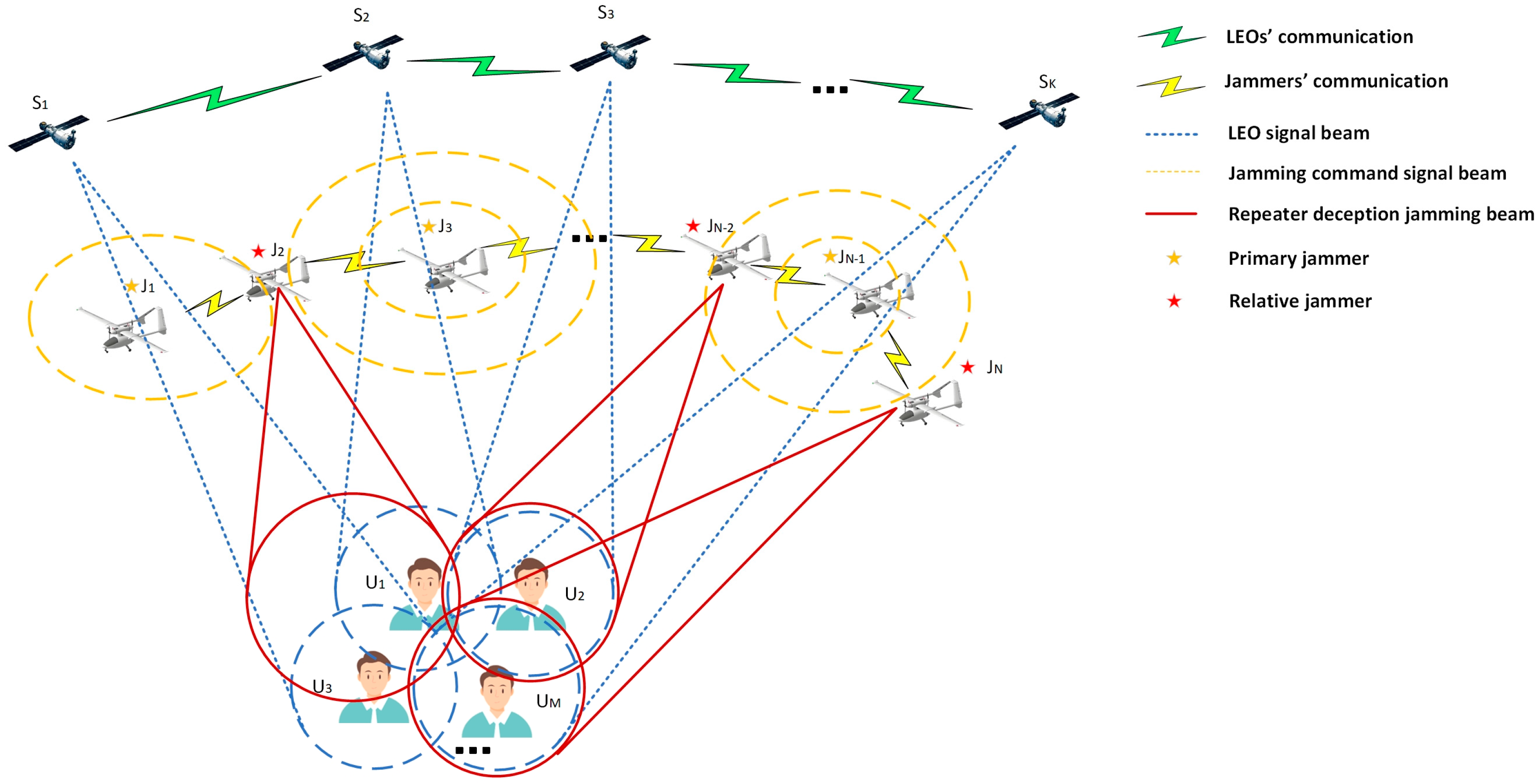
3. Distributed Jamming System Model for LEO Signal
3.1. Distributed Interference Scenario
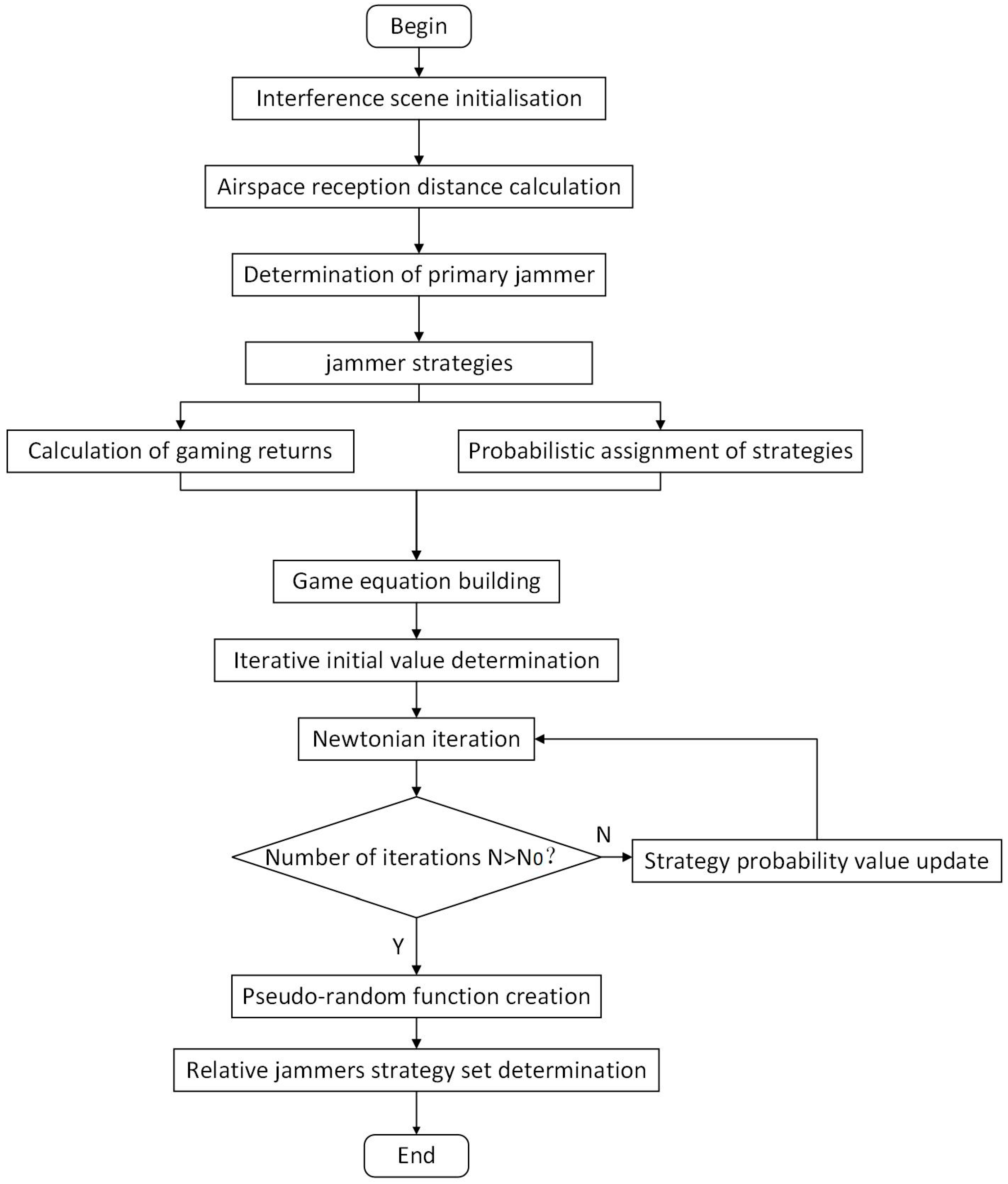
3.2. Distributed Interference Optimisation Implementation Process
3.3. Identification of Primary and Relative Jammers
4. Relative Jammer Screening Algorithm Based on Mixed-Strategy Game
4.1. Primary Jammer Set and Strategy Set
4.2. Multidimensional Utility Function Construction
- (1)
- Forwarding interference time loss model
- (2)
- Interference power loss model
- (3)
- Doppler shift loss mode
4.3. Nash Equilibrium Point Solution
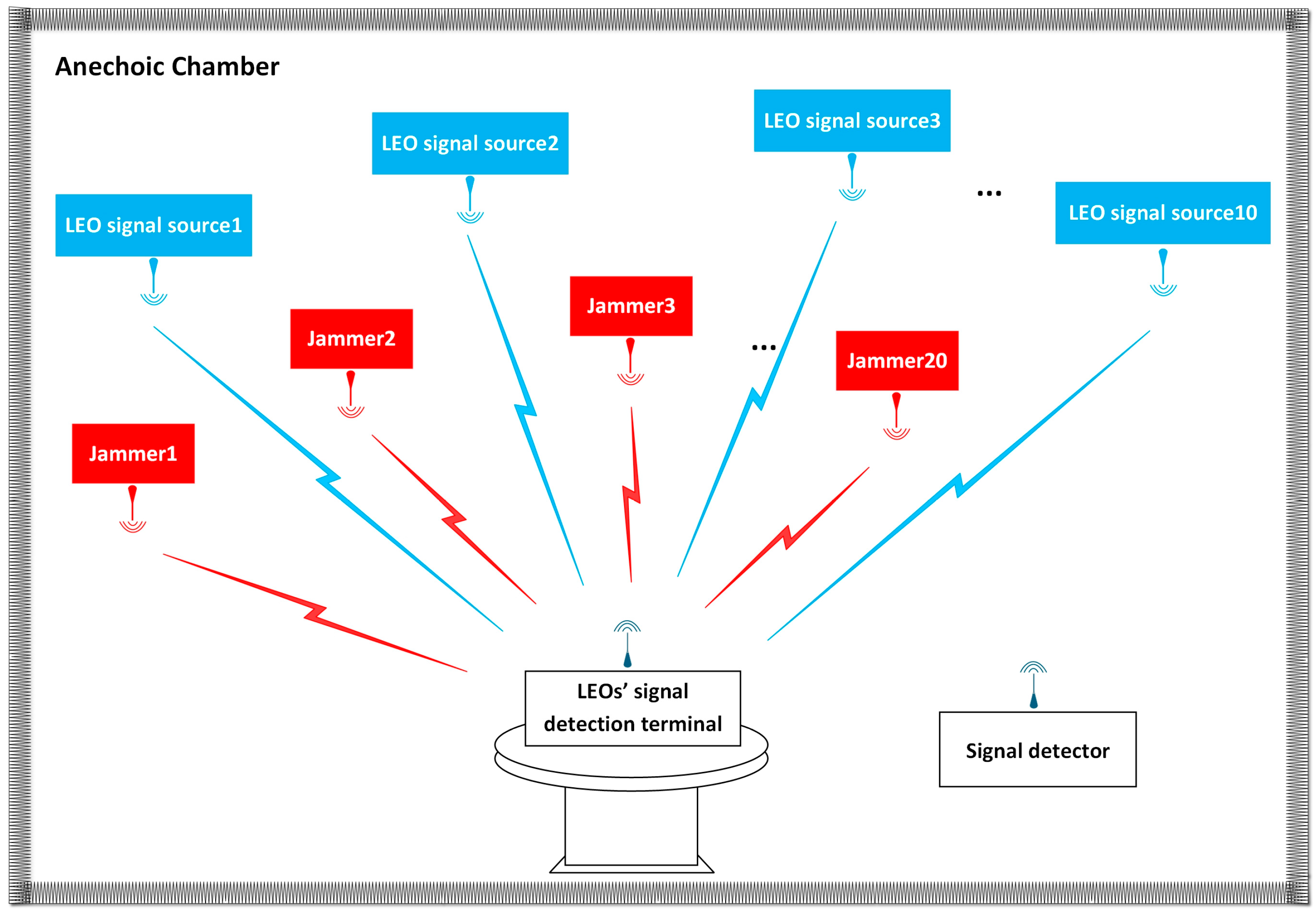
5. Simulation and Analysis
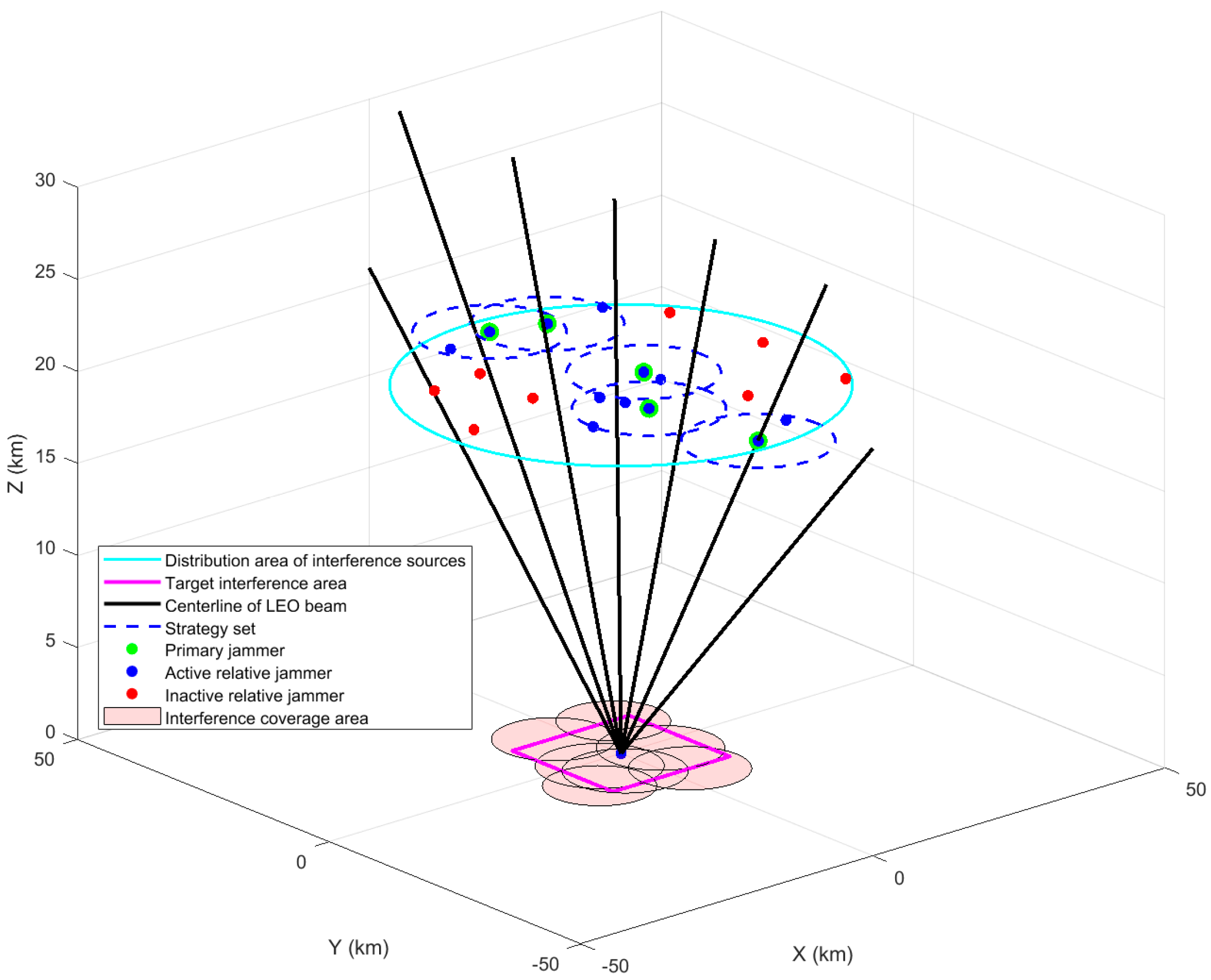
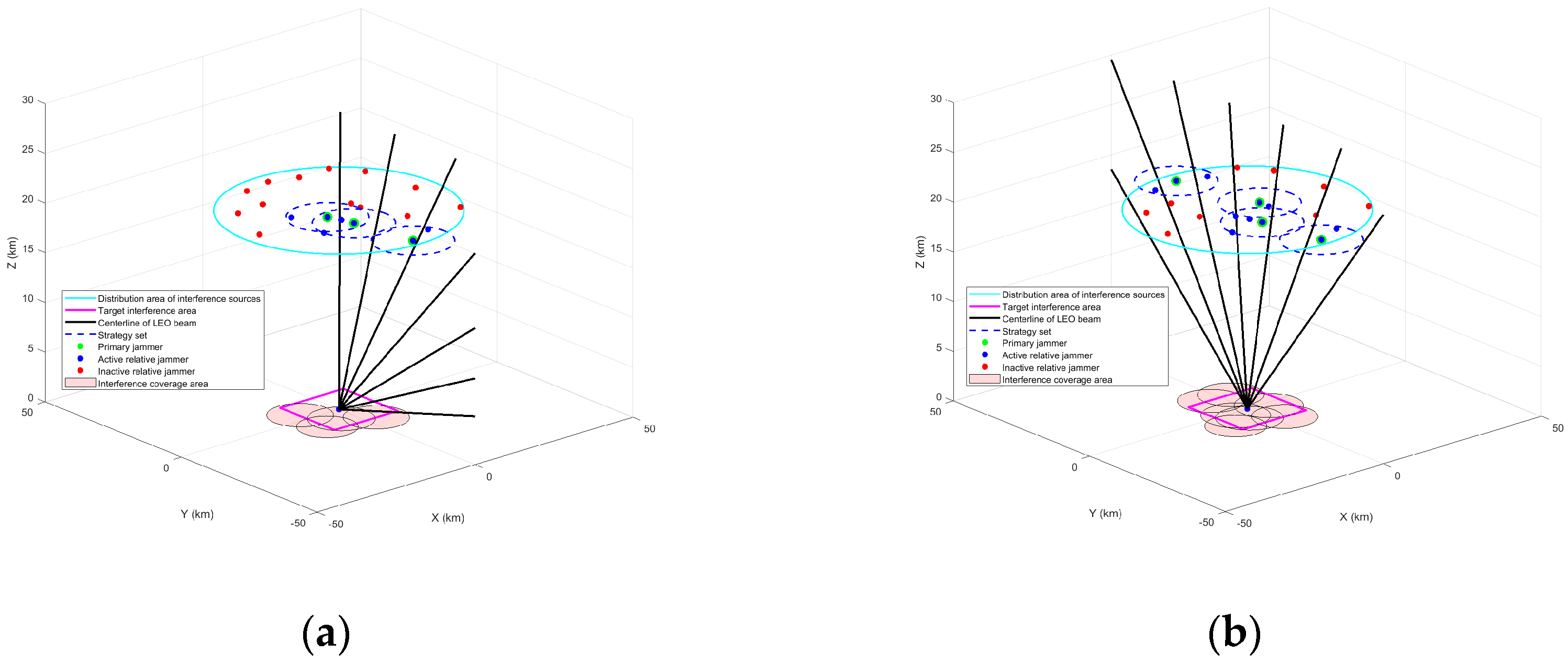
5.1. Interference Verification Scenario
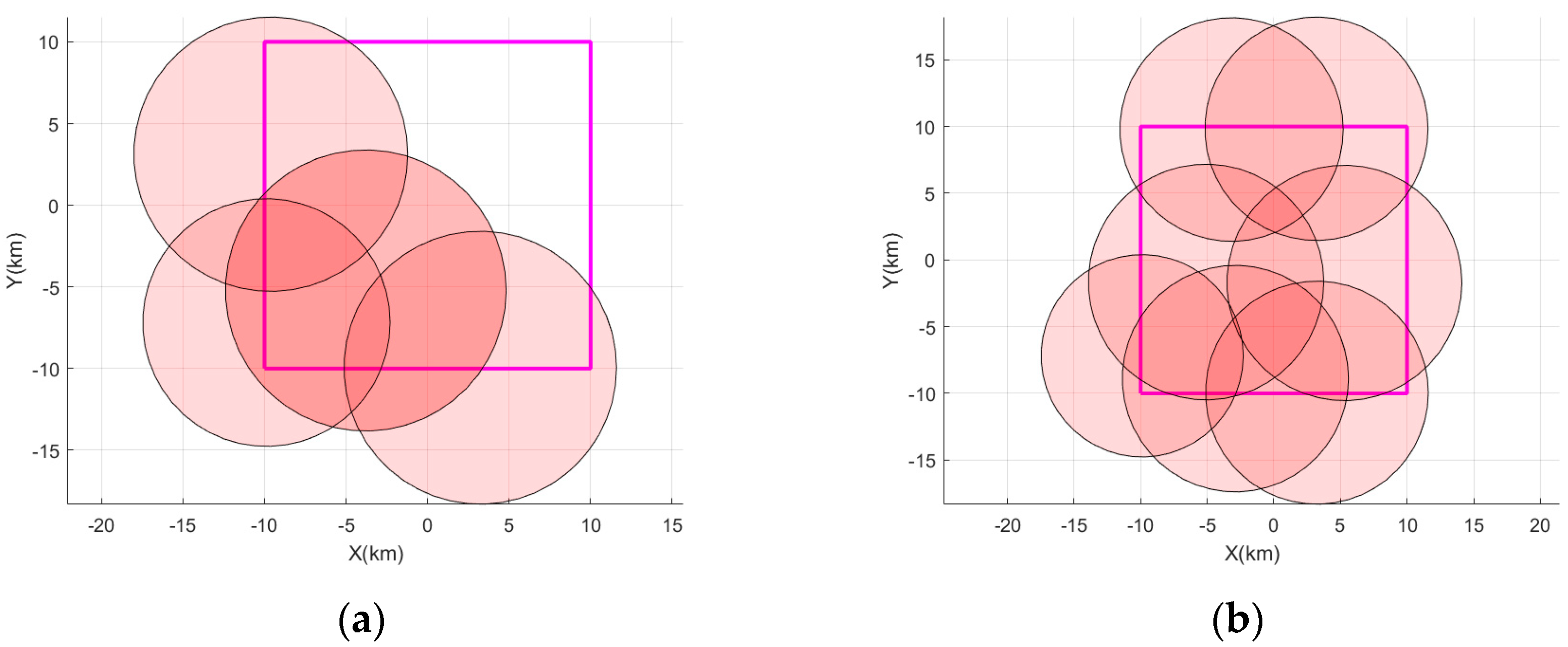
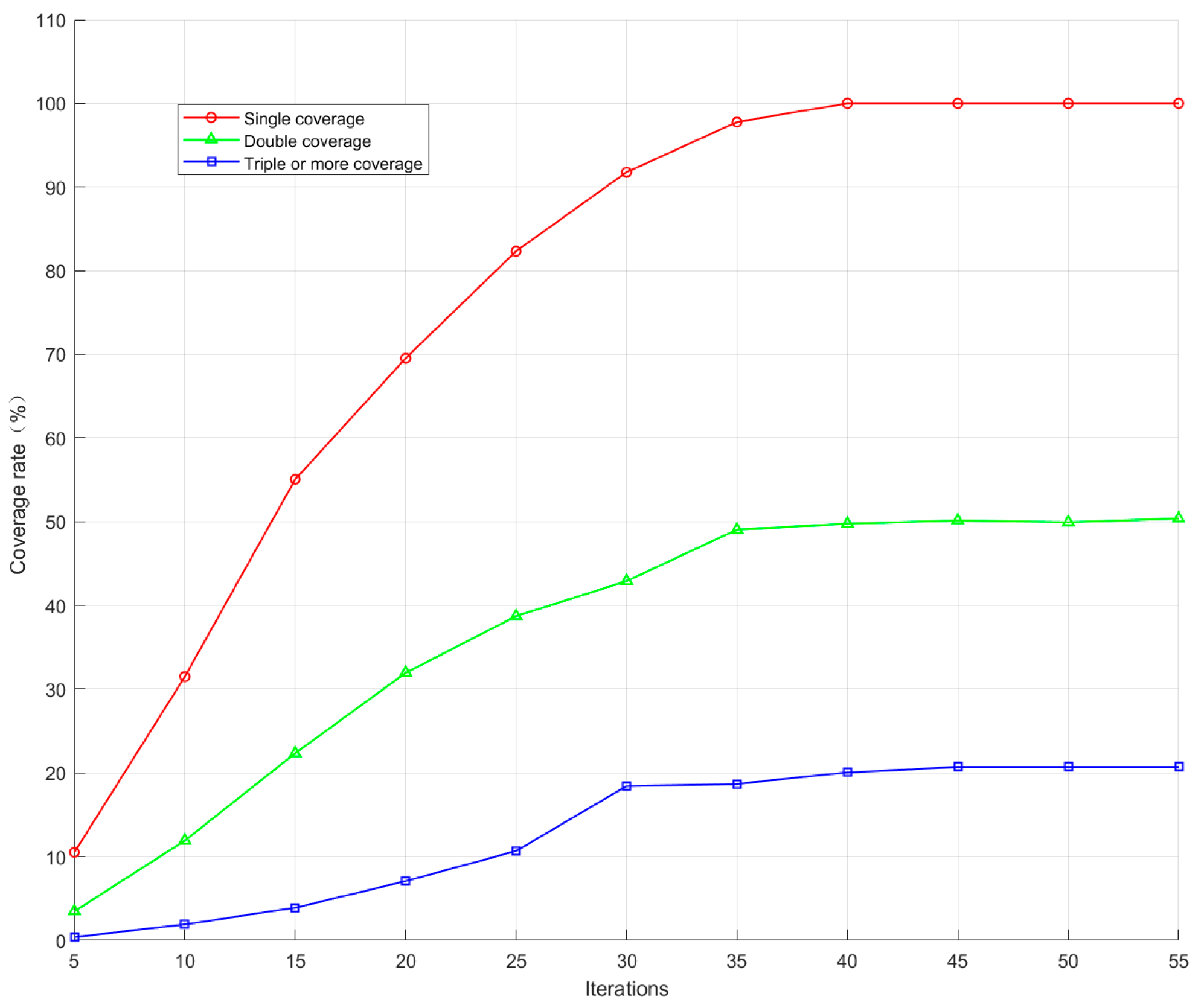
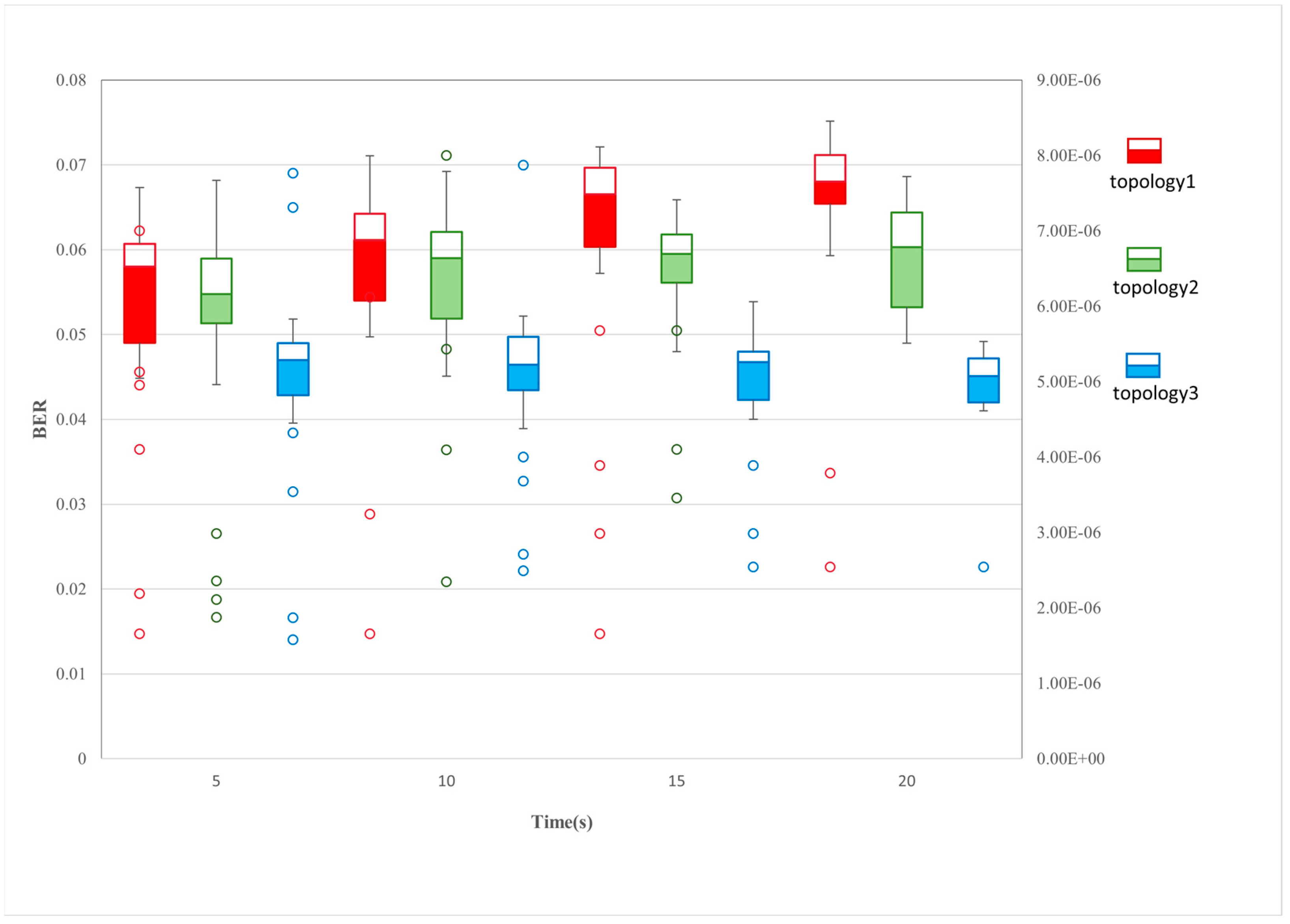
5.2. Distributed Jammers of Same Topology in Different Scenarios
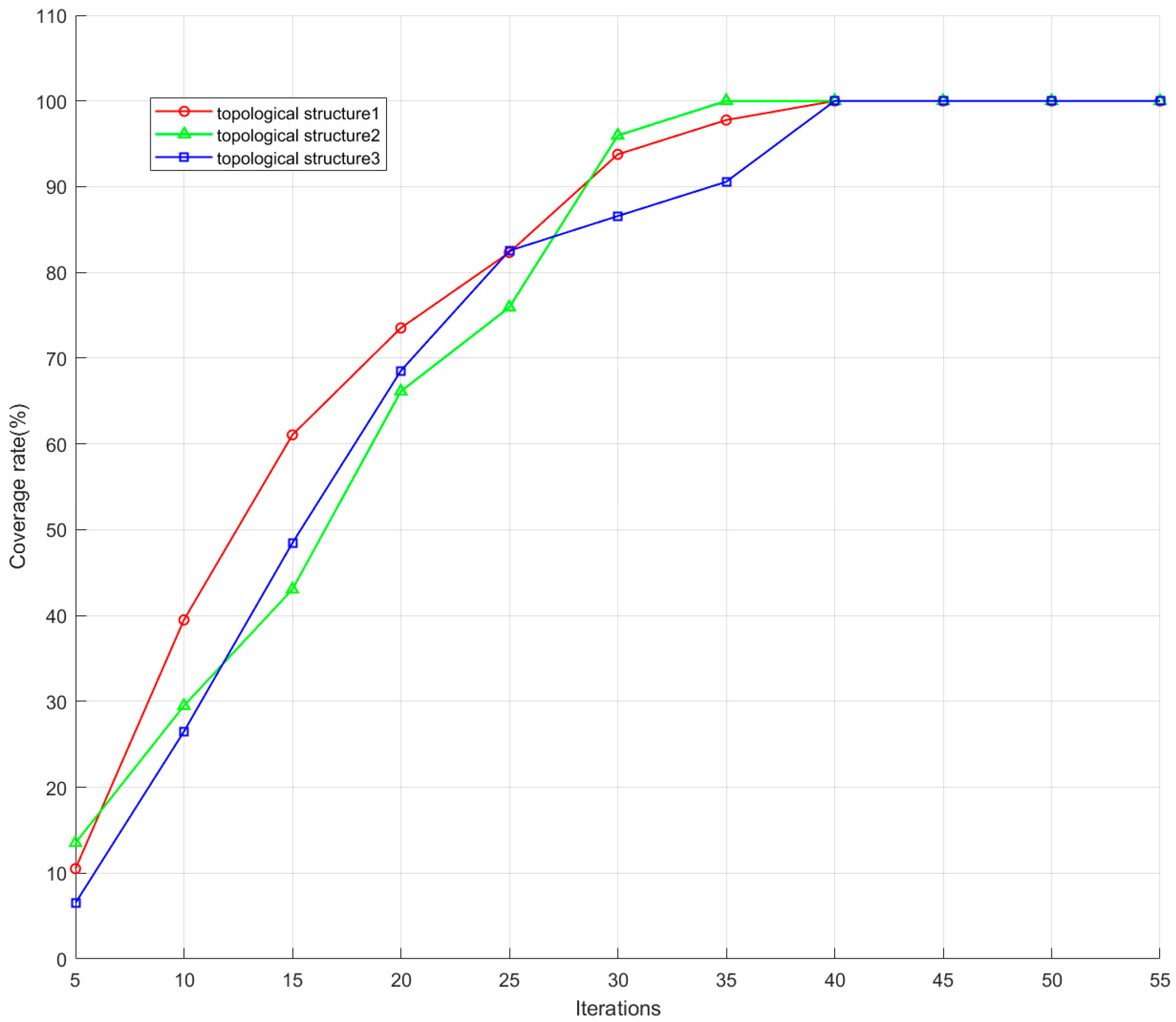
5.3. Distributed Jammers in Different Topologies
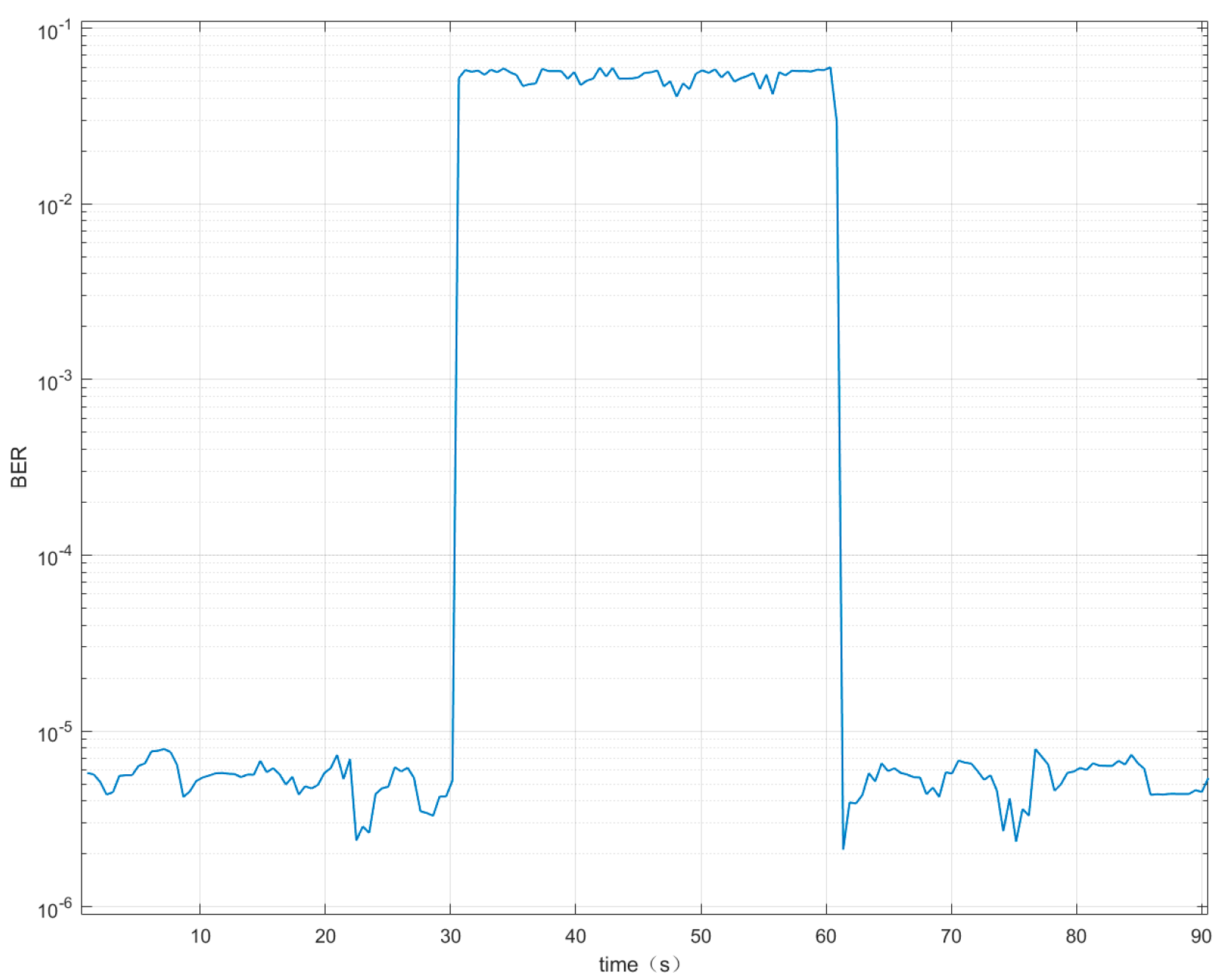
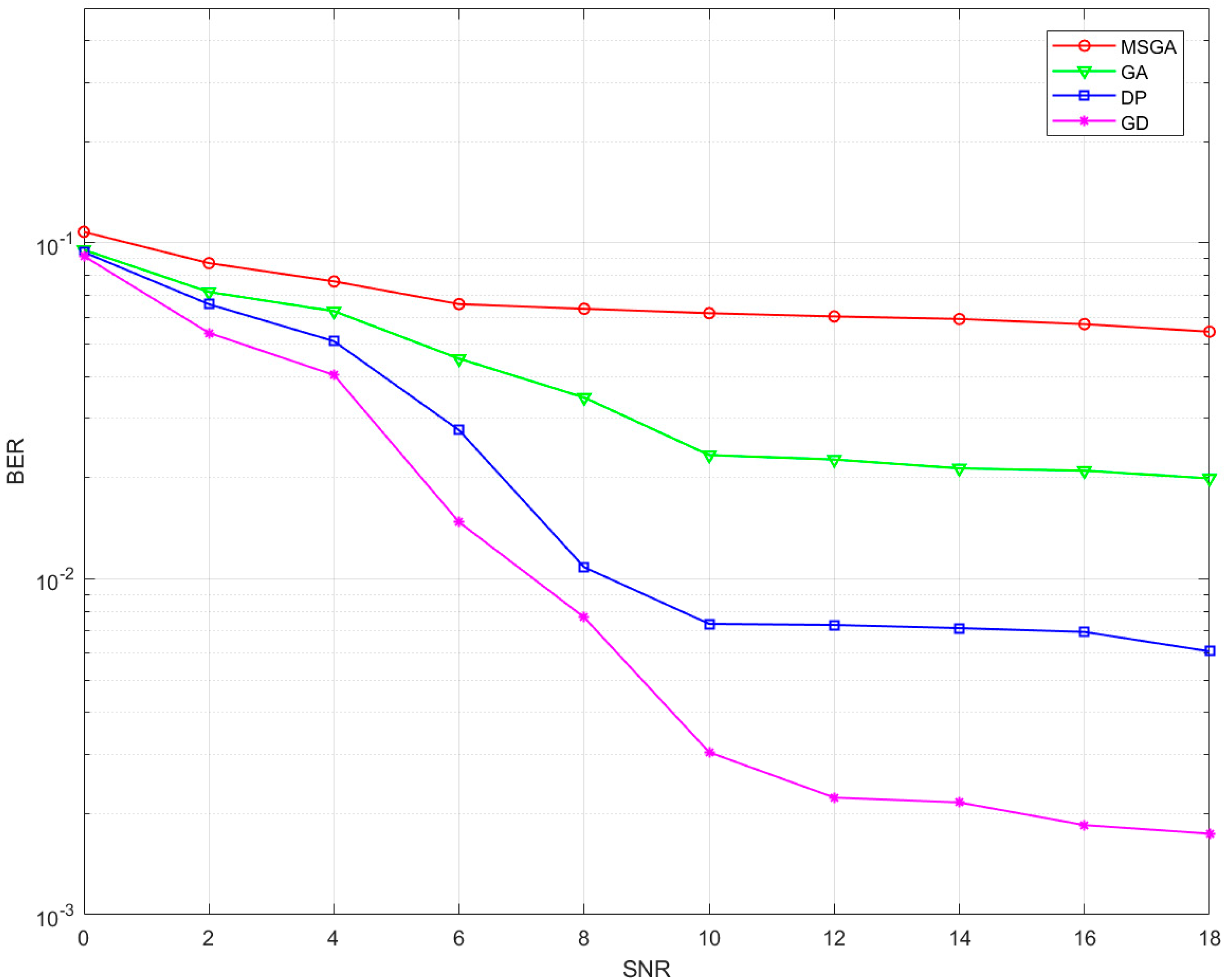
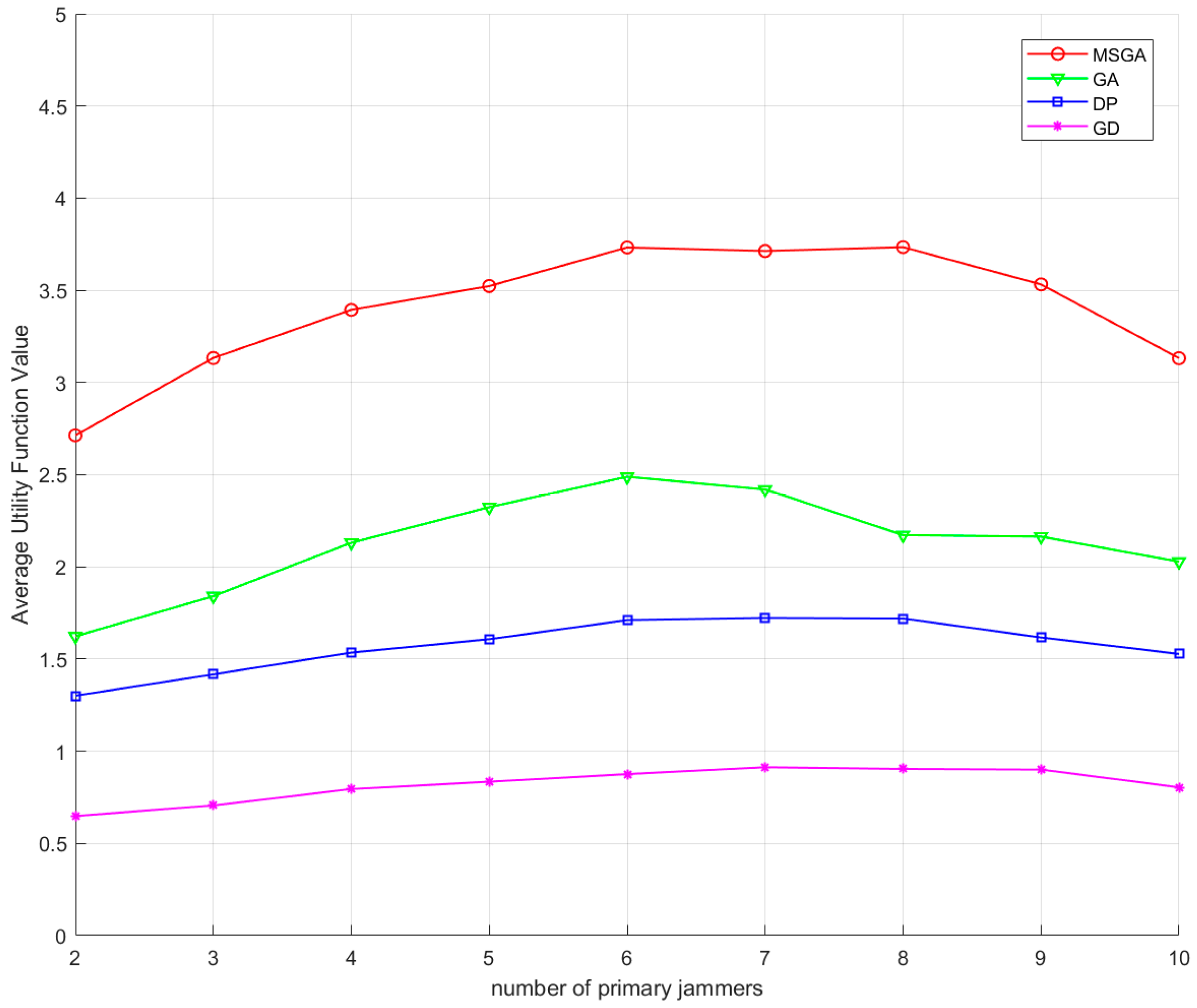
5.4. Comparison of Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shayea, I.; El-Saleh, A.A.; Ergen, M.; Saoud, B.; Hartani, R.; Turan, D.; Kabbani, A. Integration of 5G, 6G and IoT with Low Earth Orbit (LEO) networks: Opportunity, challenges and future trends. Results Eng. 2024, 23, 102409. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, Y.; Lyu, D.; Wu, M.; Wang, Y.; Cao, X.; Shen, F. LEO satellite clock modeling and its benefits for real-time LEO PPP timing. Measurement 2025, 242, 116035. [Google Scholar] [CrossRef]
- Klír, R.; Rozenberg, R.; Ďurčo, S. Celestial Navigation. In Proceedings of the International Multidisciplinary Scientific Geo Conference Surveying Geology and Mining Ecology Management, Albena, Bulgaria, 18–24 August 2020; pp. 311–318. [Google Scholar]
- She, H.; Huang, G.; Wang, L.; Qin, Z.; Xie, S.; Lai, W.; Tian, J. A simplified GNSS/LEO joint orbit determination method. Measurement 2024, 236, 115029. [Google Scholar] [CrossRef]
- Fang, J.; Tu, R.; Zhang, P.; Zhang, R.; Lu, X. UPDs estimation and ambiguity resolution performance evaluation of LEO navigation system. Adv. Space Res. 2024, 74, 2883–2900. [Google Scholar] [CrossRef]
- Wu, Z.; Jing, G.; Ding, J.; Zhao, X. SCMA-Q-learning with overload control for random access in LEO satellite mMTC networks. Phys. Commun. 2025, 69, 102584. [Google Scholar] [CrossRef]
- Chang, C.; Zhao, Q.; Li, M.; Li, W. Augmentation message design for LEO-enhanced precise positioning: In-orbit performance assessment. Measurement 2025, 243, 116314. [Google Scholar] [CrossRef]
- Ge, H.; Meng, G.; Li, B. LEO enhanced GNSS (LeGNSS) precise point positioning with emphasis on model comparison. Adv. Space Res. 2024, 74, 2156–2168. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Yang, Y.; Liang, C.; Liu, R. Spoofing and anti-spoofing technologies of global navigation satellite system: A survey. IEEE Access 2020, 8, 165444–165496. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, J.; Zhang, Y.; Yang, X.; Huang, H. Global Navigation Satellite System Terminal Spoofing and Defense Techniques. In Proceedings of the 2024 4th International Conference on Neural Networks, Information and Communication (NNICE), Guangzhou, China, 19–21 January 2024; pp. 1118–1127. [Google Scholar]
- Norhashim, N.; Kamal, N.M.; Sahwee, Z.; Shah, S.A.; Sathyamoorthy, D.; Alfian, N. Effect of Global Navigation Satellite Signal (GNSS) spoofing on unmanned aerial vehicles (UAVs) via field measurement. In Proceedings of the 2023 IEEE 16th Malaysia International Conference on Communication (MICC), Kuala Lumpur, Malaysia, 10–12 December 2023; pp. 41–45. [Google Scholar]
- Liu, Y.L.; Zhang, H.P.; Xu, Y.T. The Status and Progress of Global Satellite Navigation Systems. J. Navig. Position. 2019, 7, 18–21. [Google Scholar]
- Meng, L.; Yang, L.; Yang, W.; Zhang, L. A survey of GNSS spoofing and anti-spoofing technology. Remote Sens. 2022, 14, 4826. [Google Scholar] [CrossRef]
- Alrefaei, F.; Alzahrani, A.; Song, H.; Alrefaei, S. A survey on the jamming and spoofing attacks on the unmanned aerial vehicle networks. In Proceedings of the 2022 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS), Toronto, ON, Canada, 1–4 June 2022; pp. 1–7. [Google Scholar]
- Tedeschi, P.; Sciancalepore, S.; Di Pietro, R. Satellite-based communications security: A survey of threats, solutions, and research challenges. Comput. Netw. 2022, 216, 109246. [Google Scholar] [CrossRef]
- Gu, N.; Xing, F.; You, Z. Visual/Inertial/GNSS Integrated Navigation System under GNSS Spoofing Attack. Remote Sens. 2022, 14, 5975. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Liu, K.; Xu, K.; Luo, C.; Lv, Y.; Deng, Y. A Broadband Information Metasurface-Assisted Target Jamming System for Synthetic Aperture Radar. Remote Sens. 2024, 16, 1499. [Google Scholar] [CrossRef]
- Hills, A.; Peha, J.M.; Munk, J.; Pogorelc, S. Controlling antenna sidelobe radiation to mitigate ku-band leo-to-geo satellite interference. IEEE Access 2023, 11, 71154–71163. [Google Scholar] [CrossRef]
- Ries, L.; Limon, M.C.; Grec, F.C.; Anghileri, M.; Prieto-Cerdeira, R.; Abel, F.; Miguez, J.; Perello-Gisbert, J.V.; D’addio, S.; Ioannidis, R.; et al. LEO-PNT for augmenting Europe’s space-based PNT capabilities. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023; pp. 329–337. [Google Scholar]
- Shang, F.; Li, X.; Zhai, D.; Lu, Y.; Zhang, D.; Qian, Y. On the distributed jamming system of covert timing channels in 5G networks. In Proceedings of the 2020 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 27–29 June 2020; pp. 1107–1111. [Google Scholar]
- Qi, J.; Li, S.; Li, H.; Chen, J. Distributed Jamming Method Based on Spatial Superposition Effect: A Review. In Proceedings of the 2023 3rd International Conference on Electronic Information Engineering and Computer Science (EIECS), Changchun, China, 22–24 September 2023; pp. 654–660. [Google Scholar]
- Medina, D.; Lass, C.; Marcos, E.P.; Ziebold, R.; Closas, P.; García, J. On GNSS jamming threat from the maritime navigation perspective. In Proceedings of the 2019 22th International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, 2–5 July 2019; pp. 1–7. [Google Scholar]
- Silva Lorraine, K.J.; Ramarakula, M. A comprehensive survey on GNSS interferences and the application of neural networks for anti-jamming. IETE J. Res. 2023, 69, 4286–4305. [Google Scholar] [CrossRef]
- Tan, R.; Bu, Y.; Pan, B.; Yu, X.; Cui, G. Cooperative waveforms design for distributed sites in multiple blanket jamming. IEEE Sens. J. 2024, 24, 8774–8787. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, C.; Zhang, K.; Zhou, Q.; Yang, Z.; Zhang, J. A fast jamming waveform design method based on distributed precision jamming. In Proceedings of the 2022 2nd International Conference on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI), Nanjing, China, 23–25 September 2022; pp. 94–98. [Google Scholar]
- Yang, Y.; Zhu, L.; He, Q.; Deng, X. A simple high-performance generation method for spoofing jamming signals. In Proceedings of the 2022 International Symposium on Networks, Computers and Communications (ISNCC), Shenzhen, China, 19–22 July 2022; pp. 1–5. [Google Scholar]
- Sarikaya, B.S.; Bahtiyar, Ş. Generative Adversarial Networks for Synthetic Jamming Attacks on UAVs. In Proceedings of the 2024 9th International Conference on Computer Science and Engineering (UBMK), Antalya, Türkiye, 26–28 October 2024; pp. 760–765. [Google Scholar]
- Ji, N.; Rao, Y.; Wang, X.; Zou, D.; Chen, X.; Guo, Y. Spoofing Traction Strategy Based on the Generation of Traction Code. Remote Sens. 2023, 15, 500. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Cao, N. Research on spoofing jamming of integrated navigation system on uav. In Proceedings of the Artificial Intelligence and Security: 7th International Conference, ICAIS, Dublin, Ireland, 19–23 July 2021; Springer: Dublin, Ireland, 2021; pp. 3–13. [Google Scholar]
- Bian, S.; Hu, Y.; Chen, C.; Li, Z.; Ji, B. Research on GNSS repeater spoofing technique for fake Position, fake Time & fake Velocity. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1430–1434. [Google Scholar]
- Tang, X.; Wang, D.; Zhang, R.; Chu, Z.; Han, Z. Jamming mitigation via aerial reconfigurable intelligent surface: Passive beamforming and deployment optimization. IEEE Trans. Veh. Technol. 2021, 70, 6232–6237. [Google Scholar] [CrossRef]
- Liu, R.; Yang, Z.; Chen, Q.; Liao, G.; Zhen, W. GNSS multi-interference source centroid location based on clustering centroid convergence. IEEE Access 2021, 9, 108452–108465. [Google Scholar] [CrossRef]
- Zhang, K.; Zeng, F.; Zhao, Y.; Zeng, R. Study on index system of GPS interference effect evaluation. J. Phys. Conf. Ser. 2018, 1060, 020029. [Google Scholar]
- Tian, T.; Zhou, F.; Li, Y.; Fan, W. Evaluation of SAR Deception Jamming Effect based on Convolutional Neural Network. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–5. [Google Scholar]
- Wang, Y.; Sun, F.; Wang, X.; Hao, J.; Xiao, K. Full-domain collaborative deployment method of multiple interference sources and evaluation of its deployment effect. Def. Technol. 2024, 32, 572–595. [Google Scholar] [CrossRef]
- Li, J.J.; Rong, C.; Xiong, J. Dynamic WTA optimization model of air defense operation of warships’ formation. J. Syst. Eng. Electron. 2006, 17, 126–131. [Google Scholar]
- Chen, X.; Shi, H. Multi-platform air defence scheduling based on 0-1 integer linear programming. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 480–483. [Google Scholar]
- Zhao, J.; Liu, Y.; Song, H. Research on Jamming Resource Allocation Based on Improved Pelican Optimization Algorithm. In Proceedings of the 2022 21st International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Chizhou, China, 14–18 October 2022; pp. 123–127. [Google Scholar]
- Xia, J.; Ma, J.; Li, Y.; Song, M. Cooperative jamming resource allocation based on integer-encoded directed mutation artificial bee colony algorithm. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 695–700. [Google Scholar]
- Zhang, C.; Song, Y.; Jiang, R.; Hu, J.; Xu, S. A cognitive electronic jamming decision-making method based on Q-learning and ant colony fusion algorithm. Remote Sens. 2023, 15, 3108. [Google Scholar] [CrossRef]
- Xin, Q.; Xin, Z.; Chen, T. Cooperative Jamming Resource Allocation with Joint Multi-Domain Information Using Evolutionary Reinforcement Learning. Remote Sens. 2024, 16, 1955. [Google Scholar] [CrossRef]
- Gautam, M.; Bhusal, N.; Benidris, M. A cooperative game theory-based approach to sizing and siting of distributed energy resources. In Proceedings of the 2021 North American Power Symposium (NAPS), College Station, TX, USA, 14–16 November 2021; pp. 1–6. [Google Scholar]
- Sudhakar, M.; Srinivas, R.; Kamireddy, R.; Lokeshgupta, B. A Multi-Objective Optimization Model for Microgrid Optimal Operation with Cooperative Game Theory Approach. In Proceedings of the 2023 IEEE 20th India Council International Conference (INDICON), Hyderabad, India, 14–17 December 2023; pp. 299–304. [Google Scholar]
- Lee, J.; Noh, S.; Jung, S.; Lee, N. Coverage Analysis of LEO Satellite Downlink Networks: Orbital Geometry Dependent Approach. IEEE Access 2024, 12, 196939–196953. [Google Scholar] [CrossRef]
- Kang, E.; Park, Y.; Kim, J.; Choo, H. Downlink Analysis of a Low-Earth Orbit Satellite Considering an Airborne Interference Source Moving on Various Trajectories. Remote Sens. 2024, 16, 321. [Google Scholar] [CrossRef]


| SNR/dB | VR | A | B | C |
|---|---|---|---|---|
| 3 | 1 | 1.22 | 1.80 | 1.31 |
| 5 | 1 | 1.13 | 1.61 | 1.31 |
| 7 | 1 | 1.05 | 1.37 | 1.31 |
| 6 | 0.7 | 1.18 | 1.54 | 1.53 |
| 6 | 1.5 | 1.25 | 1.54 | 1.66 |
| 6 | 2 | 1.83 | 1.54 | 1.94 |
| Method | Time Complexity | Interference Success Rate |
|---|---|---|
| MSGA | 95.682% | |
| GA | 91.492% | |
| DP | 87.403% | |
| GD | 60.733% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, C.; Zhou, X.; Zhang, L.; Liu, Y.; Dan, Z. LEO Satellite Navigation Signal Multi-Dimensional Interference Optimisation Method Based on Hybrid Game Theory. Remote Sens. 2025, 17, 1444. https://doi.org/10.3390/rs17081444
Tang C, Zhou X, Zhang L, Liu Y, Dan Z. LEO Satellite Navigation Signal Multi-Dimensional Interference Optimisation Method Based on Hybrid Game Theory. Remote Sensing. 2025; 17(8):1444. https://doi.org/10.3390/rs17081444
Chicago/Turabian StyleTang, Chengkai, Xunbin Zhou, Lingling Zhang, Yangyang Liu, and Zesheng Dan. 2025. "LEO Satellite Navigation Signal Multi-Dimensional Interference Optimisation Method Based on Hybrid Game Theory" Remote Sensing 17, no. 8: 1444. https://doi.org/10.3390/rs17081444
APA StyleTang, C., Zhou, X., Zhang, L., Liu, Y., & Dan, Z. (2025). LEO Satellite Navigation Signal Multi-Dimensional Interference Optimisation Method Based on Hybrid Game Theory. Remote Sensing, 17(8), 1444. https://doi.org/10.3390/rs17081444







