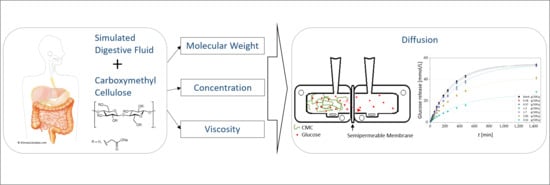
Effect of Physicochemical Properties of Carboxymethyl Cellulose on Diffusion of Glucose
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. CMC Solution Preparation
2.2.1. Solutions for Determining the Critical Concentration c*
2.2.2. Solutions for Determining the Glucose Diffusion
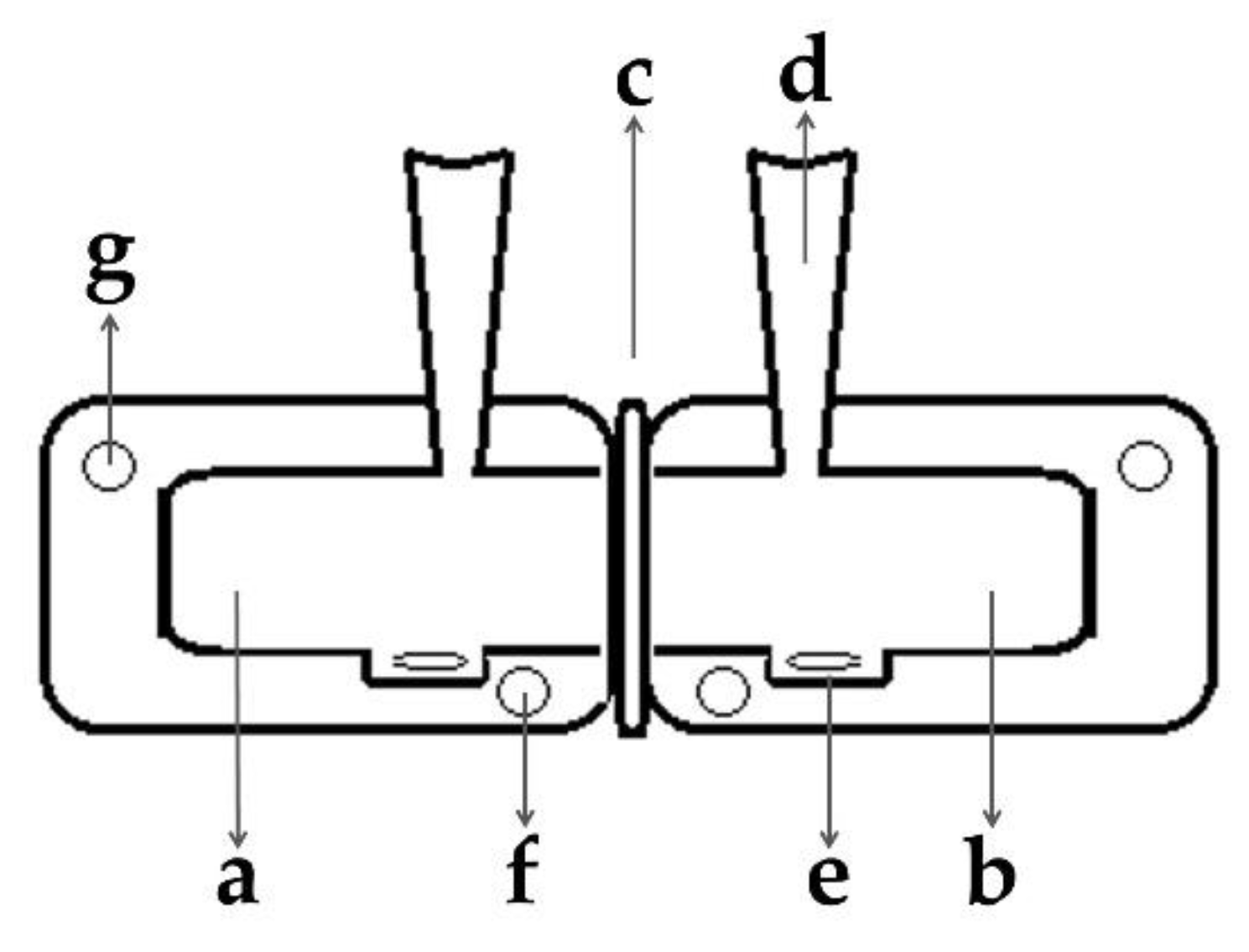
2.3. In Vitro Glucose Release (IVGR) Measurement and Glucose Determination
2.3.1. IVGR
2.3.2. Glucose Determination
2.4. Glucose Release Kinetics and Determination of the Diffusion Coefficient
2.4.1. Glucose Release Kinetics
2.4.2. Determination of the Diffusion Coefficient
2.5. Rheological Investigation
2.5.1. Zero-Shear Viscosity
2.5.2. Determination of Viscosity of CMC Solutions for Correlation to IVGR
2.5.3. Curve Fitting and Determination of the Critical Concentration c*
2.5.4. Determination of the Reynolds Number
2.6. Optical Density
2.7. Absolute Density
2.8. Cryo Scanning Electron Microscopy of CMC Solutions
2.9. Statistical Analysis
3. Results and Discussion
3.1. Flow Behavior and Determination of Critical Overlap Concentration c*
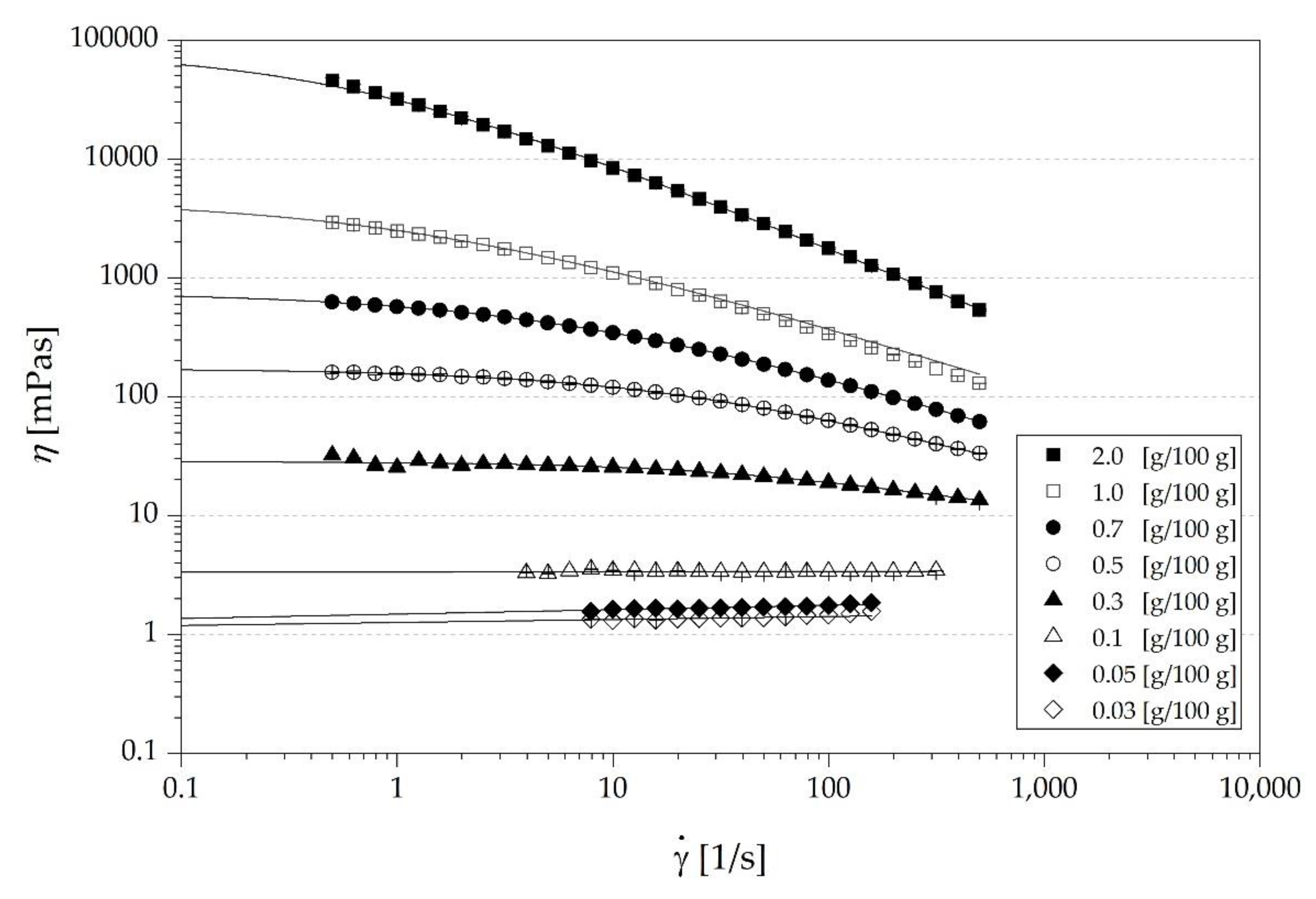
3.1.1. Flow Behavior of the CMC Solutions
3.1.2. Determination of c* of the CMC Solutions
3.2. Concentration-Dependent Diffusion of Glucose
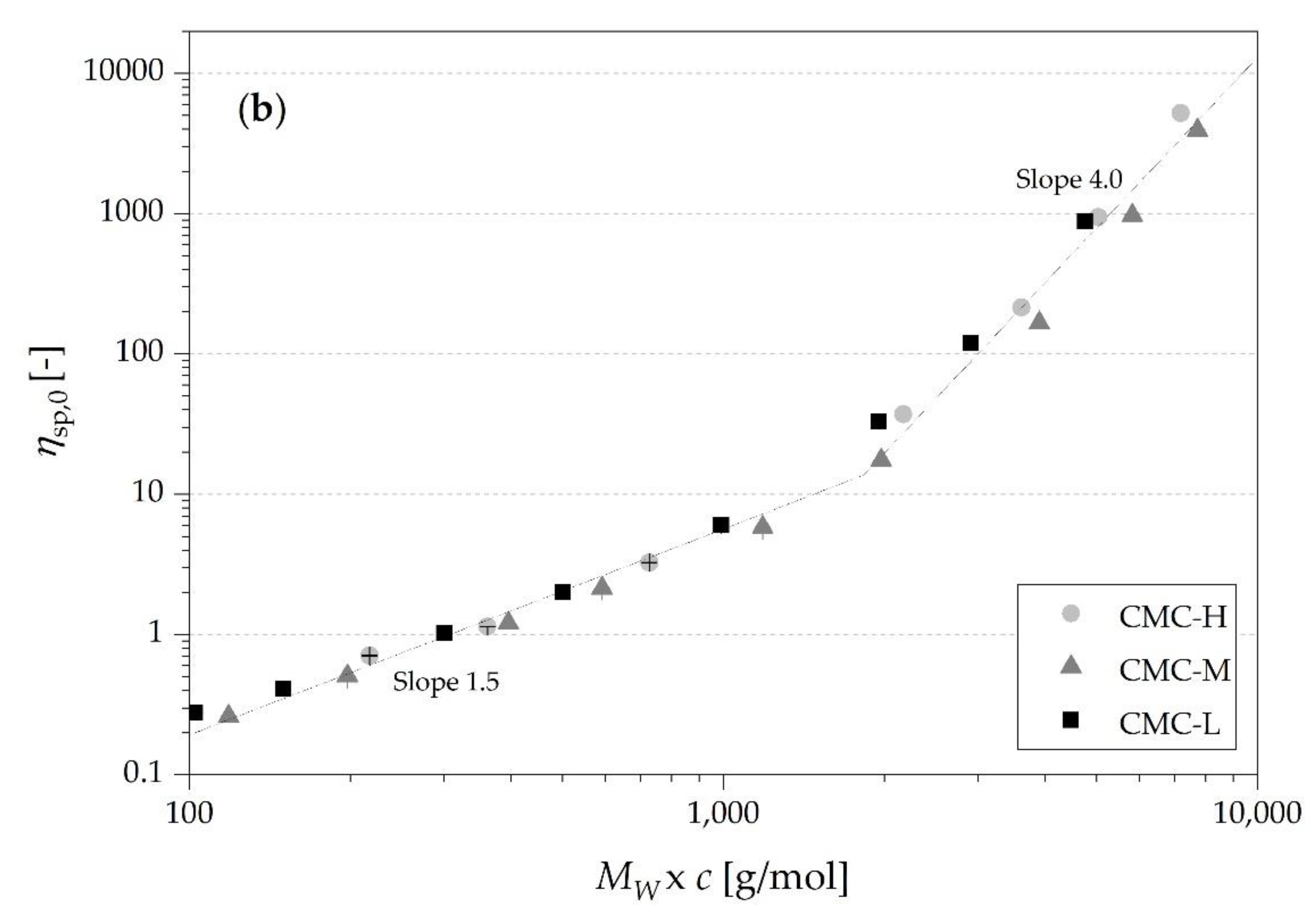
3.3. Correlations between Diffusion Coefficients, Concentrations and Molecular Weight
3.4. Correlations between Diffusion Coefficients and Viscosity—Deviation from Stokes-Einstein Equation
3.5. Impact of Convection
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jenkins, D.; Wolever, T.; Leeds, A.R.; Gassull, M.A.; Haisman, P.; Dilawari, J.; Goff, D.V.; Metz, G.L.; Alberti, K. Dietary fibres, fibre analogues, and glucose tolerance: Importance of viscosity. Br. Med. J. 1978, 1, 1392–1394. [Google Scholar] [CrossRef] [Green Version]
- Dikeman, C.L.; Murphy, M.R.; Fahey, G.C., Jr. Dietary fibers affect viscosity of solutions and simulated human gastric and small intestinal digesta. J. Nutr. 2006, 136, 913–919. [Google Scholar] [CrossRef] [Green Version]
- Fabek, H.; Messerschmidt, S.; Brulport, V.; Goff, H.D. The effect of in vitro digestive processes on the viscosity of dietary fibres and their influence on glucose diffusion. Food Hydrocoll. 2014, 35, 718–726. [Google Scholar] [CrossRef]
- Ou, S.; Kwok, K.-c.; Li, Y.; Fu, L. In vitro study of possible role of dietary fiber in lowering postprandial serum glucose. J. Agric. Food Chem. 2001, 49, 1026–1029. [Google Scholar] [CrossRef] [PubMed]
- Srichamroen, A.; Chavasit, V. In vitro retardation of glucose diffusion with gum extracted from malva nut seeds produced in thailand. Food Chem. 2011, 127, 455–460. [Google Scholar] [CrossRef] [PubMed]
- Eastwood, M.; Brydon, W.; Anderson, D. The effect of the polysaccharide composition and structure of dietary fibers on cecal fermentation and fecal excretion. Am. J. Clin. Nutr. 1986, 44, 51–55. [Google Scholar] [CrossRef]
- Adiotomre, J.; Eastwood, M.A.; Edwards, C.; Brydon, W.G. Dietary fiber: In vitro methods that anticipate nutrition and metabolic activity in humans. Am. J. Clin. Nutr. 1990, 52, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Brownlee, I.A. The physiological roles of dietary fibre. Food Hydrocoll. 2011, 25, 238–250. [Google Scholar] [CrossRef]
- Lentle, R.; Janssen, P. Physical characteristics of digesta and their influence on flow and mixing in the mammalian intestine: A review. J. Comp. Physiol. B 2008, 178, 673–690. [Google Scholar] [CrossRef] [PubMed]
- Johnson, I.; Gee, J.M. Effect of gel-forming gums on the intestinal unstirred layer and sugar transport in vitro. Gut 1981, 22, 398–403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lund, E.K.; Gee, J.; Brown, J.; Wood, P.; Johnson, I. Effect of oat gum on the physical properties of the gastrointestinal contents and on the uptake of d-galactose and cholesterol by rat small intestine in vitro. Br. J. Nutr. 1989, 62, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Macagno, E.; Christensen, J.; Lee, C. Modeling the effect of wall movement on absorption in the intestine. Am. J. Physiol. Gastrointest. Liver Physiol. 1982, 243, G541–G550. [Google Scholar] [CrossRef] [PubMed]
- Edwards, C.; Johnson, I.; Read, N. Do viscous polysaccharides slow absorption by inhibiting diffusion or convection? Eur. J. Clin. Nutr. 1988, 42, 307–312. [Google Scholar] [PubMed]
- Goff, H.D.; Repin, N.; Fabek, H.; El Khoury, D.; Gidley, M.J. Dietary fibre for glycaemia control: Towards a mechanistic understanding. Bioact. Carbohydr. Diet. Fibre 2018, 14, 39–53. [Google Scholar] [CrossRef]
- Nsor-Atindana, J.; Goff, H.D.; Liu, W.; Chen, M.; Zhong, F. The resilience of nanocrystalline cellulose viscosity to simulated digestive processes and its influence on glucose diffusion. Carbohydr. Polym. 2018, 200, 436–445. [Google Scholar] [CrossRef] [PubMed]
- Wood, P.J.; Braaten, J.T.; Scott, F.W.; Riedel, K.D.; Wolynetz, M.S.; Collins, M.W. Effect of dose and modification of viscous properties of oat gum on plasma glucose and insulin following an oral glucose load. Br. J. Nutr. 1994, 72, 731–743. [Google Scholar] [CrossRef]
- Morris, E.; Cutler, A.; Ross-Murphy, S.; Rees, D.; Price, J. Concentration and shear rate dependence of viscosity in random coil polysaccharide solutions. Carbohydr. Polym. 1981, 1, 5–21. [Google Scholar] [CrossRef]
- Alvarez-Manceñido, F.; Braeckmans, K.; De Smedt, S.C.; Demeester, J.; Landin, M.; Martínez-Pacheco, R. Characterization of diffusion of macromolecules in konjac glucomannan solutions and gels by fluorescence recovery after photobleaching technique. Int. J. Pharm. 2006, 316, 37–46. [Google Scholar] [CrossRef]
- Won, J.; Onyenemezu, C.; Miller, W.G.; Lodge, T.P. Diffusion of spheres in entangled polymer solutions: A return to stokes-einstein behavior. Macromolecules 1994, 27, 7389–7396. [Google Scholar] [CrossRef]
- Shelat, K.J.; Vilaplana, F.; Nicholson, T.M.; Gidley, M.J.; Gilbert, R.G. Diffusion and rheology characteristics of barley mixed linkage β-glucan and possible implications for digestion. Carbohydr. Polym. 2011, 86, 1732–1738. [Google Scholar] [CrossRef]
- Shelat, K.J.; Vilaplana, F.; Nicholson, T.M.; Wong, K.H.; Gidley, M.J.; Gilbert, R.G. Diffusion and viscosity in arabinoxylan solutions: Implications for nutrition. Carbohydr. Polym. 2010, 82, 46–53. [Google Scholar] [CrossRef]
- Tosh, S.M.; Brummer, Y.; Wolever, T.M.; Wood, P.J. Glycemic response to oat bran muffins treated to vary molecular weight of β-glucan. Cereal Chem. 2008, 85, 211–217. [Google Scholar] [CrossRef]
- Rieder, A.; Knutsen, S.H.; Ballance, S. In vitro digestion of beta-glucan rich cereal products results in extracts with physicochemical and rheological behavior like pure beta-glucan solutions—A basis for increased understanding of in vivo effects. Food Hydrocoll. 2017, 67, 74–84. [Google Scholar] [CrossRef]
- Wüstenberg, T. Cellulose and Cellulose Derivatives in the Food Industry: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Benchabane, A.; Bekkour, K. Rheological properties of carboxymethyl cellulose (cmc) solutions. Colloid Polym. Sci. 2008, 286, 1173. [Google Scholar] [CrossRef]
- Charpentier, D.; Mocanu, G.; Carpov, A.; Chapelle, S.; Merle, L.; Müller, G. New hydrophobically modified carboxymethylcellulose derivatives. Carbohydr. Polym. 1997, 33, 177–186. [Google Scholar] [CrossRef]
- Wagoner, T.B.; Çakır-Fuller, E.; Drake, M.; Foegeding, E.A. Sweetness perception in protein-polysaccharide beverages is not explained by viscosity or critical overlap concentration. Food Hydrocoll. 2019, 94, 229–237. [Google Scholar] [CrossRef]
- Cross, M.M. Rheology of non-newtonian fluids: A new flow equation for pseudoplastic systems. J. Colloid Sci. 1965, 20, 417–437. [Google Scholar] [CrossRef]
- Kpodo, F.; Agbenorhevi, J.; Alba, K.; Bingham, R.; Oduro, I.; Morris, G.; Kontogiorgos, V. Pectin isolation and characterization from six okra genotypes. Food Hydrocoll. 2017, 72, 323–330. [Google Scholar] [CrossRef] [Green Version]
- Minekus, M.; Alminger, M.; Alvito, P.; Ballance, S.; Bohn, T.; Bourlieu, C.; Carriere, F.; Boutrou, R.; Corredig, M.; Dupont, D. A standardised static in vitro digestion method suitable for food–an international consensus. Food Funct. 2014, 5, 1113–1124. [Google Scholar] [CrossRef] [Green Version]
- Macheras, P.; Koupparis, M.; Tsaprounis, C. An automated flow injection-serial dynamic dialysis technique for drug-protein binding studies. Int. J. Pharm. 1986, 30, 123–132. [Google Scholar] [CrossRef]
- Naumann, S.; Schweiggert-Weisz, U.; Bader-Mittermaier, S.; Haller, D.; Eisner, P. Differentiation of adsorptive and viscous effects of dietary fibres on bile acid release by means of in vitro digestion and dialysis. Int. J. Mol. Sci. 2018, 19, 2193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Espinal-Ruiz, M.; Restrepo-Sánchez, L.-P.; Narváez-Cuenca, C.-E. Effect of pectins on the mass transfer kinetics of monosaccharides, amino acids, and a corn oil-in-water emulsion in a franz diffusion cell. Food Chem. 2016, 209, 144–153. [Google Scholar] [CrossRef]
- Higuchi, W.I. Analysis of data on the medicament release from ointments. J. Pharm. Sci. 1962, 51, 802–804. [Google Scholar] [CrossRef] [PubMed]
- Mass and Density. Food Physics: Physical Properties—Measurement and Applications; Springer: Berlin/Heidelberg, Germany, 2007; pp. 41–72. [Google Scholar]
- Morris, E.R. Assembly and rheology of non-starch polysaccharides. Adv. Diet. Fibre Technol. 2001, 30–41. [Google Scholar] [CrossRef]
- Cook, D.J.; Hollowood, T.A.; Linforth, R.S.; Taylor, A.J. Perception of taste intensity in solutions of random-coil polysaccharides above and below c*. Food Qual. Prefer. 2002, 13, 473–480. [Google Scholar] [CrossRef]
- Wang, Q.; Ellis, P.R.; Ross-Murphy, S.B.; Burchard, W. Solution characteristics of the xyloglucan extracted from detarium senegalense gmelin. Carbohydr. Polym. 1997, 33, 115–124. [Google Scholar] [CrossRef]
- Qi, J.; Li, Y.; Masamba, K.G.; Shoemaker, C.F.; Zhong, F.; Majeed, H.; Ma, J. The effect of chemical treatment on the in vitro hypoglycemic properties of rice bran insoluble dietary fiber. Food Hydrocoll. 2016, 52, 699–706. [Google Scholar] [CrossRef]
- Liu, L.; Kerr, W.L.; Kong, F.; Dee, D.R.; Lin, M. Influence of nano-fibrillated cellulose (nfc) on starch digestion and glucose absorption. Carbohydr. Polym. 2018, 196, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Xu, S.-Z.; Dong, W.-R.; Wu, Z.; Wang, R.-H.; Chen, Z.-X. Influence of carboxymethyl cellulose and sodium alginate on sweetness intensity of aspartame. Food Chem. 2014, 164, 278–285. [Google Scholar] [CrossRef]
- Fujita, H. Diffusion in polymer-diluent systems. In Fortschritte der Hochpolymeren-Forschung; Springer: Berlin/Heidelberg, Germany, 1961; pp. 1–47. [Google Scholar]
- Liu, S.P.; Sa, C.; li Hu, X.; Kong, L. Fluorescence quenching method for the determination of sodium carboxymethyl cellulose with acridine yellow or acridine orange. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2006, 64, 817–822. [Google Scholar] [CrossRef]
- Szyper, M.; Zuman, P. Electronic absorption of carboxylic acids and their anions. Anal. Chim. Acta 1976, 85, 357–373. [Google Scholar] [CrossRef]
- Dhital, S.; Dolan, G.; Stokes, J.R.; Gidley, M.J. Enzymatic hydrolysis of starch in the presence of cereal soluble fibre polysaccharides. Food Funct. 2014, 5, 579–586. [Google Scholar] [CrossRef] [PubMed]

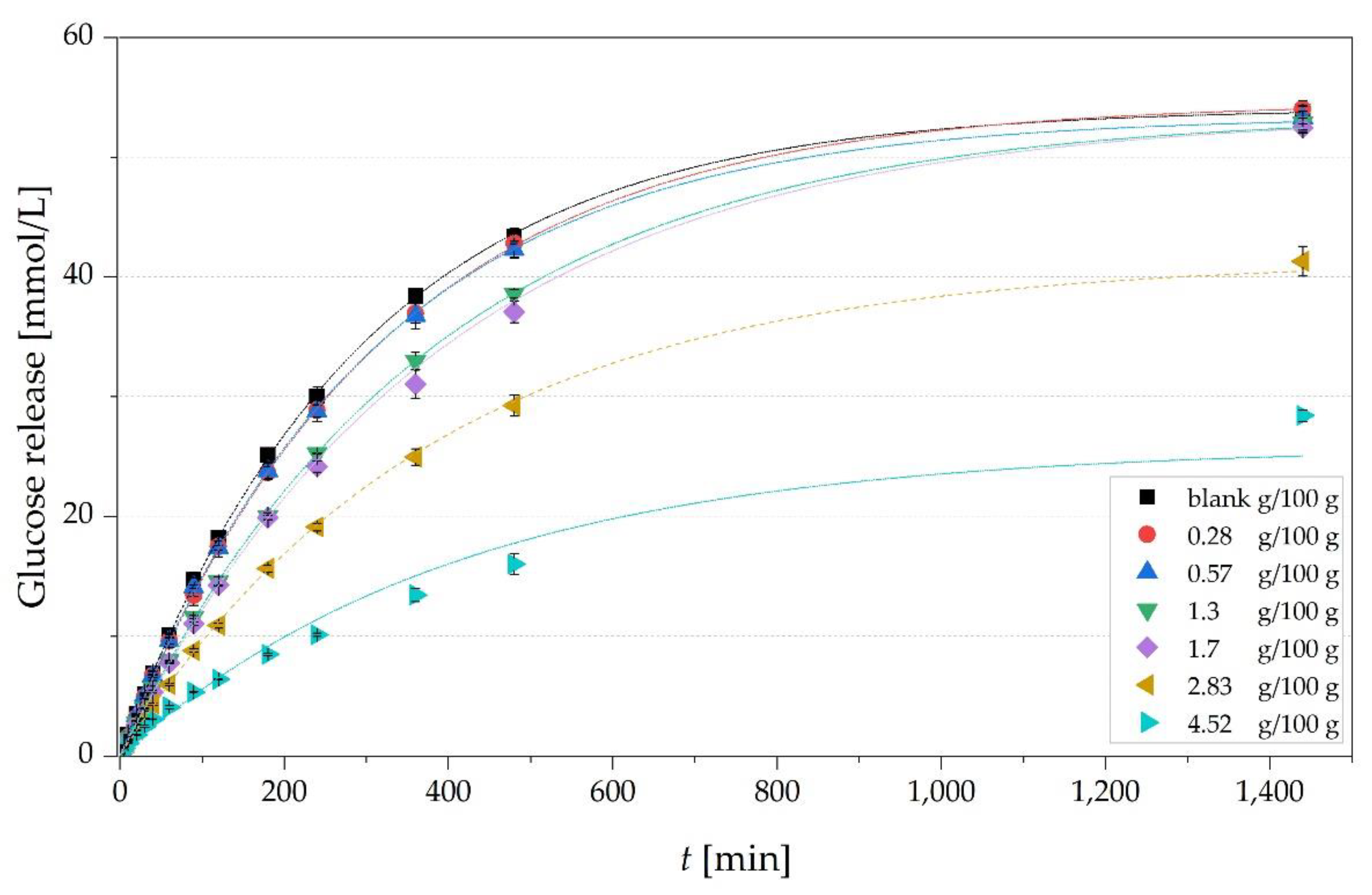
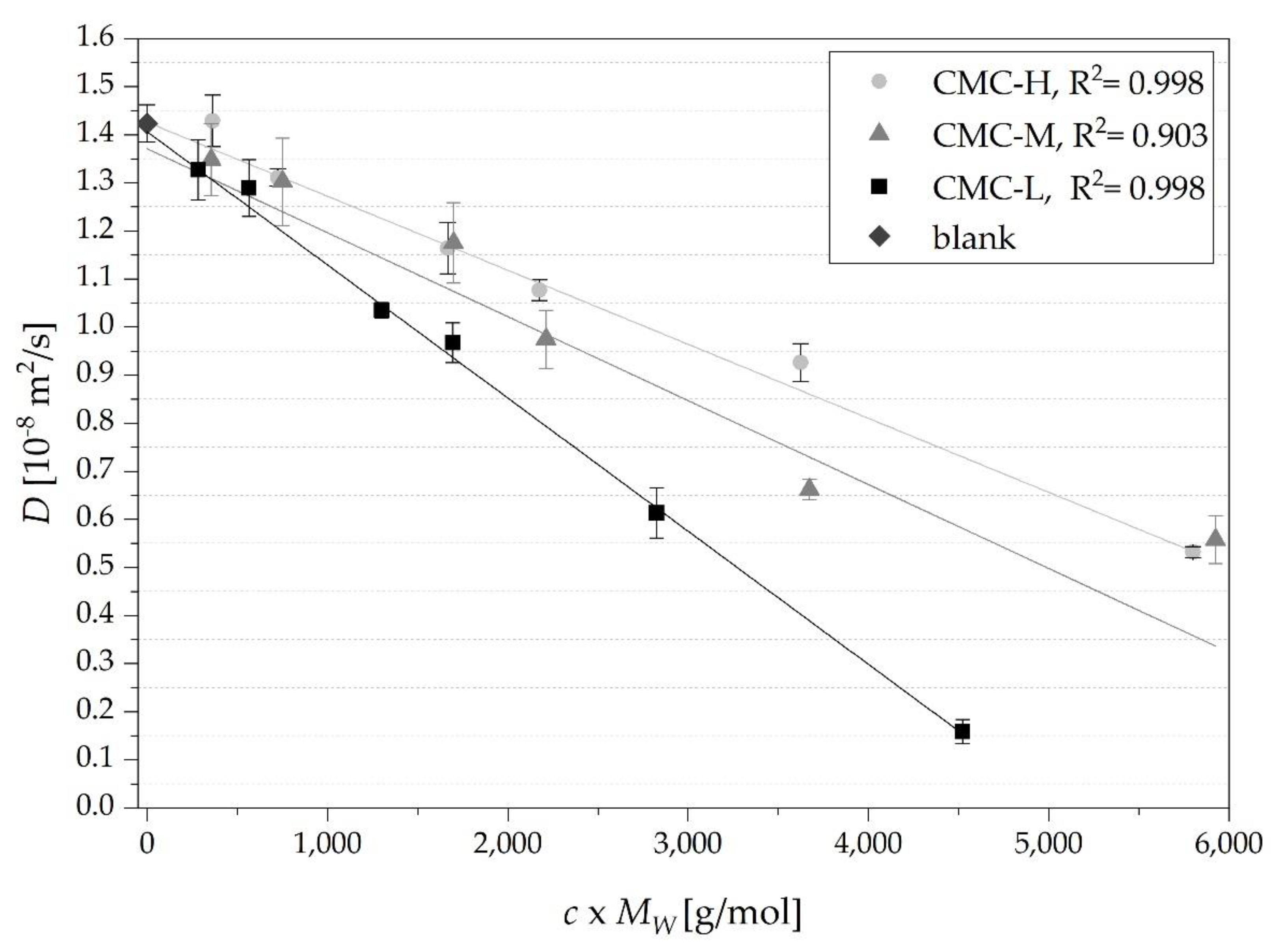


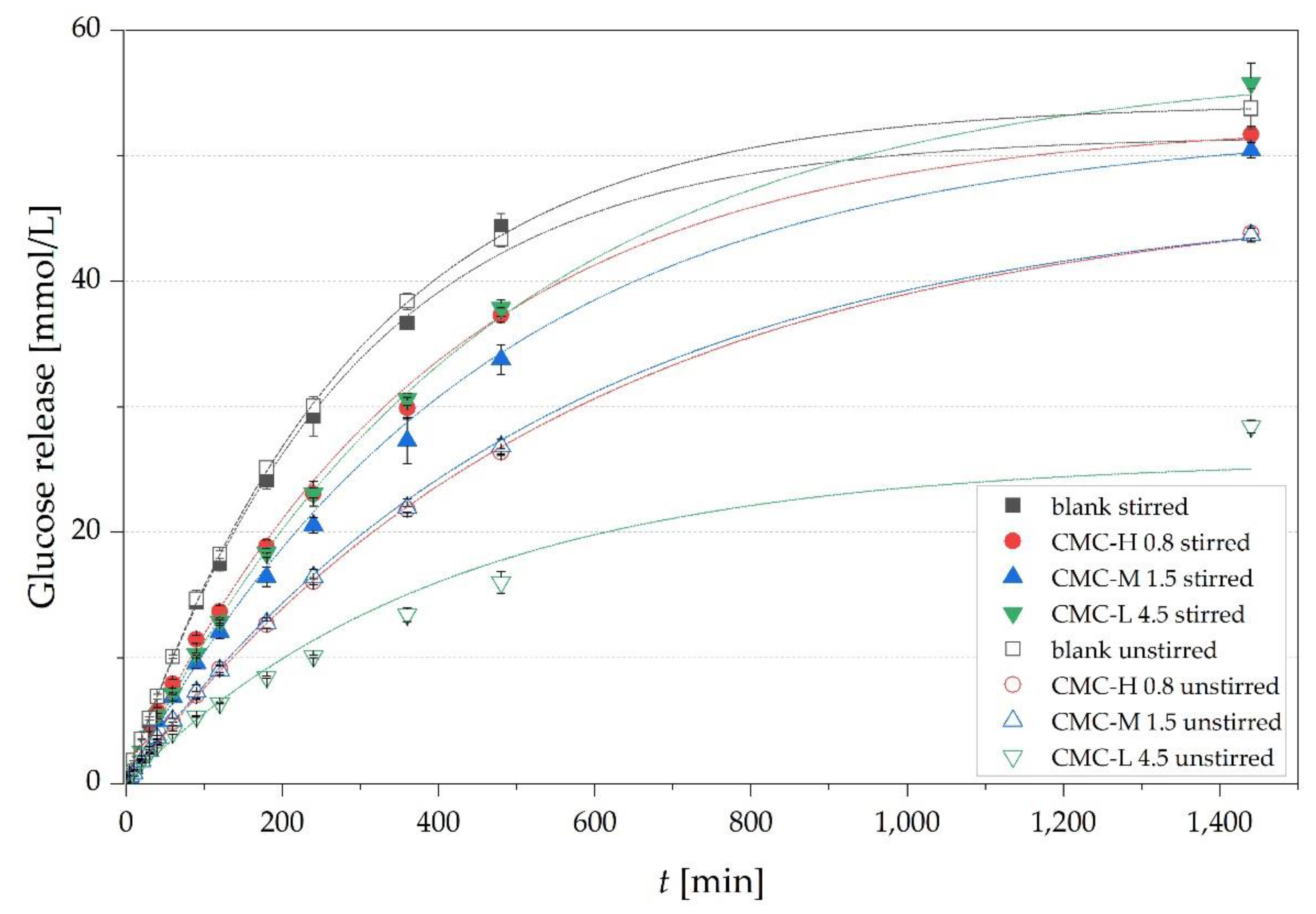
| Calculation | Concentration [g/100 g] | ||
|---|---|---|---|
| CMC-L | CMC-M | CMC-H | |
| c0 = 0 | 0 | 0 | 0 |
| c1 = 0.22 × c* | 0.28 | 0.09 | 0.05 |
| c2 = 0.43 × c* | 0.57 | 0.19 | 0.10 |
| c* | 1.30 | 0.43 | 0.23 |
| c4 = 1.30 × c* | 1.70 | 0.56 | 0.30 |
| c5 = 2.17 × c* | 2.83 | 0.93 | 0.50 |
| c6 = 3.48 × c* | 4.52 | 1.50 | 0.80 |
| Concentration | η0 [mPa s] | η0 after 24 h [mPa s] | Diffusion Coefficient (D) [10−8 m2s−1] | Maximum GTI [%] | Optical Density at 285 nm |
|---|---|---|---|---|---|
| 0 × c* (blank) | 0.8 ± 0.0 a | 0.8 ± 0.0 a | 1.42 ± 0.04 a | 100.0 ± 0.3 a | 0.17 ± 0.0 a |
| CMC-L | |||||
| 0.2 × c* (0.28 g/100 g) | 1.5 ± 0.0 a | 1.6 ± 0.0 a | 1.33 ± 0.06 a,b | 100.9 ± 0.5 a | 0.23 ± 0.0 a |
| 0.4 × c* (0.57 g/100 g) | 2.6 ± 0.1 a | 2.7 ± 0.0 a | 1.29 ± 0.06 a,b | 98.7 ± 0.6 a | 0.28 ± 0.03 a |
| c* (1.30 g/100 g) | 8.3 ± 0.1 a | 8.8 ± 0.2 a | 1.03 ± 0.02 c | 99.1 ± 1.0 a | 0.48 ± 0.02 b |
| 1.3 × c* (1.70 g/100 g) | 14.5 ± 0.2 b | 15.3 ± 1.1 a | 0.97 ± 0.04 c | 99.3 ± 0.5 a | 0.55 ± 0.07 b |
| 2.2 × c* (2.83 g/100 g) | 78.7 ± 2.0 c | 66.9 ± 5.4 b | 0.61 ± 0.05 d | 76.5 ± 1.5 b | 0.88 ± 0.02 c |
| 3.5 × c* (4.52 g/100 g) | 519 ± 9.1 d | 559.5 ± 16.1 c | 0.16 ± 0.02 e | 47.8 ± 6.3 c | 1.4 ± 0.04 d |
| CMC-M | |||||
| 0.2 × c* (0.09 g/100 g) | 1.7 ± 0 a | 1.8 ± 0.1 a | 1.35 ± 0.08 a,b | 101.5 ± 0.7 a | 0.18 ± 0.0 a |
| 0.4 × c* (0.19 g/100 g) | 3.4 ± 0.1 a | 2.9 ± 0 a | 1.3 ± 0.09 a,b | 98.3 ± 0.9 a | 0.2 ± 001 a |
| c* (0.43 g/100 g) | 11.3 ± 0.4 a,b | 11 ± 0.2 a | 1.18 ± 0.08 b,c | 97.0 ± 1.8 a | 0.25 ± 0.0 b |
| 1.3 × c* (0.56 g/100 g) | 17.9 ± 0.1 b | 19.5 ± 0.4 a | 0.97 ± 0.06 c | 89.6 ± 1.0 b | 0.28 ± 0.01 b |
| 2.2 × c* (0.93 g/100 g) | 99.8 ± 3.1 c | 99.1 ± 6.3 b | 066 ± 0.02 d | 88.0 ± 1.2 b | 0.35 ± 0.03 c |
| 3.5 × c* (1.50 g/100 g) | 816.2 ± 12.6 d | 1010.2 ± 18.0 c | 0.56 ± 0.02 d | 86.5 ± 1.3 b | 0.51 ± 0.01 d |
| CMC-H | |||||
| 0.2 × c* (0.05 g/100 g) | 1.9 ± 0.1 a | 1.7 ± 0.0 a | 1.43 ± 0.05 a | 102.7 ± 3.3 a | 0.18 ± 0.0 a |
| 0.4 × c* (0.10 g/100 g) | 3.5 ± 0.5 a | 3.7 ± 0.2 a | 1.31 ± 0.02 a | 102.5 ± 1.0 a | 0.2 ± 0.0 a |
| c* (0.23 g/100 g) | 14.9 ± 1.2 a | 15.2 ± 1 a | 1.16 ± 0.05 b | 98.6 ± 1.1 a | 0.24 ± 0.0 b |
| 1.3 × c* (0.30 g/100 g) | 15 ± 0.7 a | 15.1 ± 0.3 a | 1.08 ± 0.02 b | 97.8 ± 1.8 a | 0.26 ± 0.0 b |
| 2.2 × c* (0.50 g/100 g) | 159.2 ± 4.1 b | 165.1 ± 3.1 b | 0.93 ± 0.04 c | 94.7 ± 1.2 b | 0.32 ± 0.01 c |
| 3.5 × c* (0.80 g/100 g) | 1355.3 ± 41.2 c | 1744.5 ± 30 c | 0.53 ± 0.01 d | 87.3 ± 2.0 c | 0.46 ± 0.02 d |
| Sample | Maximum GTI [%] | K [Pa s] | n [-] | = 158 s−1) [mPa s] | Re [-] | Density [kg/m3] |
|---|---|---|---|---|---|---|
| CMC-L 4.52 g/100 g | 111.2 ± 3.2 a | 0.5 ± 0.01 a | 0.91 ± 0 a | 320 ± 6.3 a | 0.13 ± 0 a | 1027 ± 0.8 a |
| CMC-M 1.5 g/100 g | 101.6 ± 1.4 a | 0.76± 0.02 b | 0.77 ± 0 b | 221.5 ± 4 b | 0.08 ± 0.02 a,b | 1011.5 ± 2.1 b |
| CMC-H 0.8 g/100 g | 102.3 ± 1.6 a | 1.09 ± 0.04 c | 0.66 ± 0.01 c | 175 ± 4.3 c | 0.06 ± 0.02 b | 1007.9 ± 0.7 b |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miehle, E.; Bader-Mittermaier, S.; Schweiggert-Weisz, U.; Hauner, H.; Eisner, P. Effect of Physicochemical Properties of Carboxymethyl Cellulose on Diffusion of Glucose. Nutrients 2021, 13, 1398. https://doi.org/10.3390/nu13051398
Miehle E, Bader-Mittermaier S, Schweiggert-Weisz U, Hauner H, Eisner P. Effect of Physicochemical Properties of Carboxymethyl Cellulose on Diffusion of Glucose. Nutrients. 2021; 13(5):1398. https://doi.org/10.3390/nu13051398
Chicago/Turabian StyleMiehle, Elisabeth, Stephanie Bader-Mittermaier, Ute Schweiggert-Weisz, Hans Hauner, and Peter Eisner. 2021. "Effect of Physicochemical Properties of Carboxymethyl Cellulose on Diffusion of Glucose" Nutrients 13, no. 5: 1398. https://doi.org/10.3390/nu13051398
APA StyleMiehle, E., Bader-Mittermaier, S., Schweiggert-Weisz, U., Hauner, H., & Eisner, P. (2021). Effect of Physicochemical Properties of Carboxymethyl Cellulose on Diffusion of Glucose. Nutrients, 13(5), 1398. https://doi.org/10.3390/nu13051398