Development of an Electromagnetic Micromanipulator Levitation System for Metal Additive Manufacturing Applications
Abstract
:1. Introduction
2. Theory
2.1. Working Principle
- According to Ampere’s Law, the time varying currents of the coil will produce time-varying magnetic fields
- According to Faraday’s Law, the axial component of the time-varying magnetic fields will induce a voltage in conductors placed in close proximity to the micromanipulator levitation system. This will result in the induction of currents in the conductors. These induced currents are called eddy currents.
- According to Lorentz’ Law, the induced eddy currents will interact with the radial component of the source magnetic field to generate repulsive force. This resulting force will be responsible for the levitation of the levitated object.
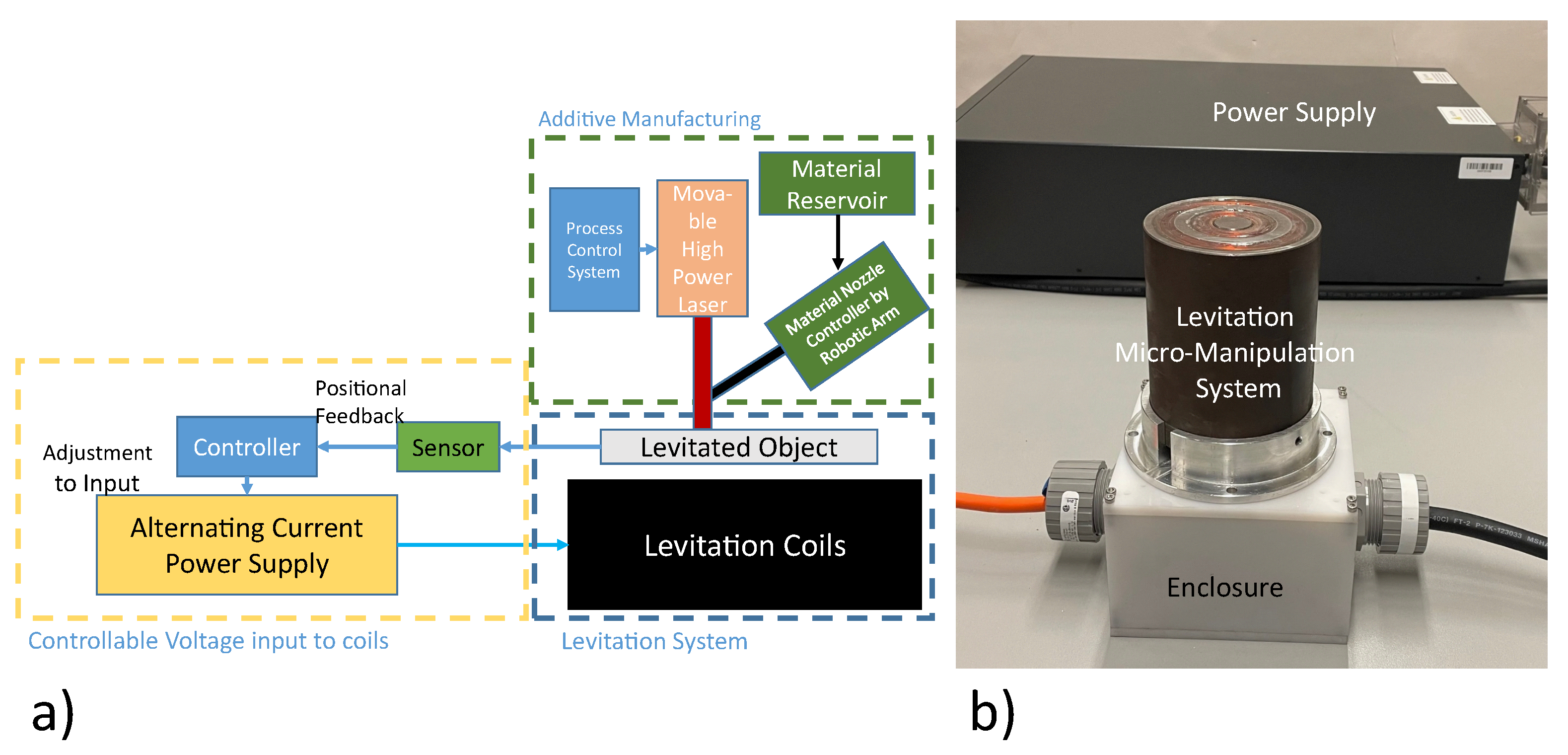
2.2. Electromagnetic Micromanipulator Levitation System
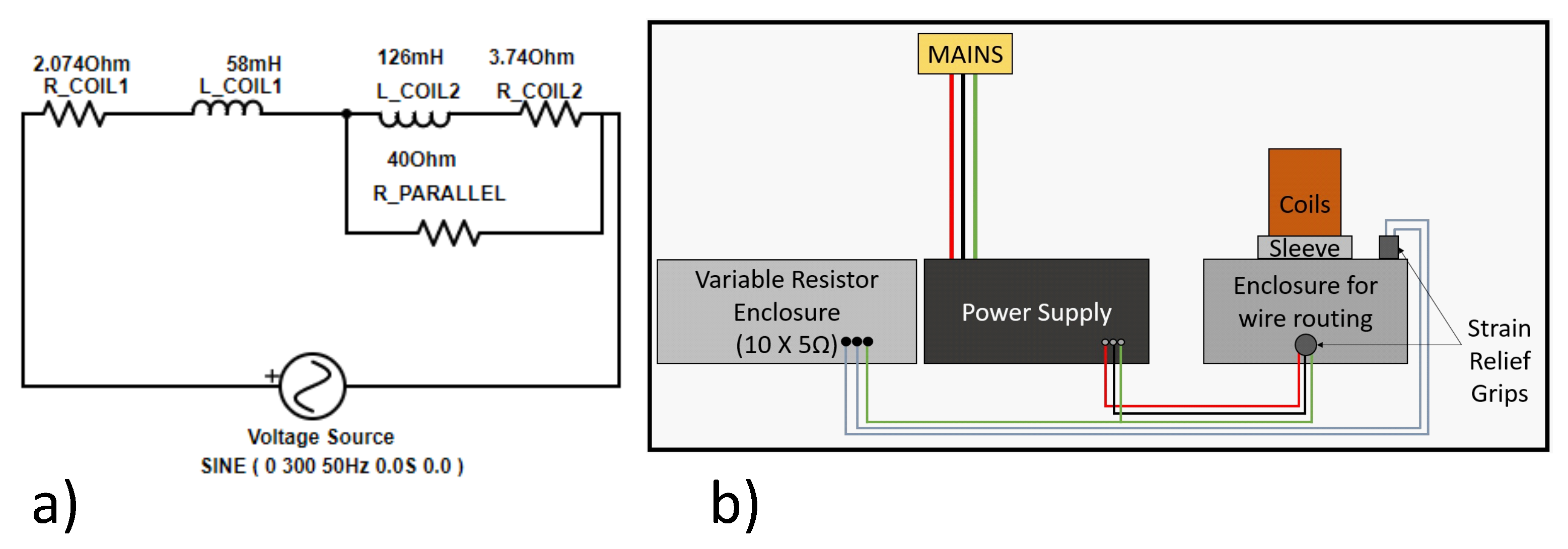
2.3. Micromanipulator Levitation System as a Series RLC Circuit
2.4. Magnetomotive Force of Coils
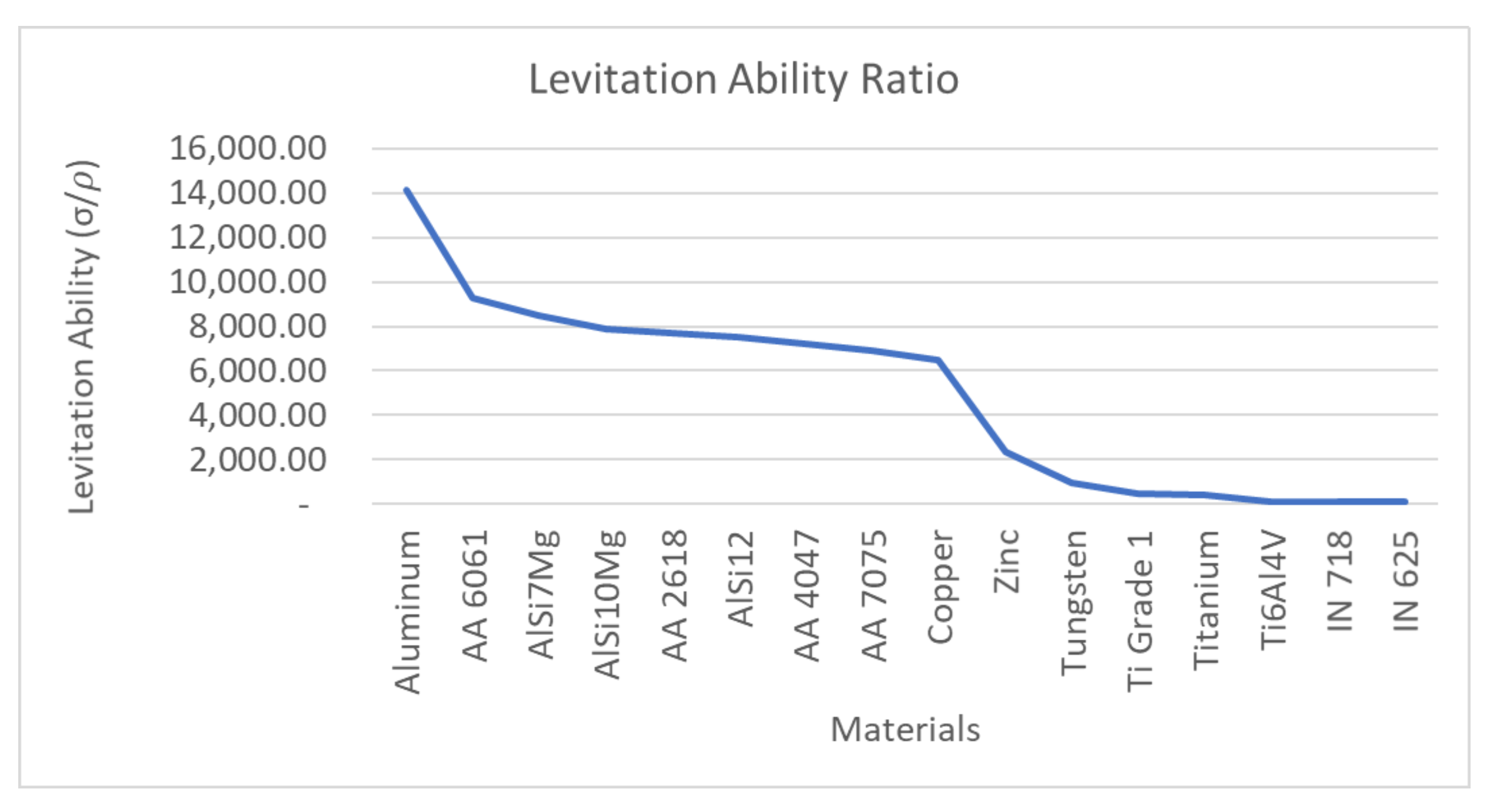
2.5. Levitation Ability
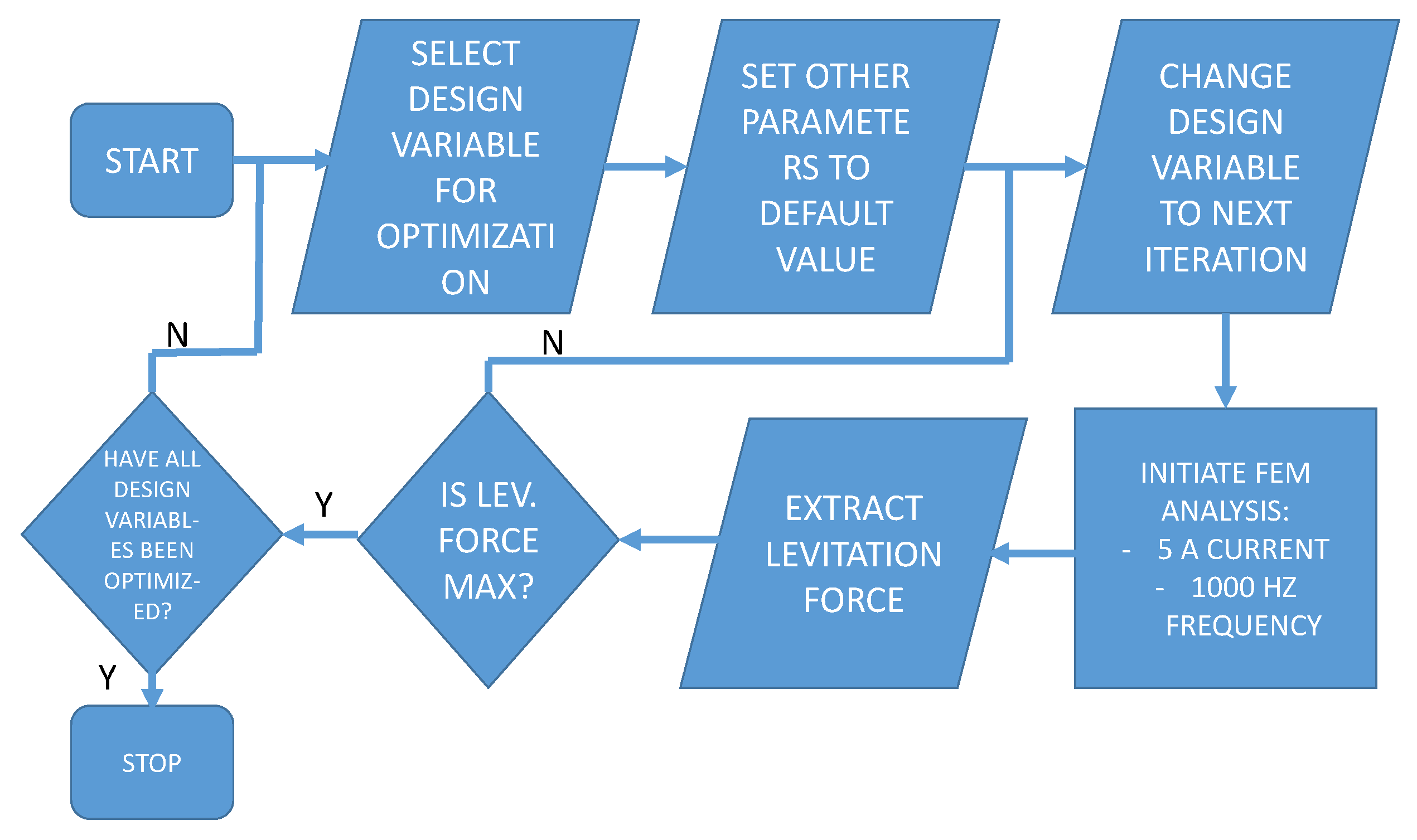
3. Design and Optimization of the Micromanipulator Levitation System
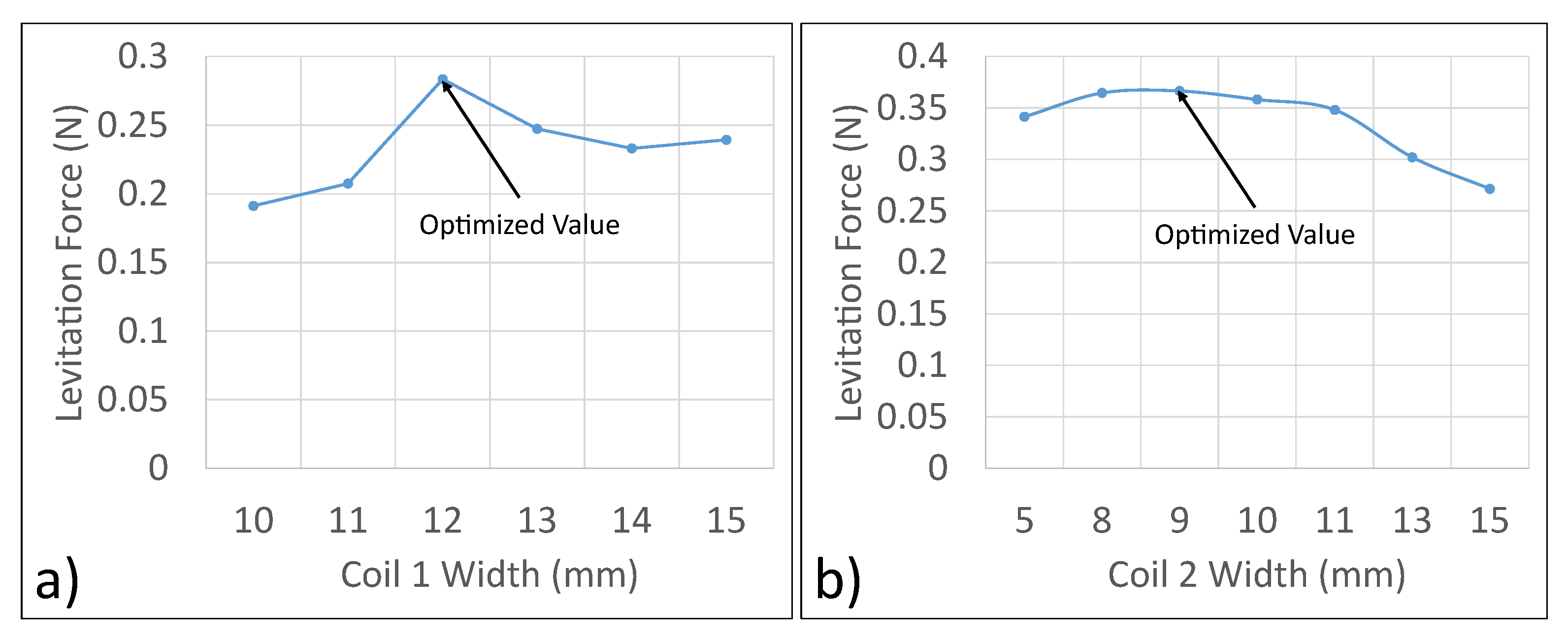
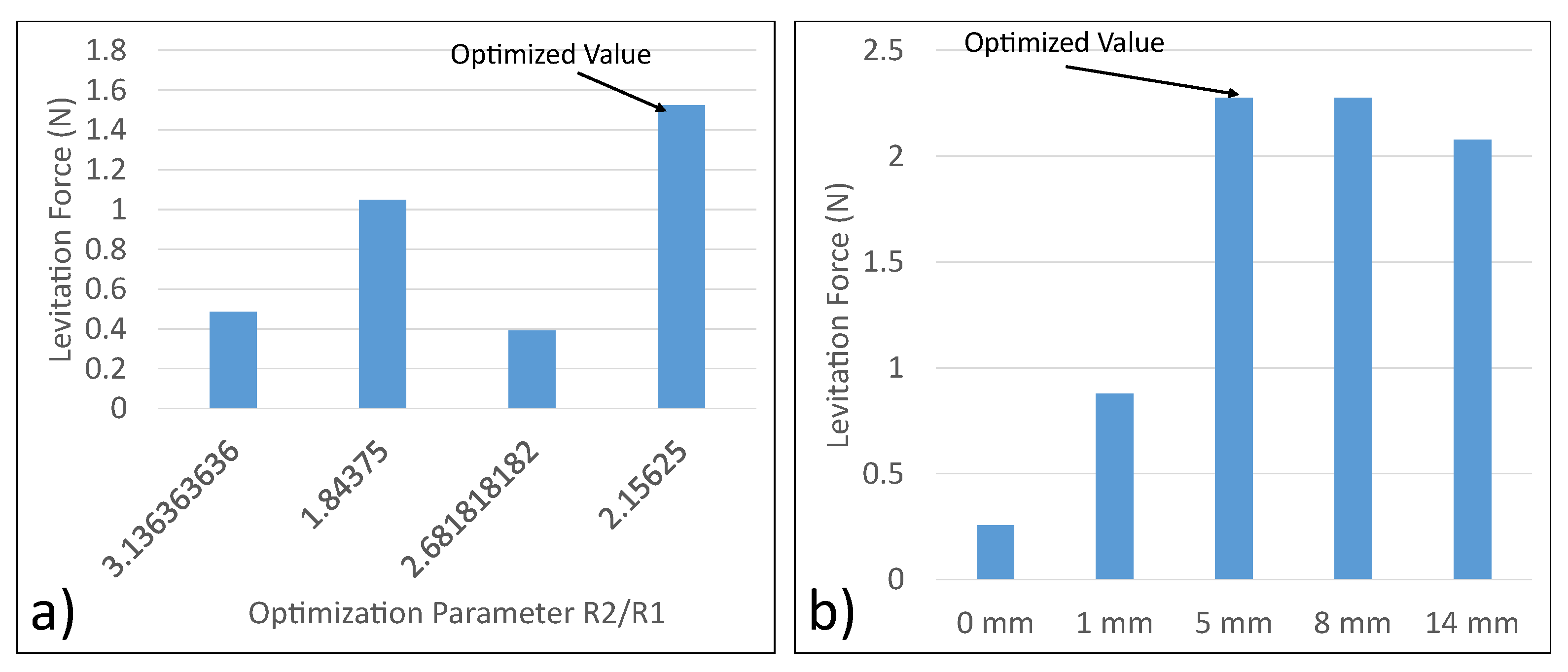
3.1. Optimization of Width of Coils
3.2. Optimization of the Radial Placement of Teh Coil
3.3. Calculation of Coil Height
3.4. Optimization of Baseplate
3.5. Selection of Core Material
3.6. Frequency of Operation
4. Free Levitation Experiment
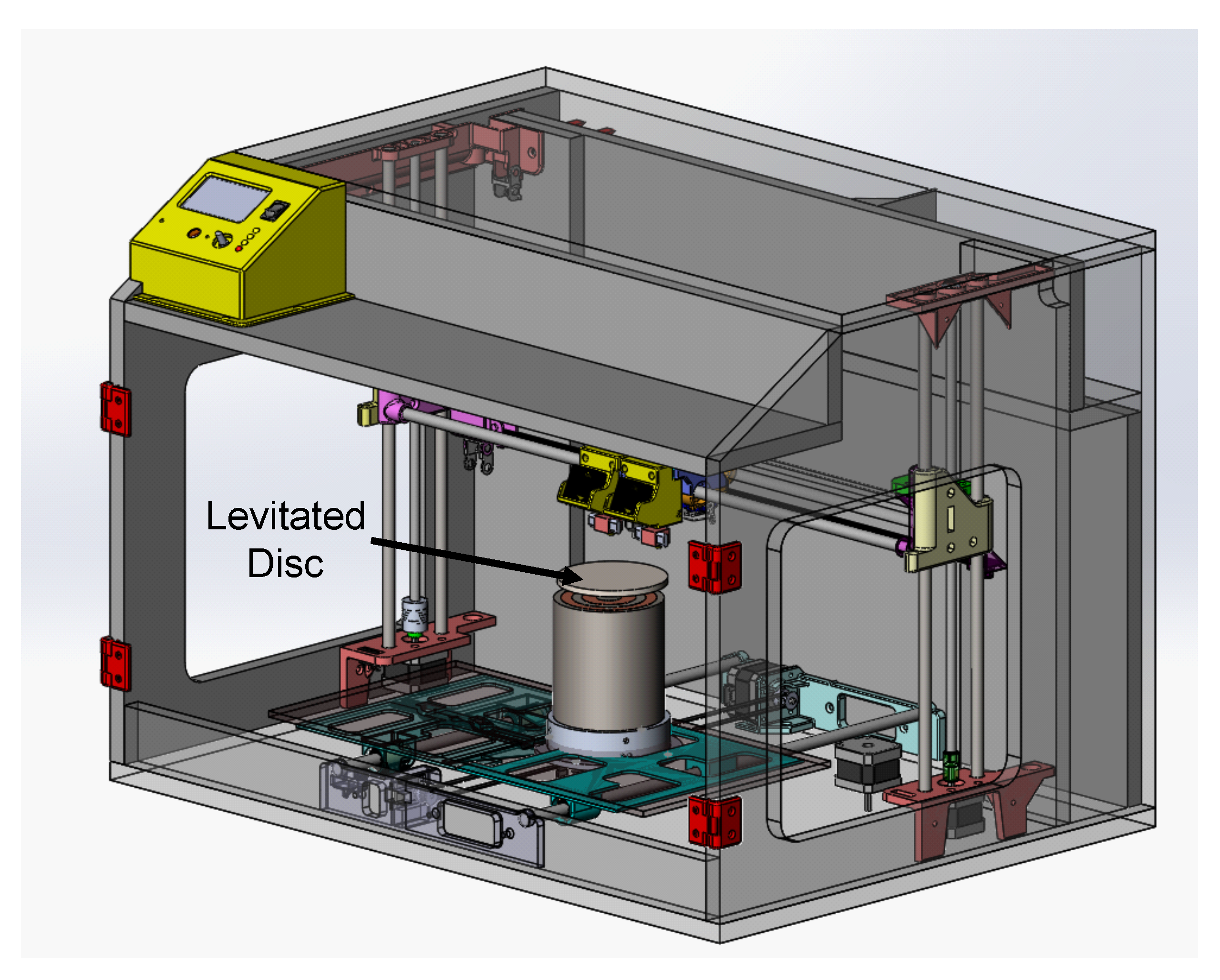
4.1. Initial Levitation Experiment
4.2. Strength of Coils
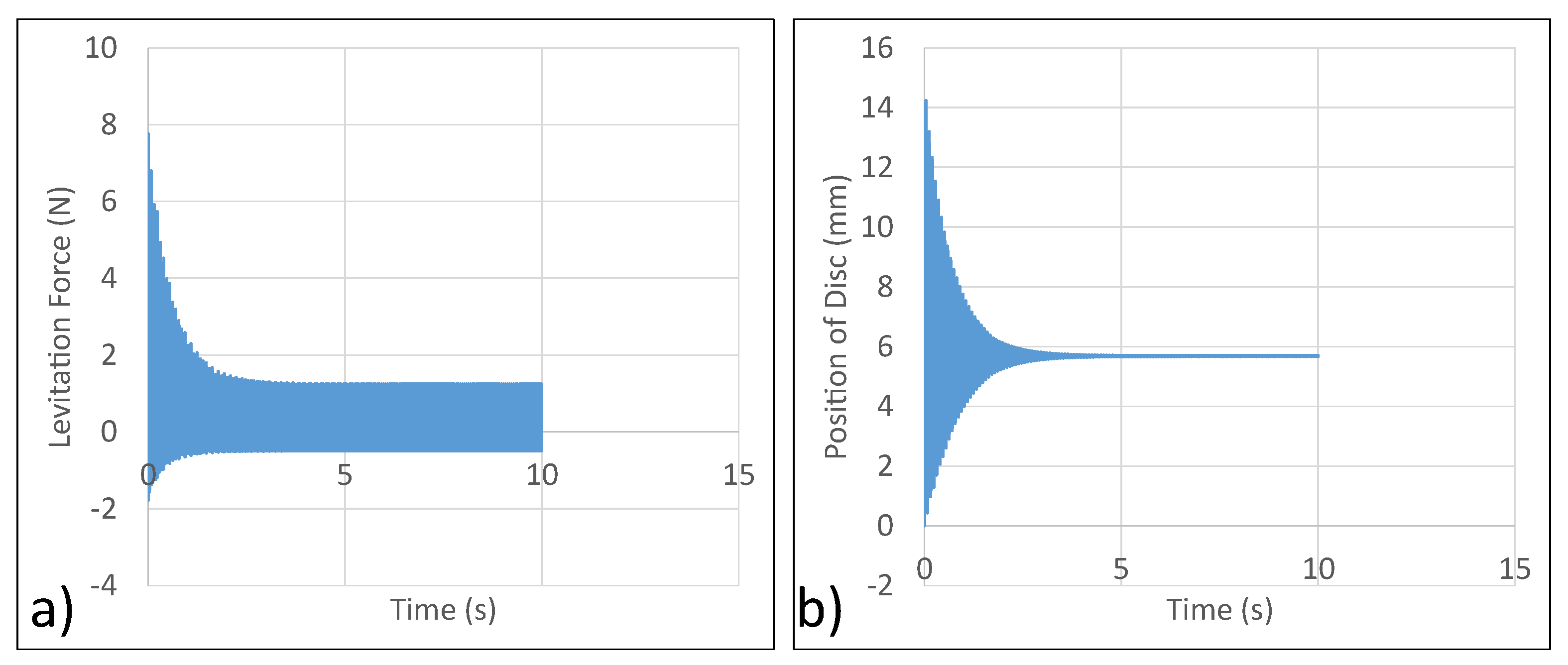
4.3. Simulation Analysis
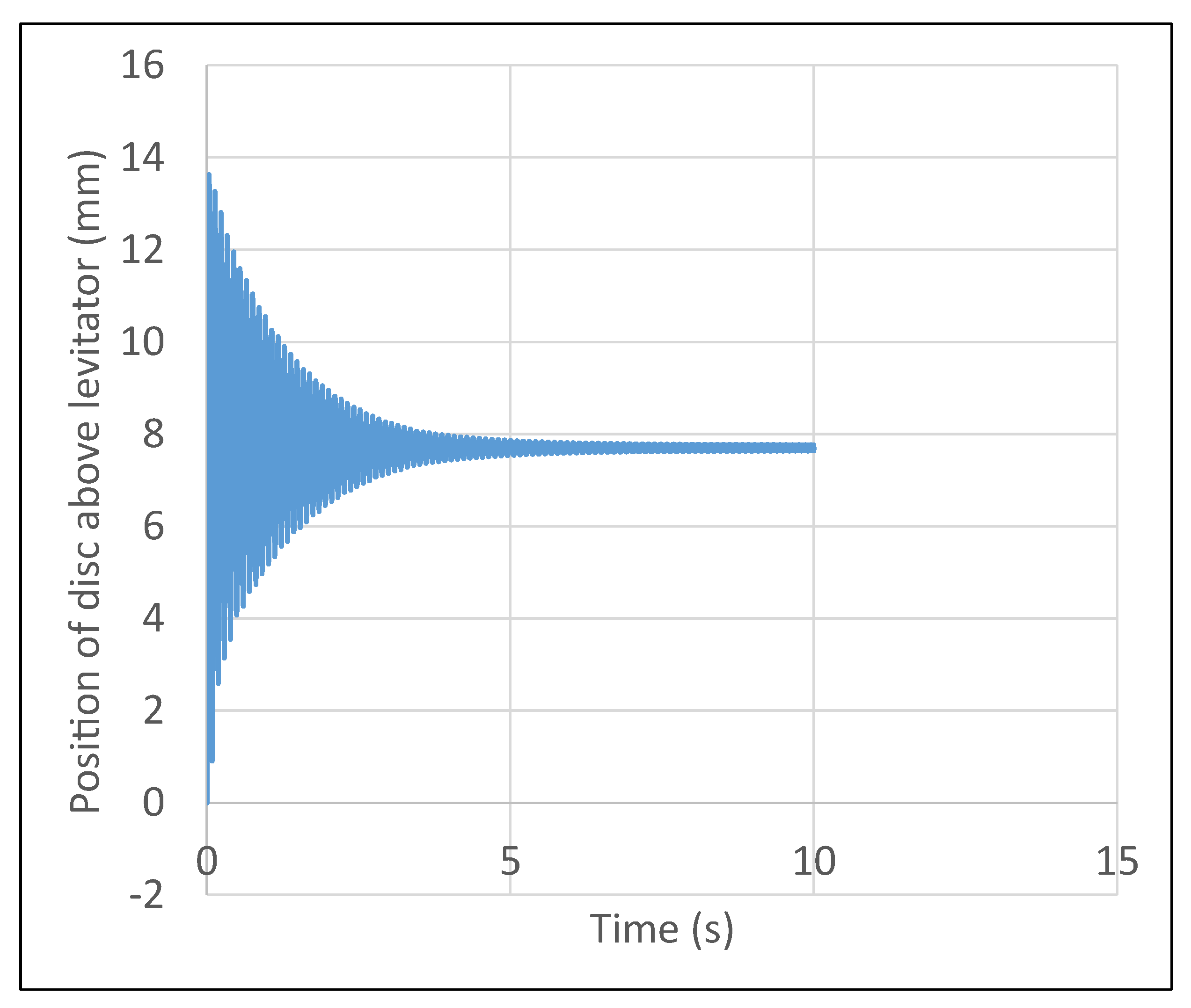
4.4. Experimental Analysis
4.5. Experimental Analysis with Additional Payload
5. Semi-Levitation Experiment
5.1. Need for Semi-Levitation Experiment
5.2. Working Principle
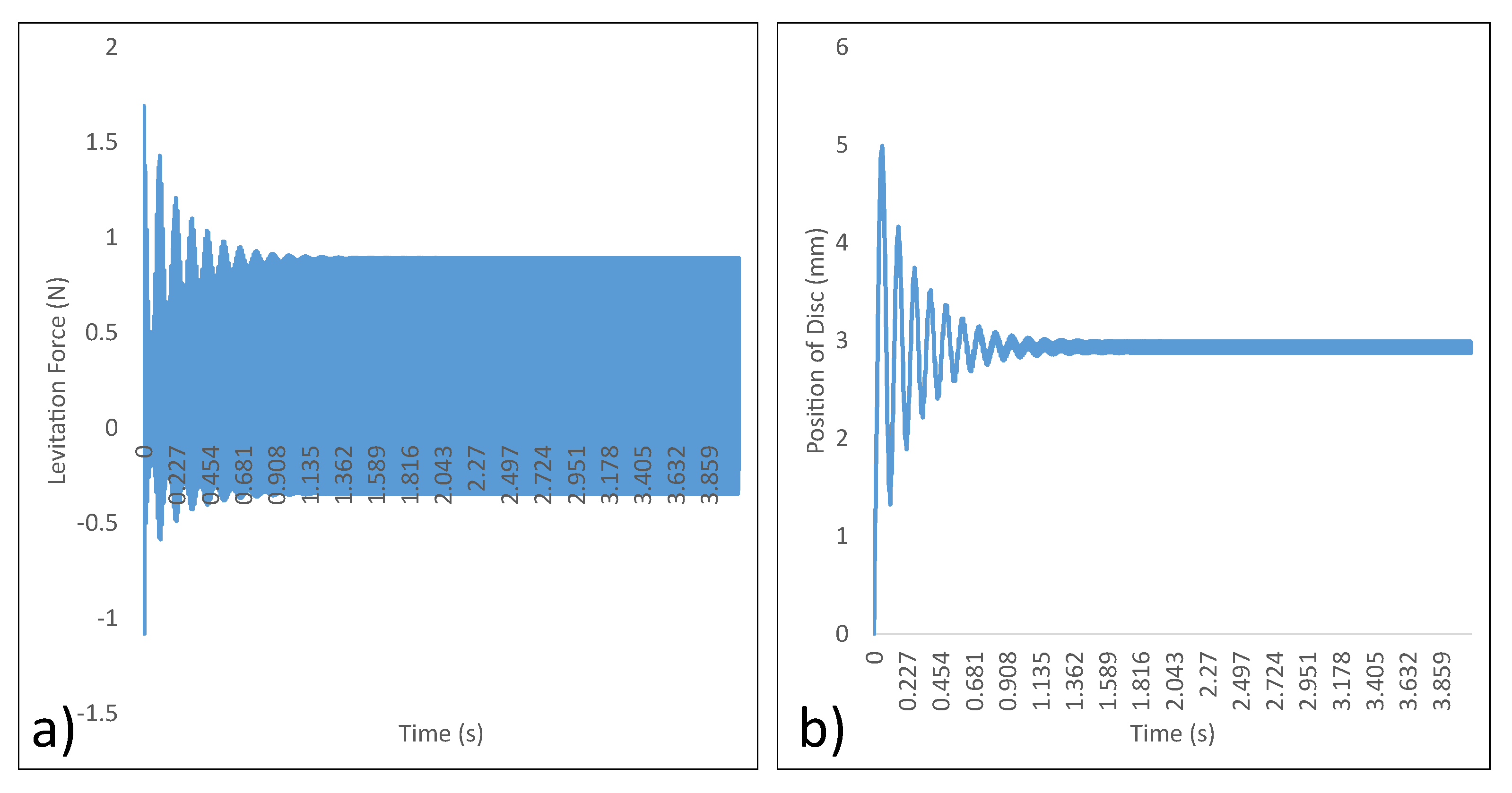
5.3. Simulation and Experimental Analyses
6. Compatibility of Micromanipulator Levitation System with Additive Manufacturing Applications
6.1. Context
6.2. Axial Stability
- The analysis assumes steady flow of powders and the impact of air friction is negligible. Since AM operations occur in a vacuum, this assumption is fair.
- Since the size of the particles are very small and originating at the same source, the collisions between the particles can be ignored.
- The nozzle angle is 0 degrees. This ensures all the force of powder deposition only acts in the axial axis.
- The coefficient of restitution is 0. This implies that all the kinetic energy of the powder is transferred to the levitated geometry and the final velocity of the powder is 0 m/s.
- The mass deposition is assumed to be continuous at 5 g/s (higher than the expected mass deposition rate)
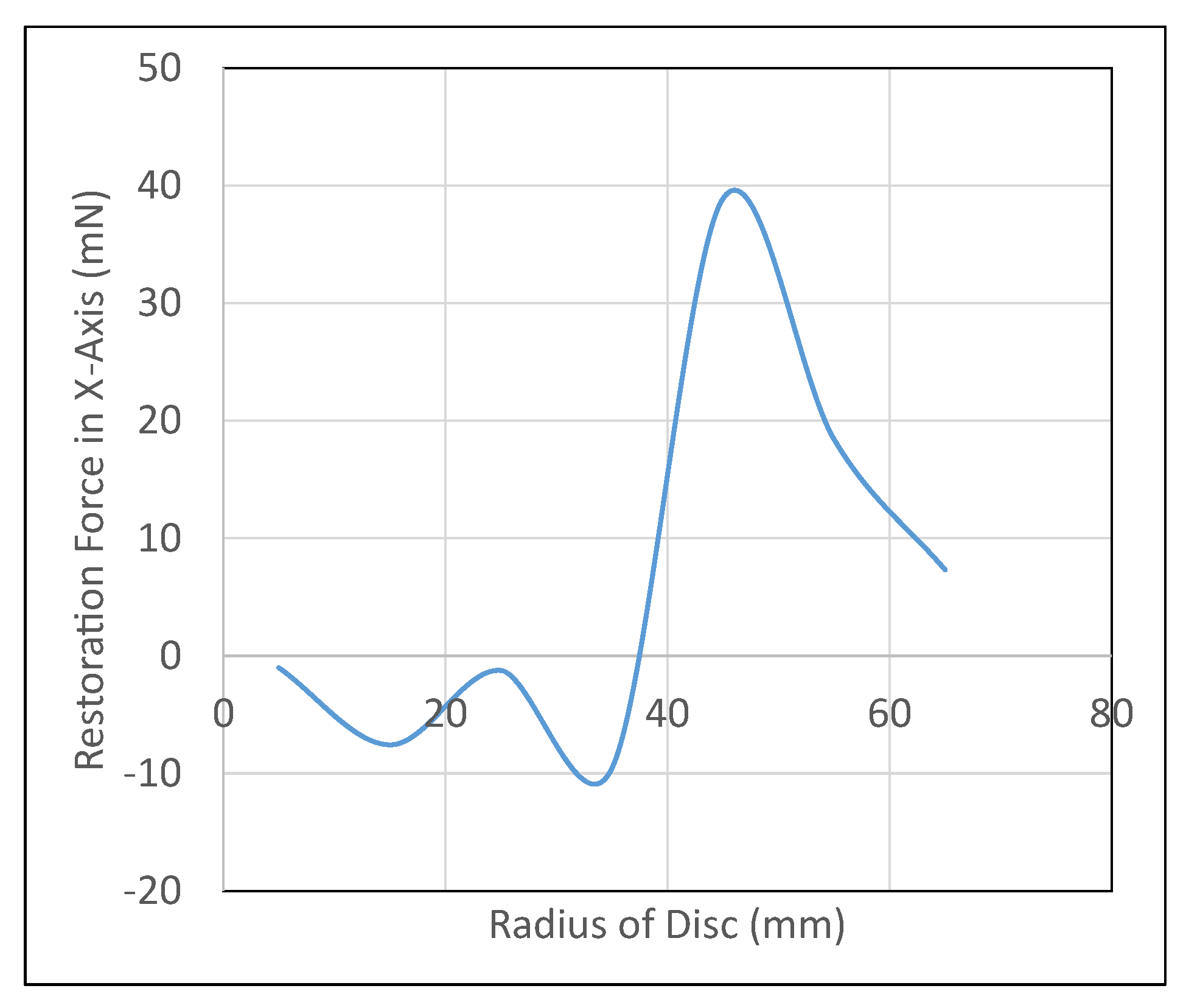
6.3. Lateral Stability
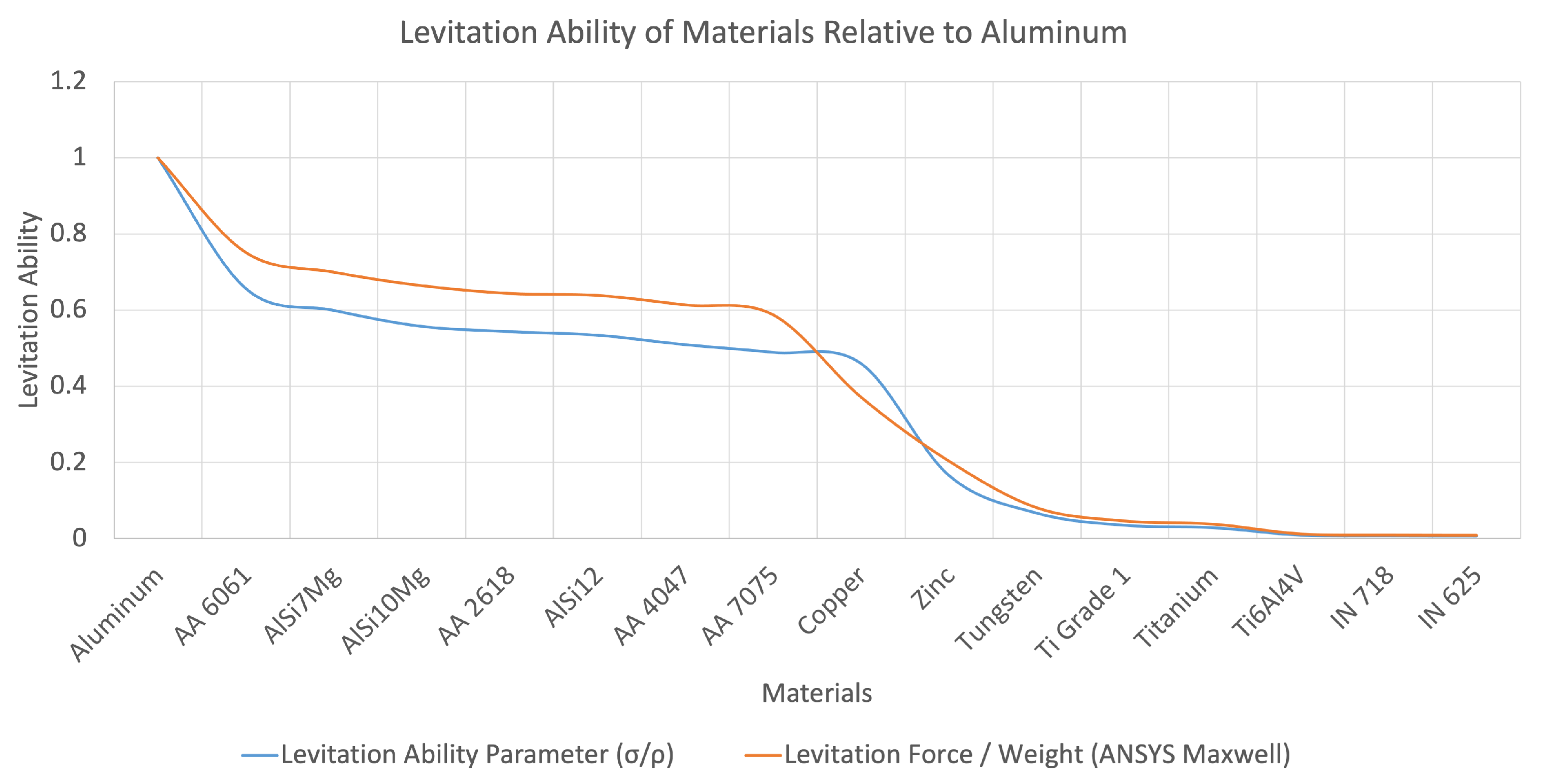
7. Verification of Levitation Ability
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fúnez, G.E.; Carrasco, A.M.; Ordoñez-Ávila, J.L. Study Case: Electromechanical Design of a Magnetic Damper for Robotic Systems. Int. J. Mech. Eng. Robot. Res. 2022. [Google Scholar] [CrossRef]
- Zhang, X.; Trakarnchaiyo, C.; Zhang, H.; Khamesee, M.B. MagTable: A tabletop system for 6-DOF large range and completely contactless operation using magnetic levitation. Mechatronics 2021, 77, 102600. [Google Scholar] [CrossRef]
- Zhou, R.; Yan, M.; Sun, F.; Jin, J.; Li, Q.; Xu, F.; Zhang, M.; Zhang, X.; Nakano, K. Experimental validations of a magnetic energy-harvesting suspension and its potential application for self-powered sensing. Energy 2022, 239, 122205. [Google Scholar] [CrossRef]
- Aldawood, G.; Bardaweel, H. Self-Powered Self-Contained Wireless Vibration Synchronous Sensor for Fault Detection. Sensors 2022, 22, 2352. [Google Scholar] [CrossRef]
- Widodo, P.J.; Budiana, E.P.; Ubaidillah, U.; Imaduddin, F.; Choi, S.B. Effect of Time and Frequency of Magnetic Field Application on MRF Pressure Performance. Micromachines 2022, 13, 222. [Google Scholar] [CrossRef]
- Liu, J.; Li, W.; Jin, L.; Lin, G.; Sun, Y.; Zhang, Z. Analysis of linear eddy current brakes for maglev train using an equivalent circuit method. IET Electr. Syst. Transp. 2021, 11, 218–226. [Google Scholar] [CrossRef]
- Bai, Y.W.; Lee, C.F. Magnetic Levitation Wireless Charging Platform with Adjustable Magnetic Levitation Height and Resonant Frequency for a Better Charging Efficiency. In Proceedings of the 2018 IEEE seventh Global Conference on Consumer Electronics (GCCE), Nara, Japan, 9–12 October 2018; pp. 784–785. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Bi, C.; Cappelleri, D.J.; Ciuti, G.; Conn, A.T.; Faivre, D.; Habibi, N.; Hošovskỳ, A.; Iacovacci, V.; Khalil, I.S.; et al. Magnetic actuation methods in bio/soft robotics. Adv. Funct. Mater. 2021, 31, 2005137. [Google Scholar] [CrossRef]
- Kazemzadeh Heris, P.; Khamesee, M.B. Design and Fabrication of a Magnetic Actuator for Torque and Force Control Estimated by the ANN/SA Algorithm. Micromachines 2022, 13, 327. [Google Scholar] [CrossRef]
- Uvet, H.; Demircali, A.A.; Kahraman, Y.; Varol, R.; Kose, T.; Erkan, K. Micro-UFO (Untethered Floating Object): A Highly Accurate Microrobot Manipulation Technique. Micromachines 2018, 9, 126. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Li, X.; Wang, Y.; Su, Y. Levitation Characteristics Analysis of a Diamagnetically Stabilized Levitation Structure. Micromachines 2021, 12, 982. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, L.; Zhang, L. Micromanipulation Using Reconfigurable Self-Assembled Magnetic Droplets With Needle Guidance. IEEE Trans. Autom. Sci. Eng. 2021, 19, 759–771. [Google Scholar] [CrossRef]
- Wang, L.; Meng, Z.; Chen, Y.; Zheng, Y. Engineering magnetic micro/nanorobots for versatile biomedical applications. Adv. Intell. Syst. 2021, 3, 2000267. [Google Scholar] [CrossRef]
- Golubev, I. Possibilities of 3D scanning of parts during repair of agricultural machinery. In BIO Web of Conferences; EDP Sciences: Les Ulis, France, 2021; Volume 37, p. 00003. [Google Scholar]
- Mohanavel, V.; Ali, K.A.; Ranganathan, K.; Jeffrey, J.A.; Ravikumar, M.; Rajkumar, S. The roles and applications of additive manufacturing in the aerospace and automobile sector. Mater. Today Proc. 2021, 47, 405–409. [Google Scholar] [CrossRef]
- Basgul, C.; Spece, H.; Sharma, N.; Thieringer, F.M.; Kurtz, S.M. Structure, properties, and bioactivity of 3D printed PAEKs for implant applications: A systematic review. J. Biomed. Mater. Res. Part B Appl. Biomater. 2021, 109, 1924–1941. [Google Scholar] [CrossRef]
- Velásquez-García, L.F.; Kornbluth, Y. Biomedical Applications of Metal 3D Printing. Annu. Rev. Biomed. Eng. 2021, 23, 307–338. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, C.; Xu, X.; Wang, J.; Hou, X.; Li, K.; Lu, X.; Shi, H.; Lee, E.S.; Jiang, H.B. A review of 3D printing in dentistry: Technologies, affecting factors, and applications. Scanning 2021, 2021, 9950131. [Google Scholar] [CrossRef]
- Li, J.; Pumera, M. 3D printing of functional microrobots. Chem. Soc. Rev. 2021, 50, 2794–2838. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Alimardani, M.; Toyserkani, E.; Huissoon, J.P.; Paul, C.P. On the delamination and crack formation in a thin wall fabricated using laser solid freeform fabrication process: An experimental—Numerical investigation. Opt. Lasers Eng. 2009, 47, 1160–1168. [Google Scholar] [CrossRef]
- Manoharan, M.; Kumaraguru, S. Path Planning for Direct Energy Deposition with Collaborative Robots: A Review. In Proceedings of the 2018 Conference on Information and Communication Technology (CICT), Jabalpur, India, 26–28 October 2018; pp. 1–6. [Google Scholar]
- Palmero, E.M.; Bollero, A. 3D and 4D Printing of Functional and Smart Composite Materials. In Encyclopedia of Materials: Composites; Brabazon, D., Ed.; Elsevier: Oxford, UK, 2021; pp. 402–419. [Google Scholar] [CrossRef]
- Huang, Yuze. Comprehensive Analytical Modeling of Laser Powder-Bed/Fed Additive Manufacturing Processes and an Associated Magnetic Focusing Module. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2019.
- Huang, Y.; Khamesee, M.B.; Toyserkani, E. A comprehensive analytical model for laser powder-fed additive manufacturing. Addit. Manuf. 2016, 12, 90–99. [Google Scholar] [CrossRef]
- Harkness, W.A.; Goldschmid, J.H. Free-Form Spatial 3-D Printing Using Part Levitation. U.S. Patent 9,908,288, 6 March 2018. [Google Scholar]
- Bo, K.; Xiong, Y.; Yu, X.; Wu, J.; Wang, Y. Study on Transient Electromagnetic Characteristics Based on Typical Soft Magnetic Material for EMS Maglev Train. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–4. [Google Scholar]
- Huang, C.G.; Zhou, Y.H. Levitation properties of maglev systems using soft ferromagnets. Supercond. Sci. Technol. 2015, 28, 035005. [Google Scholar] [CrossRef]
- Ghayoor, F.; Swanson, A. Modelling and analysis of electrodynamic suspension of an aluminium disc as a complex engineering problem. Int. J. Electr. Eng. Educ. 2018, 55, 91–108. [Google Scholar] [CrossRef]
- Lee, S.M.; Lee, S.H.; Choi, H.S.; Park, I.H. Reduced modeling of eddy current-driven electromechanical system using conductor segmentation and circuit parameters extracted by FEA. IEEE Trans. Magn. 2005, 41, 1448–1451. [Google Scholar]
- Nan, W.; Wen-Jun, X.; Bing-Bo, W. Physical characteristics of electromagnetic levitation processing. Chin. Phys. B 1999, 8, 503–513. [Google Scholar] [CrossRef]
- Kumar, P.; Huang, Y.; Toyserkani, E.; Khamesee, M.B. Development of a Magnetic Levitation System for Additive Manufacturing: Simulation Analyses. IEEE Trans. Magn. 2020, 56, 8000407. [Google Scholar] [CrossRef]
- Bird, J.O.; Chivers, P.J. 10—Electromagnetism and magnetic circuits. In Newnes Engineering and Physical Science Pocket Book; Bird, J.O., Chivers, P.J., Eds.; Newnes: London, UK, 1993; pp. 77–87. [Google Scholar] [CrossRef]
- MSAM, U.O.W. Our Equipment & Facilities. Available online: https://msam.uwaterloo.ca/infrastructure/ (accessed on 1 May 2021).
- Chemetals, S. Iron Rod, 99.6% Pure. Available online: https://www.surepure.com/Iron-Rod-99.6-Percent-pure-4.125-in.-diameter-x-12-inches-long-x-2-rods/p/5593 (accessed on 8 March 2022).
- Carty, S.; Owen, I.; Steen, W.; Bastow, B.; Spencer, J. Catchment efficiency for novel nozzle designs used in laser cladding and alloying. In Laser Processing: Surface Treatment and Film Deposition; Springer: Berlin/Heidelberg, Germany, 1996; pp. 395–410. [Google Scholar]







| Parameter | Value |
|---|---|
| Outer Diameter of Levitation System | 90 mm |
| Height of Levitation System | 115 mm |
| Core Material | Pure Iron |
| No. of turns Coil 1 N1 | 920 |
| No. of turns Coil 2 N2 | 800 |
| Distance between disc and levitator | 0 mm |
| Wire AWG | 18 AWG |
| Disc Radius | 25 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Malik, S.; Toyserkani, E.; Khamesee, M.B. Development of an Electromagnetic Micromanipulator Levitation System for Metal Additive Manufacturing Applications. Micromachines 2022, 13, 585. https://doi.org/10.3390/mi13040585
Kumar P, Malik S, Toyserkani E, Khamesee MB. Development of an Electromagnetic Micromanipulator Levitation System for Metal Additive Manufacturing Applications. Micromachines. 2022; 13(4):585. https://doi.org/10.3390/mi13040585
Chicago/Turabian StyleKumar, Parichit, Saksham Malik, Ehsan Toyserkani, and Mir Behrad Khamesee. 2022. "Development of an Electromagnetic Micromanipulator Levitation System for Metal Additive Manufacturing Applications" Micromachines 13, no. 4: 585. https://doi.org/10.3390/mi13040585
APA StyleKumar, P., Malik, S., Toyserkani, E., & Khamesee, M. B. (2022). Development of an Electromagnetic Micromanipulator Levitation System for Metal Additive Manufacturing Applications. Micromachines, 13(4), 585. https://doi.org/10.3390/mi13040585







