A Timing-Based Split-Path Sensing Circuit for STT-MRAM

Abstract

Spin-transfer torque magnetoresistive random access memory (STT-MRAM) applications have received considerable attention as a possible alternative for universal memory applications because they offer a cost advantage comparable to that of a dynamic RAM with fast performance comparable to that of a static RAM, while solving the scaling issues faced by conventional MRAMs. However, owing to the decrease in supply voltage (V_DD) and increase in process fluctuations, STT-MRAMs require an advanced sensing circuit (SC) to ensure a sufficient read yield in deep submicron technology. In this study, we propose a timing-based split-path SC (TSSC) that can achieve a greater read yield compared to a conventional split-path SC (SPSC) by employing a timing-based dynamic reference voltage technique to minimize the threshold voltage mismatch effects. Monte Carlo simulation results based on industry-compatible 28-nm model parameters reveal that the proposed TSSC method obtains a 42% higher read access pass yield at a nominal V_DD of 1.0 V compared to the SPSC in terms of iso-area and -power, trading off 1.75× sensing time.

1. Introduction

To prolong the battery life in lithium-ion battery-powered applications, such as smartphones, wearable devices, and wireless sensor nodes, it is crucial to achieve good performance with low power consumption [1]. Even though a conventional magnetoresistive random access memory (MRAM) has the speed of a static RAM (SRAM) and density of a dynamic RAM (DRAM), it has unique problems, including poor scalability and excessive power consumption owing to large write currents. Therefore, spin-transfer torque MRAM (STT-MRAM) has emerged as the top choice for universal memory applications owing to its short access time, low power consumption, and high density [2]. In addition, STT-MRAM has outstanding scalability, as the critical switching current of the magnetic tunnel junction (MTJ) decreases with device size to overcome the scaling problems faced by conventional memories, such as DRAM, SRAM, and flash memories [3,4,5]. In other words, STT-MRAM can achieve a higher performance than DRAM and smaller cell size than SRAM, with the nonvolatility of flash memory [6,7,8,9].

However, STT-MRAM faces a read yield degradation problem when used in deep submicron technologies because of the large process variations in low supply voltage (V_DD) and small resistance difference between the low resistance (state 0) and high resistance (state 1) states of the MTJ [10,11]. The current (ΔI₀ or ΔI₁) or voltage differences (ΔV₀ or ΔV₁) generated in a sensing circuit (SC), which are then conveyed to a sense amplifier (SA), can be expressed as:

$$\Delta I_{0,1}=\left|I_{\mathrm{data}0,1}-I_{\mathrm{ref}}\right|$$

(1)

$$\Delta V_{0,1}=\left|V_{\mathrm{data}0,1}-V_{\mathrm{ref}}\right|=\Delta I_{0,1}\cdot r_{\mathrm{O}\_\mathrm{PLD}}$$

(2)

where I_data0 (I_data1) and I_ref are the currents flowing through the data cell in state 0 (state 1) and reference cell, respectively. V_data0 (V_data1) and V_ref are the output voltages of the data and reference branches in the SC, respectively, and r_{O_PLD} is the output resistance of the load PMOS. Assuming a fixed V_ref, ΔV_0,1 is approximately half of the difference between V_data0 and V_data1 because V_ref is ideally equal to (V_data0 + V_data1)/2 [10]. To overcome the read yield degradation, a higher ΔV_0,1 and lower impact of process variation are required in deep submicron technology nodes. However, ΔV_0,1 is limited by V_DD and current, and the variations in the process parameters inevitably increase as the technology node scales down.

Furthermore, the offset voltage of the SA (V_{SA_OS}) must be considered for a successful read operation. Thus, ΔV_0,1 must be larger than V_{SA_OS} to generate the read-access path. The statistical distributions between ΔV_0,1 and V_{SA_OS} can be modeled using a Gaussian distribution [11]. The read-access pass yield for a single cell with states 0 or 1 (RAPY_CELL0,1) [12] is expressed as

$$RAP{Y}_{\mathrm{CELL}0,1}=\frac{{\mu }_{\Delta \mathrm{V}0,1}-{\mu }_{\mathrm{SA}\_\mathrm{OS}}}{\sqrt{{\sigma }_{\Delta \mathrm{V}0,1}^2-{\sigma }_{\mathrm{SA}\_\mathrm{OS}}^2}}$$

(3)

where μ_ΔV0,1 and μ_{SA_OS} are the means of ΔV_0,1 and V_{SA_OS}, respectively, and σ_ΔV0,1 and σ_{SA_OS} are the standard deviations of ΔV_0,1 and V_{SA_OS}, respectively. RAPY_CELL is defined as the minimum value between RAPY_CELL0 and RAPY_CELL1.

$$RAP{Y}_{\mathrm{CELL}}=\min (RAP{Y}_{\mathrm{CELL}0}, RAP{Y}_{\mathrm{CELL}1})$$

(4)

In this study, a novel timing-based split-path sensing circuit (TSSC) that is tolerant to process variations and increases ΔV_0,1 value is proposed and compared with various SCs with respect to RAPY_CELL, delay, and power consumption. It improves μ_ΔV0,1 using the dynamic reference voltage (DRV) technique that modifies V_ref according to the MTJ state. It also reduces σ_ΔV0,1 by compensating the transistor mismatch and effectively increasing the sensing current. Even though the split-path sensing circuit (SPSC) [10] is considered to have optimal performance in terms of read yield, Monte Carlo HSPICE simulation results based on industry-compatible 28-nm model parameters reveal that the proposed TSSC achieves a 42% boost in RAPY_CELL at a V_DD of 1.0 V when compared to the SPSC in terms of iso-area and -power. The remainder of this paper is organized as follows: Section 2 describes the operational principles and characteristics of the conventional SCs and proposed TSSC. Section 3 compares the performance of the proposed SC and conventional SCs. Finally, Section 4 presents the conclusions drawn from our study.

2. Previous SCs and Proposed TSSC

In this section, the characteristics and operation principles of the existing and proposed SCs are described.

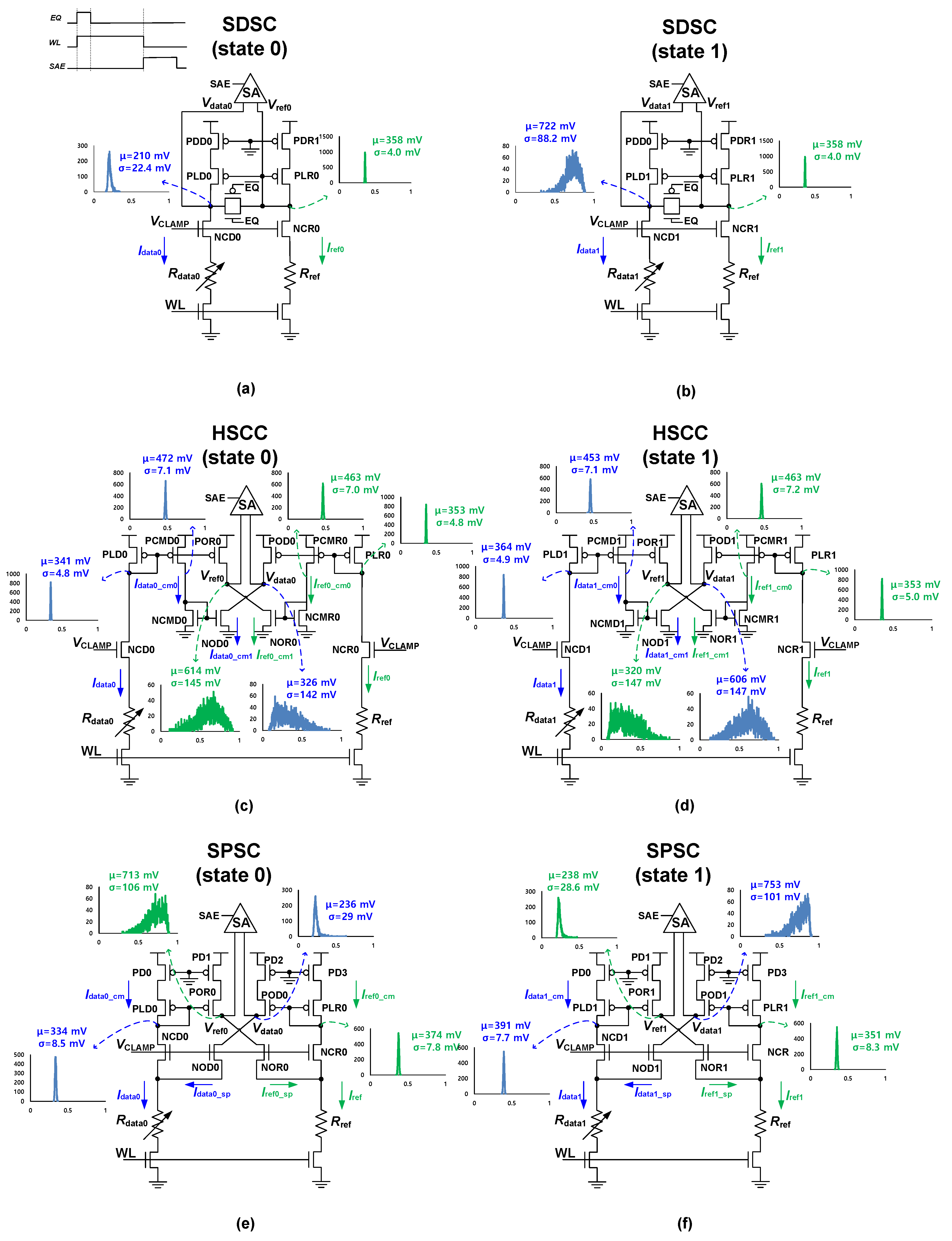
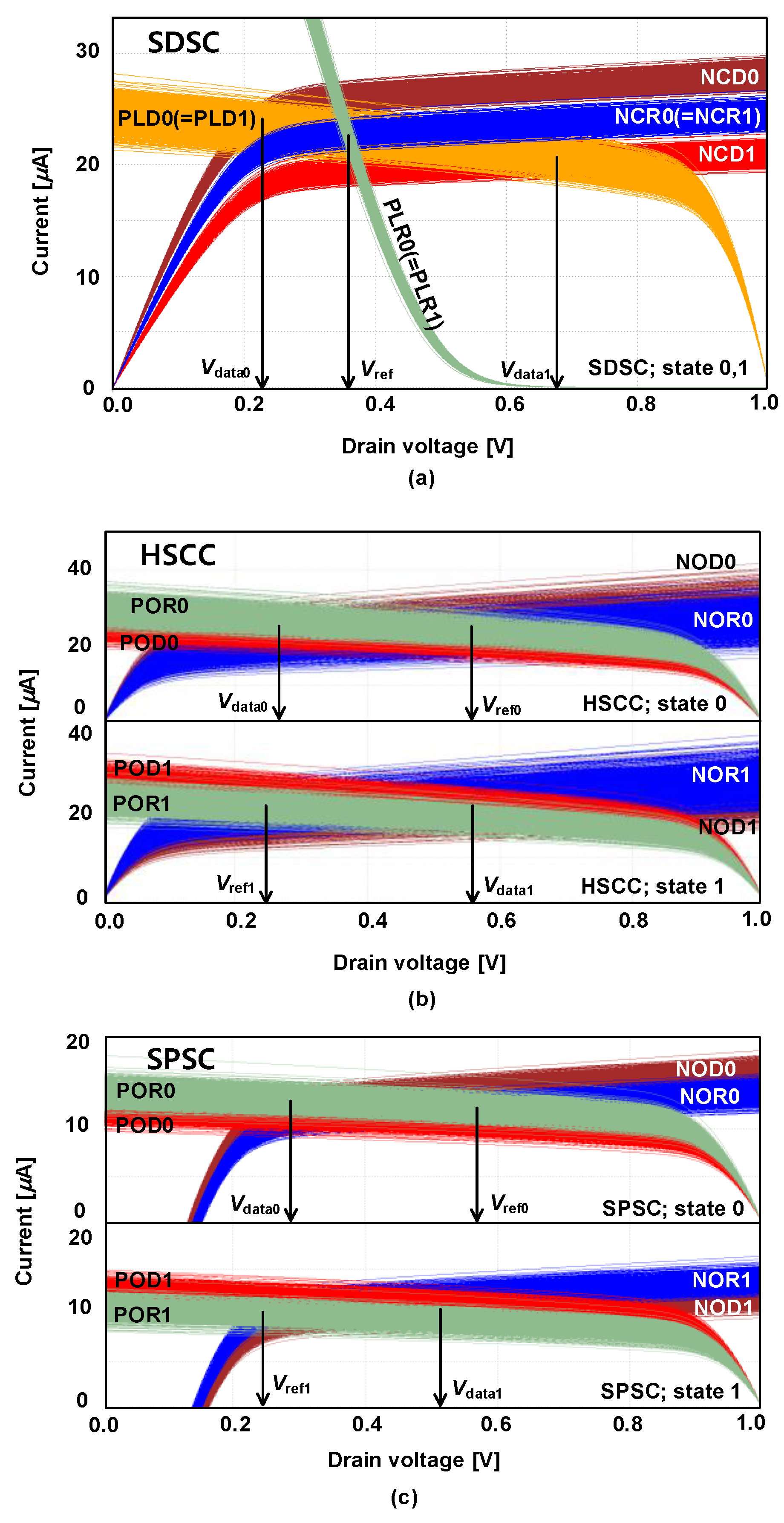
2.1. Existing SCs

Three conventional SCs [10,11,13] for STT-MRAM are shown in Figure 1 along with their output voltage distributions. To analyze the voltage distributions, industry-compatible 28-nm model parameter libraries were used. Temperature was set to room temperature (25 °C) and, to compare in terms of iso-area and -power, the layout area of SCs were set to be identical by varying the transistor sizes. In addition, the gate voltage of the clamp NMOS (V_CLAMP) was used differently for each SC to set the sensing current to 20 μA at state 1.

Figure 1a,b illustrate the schematics and output voltage distributions of the source degeneration sensing circuit (SDSC) [11] at states 0 and 1, respectively. In the SDSC, the clamp NMOS (NCD, NCR) is used to generate ΔI, which is then converted to ΔV via a load PMOS (PLD, PLR) using a current mirror; then, ΔV is fed to the SA. In addition, SDSC achieves a PMOS (PDD, PDR) degeneration between V_DD and load PMOS for source degeneration purposes. The source degeneration effect reduces the variation in the load PMOS and increases r_{O_PLD}, leading to an improvement in the RAPY_CELL. The I-V curve shown in Figure 2a represents the relationship between the drain voltage of each MOSFET and current through each MOSFET in the SDSC. The crossing points of the I-V curve for the load PMOS and clamp NMOS denote the operating points. For example, the crossing points for PLR and NCR, PLD0 and NCD0, and PLD1 and NCD1 are the operating points for V_ref, V_data0, and V_data1, respectively. PLD0 (PLD1) passes through the operating point between PLR and NCR, as V_ref denotes the gate voltage of PLD0 (PLD1). The drain voltage distribution of the PLR shown in Figure 1a has a small standard deviation because of the large slope (i.e., the output resistance is small) of the diode-connected PLR. When the output resistance is small, the voltage variation is small as well, expressed in (2). The PLD has a relatively large standard deviation owing to the small slope of the PLD I-V curve and current mirror variation. Thus, to obtain a proper sensing margin in SDSC, the PLD variation must be reduced. SDSC can obtain an adequate read yield in 65-nm process technology because the degeneration effect reduces the process variation in the SC. However, under 65-nm process technology, the SDSC suffers from significant read yield degradation because the fixed V_ref limits μ_ΔV0,1 and process variation increment increases σ_ΔV0,1.

Figure 1c,d illustrate the SC with a highly symmetric cross-coupled current mirror (HSCC) [13] at states 0 and 1, respectively. To address the fixed V_ref issue observed in SDSC, the HSCC uses the DRV technique that adjusts V_ref according to the data state to enhance the sensing margin [14]. Figure 2b shows the I-V curve of HSCC, where crossing point of POR and NOR transistors’ I-V curves represents V_ref. As demonstrated, V_ref decreases at state 1 (V_ref1) and increases at state 0 (V_ref0). The DRV technique can almost double μ_ΔV0,1 compared to the fixed V_ref approach used in the SDSC. However, in the HSCC, three current mirrors from the PLD to the NCMD are employed to generate V_data0,1. Consequently, these current mirrors induce a substantial current mismatch, which increases σ_ΔV0,1. Neglecting the channel-length modulation, the current through the NCD (I_NCD) for the current mirror is expressed as

$$I_{\mathrm{NCD}}=A{(V_{\mathrm{GS}}-V_{\mathrm{TH}})}^2$$

(5)

where A is the transconductance parameter, V_GS is the gate-to-source voltage of the NCD, and V_TH is the threshold voltage. The current through the PCMD (I_{data_cm0}), including the mismatch effects, is given by

$$I_{\mathrm{data}\_\mathrm{cm}0}=(A+\Delta A){(V_{\mathrm{GS}}-V_{\mathrm{TH}}-\Delta V_{\mathrm{TH}})}^2$$

(6)

where ΔA is the transconductance mismatch that results in a gain error and ΔV_TH is the threshold voltage mismatch that results in voltage offsets [15]. The current through the NOD (I_{data_cm1}), including the mismatch effects, is given by

$$I_{\mathrm{data}\_\mathrm{cm}1}=(A+2\Delta A){(V_{\mathrm{GS}}-V_{\mathrm{TH}}-2\Delta V_{\mathrm{TH}})}^2$$

(7)

The current through the POD is similar to I_{data_cm0}. Furthermore, PMOS-based circuits are vulnerable to mismatches because of poor gate oxide capacitance matching and high mobility variations [16]. Thus, when numerous current mirrors are used, the current mismatch increases, as expressed in (7). The standard deviations of V_data0,1 (V_ref0,1) shown in Figure 1c,d are relatively large because of the many steps in the current mirror and small slope of the POD0,1 (POR0,1) I-V curve. Consequently, even though the HSSC doubles μ_ΔV0,1 using the DRV technique, it cannot guarantee a sufficient read yield in deep submicron technology.

Figure 1e,f show the SPSC [10] at states 0 and 1, respectively. The SPSC uses a split path to employ the DRV technique and achieves PMOS degeneration to reduce the variation. Figure 2c shows that the SPSC successfully modifies V_ref according to the MTJ state; the subsequent V_ref0 and V_ref1 values that confirm this are presented in Figure 1e,f. Furthermore, to overcome the process variation issue faced by the HSCC, the SPSC utilizes a split-path technique instead of current mirrors. Instead of employing current mirrors to transmit the NCD saturation current to the NOD as HSCC does, the SPSC uses the split path on the NCD source and applies the same gate-to-source voltage to both the NCD and NOD. As a result, even without a current mirror, the saturation currents of the NCD and NOD are equalized. The standard deviations of V_data0,1 (V_ref0,1) presented in Figure 1e,f is smaller than those of the HSCC because the number of current mirrors is reduced. Therefore, among the existing SCs, SPSC is superior in terms of the RAPY_CELL. However, as shown in Figure 1e,f, the standard deviations of V_ref0 and V_data1 remain large (i.e., 106 mV and 101 mV). This is because the data current (I_data) is split in half by the split-path scheme (I_data = I_{data_cm} + I_{data_sp}), and the lowered current is sensitive to the increased process variations in deep submicron technology.

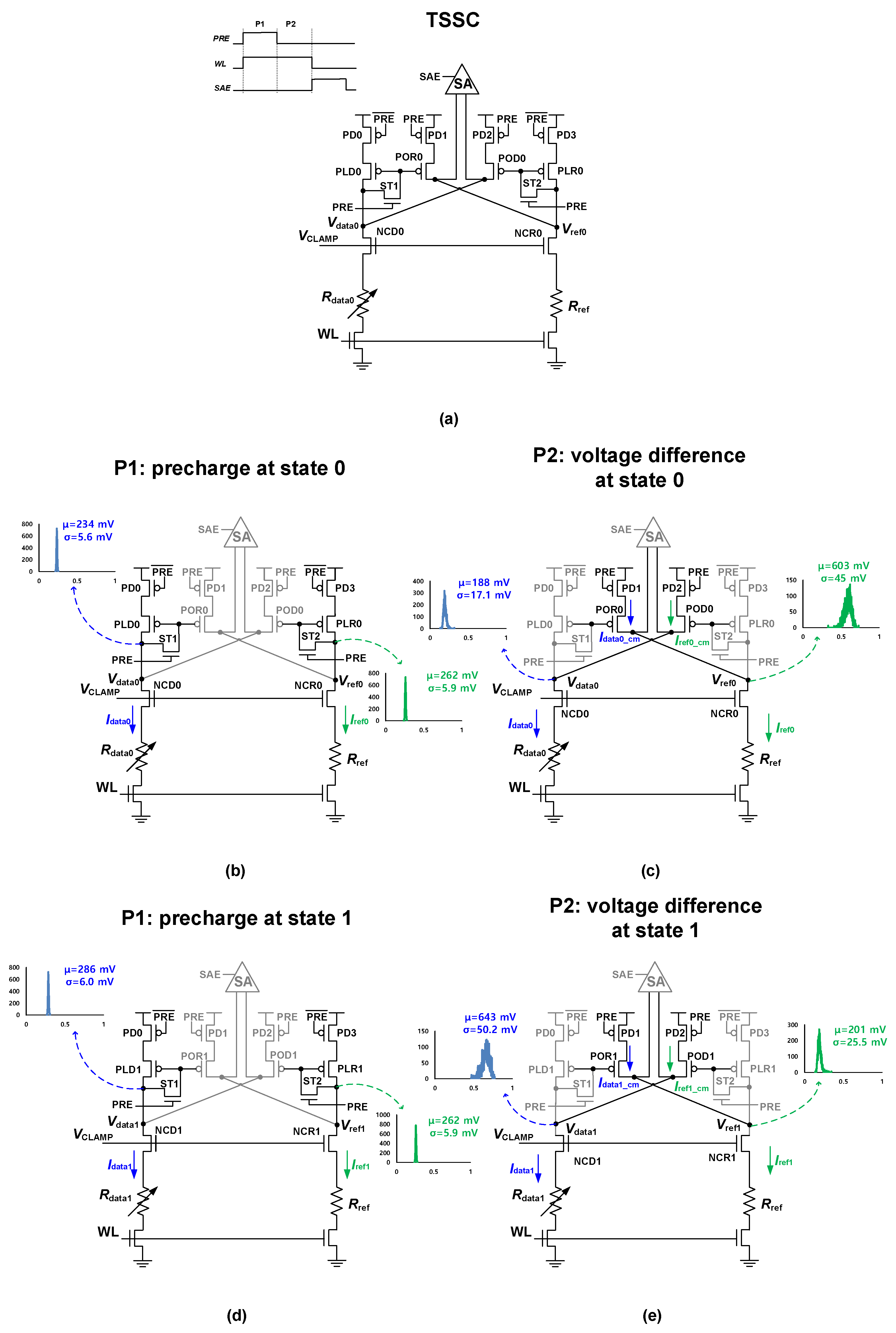
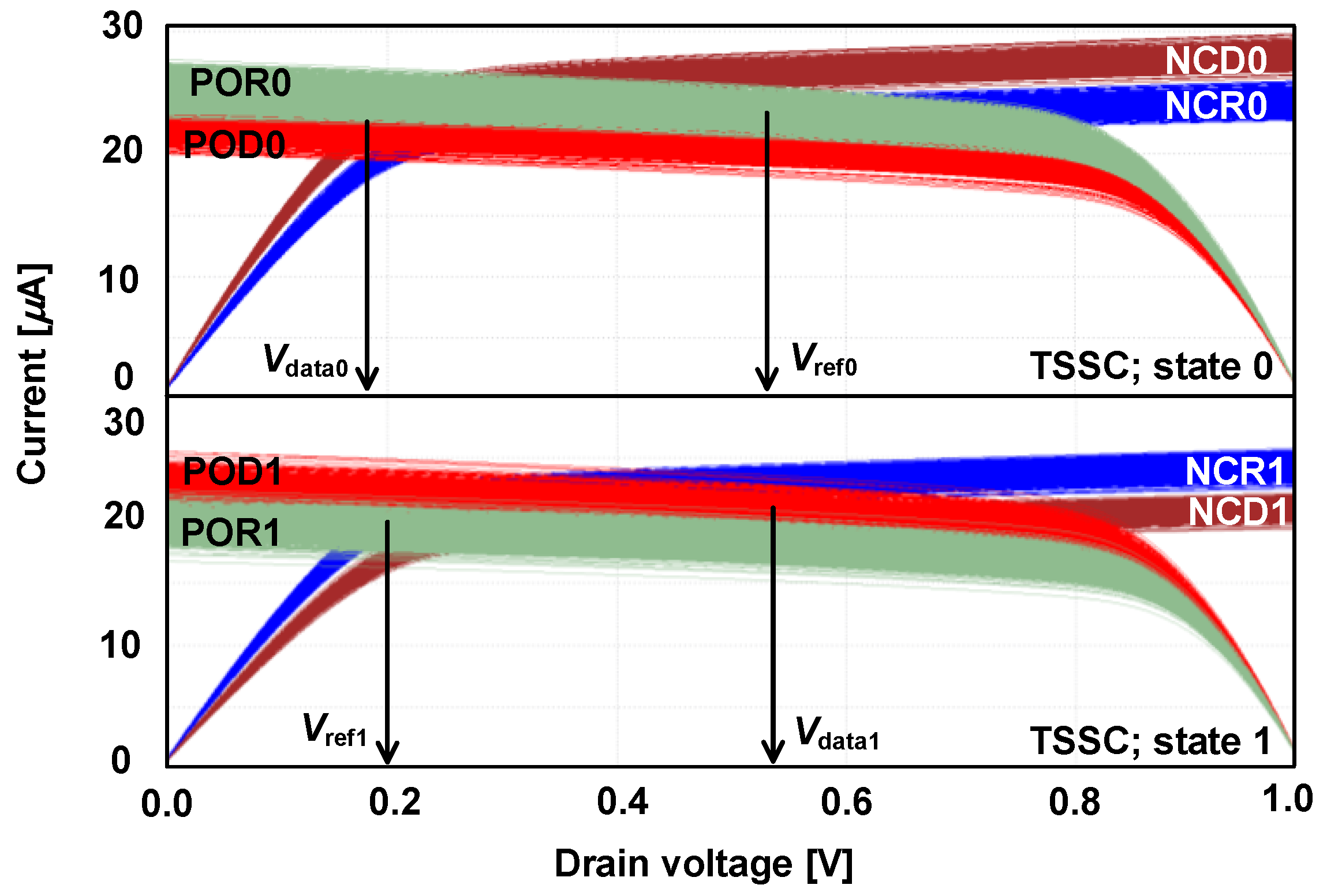
2.2. Proposed TSSC

In SPSC, the lowered saturation current caused by the split path is vulnerable against process variations. The TSSC maintains the advantages of SPSC (i.e., the DRV technique, thereby increasing the sensing margin ΔV_0,1) but overcomes the lowered saturation current problem. Figure 3a shows the schematic and timing diagram of the proposed TSSC. The key circuit design differences between the TSSC and SPSC are the inclusion of two transistors as switches (ST1 and ST2) and exclusion of NOD and NOR by implementing a timing-based split-path scheme. To reduce σ_ΔV0,1 by enhancing the current for each path, the MOSFET operating times are controlled by the PRE signal. Figure 3b shows the TSSC operation in phase 1 (P1) at state 0. In P1, the PRE signal is high; thus, PD0, PD3, ST1, and ST2 are turned on at the beginning. The gate voltage of POR0 (POD0) starts to pre-charge as ST1 and ST2 are turned on. PLD0 and PLR0 reach saturation points after a sufficient pre-charge time if I_data0 and I_ref0 are constant in P1, regardless of the process variations in PLD0 (PLR0). At the end of P1, the gate voltage of POR0 (POD0) is kept at the same value as V_data0 (V_ref0). However, POR0 and POD0 cannot operate because PD1 and PD2 are turned off, respectively. Figure 3c shows the TSSC operation in phase 2 (P2) at state 0. At the beginning of P2, the PRE signal is turned off. Thus, PD0, PD3, ST1, and ST2 are turned off, and PD1 and PD2 are turned on. When PLD0 and PLR0 are cut off from V_DD, POR0 and POD0 can operate because the gate voltages of POR0 and POD0 are pre-charged to V_data0 and V_ref0, respectively, in P1. Thus, the saturation current of POR0 is transmitted from NCD0 as the SPSC. However, for TSSC, the saturation current of POR0 is approximately two times larger than that of the SPSC, regardless of process variation. This is because PLD0 is turned off in P2 and there is no current division. In addition, in the TSSC, without current division, the clamp NMOS number is less than that of the SPSC, which is achieved by shifting the split-path position to the drain of the clamp NMOS. Therefore, the TSSC implements the DRV technique with the minimization of σ_ΔV0,1, which is confirmed by the TSSC voltage distribution diagram shown in Figure 3c,e. The process variation in the TSSC can be further decreased compared to the SPSC because in terms of iso-area, the size of MOSFETs in the TSSC can be increased as the number of clamp NMOS is reduced. Figure 3d,e show the TSSC operation at state 1 in P1 and P2, respectively. The TSSC operation at state 1 is nearly identical to that at state 0, with only a change in the MTJ state. Figure 4 shows the TSSC I-V curves, from which V_data0,1 and V_ref0,1 can be estimated. The crossing point in the I-V curves for NCD0 (NCD1) and POD0 (POD1) is the operating point for V_data0 (V_data1). Furthermore, the crossing point in the I-V curves of NCR0 (NCR1) and POR0 (POR1) is the operating point for V_ref0 (V_ref1). V_ref is successfully modified according to the MTJ state, and operation current is nearly doubled compared to that of SPSC.

3. Simulation Results

3.1. Simulation Conditions

All simulation results included in this section were obtained using Monte Carlo HSPICE simulations implemented in industry-compatible 28-nm model parameter libraries. The μ_{SA_OS} and σ_{SA_OS} values for calculating RAPY_CELL were set to 0 and 20 mV, respectively [17]. Furthermore, a standard deviation of 4% was considered for the MTJ variation. The MTJ model used in this study had an R₁ (R_H, anti-parallel) of 6 kΩ and R₀ (R_L, parallel) of 3 kΩ, considering a tunnel magnetoresistance (TMR) ratio of 100%. For a fair comparison between SCs in terms of iso-area and iso-power, all transistor sizes were chosen such that the layout area (=sum of each transistor’s area (width × length)) of each SC was 1.76 μm². Moreover, the V_CLAMP for each SC was precisely set such that it generated 20 μA at state 1. In addition, the optimal R_ref for each circuit was used for architectural analysis.

3.2. Results and Comparison

RAPY_CELL0 and RAPY_CELL1 increased when R_ref increased and decreased, respectively. Accordingly, the crossing points for RAPY_CELL0 and RAPY_CELL1 were the maximum values of RAPY_CELL. Figure 5 shows RAPY_CELL0,1 for SDSC, HSCC, SPSC, and TSSC with respect to R_ref when the temperature was set to room temperature (25 °C). The HSCC achieved the lowest RAPY_CELL value owing to the large output variation due to the current mismatch of the multiple current mirrors. Despite the large μ_ΔV0,1, the SDSC and SPSC exhibited the same value for RAPY_CELL in terms of iso-area because the SDSC transistor size was twice as large as that of the SPSC. The RAPY_CELL value of TSSC was the largest compared with that of the conventional SC because the DRV technique was successfully implemented and a timing-based split-path scheme overcame the lowered data current problem faced by SPSC.

Figure 6 shows the RAPY_CELL for SDSC, HSCC, SPSC, and TSSC with respect to V_DD and V_CLAMP. To analyze the SCs in terms of iso-power, V_CLAMP for each SC was precisely set such that it generates 20 μA at state 1. The temperature range was set in the range from −45 to 90 °C, and the worst case was chosen for RAPY_CELL calculation. As shown in Figure 6a, the HSCC exhibited minimal variations in RAPY_CELL when V_DD increased because σ_ΔV0,1 was excessively large owing to the number of current mirrors. When V_DD was less than 0.9 V, RAPY_CELL for the SPSC was greater than that for the TSSC. In the TSSC, RAPY_CELL was significantly reduced at low V_DD because the decrease rate of μ_ΔV0,1 was high. When V_DD was greater than 0.9 V, the TSSC achieved a large value for RAPY_CELL because the increase rate of μ_ΔV0,1 was higher than that of σ_ΔV0,1. Figure 6b shows RAPY_CELL with respect to V_CLAMP when V_DD = 1.0 V. RAPY_CELL value’s reliance on V_CLAMP is not linear because when V_CLAMP is low, the operating current is not enough, and when V_CLAMP is high μ_ΔV0,1 decreases because of the decreased r_{O_PLD}. Thus, V_CLAMP has an optimal value that maximizes the read yield. The HSCC has low RAPY_CELL and no optimal value according to V_CLAMP in the range from 0.55 to 0.8 V. The optimal V_CLAMP values for SDSC and SPSC are 0.65 V and 0.7 V, respectively. However, STT-MRAM requires low sensing current to prevent read disturbances. An unintentional write operation occurs during a read operation when the critical MTJ switching current is lower than the read current [11]. In the TSSC, the optimal V_CLAMP value, 0.6 V, is lower than that of conventional SCs, and the RAPY_CELL value is the highest. Therefore, the TSSC is suitable to be implemented in STT-MRAM, which requires low sensing current.

Figure 7a illustrates the RAPY_CELL values of the SDSC, HSCC, SPSC, and proposed TSSC with respect to the TMR of MTJ when V_DD is set to 1 V and V_CLAMP is set to 0.6 V. The temperature range was set in the range from −45 to 90 °C and the worst case was chosen for RAPY_CELL calculation. TMR is calculated as (R₁ − R₀)/R₀ and ideally assumes a high values because it influences the sensing speed, read margin, and noise margin of the memory cell. However, the SCs for STT-MRAM must be built to compensate for process-related fluctuations in the TMR value. As shown in Figure 7a, for low sensing current applications, even when the TMR value is decreased to 60%, the proposed TSSC maintains a greater RAPY_CELL value compared to existing SCs. Figure 7b plots the RAPY_CELL as a function of sensing time when V_DD was set to 1 V and V_CLAMP was set to 0.6 V. Because the TSSC uses a two-phase sensing operation for the timing-split-based DRV technique, it requires sufficient time for charging and discharging. Thus, a sharp increase in RAPY_CELL can be observed at approximately 8 ns, and the RAPY_CELL value is saturated at approximately 14 ns. The existing designs are not sensitive to the sensing time compared to the proposed TSSC, which provides more accurate sensing at the expense of increased sensing times.

As mentioned earlier, the TSSC exploits the gate capacitance of the PLD, POR, POD, and PLR transistors to accumulate charge during P1, which raises the question of whether the capacitor-less design is better than using a capacitor. Figure 8 shows the TSSC RAPY_CELL value with respect to the additional capacitor capacitance when two capacitors are added at the gates of the PLD and PLR. The RAPY_CELL value increases until the additional capacitor capacitance reaches 2 fF but the increment is insignificant and starts to decrease as the capacitance increases further because of the limited sensing time. Moreover, if a capacitor is added to the design, the sizes of all transistors need to be reduced in terms of iso-area, which results in a decrease in the gate capacitance and performance degradation. Accordingly, Figure 8 indicates that the gate capacitances of PLD, POR and POD, PLR pairs are sufficient for the TSSC to accumulate charge during P1 to mirror the data current during P2.

Table 1. Summary of the simulation results in terms of iso-area (identical Tr. size) and iso-power.

	SDSC [11]	HSSC [13]	SPSC [10]	TSSC (Proposed)
Process technology	28 nm
DRV technique	X	O	O	O
ICELL [μA] @ state 1	20.0
Layout Area of SC [μm2] @ iso-area (Layout Area of SC [μm2] @ identical Tr. size(1))	1.76 (1.28)	1.76 (3.04)	1.76 (2.56)	1.76 (1.76)
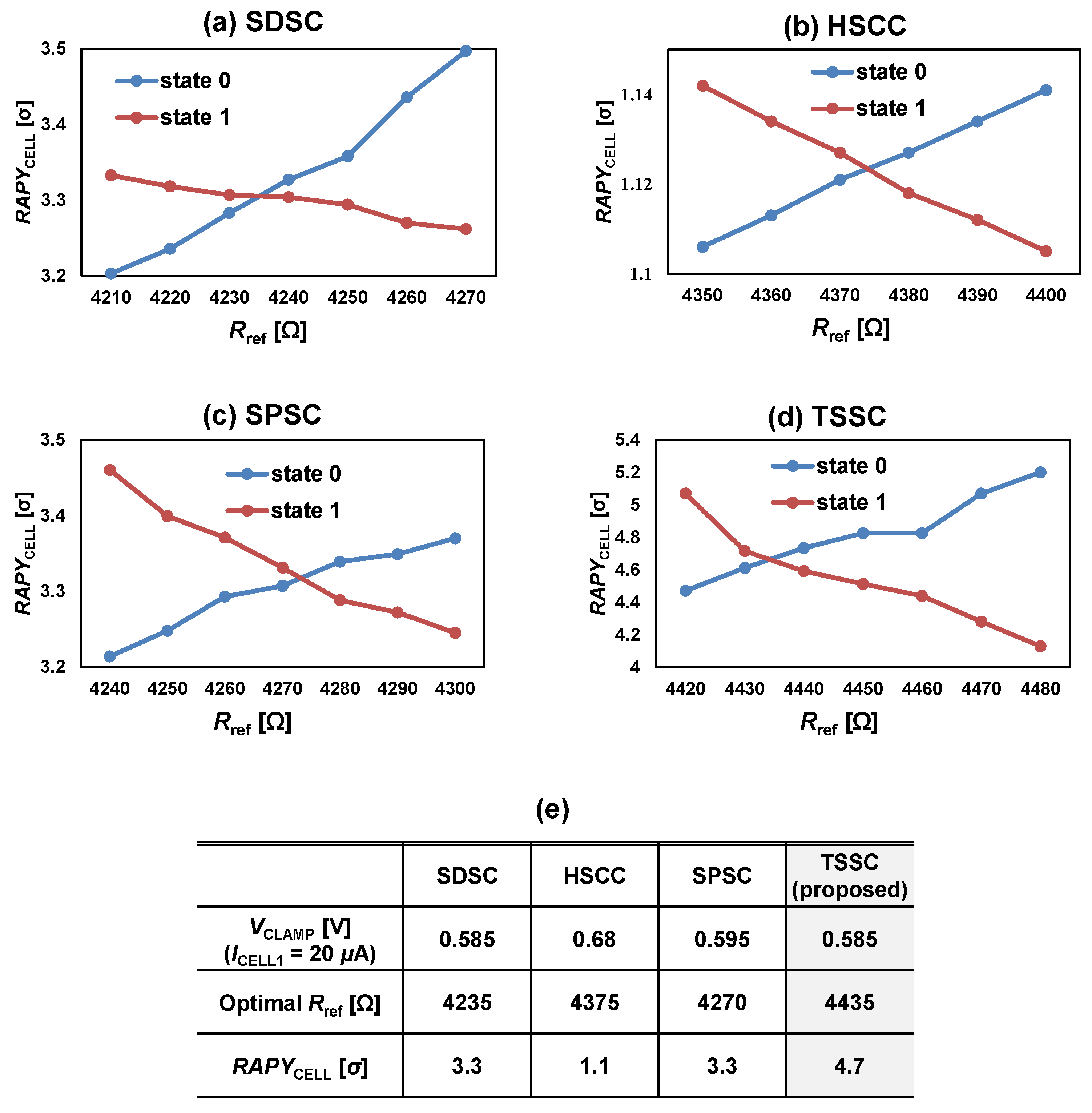
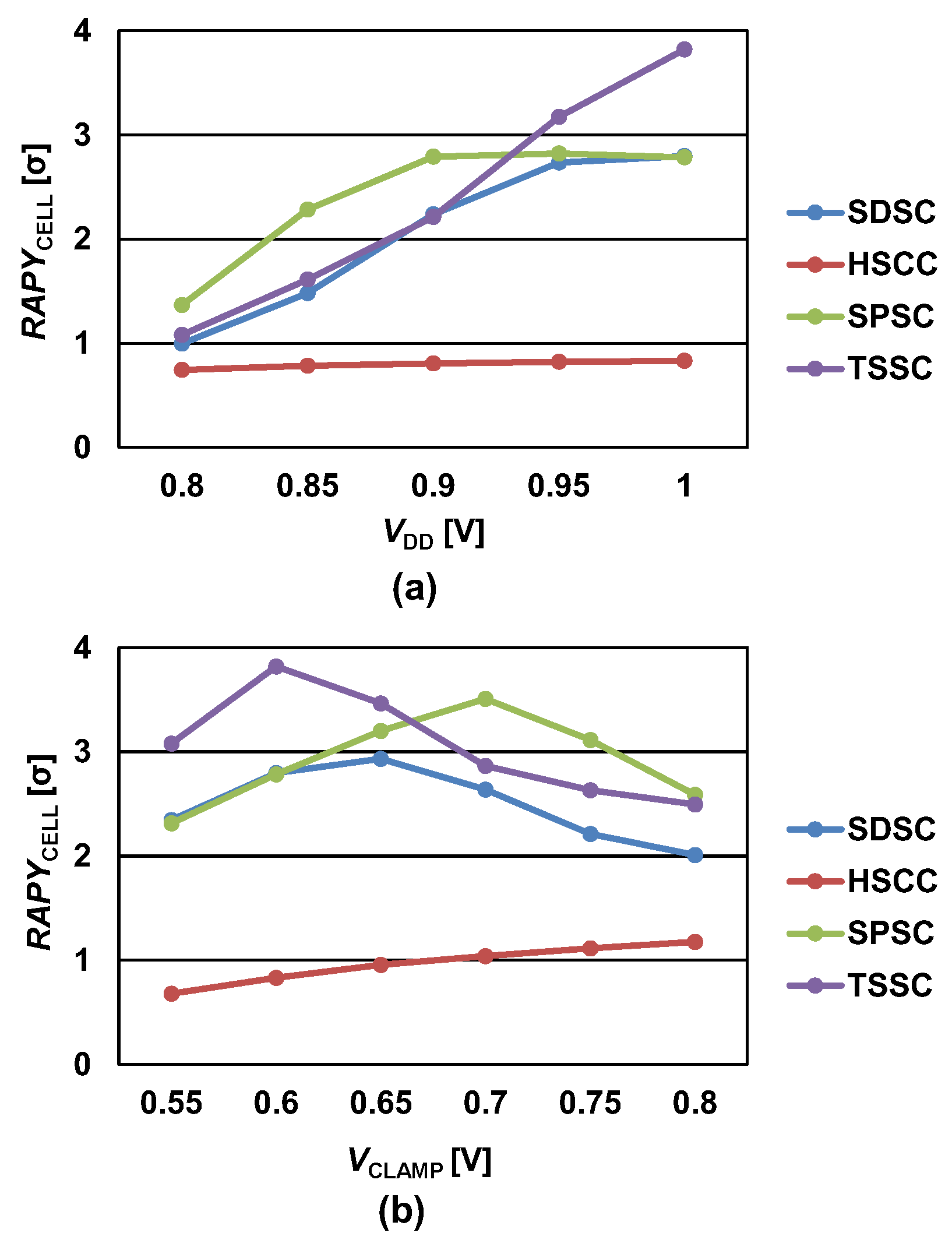
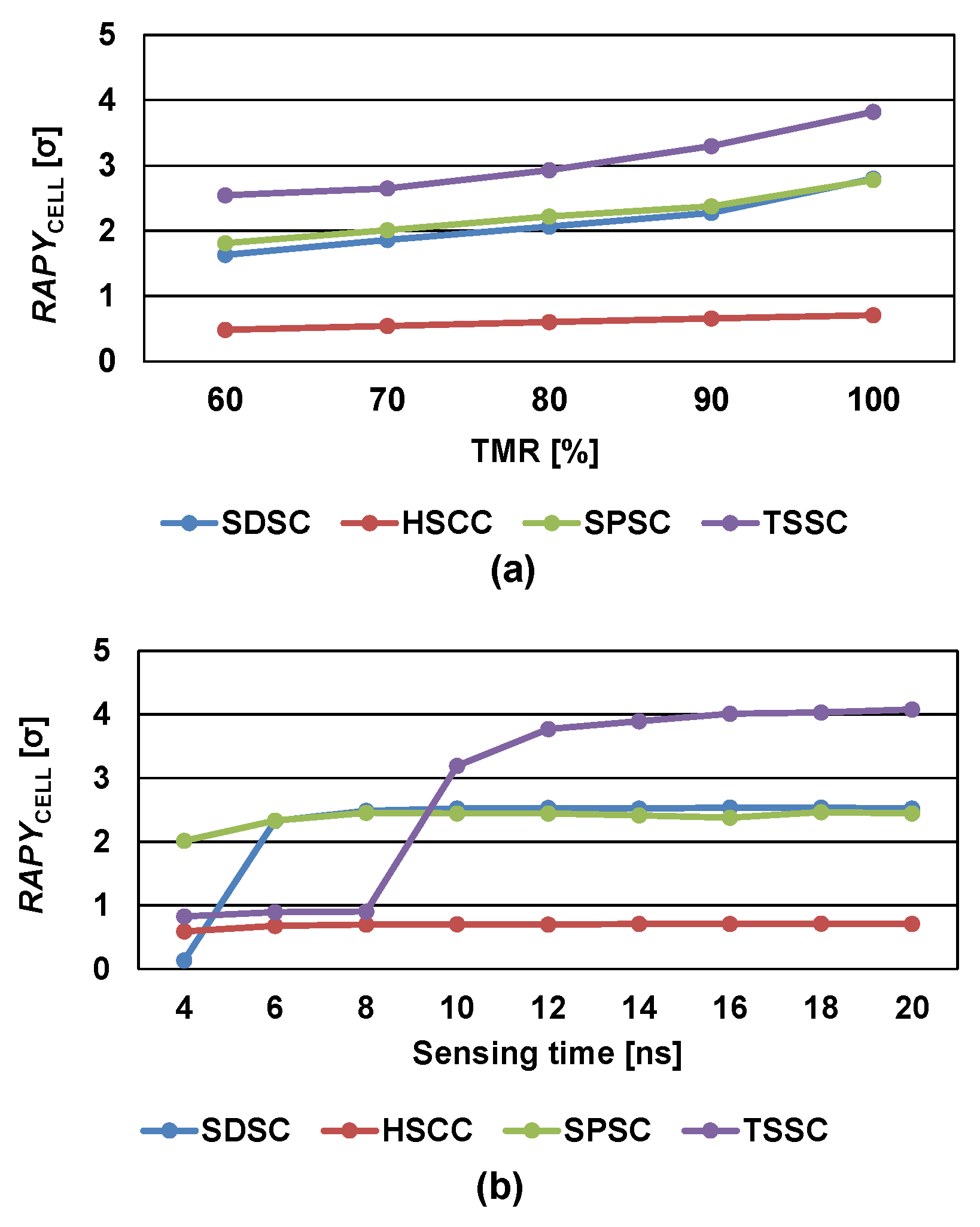
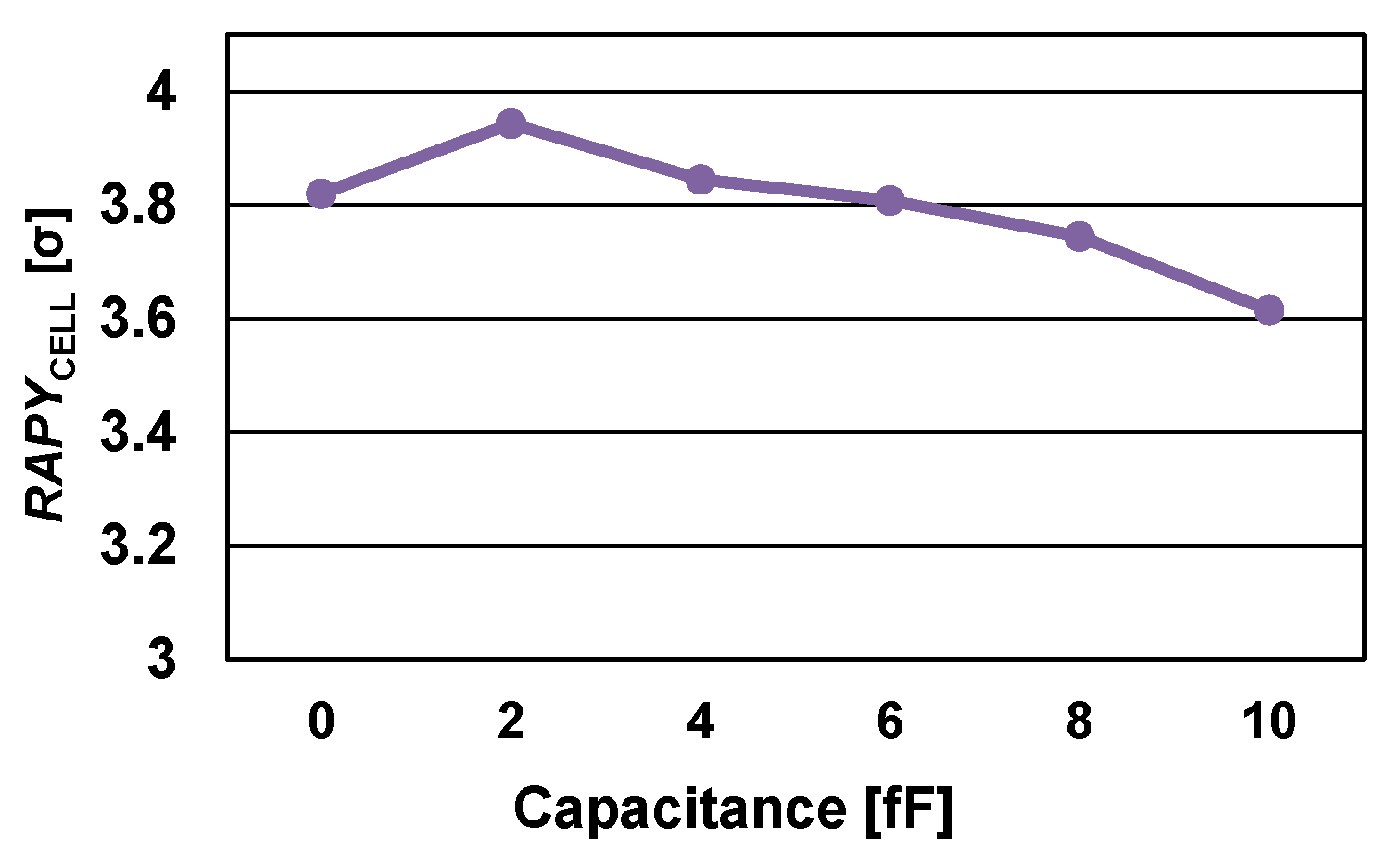
RAPYCELL(2) [σ] @ VDD = 1.0 V, iso-area (RAPYCELL(2) [σ] @ VDD = 1.0 V, identical Tr. size)	3.3 (3.12)	1.1 (1.19)	3.3 (3.36)	4.7 (4.7)
RAPYCELL(3) [σ] @ VDD = 1.0 V, iso-area (RAPYCELL(3) [σ] @ VDD = 1.0 V, identical Tr. size)	2.80 (2.68)	0.83 (0.89)	2.78 (2.79)	3.82 (3.82)
Average sensing time [ns] @ VDD = 1.0 V, iso-area (Average sensing time [ns] @ VDD = 1.0 V, identical Tr. size)	7 (7)	8 (8)	8 (8)	14 (14)
PAVG [μA] @ state 0, VDD = 1.0 V, iso-area (PAVG [μA] @ state 0, VDD = 1.0 V, identical Tr. size)	50.1 (48.1)	153 (213)	53.0 (62.9)	48.9 (48.9)
PAVG [μA] @ state 1, VDD = 1.0 V, iso-area (PAVG [μA] @ state 1, VDD = 1.0 V, identical Tr. size)	46.6 (44.7)	137 (188.7)	47.0 (55.8)	44.0 (44.0)

(1) For the identical transistor size (width/length), load PMOS of 2 μm/0.1 μm, clamp NMOS of 4 μm/0.1 μm, and switch of 0.3 μm/0.05 μm were used. (2) Temperature was set to room temperature (25 °C) and V_CLAMP was set to the values depicted in Figure 5. (3) The worst RAPY_CELL value was calculated by comparing the results obtained at 45 °C and 90 °C when V_CLAMP was set to 0.6 V.

summarizes the simulation results and compares the proposed TSSC with conventional SCs. The simulation to calculate the average power consumption (P_AVG) used and the V_CLAMP and R_ref values are presented in Figure 5. In both states 0 and 1, the TSSC achieved the lowest P_AVG compared with the conventional SCs. However, the proposed TSSC requires a longer sensing time because of its charging and discharging times. As shown in Table 1, the TSSC can achieve a 42% higher RAPY_CELL value compared to that of SPSC. Because of the read disturbance, sensing circuitries are required to work with low sensing currents. Moreover, the RAPY_CELL value of the proposed TSSC is the highest in low-current sensing tasks. Therefore, the TSSC is suitable for STT-MRAM applications, which require low sensing currents.

4. Conclusions

In this study, we proposed a TSSC using the DRV technique and novel split path over time, which maintains a large μ_ΔV0,1 and reduces σ_ΔV0,1. The proposed TSSC can reduce the V_TH variation effects by increasing the current and reducing the transistor mismatch. The simulation results indicate that conventional SCs exhibit low read yield because of small μ_ΔV0,1 or large σ_ΔV0,1 values. In contrast, the TSSC obtains the greatest read yield in the 28-nm process technology.