A Method for Broadband Polyimide Permittivity Measurement of Silicon Interposer Applied for High Speed Digital Microsystem
Abstract
:1. Introduction
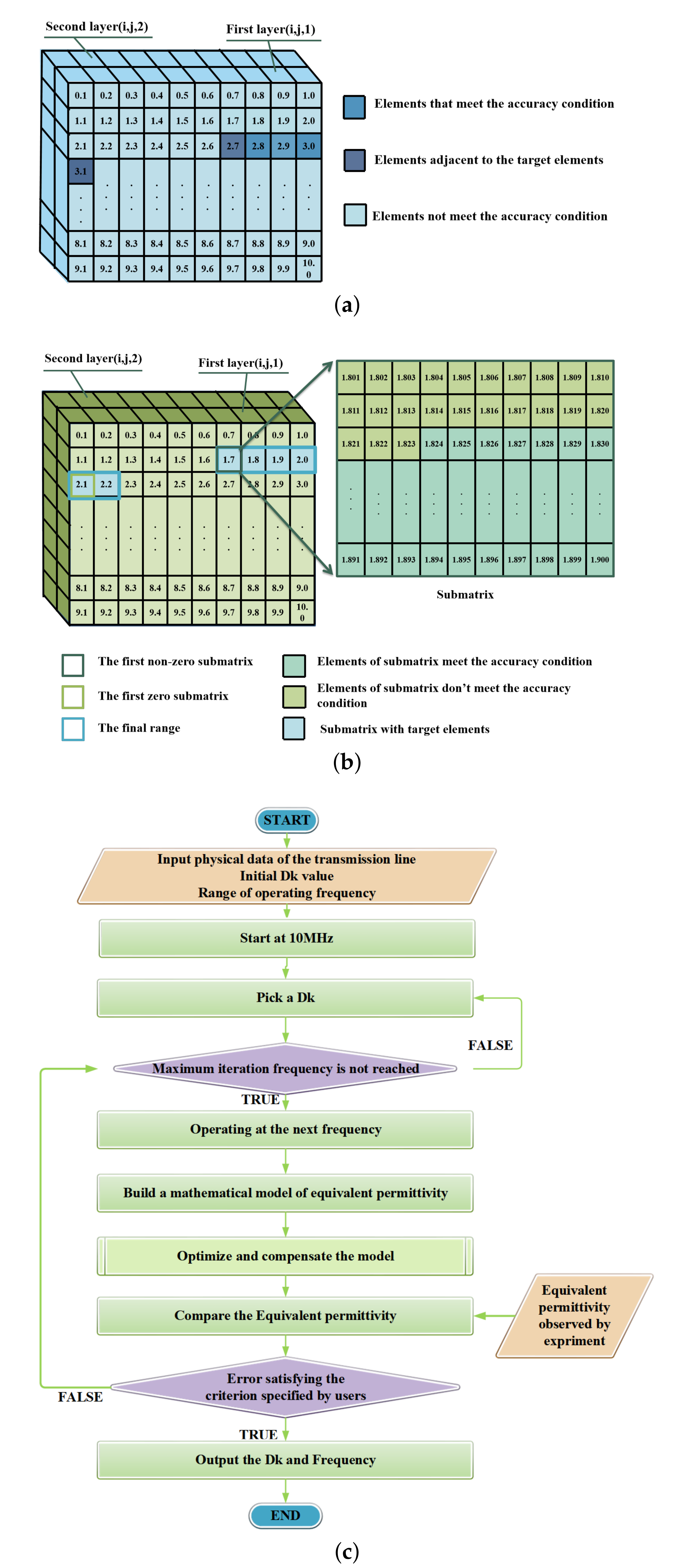
2. Methodology
3. Theory and Calculation
3.1. The Equivalent Permittivity Obtained by Microstrip Line
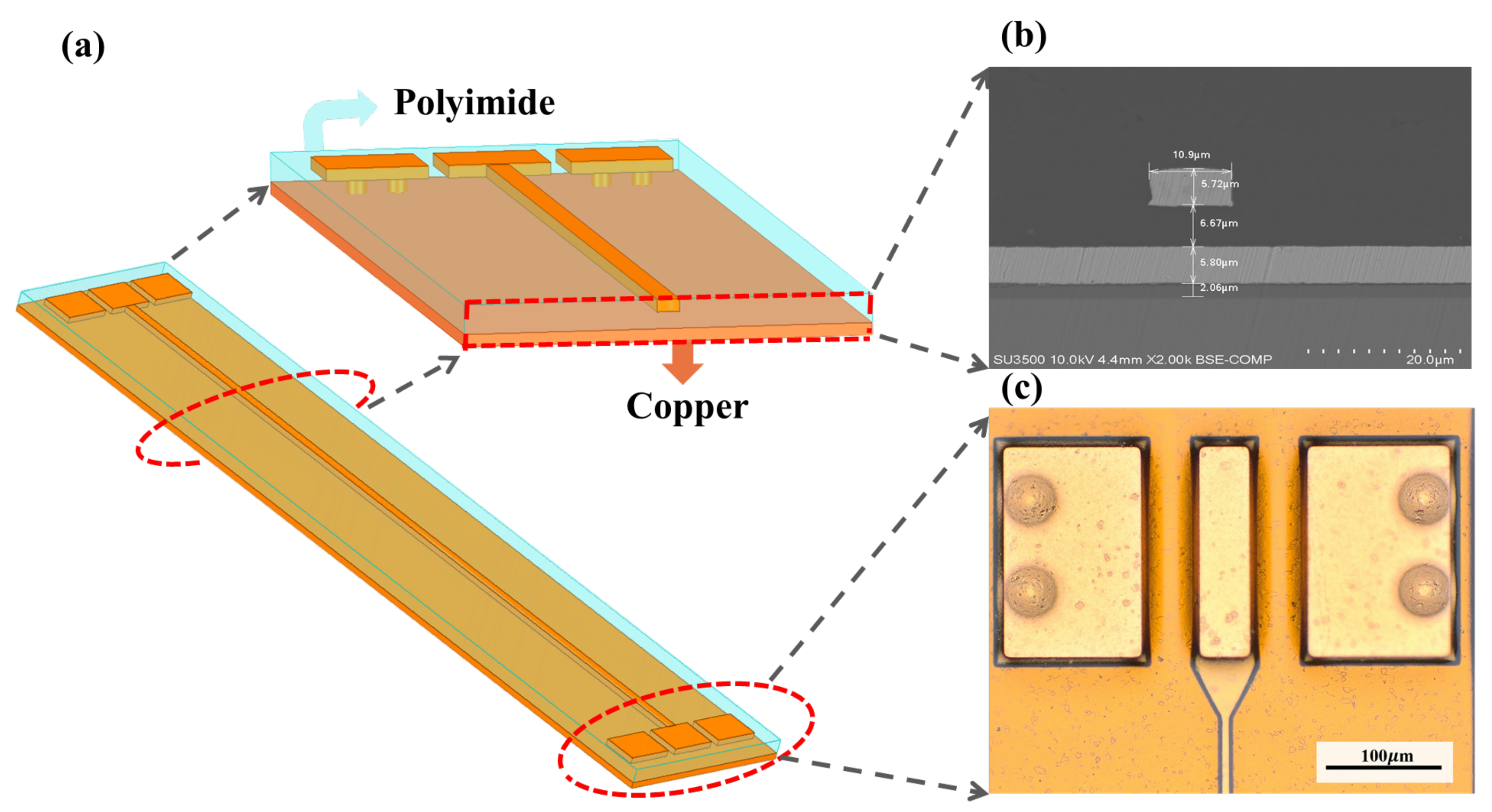
3.1.1. Fabrication
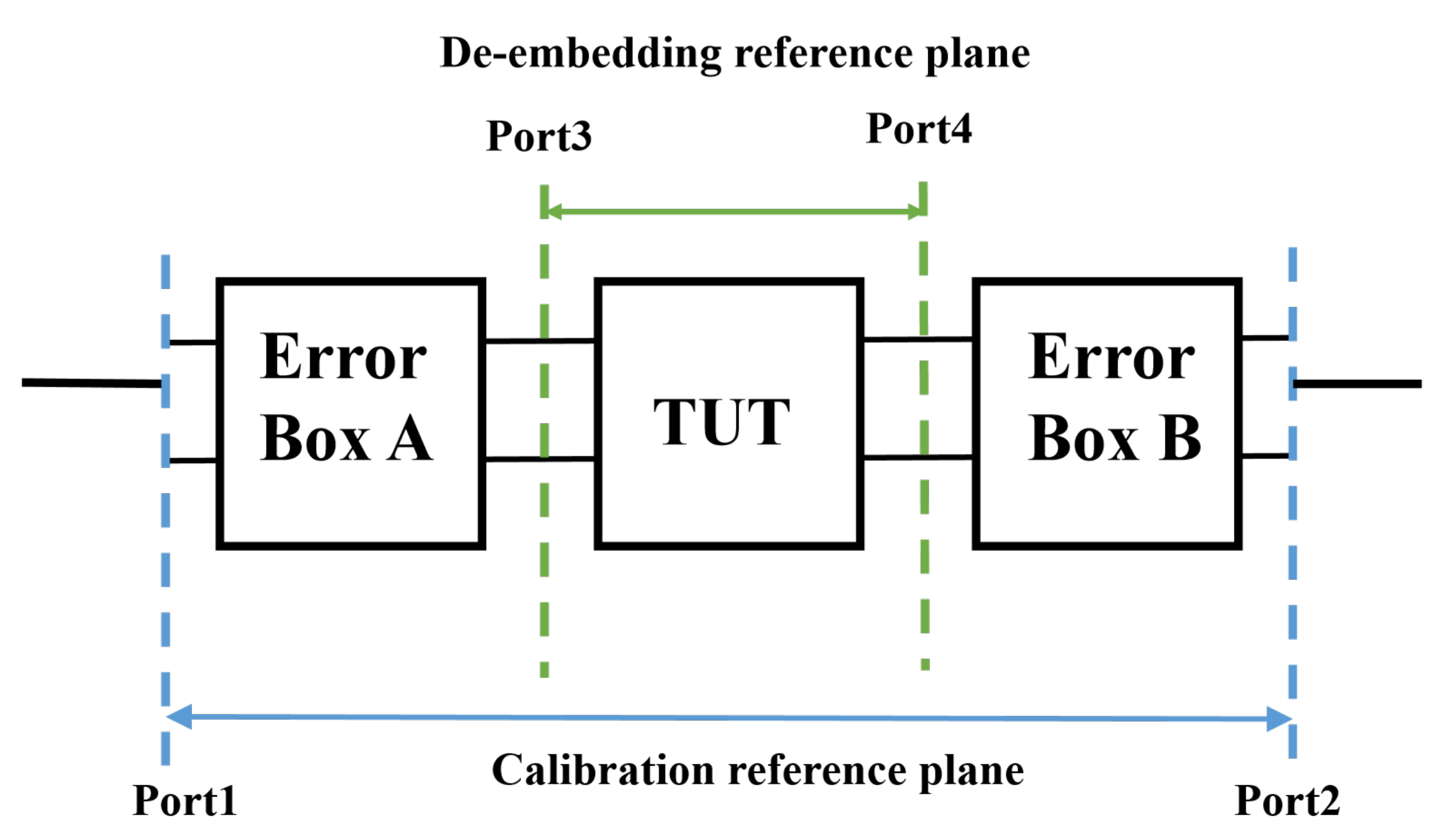
3.1.2. Calibration and Measurement
3.2. Effective Permittivity Calculated by Theory
3.3. Extraction of Df
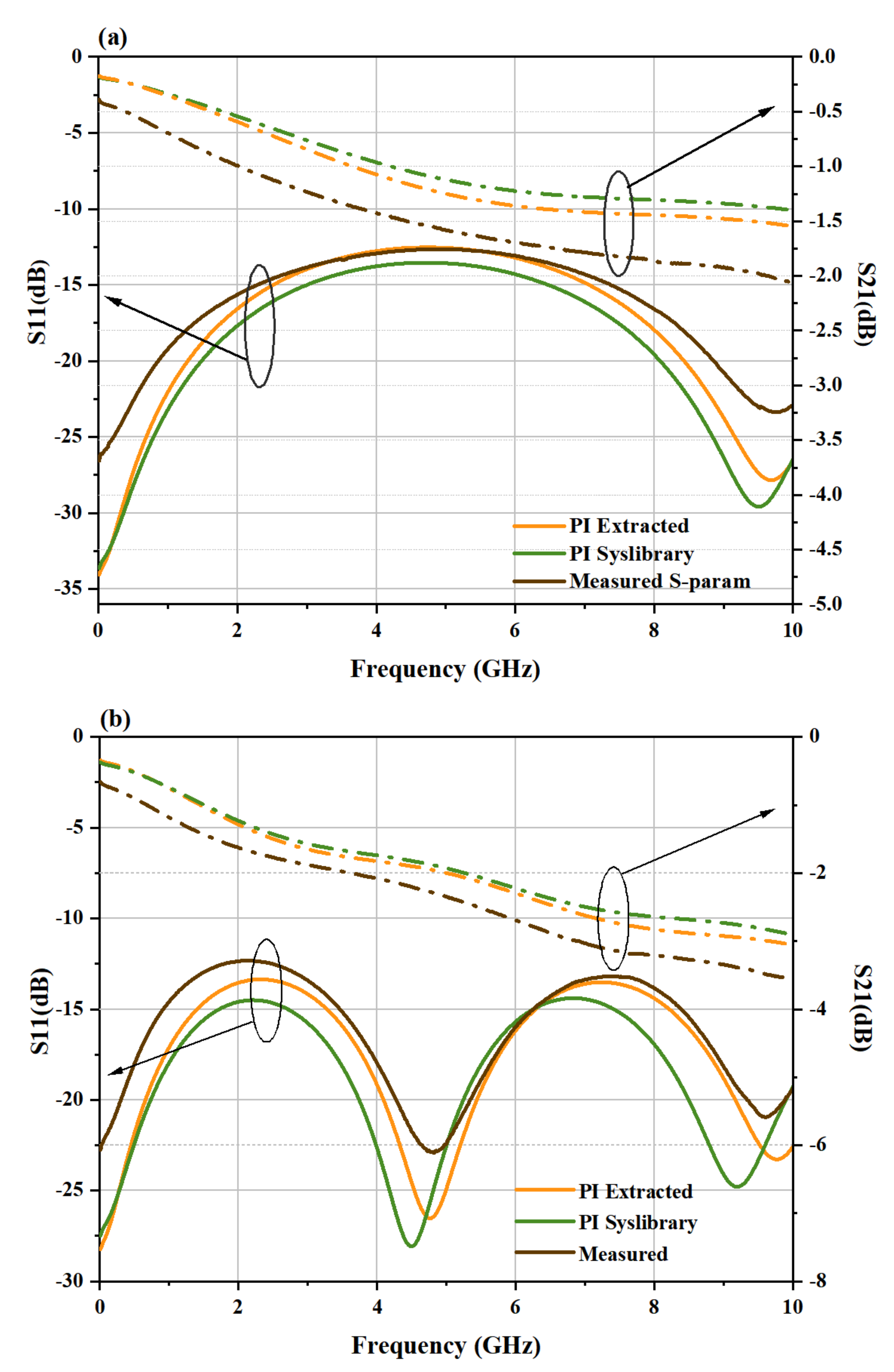
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Watanabe, A.O.; Ali, M.; Sayeed, S.; Rao, R.T.; Raj, P.M. A Review of 5G Front-End Systems Package Integration. IEEE Trans. Compon. Packag. Manuf. 2020, 11, 118–133. [Google Scholar] [CrossRef]
- Mahjabeen, N.; McIntyre, H.; Goel, Y.; Gowri, S.P.; Henderson, R. Dielectric characterization of stacked packaging substrates using a coaxial transmission line technique. In Proceedings of the 2019 IEEE Texas Symposium on Wireless and Microwave Circuits and Systems (WMCS), Waco, TX, USA, 28–29 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Wang, Z. Microsystems using three-dimensional integration and TSV technologies: Fundamentals and applications. Microelectron. Eng. 2019, 210, 35–64. [Google Scholar] [CrossRef]
- Lho, D.; Park, H.; Park, S.; Kim, S.; Kang, H.; Sim, B.; Kim, S.; Park, J.; Cho, K.; Song, J.; et al. Channel Characteristic-Based Deep Neural Network Models for Accurate Eye Diagram Estimation in High Bandwidth Memory (HBM) Silicon Interposer. IEEE Trans. Electromagn. Compat. 2022, 64, 196–208. [Google Scholar] [CrossRef]
- Bogatin, E. Signal and Power Integrity—Simplified; Pearson Education: London, UK, 2010. [Google Scholar]
- Liu, F.; Zhang, R.; De Prospo, B.H.; Dwarakanath, S.; Nimbalkar, P.; Ravichandran, S.; Weyers, D.; Kathaperumal, M.; Tummala, R.R.; Swaminathan, M. Advances in High Performance RDL Technologies for Enabling IO Density of 500 IOs/mm/layer and 8-μm IO Pitch Using Low-k Dielectrics. In Proceedings of the 2020 IEEE 70th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 3–30 June 2020; pp. 1132–1139. [Google Scholar] [CrossRef]
- Dong, X.; Zheng, M.S.; Zha, J.W. Low-k cross-linked polyimide for microelectronic packaging application. In Proceedings of the 2021 International Conference on Electrical Materials and Power Equipment (ICEMPE), Chongqing, China, 11–15 April 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Hasar, U.C.; Westgate, C.R. A Broadband and Stable Method for Unique Complex Permittivity Determination of Low-Loss Materials. IEEE Trans. Microw. Theory Tech. 2009, 57, 471–477. [Google Scholar] [CrossRef]
- Heinola, J.M.; Tolsa, K. Dielectric characterization of printed wiring board materials using ring resonator techniques: A comparison of calculation models. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 717–726. [Google Scholar] [CrossRef]
- Rautio, J.C.; Rautio, B.J. High accuracy broadband measurement of anisotropic dielectric constant using a shielded planar dual mode resonator. In Proceedings of the Microwave Measurement Symposium, Boston, MA, USA, 12 June 2009. [Google Scholar]
- Krupka, J.; Gregory, A.P.; Rochard, O.C.; Clarke, R.N.; Riddle, B.; Baker-Jarvis, J. Uncertainty of complex permittivity measurements by split-post dielectric resonator technique. J. Eur. Ceram. Soc. 2001, 21, 2673–2676. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, S.; Singh, G. Measurement of Dielectric Constant and Loss Factor of the Dielectric Material at Microwave Frequencies. Prog. Electromagn. Res. 2007, 69, 47–54. [Google Scholar] [CrossRef] [Green Version]
- Coonrod, J. Understanding the variables of dielectric constant for PCB materials used at microwave frequencies. In Proceedings of the 2011 41st European Microwave Conference, Manchester, UK, 10–13 October 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Lee, M.Q.; Nam, S. An accurate broadband measurement of substrate dielectric constant. IEEE Microw. Guid. Wave Lett. 1996, 6, 168–170. [Google Scholar] [CrossRef]
- Słobodzian, P.; Barteczka, B.; Golonka, L.; Macioszczyk, J. A comparison of two practical methods for measurement of the dielectric constant of LTCC substrates. In Proceedings of the International Conference on Microwaves, Gdansk, Poland, 16–18 June 2014. [Google Scholar]
- Narayanan, P.M. Microstrip Transmission Line Method for Broadband Permittivity Measurement of Dielectric Substrates. IEEE Trans. Microw. Theory Tech. 2014, 62, 2784–2790. [Google Scholar] [CrossRef]
- Szostak, K.; Sobodzian, P. Broadband Dielectric Measurement of PCB and Substrate Materials by Means of a Microstrip Line of Adjustable Width. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 945–947. [Google Scholar] [CrossRef]
- Huber, O.; Faseth, T.; Magerl, G.; Arthaber, H. Dielectric Characterization of RF-Printed Circuit Board Materials by Microstrip Transmission Lines and Conductor-Backed Coplanar Waveguides Up to 110 GHz. IEEE Trans. Microw. Theory Tech. 2018, 66, 237–244. [Google Scholar] [CrossRef]
- Huang, C.C.; Peng, C.L.; Lin, P.Y.; Yang, B.H.; Cheng, K.C.; Fu, W.T. Dielectric Characterization of Printed Circuit Board by Microstrip Line Up to 110 GHz. In Proceedings of the Electrical Design of Advanced Packaging and Systems Symposium, Kaohsiung, Taiwan, 16–18 December 2019. [Google Scholar]
- Kobayashi, M. A Dispersion Formula Satisfying Recent Requirements in Microstrip CAD. IEEE Trans. Microw. Theory Tech. 1988, 36, 1246–1250. [Google Scholar] [CrossRef]
- Tahar, S.; Benabed, F.; Boudra, S.; Seghiour, A. Dielectric Proprieties and R elaxation Behavior of Polyimide Films ( PI). In Proceedings of the Conference Internationale en Sciences et Technologies Electriques au Maghreb, Tunis, Tunisia, 3–6 November 2014. [Google Scholar]
- Fujiwara, T.; Tatsuta, Y.; Matsumura, K.; Kanamori, D.; Tomikawa, M. Development of Low Dielectric Loss Polyimides and Fabrication of Advanced Packagings for 5 g ApplicationS. In Proceedings of the 2020 International Wafer Level Packaging Conference (IWLPC), San Jose, CA, USA, 13–30 October 2020. [Google Scholar]
- Araki, H.; Yu, S.; Masuda, Y.; Hashimoto, K.; Tomikawa, M. Fabrication of Redistribution Structure Using Highly Reliable Photosensitive Polyimide for Fan Out Panel Level Packages. In Proceedings of the 2018 International Wafer Level Packaging Conference (IWLPC), San Jose, CA, USA, 23–25 October 2018. [Google Scholar]
- Qiu, G.; Ma, W.; Wu, L. Low dielectric constant polyimide mixtures fabricated by polyimide matrix and polyimide microsphere fillers. Polym. Int. 2020, 69, 485–491. [Google Scholar] [CrossRef]
- Araki, H.; Kiuchi, Y.; Shimada, A.; Ogasawara, H.; Tomikawa, M. Low Df Polyimide with Photosensitivity for High Frequency Applications. J. Photopolym. Sci. Technol. 2020, 33, 165–170. [Google Scholar] [CrossRef]
- Marks, R.B. A multiline method of network analyzer calibration. IEEE Trans. Microw. Theory Tech 1991, 39, 1205–1215. [Google Scholar] [CrossRef] [Green Version]
- Moon, S.J.; Ye, X.; Smith, R. Comparison of TRL calibration vs. 2x thru de-embedding methods. In Proceedings of the 2015 IEEE Symposium on Electromagnetic Compatibility and Signal Integrity, Santa Clara, CA, USA, 15–21 March 2015. [Google Scholar]
- Fuh, K.F. Broadband Continuous Extraction of Complex Propagation Constants in Methods Using Two-Line Measurements. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 671–673. [Google Scholar] [CrossRef]
- Clarricoats, P. Foundations for Microwave Engineering; IEEE: Piscataway, NJ, USA, 2001. [Google Scholar]
- Kirschning, M.; Jansen, R.H. Accurate model for effective dielectric constant of microstrip with validity up to millimetre-wave frequencies. Electr. Lett. 1982, 18, 272–273. [Google Scholar] [CrossRef]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bure, V.; Parilina, E. Probability Theory and Mathematical Statistics; Lan Publishing House: Saint Petersburg, Russia, 2013. [Google Scholar]

| Polyimide | Dk Values |
|---|---|
| ODA-PMDA | 3.10 ± 0.006 |
| Siloxane Polyimide | 2.9 |
| Rigid Polyimide | 3.3 |
| ODA-PMDA with different patterning method | 3.0 (Wet Etch Laser)/2.7 (Laser) /2.7 (Photo-Litho. Laser) |
| ODA-PMDA with Different percentages of PM (polyimide microsphere) | 2. 48 ± 0. 007 (10%)/2. 42 ± 0. 001 (20%) /2.30 ± 0.003 (40%)/2.26 ± 0.006 (50%) |
| Material | Design Value | Process Deviation |
|---|---|---|
| Copper | Thick = 5 μm | Within ±1.5 μm |
| Width = 10 μm | Within ±0.5 μm | |
| Polyimide | Thickness = 8 μm | Within ±3 μm |
| Frequency | 2 GHz | 4 GHz | 6 GHz | 8 GHz | 4 GHz |
|---|---|---|---|---|---|
| Dk ( mm) | 3.22 | 3.04 | 2.96 | 3.03 | 2.91 |
| Dk ( mm) | 3.49 | 3.15 | 3.04 | 2.94 | 2.82 |
| Df ( mm) | 0.021 | 0.025 | 0.026 | 0.026 | 0.024 |
| Df ( mm) | 0.023 | 0.026 | 0.025 | 0.024 | 0.033 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Wang, Y.; Han, L.; Wu, D.; Mo, D.; Tian, W. A Method for Broadband Polyimide Permittivity Measurement of Silicon Interposer Applied for High Speed Digital Microsystem. Micromachines 2022, 13, 1138. https://doi.org/10.3390/mi13071138
Zheng Z, Wang Y, Han L, Wu D, Mo D, Tian W. A Method for Broadband Polyimide Permittivity Measurement of Silicon Interposer Applied for High Speed Digital Microsystem. Micromachines. 2022; 13(7):1138. https://doi.org/10.3390/mi13071138
Chicago/Turabian StyleZheng, Zhuoyue, Yongkun Wang, Lei Han, Daowei Wu, Defeng Mo, and Wenchao Tian. 2022. "A Method for Broadband Polyimide Permittivity Measurement of Silicon Interposer Applied for High Speed Digital Microsystem" Micromachines 13, no. 7: 1138. https://doi.org/10.3390/mi13071138
APA StyleZheng, Z., Wang, Y., Han, L., Wu, D., Mo, D., & Tian, W. (2022). A Method for Broadband Polyimide Permittivity Measurement of Silicon Interposer Applied for High Speed Digital Microsystem. Micromachines, 13(7), 1138. https://doi.org/10.3390/mi13071138






