Impact of Generation and Relocation of Defects on Optical Degradation of Multi-Quantum-Well InGaN/GaN-Based Light-Emitting Diode
Abstract
:1. Introduction
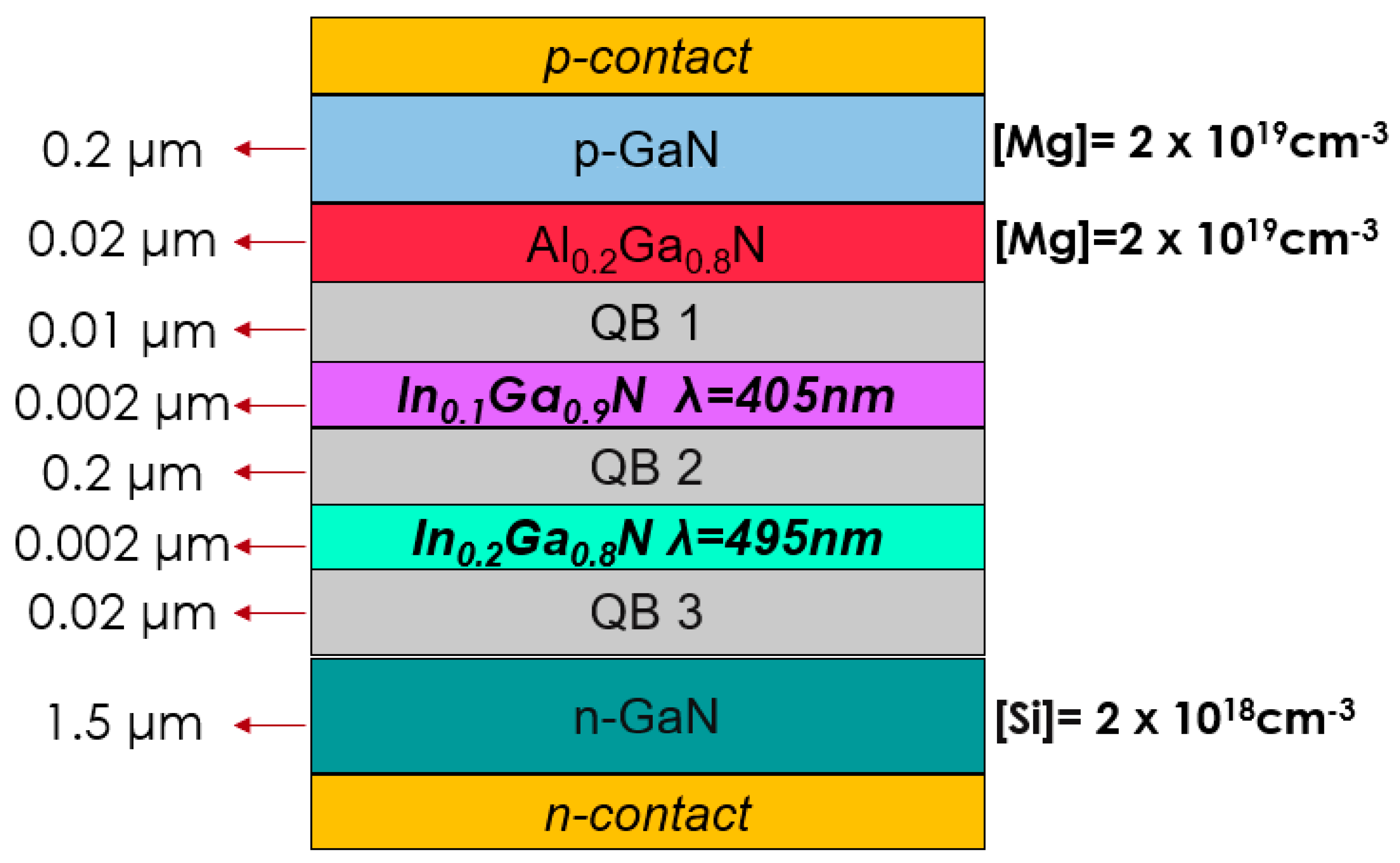
2. Materials and Methods
3. Results
3.1. Preliminary Characterization
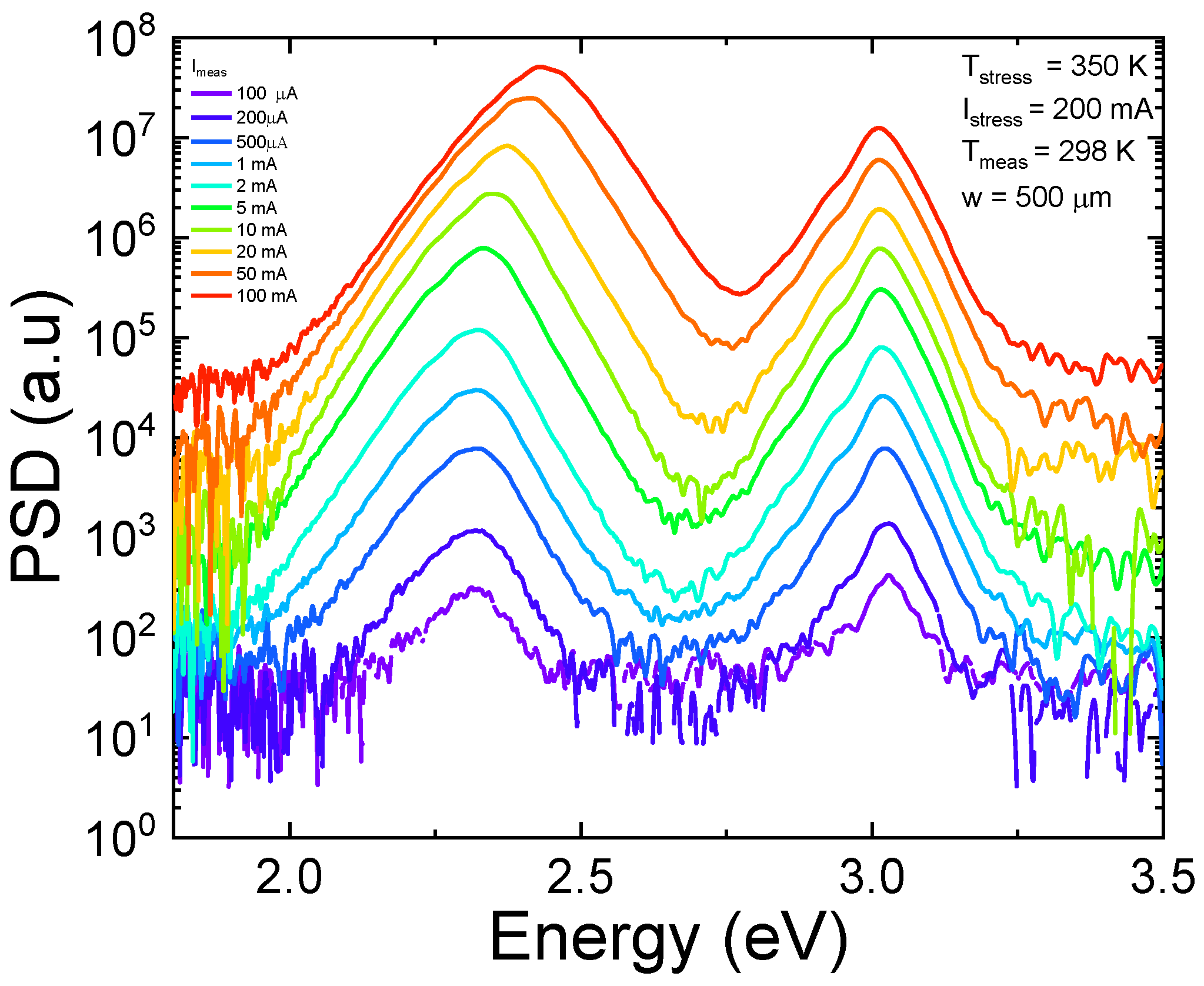
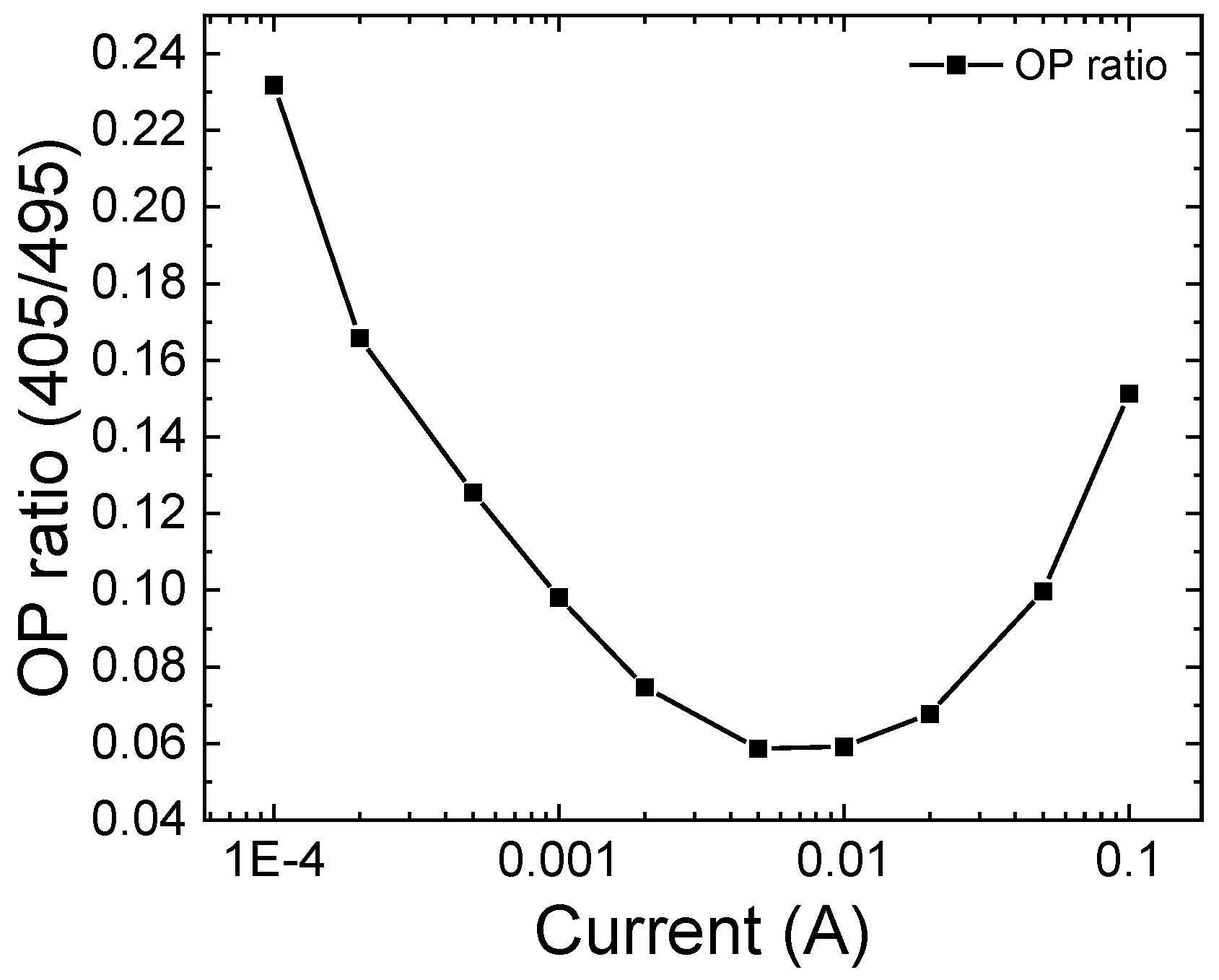
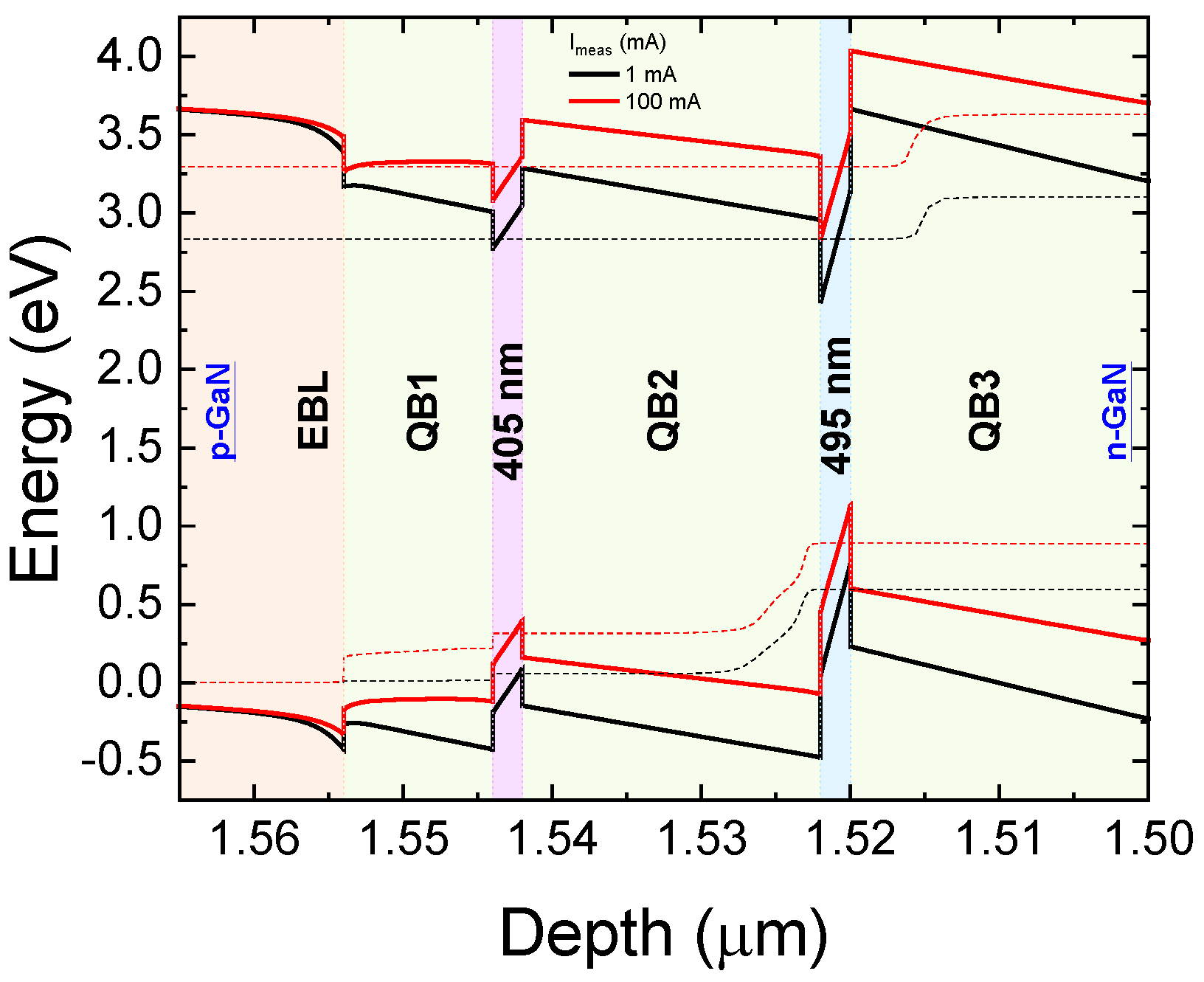
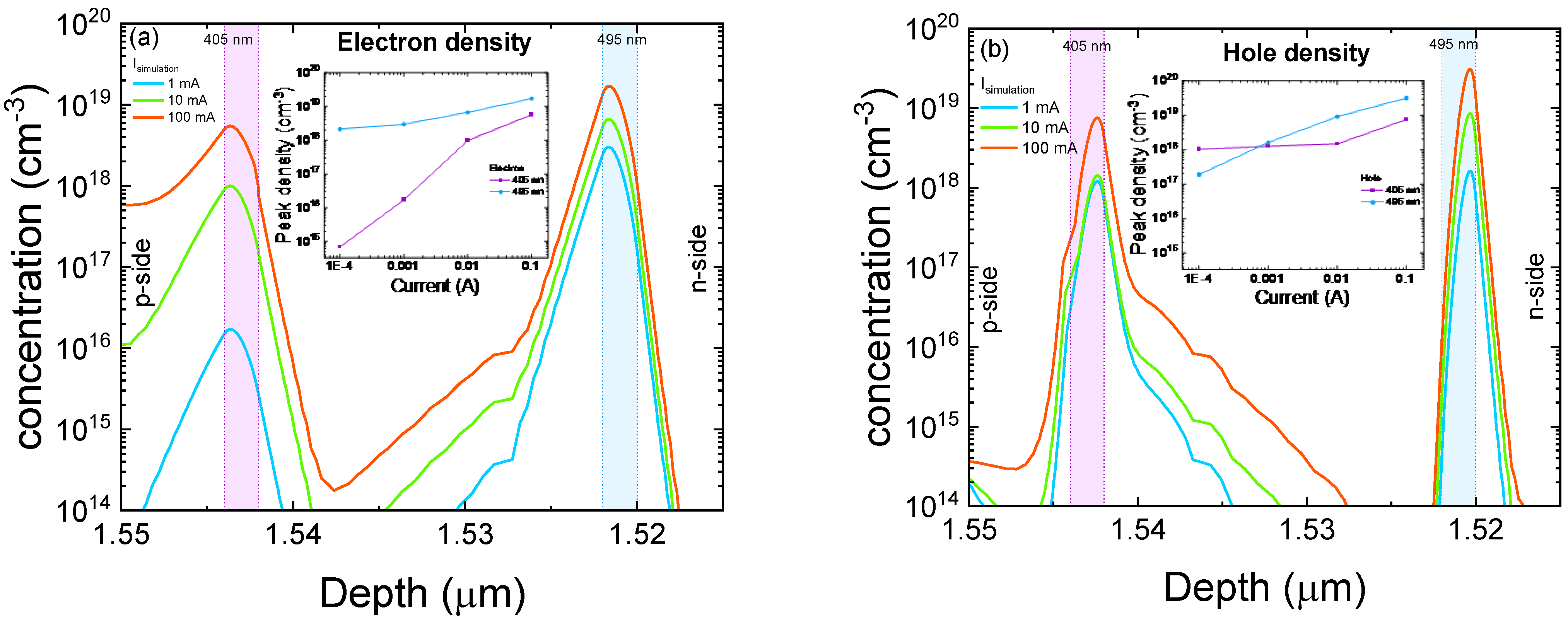
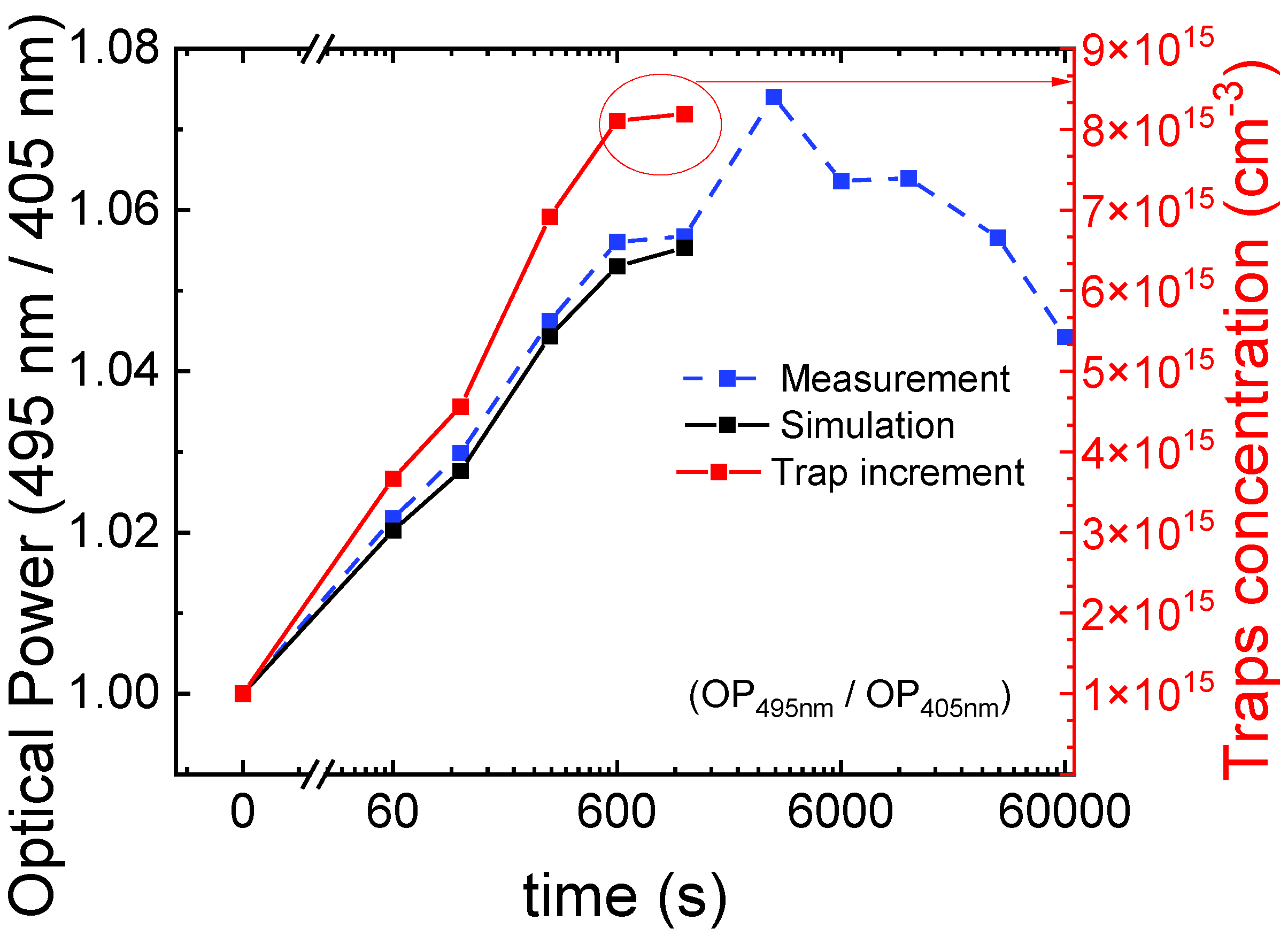
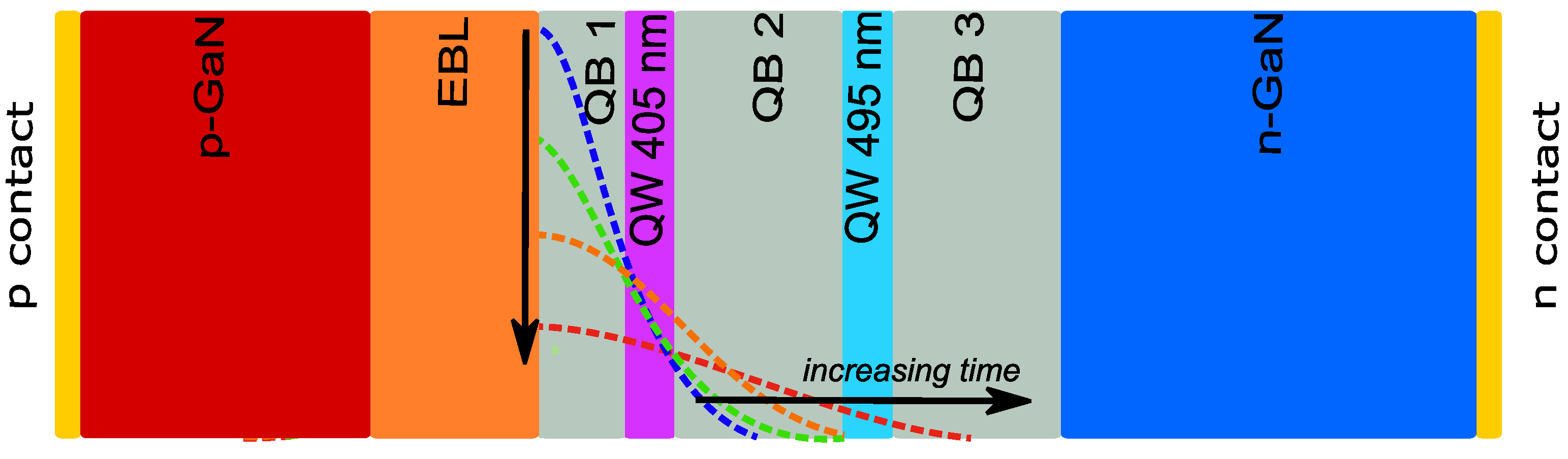
Effect of Trap Concentration and Spatial Position on Optical Characteristics
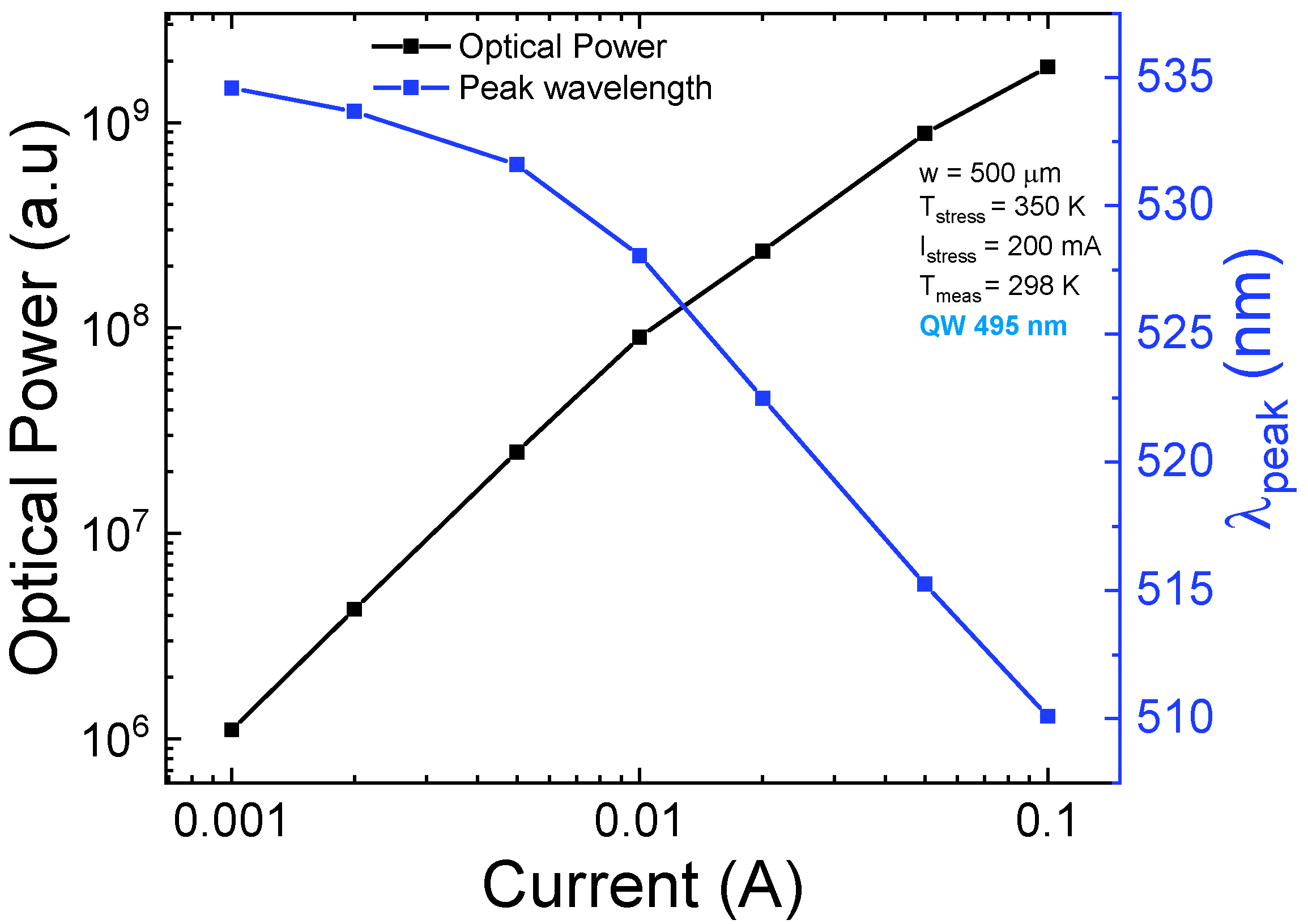
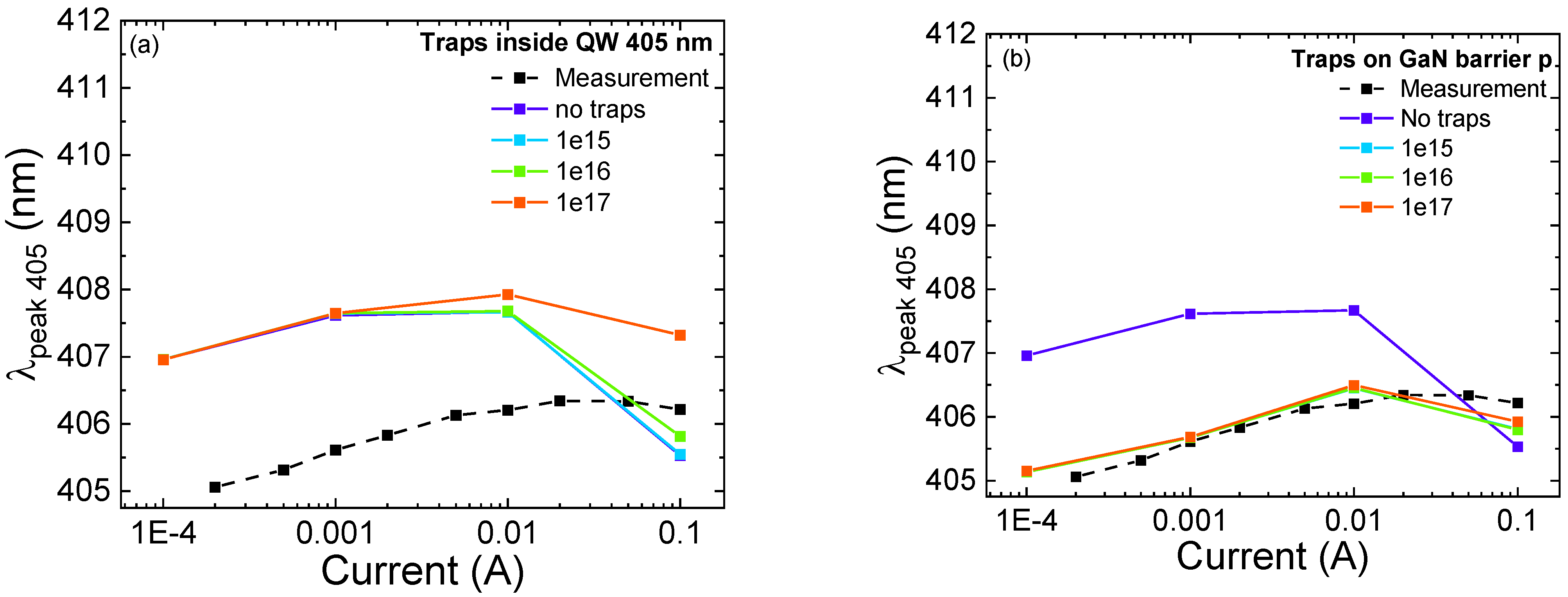
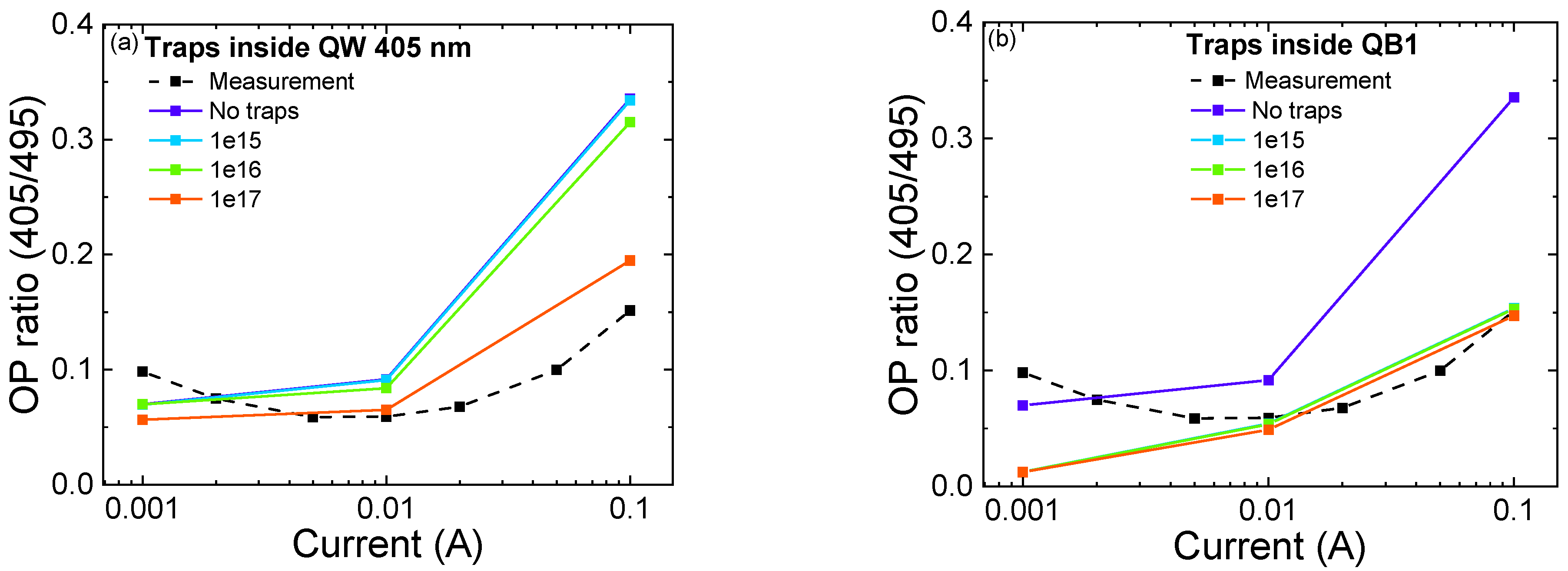
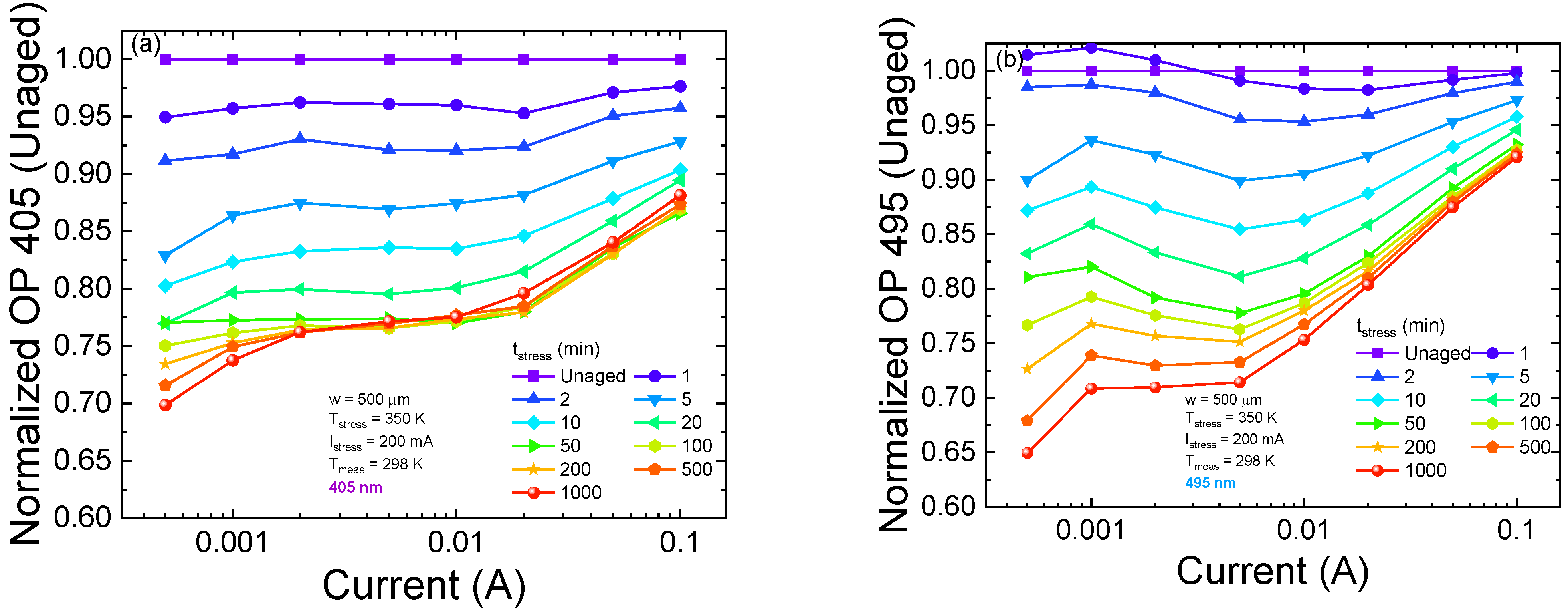
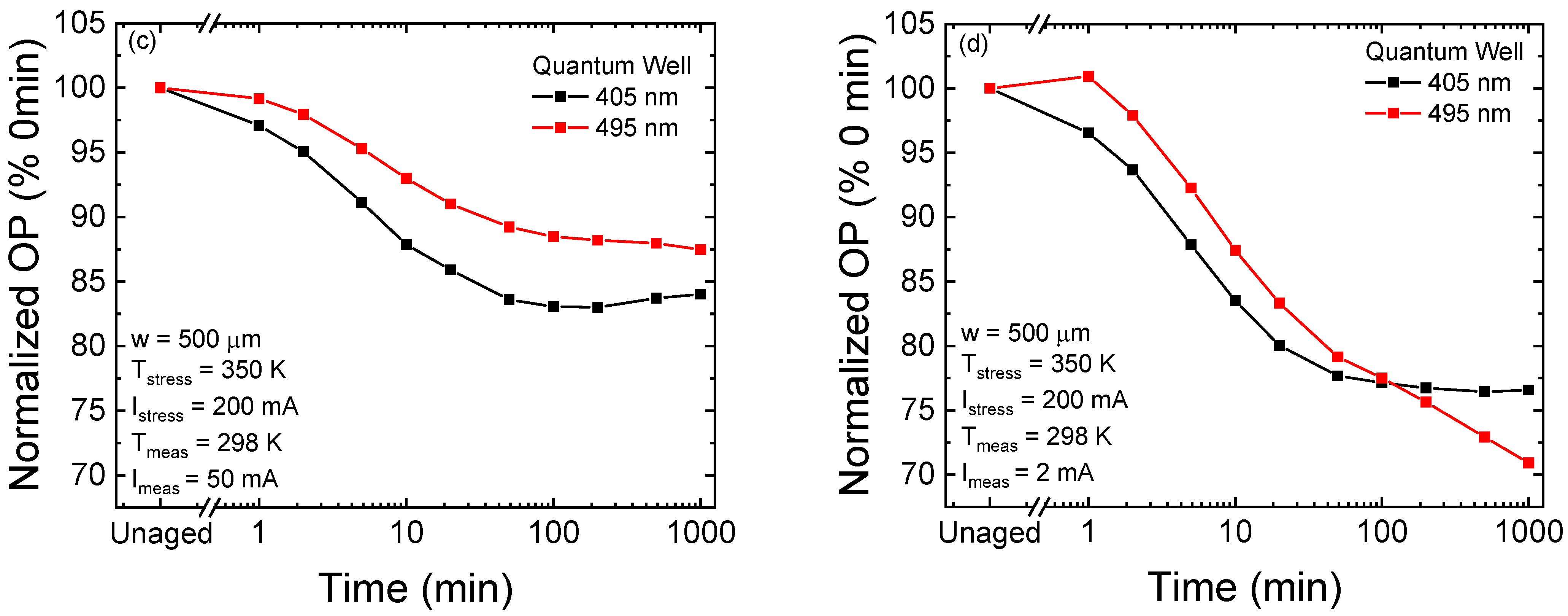
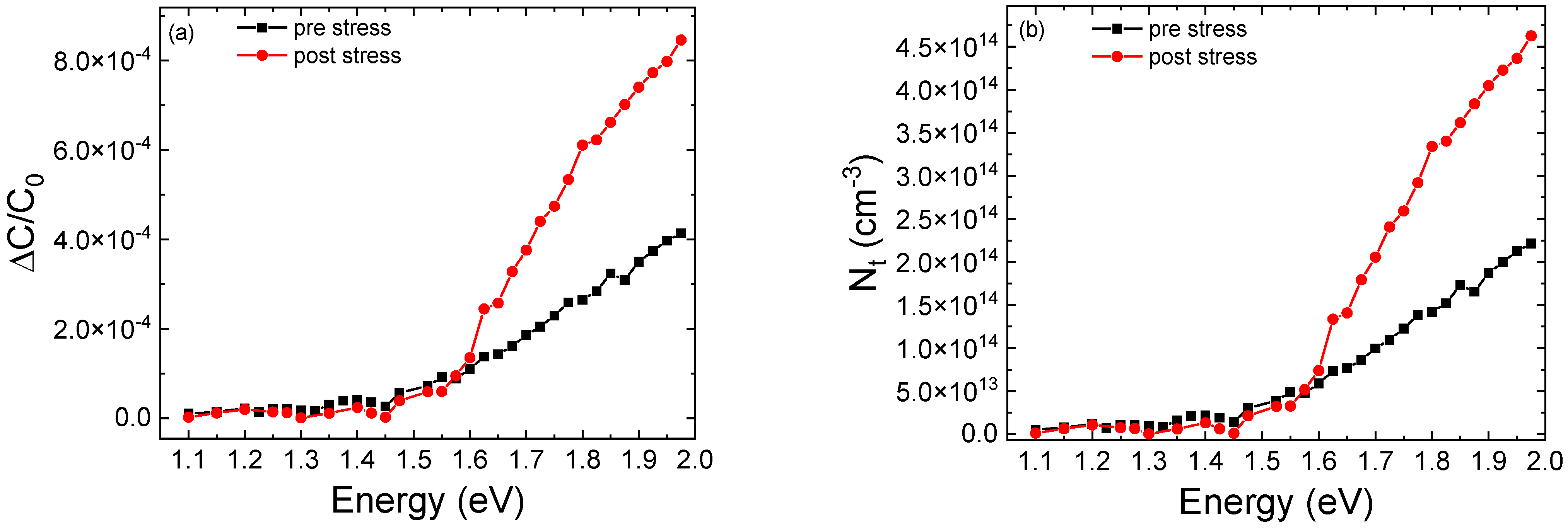
3.2. Optical Degradation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Solís-Cisneros, H.; Hernández-Gutiérrez, C.A.; Anwar, A.-R.; Sevilla-Camacho, P.Y.; Camas-Anzueto, J.L.; Grajales-Coutiño, R.; Trejo-Hernández, R.; Casallas-Moreno, Y.L.; López-López, M. Physical and technological analysis of the AlGaN-based UVC-LED: An extended discussion focused on cubic phase as an alternative for surface disinfection. Rev. Mex. Fis. 2022, 68, 1–18. [Google Scholar] [CrossRef]
- Shang, L.; Xu, B.; Ma, S.; Ouyang, H.; Shan, H.; Hao, X.; Han, B. Enhanced luminescence property of GaN-based LEDs with p-InGaN cap layer grown on p-GaN surface. Mater. Sci. Semicond. Process. 2022, 146, 106666. [Google Scholar] [CrossRef]
- Anwar, A.R.; Sajjad, M.T.; Johar, M.A.; Hernández-Gutiérrez, C.A.; Usman, M.; Łepkowski, S.P. Recent Progress in Micro-LED-Based Display Technologies. Laser Photon. Rev. 2022, 16, 1–20. [Google Scholar] [CrossRef]
- Zhou, Q.; Xu, M.; Wang, H. Internal quantum efficiency improvement of InGaN/GaN multiple quantum well green light-emitting diodes. Opto-Electron. Rev. 2016, 24, 1–9. [Google Scholar] [CrossRef]
- Armstrong, A.M.; Crawford, M.H.; Koleske, D.D. Contribution of deep-level defects to decreasing radiative efficiency of InGaN/GaN quantum wells with increasing emission wavelength. Appl. Phys. Express 2014, 7, 032101. [Google Scholar] [CrossRef]
- Pieniak, K.; Chlipala, M.; Turski, H.; Trzeciakowski, W.; Muziol, G.; Staszczak, G.; Kafar, A.; Makarowa, I.; Grzanka, E.; Skierbiszewski, C.; et al. Quantum-confined Stark effect and mechanisms of its screening in InGaN/GaN light-emitting diodes with a tunnel junction. Opt. Express 2021, 29, 1824–1837. [Google Scholar] [CrossRef]
- Lu, C.; Lu, J.; Li, D.; Liu, N.; Cao, W.; Hu, X.; Wang, L.; Li, R.; Liu, L.; Li, L.; et al. Investigation of the electroluminescence spectrum shift of InGaN/GaN multiple quantum well light-emitting diodes under direct and pulsed currents. J. Appl. Phys. 2013, 113, 013102. [Google Scholar] [CrossRef]
- Huang, C.-F.; Tang, T.-Y.; Huang, J.-J.; Shiao, W.-Y.; Yang, C.C.; Hsu, C.-W.; Chen, L.C. Prestrained effect on the emission properties of InGaN/GaN quantum-well structures. Appl. Phys. Lett. 2006, 89, 051913. [Google Scholar] [CrossRef]
- Langer, T.; Jönen, H.; Kruse, A.; Bremers, H.; Rossow, U.; Hangleiter, A. Strain-induced defects as nonradiative recombination centers in green-emitting GaInN/GaN quantum well structures. Appl. Phys. Lett. 2013, 103, 022108. [Google Scholar] [CrossRef]
- Buffolo, M.; Caria, A.; Piva, F.; Roccato, N.; Casu, C.; De Santi, C.; Trivellin, N.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Defects and reliability of GaN-based LEDs: Review and perspectives. Phys. Status Solidi 2022, 219, 2100727. [Google Scholar] [CrossRef]
- Meneghini, M.; la Grassa, M.; Vaccari, S.; Galler, B.; Zeisel, R.; Drechsel, P.; Hahn, B.; Meneghesso, G.; Zanoni, E. Characterization of the deep levels responsible for non-radiative recombination in InGaN/GaN light-emitting diodes. Appl. Phys. Lett. 2014, 104, 113505. [Google Scholar] [CrossRef]
- Cao, X.; Sandvik, P.; LeBoeuf, S.; Arthur, S. Defect generation in InGaN/GaN light-emitting diodes under forward and reverse electrical stresses. Microelectron. Reliab. 2003, 43, 1987–1991. [Google Scholar] [CrossRef]
- David, A.; Young, N.G.; Hurni, C.A.; Craven, M.D. Quantum Efficiency of III-Nitride Emitters: Evidence for Defect-Assisted Nonradiative Recombination and Its Effect on the Green Gap. Phys. Rev. Appl. 2019, 11, 031001. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Haller, C.; Chen, Y.; Weatherley, T.; Carlin, J.-F.; Jacopin, G.; Butté, R.; Grandjean, N. Impact of defects on Auger recombination in c-plane InGaN/GaN single quantum well in the efficiency droop regime. Appl. Phys. Lett. 2020, 116, 222106. [Google Scholar] [CrossRef]
- Haller, C.; Carlin, J.-F.; Mosca, M.; Rossell, M.D.; Erni, R.; Grandjean, N. InAlN underlayer for near ultraviolet InGaN based light emitting diodes. Appl. Phys. Express 2019, 12, 034002. [Google Scholar] [CrossRef]
- Haller, C.; Carlin, J.-F.; Jacopin, G.; Martin, D.; Butté, R.; Grandjean, N. Burying non-radiative defects in InGaN underlayer to increase InGaN/GaN quantum well efficiency. Appl. Phys. Lett. 2017, 111, 262101. [Google Scholar] [CrossRef] [Green Version]
- Piva, F.; De Santi, C.; Caria, A.; Haller, C.; Carlin, J.F.; Mosca, M.; Meneghesso, G.; Zanoni, E.; Grandjean, N.; Meneghini, M. Defect incorporation in In-containing layers and quantum wells: Experimental analysis via deep level profiling and optical spectroscopy. J. Phys. D Appl. Phys. 2020, 54, 025108. [Google Scholar] [CrossRef]
- Armstrong, A.M.; Bryant, B.N.; Crawford, M.H.; Koleske, D.D.; Lee, S.R.; Wierer, J.J. Defect-reduction mechanism for improving radiative efficiency in InGaN/GaN light-emitting diodes using InGaN underlayers. J. Appl. Phys. 2015, 117, 134501. [Google Scholar] [CrossRef]
- Haller, C.; Carlin, J.-F.; Jacopin, G.; Liu, W.; Martin, D.; Butté, R.; Grandjean, N. GaN surface as the source of non-radiative defects in InGaN/GaN quantum wells. Appl. Phys. Lett. 2018, 113, 111106. [Google Scholar] [CrossRef] [Green Version]
- Tessarek, C.; Figge, S.; Aschenbrenner, T.; Bley, S.; Rosenauer, A.; Seyfried, M.; Kalden, J.; Sebald, K.; Gutowski, J.; Hommel, D. Strong phase separation of strained InxGa1−xN layers due to spinodal and binodal decomposition: Formation of stable quantum dots. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 115316. [Google Scholar] [CrossRef]
- Okumura, T.; Akagi, Y. Numerical analysis of InGaN dot-like structure and compositional fluctuation caused by phase separation. J. Cryst. Growth 2001, 223, 43–54. [Google Scholar] [CrossRef]
- Hernández-Gutiérrez, C.; Kudriavtsev, Y.; Cardona, D.; Guillén-Cervantes, A.; Santana-Rodríguez, G.; Escobosa, A.; Hernández-Hernández, L.A.; López-López, M. InxGa1−xN nucleation by In+ ion implantation into GaN. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 413, 62–67. [Google Scholar] [CrossRef]
- Dong, H.; Qu, K.; Liang, J.; Zhang, A.; Jia, Z.; Jia, W.; Xu, B.; Liu, X.; Li, G.; Wu, Y. Evolution mechanism of InGaN quantum dots and their optical properties. Opt. Mater. 2019, 99, 109554. [Google Scholar] [CrossRef]
- Chichibu, S.F.; Abare, A.C.; Minsky, M.S.; Keller, S.; Fleischer, S.B.; Bowers, J.E.; Hu, E.; Mishra, U.K.; Coldren, L.A.; DenBaars, S.P.; et al. Effective band gap inhomogeneity and piezoelectric field in InGaN/GaN multiquantum well structures. Appl. Phys. Lett. 1998, 73, 2006–2008. [Google Scholar] [CrossRef] [Green Version]
- O’Donnell, K.P.; Martin, R.W.; Middleton, P.G. Origin of Luminescence from InGaN Diodes. Phys. Rev. Lett. 1999, 82, 237–240. [Google Scholar] [CrossRef]
- Pässler, R. Photoionization cross-section analysis for a deep trap contributing to current collapse in GaN field-effect transistors. J. Appl. Phys. 2004, 96, 715–722. [Google Scholar] [CrossRef]
- Crosslight Device Simulation Software. 2018. Available online: www.crosslight.com (accessed on 8 June 2022).
- Wang, C.; Maeda, N.; Tsubaki, K.; Kobayashi, N.; Makimoto, T. Electron transport properties in lightly Si-doped InGaN films grown by metalorganic vapor phase epitaxy. Jpn. J. Appl. Phys. 2004, 43, 3356–3359. [Google Scholar] [CrossRef]
- Sze, S.M. Sze_Dispositivi_a_Semiconduttore; Ulrico Hoepli: Milano, Italy, 1991; ISBN 88-203-1850-41991. [Google Scholar]
- Nakano, Y.; Jimbo, T. Electrical Properties of Acceptor Levels in Mg-Doped GaN. Phys. Status Solidi 2002, 1, 438–442. [Google Scholar] [CrossRef]
- Pan, S.; Sun, C.; Zhou, Y.; Chen, W.; Zhang, R.; Zheng, Y. Investigation of the Electroluminescence Mechanism of GaN-Based Blue and Green Light-Emitting Diodes with Junction Temperature Range of 120–373 K. Appl. Sci. 2020, 10, 444. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhao, D.G.; Jiang, D.S.; Chen, P.; Zhu, J.J.; Liu, Z.S.; Le, L.C.; Li, X.J.; He, X.G.; Liu, J.P.; et al. Optical and structural characteristics of high indium content InGaN/GaN multi-quantum wells with varying GaN cap layer thickness. J. Appl. Phys. 2015, 117, 055709. [Google Scholar] [CrossRef]
- Shapiro, N.A.; Perlin, P.; Kisielowski, C.; Mattos, L.S.; Yang, J.W.; Weber, E.R. The effects of indium concentration and well-thickness on the mechanisms of radiative recombination in InxGa1−xN quantum wells. MRS Internet J. Nitride Semicond. Res. 2000, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Quitsch, W.-A.; Sager, D.; Loewenich, M.; Meyer, T.; Hahn, B.; Bacher, G. Low injection losses in InGaN/GaN LEDs: The correlation of photoluminescence, electroluminescence, and photocurrent measurements. J. Appl. Phys. 2018, 123, 214502. [Google Scholar] [CrossRef]
- Wang, L.; Lu, C.; Lu, J.; Liu, L.; Liu, N.; Chen, Y.; Zhang, Y.; Gu, E.; Hu, X. Influence of carrier screening and band filling effects on efficiency droop of InGaN light emitting diodes. Opt. Express 2011, 19, 14182–14187. [Google Scholar] [CrossRef] [PubMed]
- Roccato, N.; Piva, F.; De Santi, C.; Buffolo, M.; Haller, C.; Carlin, J.-F.; Grandjean, N.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Effects of quantum-well indium content on deep defects and reliability of InGaN/GaN light-emitting diodes with under layer. J. Phys. D Appl. Phys. 2021, 54, 505108. [Google Scholar] [CrossRef]
- Piva, F.; De Santi, C.; Deki, M.; Kushimoto, M.; Amano, H.; Tomozawa, H.; Shibata, N.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Modeling the degradation mechanisms of AlGaN-based UV-C LEDs: From injection efficiency to mid-gap state generation. Photon. Res. 2020, 8, 1786. [Google Scholar] [CrossRef]
- De Santi, C.; Buffolo, M.; Renso, N.; Neviani, A.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Evidence for defect-assisted tunneling and recombination at extremely low current in InGaN/GaN-based LEDs. Appl. Phys. Express 2019, 12, 052007. [Google Scholar] [CrossRef]
- Lee, S.-N.; Paek, H.S.; Son, J.K.; Kim, H.; Kim, K.K.; Ha, K.H.; Nam, O.H.; Park, Y. Effects of Mg dopant on the degradation of InGaN multiple quantum wells in AlInGaN-based light emitting devices. J. Electroceramics 2008, 23, 406–409. [Google Scholar] [CrossRef]
- Orita, K.; Meneghini, M.; Ohno, H.; Trivellin, N.; Ikedo, N.; Takigawa, S.; Yuri, M.; Tanaka, T.; Zanoni, E.; Meneghesso, G. Analysis of Diffusion-Related Gradual Degradation of InGaN-Based Laser Diodes. IEEE J. Quantum Electron. 2012, 48, 1169–1176. [Google Scholar] [CrossRef]
- Renso, N.; De Santi, C.; Caria, A.; Torre, F.D.; Zecchin, L.; Meneghesso, G.; Zanoni, E.; Meneghini, M. Degradation of InGaN-based LEDs: Demonstration of a recombination-dependent defect-generation process. J. Appl. Phys. 2020, 127, 185701. [Google Scholar] [CrossRef]
- Mandurrino, M.; Verzellesi, G.; Goano, M.; Vallone, M.; Bertazzi, F.; Ghione, G.; Meneghini, M.; Meneghesso, G.; Zanoni, E. Physics-based modeling and experimental implications of trap-assisted tunneling in InGaN/GaN light-emitting diodes. Phys. Status Solidi 2015, 212, 947–953. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casu, C.; Buffolo, M.; Caria, A.; De Santi, C.; Zanoni, E.; Meneghesso, G.; Meneghini, M. Impact of Generation and Relocation of Defects on Optical Degradation of Multi-Quantum-Well InGaN/GaN-Based Light-Emitting Diode. Micromachines 2022, 13, 1266. https://doi.org/10.3390/mi13081266
Casu C, Buffolo M, Caria A, De Santi C, Zanoni E, Meneghesso G, Meneghini M. Impact of Generation and Relocation of Defects on Optical Degradation of Multi-Quantum-Well InGaN/GaN-Based Light-Emitting Diode. Micromachines. 2022; 13(8):1266. https://doi.org/10.3390/mi13081266
Chicago/Turabian StyleCasu, Claudia, Matteo Buffolo, Alessandro Caria, Carlo De Santi, Enrico Zanoni, Gaudenzio Meneghesso, and Matteo Meneghini. 2022. "Impact of Generation and Relocation of Defects on Optical Degradation of Multi-Quantum-Well InGaN/GaN-Based Light-Emitting Diode" Micromachines 13, no. 8: 1266. https://doi.org/10.3390/mi13081266
APA StyleCasu, C., Buffolo, M., Caria, A., De Santi, C., Zanoni, E., Meneghesso, G., & Meneghini, M. (2022). Impact of Generation and Relocation of Defects on Optical Degradation of Multi-Quantum-Well InGaN/GaN-Based Light-Emitting Diode. Micromachines, 13(8), 1266. https://doi.org/10.3390/mi13081266








