Hierarchical Morphing Control of an Ultra-Lightweight Electro-Actuated Polymer Telescope with Thin-Film Actuators
Abstract
:1. Introduction
- Thermal considerations: The space environment is subject to wide temperature variations, leading to significant deformations in polymer-based reflector substrates and resulting shape errors. Therefore, the selection of materials with minimal coefficients of thermal expansion (CTE) is of utmost importance. Ideally, a polymer material with zero CTE is highly desirable, as exemplified by (developed by ManTech, Herndon, VA, USA), which boasts an exceptionally low CTE of approximately [14,15]. On the other hand, thermal stability is also crucial, considering the viscoelastic properties, including creep, which significantly influence the behaviors of thin-shell mirrors constructed from polymers during moving phases, such as unfolding deployment. Maintaining long-term dimensional stability necessitates continuous monitoring of surface figures, often requiring the implementation of feedback control systems.
- Surface quality: The reflectivity of polymer thin-shell mirrors is significantly impacted by the surface roughness following the coating process. The attainment of a smooth micro-scale surface on the thin mirror substrate is imperative for the effective implementation of macro-scale active control. This underscores the critical necessity of selecting substrate materials endowed with exceptional mechanical properties suitable for the thermoplastic forming process. Typically, reported values for surface roughness in the references cited [4,5,9,12,13] consistently fall below nm. However, when considering the shape error control of the wavefront within a macro-scale clear pupil, the root mean square (RMS) error of the surface figure should conform to specific standards. For imaging applications, achieving a Strehl ratio of 0.8 necessitates [16]where represents the detection wavelength. For non-imaging applications, e.g., incoherent LiDAR, a relaxed criterion can be applied with a factor of 5, i.e., /6 should be fulfilled [5].
- Space compatibility: Particular attention is dedicated to assessing the material’s resistance to space-related threats, including exposure to solar radiation, particle radiation, and erosive factors. These environmental challenges have the potential to compromise the long-term viability of the polymer material and, consequently, the service life of the space reflector. It is worth noting that NASA has conducted an extensive series of experiments as part of the Materials International Space Station Experiment (MISSE) program to tackle these formidable challenges [17].
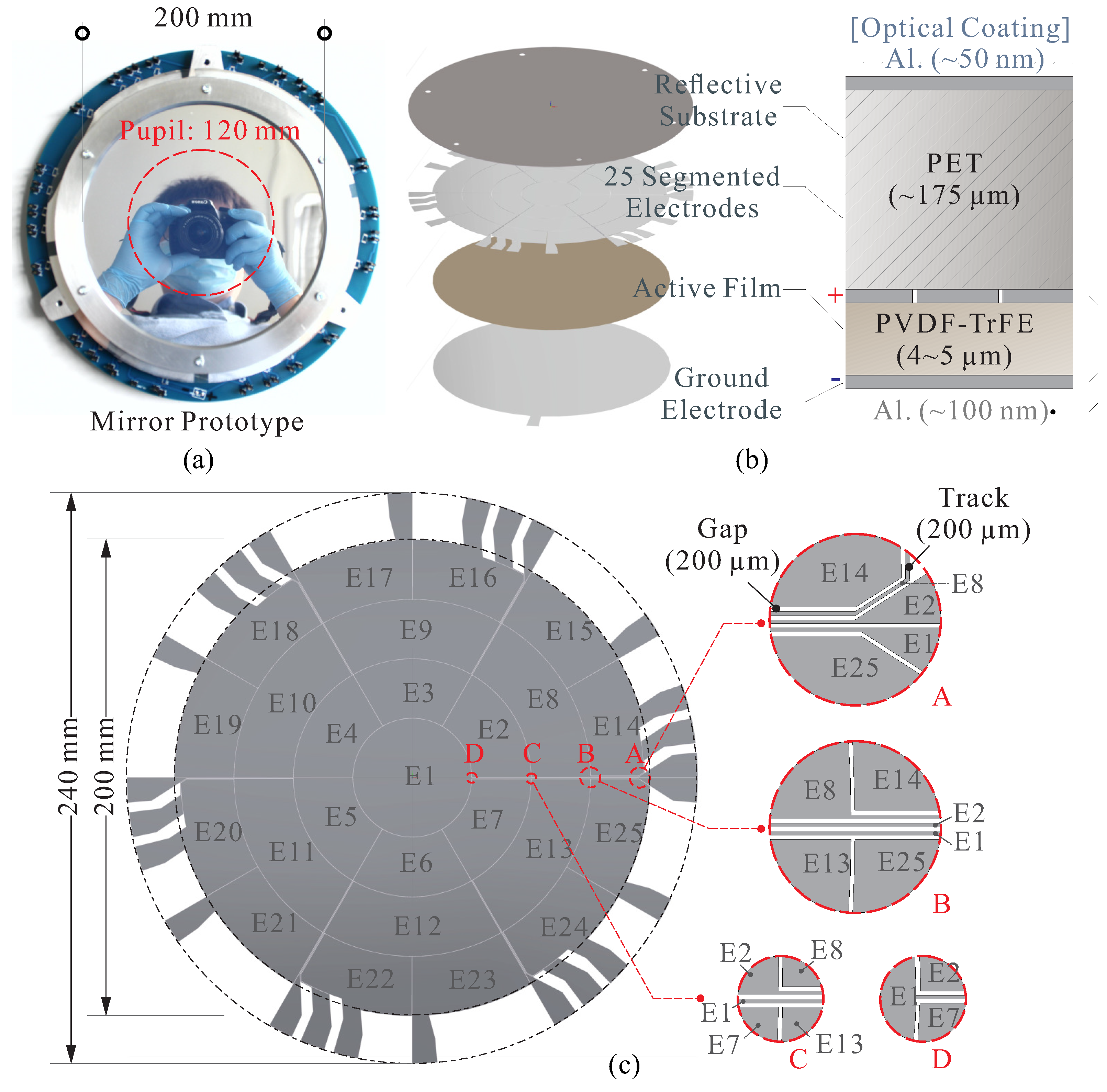
2. Development of Thin-Shell Composite with Film Actuators
3. Strain Generated by Thin-Film Actuators
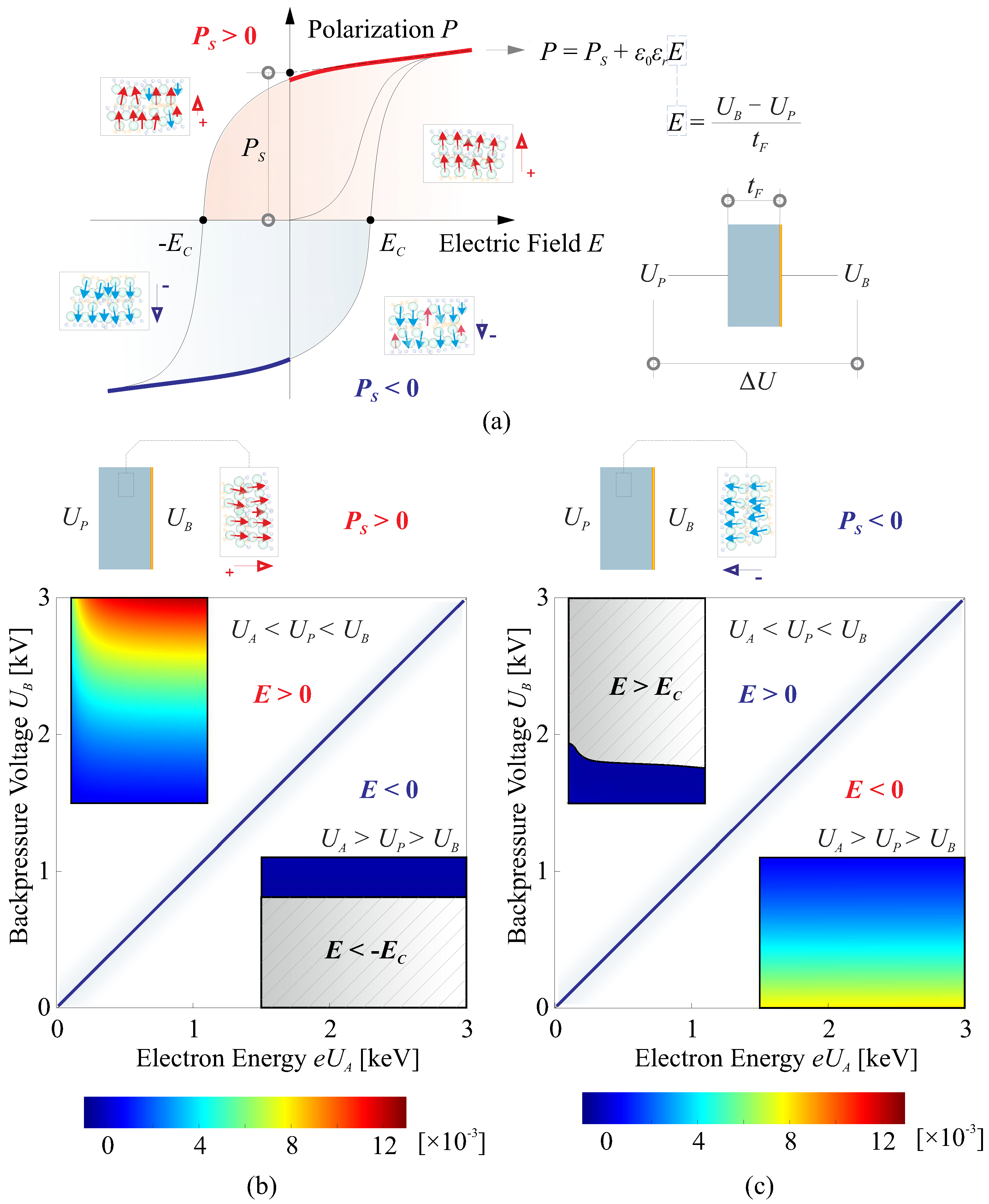
3.1. Strain Actuation by Charging a Pair of Parallel Electrodes
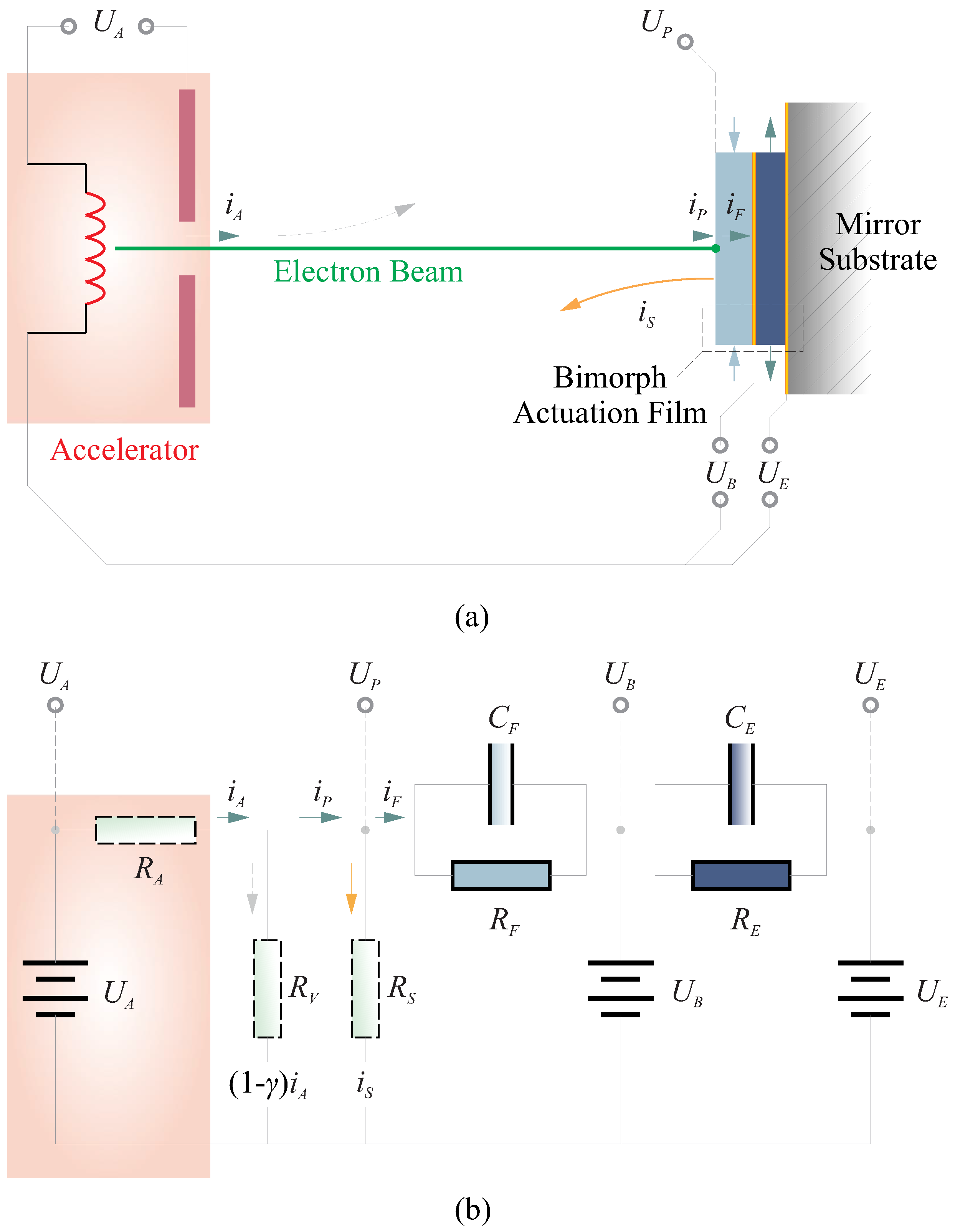
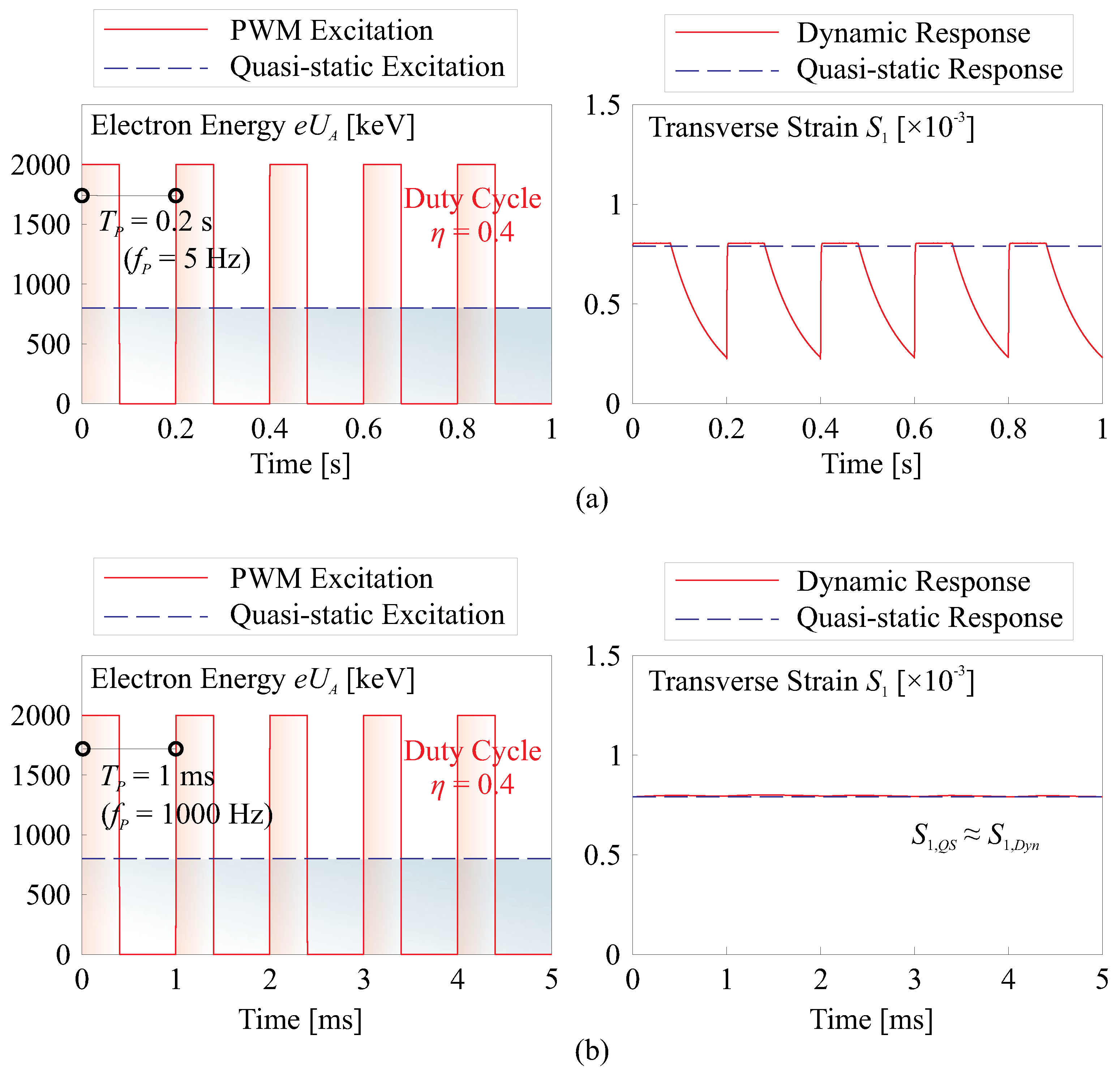
3.2. Numerical Study on Strain Excitation with Electron Flux
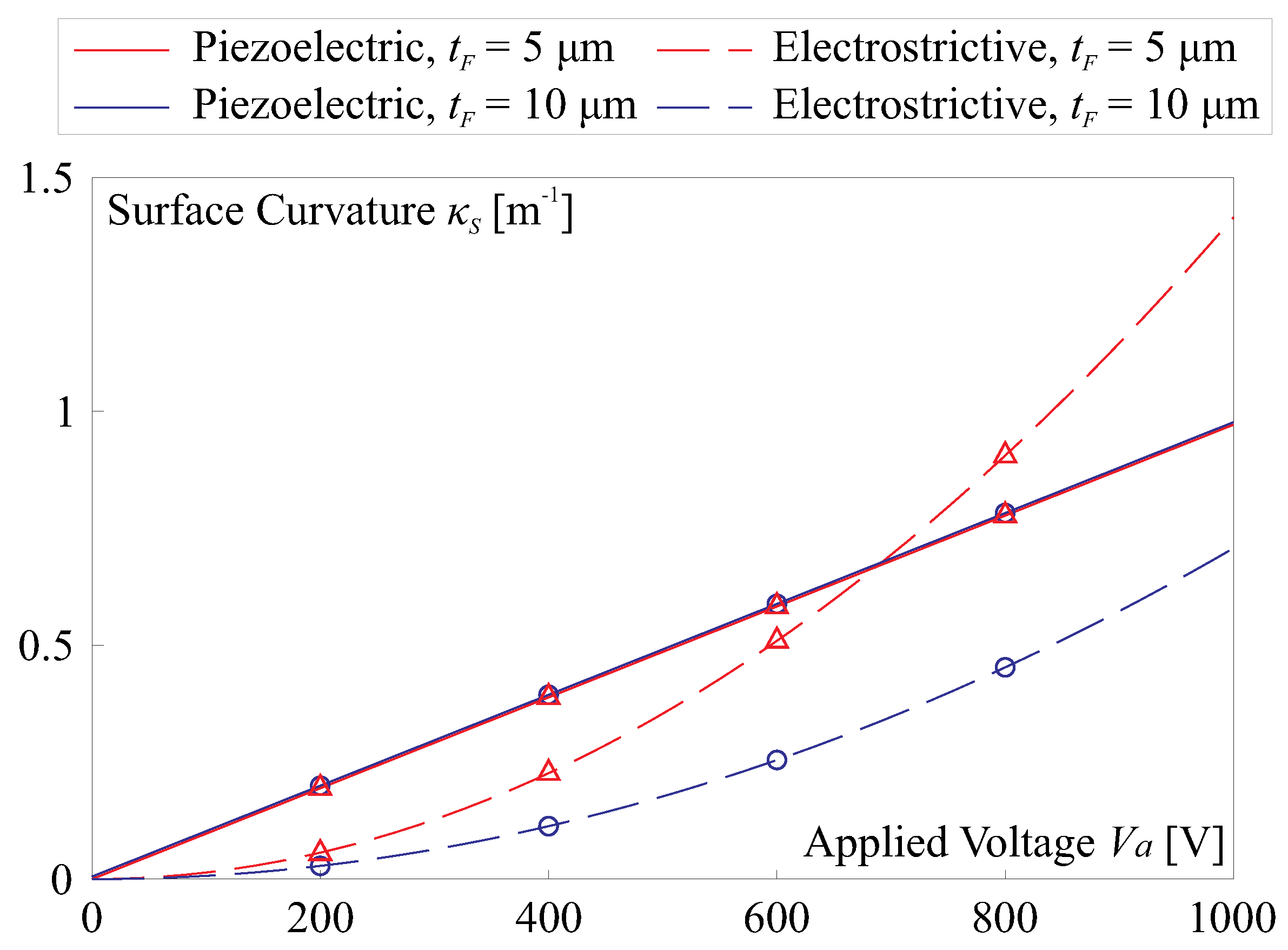
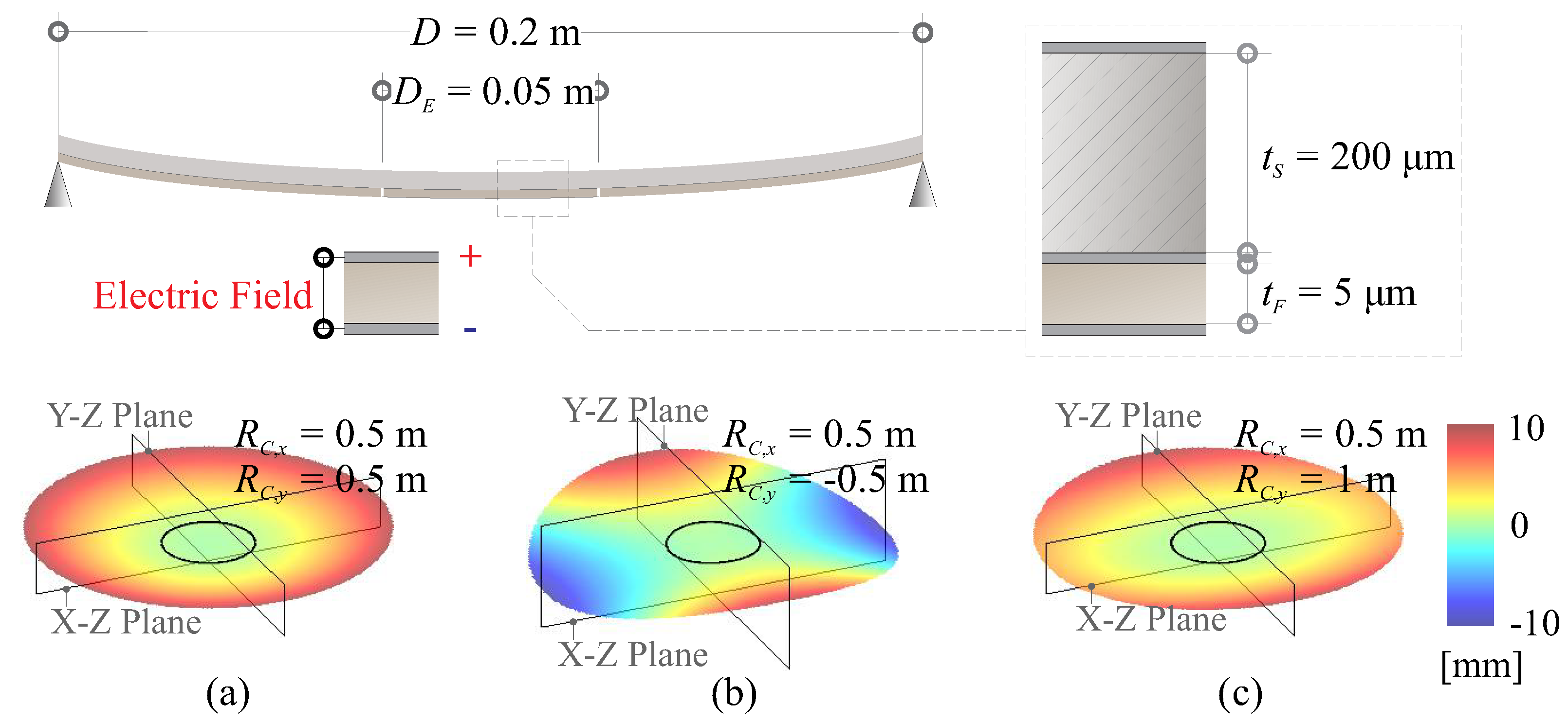
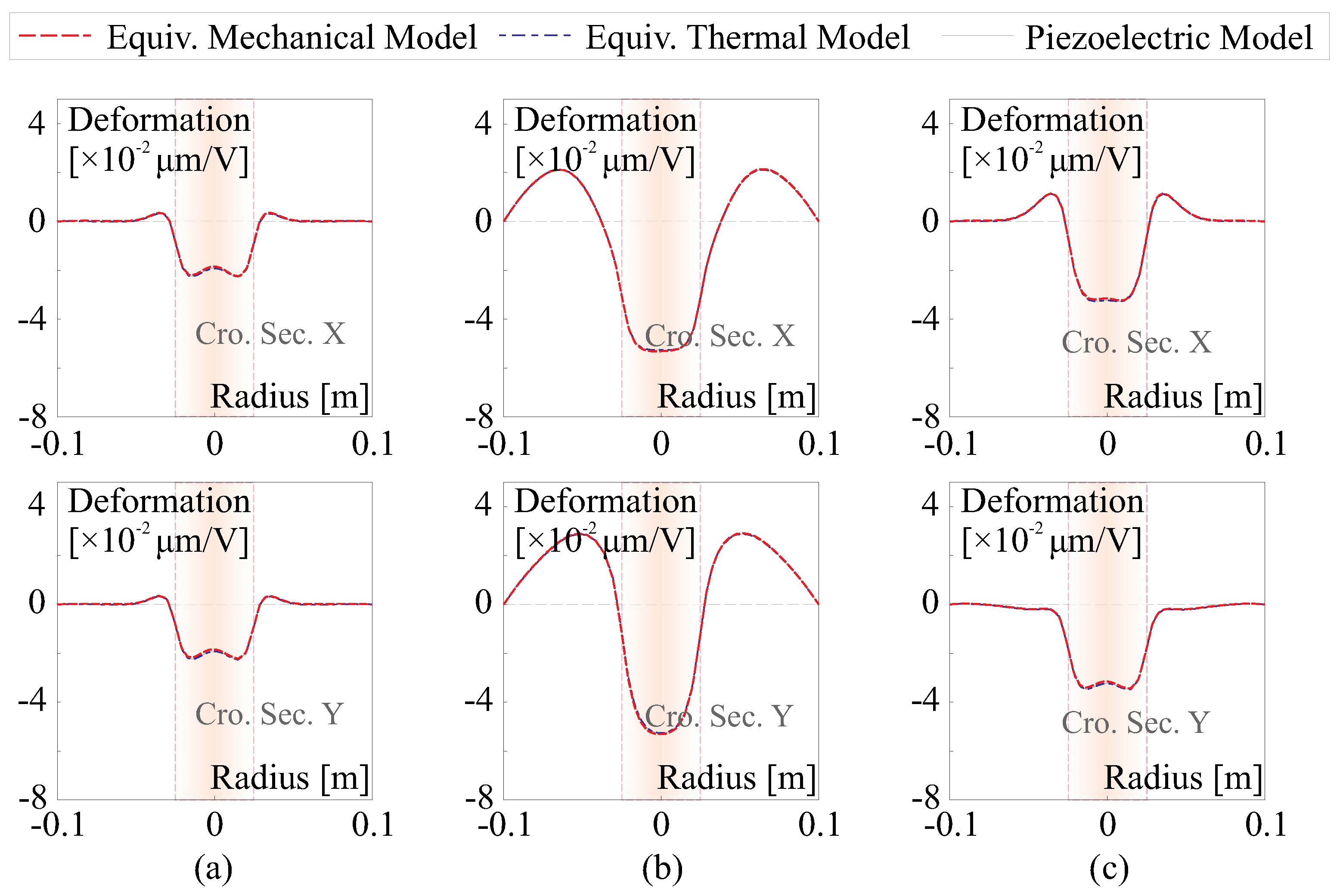
3.3. Comparative Study on Morphing Capability on a Thin-Shell Curved Reflector
- is an even function, meaning that , and at the origin (), the maximum value of V is .
- is a monotonically decreasing function within the range of , specifically, for .
- is a convex function at the origin, i.e., .
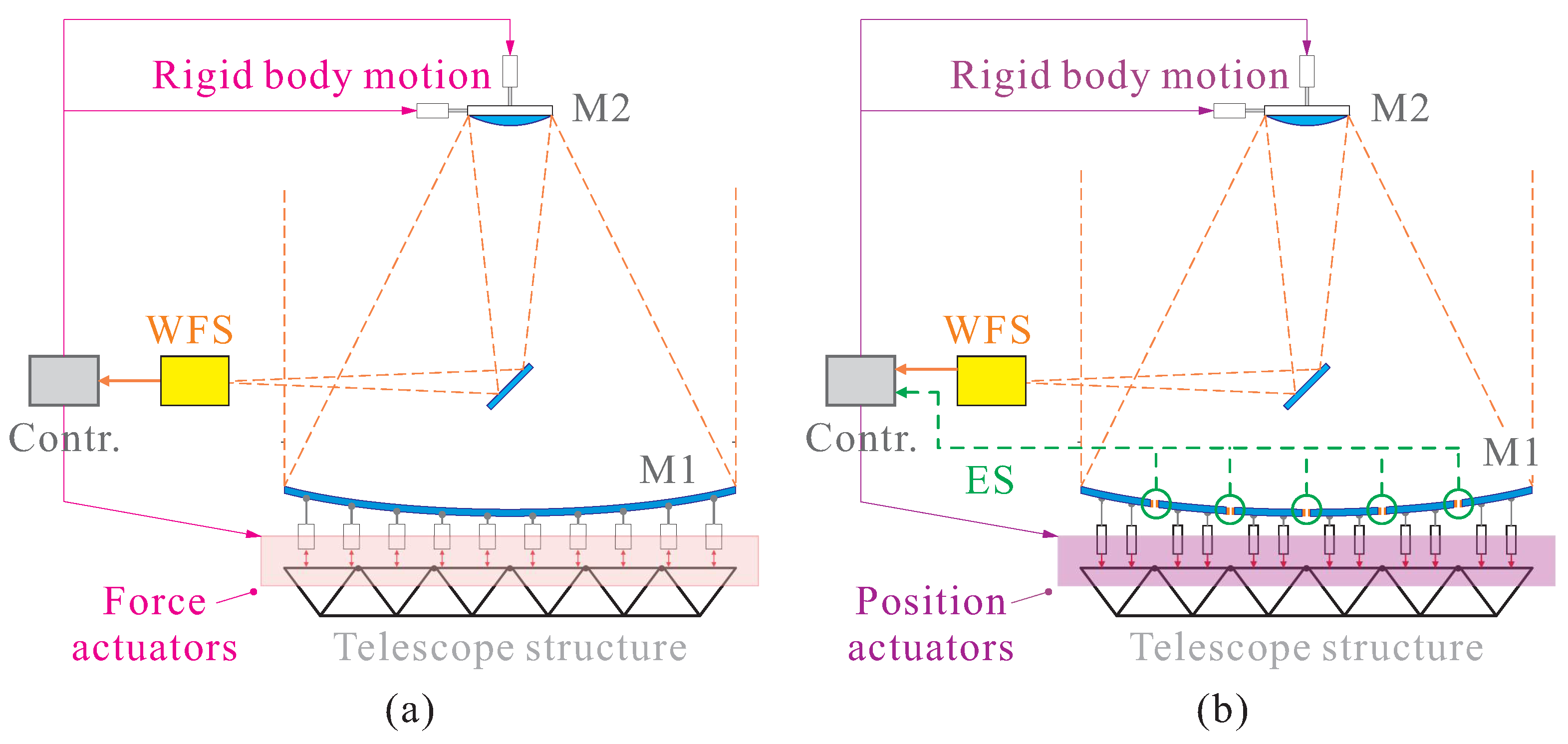
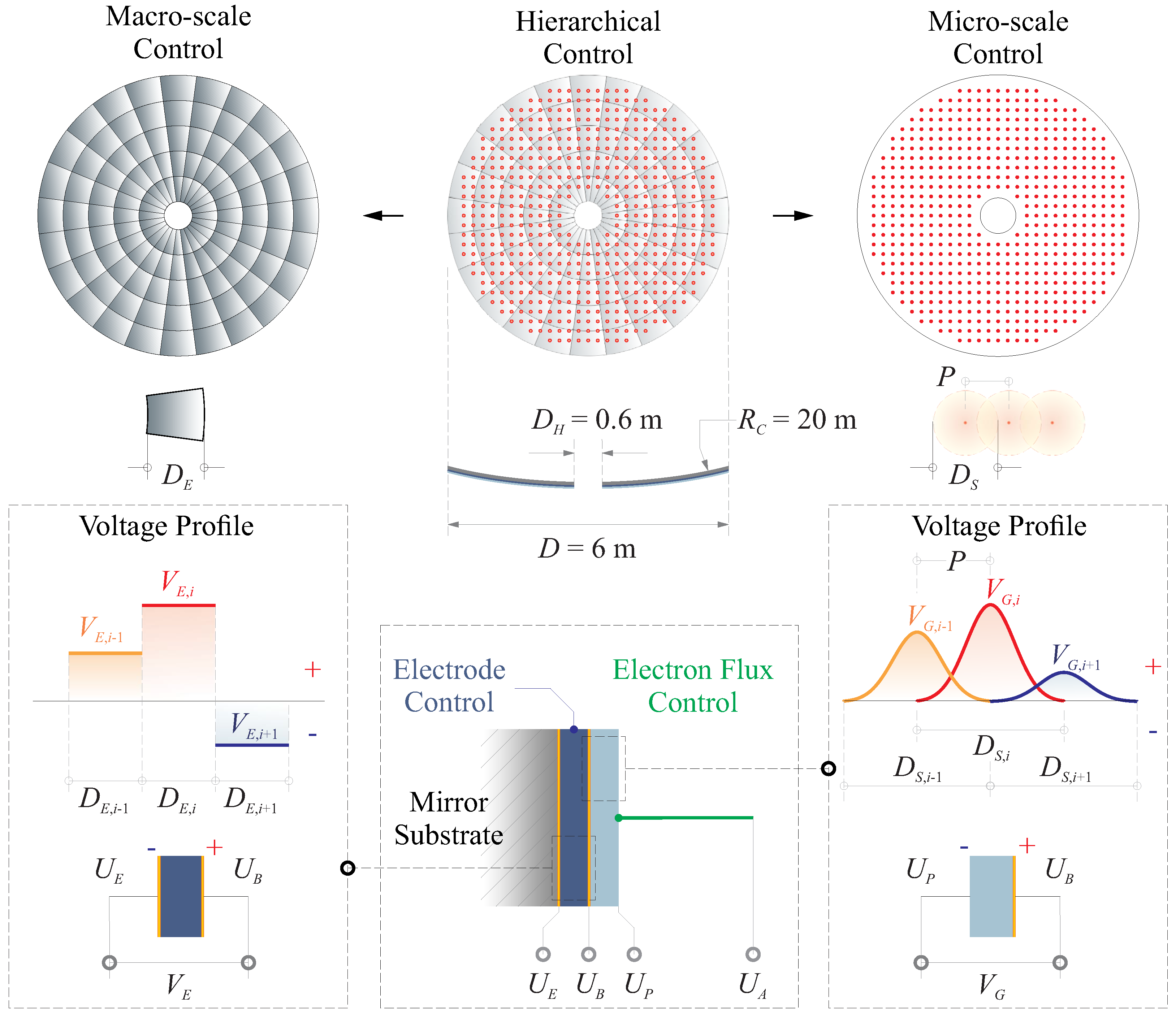
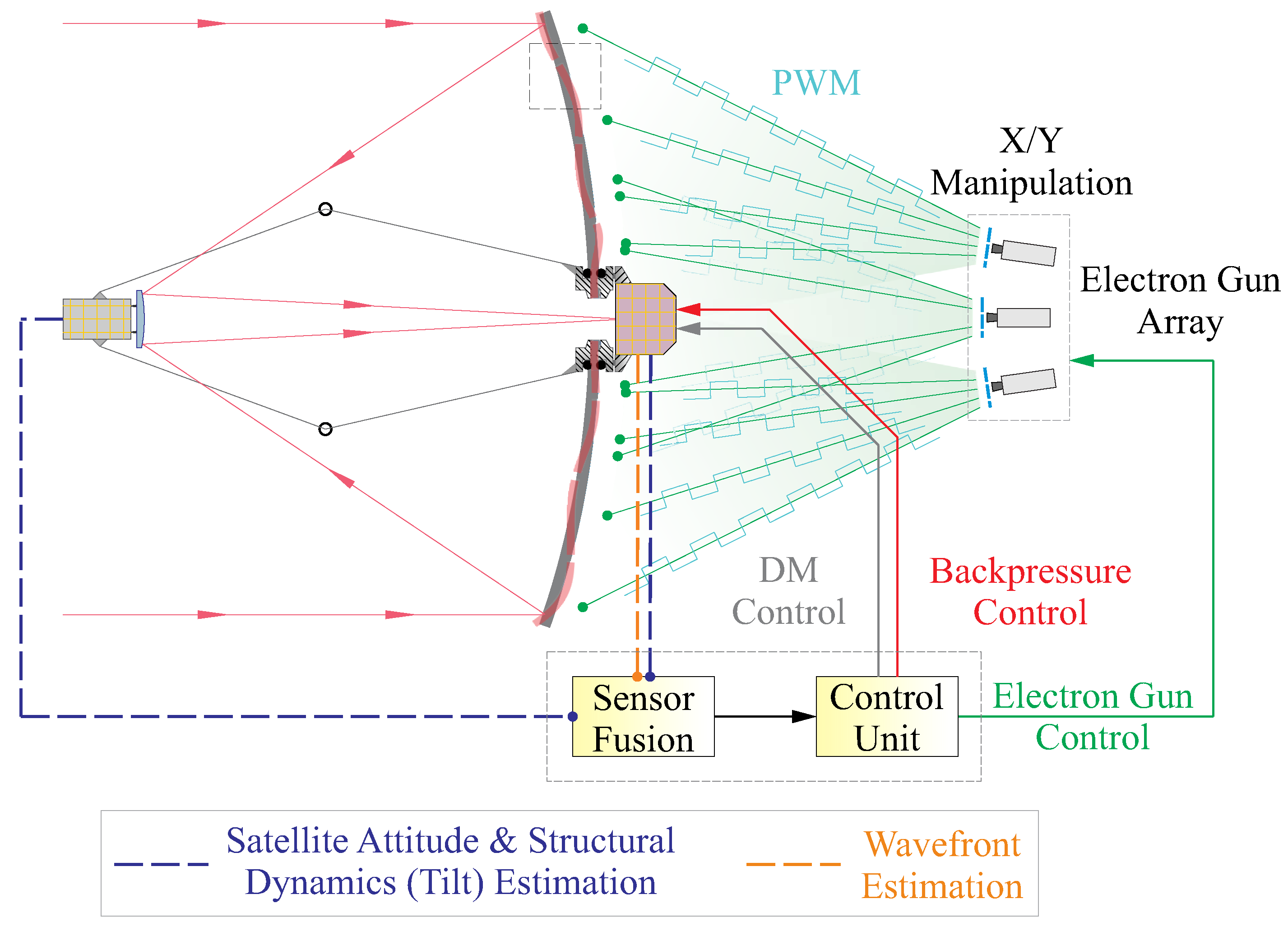
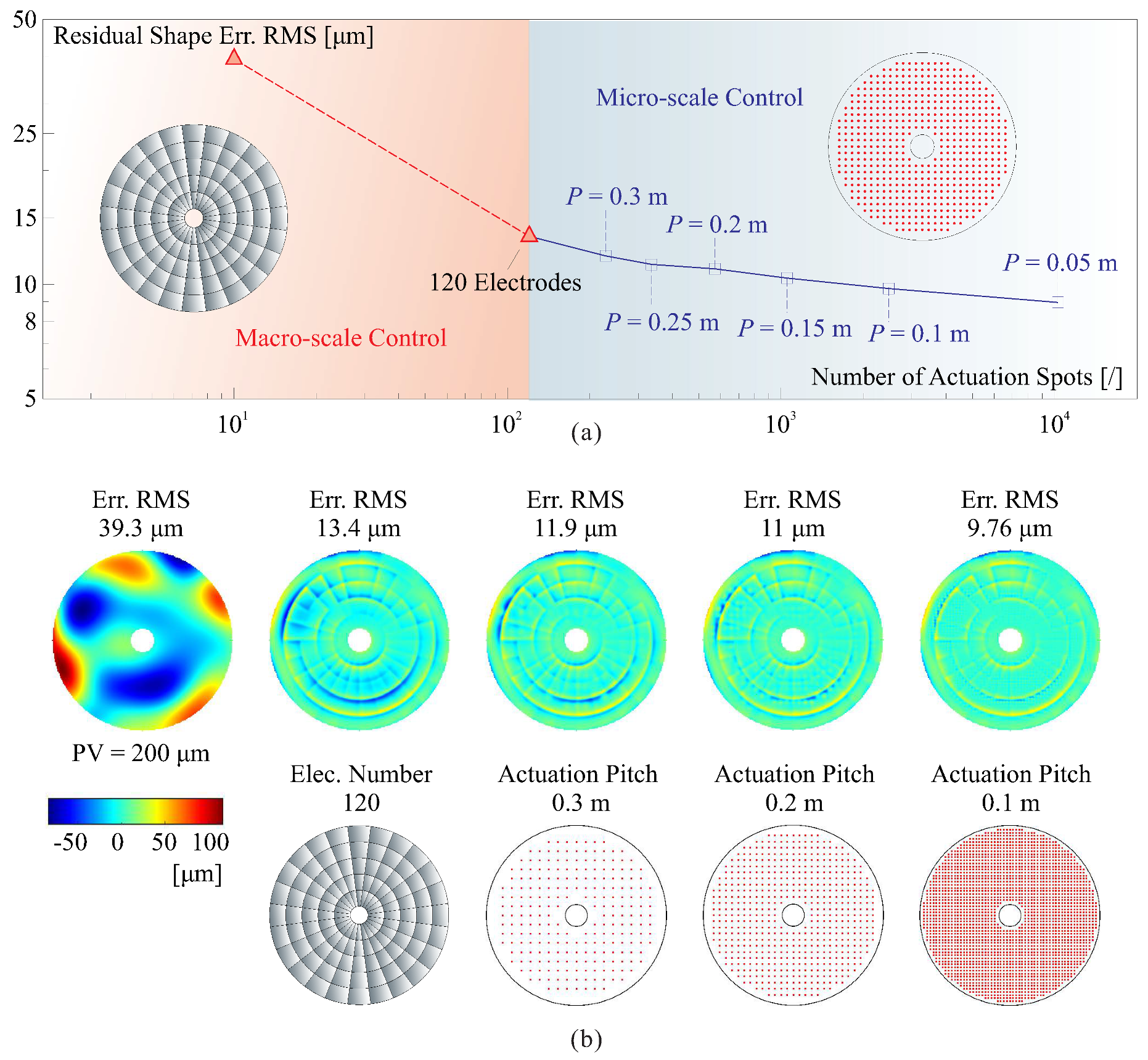
4. Hierarchical Control of a Large Thin-Shell Surface: A Future Perspective
Macro-Scale Control
Micro-Scale Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AO | adaptive optics or active optics |
| CTE | coefficient of thermal expansion |
| DLS | damped least squares |
| DM | deformable mirror |
| DoF | degree-of-freedom |
| ESA | European Space Agency |
| ESO | European Southern Observatory |
| FoV | field of view |
| IAE | inflatable antenna experiment |
| JWST | James Webb Space Telescope |
| LS | least squares |
| MISSE | Materials International Space Station Experiment |
| ULB | Université Libre de Bruxelles |
| UV | Ultraviolet |
| PET | polyethylene terephthalate |
| PI | polyimide |
| PVDF | poly(vinylidene Fluoride |
| PVDF-HFP | poly(vinylidene fluoride-co-hexafluoropropylene) |
| PVDF-TrFE | poly(vinylidene fluoride-trifluoroethylene) |
| PWM | pulse width modulation |
| RMS | root mean square |
| VLT | very large telescope |
Appendix A
| Term (Index i) | Analytical Expression | Classical Name |
|---|---|---|
| (0) | 1 | Piston |
| (1) | Vertical Tilt | |
| (2) | Horizontal Tilt | |
| (3) | Oblique Astigmatism | |
| (4) | Defocus | |
| (5) | Vertical Astigmatism | |
| (6) | Vertical Trefoil | |
| (7) | Vertical Coma | |
| (8) | Horizontal Coma | |
| (9) | Oblique Trefoil | |
| (10) | Oblique Quadrafoil | |
| (11) | Oblique Secondary Astigmatism | |
| (12) | Primary Spherical Aberration | |
| (13) | Vertical Secondary Astigmatism | |
| (14) | Vertical Quadrafoil |
References
- Palisoc, A.; Veal, G.; Cassapakis, C.; Greschik, G.; Mikulas, M. Geometry Attained by Pressurized Membranes. In SPIE Astronomical Telescopes + Instrumentation; Kona: Honolulu, HI, USA, 1998. [Google Scholar]
- Freeland, R.E.; Bilyeu, G. In-step Inflatable Antenna Experiment. Acta Astronaut. 1993, 30, 29–40. [Google Scholar] [CrossRef]
- Chodimella, S.; Moore, J.; Otto, J.; Fang, H. Design Evaluation of a Large Aperture Deployable Antenna. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006; p. 1603. [Google Scholar]
- Flint, E.; Bales, G.; Glaese, R.; Bradford, R. Experimentally Characterizing the Dynamics of 0.5 m Diameter Doubly Curved Shells Made from Thin Films. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003; p. 1831. [Google Scholar]
- Flint, E.; Lindler, J.; Hall, J.; Rankine, C.; Regelbrugge, M. Overview of Form Stiffened Thin Film Shell Characteristic Behavior. In Proceedings of the 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, RI, USA, 1–4 May 2006; p. 1900. [Google Scholar]
- Cassapakis, C.; Thomas, M. Inflatable Structures Technology Development Overview. In AIAA Space Programs and Technologies Conference; AIAA: Huntsville, AL, USA, 1995. [Google Scholar]
- Chandra, A.; Tonazzi, J.C.L.; Stetson, D.; Pat, T.; Walker, C.K. Inflatable Membrane Antennas for Small Satellites. In Proceedings of the IEEE Aerospace Conference, Big Sky, MO, USA, 7–14 March 2020. [Google Scholar]
- Chandra, A.; Pat, T.; Tonazzi, J.C.L.; Walker, C.K. Development and Flight Qualification of A Small Satellite X-band Spherical Membrane Antenna. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2021. [Google Scholar]
- Stuckey, W.K.; Meshishnek, M.J.; Hanna, W.D.; Ross, F.D. Space Environment Test of Materials for Inflatable Structures; Technical Report TR-98 (1055)-1 to Space and Missile Systems Center; Air Force Materiel Command: Dayton, OH, USA, 1998. [Google Scholar]
- Patrick, B.; Moore, J.; Jardine, P.; Maji, A. Shape Memory Alloy and Clear Polymer Integration for First Surface Mirror Applications. In Proceedings of the Engineering, Construction, and Operations in Challenging Environments: Earth and Space 2004, Houston, TX, USA, 7–10 March 2004; pp. 883–899. [Google Scholar]
- Veal, G.; Thomas, M. Highly Accurate Inflatable Reflectors; Technical Report AFRPL TR-84-021 to Air Force Space Technology Center, Space Division; Air Force Systems Command: Baltimore, MA, USA, 1984. [Google Scholar]
- Burley, G.S.; Stilburn, J.R.; Walker, G.A. Membrane Mirror and Bias Electronics. Appl. Opt. 1998, 37, 4649–4655. [Google Scholar] [CrossRef] [PubMed]
- Buske, I.; Becker, P. Compensating Aberrations of A 6-Inch Concave Membrane Mirror. SPIE Remote Sens. 2011, 8178, 81780H. [Google Scholar]
- Poe, G.D.; Patrick, B.G. Zero CTE Polyimides for Athermal Optical Membranes. SPIE Opt. Eng. Appl. 2008, 7061, 311–319. [Google Scholar]
- Copp, T.; Domber, J.L.; Atcheson, P.D.; Tandy, W.D. MOIRE: Membrane Material Property Characterizations, Testing and Lessons Learned. In Proceedings of the Spacecraft Structures Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Roddier, F. Adaptive Optics in Astronomy; Cambridge University Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Degroh, K.K.; Jaworske, D.A.; Pippin, G.; Jenkins, P.P.; Walters, R.J.; Thibeault, S.A.; Palusinski, I.; Lorentzen, J.R. Materials International Space Station Experiment (MISSE): Overview, Accomplishments and Future Needs. In Proceedings of the Annual International Space Station Research and Development, Chicago, IL, USA, 17–19 June 2014. [Google Scholar]
- Wang, K.; Godfroid, T.; Robert, D.; Preumont, A. Adaptive Shell Spherical Reflector Actuated with PVDF-TrFE Thin Film Strain Actuators. Actuators 2021, 10, 7. [Google Scholar] [CrossRef]
- Schipani, P.; Noethe, L.; Magrin, D.; Kuijken, K.; Arcidiacono, C.; Argomedo, J.; Capaccioli, M.; Dall’ora, M.; D’orsi, S.; Farinato, J.; et al. Active Optics System of the VLT Survey Telescope. Appl. Opt. 2016, 55, 1573–1583. [Google Scholar] [CrossRef]
- Ray, F.B. Active Optics Technology: An Overview. Anal. Opt. Struct. 1991, 1532, 188–206. [Google Scholar]
- Wang, K.; Yu, Y.; Preumont, A. Wavefront Control Strategies for Large Active Thin Shell Primaries with Unimorph Actuators. Actuators 2023, 12, 100. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures, an Introduction, 4th ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Wang, K.; Godfroid, T.; Robert, D.; Preumont, A. Electrostrictive PVDF-TrFE Thin Film Actuators for the Control of Adaptive Thin Shell Reflectors. Actuators 2020, 9, 53. [Google Scholar] [CrossRef]
- Bastaits, R.; Rodrigues, G.; Jetteur, P.; Hagedorn, P.; Preumont, A. Multi-layer Adaptive Thin Shells for Future Space Telescopes. Smart Mater. Struct. 2012, 21, 064004. [Google Scholar] [CrossRef]
- Stoney, G.G. The Tension of Metallic Films Deposited by Electrolysis. Proc. R. Soc. London. Ser. Contain. Pap. Math. Phys. Character 1909, 82, 172–175. [Google Scholar]
- Martin, J.W.; Main, J.A. Noncontact Electron Gun Actuation of a Piezoelectric Polymer Thin Film Bimorph Structure. J. Intell. Mater. Syst. Struct. 2002, 13, 329–337. [Google Scholar] [CrossRef]
- Nelson, G.C.; Main, J.A. Noncontact Electron Gun Strain Control of Piezoceramics. AIAA J. 2001, 39, 1808–1813. [Google Scholar] [CrossRef]
- Hadinata, P.C.; Main, J.A. Strain and Current Responses during Electron Flux Excitation of Piezoelectric Ceramics. J. Intell. Mater. Syst. Struct. 2002, 13, 339–348. [Google Scholar] [CrossRef]
- Bañón-Caballero, D.; Socuéllamos, J.M.; Mata, R.; Mercadé, L.; Gimeno, B.; Boria, V.E.; Raboso, D.; Semenov, V.E.; Rakova, E.I.; Sánchez-Royo, J.F.; et al. Study of the Secondary Electron Yield in Dielectrics Using Equivalent Circuital Models. IEEE Trans. Plasma Sci. 2018, 46, 859–867. [Google Scholar] [CrossRef]
- Lau, Y.Y. Simple Theory for the Two-dimensional Child-Langmuir Law. IPhys. Rev. Lett. 2001, 87, 278301. [Google Scholar] [CrossRef]
- Koshida, N.; Yoshida, S. Secondary Electron Emission from Polyvinylidene Fluoride (PVDF) Film. Jpn. J. Appl. Phys. 1983, 22, 1744. [Google Scholar] [CrossRef]
- Mckinney, J.E.; Davis, G.T.; Broadhurst, M.G. Plasma Poling of Poly (VinyliDene Fluoride): Piezo- and Pyroelectric Response. J. Appl. Phys. 1980, 51, 1676–1681. [Google Scholar] [CrossRef]
- Wang, K.; Yu, Y.; Preumont, A. Shape Control of a Unimorph Deformable Mirror for Space Active Optics under Uncertainties. Micromachines 2023, 14, 1756. [Google Scholar] [CrossRef]
- Upatov, V.Y. Dielectric Charging by an Electron Beam. J. Appl. Phys. 1996, 80, 2453–2457. [Google Scholar] [CrossRef]
- Persson, B.N.; Albohr, O.; Tartaglino, U.; Volokitin, A.I.; Tosatti, E. On the Nature of Surface Roughness with Application to Contact Mechanics, Sealing, Rubber Friction and Adhesion. J. Phys. Condens. Matter 2004, 17, R1. [Google Scholar] [CrossRef] [PubMed]
- Coleman, T.F.; Li, Y. A Reflective Newton Method for Minimizing a Quadratic Function Subject to Bounds on Some of the Variables. SIAM J. Optim. 1996, 6, 1040–1058. [Google Scholar] [CrossRef]
- Conan, R.; Correia, C. Object-oriented MATLAB Adaptive Optics Toolbox. SPIE Astron. Telesc. Instrum. 2014, 9148, 91486C. [Google Scholar]







| Deposition Technique | Spin Coating | Spray Coating | ||
|---|---|---|---|---|
| Annealing condition | 140 C | 140 C | 130 C | 120 C |
| Relative permittivity [/] | 11.86 | 9.6 | 9.9 | 9.5 |
| Piezoelectric constant [pC/N] | 13.54 | 12.56 | 10.9 | 9.04 |
| Electrostrictive constant [m/C] | −12.65 | −13.81 | −12.27 | −12.65 |
| Remnant polarization [C/m] | 0.0152 | 0.0157 | 0.0148 | 0.0126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Gong, Y.; Yu, Y.; Preumont, A. Hierarchical Morphing Control of an Ultra-Lightweight Electro-Actuated Polymer Telescope with Thin-Film Actuators. Micromachines 2023, 14, 1855. https://doi.org/10.3390/mi14101855
Wang K, Gong Y, Yu Y, Preumont A. Hierarchical Morphing Control of an Ultra-Lightweight Electro-Actuated Polymer Telescope with Thin-Film Actuators. Micromachines. 2023; 14(10):1855. https://doi.org/10.3390/mi14101855
Chicago/Turabian StyleWang, Kainan, Yuxuan Gong, Yian Yu, and André Preumont. 2023. "Hierarchical Morphing Control of an Ultra-Lightweight Electro-Actuated Polymer Telescope with Thin-Film Actuators" Micromachines 14, no. 10: 1855. https://doi.org/10.3390/mi14101855
APA StyleWang, K., Gong, Y., Yu, Y., & Preumont, A. (2023). Hierarchical Morphing Control of an Ultra-Lightweight Electro-Actuated Polymer Telescope with Thin-Film Actuators. Micromachines, 14(10), 1855. https://doi.org/10.3390/mi14101855








