Design and Analysis of Ultra-Precision Smart Cutting Tool for In-Process Force Measurement and Tool Nanopositioning in Ultra-High-Precision Single-Point Diamond Turning
Abstract
:1. Introduction
2. Background Overview
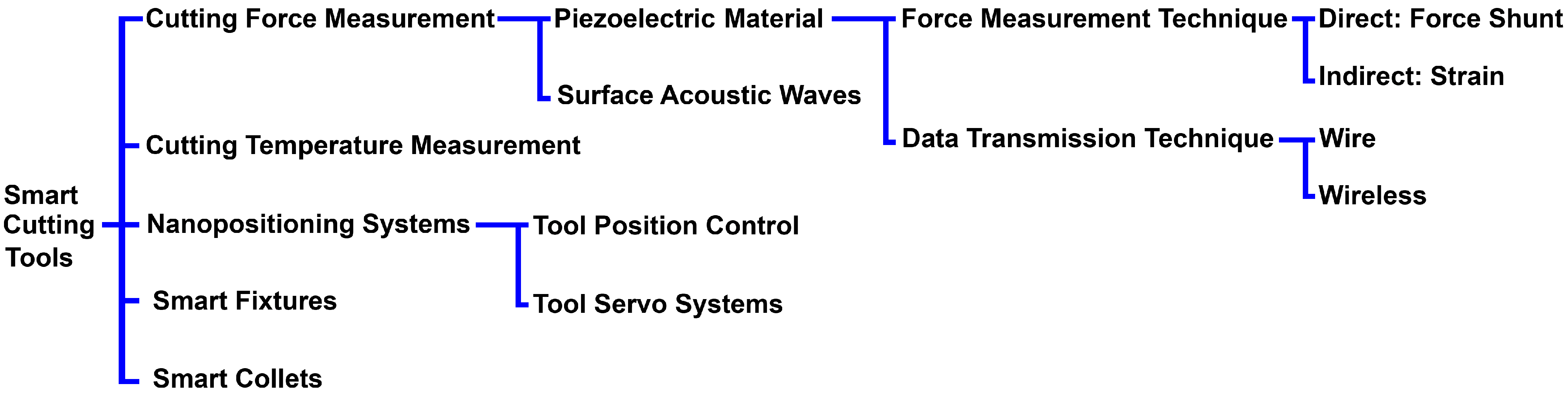
2.1. Smart Cutting Tools for In-Process Force Measurement in Ultra-Precision SPDT
2.2. Piezoelectric Actuators and Ultra-Precision Nanopositioning Systems
3. Material and Methods
3.1. Theory and Principles
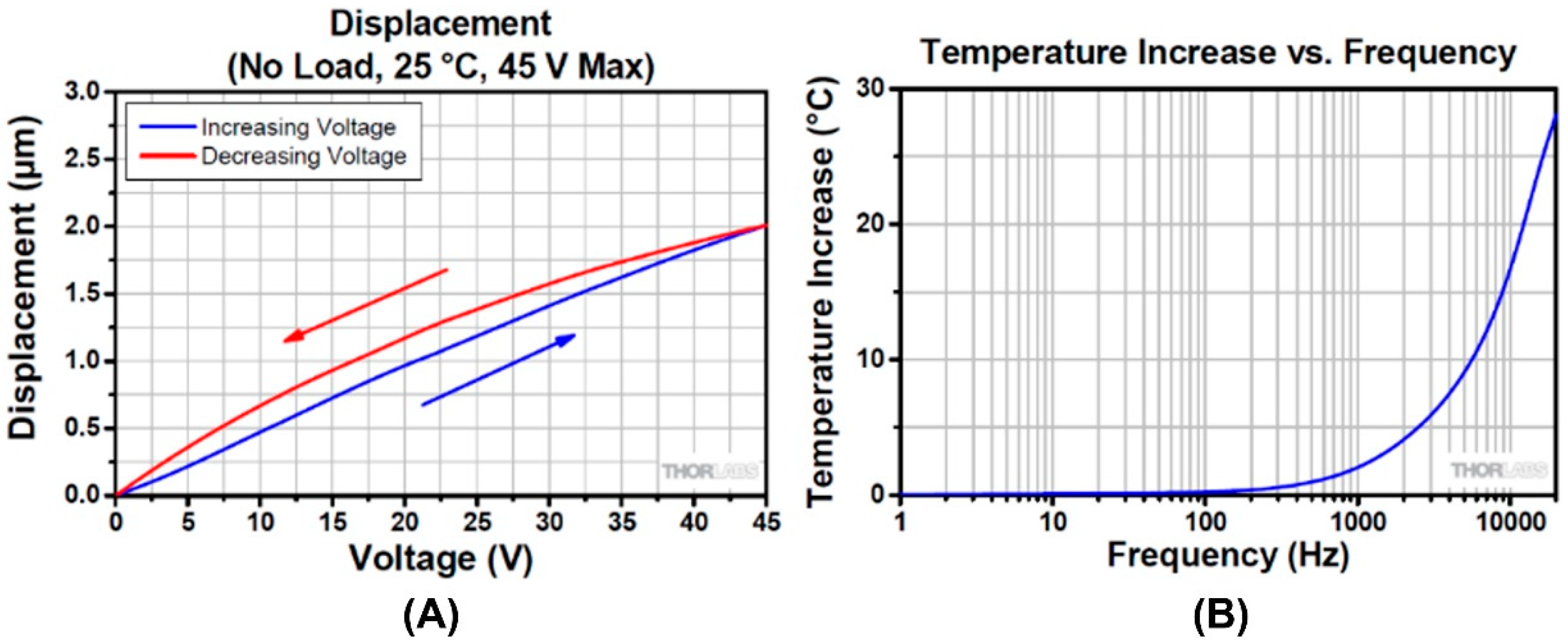
3.1.1. Characteristics of the Piezoelectric Component and Multi-Layer Piezo Stack Actuator
3.1.2. Strain Gauge Characteristics
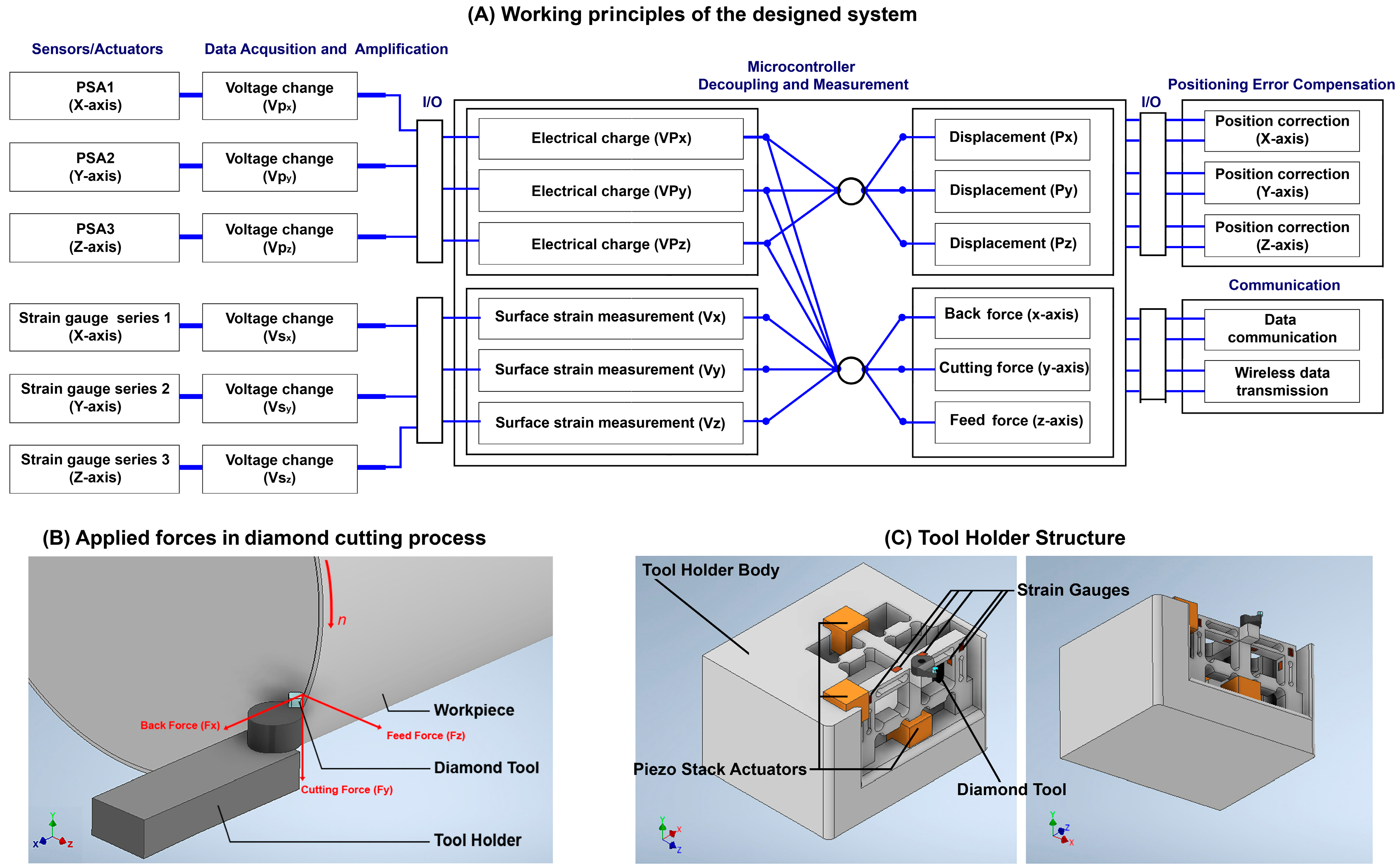
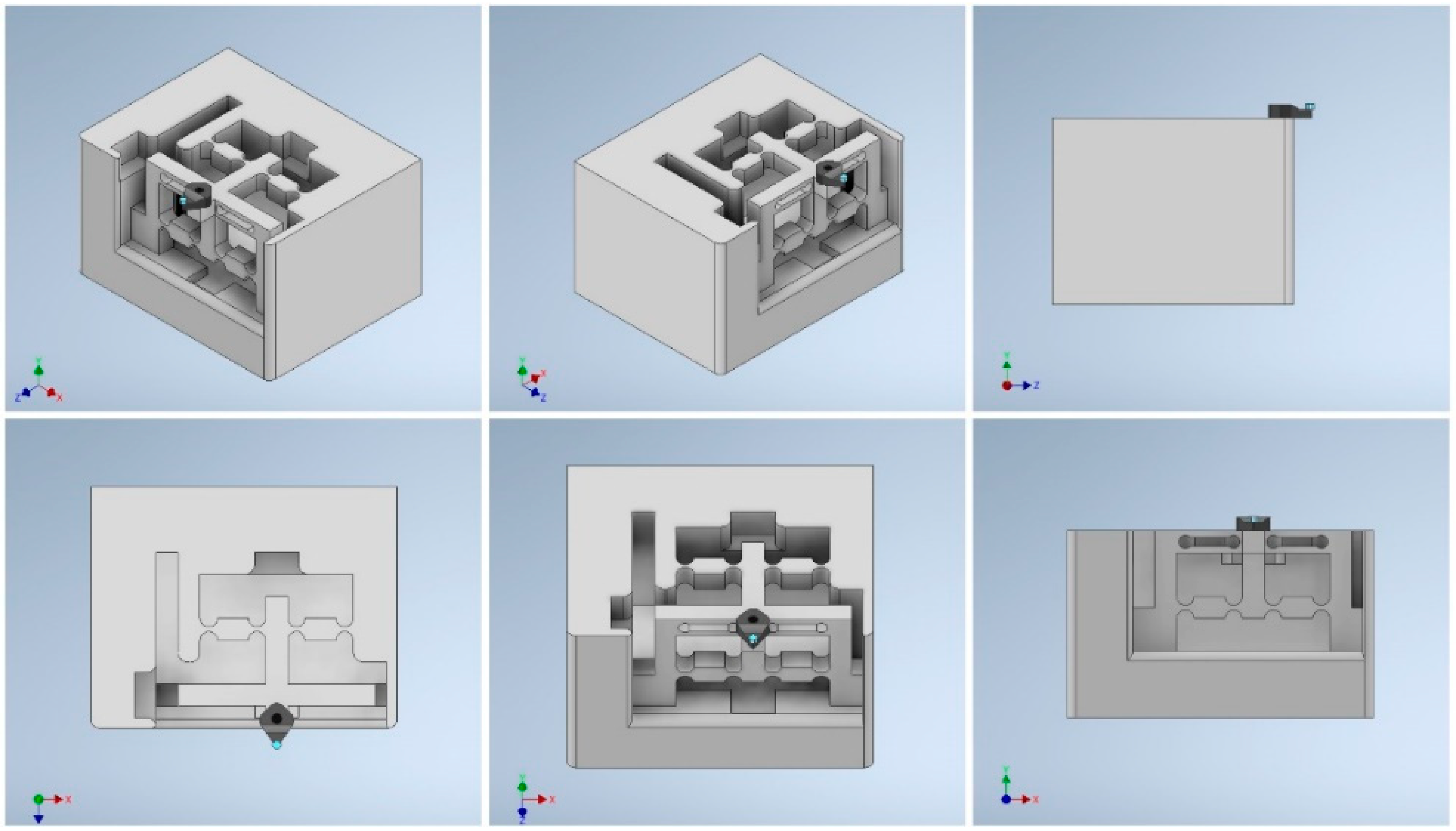
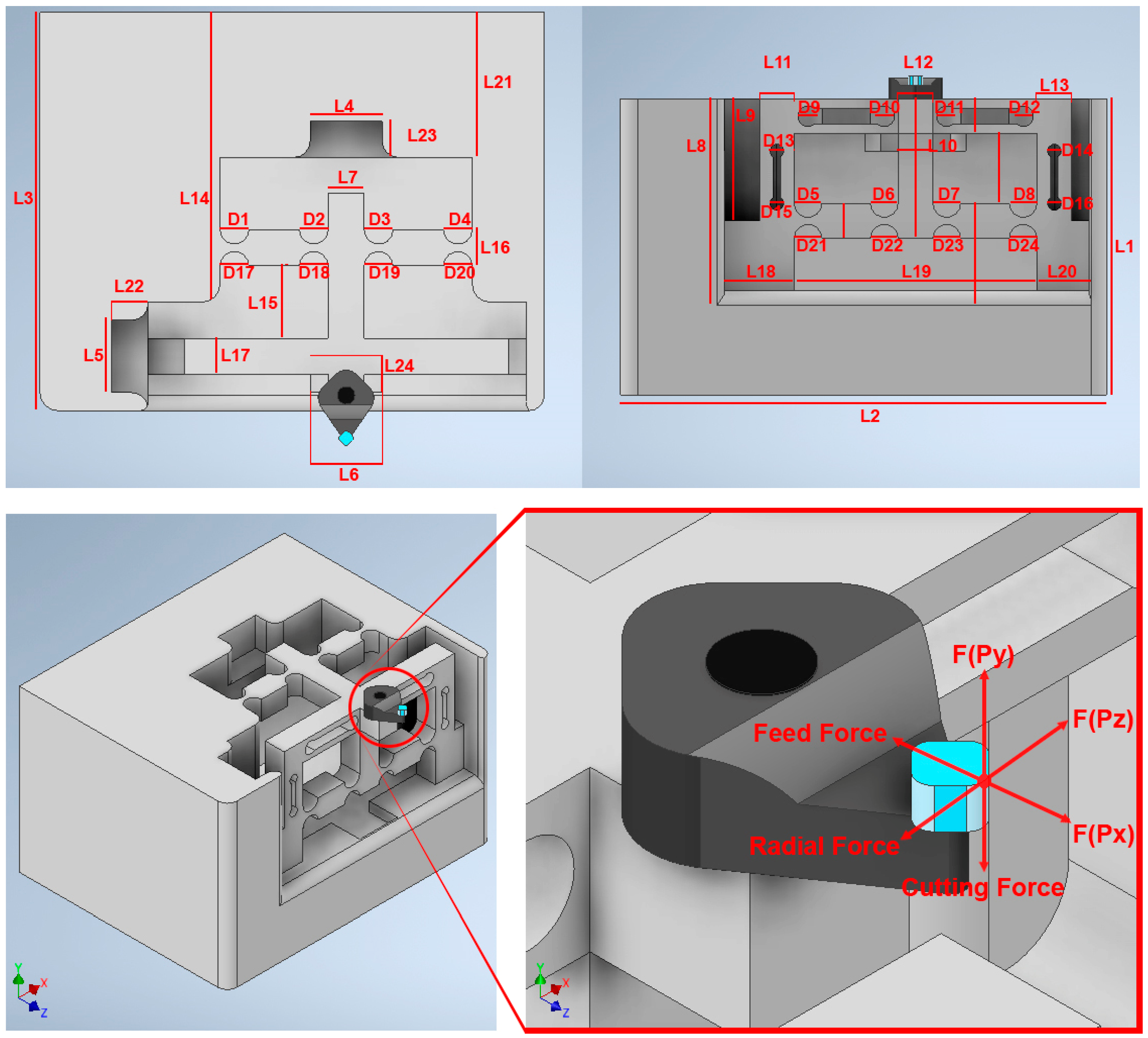
3.2. Structure Design of the Smart Cutting Tool
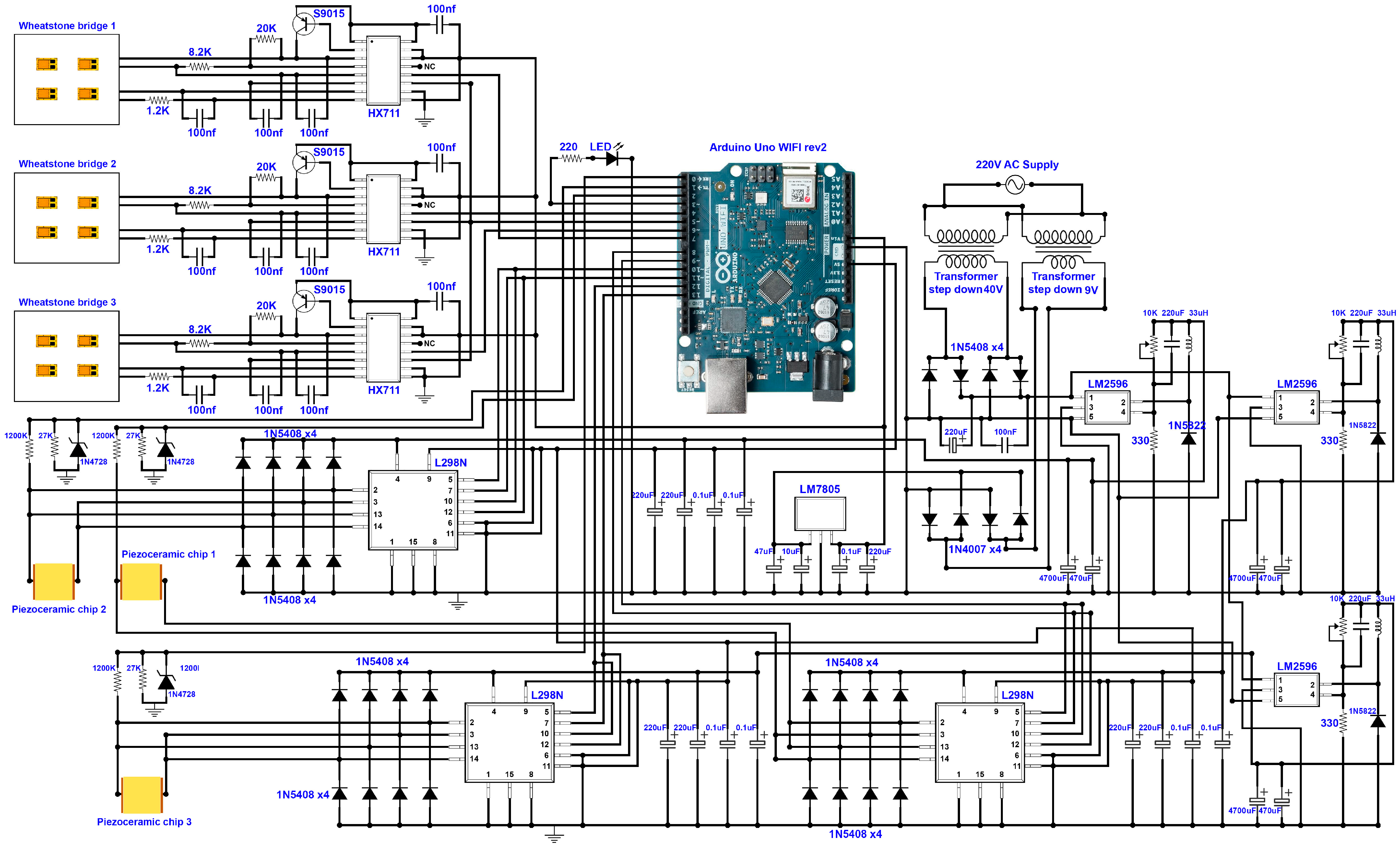
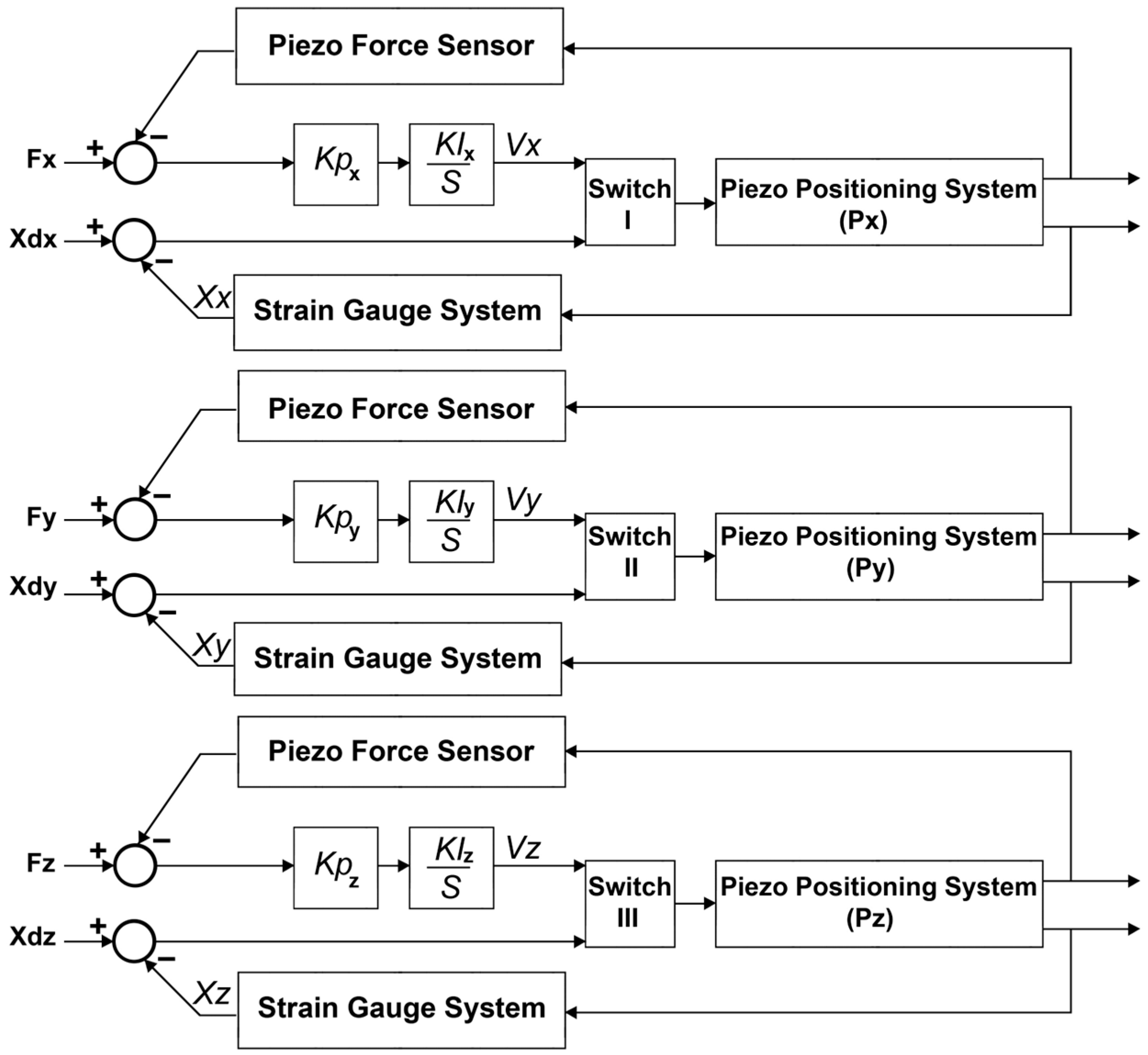
3.3. Control System
3.3.1. The Arrangement Strategy of the Strain Gauges and Piezoelectric Stack Actuators
3.3.2. Strain Gauge Outputs: Decoupling the Applied Forces and Respective Surface Strain
3.3.3. Piezo Stack Actuators: Decoupling the Applied Force and Respective Surface Strain
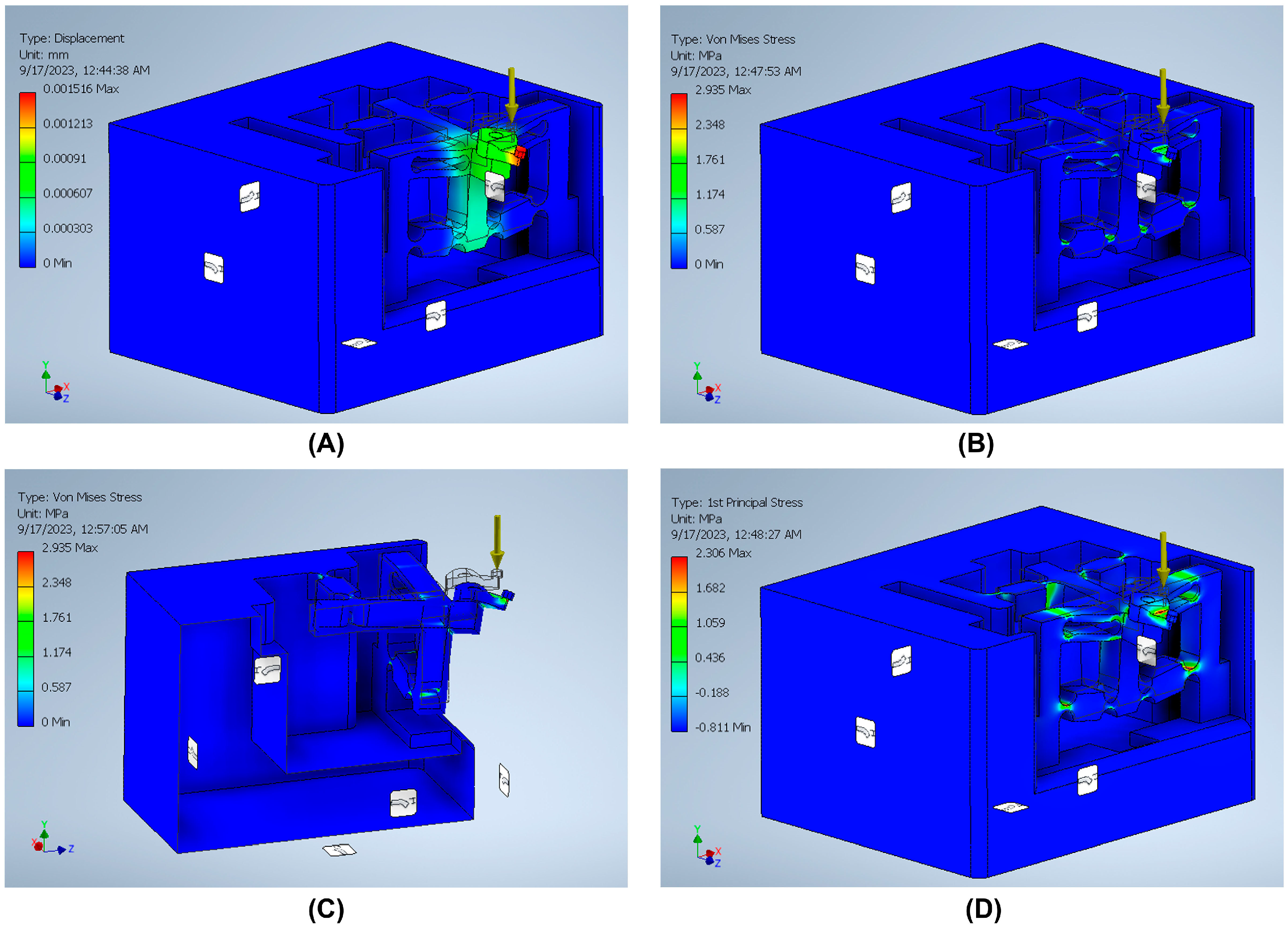
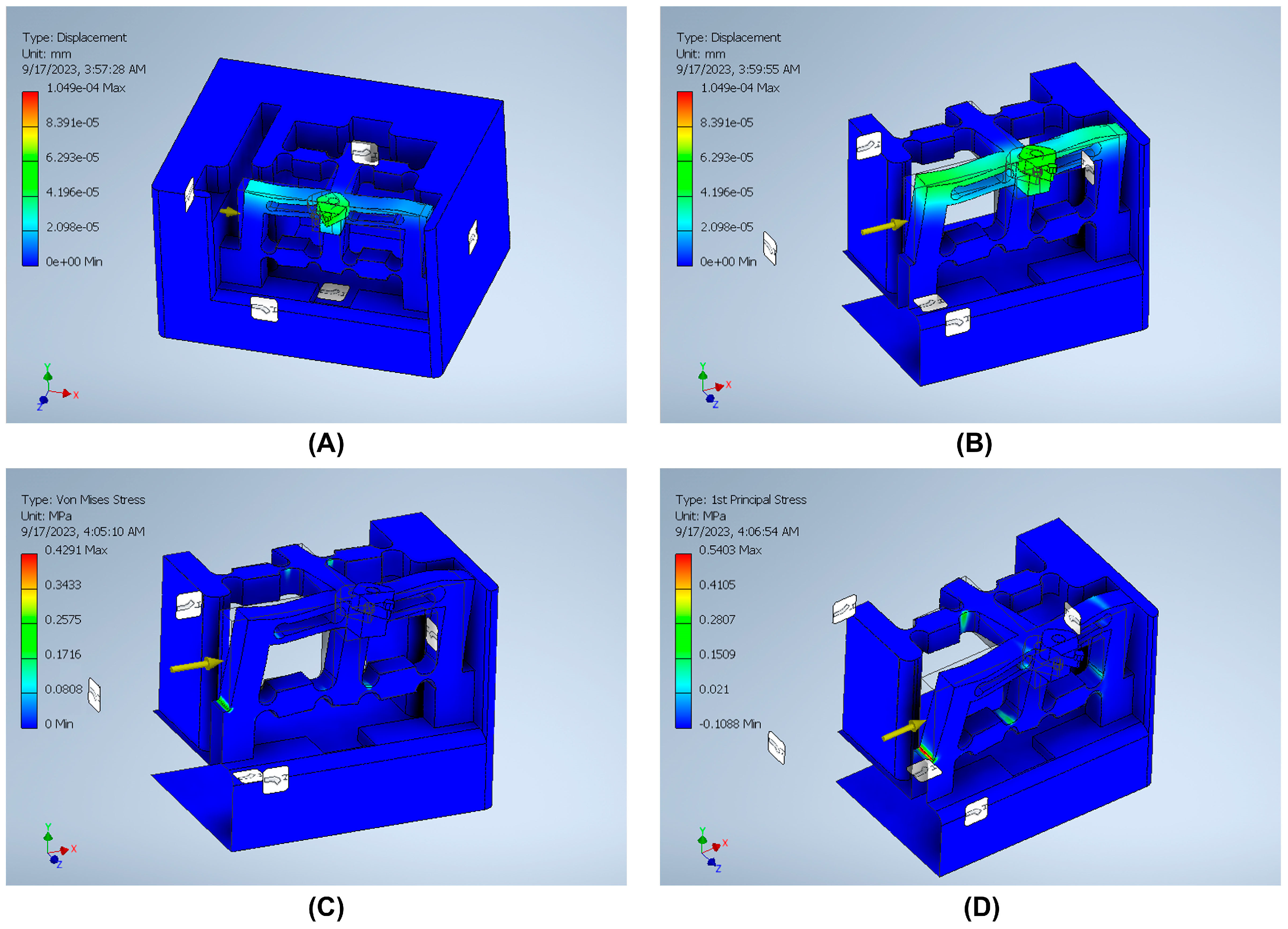
3.4. Finite Element Analysis (FEA) Validation
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goel, B.; Singh, S.; Sarepaka, R.V.; Mishra, V.; Khatri, N.; Aggarwal, V.; Nand, K.; Kumar, R. Diamond turning of optical materials: A review. Int. J. Mach. Mach. Mater. 2021, 23, 160–190. [Google Scholar] [CrossRef]
- Hatefi, S.; Abou-El-Hossein, K. Review of single-point diamond turning process in terms of ultra-precision optical surface roughness. Int. J. Adv. Manuf. Technol. 2020, 106, 2167–2187. [Google Scholar] [CrossRef]
- Ramesh, R.; Mannan, M.; Poo, A. Error compensation in machine tools—A review: Part I: Geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manuf. 2000, 40, 1235–1256. [Google Scholar] [CrossRef]
- Huang, P.; Lee, W. Cutting force prediction for ultra-precision diamond turning by considering the effect of tool edge radius. Int. J. Mach. Tools Manuf. 2016, 109, 1–7. [Google Scholar] [CrossRef]
- Nategh, M.J.; Amini, S.; Soleimanimehr, H. Modeling the Force, Surface Roughness and Cutting Temperature in Ultrasonic Vibration-Assisted Turning of Al7075. In Advanced Materials Research; Trans Tech Publications: Zurich, Switzerland, 2010. [Google Scholar]
- Sawangsri, W.; Cheng, K. An innovative approach to cutting force modelling in diamond turning and its correlation analysis with tool wear. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 405–415. [Google Scholar] [CrossRef]
- Rashid, R.R.; Sun, S.; Wang, G.; Dargusch, M.S. An investigation of cutting forces and cutting temperatures during laser-assisted machining of the Ti–6Cr–5Mo–5V–4Al beta titanium alloy. Int. J. Mach. Tools Manuf. 2012, 63, 58–69. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Wang, S.; Shimizu, Y.; Ito, S.; Gao, W.; Ju, B.-F. An in-process measurement method for repair of defective microstructures by using a fast tool servo with a force sensor. Precis. Eng. 2015, 39, 134–142. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, J.; Shang, Z.; Fan, X. Modeling of cutting force prediction in machining high-volume SiCp/Al composites. Appl. Math. Model. 2019, 70, 1–17. [Google Scholar] [CrossRef]
- Che-Haron, C.H. Tool life and surface integrity in turning titanium alloy. J. Mater. Process. Technol. 2001, 118, 231–237. [Google Scholar] [CrossRef]
- Nath, C.; Rahman, M.; Neo, K.S. A study on ultrasonic elliptical vibration cutting of tungsten carbide. J. Mater. Process. Technol. 2009, 209, 4459–4464. [Google Scholar] [CrossRef]
- Feucht, F.; Ketelaer, J.; Wolff, A.; Mori, M.; Fujishima, M. Latest machining technologies of hard-to-cut materials by ultrasonic machine tool. Procedia CIRP 2014, 14, 148–152. [Google Scholar] [CrossRef]
- Hatefi, S.; Abou-El-Hossein, K. Review of hybrid methods and advanced technologies for in-process metrology in ultra-high-precision single-point diamond turning. Int. J. Adv. Manuf. Technol. 2020, 111, 427–447. [Google Scholar] [CrossRef]
- De Oliveira, F.B.; Rodrigues, A.R.; Coelho, R.T.; de Souza, A.F. Size effect and minimum chip thickness in micromilling. Int. J. Mach. Tools Manuf. 2015, 89, 39–54. [Google Scholar] [CrossRef]
- He, C.; Zong, W.; Sun, T. Origins for the size effect of surface roughness in diamond turning. Int. J. Mach. Tools Manuf. 2016, 106, 22–42. [Google Scholar] [CrossRef]
- Guo, P.; Ehmann, K.F. An analysis of the surface generation mechanics of the elliptical vibration texturing process. Int. J. Mach. Tools Manuf. 2013, 64, 85–95. [Google Scholar] [CrossRef]
- Liu, X.; DeVor, R.; Kapoor, S. An analytical model for the prediction of minimum chip thickness in micromachining. J. Manuf. Sci. Eng. 2006, 128, 474–481. [Google Scholar] [CrossRef]
- Fang, N. Slip-line modeling of machining with a rounded-edge tool—Part I: New model and theory. J. Mech. Phys. Solids 2003, 51, 715–742. [Google Scholar] [CrossRef]
- Waldorf, D.J.; DeVor, R.E.; Kapoor, S.G. A slip-line field for ploughing during orthogonal cutting. J. Manuf. Sci. Eng. 1998, 120, 693–699. [Google Scholar] [CrossRef]
- Liu, X.; Jun, M.B.; DeVor, R.E.; Kapoor, S.G. Cutting mechanisms and their influence on dynamic forces, vibrations and stability in micro-endmilling. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13–19 November 2004. [Google Scholar]
- Bissacco, G.; Hansen, H.N.; Slunsky, J. Modelling the cutting edge radius size effect for force prediction in micro milling. CIRP Ann. 2008, 57, 113–116. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.; Leach, R.; Cheung, C.; Savio, E.; Linares, J. On-machine and in-process surface metrology for precision manufacturing. Ann. CIRP 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, K.; Wang, C. Design of a smart turning tool with application to in-process cutting force measurement in ultraprecision and micro cutting. Manuf. Lett. 2014, 2, 112–117. [Google Scholar] [CrossRef]
- Xiao, C.; Ding, H.; Cheng, K.; Chen, S. Design of an innovative smart turning tool with application to real-time cutting force measurement. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 563–568. [Google Scholar] [CrossRef]
- Liang, Q.; Zhang, D.; Coppola, G.; Mao, J.; Sun, W.; Wang, Y.; Ge, Y. Design and analysis of a sensor system for cutting force measurement in machining processes. Sensors 2016, 16, 70. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhao, Y.L.; Shao, Y.W.; Hu, T.J.; Zhang, Q.; Ge, X.H. Research of a Smart Cutting Tool Based on MEMS Strain Gauge. IOP J. Phys. Conf. Ser. 2018, 986, 012016. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Y.; Liang, S.; Zhou, G. A high performance sensor for triaxial cutting force measurement in turning. Sensors 2015, 15, 7969–7984. [Google Scholar] [CrossRef]
- Cheng, K.; Niu, Z.-C.; Wang, R.C.; Rakowski, R.; Bateman, R. Smart Cutting Tools and Smart Machining: Development Approaches, and Their Implementation and Application Perspectives. Chin. J. Mech. Eng. 2017, 30, 1162–1176. [Google Scholar] [CrossRef]
- Hatefi, S.; Abou-El-Hossein, K. Design and Development of High-Precision Hybrid Controller for Ultra-Precision Non-Conventional Single-Point Diamond Turning Processes. Majlesi J. Electr. Eng. 2020, 14, 61–70. [Google Scholar]
- Bhowmik, S.; Zindani, D. Combined Variant of Hybrid Micromachining Processes. In Hybrid Micro-Machining Processes; Springer: Berlin/Heidelberg, Germany, 2019; pp. 61–70. [Google Scholar]
- Luo, X.; Qin, Y. Hybrid Machining: Theory, Methods, and Case Studies; Academic Press: London, UK, 2018. [Google Scholar]
- Jin, W.; Venuvinod, P.; Wang, X. An optical fibre sensor based cutting force measuring device. Int. J. Mach. Tools Manuf. 1995, 35, 877–883. [Google Scholar] [CrossRef]
- Kim, J.; Chang, H.; Han, D.; Jang, D.; Oh, S. Cutting force estimation by measuring spindle displacement in milling process. CIRP Ann. 2005, 54, 67–70. [Google Scholar] [CrossRef]
- Kim, J.-D.; Kim, D.-S. Development of a combined-type tool dynamometer with a piezo-film accelerometer for an ultra-precision lathe. J. Mater. Process. Technol. 1997, 71, 360–366. [Google Scholar] [CrossRef]
- Odedeyi, P.B.; Abou-El-Hossein, K.; Hatefi, S.; Oyekunle, F. Self-sensing tool holder for in-process metrology of cutting force in ultra-high-precision single-point diamond turning applications. Int. J. Comput. Methods Exp. Meas. 2022, 10, 329–344. [Google Scholar] [CrossRef]
- Uchino, K. Chapter 1—The Development of Piezoelectric Materials and the New Perspective. In Advanced Piezoelectric Materials, 2nd ed.; Uchino, K., Ed.; Woodhead Publishing: Sawston, UK, 2017; pp. 1–92. [Google Scholar]
- Zhang, T.; Du, Z.; Zhou, C.; Cao, Z.; Wang, S.; Cheng, L.; Deng, L. Piezoelectric single crystal-based nano-scale actuator and its amplifying mechanism. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019. [Google Scholar]
- Somiya, S. Handbook of Advanced Ceramics: Materials, Applications, Processing, and Properties; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Fan, P.; Liu, K.; Ma, W.; Tan, H.; Zhang, Q.; Zhang, L.; Zhou, C.; Salamon, D.; Zhang, S.-T.; Zhang, Y.; et al. Progress and perspective of high strain NBT-based lead-free piezoceramics and multilayer actuators. J. Mater. 2021, 7, 508–544. [Google Scholar] [CrossRef]
- Uchino, K. Multilayer Technologies for Piezoceramic Materials. In Advanced Piezoelectric Materials; Elsevier: Amsterdam, The Netherlands, 2017; pp. 423–451. [Google Scholar]
- Panda, P.K.; Sahoo, B.; Raja, S.; Vijaya Kumar, M.P.; Shankar, V. Electromechanical and dynamic characterization of in-house-fabricated amplified piezo actuator. Smart Mater. Res. 2012, 2012, 8. [Google Scholar] [CrossRef]
- Yong, Y.K.; Fleming, A.J. Note: An improved low-frequency correction technique for piezoelectric force sensors in high-speed nanopositioning systems. Rev. Sci. Instrum. 2017, 88, 046105. [Google Scholar] [CrossRef]
- Yong, Y.K. Preloading piezoelectric stack actuators in high-speed nanopositioning systems. Front. Mech. Eng. 2016, 2, 8. [Google Scholar] [CrossRef]
- Low-Voltage Piezoelectric Chips. 2022. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_ID=7563 (accessed on 3 September 2023).
- Medvedeva, A. Tool Steel for Tool Holder Applications: Microstructure and Mechanical Properties. Ph.D. Thesis, Karlstad University, Karlstad, Sweden, 2008. [Google Scholar]
- ASM Handbook Committee. Properties and Selection: Irons. Steels, and High-Performance Alloys; ASM International: Almere, The Netherlands, 1990; Volume 1, p. 2195. [Google Scholar]



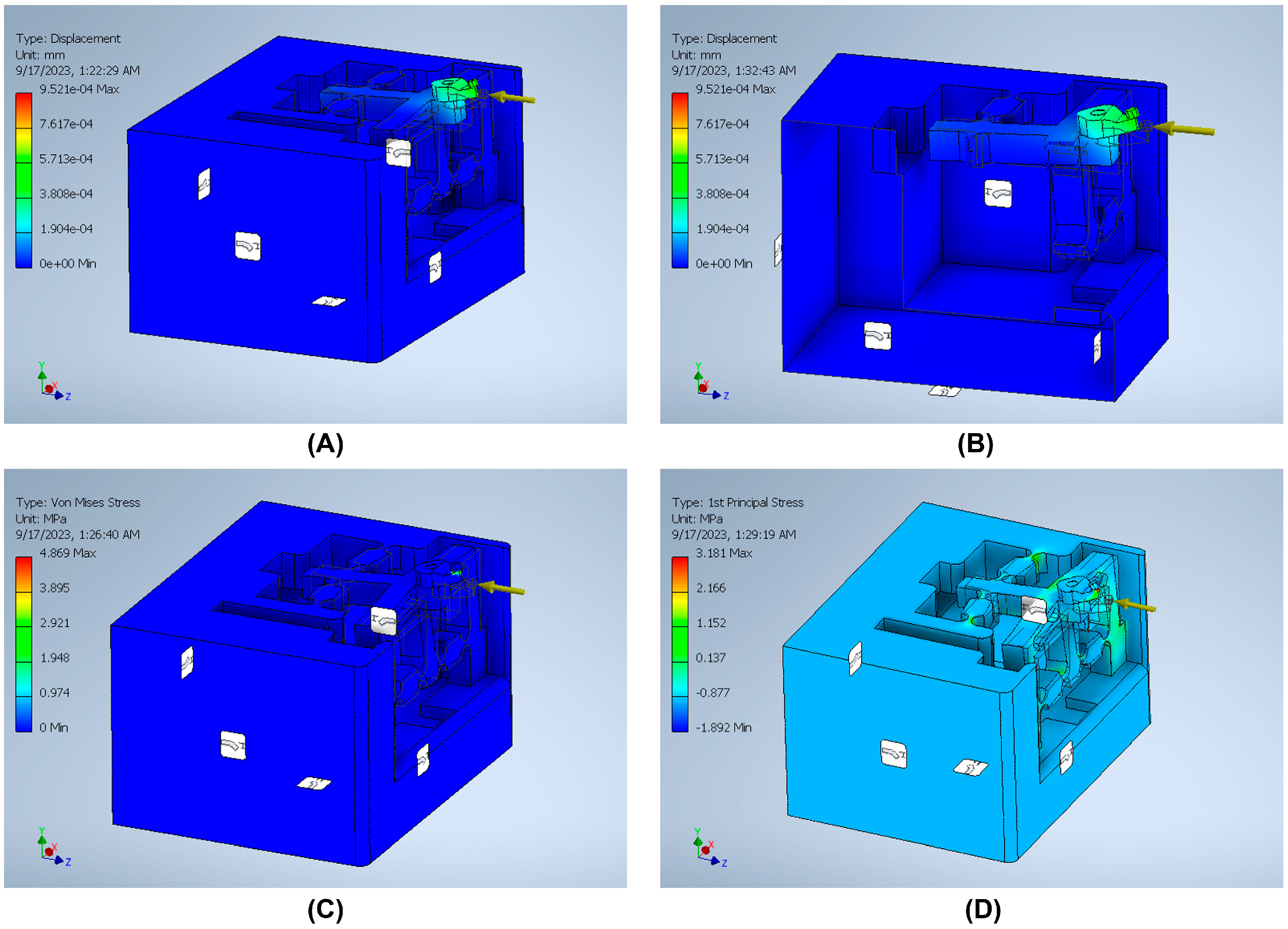
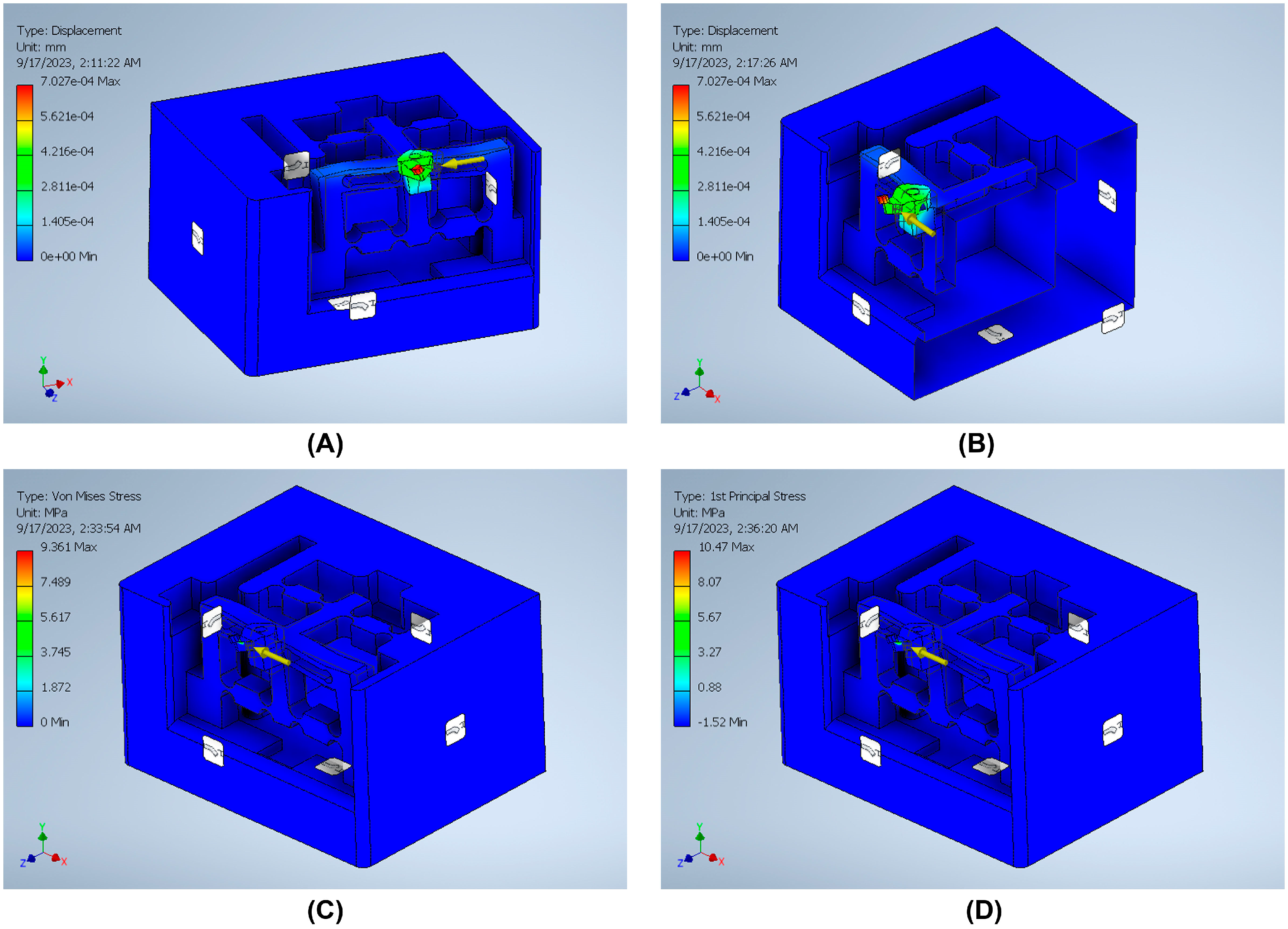
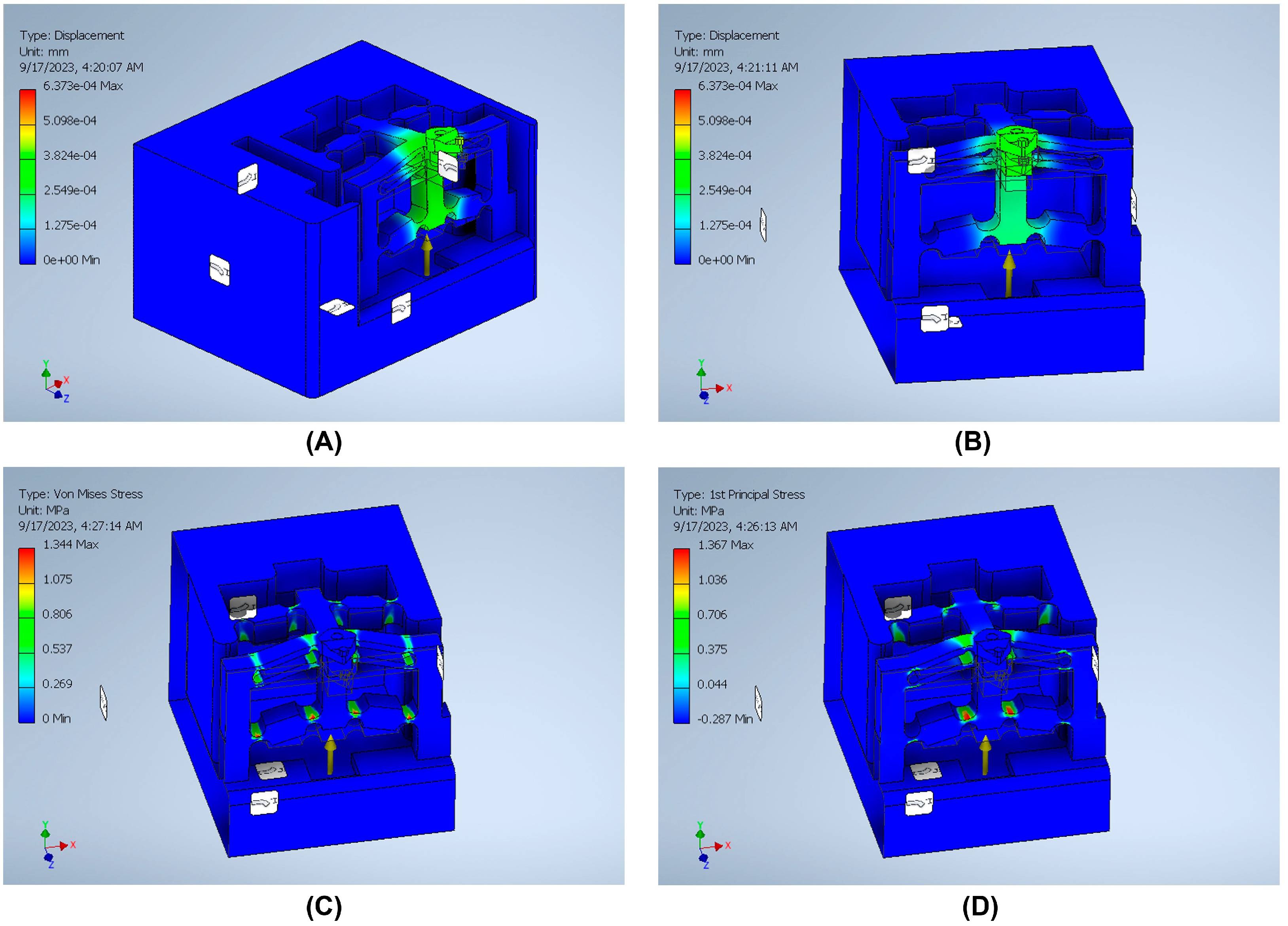
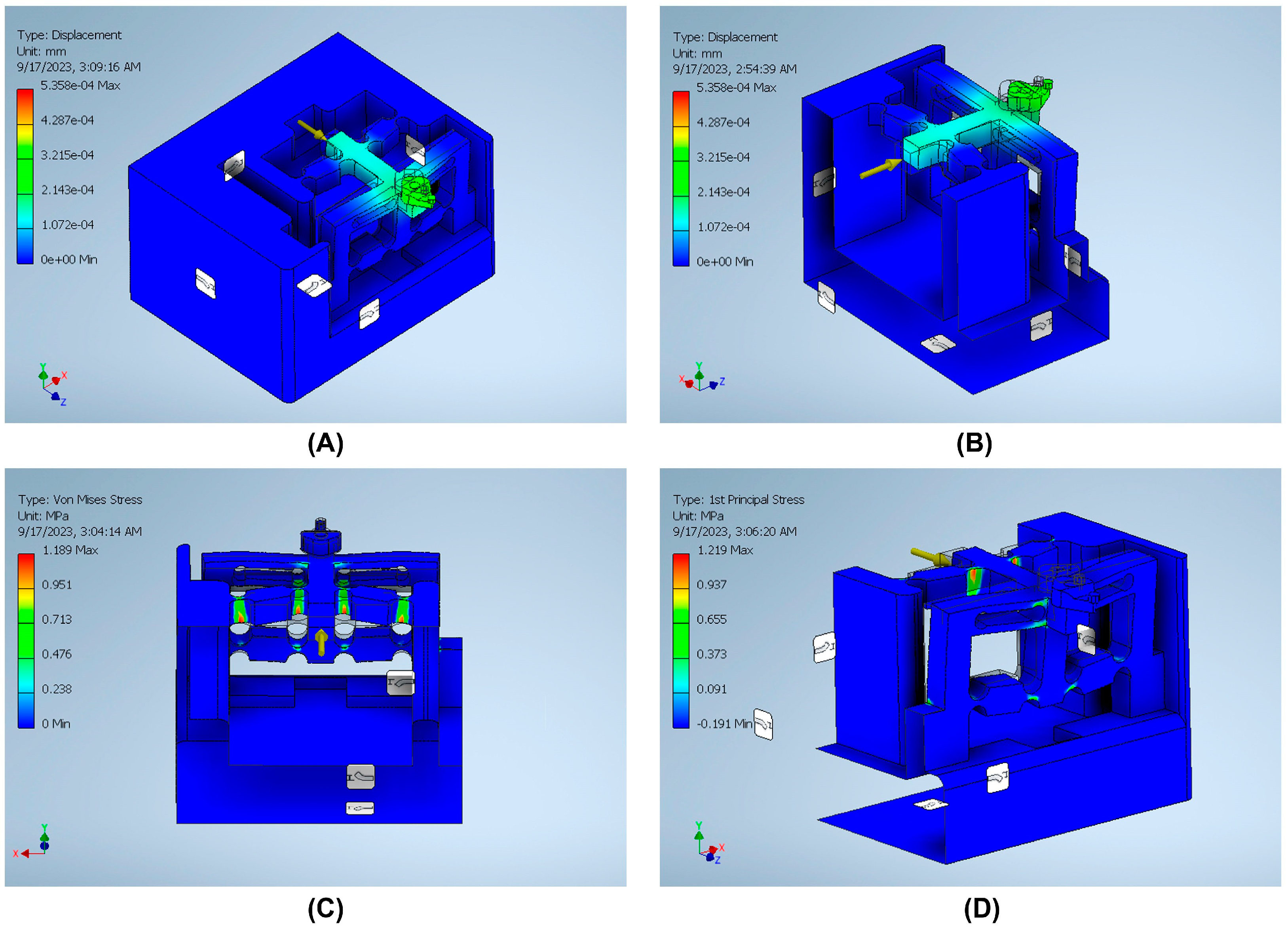
| Measurement System | Strain Gauge | Back Force (Fx) | Cutting Force (Fy) | Feed Force (Fz) |
|---|---|---|---|---|
| Wheatstone bridge I | R1 | + | 0 | 0 |
| R2 | − | 0 | 0 | |
| R3 | + | 0 | 0 | |
| R4 | − | 0 | 0 | |
| Wheatstone bridge II | R5 | 0 | + | 0 |
| R6 | 0 | − | 0 | |
| R7 | 0 | + | 0 | |
| R8 | 0 | − | 0 | |
| Wheatstone bridge III | R9 | 0 | 0 | + |
| R10 | 0 | 0 | − | |
| R11 | 0 | 0 | + | |
| R12 | 0 | 0 | − |
| Symbol | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | L11 | L12 |
| Value (mm) | 85 | 140 | 100 | 20 | 20 | 20 | 10 | 60 | 40 | 10 | 10 | 10 |
| Symbol | L13 | L14 | L15 | L16 | L17 | L18 | L19 | L20 | L21 | L22 | L23 | L24 |
| Value (mm) | 10 | 80 | 20 | 10 | 10 | 20 | 70 | 15 | 40 | 10 | 10 | 10 |
| Symbol | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | D12 |
| Value (mm) | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 6 | 6 | 6 | 6 |
| Symbol | D13 | D14 | D15 | D16 | D17 | D18 | D19 | D20 | D21 | D22 | D23 | D24 |
| Value (mm) | 4 | 4 | 4 | 4 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatefi, S.; Smith, F. Design and Analysis of Ultra-Precision Smart Cutting Tool for In-Process Force Measurement and Tool Nanopositioning in Ultra-High-Precision Single-Point Diamond Turning. Micromachines 2023, 14, 1857. https://doi.org/10.3390/mi14101857
Hatefi S, Smith F. Design and Analysis of Ultra-Precision Smart Cutting Tool for In-Process Force Measurement and Tool Nanopositioning in Ultra-High-Precision Single-Point Diamond Turning. Micromachines. 2023; 14(10):1857. https://doi.org/10.3390/mi14101857
Chicago/Turabian StyleHatefi, Shahrokh, and Farouk Smith. 2023. "Design and Analysis of Ultra-Precision Smart Cutting Tool for In-Process Force Measurement and Tool Nanopositioning in Ultra-High-Precision Single-Point Diamond Turning" Micromachines 14, no. 10: 1857. https://doi.org/10.3390/mi14101857
APA StyleHatefi, S., & Smith, F. (2023). Design and Analysis of Ultra-Precision Smart Cutting Tool for In-Process Force Measurement and Tool Nanopositioning in Ultra-High-Precision Single-Point Diamond Turning. Micromachines, 14(10), 1857. https://doi.org/10.3390/mi14101857








