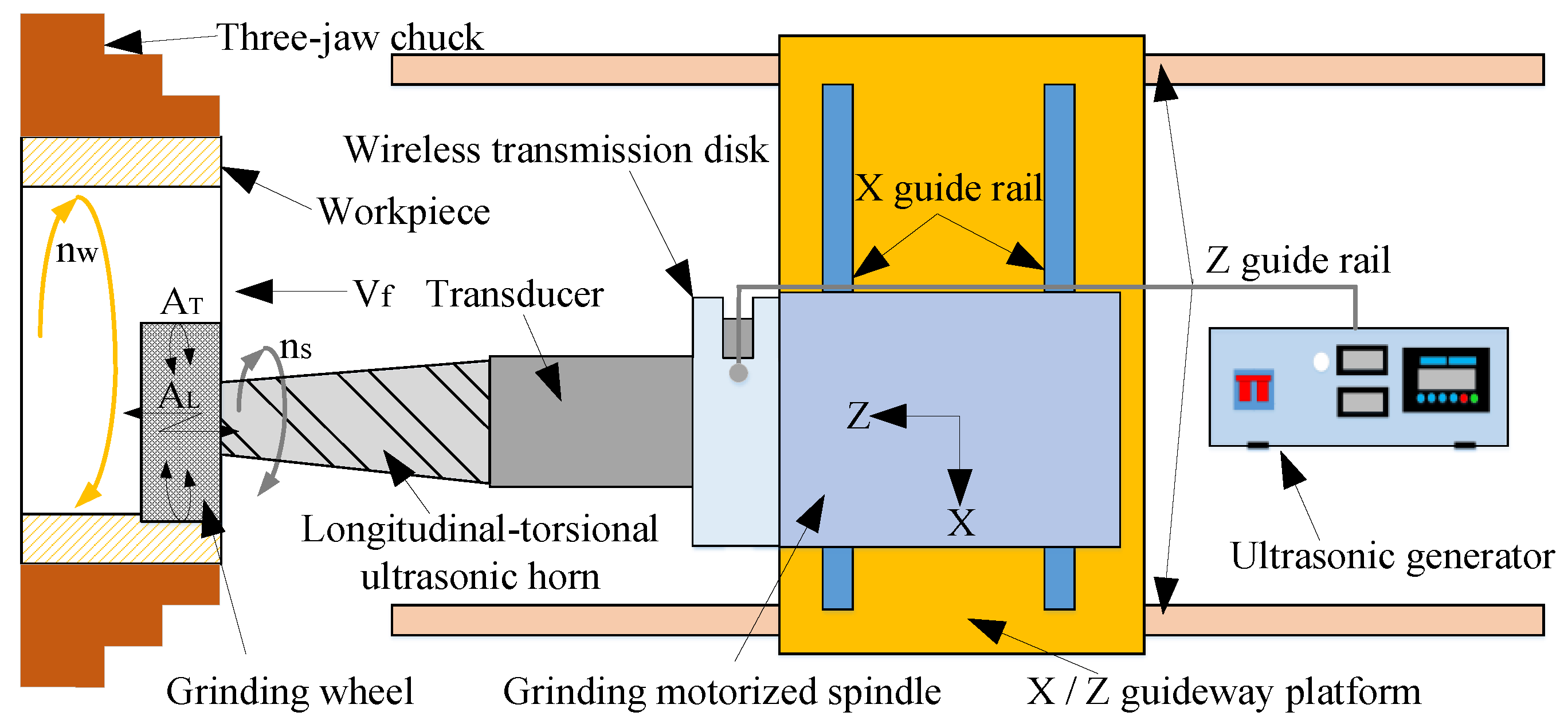
2.2. Design and Optimization of the Longitudinal Vibration Ultrasonic Horn
In the selection of horn materials, the characteristics and mechanical properties of materials should be considered comprehensively. Titanium and titanium alloys are widely used in many fields due to their high specific strength, excellent corrosion resistance, low density, and low magnetic susceptibility [
28]. They have high strength and excellent comprehensive properties. Therefore, a TC4 titanium alloy was selected as the material for the horn.
In order to realize the longitudinal-torsional ultrasonic composite vibration grinding and obtain the larger amplification coefficient and shape factor of the horn, a conical transition longitudinal-torsional ultrasonic composite horn was selected [
29]. When selecting the design frequency of the horn, the influence of the diameter of the grinding tool head, the diameter of the transducer, the length of the horn, the amplification coefficient and the shape factor should be considered.
For the full wavelength horn, the calculation of the wavelength
λ is as follows:
For the actual processing work in this paper, if the length of the horn is too short, it cannot meet the use requirements, and if too long, will lead to insufficient stiffness. Therefore, we chose a horn frequency range of 25–30 kHz.
For transducer diameter
D,
D is generally required to be less than
λ/4. Then, when
f = 30 kHz,
λ = 164.62 mm can be obtained. Due to the influence of the grinding tool head, the diameter of the transducer should be at least greater than 30 mm. Therefore, the range of transducer diameter
D is:
Considering the influence of the amplification factor and the shape characteristics of the horn, a design frequency of 28 kHz was selected. Hence, a 28 kHz piezoelectric ceramic transducer with a diameter D = 38 mm was employed in our design, while the tool head was a CBN grinding wheel with diameter of 50 mm, width of 15 mm, and made of a titanium alloy matrix.
According to the literature [
25,
30,
31], in this paper, the requirements for vibration and impedance characteristics of the horn are shown in
Table 1.
Then the design of the conical transition longitudinal-torsional ultrasonic horn is started, and the model is shown in
Figure 2.
As shown in
Figure 2, the overall structure of the conical transition longitudinal vibration ultrasonic horn is composed of a large cylindrical section I, a conical transition section II and a small cylindrical section III. The lengths and diameters of the three parts of I, II and III are
L1,
L2,
L3 and
d1,
d2,
d3, respectively. The longitudinal vibration excitation is input on the large cylindrical section I, and the whole structure resonates in the one-dimensional longitudinal direction. The force and vibration velocity on all sections are continuous, and the impedance transfer matrix method can be used to calculate the size parameters of the horn [
32].
The area function of each section can be expressed as:
The area function of I and III is expressed as
and
, respectively. The area function of conical transition section II,
, can be expressed as:
From
Figure 2, the diameter of the conical transition section II
can be expressed as:
Substitute Equation (6) into Equation (5):
Equation (7) can be simplified as follows:
where
is the taper coefficient of the conical section and
is the area coefficient.
The transfer matrix expression of the longitudinal vibration of the horn is as follows [
32]:
where
Z1,
Z2 and
Z3 are the impedance transfer matrices of the three sections of the conical transition longitudinal vibration horn, respectively. The elements in the above matrix are as follows:
where
kl =
ω/cl,
kl is the circular wave number;
ω is the circular frequency;
cl = (
E/ρ)
1/2, which is the longitudinal wave propagation velocity in the horn;
ρ is the density of the material; and
E is the Young’s modulus.
According to matrix multiplication theory, Equation (11) can be further simplified as follows:
where
,
,
and
are the elements obtained by the product of the three impedance transfer matrices of the horn, respectively. According to the boundary conditions of the horn [
33,
34], the force on the free cross-section at both ends of system is 0, then
F1 =
F3 = 0,
= 0, and the longitudinal vibration frequency equation of the conical transition horn is obtained as follows [
32]:
Further, the amplification factor of longitudinal vibration can be expressed as follows [
32]:
From Equation (20), it can be seen that this equation is a transcendental equation set about the geometric parameters of the horn shape and material characteristic parameters [
35]. In general, it is difficult to solve the numerical solution. However, in engineering applications, the material, area coefficient, and working frequency of the composite horn are often pre-set. Therefore, the material characteristic parameters such as sound velocity, density, elastic modulus, and Poisson’s ratio of composite horn are determined. The material parameters of TC4 titanium alloy are shown in
Table 2.
Due to the design requirements, it is necessary to match the existing 28 kHz transducer, and the size of the grinding wheel has been determined to be
d4 = 50 mm and
L4 = 15 mm. The known size parameters of the longitudinal-torsional composite ultrasonic horn and grinding wheel are shown in
Table 3.
Therefore, there are only three unknowns left in the longitudinal ultrasonic frequency equations: the length of the two cylindrical sections L1, L3 and the length of the conical section L2. In order to obtain the accurate numerical solution of the transcendental equations, the length L1 of the large cylindrical segment can be determined in advance.
According to traditional horn design theory, the flange is generally set at the zero point of the vibration displacement of the horn, and the position is about 1/4 of the wavelength. According to the material parameters, the full wavelength
λ of the longitudinal wave can be calculated as:
It can be seen from Equation (22) that the vibration displacement zero point
X0 is about 44.1 mm. Due to the design and use requirements, the diameter of the flange is
d5 = 70 mm, the length is
L5 = 8 mm, and the vibration displacement zero point
X0 should be in the center of the flange, then the length of the large cylindrical section I can be scheduled as follows:
Substituting all the above known parameters into Equations (20) and (21), L2 = 55.114 mm, L3 = 41.078 mm, and the amplification factor ML = 1.26 is obtained.
According to the predetermined size parameters of the horn, the horn and the grinding wheel are modeled by SolidWorks 2018 software and imported into the finite element analysis software ANSYS 16.0. The path is added in a longitudinal direction, and the modal analysis result is shown in
Figure 3a. The vibration displacement zero point has a deviation, which is considered to be the influence of the applied tool head. As shown in
Figure 3b, the zero point of vibration displacement changes to 46.667 mm.
By slightly adjusting the size of each section and performing modal analysis, the vibration mode is continuously optimized, and finally, a better vibration mode is obtained under the size of
L1 = 52 mm,
L2 = 56 mm, and
L3 = 37 mm. The modal analysis result of the longitudinal vibration horn with tool head is shown in
Figure 4. The resonance frequency is 27,759 Hz, which is 241 Hz less than the theoretical design frequency of 28,000 Hz, and the error is 0.9%. According to
Table 1, the frequency error requirement is 5%. Therefore, the frequency error is within the allowable range and meets the requirements.
The size parameters of each section of the conical transition longitudinal vibration horn with tool head are determined as shown in
Table 4:
2.3. Design and Optimization of Spiral Groove
In the design process of the longitudinal-torsional ultrasonic vibration horn, the output torsional vibration of the horn is realized through a spiral groove. Some literatures have explained the principle of applying spiral grooves to achieve longitudinal-torsional vibration [
21,
36]. As shown in
Figure 5, the conical transition section can be regarded as composed of a cylindrical section at the bottom of the groove with a radius of
R2 and an outer spiral part. When the longitudinal ultrasonic vibration force
F is applied to the large cylindrical end of the horn and transmitted to the conical transition section, part of the longitudinal ultrasonic vibration force
F1 continues to be transmitted along the cylindrical section at the bottom of the groove. Due to the angle
θ of the spiral groove in the outer layer, the longitudinal ultrasonic vibration force is transmitted to the force
F2 perpendicular to the spiral groove surface, and
F2 is further decomposed into the longitudinal force
F2L and the torsional force
F2T along the spiral angle
θ [
37]. The longitudinal ultrasonic amplitude
AL and the torsional ultrasonic amplitude
AT are output at the end of the small cylinder, so the single longitudinal ultrasonic vibration is converted into longitudinal-torsional ultrasonic vibration through the spiral groove.
According to the torsional vibration theory of ultrasonic vibration, the tangential component
F2T causes the system to produce torsional vibration. Hence. we can use the same method [
37] to deduce both the generated torque
M and longitudinal-torsional mechanical conversion coefficient
nT as follows:
It can be seen from Equation (25) that the longitudinal-torsional mechanical conversion coefficient
nT is related to
R1,
R2,
φ1,
φ2, and
θ. That is, it is related to the groove depth, the number of the spiral grooves, the groove width, and the spiral angle. As shown in
Figure 5, the width of the spiral groove is
Bg, the length is
Lg, the number is
N (generally
N = 4), and the spiral angle is
θ. Since the conical section has a tilt angle, the depth of the spiral groove is not a fixed value, so the radius
R2 of the spiral groove bottom cylinder is used to characterize the depth of the spiral groove. The larger
R2 is, the smaller the depth of spiral groove; the smaller
R2 is, the greater the depth of the spiral groove.
When selecting the parameters of the spiral groove, the influence of the spiral groove on the design frequency
f and the torsional-longitudinal ratio
i (
i =
AT/
AL) is the main target. Relevant studies have shown that, as the spiral angle
θ of the spiral groove increases from small to large,
i increases first and then decreases, and the torsional-longitudinal ratio
i reaches the maximum when the spiral angle
θ = 45°. As the length of the spiral groove
Lg increases, the torsional-longitudinal ratio
i increases [
23,
38]. Therefore, the number of the spiral grooves is
N = 4, the spiral angle
θ = 45°, and the length of the spiral groove
Lg is as long as possible. The length of the conical section is known to be
L2 = 56 mm. Considering the actual machining operation and the presence of the tool radius, a safety clearance of 6 mm is reserved and the length of the spiral groove is
Lg = 50 mm. From the relevant literature [
21,
23], it is found that the most commonly selected range of spiral groove width is 4–8 mm. And, the depth of the spiral groove also has an effect on the frequency and torsional-longitudinal ratio [
21]. The maximum value of
R2 is selected to be equal to the radius of the small cylindrical section of 15 mm, and in order to make the conical transition section III have sufficient strength, the minimum value of
R2 is selected to be 12 mm. Hence, the value of
R2 is selected in the range of 12–15 mm. The parameter optimization of the width of the spiral groove,
Bg, and the radius of bottom cylinder of spiral groove,
R2, is carried out using single factor simulation analysis approach [
39]. Parameters to be optimized are shown in
Table 5.
The results of the ANSYS analysis are shown in
Figure 6. In
Figure 6a, with the increase in
Bg, the frequency
f changes little; And,
i decreases first and then increases and then decreases again and reaches the maximum at
Bg = 6 mm, so the spiral groove width
Bg is determined to be 6 mm. Then, the effects of different
R2 on frequency
f and torsional-longitudinal ratio
i are analyzed. As shown in
Figure 6b, with the increase in
R2, the frequency
f also increases, and the torsion ratio
i increases first and then decreases, reaching the maximum when
R2 = 13 mm. Therefore, the parameters of the spiral groove are all determined, as shown in
Table 6.