Design, Fabrication, Characterization, and Simulation of AlN-Based Piezoelectric Micromachined Ultrasonic Transducer for Sonar Imaging Applications
Abstract
1. Introduction
2. Design of AlN PMUT
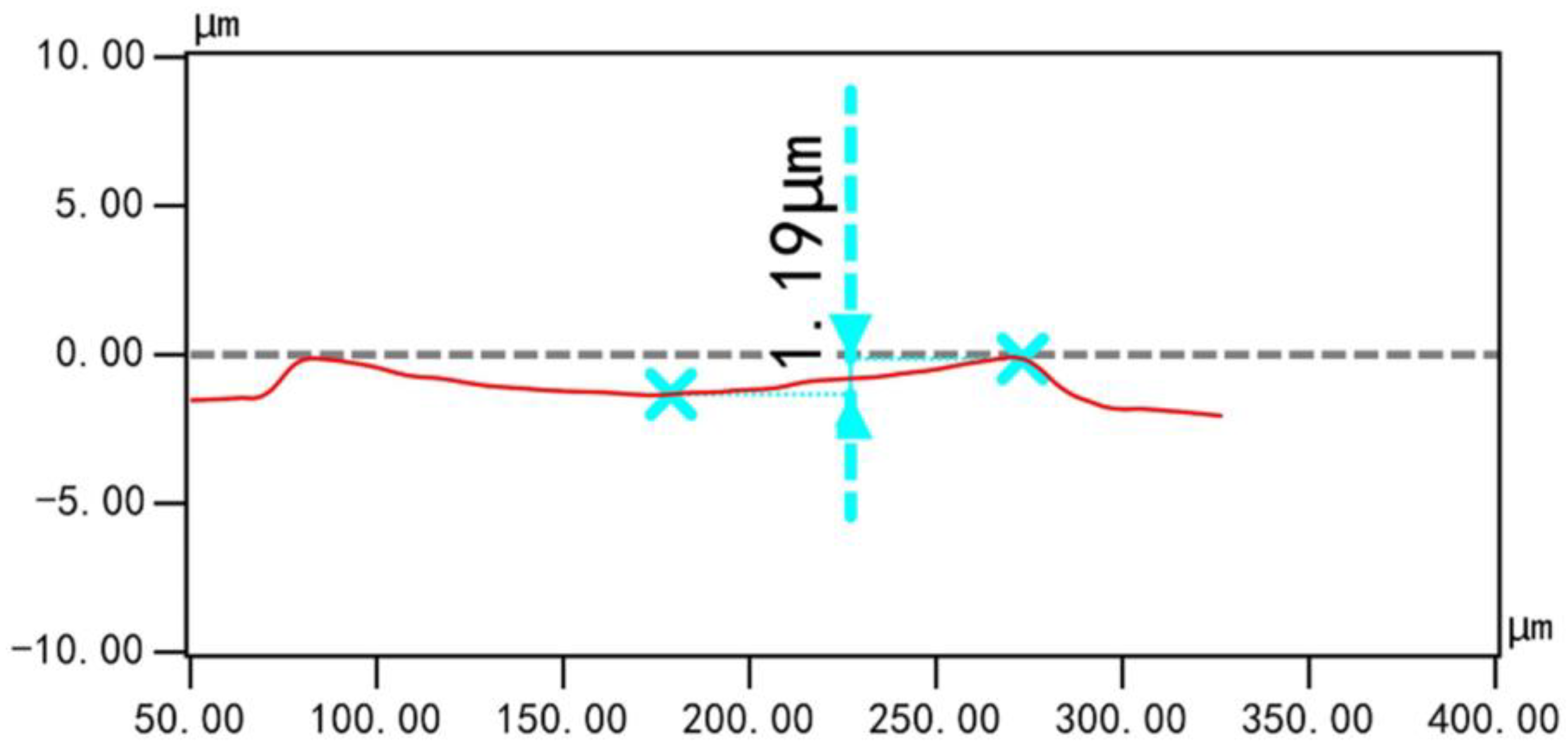
3. Fabrication of AlN PMUT
4. The Characteristic Measurement of the AlN PMUTs
4.1. Resonant Frequency Test
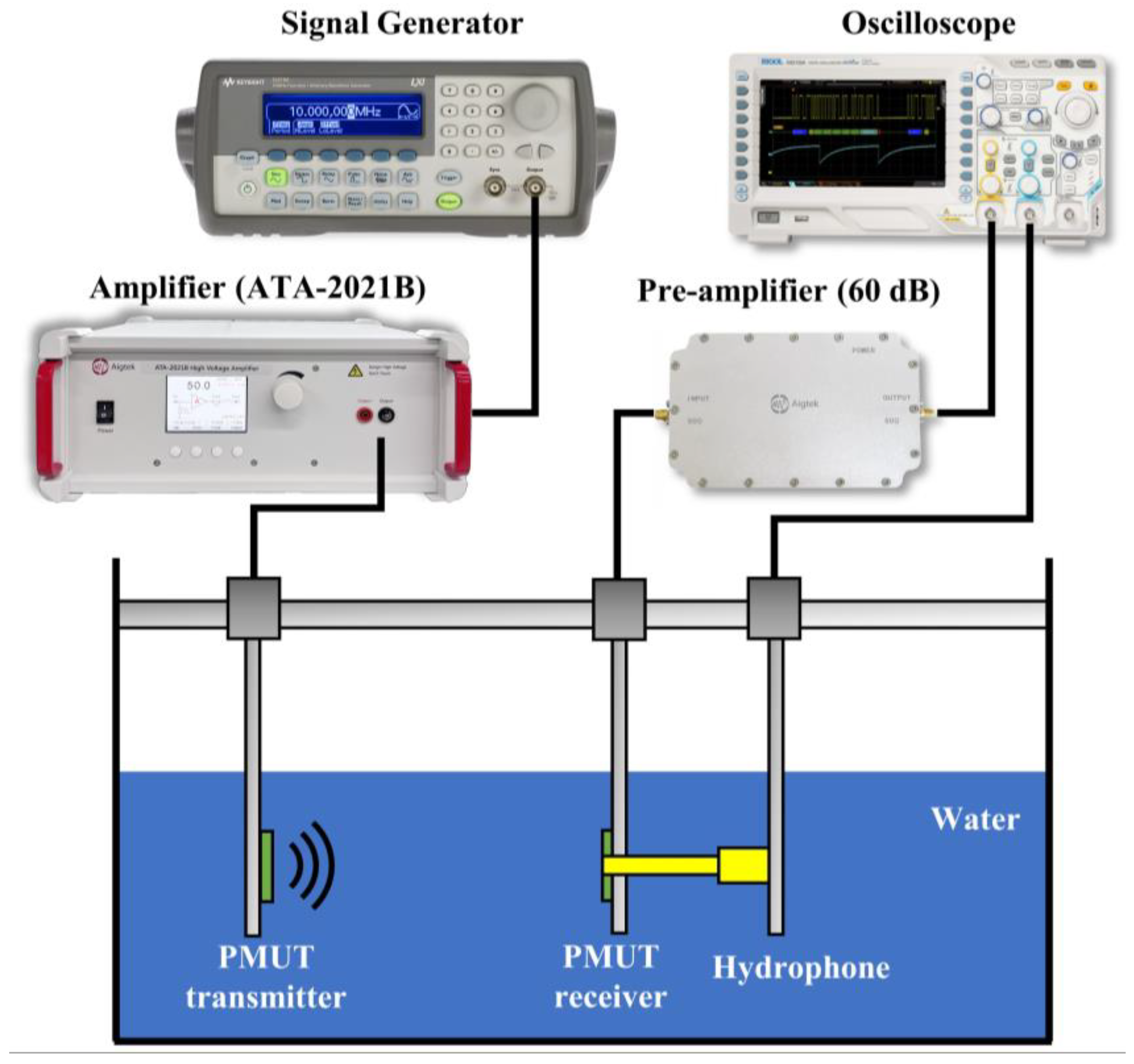
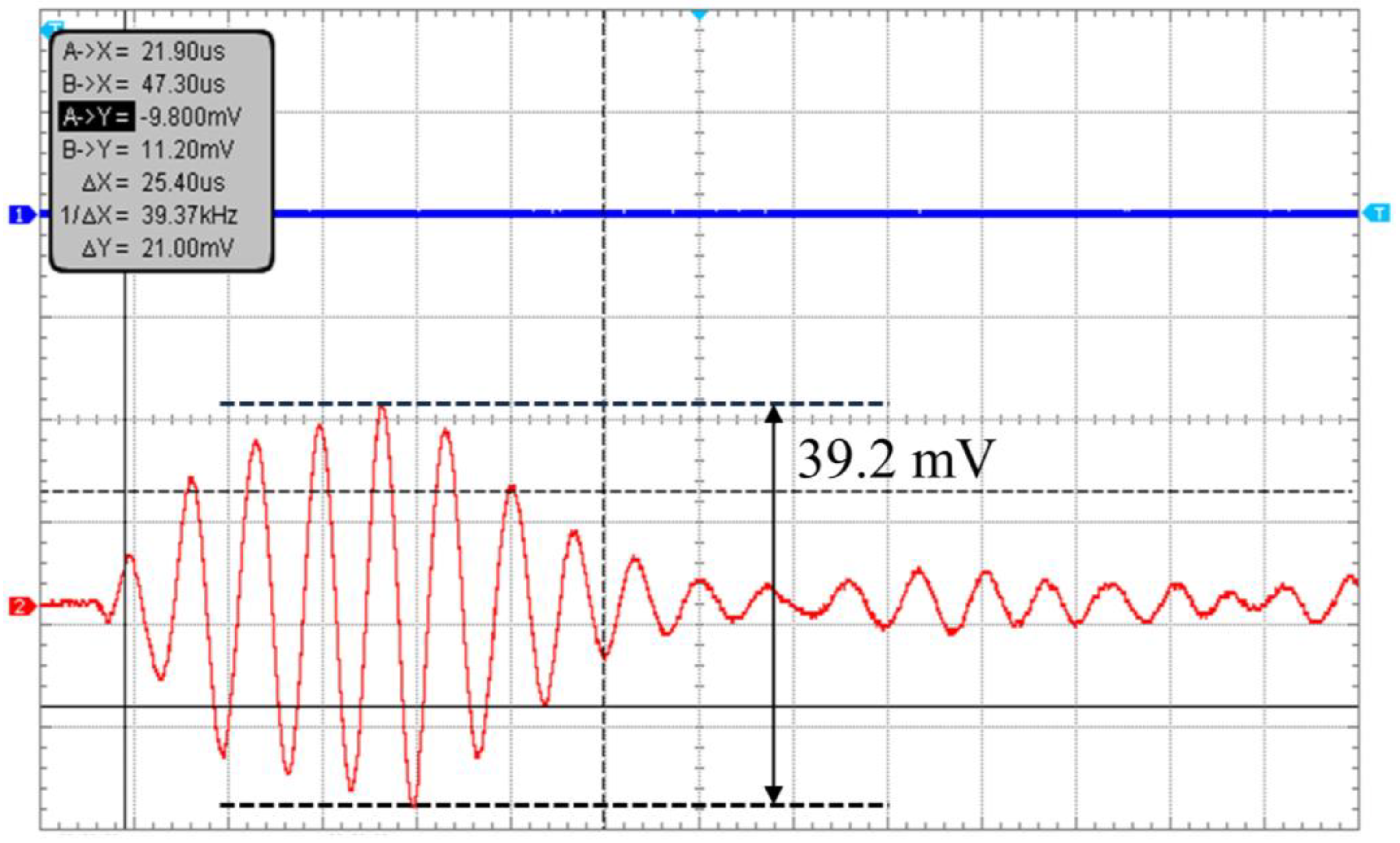
4.2. Measurement of PMUT’s Underwater Acoustic Properties
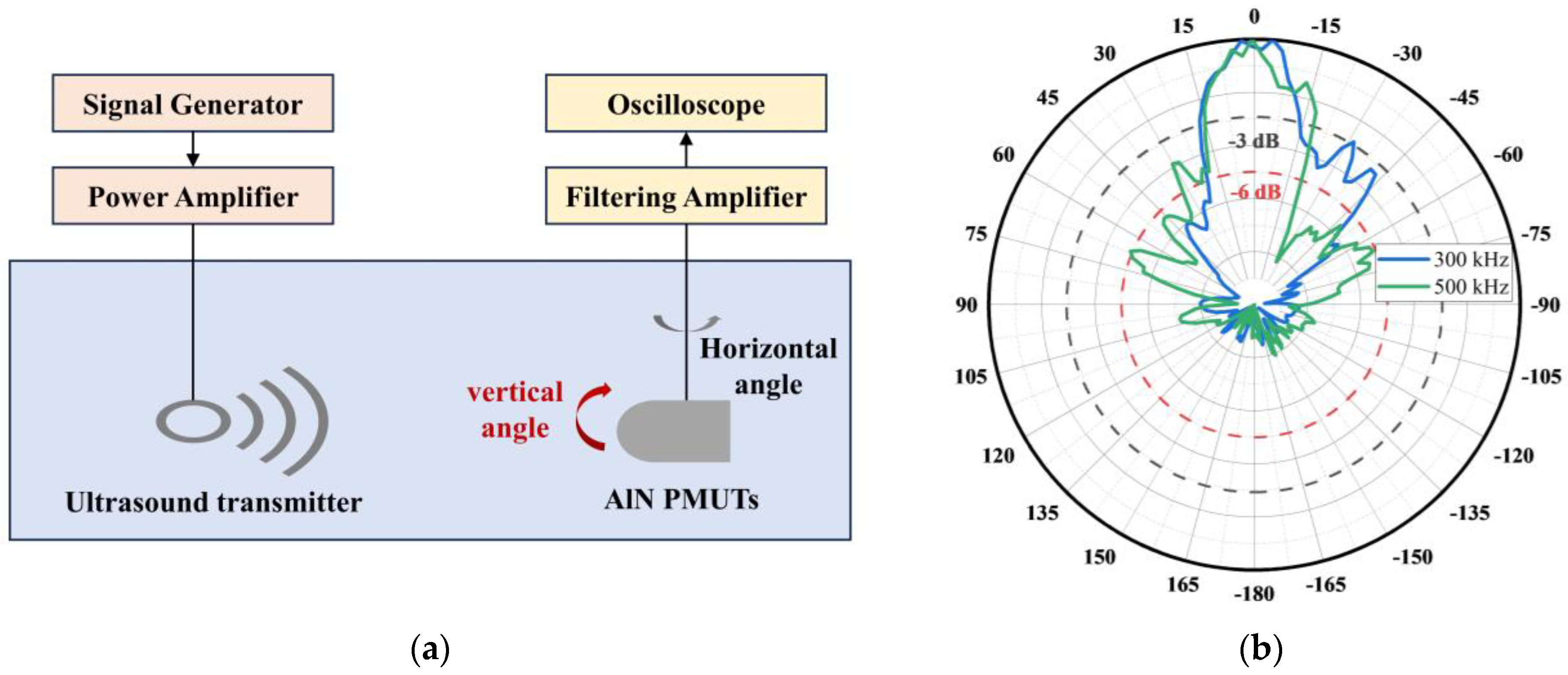
4.3. Receiving Angle of PMUT
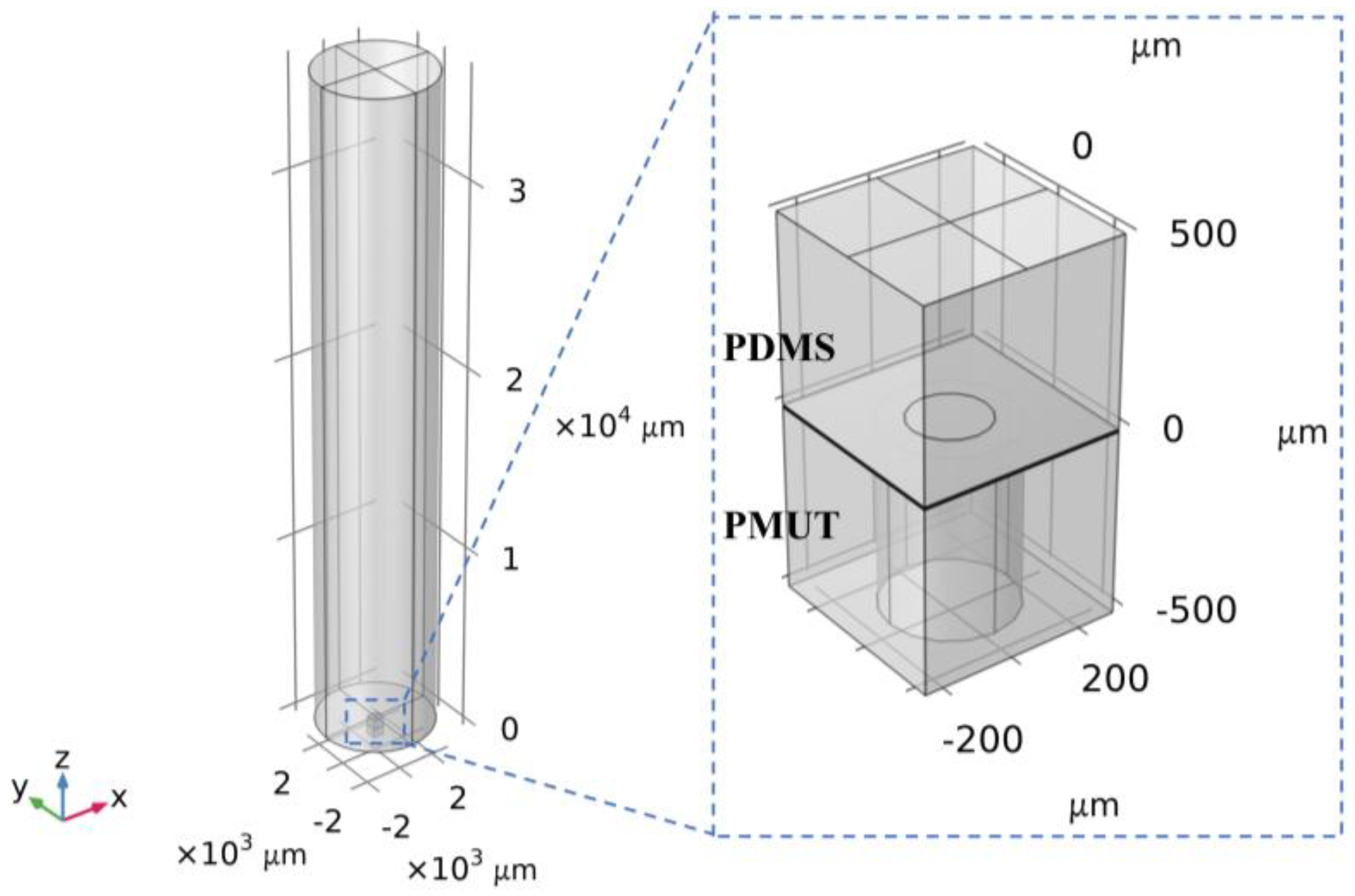
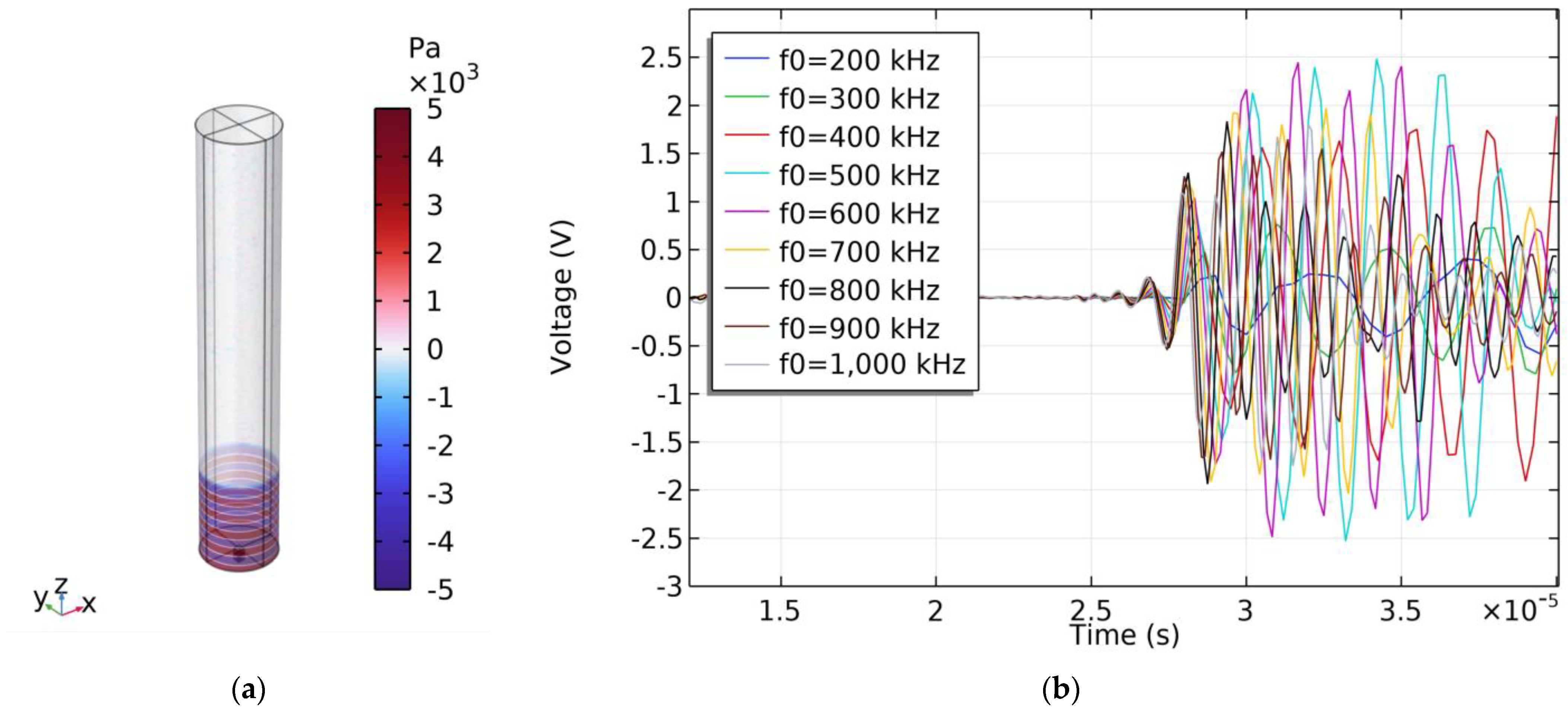
5. Simulation of PMUTs Underwater
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, Y.; Jia, L.; Liu, C.; Wang, X.; Sun, C.; Liu, S.; Wu, G. A transceiver integrated piezoelectric micromachined ultrasound transducer array for underwater imaging. Sens. Actuators A Phys. 2023, 359, 114476. [Google Scholar] [CrossRef]
- Shuyu, L. The Principle and Design of Ultrasonic Transducer; Science Press: Beijing, China, 2004. [Google Scholar]
- Roy, K.; Lee, J.E.-Y.; Lee, C. Thin-film PMUTs: A review of over 40 years of research. Microsyst. Nanoeng. 2023, 9, 95. [Google Scholar] [CrossRef] [PubMed]
- Gong, D.; Ma, S.; Chiu, Y.; Lee, H.; Jin, Y. Study of the Properties of AlN PMUT used as a Wireless Power Receiver. In Proceedings of the 2019 IEEE 69th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2019; pp. 1503–1508. [Google Scholar]
- Chiu, Y.; Wang, C.; Gong, D.; Li, N.; Ma, S.; Jin, Y. A Novel Ultrasonic TOF Ranging System Using AlN Based PMUTs. Micromachines 2021, 12, 284. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Tang, H.Y.; Fung, S.; Boser, B.E.; Horsley, D.A. Pulse-Echo Ultrasound Imaging Using an AlN Piezoelectric Micromachined Ultrasonic Transducer Array With Transmit Beam-Forming. J. Microelectromech. Syst. 2016, 25, 179–187. [Google Scholar] [CrossRef]
- Hake, A.E.; Zhao, C.; Ping, L.; Grosh, K. Ultraminiature AlN diaphragm acoustic transducer. Appl. Phys. Lett. 2020, 117, 645. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Yang, L.; Chen, X.; Qu, M.; Zhu, K.; Ding, H.; Li, D.; Bai, Y.; Ling, J.; Xu, J.; et al. A piezoelectric AlN MEMS hydrophone with high sensitivity and low noise density. Sens. Actuators A Phys. 2021, 318, 112493. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, H. Research on monometallic plate piezoelectric ceramic column array broadband high sensitivity transducer. Appl. Acoust. 2023, 205, 109281. [Google Scholar] [CrossRef]
- Chen, W.L.; Yang, S.S.; Yuan, N.H.; Zhou, W.Y.; Yang, Y.P.; Lo, H.H.; Wang, P.J.; Lai, W.; Fuh, Y.k.; Li, T.T. Minimizing residual stress of aluminum nitride (AlN) thin films using multi-step deposition of DC pulsed sputtering. In Proceedings of the 2022 China Semiconductor Technology International Conference (CSTIC), Shanghai, China, 20–21 June 2022; pp. 1–4. [Google Scholar]
- Chen, X.; Chen, D.; Liu, X.; Yang, D.; Pang, J.; Xie, J. Transmitting Sensitivity Enhancement of Piezoelectric Micromachined Ultrasonic Transducers via Residual Stress Localization by Stiffness Modification. IEEE Electron. Device Lett. 2019, 40, 796–799. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, M.L.; Sun, S.; Guo, W.L.; Sun, C.; Pang, W. Piezoelectric Micromachined Ultrasonic Transducers With Superior Frequency Control. J. Microelectromech. Syst. 2023, 32, 513–515. [Google Scholar] [CrossRef]
- Olfatnia, M.; Xu, T.; Ong, L.S.; Miao, J.M.; Wang, Z.H. Investigation of residual stress and its effects on the vibrational characteristics of piezoelectric-based multilayered microdiaphragms. J. Micromech. Microeng. 2009, 20, 015007. [Google Scholar] [CrossRef]
- Sammoura, F.; Smyth, K.; Kim, S.-G. Optimizing the electrode size of circular bimorph plates with different boundary conditions for maximum deflection of piezoelectric micromachined ultrasonic transducers. Ultrasonics 2013, 53, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Ross, G.; Dong, H.Q.; Karuthedath, C.B.; Sebastian, A.T.; Pensala, T.; Paulasto-Kröckel, M. The impact of residual stress on resonating piezoelectric devices. Mater. Des. 2020, 196, 109126. [Google Scholar] [CrossRef]
- Dangi, A.; Pratap, R. System level modeling and design maps of PMUTs with residual stresses. Sens. Actuators A Phys. 2017, 262, 18–28. [Google Scholar] [CrossRef]
- Lundh, J.S.; Coleman, K.; Song, Y.; Griffin, B.A.; Esteves, G.; Douglas, E.A.; Edstrand, A.M.; Badescu, S.C.; Moore, E.A.; Leach, J.H.; et al. Residual stress analysis of aluminum nitride piezoelectric micromachined ultrasonic transducers using Raman spectroscopy. J. Appl. Phys. 2021, 130, 044501. [Google Scholar] [CrossRef]
- Lu, Y.; Horsley, D.A. Modeling, Fabrication, and Characterization of Piezoelectric Micromachined Ultrasonic Transducer Arrays Based on Cavity SOI Wafers. J. Microelectromech. Syst. 2015, 24, 1142–1149. [Google Scholar] [CrossRef]
- Cai, J.; Wang, Y.; Jiang, D.; Zhang, S.; Gu, Y.A.; Lou, L.; Gao, F.; Wu, T. Beyond fundamental resonance mode: High-order multi-band ALN PMUT for in vivo photoacoustic imaging. Microsystems Nanoeng. 2022, 8, 116. [Google Scholar] [CrossRef]
- Latif, R.; Aziz, M.F.; Majlis, B.Y. Control of physical and microstructural properties in molybdenum by direct current magnetron sputtering deposition producing bilayer thin film. Thin Solid. Film. 2018, 665, 17–28. [Google Scholar] [CrossRef]
- Joe, H.; Cho, H.; Sung, M.; Kim, J.; Yu, S.-c. Sensor fusion of two sonar devices for underwater 3D mapping with an AUV. Auton. Robot. 2021, 45, 543–560. [Google Scholar] [CrossRef]
- Jiang, X.; Lu, Y.; Tang, H.-Y.; Tsai, J.M.; Ng, E.J.; Daneman, M.J.; Boser, B.E.; Horsley, D.A. Monolithic ultrasound fingerprint sensor. Microsyst. Nanoeng. 2017, 3, 17059. [Google Scholar] [CrossRef] [PubMed]
- Eovino, B.E.; Akhbari, S.; Lin, L. Broadband ring-shaped PMUTS based on an acoustically induced resonance. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 1184–1187. [Google Scholar]
- Wong, L.L.P.; Na, S.; Chen, A.I.; Li, Z.; Macecek, M.; Yeow, J.T.W. A feasibility study of piezoelectric micromachined ultrasonic transducers fabrication using a multi-user MEMS process. Sens. Actuators A Phys. 2016, 247, 430–439. [Google Scholar] [CrossRef]
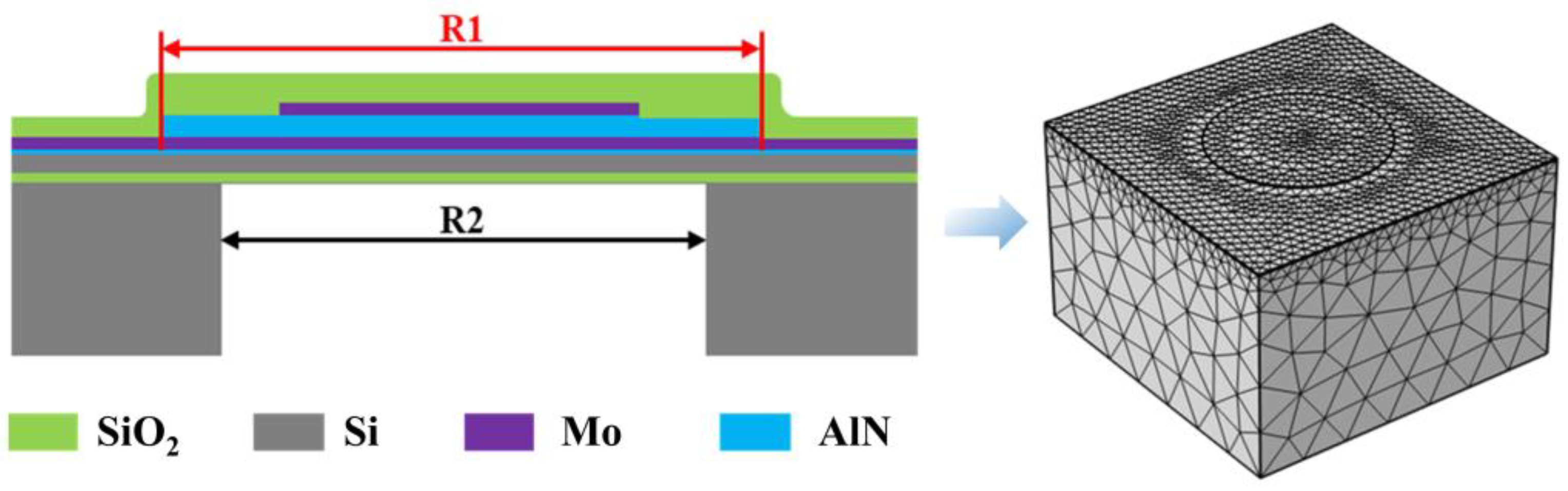
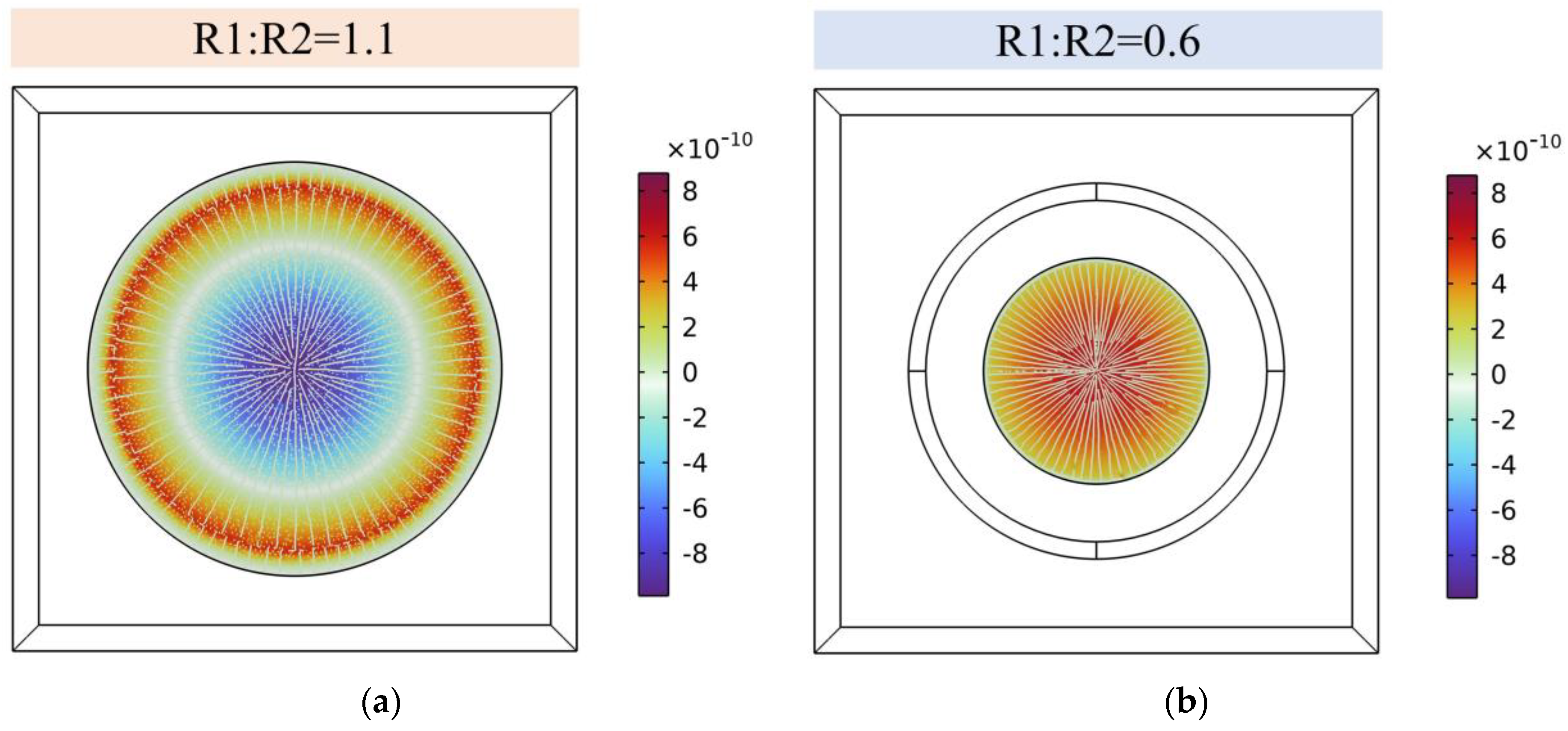
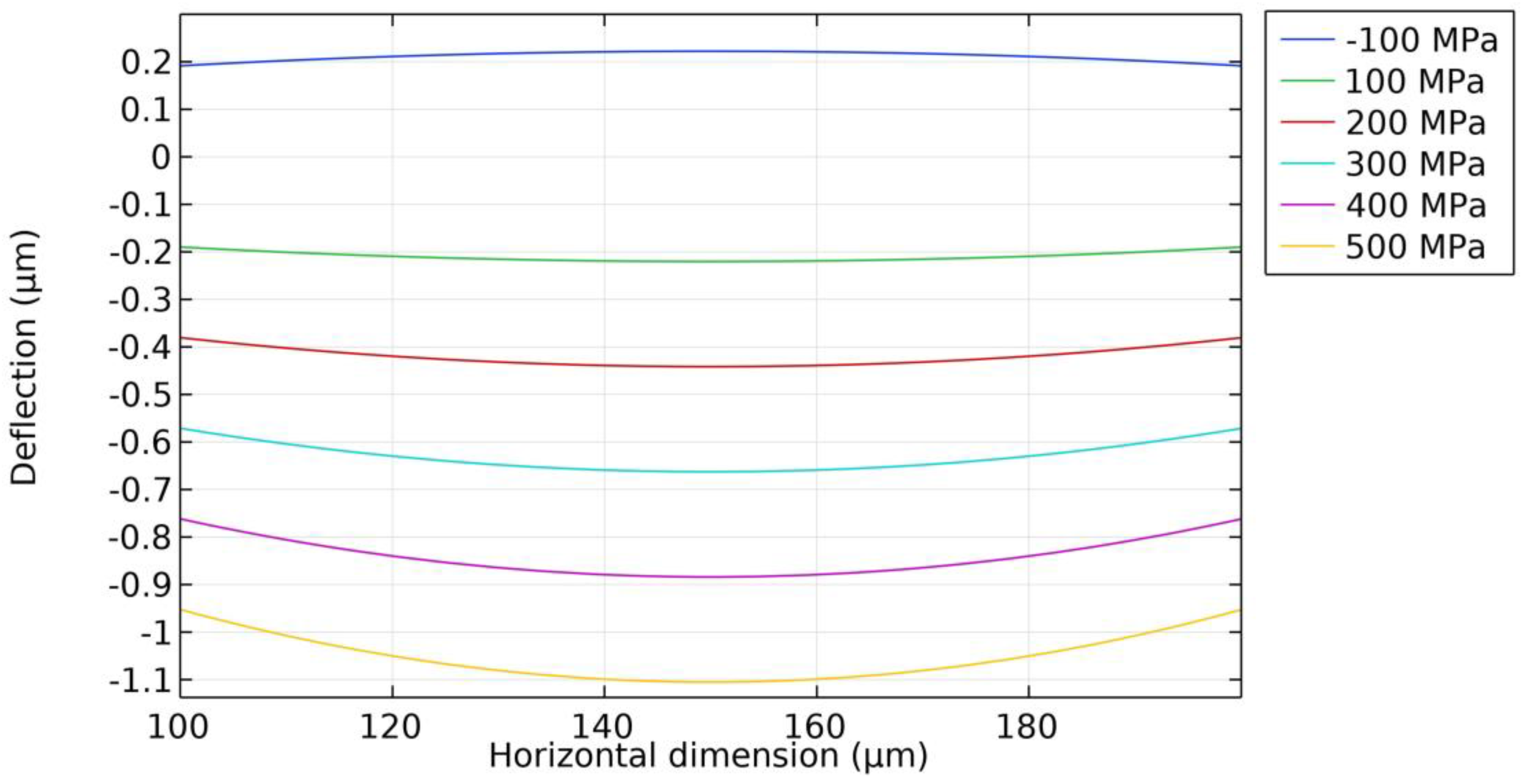




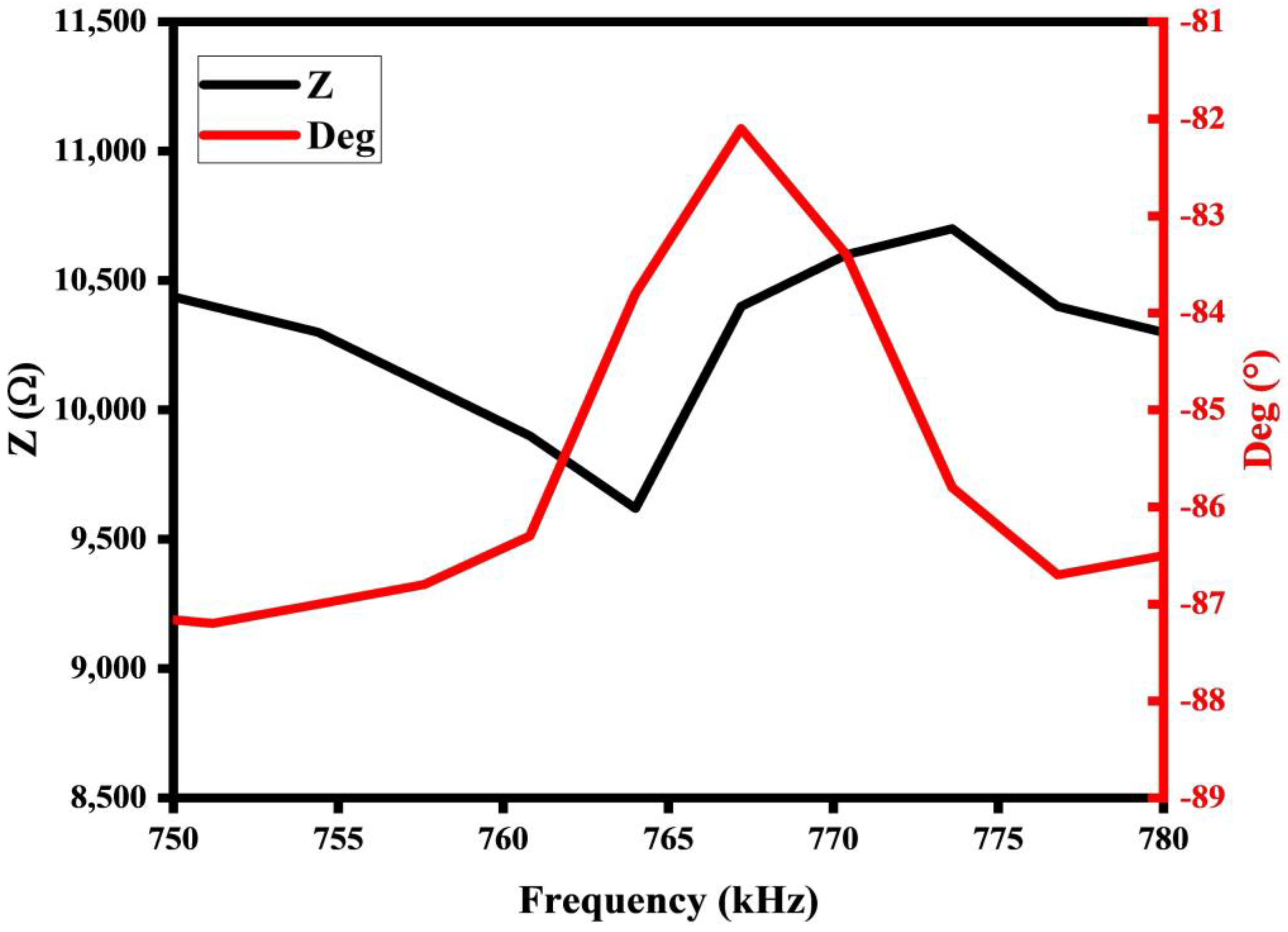

| Materials | Density (kg/m3) | Poisson’s Ratio | Young’s Modulus (GPa) | Thickness (μm) |
|---|---|---|---|---|
| Si | 2330 | 0.28 | 170 | 3 |
| Mo | 10,200 | 0.31 | 314 | 0.2 |
| AlN | 3600 | 0.24 | 340 | 2 |
| SiO2 | 2200 | 0.17 | 60 | 1 |
| Materials | UW [24] | ZJU [8] | WHU [1] | This Work |
|---|---|---|---|---|
| Cavity size (μm) | 460 | 280 | 500 | 345 |
| Geometry | square | circular | hexagonal | circular |
| Array | 3 × 3 | 10 × 10 | 7 × 8 | 2 × 2 |
| Resonant frequency (kHz, in air) | 600 | 986 | 438.62 | 767.2 |
| Piezoelectric material | AlN | AlN | Sc0.2Al0.8N | AlN |
| Receiving sensitivity (dB) (Amplifier gain) | −237.39 (0 dB) | −178 (40 dB) | −173.4 (40 dB) | −173.9 (60 dB) |
| Receiving sensitivity (dB) 1 | −237.39 | −218 | −213.4 | −233.9 |
| Receiving sensitivity per unit area (V/µPa/mm2) 1 | 0.71 | 0.53 | 0.58 | 1.37 |
| −6 dB bandwidth (kHz) | - | ~1.5 | ~68 | ~500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Ma, S.; Lai, X.; Wang, Z.; Zhao, H.; Zha, Q.; Chiu, Y.; Jin, Y. Design, Fabrication, Characterization, and Simulation of AlN-Based Piezoelectric Micromachined Ultrasonic Transducer for Sonar Imaging Applications. Micromachines 2024, 15, 781. https://doi.org/10.3390/mi15060781
Chen W, Ma S, Lai X, Wang Z, Zhao H, Zha Q, Chiu Y, Jin Y. Design, Fabrication, Characterization, and Simulation of AlN-Based Piezoelectric Micromachined Ultrasonic Transducer for Sonar Imaging Applications. Micromachines. 2024; 15(6):781. https://doi.org/10.3390/mi15060781
Chicago/Turabian StyleChen, Wenxing, Shenglin Ma, Xiaoyi Lai, Zhizhen Wang, Hui Zhao, Qiang Zha, Yihsiang Chiu, and Yufeng Jin. 2024. "Design, Fabrication, Characterization, and Simulation of AlN-Based Piezoelectric Micromachined Ultrasonic Transducer for Sonar Imaging Applications" Micromachines 15, no. 6: 781. https://doi.org/10.3390/mi15060781
APA StyleChen, W., Ma, S., Lai, X., Wang, Z., Zhao, H., Zha, Q., Chiu, Y., & Jin, Y. (2024). Design, Fabrication, Characterization, and Simulation of AlN-Based Piezoelectric Micromachined Ultrasonic Transducer for Sonar Imaging Applications. Micromachines, 15(6), 781. https://doi.org/10.3390/mi15060781







