Elasticity of Carrier Fluid: A Key Factor Affecting Mechanical Phenotyping in Deformability Cytometry
Abstract
1. Introduction
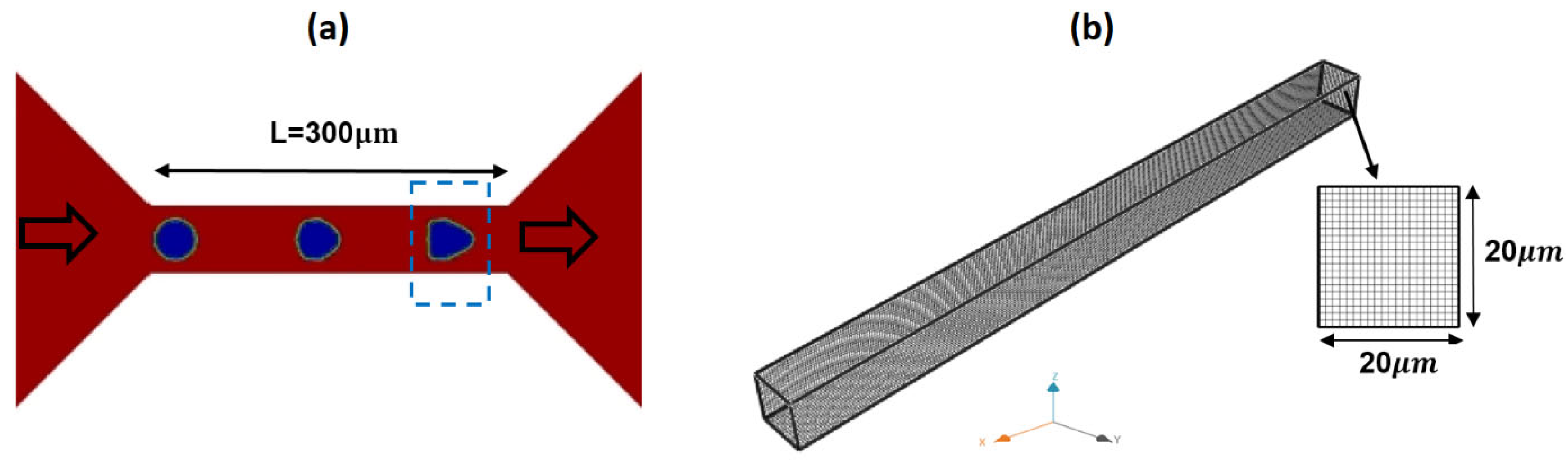
2. Numerical Method
3. Results and Discussions
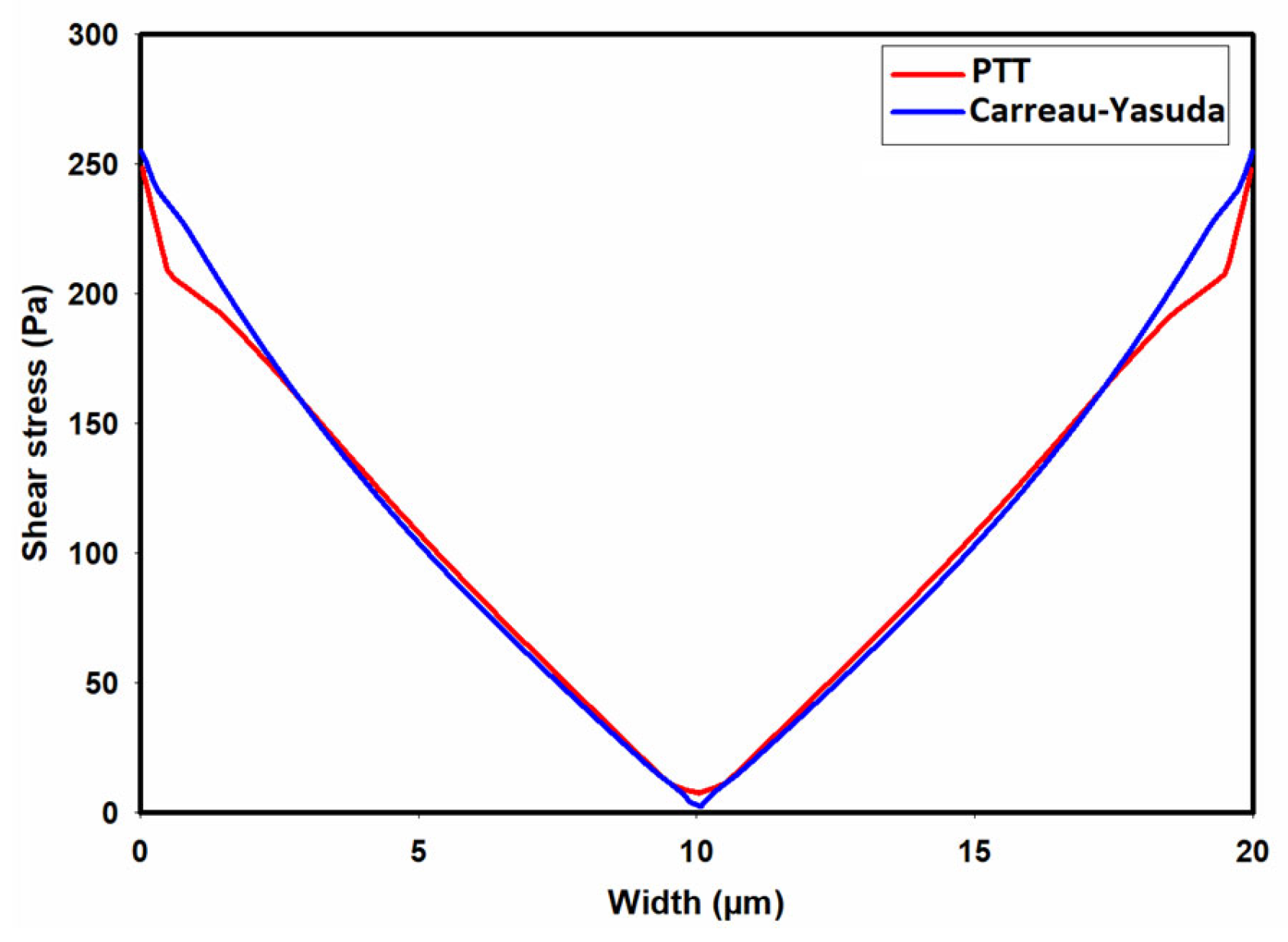
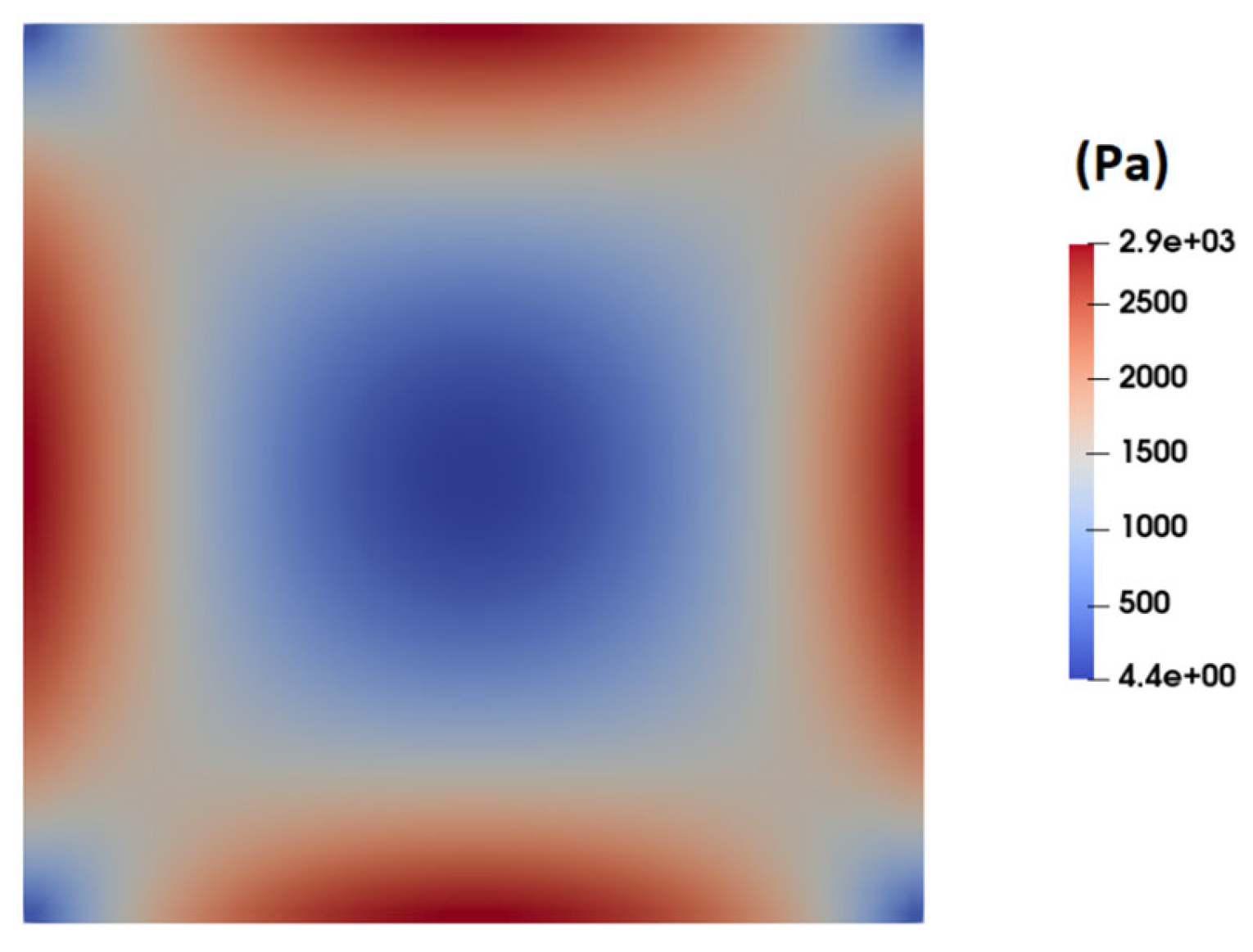
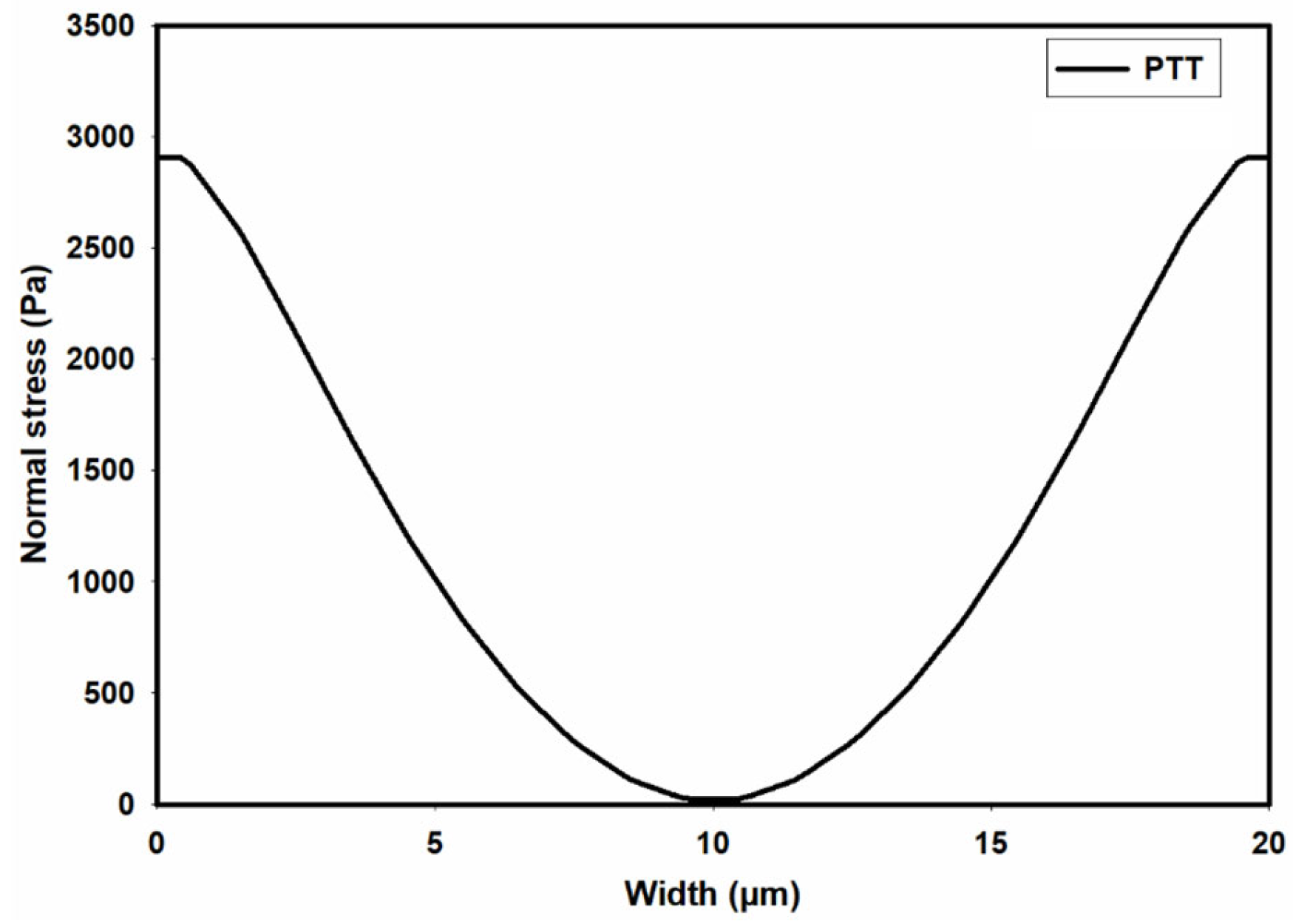
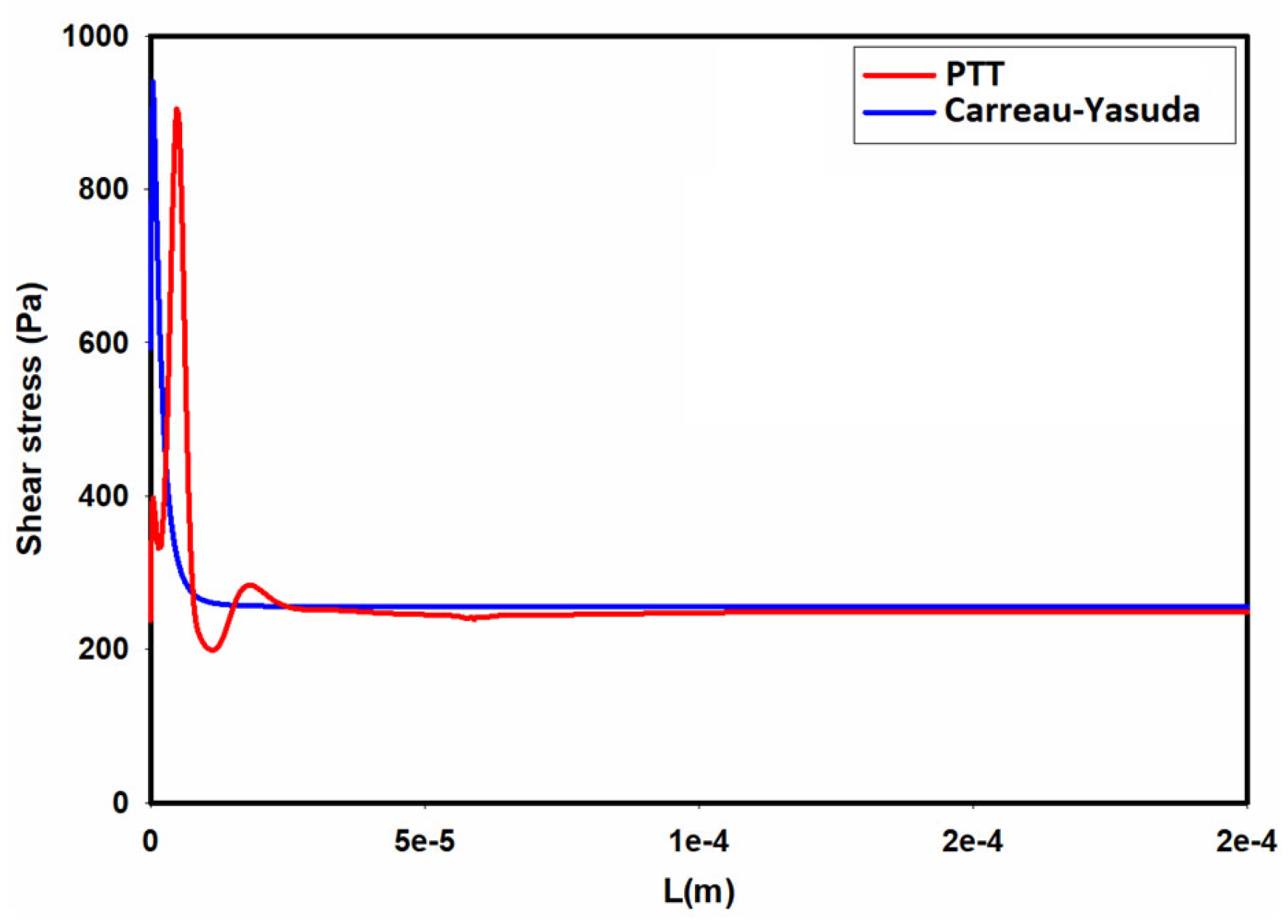
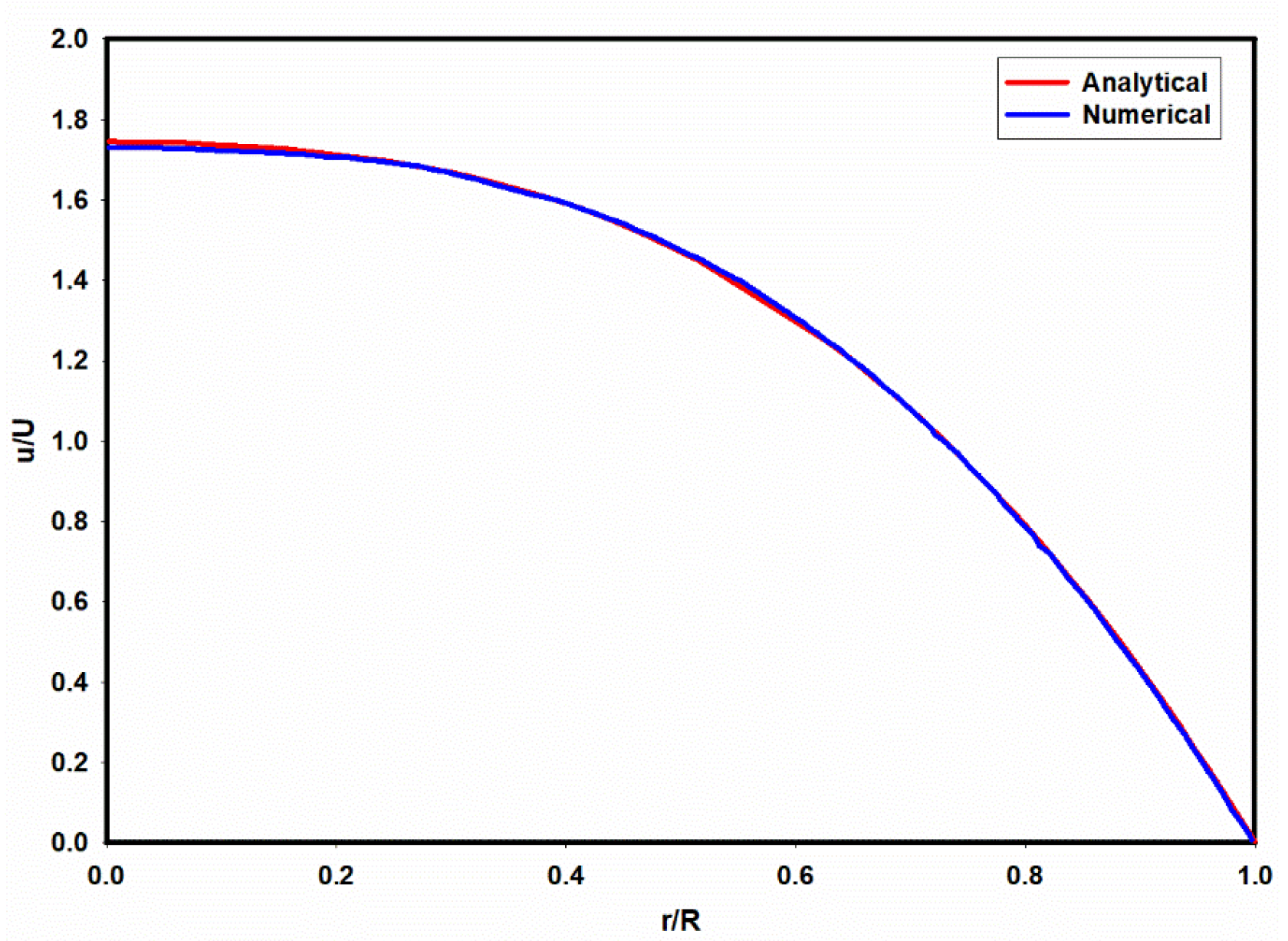
3.1. Flow Field in the Microchannel Conveying the Single-Phase MC-PBS Solution
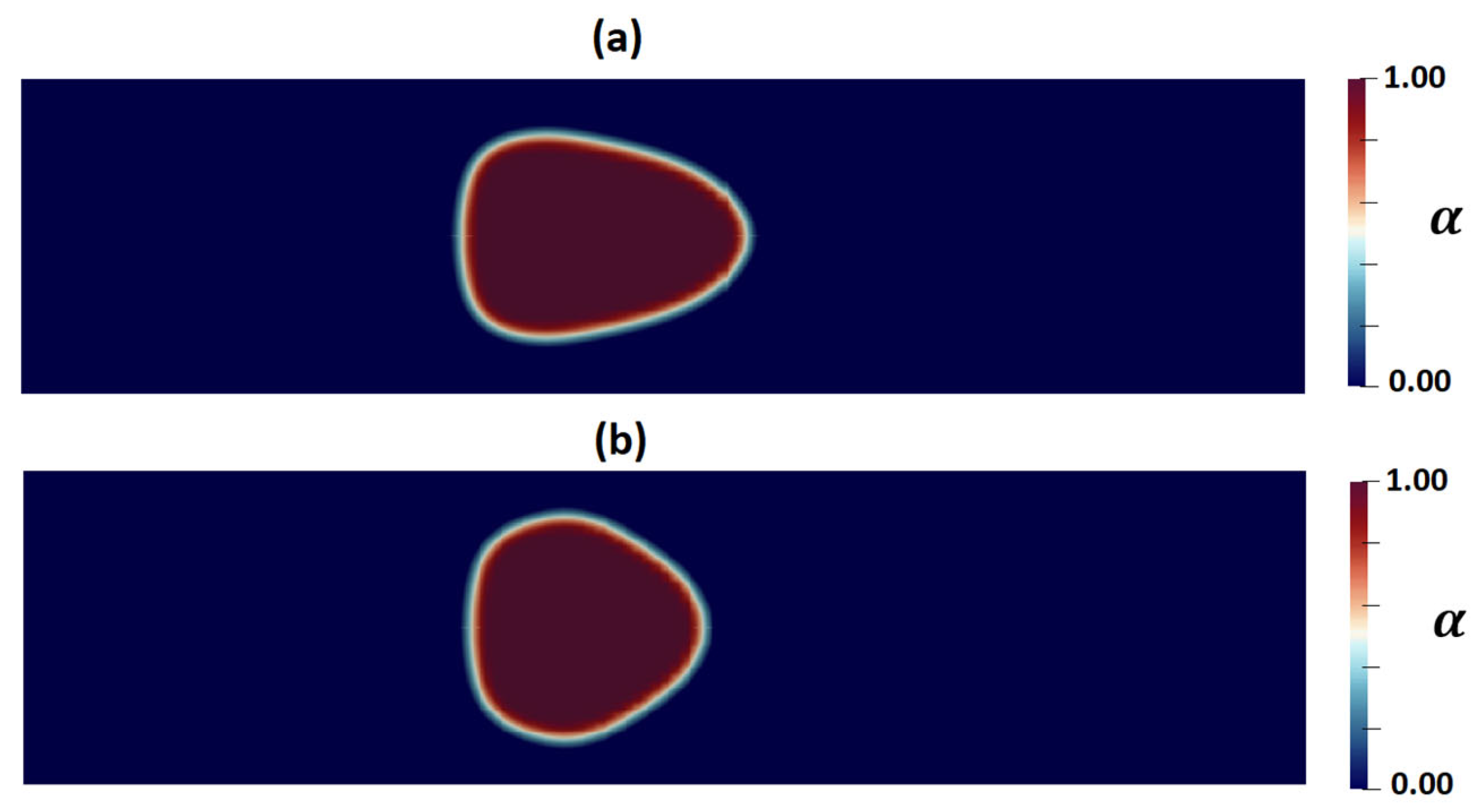
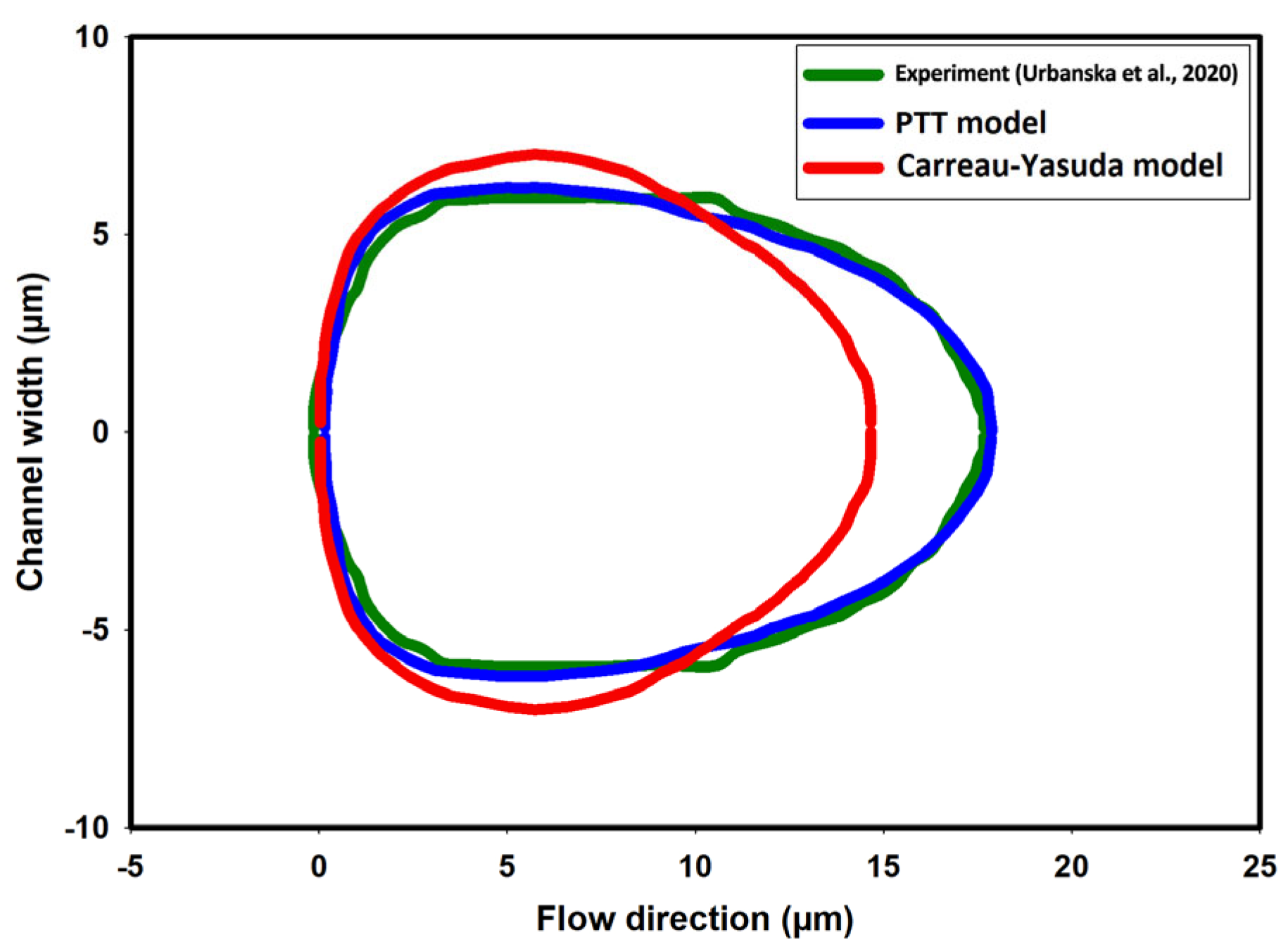
3.2. Numerical Modeling of Cell Deformation in a Hydrodynamic Constriction Channel
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nematbakhsh, Y.; Lim, C.T. Cell biomechanics and its applications in human disease diagnosis. Acta Mech. Sin. 2015, 31, 268–273. [Google Scholar] [CrossRef]
- Darling, E.M.; Di Carlo, D. High-throughput assessment of cellular mechanical properties. Annu. Rev. Biomed. Eng. 2015, 17, 35–62. [Google Scholar] [CrossRef] [PubMed]
- Otto, O.; Rosendahl, P.; Mietke, A.; Golfier, S.; Herold, C.; Klaue, D.; Girardo, S.; Pagliara, S.; Ekpenyong, A.; Jacobi, A.; et al. Real-time deformability cytometry: On-the-fly cell mechanical phenotyping. Nat. Methods 2015, 12, 199–202. [Google Scholar] [CrossRef]
- Guck, J.; Schinkinger, S.; Lincoln, B.; Wottawah, F.; Ebert, S.; Romeyke, M.; Lenz, D.; Erickson, H.M.; Ananthakrishnan, R.; Mitchell, D.; et al. Optical deformability as an inherent cell marker for testing malignant transformation and metastatic competence. Biophys. J. 2005, 88, 3689–3698. [Google Scholar] [CrossRef] [PubMed]
- Swaminathan, V.; Mythreye, K.; O’Brien, E.T.; Berchuck, A.; Blobe, G.C.; Superfine, R. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res. 2011, 71, 5075–5080. [Google Scholar] [CrossRef] [PubMed]
- Tse, H.T.K.; Gossett, D.R.; Moon, Y.S.; Masaeli, M.; Sohsman, M.; Ying, Y.; Mislick, K.; Adams, R.P.; Rao, J.; Di Carlo, D. Quantitative diagnosis of malignant pleural effusions by single-cell mechanophenotyping. Sci. Transl. Med. 2013, 5, 212ra163. [Google Scholar] [CrossRef]
- Bufi, N.; Saitakis, M.; Dogniaux, S.; Buschinger, O.; Bohineust, A.; Richert, A.; Maurin, M.; Hivroz, C.; Asnacios, A. Human primary immune cells exhibit distinct mechanical properties that are modified by inflammation. Biophys. J. 2015, 108, 2181–2190. [Google Scholar] [CrossRef]
- Bashant, K.R.; Vassallo, A.; Herold, C.; Berner, R.; Menschner, L.; Subburayalu, J.; Kaplan, M.J.; Summers, C.; Guck, J.; Chilvers, E.R.; et al. Real-time deformability cytometry reveals sequential contraction and expansion during neutrophil priming. J. Leukoc. Biol. 2019, 105, 1143–1153. [Google Scholar] [CrossRef]
- Ekpenyong, A.E.; Whyte, G.; Chalut, K.; Pagliara, S.; Lautenschläger, F.; Fiddler, C.; Paschke, S.; Keyser, U.F.; Chilvers, E.R.; Guck, J. Viscoelastic Properties of Differentiating Blood Cells Are Fate- and Function-Dependent. PLoS ONE 2012, 7, e45237. [Google Scholar] [CrossRef]
- Lin, J.; Kim, D.; Tse, H.T.; Tseng, P.; Peng, L.; Dhar, M.; Karumbayaram, S.; Di Carlo, D. High-throughput physical phenotyping of cell differentiation. Microsyst. Nanoeng. 2017, 3, 17013. [Google Scholar] [CrossRef]
- Guck, J.; Ananthakrishnan, R.; Mahmood, H.; Moon, T.J.; Cunningham, C.C.; Käs, J. The optical stretcher: A novel laser tool to micromanipulate cells. Biophys. J. 2001, 81, 767–784. [Google Scholar] [CrossRef] [PubMed]
- Radmacher, M. Studying the mechanics of cellular processes by atomic force microscopy. Methods Cell Biol. 2007, 83, 347–372. [Google Scholar] [CrossRef] [PubMed]
- Hochmuth, R.M. Micropipette aspiration of living cells. J. Biomech. 2000, 33, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Thoumine, O.; Ott, A.; Cardoso, O.; Meister, J.J. Microplates: A new tool for manipulation and mechanical perturbation of individual cells. J. Biochem. Biophys. Methods 1999, 39, 47–62. [Google Scholar] [CrossRef] [PubMed]
- Lange, J.R.; Steinwachs, J.; Kolb, T.; Lautscham, L.A.; Harder, I.; Whyte, G.; Fabry, B. Microconstriction arrays for high-throughput quantitative measurements of cell mechanical properties. Biophys. J. 2015, 109, 26–34. [Google Scholar] [CrossRef] [PubMed]
- Nyberg, K.D.; Hu, K.H.; Kleinman, S.H.; Khismatullin, D.B.; Butte, M.J.; Rowat, A.C. Quantitative deformability cytometry: Rapid, calibrated measurements of cell mechanical properties. Biophys. J. 2017, 113, 1574–1584. [Google Scholar] [CrossRef] [PubMed]
- Gossett, D.R.; Tse, H.T.K.; Lee, S.A.; Ying, Y.; Lindgren, A.G.; Yang, O.O.; Rao, J.; Clark, A.T.; Di Carlo, D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA 2012, 109, 7630–7635. [Google Scholar] [CrossRef]
- Urbanska, M.; Muñoz, H.E.; Shaw Bagnall, J.; Otto, O.; Manalis, S.R.; Di Carlo, D.; Guck, J. A comparison of microfluidic methods for high-throughput cell deformability measurements. Nat. Methods 2020, 17, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Nawaz, A.A.; Urbanska, M.; Herbig, M.; Nötzel, M.; Kräter, M.; Rosendahl, P.; Herold, C.; Toepfner, N.; Kubankova, M.; Goswami, R.; et al. Using real-time fluorescence and deformability cytometry and deep learning to transfer molecular specificity to label-free sorting. bioRxiv 2019. [Google Scholar] [CrossRef]
- Rosendahl, P.; Plak, K.; Jacobi, A.; Kraeter, M.; Toepfner, N.; Otto, O.; Herold, C.; Winzi, M.; Herbig, M.; Ge, Y.; et al. Real-time fluorescence and deformability cytometry. Nat. Methods 2018, 15, 355–358. [Google Scholar] [CrossRef]
- Fregin, B.; Czerwinski, F.; Biedenweg, D.; Girardo, S.; Gross, S.; Aurich, K.; Otto, O. High-throughput single-cell rheology in complex samples by dynamic real-time deformability cytometry. Nat. Commun. 2019, 10, 415. [Google Scholar] [CrossRef]
- Fregin, B.; Czerwinski, F.; Biedenweg, D.; Girardo, S.; Gross, S.; Aurich, K.; Otto, O. Extracting cell stiffness from real-time deformability cytometry: Theory and experiment. Biophys. J. 2015, 109, 2023–2036. [Google Scholar] [CrossRef]
- Mokbel, M.; Mokbel, D.; Mietke, A.; Träber, N.; Girardo, S.; Otto, O.; Guck, J.; Aland, S. Numerical simulation of real-time deformability cytometry to extract cell mechanical properties. ACS Biomater. Sci. Eng. 2017, 3, 2962–2973. [Google Scholar] [CrossRef] [PubMed]
- Guillou, L.; Dahl, J.B.; Lin, J.M.G.; Barakat, A.I.; Husson, J.; Muller, S.J.; Kumar, S. Measuring cell viscoelastic properties using a microfluidic extensional flow device. Biophys. J. 2016, 111, 2039–2050. [Google Scholar] [CrossRef] [PubMed]
- Armistead, F.J.; De Pablo, J.G.; Gadêlha, H.; Peyman, S.A.; Evans, S.D. Cells under stress: An inertial-shear microfluidic determination of cell behavior. Biophys. J. 2019, 116, 1127–1135. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Lu, R.; Wang, W.; Tian, F.B.; Feng, J.J.; Sui, Y. A computational model for the transit of a cancer cell through a constricted microchannel. Biomech. Model. Mechanobiol. 2023, 22, 1129–1143. [Google Scholar] [CrossRef] [PubMed]
- Büyükurgancı, B.; Basu, S.K.; Neuner, M.; Guck, J.; Wierschem, A.; Reichel, F. Shear rheology of methyl cellulose based solutions for cell mechanical measurements at high shear rates. Soft Matter 2023, 19, 1739–1748. [Google Scholar] [CrossRef] [PubMed]
- Urbanska, M. Single-Cell Mechanical Phenotyping Across Timescales and Cell State Transitions. Doctor Dissertation, Technische Universität Dresden, Dresden, Germany, 2022. Available online: https://nbn-resolving.org/urn:nbn:de:bsz:14-qucosa2-775638 (accessed on 1 February 2024).
- Wu, P.-H.; Raz-Ben Aroush, D.; Asnacios, A.; Chen, W.-C.; Dokukin, M.E.; Doss, B.L.; Durand-Smet, P.; Ekpenyong, A.; Guck, J.; Guz, N.V.; et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 2018, 15, 491–498. [Google Scholar] [CrossRef] [PubMed]
- Thien, N.P.; Tanner, R.I. A new constitutive equation derived from network theory. J. Non-Newton. Fluid Mech. 1977, 2, 353–365. [Google Scholar] [CrossRef]
- Alves, M.A.; Oliveira, P.J.; Pinho, F.T. Numerical methods for viscoelastic fluid flows. Annu. Rev. Fluid Mech. 2021, 53, 509–541. [Google Scholar] [CrossRef]
- Cruz, D.O.A.; Pinho, F.; Oliveira, P.J. Analytical solutions for fully developed laminar flow of some viscoelastic liquids with a Newtonian solvent contribution. J. Non-Newton. Fluid Mech. 2005, 132, 28–35. [Google Scholar] [CrossRef]
- Azaiez, J.; Guénette, R.; Ait-Kadi, A. Numerical simulation of viscoelastic flows through a planar contraction. J. Non-Newton. Fluid Mech. 1996, 62, 253–277. [Google Scholar] [CrossRef]
- Lizarraga-Garcia, E.; Buongiorno, J.; Al-Safran, E.; Lakehal, D. A broadly-applicable unified closure relation for Taylor bubble rise velocity in pipes with stagnant liquid. Int. J. Multiphase Flow 2017, 89, 345–358. [Google Scholar] [CrossRef]
- Caviezel, D.; Narayanan, C.; Lakehal, D. Adherence and bouncing of liquid droplets impacting on dry surfaces. Microfluid. Nanofluid. 2008, 5, 469–478. [Google Scholar] [CrossRef]
- Lakehal, D.; Larrignon, G.; Narayanan, C. Computational heat transfer and two-phase flow topology in miniature tubes. Microfluid. Nanofluid. 2008, 4, 261–271. [Google Scholar] [CrossRef]
- Available online: https://transat-cfd.com/ (accessed on 1 February 2024).
- Lakehal, D.; Meier, M.; Fulgosi, M. Interface tracking towards the direct simulation of heat and mass transfer in multiphase flows. Int. J. Heat Fluid Flow 2002, 23, 242–257. [Google Scholar] [CrossRef]
- Suzuki, T.; Kalyan, S.; Berlinicke, C.; Yoseph, S.; Zack, D.J.; Hur, S.C. Deciphering viscoelastic cell manipulation in rectangular microchannels. Phys. Fluids 2023, 35, 103117. [Google Scholar] [CrossRef]
- Pouraria, H.; Foudazi, R.; Houston, J.P. Exploitation of elasto-inertial fluid flow for the separation of nano-sized particles: Simulating the isolation of extracellular vesicles. Cytom. Part A 2023, 103, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Poryles, R.; Zenit, R. Encapsulation of droplets using cusp formation behind a drop rising in a non-Newtonian fluid. Fluids 2018, 3, 54. [Google Scholar] [CrossRef]
- Ohta, M.; Kobayashi, N.; Shigekane, Y.; Yoshida, Y.; Iwata, S. The dynamic motion of single bubbles with unique shapes rising freely in hydrophobically modified alkali-soluble emulsion polymer solutions. J. Rheol. 2015, 59, 303–316. [Google Scholar] [CrossRef]
- Esposito, G.; Dimakopoulos, Y.; Tsamopoulos, J. Buoyancy driven flow of a viscous drop in viscoelastic materials. J. Non-Newton. Fluid Mech. 2023, 321, 105124. [Google Scholar] [CrossRef]
- Poole, R.J. Inelastic and flow-type parameter models for non-Newtonian fluids. J. Non-Newton. Fluid Mech. 2023, 320, 105106. [Google Scholar] [CrossRef]
- Badami, M.M.; Alizadeh, P.; Almasi, S.; Riasi, A.; Sadeghy, K. Numerical study of blood hammer phenomenon considering blood viscoelastic effects. Eur. J. Mech. B/Fluids 2022, 95, 212–220. [Google Scholar] [CrossRef]
- Mirzaaghaian, A.; Ramiar, A.; Ranjbar, A.A.; Warkiani, M.E. Application of level-set method in simulation of normal and cancer cells deformability within a microfluidic device. J. Biomech. 2020, 112, 110066. [Google Scholar] [CrossRef] [PubMed]
- Nooranidoost, M.; Kumar, R. Improving viability of leukemia cells by tailoring shell fluid rheology in constricted microcapillary. Sci. Rep. 2020, 10, 11570. [Google Scholar] [CrossRef]
- Tsai, M.A.; Waugh, R.E.; Keng, P.C. Cell cycle-dependence of HL-60 cell deformability. Biophys. J. 1996, 70, 2023–2029. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rosenbluth, M.J.; Lam, W.A.; Fletcher, D.A. Force microscopy of nonadherent cells: A comparison of leukemia cell deformability. Biophys. J. 2006, 90, 2994–3003. [Google Scholar] [CrossRef]
- Wittwer, L.D.; Reichel, F.; Müller, P.; Guck, J.; Aland, S. A new hyperelastic lookup table for RT-DC. Soft Matter 2023, 19, 2064–2073. [Google Scholar] [CrossRef]
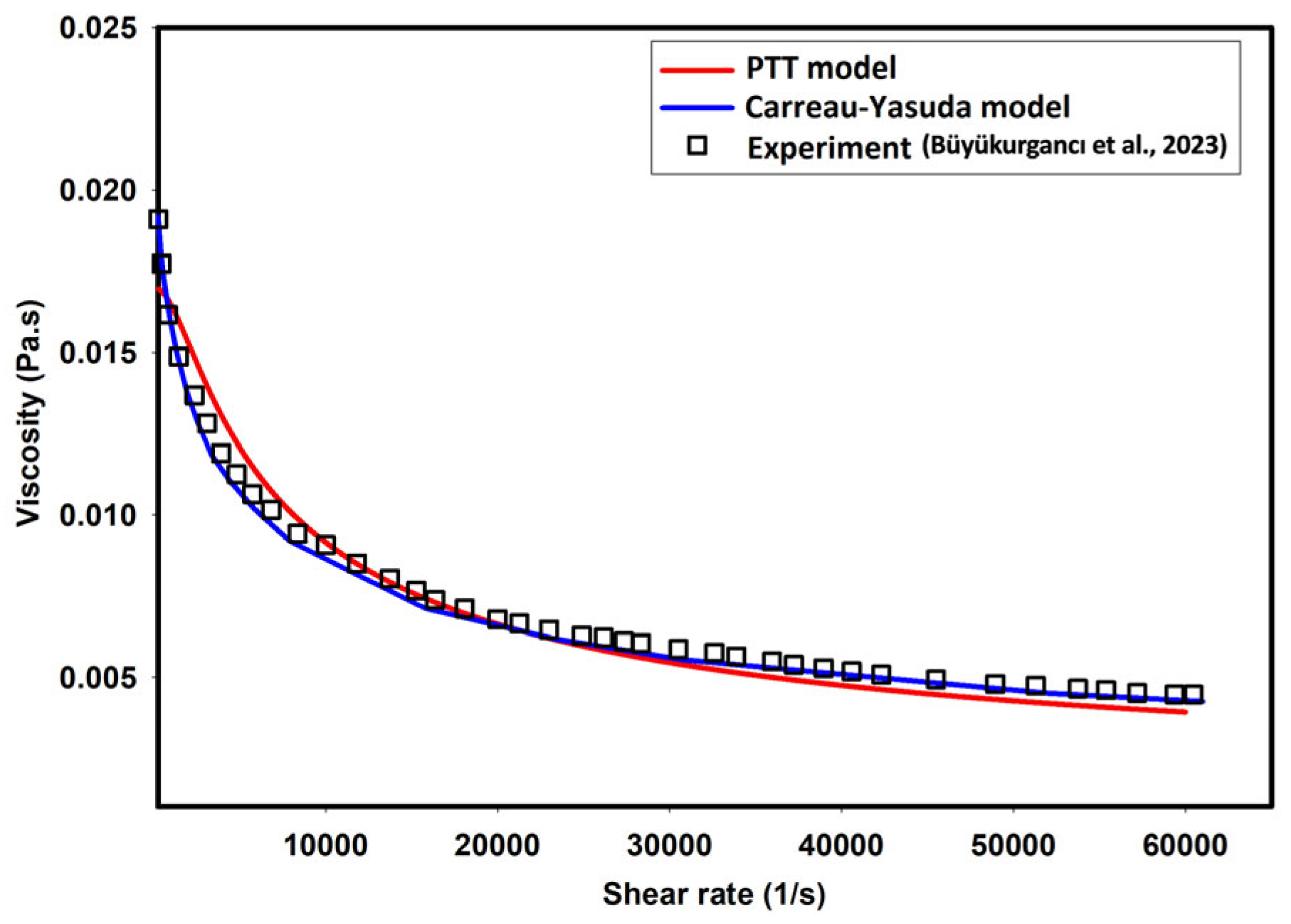









| Fluid | ϻ0 | ϻ∞ | λ | v | α |
|---|---|---|---|---|---|
| 0.5% MC-PBS | 20 mPa.s | 1 mPa.s | 0.0012 | 0.65 | 1.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pouraria, H.; Houston, J.P. Elasticity of Carrier Fluid: A Key Factor Affecting Mechanical Phenotyping in Deformability Cytometry. Micromachines 2024, 15, 822. https://doi.org/10.3390/mi15070822
Pouraria H, Houston JP. Elasticity of Carrier Fluid: A Key Factor Affecting Mechanical Phenotyping in Deformability Cytometry. Micromachines. 2024; 15(7):822. https://doi.org/10.3390/mi15070822
Chicago/Turabian StylePouraria, Hassan, and Jessica P. Houston. 2024. "Elasticity of Carrier Fluid: A Key Factor Affecting Mechanical Phenotyping in Deformability Cytometry" Micromachines 15, no. 7: 822. https://doi.org/10.3390/mi15070822
APA StylePouraria, H., & Houston, J. P. (2024). Elasticity of Carrier Fluid: A Key Factor Affecting Mechanical Phenotyping in Deformability Cytometry. Micromachines, 15(7), 822. https://doi.org/10.3390/mi15070822







