Experimental and Numerical Study on Various Liquid-Cooled Heat Sinks Including Topology Optimization
Abstract
1. Introduction
2. Topology Optimization Design of Heat Sink
2.1. Topology Optimization Model
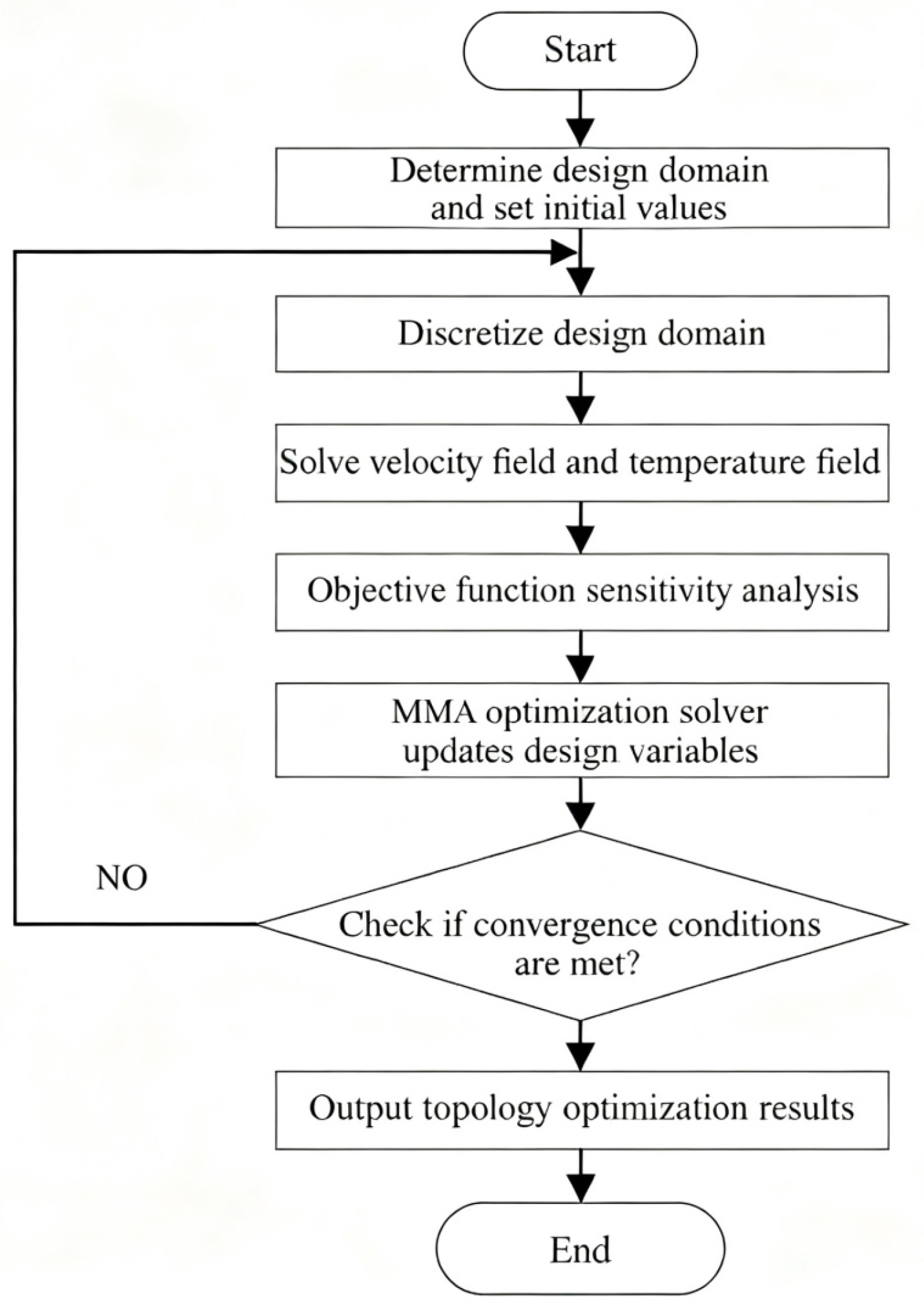
2.2. Computational Methods for Topology Optimization
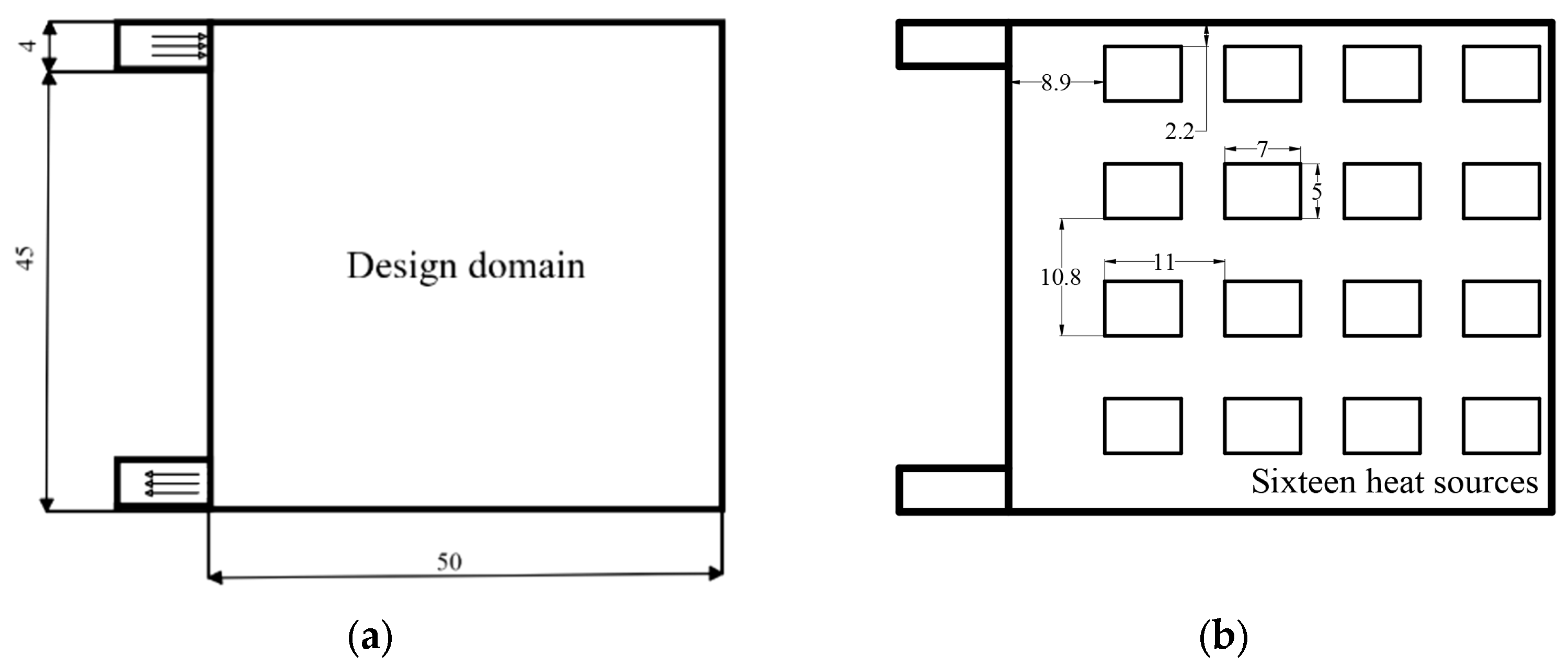
2.2.1. Boundary Conditions
2.2.2. Calculation of Material Interpolation
2.2.3. Density Filtering and Projection
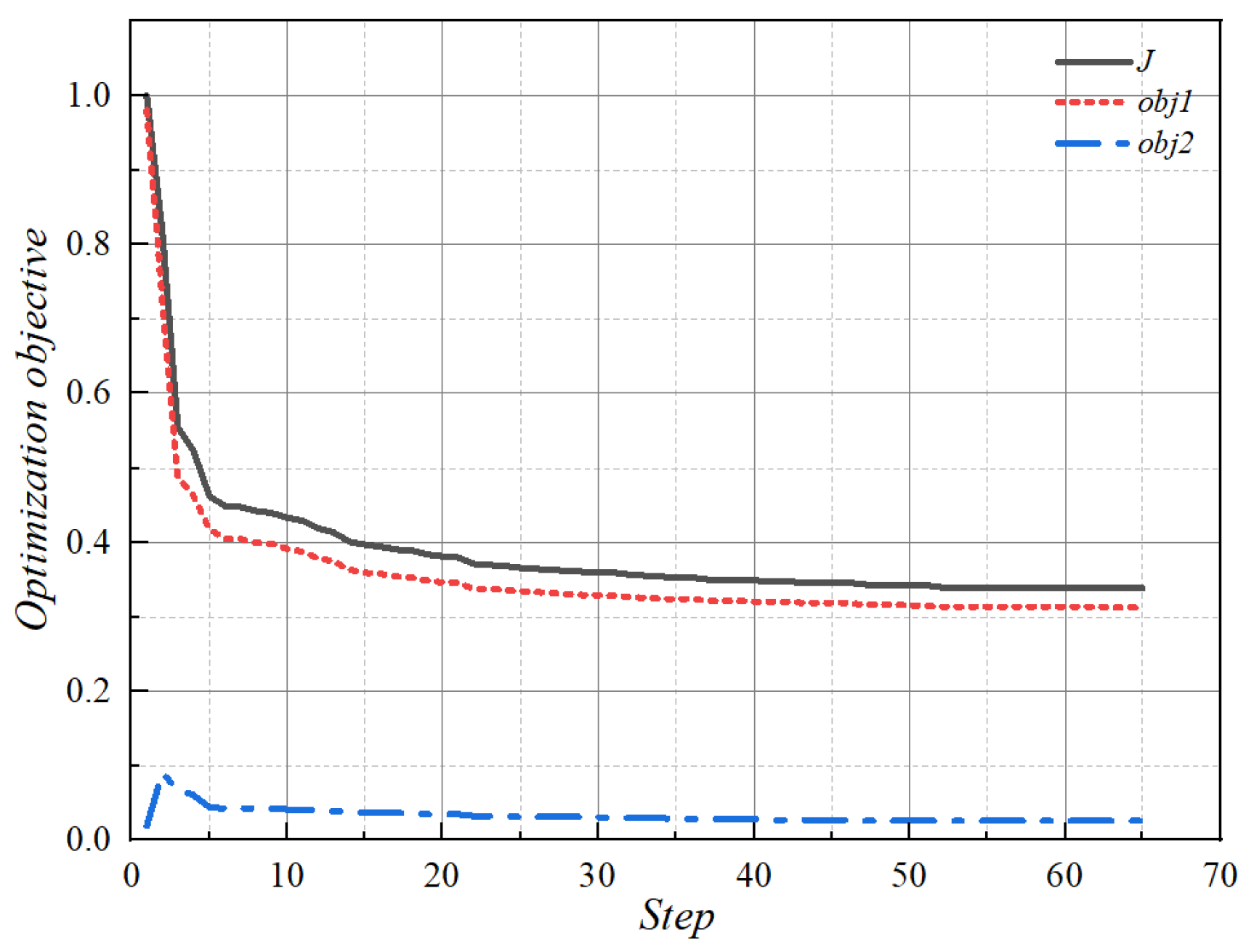
2.2.4. Topology Optimization Objective
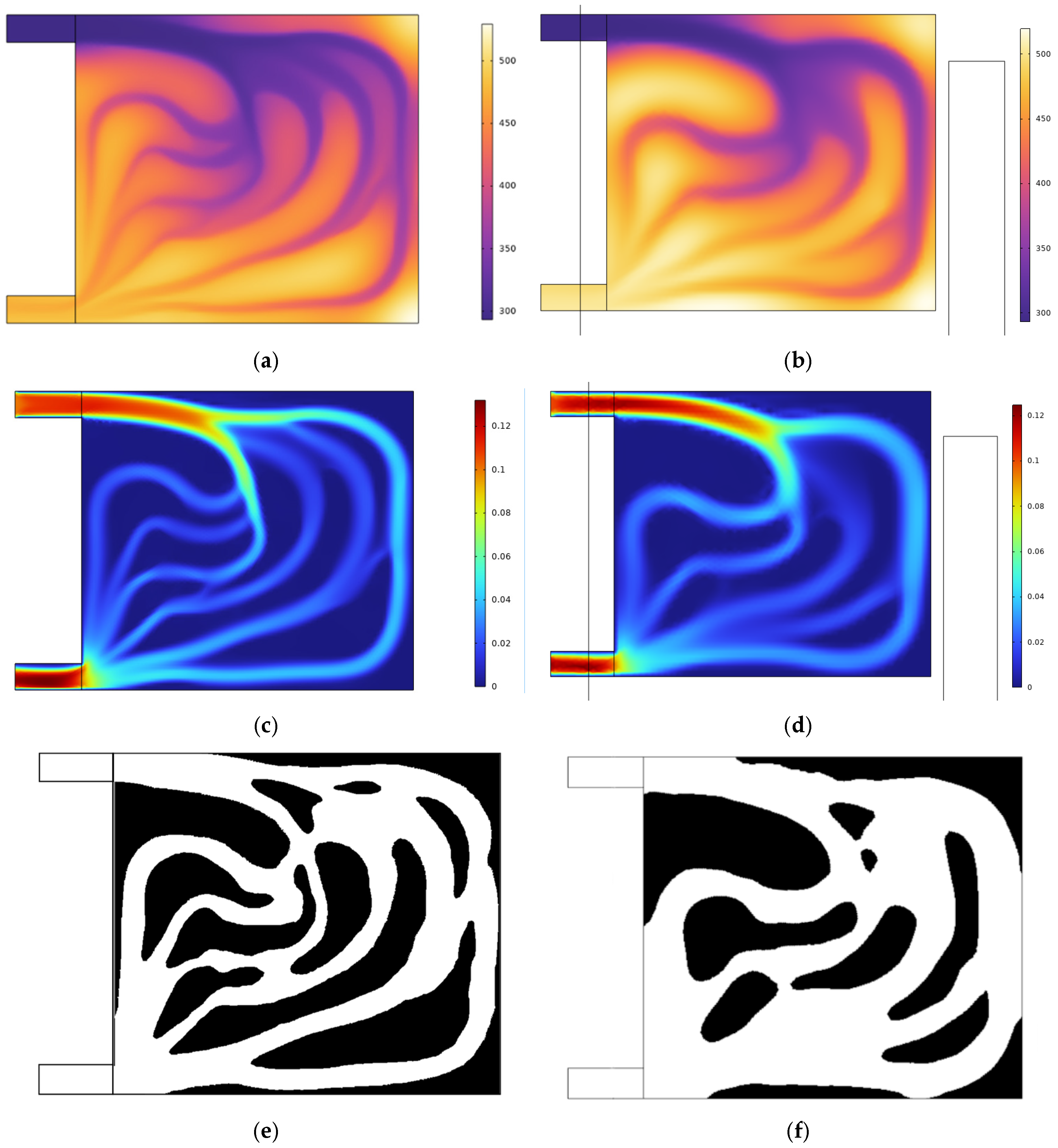
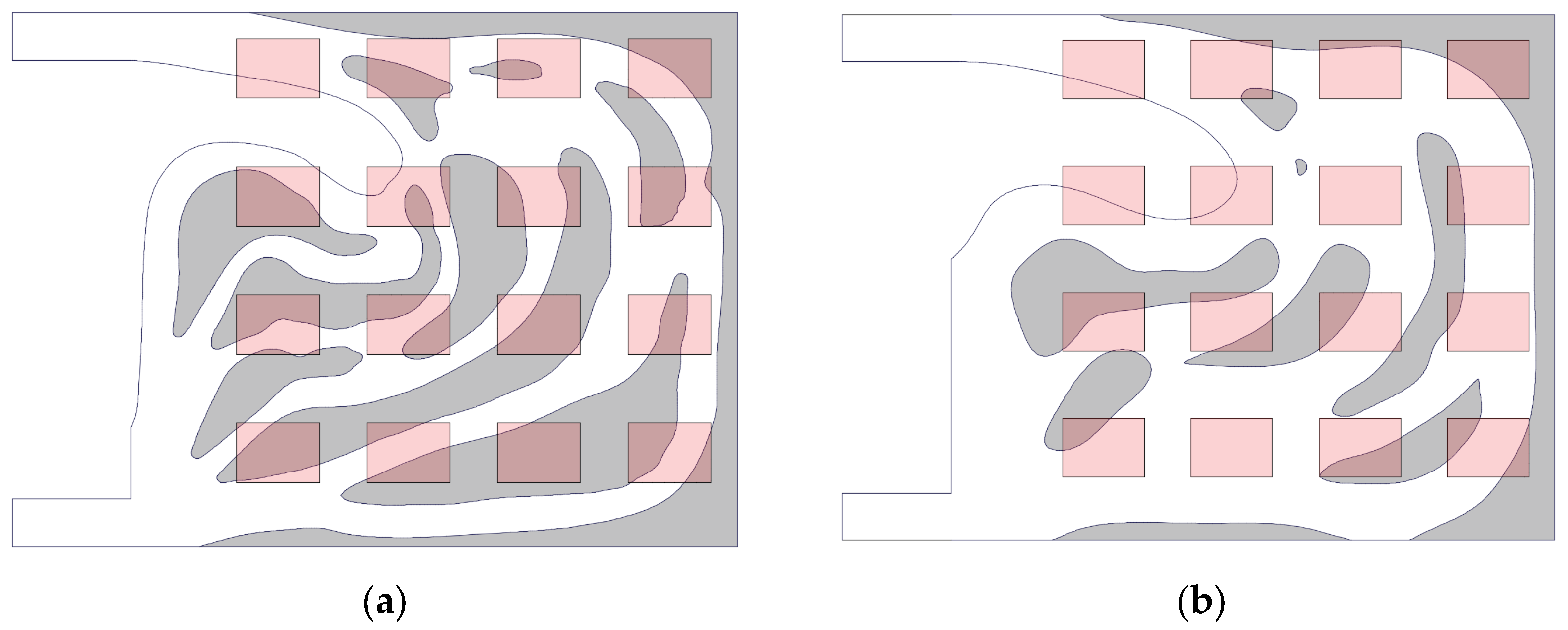
2.3. Topology Optimization Results
3. Numerical Investigation of Liquid-Cooled Heat Sink
3.1. Numerical Modeling and Boundary Conditions
3.2. Mesh Sensitivity Analysis
3.3. Simulation Results
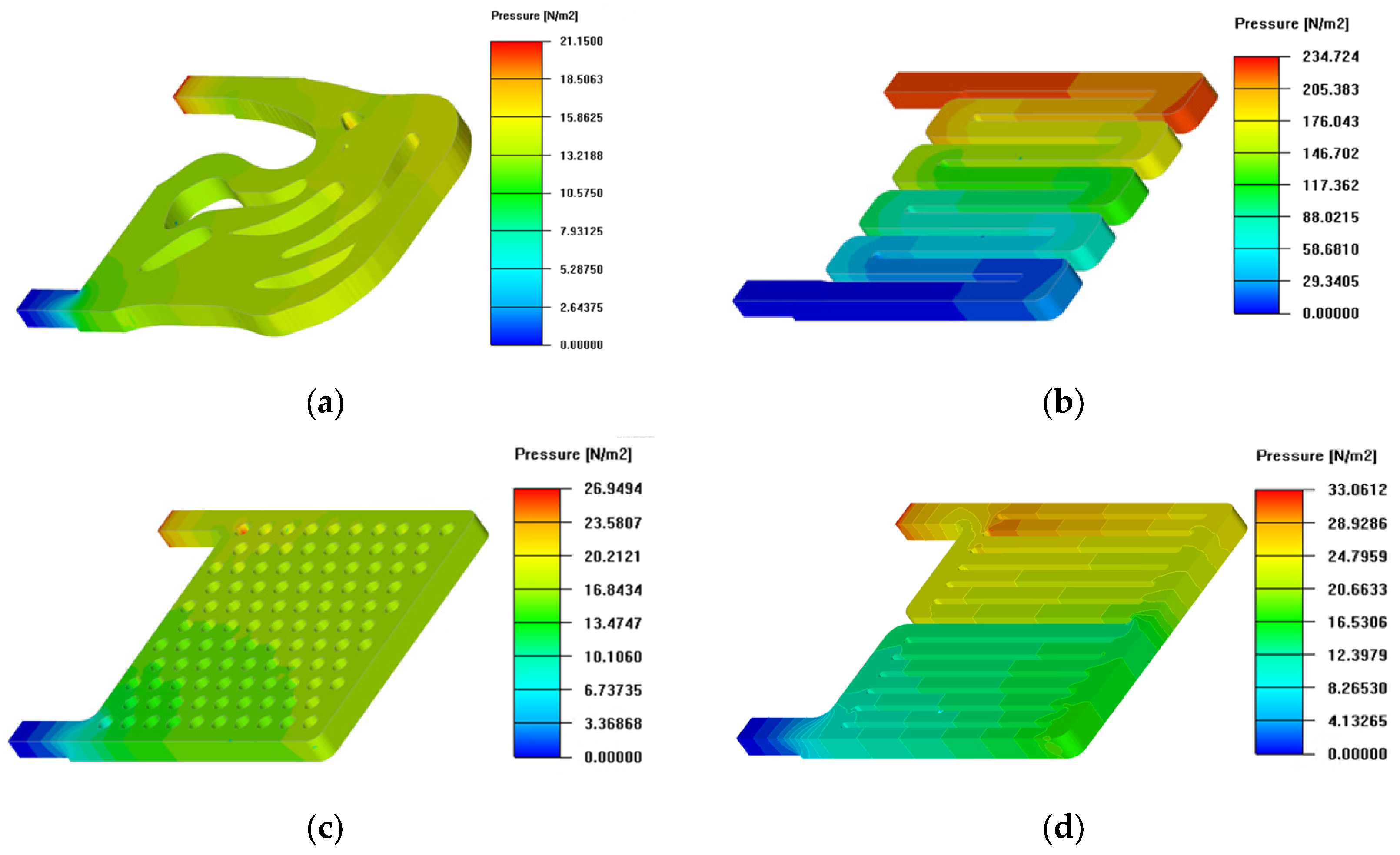
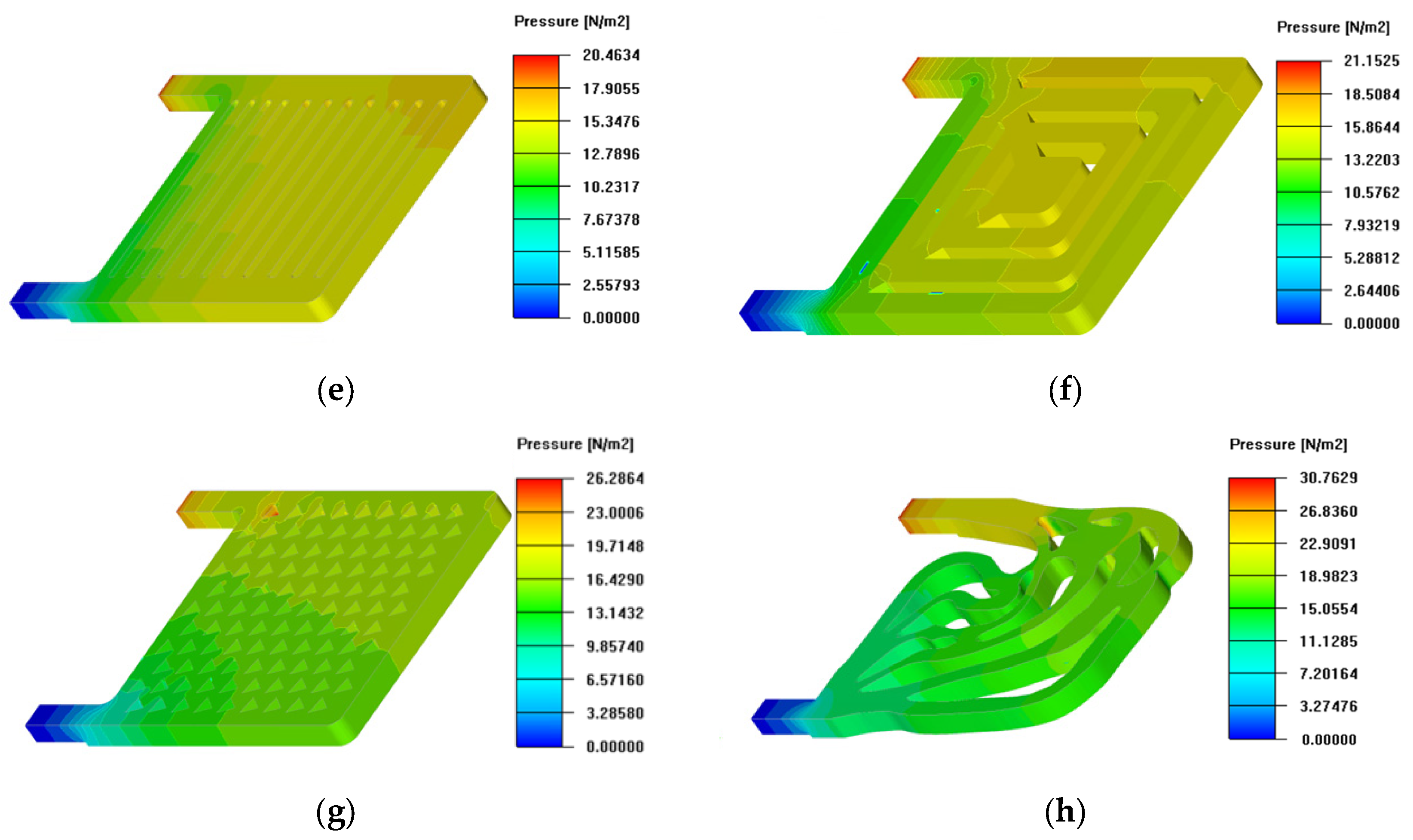
3.3.1. Simulation Results of Heat Dissipation Performance
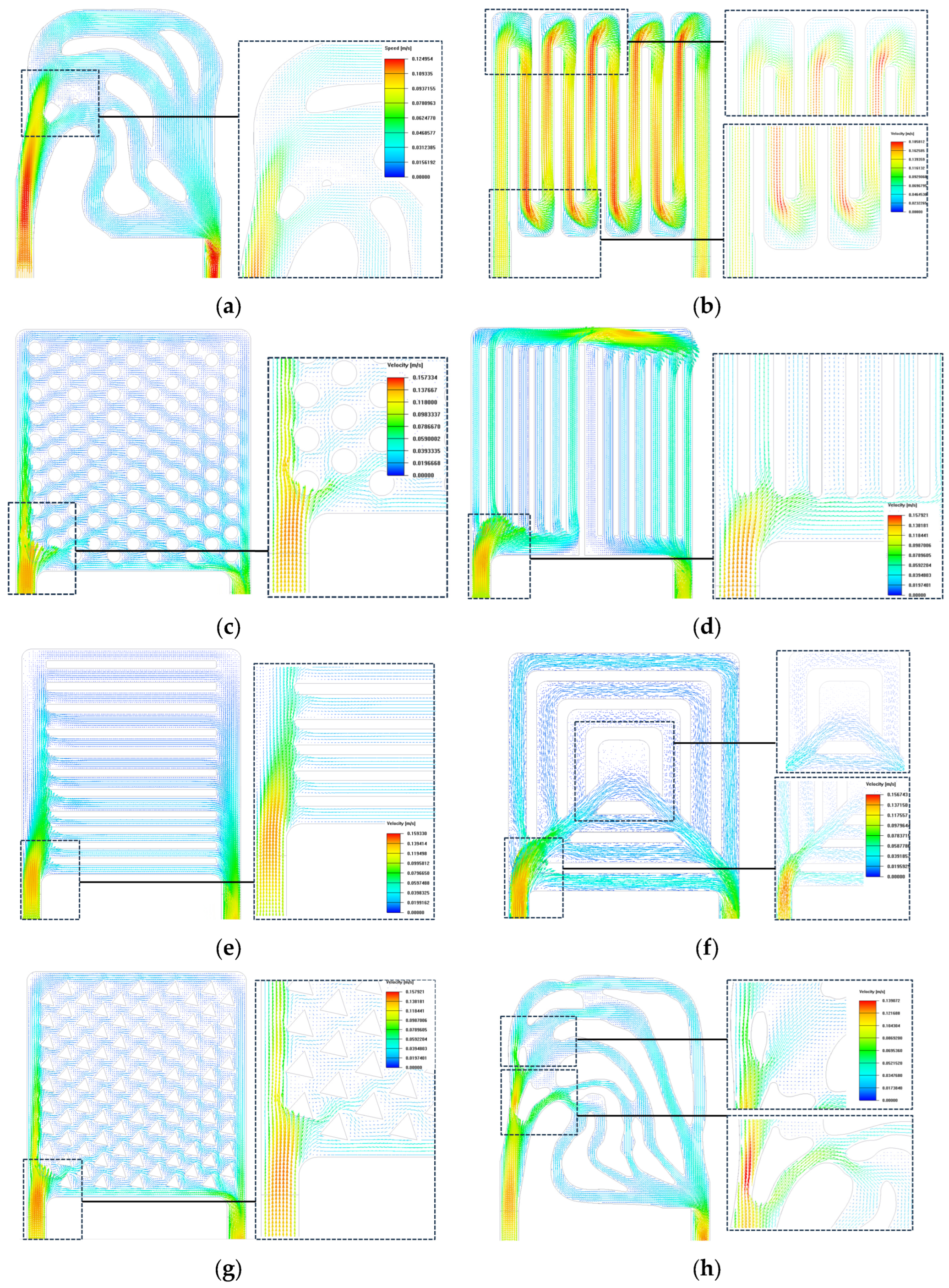
3.3.2. Simulation Results of Fluid Characteristics
4. Experimental Verification
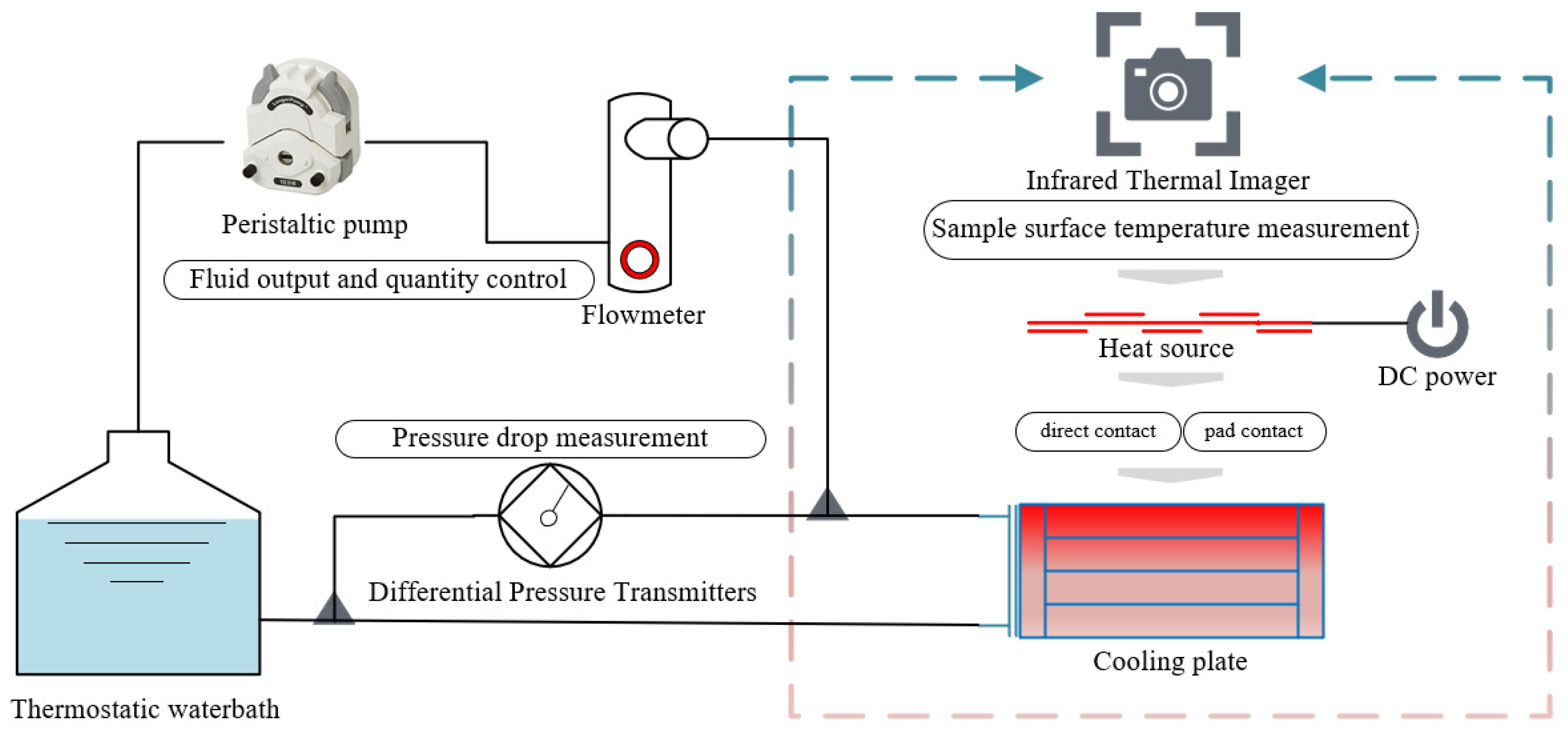
4.1. Experimental Setup
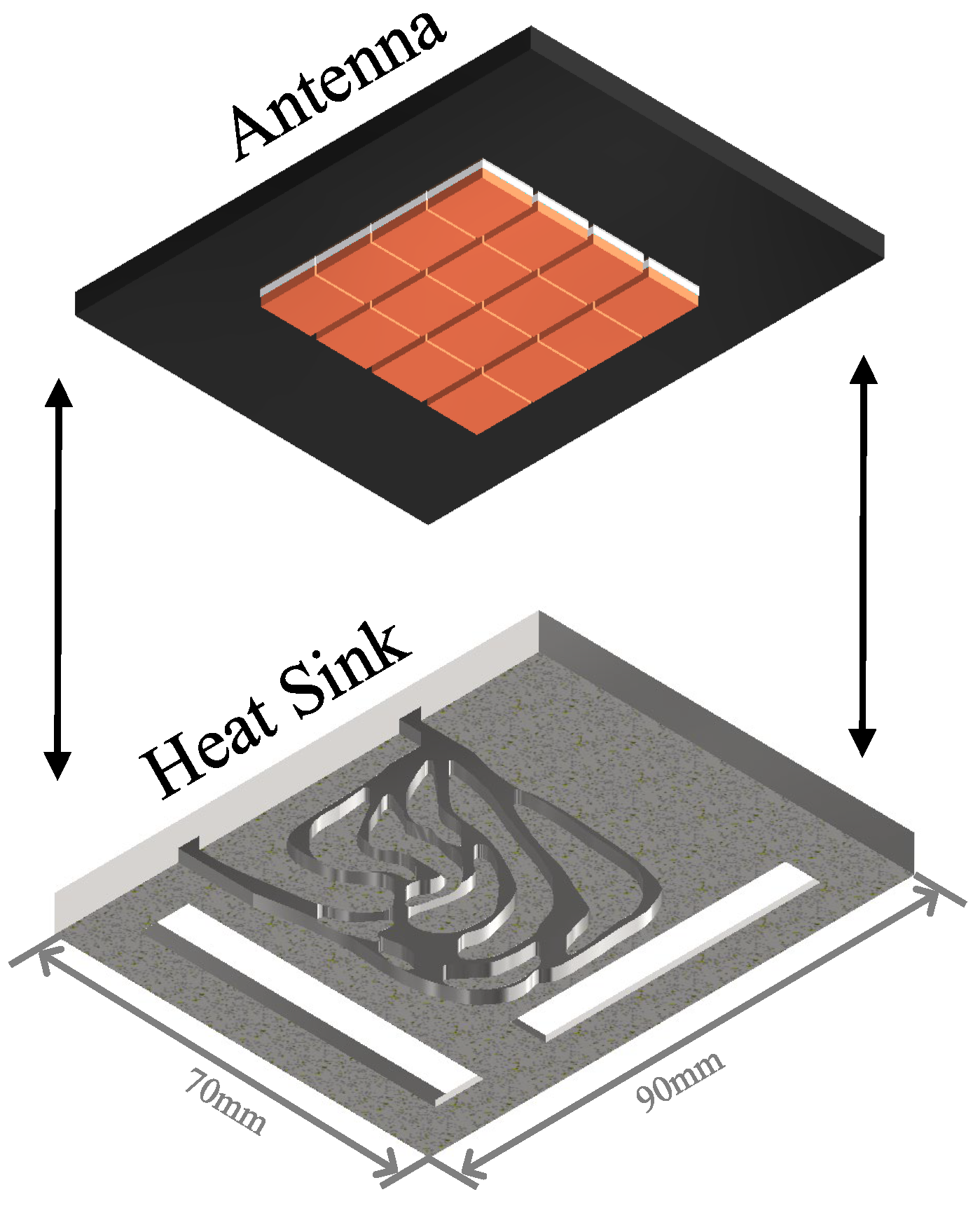
4.1.1. Experimental Platform
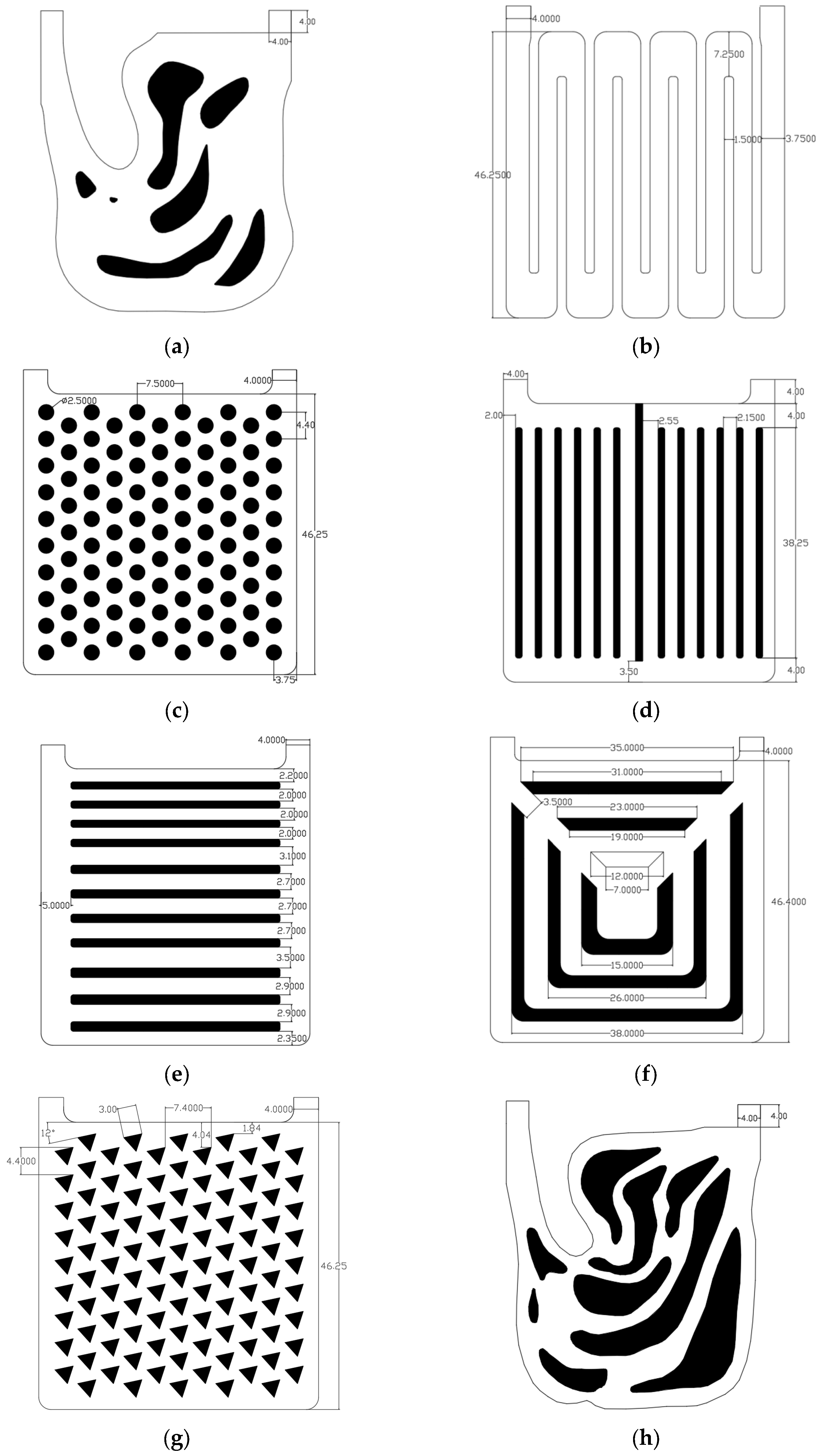
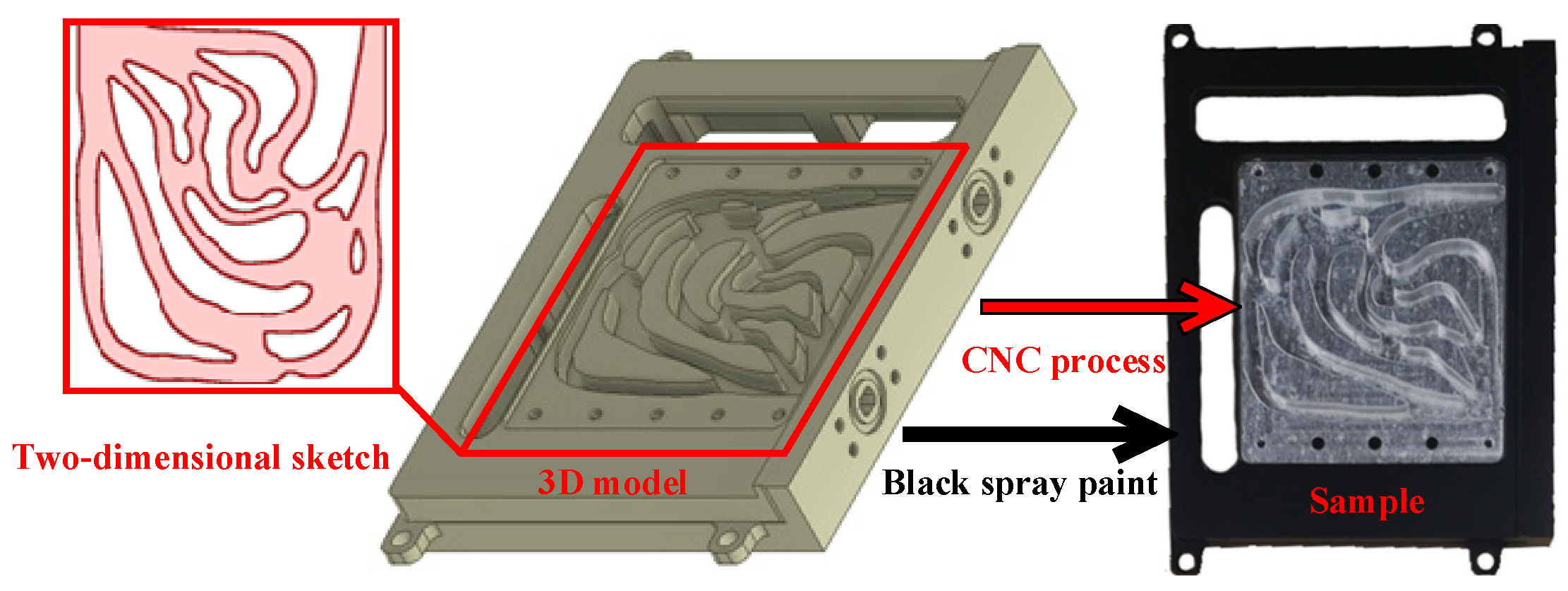
4.1.2. Design and Manufacture of Samples
4.1.3. Obtaining of Experimental Results
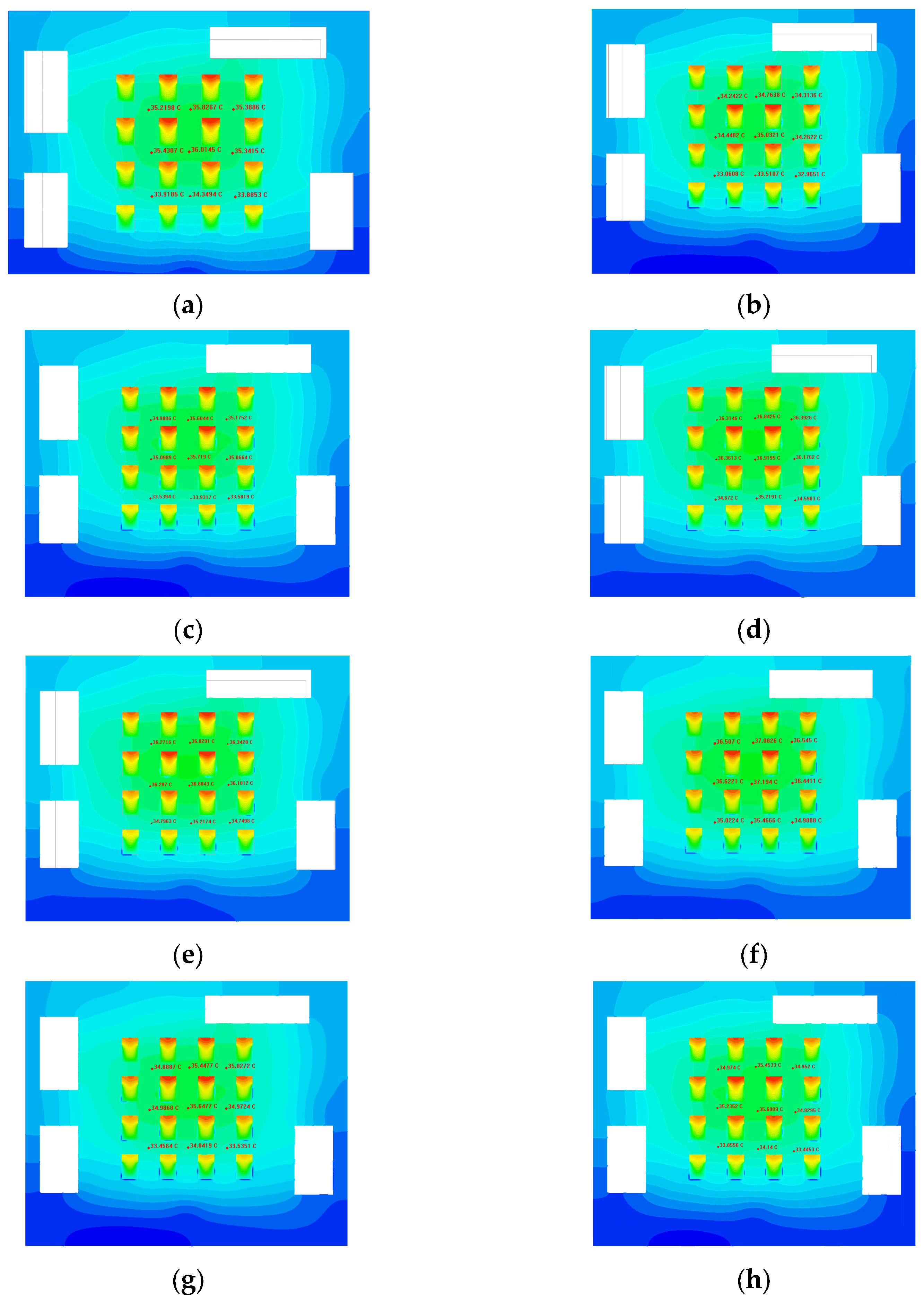
4.2. Experimental Results and Discussion
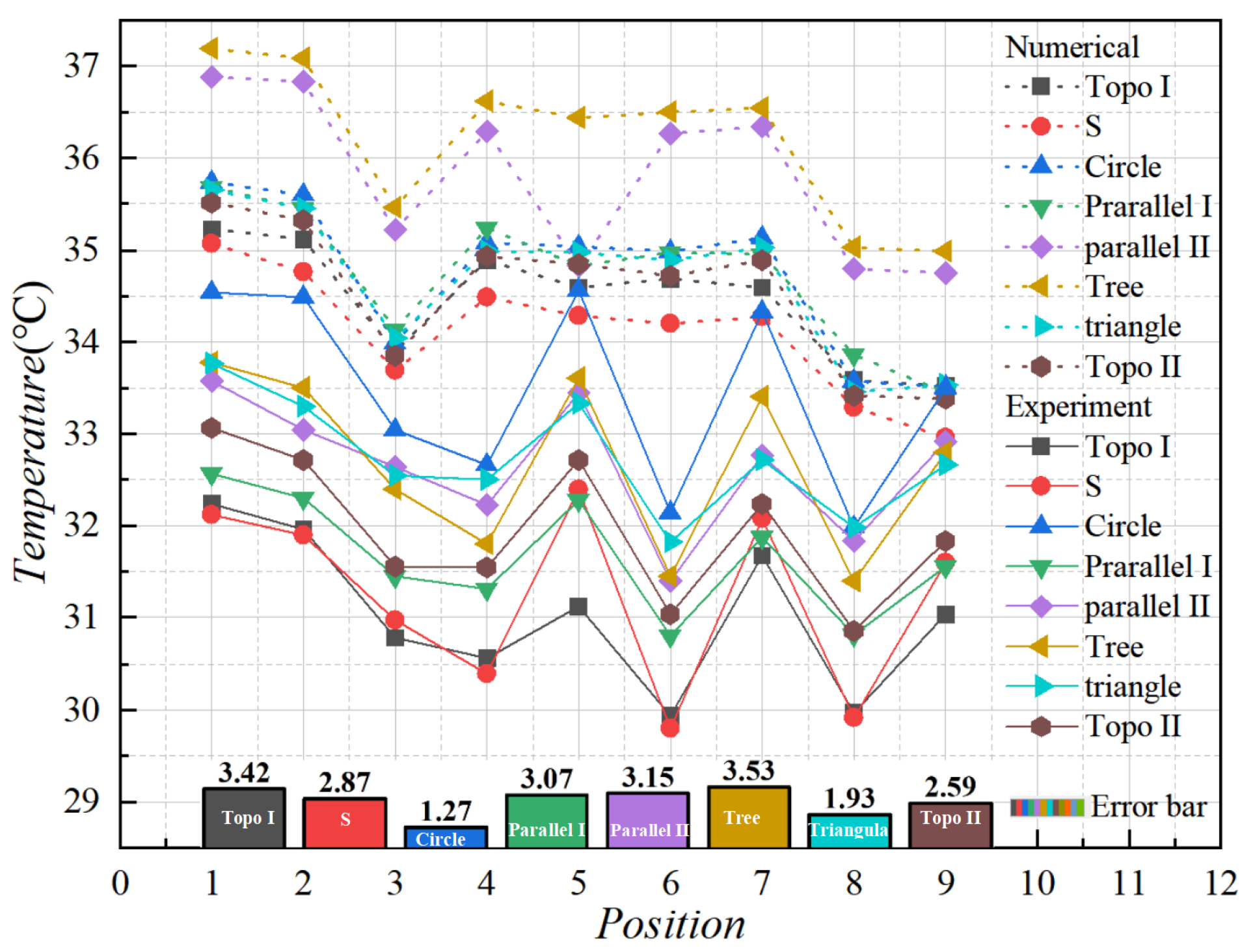
4.2.1. Temperature Results
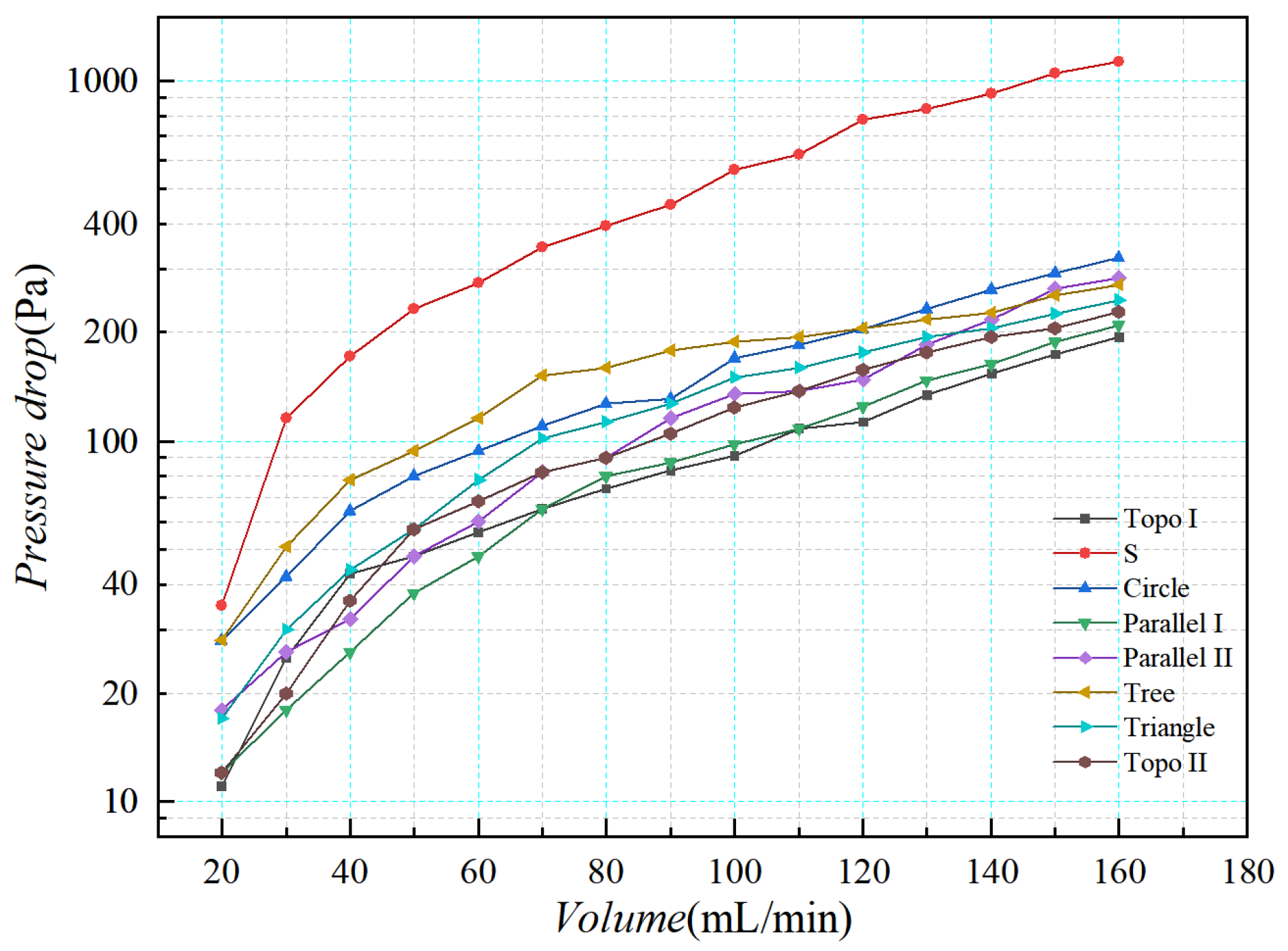
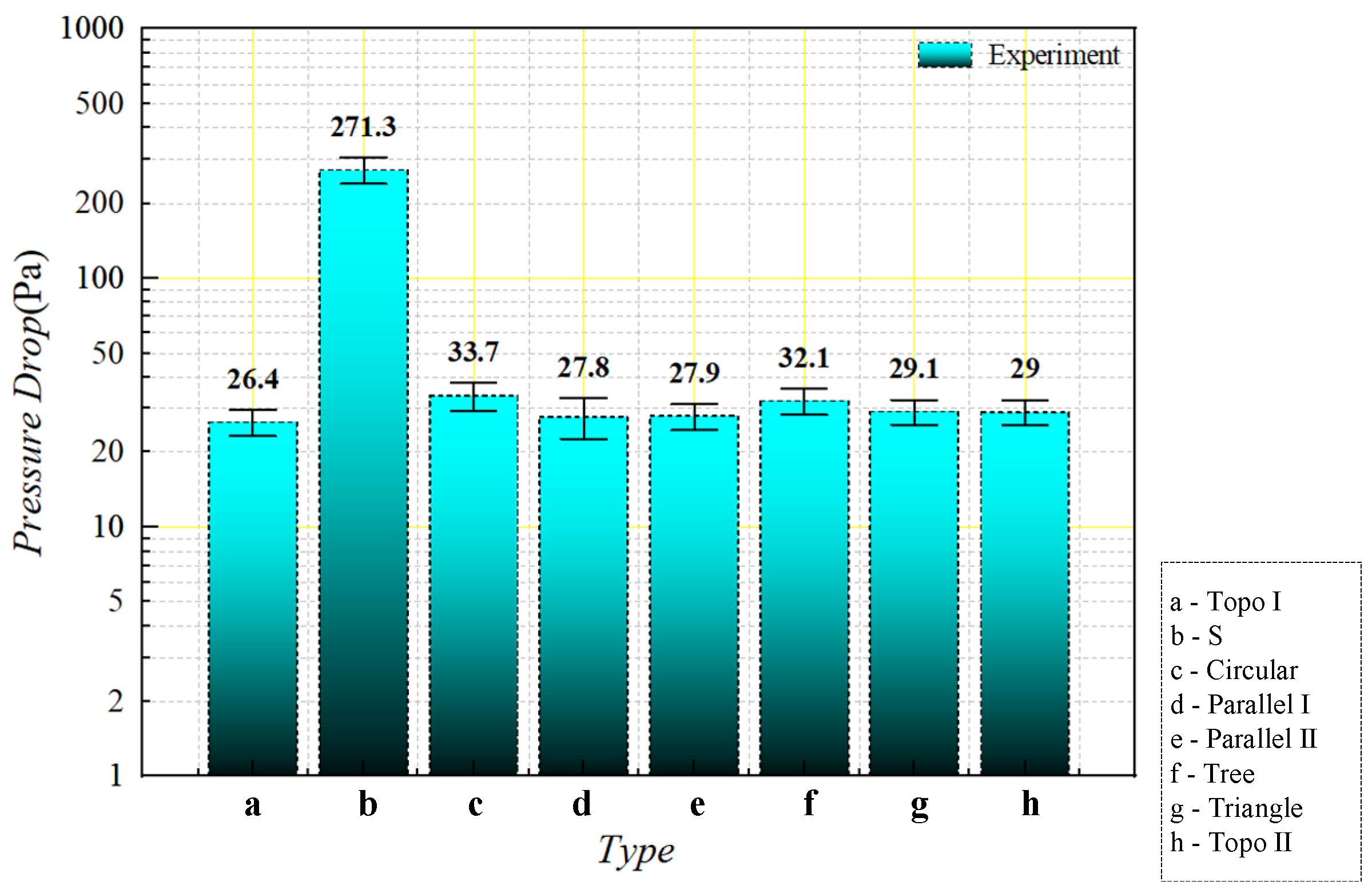
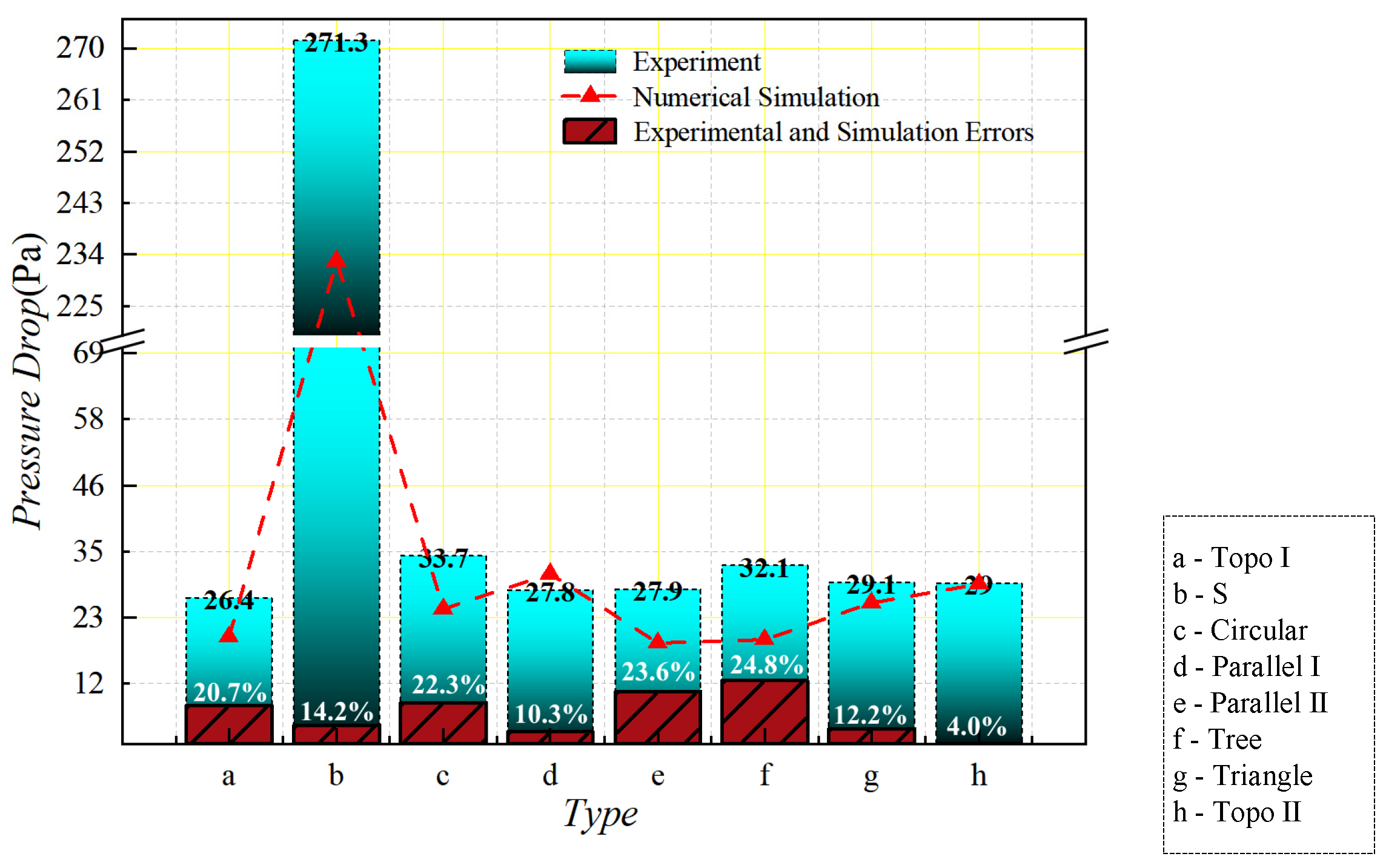
4.2.2. Pressure Drop Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.; Yang, S.; Pan, M.; Xu, J. Experimental investigation on thermal management of lithium-ion battery with roll bond liquid cooling plate. Appl. Therm. Eng. 2022, 206, 118106. [Google Scholar] [CrossRef]
- Moore, G.E. Cramming More Components onto Integrated Circuits. Proc. IEEE 1998, 86, 82–85. [Google Scholar] [CrossRef]
- Erp, R.V.; Kampitsis, G.; Matioli, E. Efficient Microchannel Cooling of Multiple Power Devices with Compact Flow Distribution for High Power-Density Converters. IEEE Trans. Power Electron. 2020, 35, 7235–7245. [Google Scholar] [CrossRef]
- Hassan, H.; Shafey, N.Y.A. 3D study of convection-radiation heat transfer of electronic chip inside enclosure cooled by heat sink. Int. J. Therm. Sci. 2021, 159, 106585. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, H.; Qiu, Y.; Zeng, H.; Dong, X. Numerical analysis of topology-optimized cold plates for thermal management of battery packs. Appl. Therm. Eng. 2024, 238, 121983. [Google Scholar] [CrossRef]
- Doty, J.; Yerkes, K.; Byrd, L.; Murthy, J.; Alleyne, A.; Wolff, M.; Heister, S.; Fisher, T.S.; Transfer, H. Dynamic Thermal Management for Aerospace Technology: Review and Outlook. J. Thermophys. Heat Transf. 2017, 31, 86–98. [Google Scholar] [CrossRef]
- Brookner, E. Phased-Array and Radar Breakthroughs. In Proceedings of the 2007 IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 37–42. [Google Scholar]
- Habibi Khalaj, A.; Halgamuge, S.K. A Review on efficient thermal management of air- and liquid-cooled data centers: From chip to the cooling system. Appl. Energy 2017, 205, 1165–1188. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Mujumdar, A.S. Numerical investigation of laminar heat transfer performance of various cooling channel designs. Appl. Therm. Eng. 2011, 31, 1293–1304. [Google Scholar] [CrossRef]
- Mohamad Rohaizan, M.H.K.; Nor Azwadi Che, S.; Kamyar, S. Numerical Analysis of Heat Transfer in Microchannel Heat Transfer in Microchannel Heat Sink using Flow Disruption. J. Adv. Res. Des. 2024, 106, 1–14. [Google Scholar] [CrossRef]
- Palumbo, J.; Tayyara, O.; Amon, C.H.; Chandra, S. Topologically optimized mini-channel heat sinks for reduced temperature non-uniformity. Int. J. Heat Mass Transf. 2023, 214, 124421. [Google Scholar] [CrossRef]
- Choudhury, B.K.; Gouda, M.K. CFD Analysis of Heat Transfer in Liquid-Cooled Heat Sink for Different Microchannel Flow Field Configuration. In Advances in Air Conditioning and Refrigeration, Select Proceedings of RAAR 2019; Springer: Singapore, 2020. [Google Scholar]
- Rao, Z.; Wang, S. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Qureshi, Z.A.; Al-Omari, S.A.B.; Elnajjar, E.; Al-Ketan, O.; Al-Rub, R.A.; Transfer, M. Using triply periodic minimal surfaces (TPMS)-based metal foams structures as skeleton for metal-foam-PCM composites for thermal energy storage and energy management applications. Int. Commun. Heat Mass Transf. 2021, 124, 105265. [Google Scholar] [CrossRef]
- Qureshi, Z.A.; Elnajjar, E.; Al-Ketan, O.; Al-Rub, R.A.; Al-Omari, S.B. Heat transfer performance of a finned metal foam-phase change material (FMF-PCM) system incorporating triply periodic minimal surfaces (TPMS). Int. J. Heat Mass Transf. 2021, 170, 121001. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, P. Flow and thermal transport characteristics of Triply-Periodic Minimal Surface (TPMS)-based gyroid and Schwarz-P cellular materials. Numer. Heat Transf. Part A Appl. 2021, 79, 553–569. [Google Scholar] [CrossRef]
- Wang, S.; Li, K.; Tian, Y.; Wang, J.; Wu, Y.; Ji, S. Improved thermal performance of a large laminated lithium-ion power battery by reciprocating air flow. Appl. Therm. Eng. 2019, 152, 445–454. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Zhang, J.; Liu, Z. Shortcut computation for the thermal management of a large air-cooled battery pack. Appl. Therm. Eng. 2014, 66, 445–452. [Google Scholar] [CrossRef]
- Liu, W.; Gou, J.; Luo, Y.; Zhang, M. The experimental investigation of a vapor chamber with compound columns under the influence of gravity. Appl. Therm. Eng. 2018, 140, 131–138. [Google Scholar] [CrossRef]
- Ramos-Alvarado, B.; Li, P.; Liu, H.; Hernandez-Guerrero, A. CFD study of liquid-cooled heat sinks with microchannel flow field configurations for electronics, fuel cells, and concentrated solar cells. Appl. Therm. Eng. 2011, 31, 2494–2507. [Google Scholar] [CrossRef]
- Shen, J.; Wang, Y.; Yu, G.; Li, H. Thermal Management of Prismatic Lithium-Ion Battery with Minichannel Cold Plate. J. Energy Eng. 2020, 146, 04019033. [Google Scholar] [CrossRef]
- Husain, A.; Kim, K.Y. Shape Optimization of Micro-Channel Heat Sink for Micro-Electronic Cooling. IEEE Trans. Compon. Packag. Technol. 2008, 31, 322–330. [Google Scholar] [CrossRef]
- Peles, Y.; Koşar, A.; Mishra, C.; Kuo, C.-J.; Schneider, B. Forced convective heat transfer across a pin fin micro heat sink. Int. J. Heat Mass Transf. 2005, 48, 3615–3627. [Google Scholar] [CrossRef]
- Michell, A.G.M. LVIII. The limits of economy of material in frame-structures. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1904, 8, 589–597. [Google Scholar] [CrossRef]
- Baker, W.F.; Beghini, L.L.; Mazurek, A.; Carrion, J.; Beghini, A. Maxwell’s reciprocal diagrams and discrete Michell frames. Struct. Multidiscip. Optim. 2013, 48, 267–277. [Google Scholar] [CrossRef]
- Yulin, M.; Xiaoming, W. A level set method for structural topology optimization and its applications. Adv. Eng. Softw. 2004, 35, 415–441. [Google Scholar] [CrossRef]
- Nelli Silva, E.C.; Ono Fonseca, J.S.; Kikuchi, N. Optimal design of periodic piezocomposites. Comput. Methods Appl. Mech. Eng. 1998, 159, 49–77. [Google Scholar] [CrossRef]
- Varanasi, S.; Ananthasuresh, G. Analysis and Topology Optimization of Heat Sinks with a Phase-Change Material on COMSOL Multiphysics™ Platform. In Proceedings of the COMSOL Users Conference, Shanghai, China, 12 December 2006. [Google Scholar]
- Bajaj, N.; Subbarayan, G.; Garimella, S.V. Topological design of channels for squeeze flow optimization of thermal interface materials. Int. J. Heat Mass Transf. 2012, 55, 3560–3575. [Google Scholar] [CrossRef]
- Li, H.; Ding, X.; Meng, F.; Jing, D.; Xiong, M. Optimal design and thermal modelling for liquid-cooled heat sink based on multi-objective topology optimization: An experimental and numerical study. Int. J. Heat Mass Transf. 2019, 144, 118638. [Google Scholar] [CrossRef]
- Sun, Y.; Dastidar, A.G.; Agazzi, A.; Le Goff, R.; Alexandersen, J. Topology optimization of conformal cooling channels in injection moulding: A scaling strategy for forced convection in high Reynolds number flows. Struct. Multidiscip. Optim. 2025, 68, 156. [Google Scholar] [CrossRef]
- Wu, T.; Tovar, A. Design for Additive Manufacturing of Conformal Cooling Channels Using Thermal-Fluid Topology Optimization and Application in Injection Molds. In Proceedings of the Design Automation Conference, San Francisco, CA, USA, 24–28 June 2018. [Google Scholar]
- Jahan, S.; Wu, T.; Shin, Y.; Tovar, A.; El-Mounayri, H.J.E. Thermo-fluid Topology Optimization and Experimental Study of Conformal Cooling Channels for 3D Printed Plastic Injection Molds. Procedia Manuf. 2019, 34, 631–639. [Google Scholar] [CrossRef]
- San, J.-Y.; Lin, G.-S.; Pai, K.-L. Performance of a serpentine heat exchanger: Part I–Effectiveness and heat transfer characteristics. Appl. Therm. Eng. 2009, 29, 3081–3087. [Google Scholar] [CrossRef]
- San, J.-Y.; Pai, K.-L. Performance of a serpentine heat exchanger: Part II–Second-law efficiency. Appl. Therm. Eng. 2009, 29, 3088–3093. [Google Scholar] [CrossRef]
- Husain, A.; Kim, K.-Y. Optimization of a microchannel heat sink with temperature dependent fluid properties. Appl. Therm. Eng. 2008, 28, 1101–1107. [Google Scholar] [CrossRef]
- Gersborg-Hansen, A.; Sigmund, O.; Haber, R.B.J.S.; Optimization, M. Topology optimization of channel flow problems. Struct. Multidiscip. Optim. 2005, 30, 181–192. [Google Scholar] [CrossRef]
- Olesen, L.H.J.; Okkels, F.; Bruus, H. A high-level programming-language implementation of topology optimization applied to steady-state Navier-Stokes flow. Int. J. Numer. Methods Eng. 2006, 65, 975–1001. [Google Scholar] [CrossRef]
- Chen, L.; Wei, S.; Sun, F. The area–point constructal entransy dissipation rate minimization for a discrete variable cross-section conducting path. Int. J. Low-Carbon Technol. 2014, 9, 20–28. [Google Scholar] [CrossRef]
- Dede, E.M.; Joshi, S.N.; Zhou, F. Topology Optimization, Additive Layer Manufacturing, and Experimental Testing of an Air-Cooled Heat Sink. J. Mech. Des. 2015, 137. [Google Scholar] [CrossRef]
- Okkels, F.; Olesen, L.; Bruus, H. Applications of topology optimization in the design of micro-and nanofluidic systems. In Proceedings of the 2005 NSTI Nanotechnology Conference and Trade Show-NSTI Nanotech 2005 Technical Proceedings, Anaheim, CA, USA, 8–12 May 2005; Volume 1. [Google Scholar]
- Borrvall, T.; Petersson, J. Topology optimization of fluids in Stokes flow. Int. J. Numer. Methods Fluids 2003, 41, 77–107. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G.I.N. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Kawamoto, A.; Matsumori, T.; Yamasaki, S.; Nomura, T.; Kondoh, T.; Nishiwaki, S. Heaviside projection based topology optimization by a PDE-filtered scalar function. Struct. Multidiscip. Optim. 2011, 44, 19–24. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S.; Yap, C. Thermal characteristics of tree-shaped microchannel nets for cooling of a rectangular heat sink. Int. J. Therm. Sci. 2006, 45, 1103–1112. [Google Scholar] [CrossRef]













| q | Da | V0 | L (mm) | γβ | μ (N·s/m2) |
|---|---|---|---|---|---|
| 0.01 | 1 × 10−4 | 0.5 | 4 | 0.5 | 0.001 |
| Component | Material | Density ρ (kg/m3) | Heat Conductivity k (W(m·K)) | Specific Heat (J/kg K) Cp | Dynamic Viscosity μ (N·s/m2) |
|---|---|---|---|---|---|
| Heat sink | Aluminum 6061 | 2700 | 240 | 336 | — |
| Carrying plate | Aluminum 6061 | 2700 | 240 | 336 | — |
| MCH | 96 Alumina | 3970 | 15 | 61 | — |
| Thermal pad | Alumina | 3200 | 3 | 1000 | — |
| Coolant | Deionized water | 998.2 | 0.61 | 4180 | 0.001 |
| Mesh Number | [°C] | |
|---|---|---|
| 968,718 | 51.5 | -- |
| 1,736,644 | 48.8 | 5.5% |
| 2,902,755 | 47 | 3.8% |
| 4,308,285 | 45.9 | 2.4% |
| 6,568,243 | 45.6 | 0.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Dai, Y.; Yu, Z.; Zeng, X.; Tan, C.; Zhang, H.; Yang, G.; Qin, F. Experimental and Numerical Study on Various Liquid-Cooled Heat Sinks Including Topology Optimization. Micromachines 2025, 16, 1213. https://doi.org/10.3390/mi16111213
Shi G, Dai Y, Yu Z, Zeng X, Tan C, Zhang H, Yang G, Qin F. Experimental and Numerical Study on Various Liquid-Cooled Heat Sinks Including Topology Optimization. Micromachines. 2025; 16(11):1213. https://doi.org/10.3390/mi16111213
Chicago/Turabian StyleShi, Ge, Yanwei Dai, Zhongjun Yu, Xingyao Zeng, Cheng Tan, Haibo Zhang, Guang Yang, and Fei Qin. 2025. "Experimental and Numerical Study on Various Liquid-Cooled Heat Sinks Including Topology Optimization" Micromachines 16, no. 11: 1213. https://doi.org/10.3390/mi16111213
APA StyleShi, G., Dai, Y., Yu, Z., Zeng, X., Tan, C., Zhang, H., Yang, G., & Qin, F. (2025). Experimental and Numerical Study on Various Liquid-Cooled Heat Sinks Including Topology Optimization. Micromachines, 16(11), 1213. https://doi.org/10.3390/mi16111213









