Design Parameters Affecting the Performance of Vortex-Induced Vibration Harvesters
Abstract
:1. Introduction
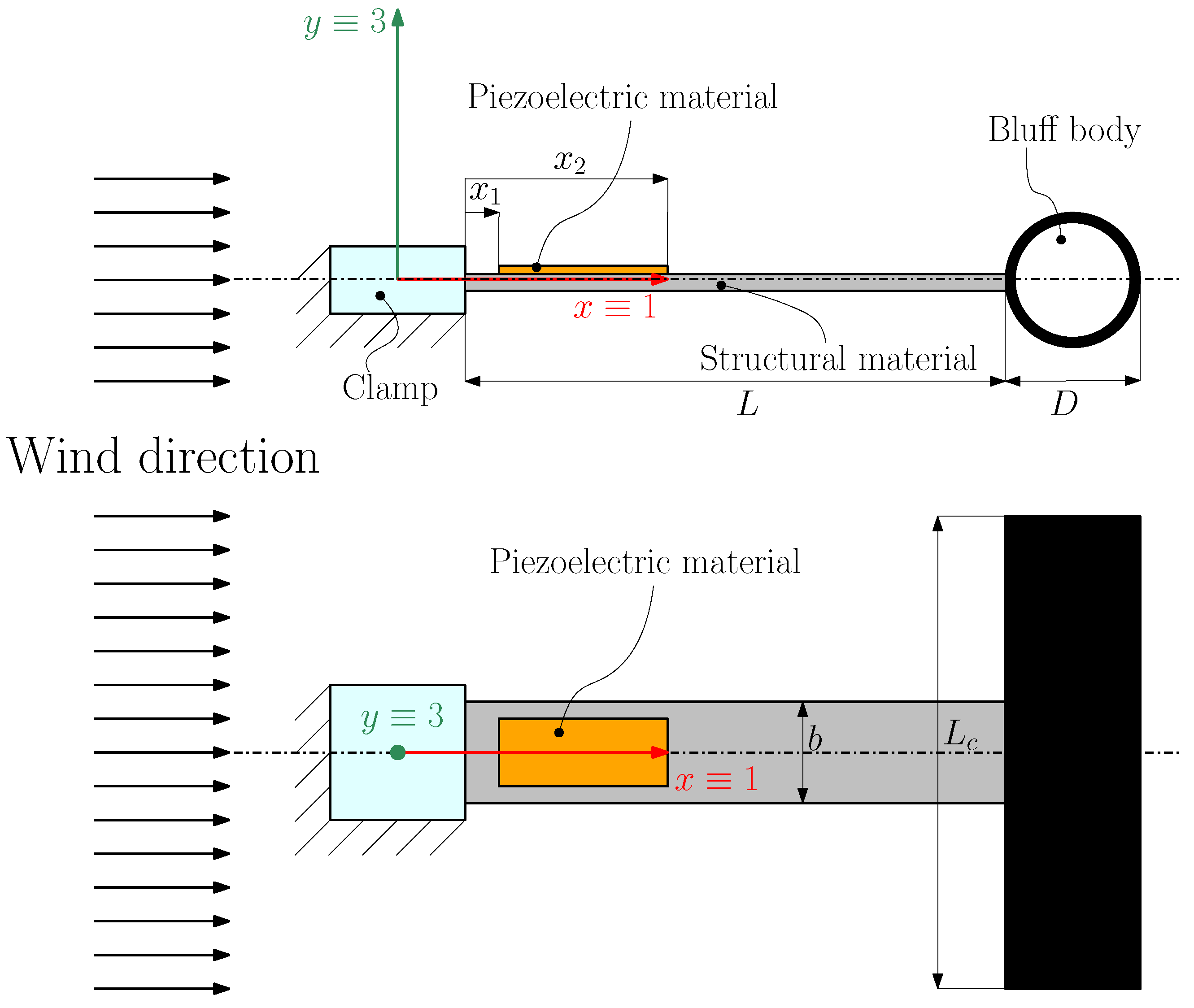
2. Mathematical Model of the VIV Harvester
2.1. Electromechanical Model
2.2. Aerodynamic Force
2.3. Dimensionless Harmonic Solution
2.4. Calculated Results
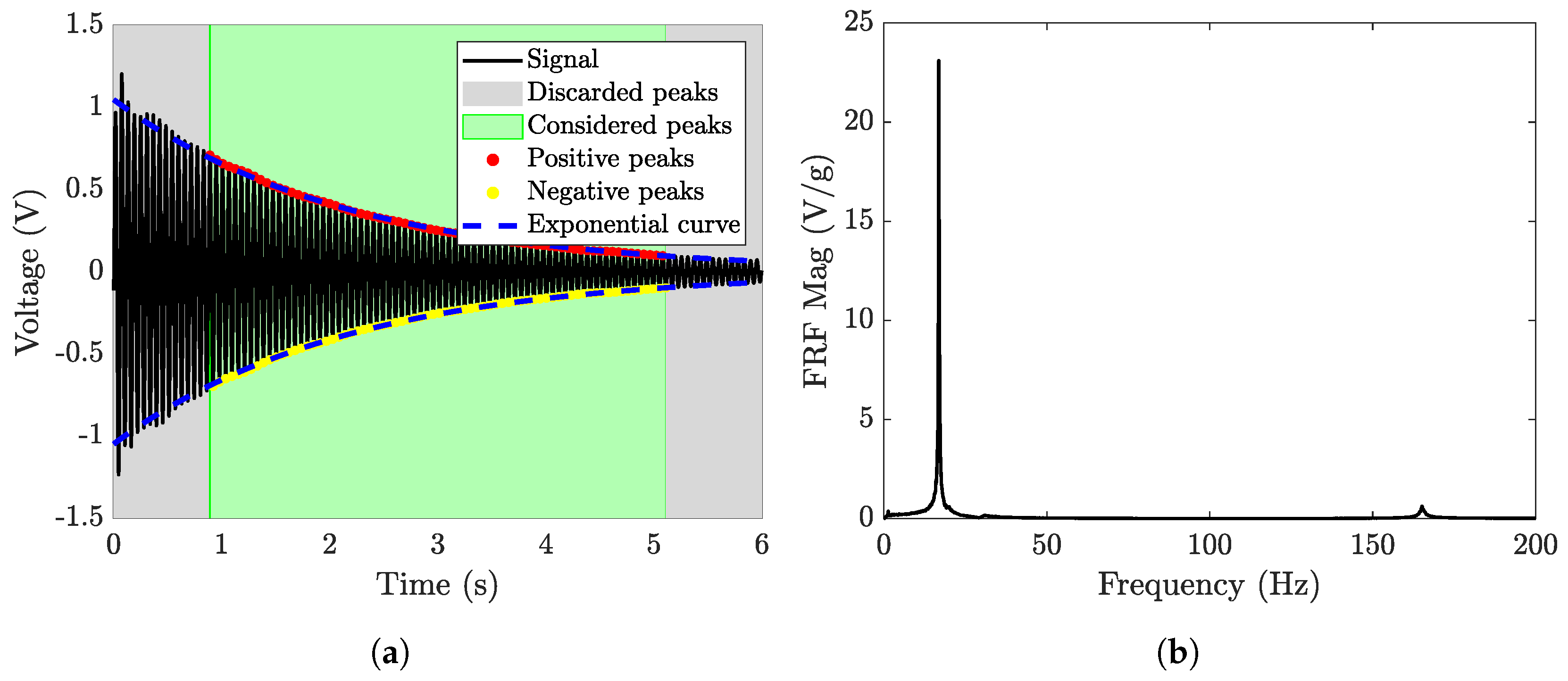
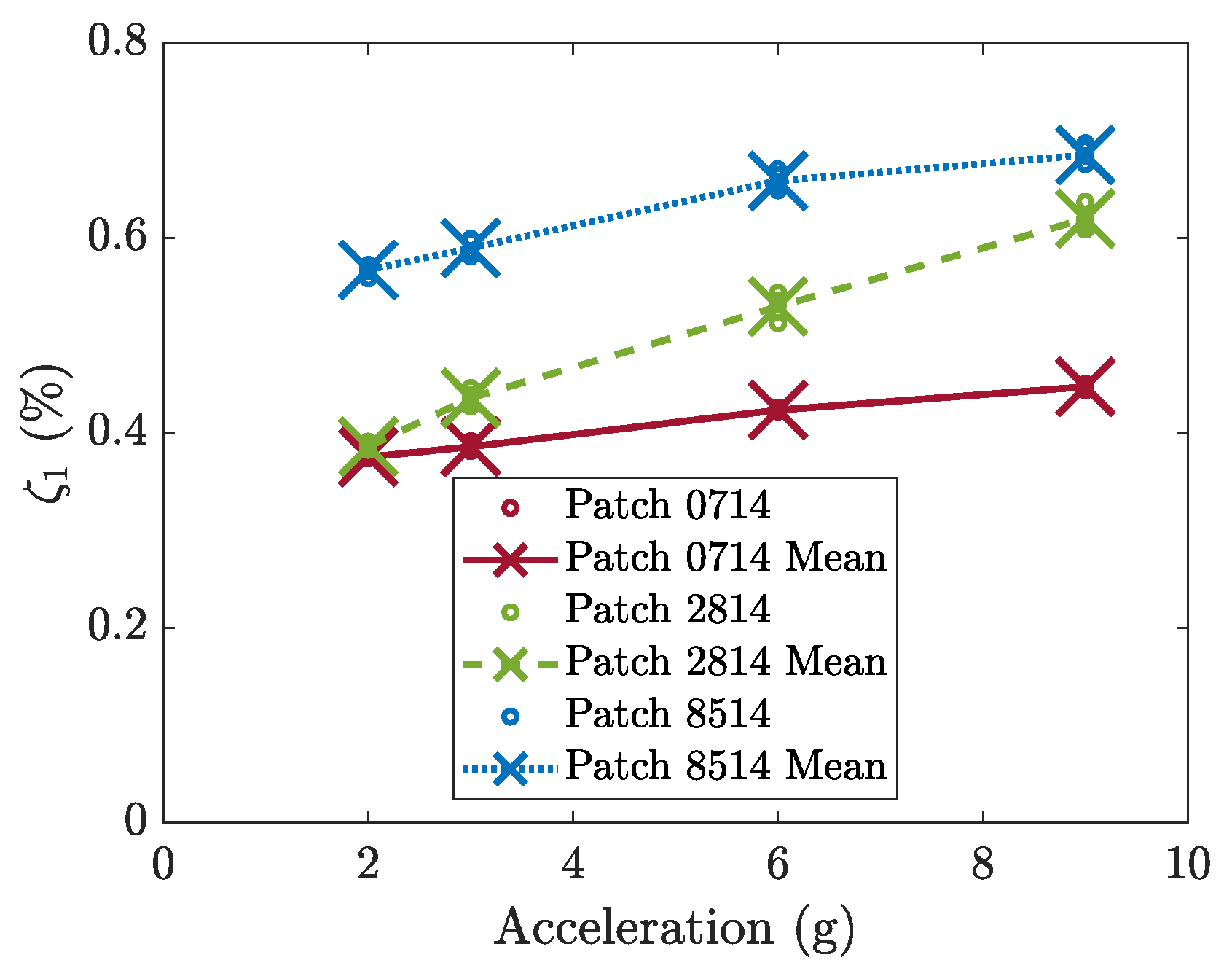
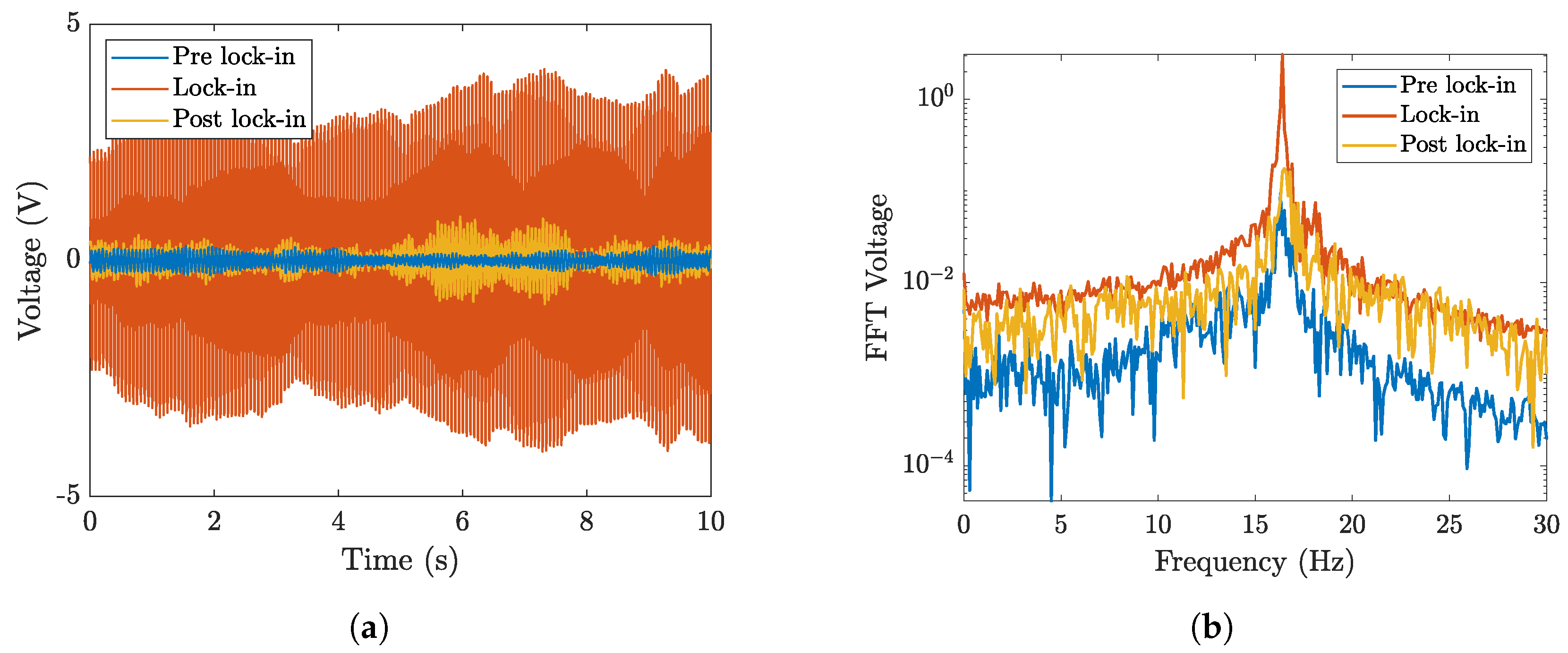
3. Experimental Characterization of the Harvester by Means of Impulsive Tests
4. Effects of the Design Parameters of the Harvester in Wind Tunnel Experiments
4.1. Experimental Equipment—Wind Tunnel
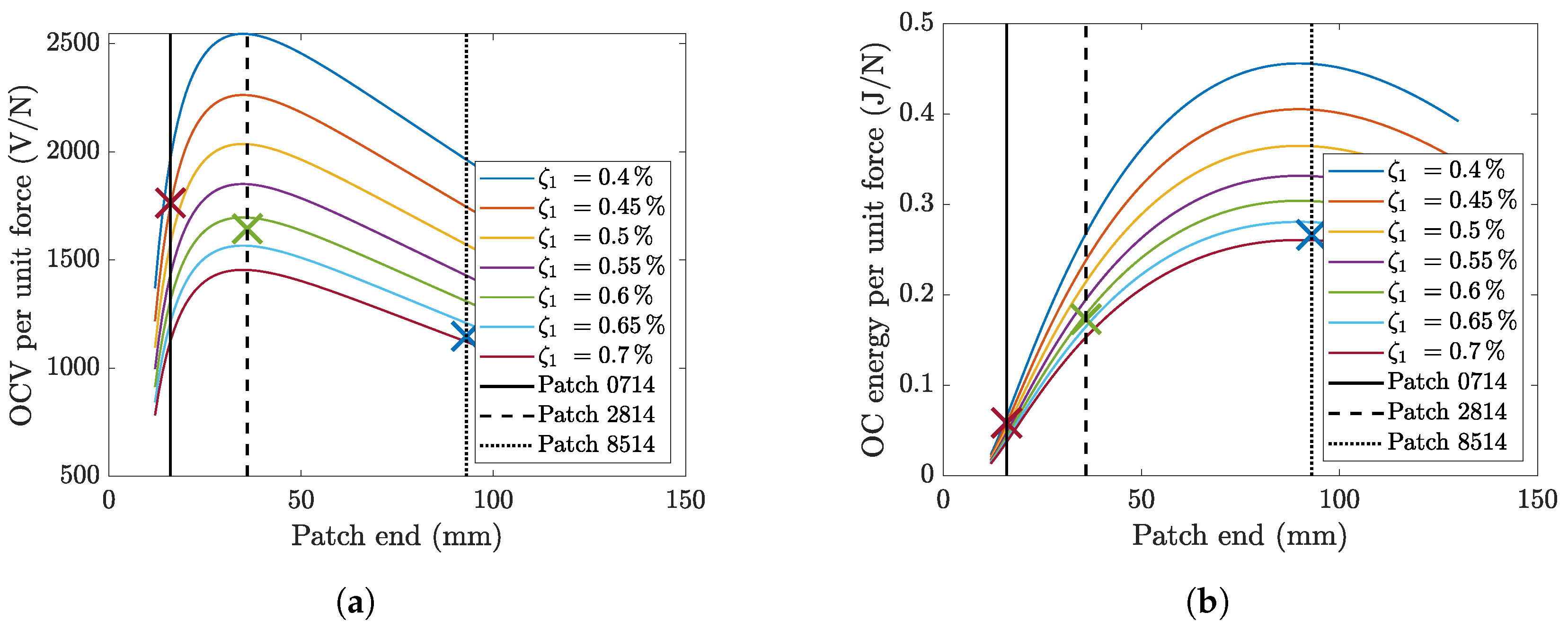
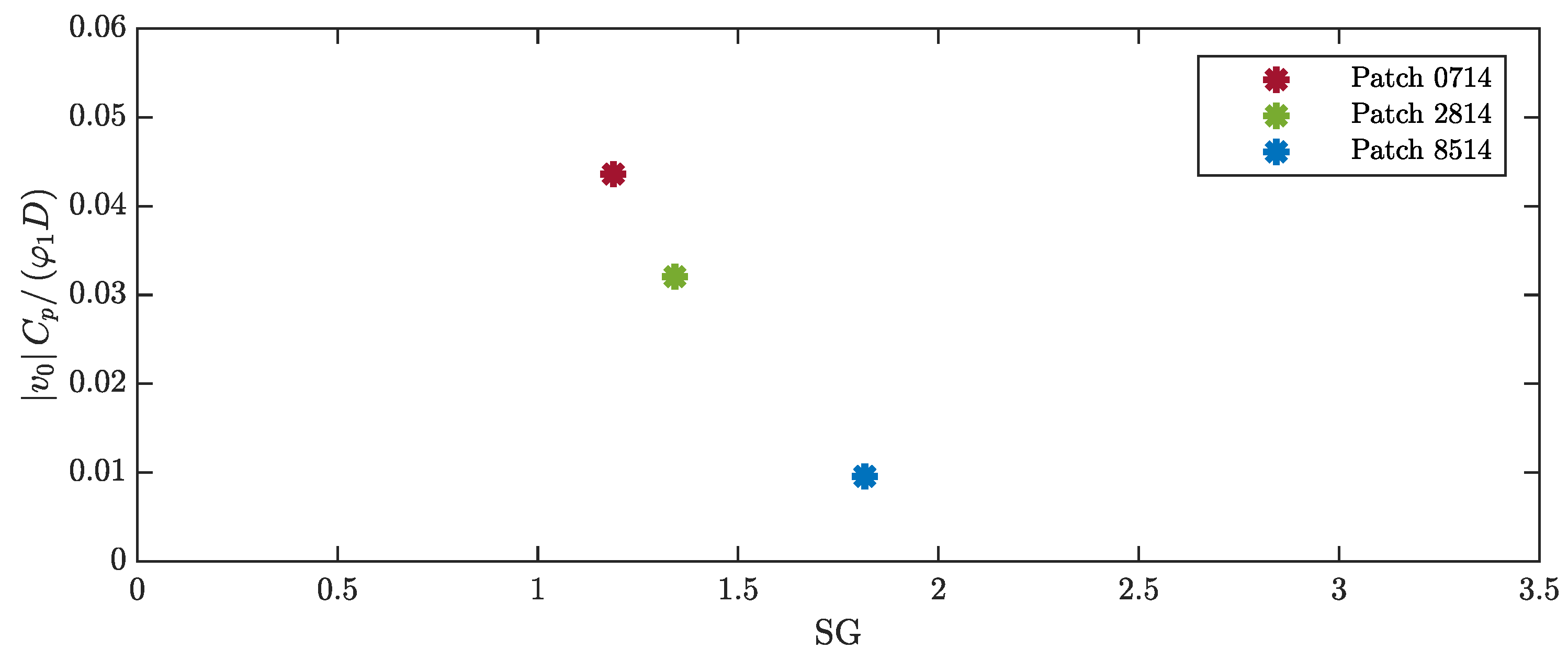
4.2. Effect of Patch Length
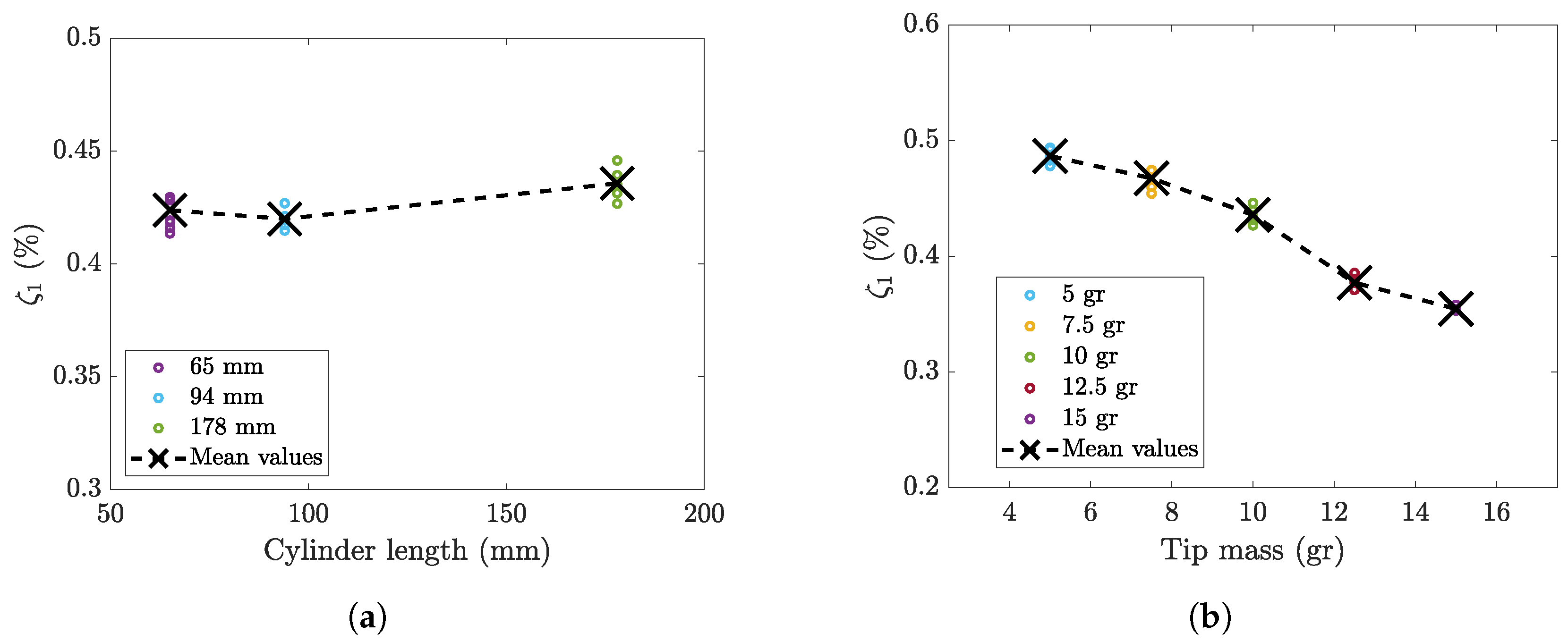
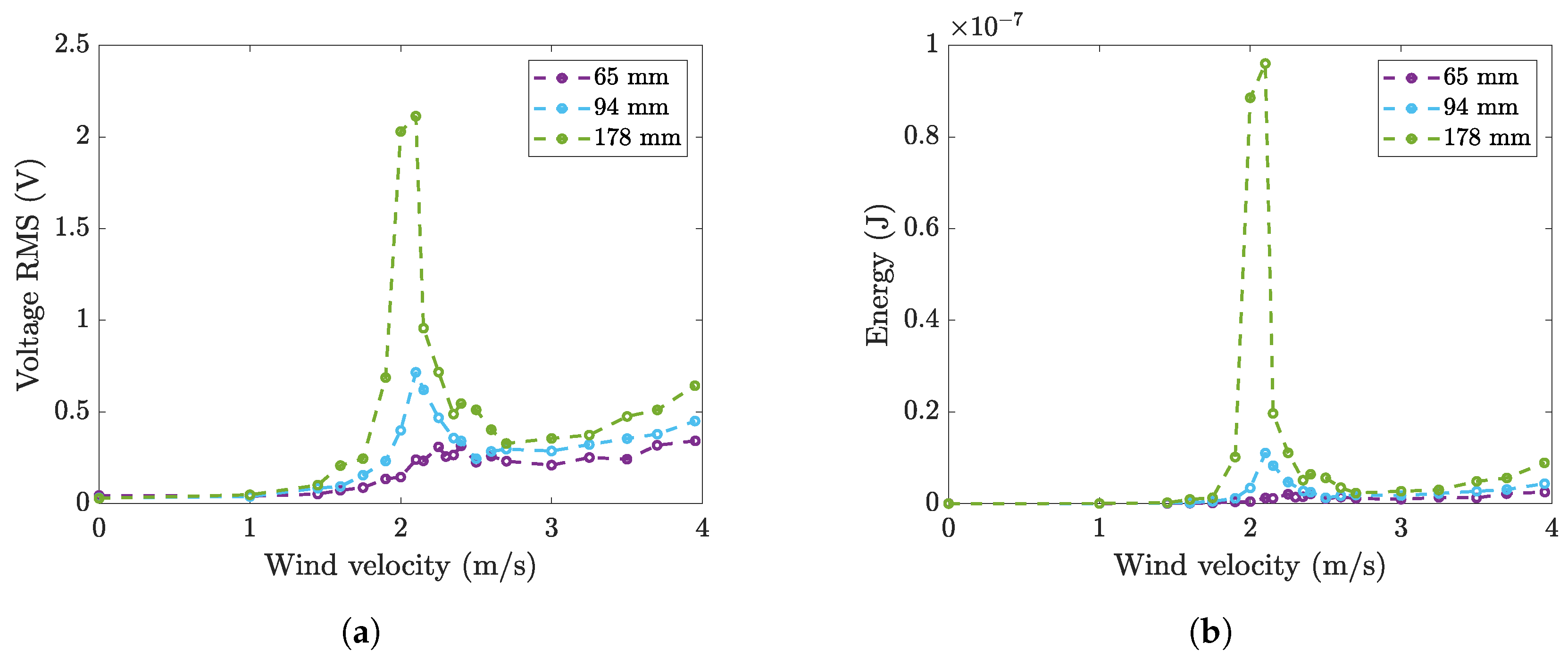
4.3. Effect of Cylinder Length
4.4. Effect of Cylinder Mass
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| patch start from clamp | |
| patch end from clamp | |
| L | cantilever length |
| b | cantilever width |
| D | cylinder external diameter |
| cylinder length | |
| shedding frequency | |
| U | wind speed |
| t | time variable |
| M | bending moment of the cantilever |
| equivalent coefficient of strain rate damping | |
| I | equivalent moment of inertia of the composite cross section |
| viscous air damping coefficient | |
| m | mass per unit length of the beam |
| F | generic force applied to the cantilever tip |
| harmonic lift applied to the cylinder axis | |
| Dirac delta function | |
| bending stiffness of the composite cross section of the cantilever | |
| H | Heaviside function |
| piezoelectric constant | |
| thickness of the piezoelectric layer | |
| position of the bottom of the piezoelectric layer from the neutral axis | |
| position of the top of the piezoelectric layer from the neutral axis | |
| distance of the center of the piezoelectric patch cross section from the neutral axis | |
| nth mode of vibration | |
| nth modal displacement | |
| modal mass of the nth mode of vibration | |
| modal damping coefficient of the nth mode of vibration | |
| modal stiffness of the nth mode of vibration | |
| forward modal coupling coefficient nth mode of vibration | |
| modal force of the nth mode of vibration | |
| modal damping ratio of the nth mode of vibration | |
| surface of the positive electrode |
| electric displacement | |
| unit normal vector of | |
| strain within the piezoelectric layer | |
| transverse component of the electric field | |
| transverse component of electric displacement | |
| piezoelectric stress charge coefficient | |
| permittivity at constant strain | |
| v | electric voltage |
| open-circuit voltage | |
| i | output current |
| piezoelectric patch capacitance | |
| electric potential energy stored in the harvester | |
| average electric potential energy stored in the harvester | |
| root mean square (RMS) value of the open-circuit voltage | |
| fluid density | |
| lift coefficient | |
| torque applied to the tip | |
| modal constant of the nth mode | |
| natural angular frequency of the first mode of the coupled system | |
| angular frequency of vortex shedding | |
| SG | Skop–Griffin number |
| St | Strouhal number |
| mass ratio between the vibrating mass and the mass of fluid having the same volume of the cylinder |
References
- Blevins, R.D. Flow-Induced Vibration; Van Nostrand Reinhold Company: New York, NY, USA, 1977. [Google Scholar]
- Matsumoto, M. Vortex shedding of bluff bodies: A review. J. Fluids Struct. 1999, 13, 791–811. [Google Scholar] [CrossRef]
- Assi, G.; Bearman, P.; Kitney, N. Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 2009, 25, 666–675. [Google Scholar] [CrossRef]
- Azadeh-Ranjbar, V.; Elvin, N.; Andreopoulos, Y. Vortex-induced vibration of finite-length circular cylinders with spanwise free-ends: Broadening the lock-in envelope. Phys. Fluids 2018, 30, 105104. [Google Scholar] [CrossRef]
- Khalak, A.; Williamson, C. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 1999, 13, 813–851. [Google Scholar] [CrossRef]
- Goswami, I.; Scanlan, R.; Jones, N. Vortex-induced vibration of circular cylinders. I: Experimental data. J. Eng. Mech. 1993, 119, 2270–2287. [Google Scholar] [CrossRef]
- Choi, C.K.; Kwon, D.K. Wind tunnel blockage effects on aerodynamic behavior of bluff body. Wind. Struct. Int. J. 1998, 1, 351–364. [Google Scholar] [CrossRef]
- Wang, J.; Geng, L.; Ding, L.; Zhu, H.; Yurchenko, D. The state-of-the-art review on energy harvesting from flow-induced vibrations. Appl. Energy 2020, 267, 114902. [Google Scholar] [CrossRef]
- Tukymbekov, D.; Saymbetov, A.; Nurgaliyev, M.; Kuttybay, N.; Dosymbetova, G.; Svanbayev, Y. Intelligent autonomous street lighting system based on weather forecast using LSTM. Energy 2021, 231, 120902. [Google Scholar] [CrossRef]
- Xia, L.; Ma, S.; Tao, P.; Pei, W.; Liu, Y.; Tao, L.; Wu, Y. A Wind-Solar Hybrid Energy Harvesting Approach Based on Wind-Induced Vibration Structure Applied in Smart Agriculture. Micromachines 2023, 14, 58. [Google Scholar] [CrossRef] [PubMed]
- Doria, A.; Fanti, G.; Filipi, G.; Moro, F. Development of a novel piezoelectric harvester excited by raindrops. Sensors 2019, 19, 3653. [Google Scholar] [CrossRef] [PubMed]
- Palomba, I.; Tonan, M.; Doria, A. Design of cantilever harvesters excited by raindrop impacts. Mech. Syst. Signal Process. 2025, 225, 112284. [Google Scholar] [CrossRef]
- Akaydin, H.; Elvin, N.; Andreopoulos, Y. The performance of a self-excited fluidic energy harvester. Smart Mater. Struct. 2012, 21, 025007. [Google Scholar] [CrossRef]
- Dai, H.; Abdelkefi, A.; Wang, L. Theoretical modeling and nonlinear analysis of piezoelectric energy harvesting from vortex-induced vibrations. J. Intell. Mater. Syst. Struct. 2014, 25, 1861–1874. [Google Scholar] [CrossRef]
- Zhao, D.; Hu, X.; Tan, T.; Yan, Z.; Zhang, W. Piezoelectric galloping energy harvesting enhanced by topological equivalent aerodynamic design. Energy Convers. Manag. 2020, 222, 113260. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, Q.; Wang, W. Optimization of galloping piezoelectric energy harvester with V-shaped groove in low wind speed. Energies 2019, 12, 4619. [Google Scholar] [CrossRef]
- Orrego, S.; Shoele, K.; Ruas, A.; Doran, K.; Caggiano, B.; Mittal, R.; Kang, S. Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 2017, 194, 212–222. [Google Scholar] [CrossRef]
- Hobeck, J.; Inman, D. Artificial piezoelectric grass for energy harvesting from turbulence-induced vibration. Smart Mater. Struct. 2012, 21, 105024. [Google Scholar] [CrossRef]
- Lai, Z.; Wang, S.; Zhu, L.; Zhang, G.; Wang, J.; Yang, K.; Yurchenko, D. A hybrid piezo-dielectric wind energy harvester for high-performance vortex-induced vibration energy harvesting. Mech. Syst. Signal Process. 2021, 150, 107212. [Google Scholar] [CrossRef]
- Dai, H.; Abdelkefi, A.; Yang, Y.; Wang, L. Orientation of bluff body for designing efficient energy harvesters from vortex-induced vibrations. Appl. Phys. Lett. 2016, 108, 053902. [Google Scholar] [CrossRef]
- Fershalov, A.; Albano, J.; Orlandini, P.; Elvin, N.; Liu, Y. Harvesting sustainable energy through vortex-induced cylinder vibrations. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2024; Volume 88124, p. V001T03A004. [Google Scholar] [CrossRef]
- Boddapati, K.; Arrieta, A.F. Structural multistability for multi-speed wind energy harvesting from vortex-induced vibrations. Smart Mater. Struct. 2024, 33, 105048. [Google Scholar] [CrossRef]
- Facchinetti, M.; de Langre, E.; Biolley, F. Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 2004, 19, 123–140. [Google Scholar] [CrossRef]
- Akaydin, H.D.; Elvin, N.; Andreopoulos, Y. Experimental study of a self-excited piezoelectric energy harvester. In Proceedings of the ASME 2010 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, SMASIS 2010, Philadelphia, PA, USA, 28 September–1 October 2010; Volume 1, pp. 179–185. [Google Scholar] [CrossRef]
- Mehmood, A.; Abdelkefi, A.; Hajj, M.; Nayfeh, A.; Akhtar, I.; Nuhait, A. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder. J. Sound Vib. 2013, 332, 4656–4667. [Google Scholar] [CrossRef]
- Pasetto, A.; Tonan, M.; Doria, A. Development of a Hybrid Harvester for Collecting Energy From Wind and Vibrations in Light Vehicles. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 25–28 August 2024; Volume 1, 26th International Conference on Advanced Vehicle Technologies (AVT). p. V001T01A012. [Google Scholar] [CrossRef]
- Smart Material Corporation. Home of the MFC. Available online: https://www.smart-material.com/MFC-product-mainV2.html (accessed on 25 November 2024).
- Malefaki, I.; Konstantinidis, E. Assessment of a hydrokinetic energy converter based on vortex-induced angular oscillations of a cylinder. Energies 2020, 13, 717. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D. On Mechanical Modeling of Cantilevered Piezoelectric Vibration Energy Harvesters. J. Intell. Mater. Syst. Struct. 2008, 19, 1311–1325. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. A Distributed Parameter Electromechanical Model for Cantilevered Piezoelectric Energy Harvesters. J. Vib. Acoust. 2008, 130, 041002. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D. Piezoelectric Energy Harvesting; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Doria, A.; Marconi, E.; Moro, F. Energy Harvesting from Bicycle Vibrations by Means of Tuned Piezoelectric Generators. Electronics 2020, 9, 1377. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 5th ed.; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar] [CrossRef]
- Rao, S.S.; Yap, F.F. Mechanical Vibrations; Addison-Wesley: New York, NY, USA, 1995; Volume 4. [Google Scholar]
- Bearman, P.W. Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 1984, 16, 195–222. [Google Scholar] [CrossRef]
- Williamson, C.H.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Tommasino, D.; Tonan, M.; Moro, F.; Doria, A. Identification of the Piezoelectric Properties of Materials From Impulsive Tests on Cantilever Harvesters. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 20–23 August 2023; Volume 12, 35th Conference on Mechanical Vibration and Sound (VIB). p. V012T12A005. [Google Scholar] [CrossRef]
- Morse, T.; Govardhan, R.; Williamson, C. The effect of end conditions on the vortex-induced vibration of cylinders. J. Fluids Struct. 2008, 24, 1227–1239. [Google Scholar] [CrossRef]
- Unal, M.; Rockwell, D. On vortex formation from a cylinder. Part 2. Control by splitter-plate interference. J. Fluid Mech. 1988, 190, 513–529. [Google Scholar] [CrossRef]



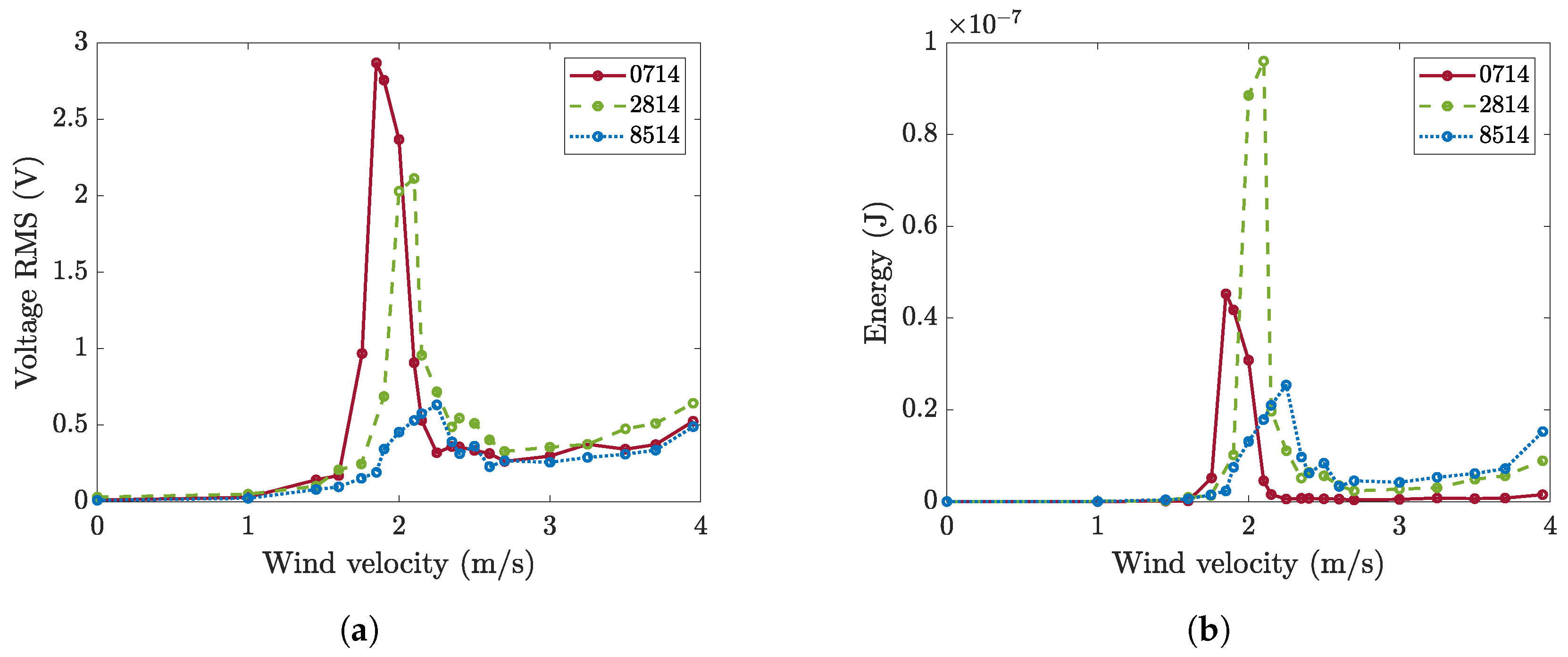



| Patch 0714 | Patch 2814 | Patch 8514 | |
|---|---|---|---|
| (Hz) | 16.0 | 16.8 | 19.2 |
| 0.45 | 0.62 | 0.68 |
| Cylinder Length | 65 mm | 94 mm | 178 mm |
|---|---|---|---|
| AR | 3.4 | 5.0 | 9.4 |
| 0.32 | 0.22 | 0.12 | |
| ∼570 | ∼430 | ∼210 |
| Cylinder Mass | 5 gr | 7.5 gr | 10 gr | 12.5 gr | 15 gr |
|---|---|---|---|---|---|
| (Hz) | 20.7 | 18.1 | 16.8 | 15.1 | 14.1 |
| ∼130 | ∼170 | ∼210 | ∼250 | ∼290 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasetto, A.; Tonan, M.; Moro, F.; Doria, A. Design Parameters Affecting the Performance of Vortex-Induced Vibration Harvesters. Micromachines 2025, 16, 122. https://doi.org/10.3390/mi16020122
Pasetto A, Tonan M, Moro F, Doria A. Design Parameters Affecting the Performance of Vortex-Induced Vibration Harvesters. Micromachines. 2025; 16(2):122. https://doi.org/10.3390/mi16020122
Chicago/Turabian StylePasetto, Alberto, Michele Tonan, Federico Moro, and Alberto Doria. 2025. "Design Parameters Affecting the Performance of Vortex-Induced Vibration Harvesters" Micromachines 16, no. 2: 122. https://doi.org/10.3390/mi16020122
APA StylePasetto, A., Tonan, M., Moro, F., & Doria, A. (2025). Design Parameters Affecting the Performance of Vortex-Induced Vibration Harvesters. Micromachines, 16(2), 122. https://doi.org/10.3390/mi16020122








