Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data
Abstract
:Simple Summary
Abstract
1. Introduction
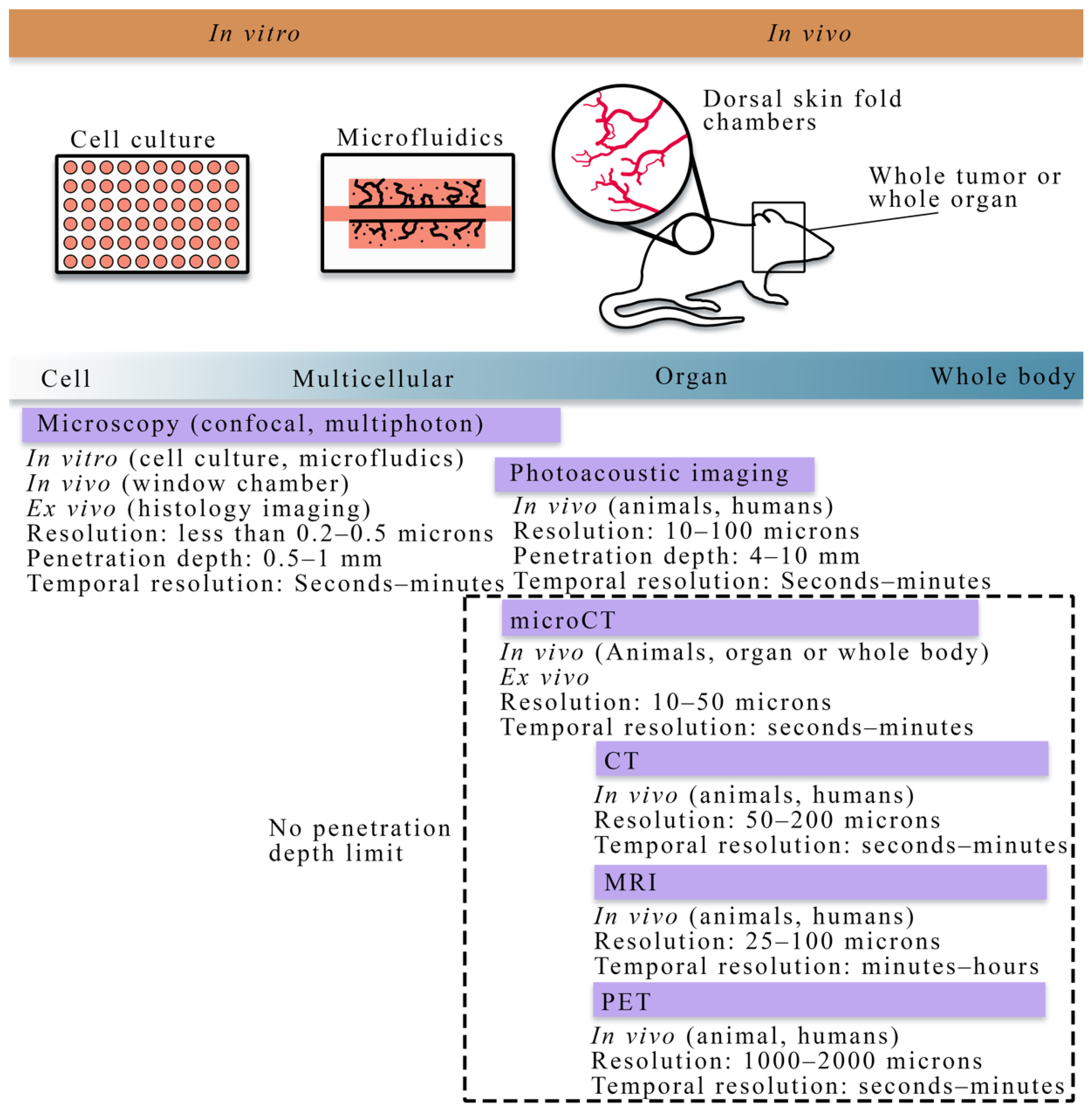
2. Overview of Experimental Techniques across Scales
2.1. Quantitative Techniques for Observing Tumor Vasculature and Angiogenesis at the Cellular Scale
2.2. Quantitative Techniques for Observing Tumor Vasculature and Angiogenesis at the Tissue Scale
| Modality | Scale | Measurement | Uses in Literature |
|---|---|---|---|
| Microscopy (confocal, multiphoton, optical projection tomography, histology imaging) | Cell to tissue | Vascular structure, individual cell types, vessel porosity, flow | [18,76,77,78,79,80] |
| Photoacoustic imaging | Cell to tissue | Vascular structure, blood oxygenation | [81,82] |
| Angiography (X-ray, CT, MRI) | Tissue | Vascular structure | [47,48,83,84] |
| Dynamic contrast-enhanced MRI or CT | Tissue | Perfusion, permeability, blood volume fraction | [28,32,33,85,86] |
| PET | Tissue | Perfusion, permeability, blood volume fraction | [83,84] |
| microCT | Tissue | Vascular structure | [47,48,83,84] |
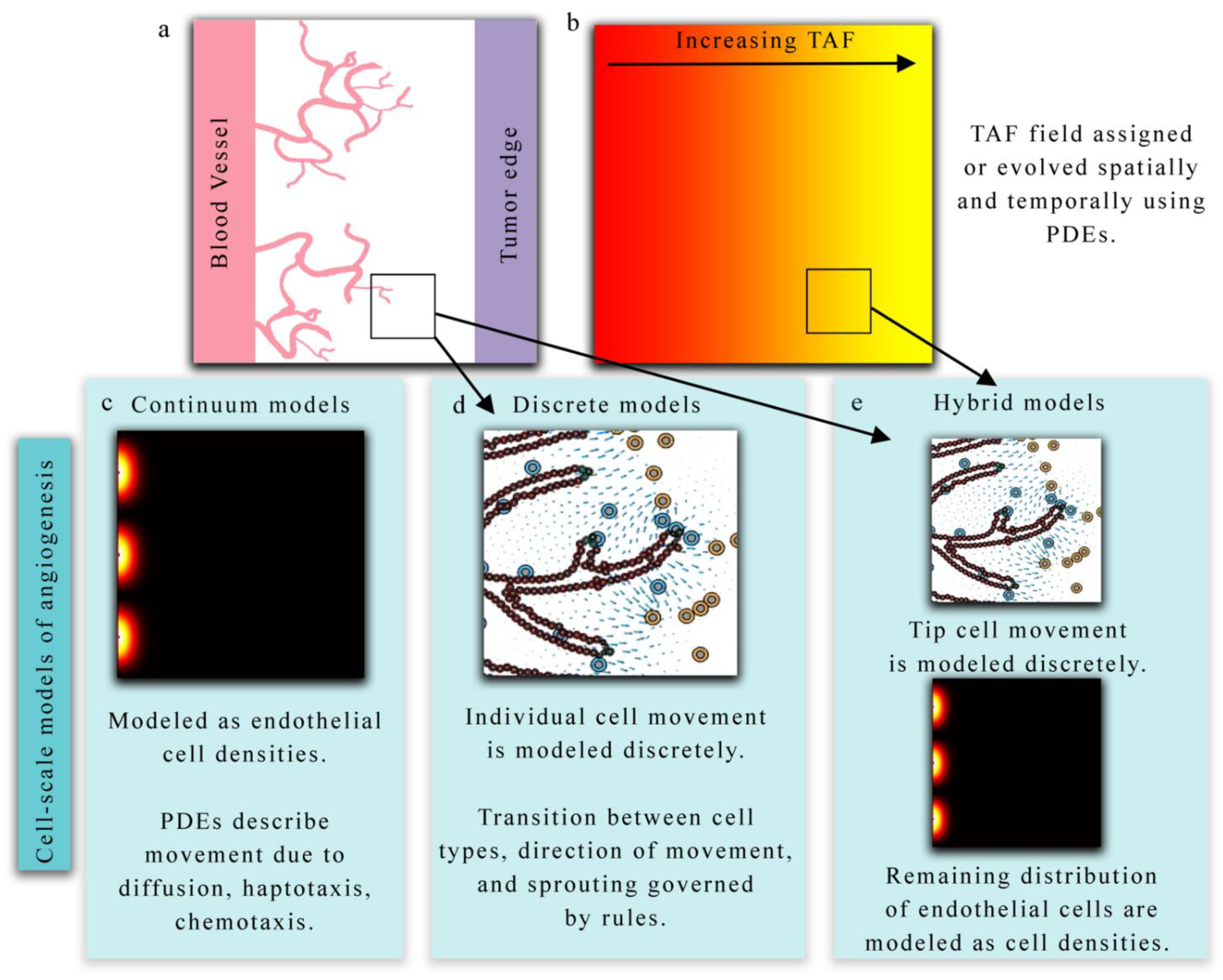
3. Approaches for Modeling Tumor Vasculature at the Cell Scale
3.1. Mathematical Modeling of Tumor Vasculature and Angiogenesis at the Cell Scale
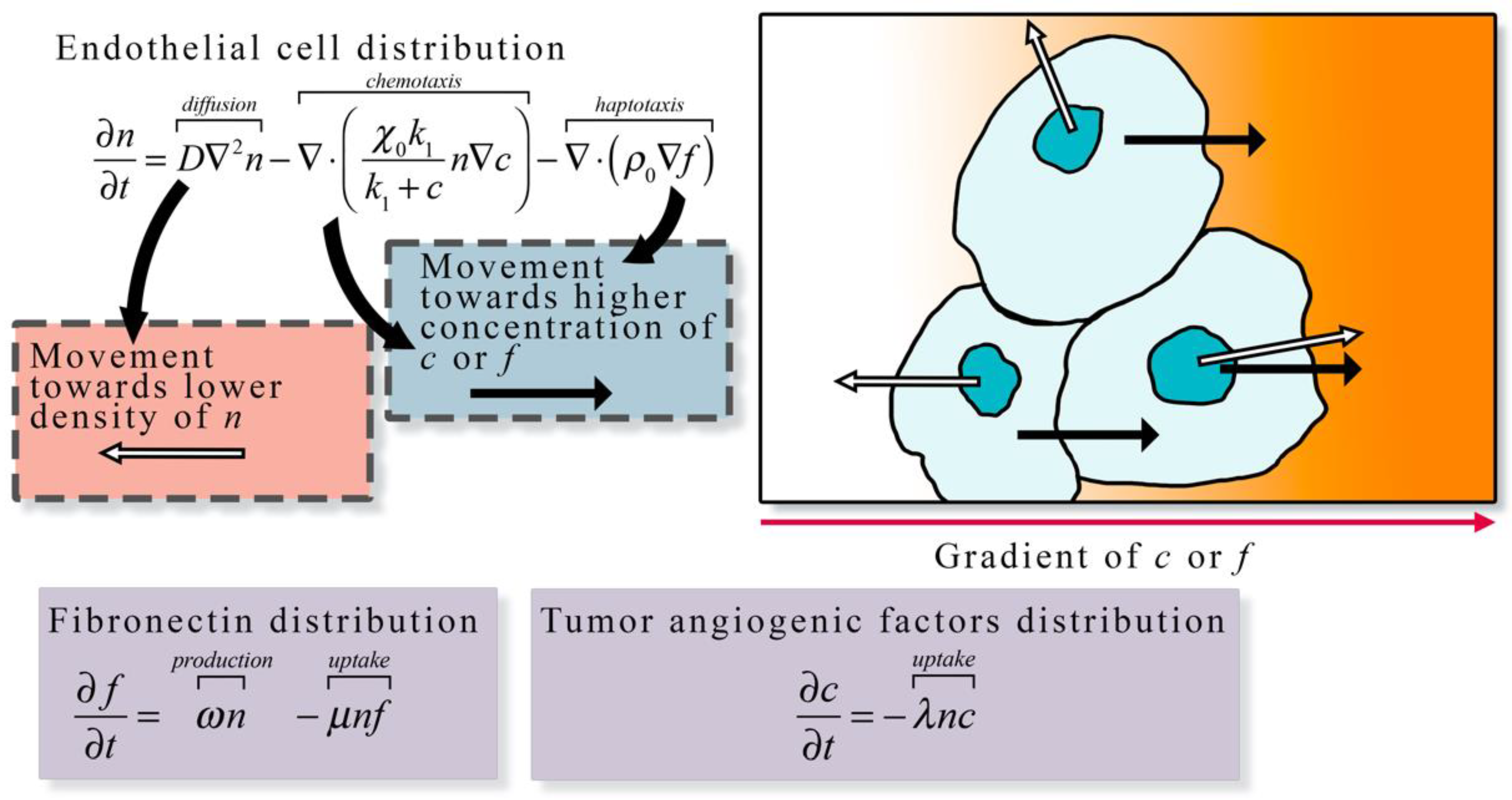
3.1.1. Continuum Models
3.1.2. Discrete Models
3.1.3. Hybrid Models
3.1.4. Summary
3.2. Integrating Theory and Experimental Data at the Cellular Scale
4. Approaches for Modeling Tumor Vasculature and Angiogenesis at the Tissue Scale
4.1. Mathematical Modeling of Tumor Vasculature and Angiogenesis at the Tissue Scale
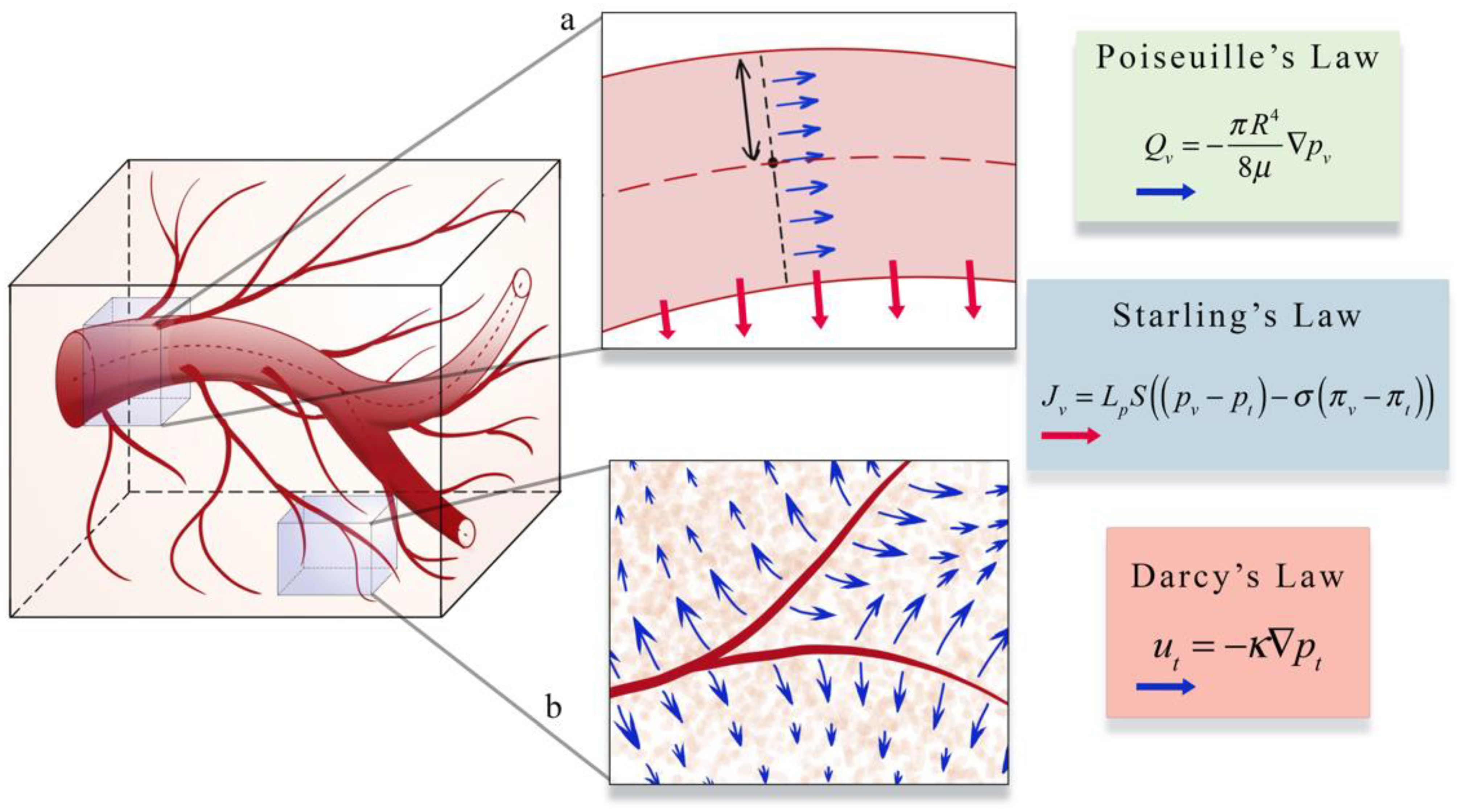
4.1.1. Models of Evolving Tumor Vascular Network
4.1.2. Models of Blood Flow and Blood-Driven Transport
4.1.3. Models of Tumor and Vasculature Growth and Response to Therapy
4.2. Integrating Theory and Experimental Data at the Tissue Scale
4.2.1. Applications to Estimate Perfusion and Delivery
4.2.2. Applications to Treatment Response
5. Opportunities for Multiscale Modeling of Angiogenesis
6. Future Directions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Folkman, J.; Bach, M.; Rowe, J.W.; Davidoff, F.; Lambert, P.; Hirsch, C.; Goldberg, A.; Hiatt, H.H.; Glass, J.; Henshaw, E. Tumor Angiogenesis—Therapeutic Implications. N. Engl. J. Med. 1971, 285, 1182–1186. [Google Scholar]
- Folkman, J. Tumor Angiogenesis; Klein, G., Weinhouse, S., Haddow, A.B.T.-A., Eds.; Academic Press: Cambridge, MA, USA, 1974; Volume 19, pp. 331–358. ISBN 0065230X. [Google Scholar]
- Carmeliet, P. Angiogenesis in health and disease. Nat. Med. 2003, 9, 653–660. [Google Scholar] [CrossRef]
- Jain, R.K.; di Tomaso, E.; Duda, D.G.; Loeffler, J.S.; Sorensen, A.G.; Batchelor, T.T. Angiogenesis in brain tumours. Nat. Rev. Neurosci. 2007, 8, 610–622. [Google Scholar] [CrossRef] [PubMed]
- Folkman, J. Angiogenesis in cancer, vascular, rheumatoid and other disease. Nat. Med. 1995, 1, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Plate, K.H.; Breier, G.; Weich, H.A.; Risau, W. Vascular endothelial growth factor is a potential tumour angiogenesis factor in human gliomas in vivo. Nature 1992, 359, 845–848. [Google Scholar] [CrossRef] [PubMed]
- Carmeliet, P. Angiogenesis in life, disease and medicine. Nature 2005, 438, 932–936. [Google Scholar] [CrossRef] [PubMed]
- Gillies, R.J.; Schornack, P.A.; Secomb, T.W.; Raghunand, N. Causes and effects of heterogeneous perfusion in tumors. Neoplasia 1999, 1, 197–207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, M.C.; Mushawah, F.A.; Gao, F.; Aft, R.L.; Gillanders, W.E.; Eberlein, T.J.; Margenthaler, J.A. Predictors of Complete Pathologic Response After Neoadjuvant Systemic Therapy for Breast Cancer. Am. J. Surg. 2009, 198, 520–525. [Google Scholar] [CrossRef] [Green Version]
- Jain, R.K. Normalizing Tumor Microenvironment to Treat Cancer: Bench to Bedside to Biomarkers. J. Clin. Oncol. 2013, 31, 2205–2218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whisenant, J.G.; Sorace, A.G.; McIntyre, J.O.; Kang, H.; Sánchez, V.; Loveless, M.E.; Yankeelov, T.E. Evaluating treatment response using DW-MRI and DCE-MRI in trastuzumab responsive and resistant HER2-overexpressing human breast cancer xenografts. Transl. Oncol. 2014, 7, 768–779. [Google Scholar] [CrossRef] [Green Version]
- Gray, L.H.; Conger, A.D.; Ebert, M.; Hornsey, S.; Scott, O.C.A. The Concentration of Oxygen Dissolved in Tissues at the Time of Irradiation as a Factor in Radiotherapy. Br. J. Radiol. 1953, 26, 638–648. [Google Scholar] [CrossRef]
- Bertout, J.A.; Patel, S.A.; Simon, M.C. Hypoxia and Metabolism Series—Timeline The impact of O(2) availability on human cancer. Nat. Rev. Cancer 2008, 8, 967–975. [Google Scholar] [CrossRef] [Green Version]
- Rong, Y.; Durden, D.L.; Van Meir, E.G.; Brat, D.J. “Pseudopalisading” Necrosis in Glioblastoma: A Familiar Morphologic Feature That Links Vascular Pathology, Hypoxia, and Angiogenesis. J. Neuropathol. Exp. Neurol. 2006, 65, 529–539. [Google Scholar] [CrossRef]
- Kallman, R.F.; Dorie, M.J. Tumor oxygenation and reoxygenation during radiation theraphy: Their importance in predicting tumor response. Int. J. Radiat. Oncol. 1986, 12, 681–685. [Google Scholar] [CrossRef]
- Boss, M.-K.; Bristow, R.; Dewhirst, M.W. Linking the History of Radiation Biology to the Hallmarks of Cancer. Radiat. Res. 2014, 181, 561–577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hormuth, D.A.; Jarrett, A.M.; Lorenzo, G.; Ernesto, A.B.F.; Wu, C.; Chung, C.; Patt, D.; Yankeelov, T.E.; Hormuth, D.A.; Jarrett, A.M.; et al. Math, magnets, and medicine: Enabling personalized oncology. Expert Rev. Precis. Med. Drug Dev. 2021, 6, 79–81. [Google Scholar] [CrossRef]
- Kazerouni, A.S.; Gadde, M.; Gardner, A.; Hormuth, D.A.; Jarrett, A.M.; Johnson, K.E.; Lima, E.A.B.F.; Lorenzo, G.; Phillips, C.; Brock, A.; et al. Integrating quantitative assays with biologically-based mathematical modeling for predictive oncology. iScience 2020, 23, 101807. [Google Scholar] [CrossRef] [PubMed]
- Hormuth II, D.; Jarrett, A.; Lima, E.A.B.F.; McKenna, M.; Fuentes, D.; Yankeelov, T. Mechanism-Based Modeling of Tumor Growth and Treatment Response Constrained by Multiparametric Imaging Data. J. Clin. Oncol. Clin. Cancer Inform. 2019, 3, 1–10. [Google Scholar] [CrossRef]
- Yankeelov, T.E.; Atuegwu, N.; Hormuth, D.A.; Weis, J.A.; Barnes, S.L.; Miga, M.I.; Rericha, E.C.; Quaranta, V. Clinically Relevant Modeling of Tumor Growth and Treatment Response. Sci. Transl. Med. 2013, 5, 187ps9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rockne, R.C.; Hawkins-Daarud, A.; Swanson, K.R.; Sluka, J.P.; Glazier, J.A.; Macklin, P.; Hormuth, D.A.; Jarrett, A.M.; Lima, E.A.B.F.; Tinsley Oden, J.; et al. The 2019 mathematical oncology roadmap. Phys. Biol. 2019, 16, 41005. [Google Scholar] [CrossRef]
- Chaplain, M.A.J.; McDougall, S.R.; Anderson, A.R.A. Mathematical modeling of tumor-induced angiogenesis. Annu. Rev. Biomed. Eng. 2006, 8, 233–257. [Google Scholar] [CrossRef] [Green Version]
- Anderson, A.R.A.; Chaplain, M.A.J. Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull. Math. Biol. 1998, 60, 857–899. [Google Scholar] [CrossRef] [PubMed]
- Yankeelov, T.E.; An, G.; Saut, O.; Luebeck, E.G.; Popel, A.S.; Ribba, B.; Vicini, P.; Zhou, X.; Weis, J.A.; Ye, K.; et al. Multi-scale Modeling in Clinical Oncology: Opportunities and Barriers to Success. Ann. Biomed. Eng. 2016, 44, 2626–2641. [Google Scholar] [CrossRef]
- Jarrett, A.M.; Lima, E.A.B.F.; Hormuth, D.A.; McKenna, M.T.; Feng, X.; Ekrut, D.A.; Resende, A.C.M.; Brock, A.; Yankeelov, T.E. Mathematical models of tumor cell proliferation: A review of the literature. Expert Rev. Anticancer Ther. 2018, 18, 1271–1286. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, L.; Tan, H.; Bao, J.; Strouthos, C.; Zhou, X. Multi-scale agent-based brain cancer modeling and prediction of TKI treatment response: Incorporating EGFR signaling pathway and angiogenesis. BMC Bioinform. 2012, 13, 218. [Google Scholar] [CrossRef] [Green Version]
- Olsen, M.M.; Siegelmann, H.T. Multiscale agent-based model of tumor angiogenesis. Procedia Comput. Sci. 2013, 18, 1016–1025. [Google Scholar] [CrossRef] [Green Version]
- Jarrett, A.M.; Hormuth, D.A.; Wu, C.; Syed, A.K.; Virostko, J.; Sorace, A.; DiCarlo, J.C.; Kowalski, J.; Patt, D.; Goodgame, B.; et al. Evaluating patient-specific neoadjuvant regimens for breast cancer via a mathematical model constrained by quantitative magnetic resonance imaging data. Neoplasia 2020, 22, 820–830. [Google Scholar] [CrossRef] [PubMed]
- Vilanova, G.; Colominas, I.; Gomez, H. Computational Modeling of Tumor-Induced Angiogenesis. Arch. Comput. Methods Eng. 2017, 24, 1071–1102. [Google Scholar] [CrossRef]
- Scianna, M.; Bell, C.G.; Preziosi, L. A review of mathematical models for the formation of vascular networks. J. Theor. Biol. 2013, 333, 174–209. [Google Scholar] [CrossRef] [Green Version]
- Dorraki, M.; Fouladzadeh, A.; Allison, A.; Bonder, C.S.; Abbott, D. Angiogenic Networks in Tumors—Insights via Mathematical Modeling. IEEE Access 2020, 8, 43215–43228. [Google Scholar] [CrossRef]
- Hormuth, D.A.; Jarrett, A.M.; Feng, X.; Yankeelov, T.E. Calibrating a Predictive Model of Tumor Growth and Angiogenesis with Quantitative MRI. Ann. Biomed. Eng. 2019, 47, 1539–1551. [Google Scholar] [CrossRef]
- Wu, C.; Hormuth, D.A.; Oliver, T.A.; Pineda, F.; Lorenzo, G.; Karczmar, G.S.; Moser, R.D.; Yankeelov, T.E. Patient-Specific Characterization of Breast Cancer Hemodynamics Using Image-Guided Computational Fluid Dynamics. IEEE Trans. Med. Imaging 2020, 39, 2760–2771. [Google Scholar] [CrossRef]
- Gurcan, M.N.; Boucheron, L.E.; Can, A.; Madabhushi, A.; Rajpoot, N.M.; Yener, B. Histopathological Image Analysis: A Review. IEEE Rev. Biomed. Eng. 2009, 2, 147–171. [Google Scholar] [CrossRef] [Green Version]
- Heindl, A.; Nawaz, S.; Yuan, Y. Mapping spatial heterogeneity in the tumor microenvironment: A new era for digital pathology. Lab. Investig. 2015, 95, 377–384. [Google Scholar] [CrossRef] [Green Version]
- Saucedo, A.M.; De La Cerda, J.; Suami, H.; Serda, R.E. Multimodal imaging of the tumor microenvironment and biological responses to immune therapy. Biomed. Microdevices 2018, 20, 105. [Google Scholar] [CrossRef]
- Wu, N.Z.; Klitzman, B.; Rosner, G.; Needham, D.; Dewhirst, M.W. Measurement of material extravasation in microvascular networks using fluorescence video-microscopy. Microvasc. Res. 1993, 46, 231–253. [Google Scholar] [CrossRef] [PubMed]
- Hori, K.; Saito, S.; Tamai, M. Effect of irradiation on neovascularization in rat skinfold chambers: Implications for clinical trials of low-dose radiotherapy for wet-type age-related macular degeneration. Int. J. Radiat. Oncol. Biol. Phys. 2004, 60, 1564–1571. [Google Scholar] [CrossRef]
- Dewhirst, M.W.; Ong, E.T.; Braun, R.D.; Smith, B.; Klitzman, B.; Evans, S.M.; Wilson, D. Quantification of longitudinal tissue pO2 gradients in window chamber tumours: Impact on tumour hypoxia. Br. J. Cancer 1999, 79, 1717–1722. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dewhirst, M.W.; Ong, E.T.; Klitzman, B.; Secomb, T.W.; Vinuya, R.Z.; Dodge, R.; Brizel, D.; Gross, J.F. Perivascular oxygen tensions in a transplantable mammary tumor growing in a dorsal flap window chamber. Radiat. Res. 1992, 130, 171. [Google Scholar] [CrossRef]
- Koehl, G.E.; Gaumann, A.; Geissler, E.K. Intravital microscopy of tumor angiogenesis and regression in the dorsal skin fold chamber: Mechanistic insights and preclinical testing of therapeutic strategies. Clin. Exp. Metastasis 2009, 26, 329–344. [Google Scholar] [CrossRef] [PubMed]
- Tozer, G.M.; Ameer-Beg, S.M.; Baker, J.; Barber, P.R.; Hill, S.A.; Hodgkiss, R.J.; Locke, R.; Prise, V.E.; Wilson, I.; Vojnovic, B. Intravital imaging of tumour vascular networks using multi-photon fluorescence microscopy. Adv. Drug Deliv. Rev. 2005, 57, 135–152. [Google Scholar] [CrossRef]
- Brown, E.; Brunker, J.; Bohndiek, S.E. Photoacoustic imaging as a tool to probe the tumour microenvironment. DMM Dis. Model. Mech. 2019, 12, dmm039636. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jathoul, A.P.; Laufer, J.; Ogunlade, O.; Treeby, B.; Cox, B.; Zhang, E.; Johnson, P.; Pizzey, A.R.; Philip, B.; Marafioti, T.; et al. Deep in vivo photoacoustic imaging of mammalian tissues using a tyrosinase-based genetic reporter. Nat. Photonics 2015, 9, 239–246. [Google Scholar] [CrossRef]
- Fox, S.B.; Harris, A.L. Histological quantitation of tumour angiogenesis. APMIS 2004, 112, 413–430. [Google Scholar] [CrossRef] [PubMed]
- Ehling, J.; Theek, B.; Gremse, F.; Baetke, S.; Möckel, D.; Maynard, J.; Ricketts, S.A.; Grüll, H.; Neeman, M.; Knuechel, R.; et al. Micro-CT imaging of tumor angiogenesis: Quantitative measures describing micromorphology and vascularization. Am. J. Pathol. 2014, 184, 431–441. [Google Scholar] [CrossRef]
- Stamatelos, S.K.; Kim, E.; Pathak, A.P.; Popel, A.S. A bioimage informatics based reconstruction of breast tumor microvasculature with computational blood flow predictions. Microvasc. Res. 2014, 91, 8–21. [Google Scholar] [CrossRef] [Green Version]
- Stamatelos, S.K.; Bhargava, A.; Kim, E.; Popel, A.S.; Pathak, A.P. Tumor Ensemble-Based Modeling and Visualization of Emergent Angiogenic Heterogeneity in Breast Cancer. Sci. Rep. 2019, 9, 5276. [Google Scholar] [CrossRef]
- McDonald, D.M.; Choyke, P.L. Imaging of angiogenesis: From microscope to clinic. Nat. Med. 2003, 9, 713–725. [Google Scholar] [CrossRef] [PubMed]
- Iwazawa, J.; Ohue, S.; Mitani, T.; Abe, H.; Hashimoto, N.; Hamuro, M.; Nakamura, K. Identifying feeding arteries during TACE of hepatic tumors: Comparison of C-Arm CT and digital subtraction angiography. Am. J. Roentgenol. 2009, 192, 1057–1063. [Google Scholar] [CrossRef]
- Drescher, R.; Freesmeyer, M. PET angiography: Application of early dynamic PET/CT to the evaluation of arteries. Am. J. Roentgenol. 2013, 201, 908–911. [Google Scholar] [CrossRef]
- Cuenod, C.A.; Fournier, L.; Balvay, D.; Guinebretière, J.M. Tumor angiogenesis: Pathophysiology and implications for contrast-enhanced MRI and CT assessment. Abdom. Imaging 2006, 31, 188–193. [Google Scholar] [CrossRef] [PubMed]
- Soriano, A.; Castells, A.; Ayuso, C.; Ayuso, J.R.; De Caralt, M.T.; Ginès, M.À.; Real, M.I.; Gilabert, R.; Quintó, L.; Trilla, A.; et al. Preoperative Staging and Tumor Resectability Assessment of Pancreatic Cancer: Prospective Study Comparing Endoscopic Ultrasonography, Helical Computed Tomography, Magnetic Resonance Imaging, and Angiography. Am. J. Gastroenterol. 2004, 99, 492–501. [Google Scholar] [CrossRef]
- Mullani, N.A.; Herbst, R.S.; O’Neil, R.G.; Gould, K.L.; Barron, B.J.; Abbruzzese, J.L. Tumor blood flow measured by PET dynamic imaging of first-pass 18F-FDG uptake: A comparison with 15O-labeled water-measured blood flow. J. Nucl. Med. 2008, 49, 517–523. [Google Scholar] [CrossRef] [Green Version]
- Massaro, A.; Ferretti, A.; Secchiero, C.; Cittadin, S.; Milan, E.; Tamiso, L.; Pavan, L.; Tommasi, E.; Marzola, M.C.; Chondrogiannis, S.; et al. Optimising 18F-Choline PET/CT acquisition protocol in prostate cancer patients. N. Am. J. Med. Sci. 2012, 4, 416–420. [Google Scholar] [PubMed] [Green Version]
- Van Vliet, M.; Van Dijke, C.F.; Wielopolski, P.A.; Ten Hagen, T.L.M.; Veenland, J.F.; Preda, A.; Loeve, A.J.; Eggermont, A.M.M.; Krestin, G.P. MR angiography of tumor-related vasculature: From the clinic to the microenvironment. Radiographics 2005, 25, 85–98. [Google Scholar] [CrossRef]
- Brubaker, L.M.; Bullitt, E.; Yin, C.; Van Dyke, T.; Lin, W. Magnetic resonance angiography visualization of abnormal tumor vasculature in genetically engineered mice. Cancer Res. 2005, 65, 8218–8223. [Google Scholar] [CrossRef] [Green Version]
- Bullitt, E.; Zeng, D.; Gerig, G.; Aylward, S.; Joshi, S.; Smith, J.K.; Lin, W.; Ewend, M.G. Vessel tortuosity and brain tumor malignancy: A blinded study. Proc. Acad. Radiol. 2005, 12, 1232–1240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neves, F.; Huwart, L.; Jourdan, G.; Reizine, D.; Herman, P.; Vicaut, E.; Guichard, J.P. Head and neck paragangliomas: Value of contrast-enhanced 3D MR angiography. Proc. Am. J. Neuroradiol. 2008, 29, 883–889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuss, M.; Wenz, F.; Essig, M.; Muenter, M.; Debus, J.; Herman, T.S.; Wannenmacher, M. Tumor angiogenesis of low-grade astrocytomas measured by dynamic susceptibility contrast-enhanced MRI (DSC-MRI) is predictive of local tumor control after radiation therapy. Int. J. Radiat. Oncol. Biol. Phys. 2001, 51, 478–482. [Google Scholar] [CrossRef]
- Kickingereder, P.; Brugnara, G.; Hansen, M.B.; Nowosielski, M.; Pflüger, I.; Schell, M.; Isensee, F.; Foltyn, M.; Neuberger, U.; Kessler, T.; et al. Noninvasive characterization of tumor angiogenesis and oxygenation in bevacizumab-treated recurrent glioblastoma by using dynamic susceptibility MRI: Secondary analysis of the European Organization for Research and Treatment of Cancer 26101 Trial. Radiology 2020, 297, 164–175. [Google Scholar] [CrossRef]
- Puig, J.; Blasco, G.; Daunis-i-Estadella, J.; Alberich-Bayarri, A.; Essig, M.; Jain, R.; Remollo, S.; Hernández, D.; Puigdemont, M.; Sánchez-González, J.; et al. High-resolution blood-pool-contrast-enhanced MR angiography in glioblastoma: Tumor-associated neovascularization as a biomarker for patient survival. A preliminary study. Neuroradiology 2016, 58, 17–26. [Google Scholar] [CrossRef]
- Cai, W.; Shin, D.W.; Chen, K.; Gheysens, O.; Cao, Q.; Wang, S.X.; Gambhir, S.S.; Chen, X. Peptide-labeled near-infrared quantum dots for imaging tumor vasculature in living subjects. Nano Lett. 2006, 6, 669–676. [Google Scholar] [CrossRef]
- Senarathna, J.; Prasad, A.; Bhargava, A.; Gil, S.; Thakor, N.V.; Pathak, A.P. HemoSYS: A Toolkit for Image-based Systems Biology of Tumor Hemodynamics. Sci. Rep. 2020, 10, 2372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sze, D.Y.; Razavi, M.K.; So, S.K.S.; Jeffrey, J. Impact of multidetector CT hepatic arteriography on the planning of chemoembolization treatment of hepatocellular carcinoma. Am. J. Roentgenol. 2001, 177, 1339–1345. [Google Scholar] [CrossRef] [PubMed]
- Fishman, E.K.; Horton, K.M. Imaging Pancreatic Cancer: The Role of Multidetector CT with Three-Dimensional CT Angiography. Pancreatology 2001, 1, 610–624. [Google Scholar] [CrossRef]
- Horton, K.M.; Fishman, E.K. Volume-rendered 3D CT of the mesenteric vasculature: Normal anatomy, anatomic variants, and pathologic conditions. Radiographics 2002, 22, 161–172. [Google Scholar] [CrossRef] [PubMed]
- Bullitt, E.; Gerig, G.; Pizer, S.M.; Lin, W.; Aylward, S.R. Measuring Tortuosity of the Intracerebral Vasculature from MRA Images. IEEE Trans. Med. Imaging 2003, 22, 1163–1171. [Google Scholar] [CrossRef] [Green Version]
- Mustafi, D.; Leinroth, A.; Fan, X.; Markiewicz, E.; Zamora, M.; Mueller, J.; Conzen, S.D.; Karczmar, G.S. Magnetic resonance angiography shows increased arterial blood supply associated with murine mammary cancer. Int. J. Biomed. Imaging 2019, 2019. [Google Scholar] [CrossRef] [PubMed]
- Kan, Z.; Phongkitkaran, S.; Kobayashi, S.; Tang, Y.; Ellis, L.M.; Lee, T.Y.; Charnsangavej, C. Functional CT for quantifying tumor perfusion in antiangiogenic therapy in a rat model. Radiology 2005, 237, 151–158. [Google Scholar] [CrossRef]
- Yankeelov, T.E.; Cron, G.O.; Addison, C.L.; Wallace, J.C.; Wilkins, R.C.; Pappas, B.A.; Santyr, G.E.; Gore, J.C. Comparison of a reference region model with direct measurement of an AIF in the analysis of DCE-MRI data. Magn. Reson. Med. 2007, 57, 353–361. [Google Scholar] [CrossRef]
- Pineda, F.D.; Medved, M.; Wang, S.; Fan, X.; Schacht, D.V.; Sennett, C.; Oto, A.; Newstead, G.M.; Abe, H.; Karczmar, G.S. Ultrafast Bilateral DCE-MRI of the Breast with Conventional Fourier Sampling: Preliminary Evaluation of Semi-quantitative Analysis. Acad. Radiol. 2016, 23, 1137–1144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, C.; Pineda, F.; Hormuth, D.A., II; Karczmar, G.S.; Yankeelov, T.E. Quantitative analysis of vascular properties derived from ultrafast DCE-MRI to discriminate malignant and benign breast tumors. Magn. Reson. Med. 2019, 81, 2147–2160. [Google Scholar] [CrossRef]
- Li, C.Y.; Shan, S.; Huang, Q.; Braun, R.D.; Lanzen, J.; Hu, K.; Lin, P.; Dewhirst, M.W. Initial stages of tumor cell-induced angiogenesis: Evaluation via skin window chambers in rodent models. J. Natl. Cancer Inst. 2000, 92, 143–147. [Google Scholar] [CrossRef] [Green Version]
- Hak, S.; Reitan, N.K.; Haraldseth, O.; De Lange Davies, C. Intravital microscopy in window chambers: A unique tool to study tumor angiogenesis and delivery of nanoparticles. Angiogenesis 2010, 13, 113–130. [Google Scholar] [CrossRef] [PubMed]
- Perfahl, H.; Byrne, H.M.; Chen, T.; Estrella, V.; Alarcón, T.; Lapin, A.; Gatenby, R.A.; Gillies, R.J.; Lloyd, M.C.; Maini, P.K.; et al. Multiscale Modelling of Vascular Tumour Growth in 3D: The Roles of Domain Size and Boundary Conditions. PLoS ONE 2011, 6, e14790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stepanova, D.; Byrne, H.M.; Maini, P.K.; Alarcon, T. A multiscale model of complex endothelial cell dynamics in early angiogenesis. PLoS Comput. Biol. 2021, 17, 1–44. [Google Scholar] [CrossRef]
- Jakobsson, L.; Franco, C.A.; Bentley, K.; Collins, R.T.; Ponsioen, B.; Aspalter, I.M.; Rosewell, I.; Busse, M.; Thurston, G.; Medvinsky, A.; et al. Endothelial cells dynamically compete for the tip cell position during angiogenic sprouting. Nat. Cell Biol. 2010, 12, 943–953. [Google Scholar] [CrossRef]
- Gadde, M.; Lima, E.A.B.F.; Phillips, C.M.; Rylander, M.N.; Yankeelov, T.E. A multi-scale model of tumor growth and angiogenesis calibrated by data from a tissue-mimicking, 3D, microfluidic platform. In Proceedings of the Cancer Research UK-AACR Joint Conference on Engineering and Physical Sciences in Oncology, London, England, 15–17 October 2019. [Google Scholar]
- D’Esposito, A.; Sweeney, P.W.; Ali, M.; Saleh, M.; Ramasawmy, R.; Roberts, T.A.; Agliardi, G.; Desjardins, A.; Lythgoe, M.F.; Pedley, R.B.; et al. Computational fluid dynamics with imaging of cleared tissue and of in vivo perfusion predicts drug uptake and treatment responses in tumours. Nat. Biomed. Eng. 2018, 2, 773–787. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Vilanova, G.; Gomez, H. Phase-field model of vascular tumor growth: Three-dimensional geometry of the vascular network and integration with imaging data. Comput. Methods Appl. Mech. Eng. 2020, 359, 112648. [Google Scholar] [CrossRef]
- Vilanova, G.; Burés, M.; Colominas, I.; Gomez, H. Computational modelling suggests complex interactions between interstitial flow and tumour angiogenesis. J. R. Soc. Interface 2018, 15, 20180415. [Google Scholar] [CrossRef] [Green Version]
- Vikram, A.; Robert, J. An imaging-based stochastic model for simulation of tumour vasculature. Phys. Med. Biol. 2012, 57, 6103. [Google Scholar]
- Adhikarla, V.; Jeraj, R. An imaging-based computational model for simulating angiogenesis and tumour oxygenation dynamics. Phys. Med. Biol. 2016, 61, 3885–3902. [Google Scholar] [CrossRef] [PubMed]
- Hormuth, D.A.; Jarrett, A.M.; Yankeelov, T.E. Forecasting tumor and vasculature response dynamics to radiation therapy via image based mathematical modeling. Radiat. Oncol. 2020, 15, 4. [Google Scholar] [CrossRef]
- Jarrett, A.; Hormuth, D., II; Barnes, S.; Feng, X.; Huang, W.; Yankeelov, T. Incorporating drug delivery into an imaging-driven, mechanics-coupled reaction diffusion model for predicting the response of breast cancer to neoadjuvant chemotherapy: Theory and preliminary clinical results. Phys. Med. Biol. 2018, 63, 105015. [Google Scholar] [CrossRef]
- Frieboes, H.B.; Jin, F.; Chuang, Y.-L.; Wise, S.M.; Lowengrub, J.S.; Cristini, V. Three-dimensional multispecies nonlinear tumor growth-II: Tumor invasion and angiogenesis. J. Theor. Biol. 2010, 264, 1254–1278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vavourakis, V.; Wijeratne, P.A.; Shipley, R.; Loizidou, M.; Stylianopoulos, T.; Hawkes, D.J. A Validated Multiscale In-Silico Model for Mechano-sensitive Tumour Angiogenesis and Growth. PLoS Comput. Biol. 2017, 13, e1005259. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.M.; Chaplain, M.A.J. Explicit solutions of a simplified model of capillary sprout growth during tumour angiogenesis. Appl. Math. Lett. 1995, 8, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Cristini, V.; Lowengrub, J.; Nie, Q. Nonlinear simulation of tumor growth. J. Math. Biol. 2003, 46, 191–224. [Google Scholar] [CrossRef]
- Chaplain, M.A.J. Avascular growth, angiogenesis and vascular growth in solid tumours: The mathematical modelling of the stages of tumour development. Math. Comput. Model. 1996, 23, 47–87. [Google Scholar] [CrossRef]
- Owen, M.R.; Alarcón, T.; Maini, P.K.; Byrne, H.M. Angiogenesis and vascular remodelling in normal and cancerous tissues. J. Math. Biol. 2009, 58, 689–721. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alarcón, T.; Byrne, H.M.; Maini, P.K. A cellular automaton model for tumour growth in inhomogeneous environment. J. Theor. Biol. 2003, 225, 257–274. [Google Scholar] [CrossRef] [Green Version]
- Szabo, A.; Merks, R.M.H. Cellular Potts modeling of tumor growth, tumor invasion and tumor evolution. Front. Oncol. 2013, 3, 87. [Google Scholar] [CrossRef] [Green Version]
- Boas, S.E.M.; Merks, R.M.H. Synergy of cell-cell repulsion and vacuolation in a computational model of lumen formation. J. R. Soc. Interface 2014, 11, 20131049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McDougall, S.R.; Anderson, A.R.A.; Chaplain, M.A.J. Mathematical modelling of dynamic adaptive tumour-induced angiogenesis: Clinical implications and therapeutic targeting strategies. J. Theor. Biol. 2006, 241, 564–589. [Google Scholar] [CrossRef]
- Merks, R.M.H.; Perryn, E.D.; Shirinifard, A.; Glazier, J.A. Contact-inhibited chemotaxis in de novo and sprouting blood-vessel growth. PLoS Comput. Biol. 2008, 4, e1000163. [Google Scholar] [CrossRef] [Green Version]
- Walpole, J.; Chappell, J.C.; Cluceru, J.G.; Mac Gabhann, F.; Bautch, V.L.; Peirce, S.M. Agent-based model of angiogenesis simulates capillary sprout initiation in multicellular networks. Integr. Biol. 2015, 7, 987–997. [Google Scholar] [CrossRef] [Green Version]
- Plank, M.J.; Sleeman, B.D. A reinforced random walk model of tumour angiogenesis and anti-angiogenic strategies. Math. Med. Biol. 2003, 20, 135–181. [Google Scholar] [CrossRef]
- Phillips, C.M.; Lima, E.A.B.F.; Woodall, R.T.; Brock, A.; Yankeelov, T.E. A hybrid model of tumor growth and angiogenesis: In silico experiments. PLoS ONE 2020, 15, e0231137. [Google Scholar] [CrossRef] [PubMed]
- Vilanova, G.; Colominas, I.; Gomez, H. A mathematical model of tumour angiogenesis: Growth, regression and regrowth. J. R. Soc. Interface 2017, 14, 20160918. [Google Scholar] [CrossRef]
- Bauer, A.L.; Jackson, T.L.; Jiang, Y. A cell-based model exhibiting branching and anastomosis during tumor-induced angiogenesis. Biophys. J. 2007, 92, 3105–3121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, A.R. A hybrid mathematical model of solid tumour invasion: The importance of cell adhesion. Math. Med. Biol. 2005, 22, 163–186. [Google Scholar] [CrossRef]
- Norton, K.A.; Popel, A.S. Effects of endothelial cell proliferation and migration rates in a computational model of sprouting angiogenesis. Sci. Rep. 2016, 6, 1–10. [Google Scholar] [CrossRef]
- Lyu, J.; Cao, J.; Zhang, P.; Liu, Y.; Cheng, H. Coupled hybrid continuum-discrete model of tumor angiogenesis and growth. PLoS ONE 2016, 11, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Capasso, V.; Morale, D. Stochastic modelling of tumour-induced angiogenesis. J. Math. Biol. 2009, 58, 219–233. [Google Scholar] [CrossRef]
- Lima, E.A.B.F.; Oden, J.T.; Almeida, R.C. A hybrid ten-species phase-field model of tumor growth. Math. Model. Methods Appl. Sci. 2014, 24, 2569–2599. [Google Scholar] [CrossRef]
- Meyvantsson, I.; Beebe, D.J. Cell culture models in microfluidic systems. Annu. Rev. Anal. Chem. 2008, 1, 423–449. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Sun, Q.; Pei, J. Microfluidic-based 3D engineered microvascular networks and their applications in vascularized microtumor models. Micromachines 2018, 9, 493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsu, Y.H.; Moya, M.L.; Hughes, C.C.W.; George, S.C.; Lee, A.P. A microfluidic platform for generating large-scale nearly identical human microphysiological vascularized tissue arrays. Lab Chip 2013, 13, 2990–2998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hsu, Y.H.; Moya, M.L.; Abiri, P.; Hughes, C.C.W.; George, S.C.; Lee, A.P. Full range physiological mass transport control in 3D tissue cultures. Lab Chip 2013, 13, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Moya, M.L.; Hsu, Y.H.; Lee, A.P.; Christopher, C.W.H.; George, S.C. In vitro perfused human capillary networks. Tissue Eng. Part C Methods 2013, 19, 730–737. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raghavan, S.; Nelson, C.M.; Baranski, J.D.; Lim, E.; Chen, C.S. Geometrically controlled endothelial tubulogenesis in micropatterned gels. Tissue Eng. Part A 2010, 16, 2255–2263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vickerman, V.; Kamm, R.D. Mechanism of a flow-gated angiogenesis switch: Early signaling events at cell-matrix and cell-cell junctions. Integr. Biol. 2012, 4, 863–874. [Google Scholar] [CrossRef] [Green Version]
- Shin, Y.; Jeon, J.S.; Han, S.; Jung, G.S.; Shin, S.; Lee, S.H.; Sudo, R.; Kamm, R.D.; Chung, S. In vitro 3D collective sprouting angiogenesis under orchestrated ANG-1 and VEGF gradients. Lab Chip 2011, 11, 2175–2181. [Google Scholar] [CrossRef]
- Kim, S.; Chung, M.; Ahn, J.; Lee, S.; Jeon, N.L. Interstitial flow regulates the angiogenic response and phenotype of endothelial cells in a 3D culture model. Lab Chip 2016, 16, 4189–4199. [Google Scholar] [CrossRef] [PubMed]
- Gadde, M.; Phillips, C.; Ghousifam, N.; Sorace, A.G.; Wong, E.; Krishnamurthy, S.; Syed, A.; Rahal, O.; Yankeelov, T.E.; Woodward, W.A.; et al. In vitro vascularized tumor platform for modeling tumor-vasculature interactions of inflammatory breast cancer. Biotechnol. Bioeng. 2020, 117, 3572–3590. [Google Scholar] [CrossRef]
- Sobrino, A.; Phan, D.T.T.; Datta, R.; Wang, X.; Hachey, S.J.; Romero-López, M.; Gratton, E.; Lee, A.P.; George, S.C.; Hughes, C.C.W. 3D microtumors in vitro supported by perfused vascular networks. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Moreira-Soares, M.; Coimbra, R.; Rebelo, L.; Carvalho, J.; Travasso, R.D.M. Angiogenic Factors produced by Hypoxic Cells are a leading driver of Anastomoses in Sprouting Angiogenesis-a computational study. Sci. Rep. 2018, 8, 8726. [Google Scholar] [CrossRef] [PubMed]
- Travasso, R.D.M.; Poiré, E.C.; Castro, M.; Rodrguez-Manzaneque, J.C.; Hernández-Machado, A. Tumor angiogenesis and vascular patterning: A mathematical model. PLoS ONE 2011, 6, e19989. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Vilanova, G.; Gomez, H. Full-scale, three-dimensional simulation of early-stage tumor growth: The onset of malignancy. Comput. Methods Appl. Mech. Eng. 2017, 314, 126–146. [Google Scholar] [CrossRef]
- Fritz, M.; Jha, P.K.; Köppl, T.; Oden, J.T.; Wohlmuth, B. Analysis of a new multispecies tumor growth model coupling 3D phase-fields with a 1D vascular network. Nonlinear Anal. Real World Appl. 2021, 61, 103331. [Google Scholar] [CrossRef]
- Fritz, M.; Jha, P.K.; Köppl, T.; Tinsley Oden, J.; Wagner, A.; Wohlmuth, B. Modeling and Simulation of Vascular Tumors Embedded in Evolving Capillary Networks. arXiv 2021, arXiv:2101.10183v2. [Google Scholar]
- Vavourakis, V.; Stylianopoulos, T.; Wijeratne, P.A. In-silico dynamic analysis of cytotoxic drug administration to solid tumours: Effect of binding affinity and vessel permeability. PLoS Comput. Biol. 2018, 14, e1006460. [Google Scholar] [CrossRef]
- Wijeratne, P.A.; Vavourakis, V. A quantitative in silico platform for simulating cytotoxic and nanoparticle drug delivery to solid tumours. Interface Focus 2019, 9, 20180063. [Google Scholar] [CrossRef] [Green Version]
- Koch, T.; Flemisch, B.; Helmig, R.; Wiest, R.; Obrist, D. A multiscale subvoxel perfusion model to estimate diffusive capillary wall conductivity in multiple sclerosis lesions from perfusion MRI data. Int. J. Numer. Method. Biomed. Eng. 2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kremheller, J.; Vuong, A.T.; Schrefler, B.A.; Wall, W.A. An approach for vascular tumor growth based on a hybrid embedded/homogenized treatment of the vasculature within a multiphase porous medium model. Int. J. Numer. Method. Biomed. Eng. 2019, 35, e3253. [Google Scholar] [CrossRef] [Green Version]
- Hinow, P.; Gerlee, P.; McCawley, L.J.; Quaranta, V.; Ciobanu, M.; Wang, S.Z.; Graham, J.M.; Ayati, B.P.; Claridge, J.; Swanson, K.R.; et al. A Spatial Model of Tumor-Host Interaction: Application of Chemotherapy. Math. Biosci. Eng. 2009, 6, 521–546. [Google Scholar] [CrossRef] [PubMed]
- Swanson, K.R.; Rockne, R.C.; Claridge, J.; Chaplain, M.A.; Alvord, E.C.; Anderson, A.R.A. Quantifying the role of angiogenesis in malignant progression of gliomas: In silico modeling integrates imaging and histology. Cancer Res. 2011, 71, 7366–7375. [Google Scholar] [CrossRef] [Green Version]
- D’Angelo, C. Multiscale modelling of metabolism and transport phenomena in living tissues. Lausanne EPFL 2007. [Google Scholar] [CrossRef]
- D’Angelo, C.; Quarteroni, A. On the coupling of 1D and 3D diffusion-reaction equations. Application to tissue perfusion problems. Math. Model. Methods Appl. Sci. 2008, 18, 1481–1504. [Google Scholar] [CrossRef] [Green Version]
- Köppl, T.; Vidotto, E.; Wohlmuth, B. A 3D-1D coupled blood flow and oxygen transport model to generate microvascular networks. Int. J. Numer. Method. Biomed. Eng. 2020, 36, e3386. [Google Scholar] [CrossRef]
- Hawkins-Daarud, A.; Rockne, R.C.; Anderson, A.R.A.; Swanson, K.R. Modeling tumor-associated edema in gliomas during anti-angiogenic therapy and its impact on imageable tumor. Front. Oncol. 2013, 3, 66. [Google Scholar] [CrossRef] [Green Version]
- Kohandel, M.; Kardar, M.; Milosevic, M.; Sivaloganathan, S. Dynamics of tumor growth and combination of anti-angiogenic and cytotoxic therapies. Phys. Med. Biol. 2007, 52, 3665–3677. [Google Scholar] [CrossRef] [PubMed]
- Vidotto, E.; Koch, T.; Köppl, T.; Helmig, R.; Wohlmuth, B. Hybrid Models for Simulating Blood Flow in Microvascular Networks. Multiscale Model. Simul. 2019, 17, 1076–1102. [Google Scholar] [CrossRef] [Green Version]
- Shipley, R.J.; Smith, A.F.; Sweeney, P.W.; Pries, A.R.; Secomb, T.W. A hybrid discrete-continuum approach for modelling microcirculatory blood flow. Math. Med. Biol. 2020, 37, 40–57. [Google Scholar] [CrossRef]
- Lima, E.A.B.F.; Oden, J.T.; Wohlmuth, B.; Shahmoradi, A.; Hormuth, D.A.; Yankeelov, T.E.; Scarabosio, L.; Horger, T. Selection and validation of predictive models of radiation effects on tumor growth based on noninvasive imaging data. Comput. Methods Appl. Mech. Eng. 2017, 327, 277–305. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, G.; Hormuth, D.A.; Jarrett, A.M.; Lima, E.A.B.F.; Subramanian, S.; Biros, G.; Oden, J.T.; Hughes, T.J.R.; Yankeelov, T.E. Quantitative in vivo imaging to enable tumor forecasting and treatment optimization. arXiv 2021, arXiv:2102.12602. [Google Scholar]
- Hahnfeldt, P.; Panigrahy, D.; Folkman, J.; Hlatky, L. Tumor development under angiogenic signaling: A dynamical theory of tumor growth, treatment response, and postvascular dormancy. Cancer Res. 1999, 59, 4770–4775. [Google Scholar]
- Oden, J.T.; Hawkins, A.; Prudhomme, S. General Diffuse-interface theories and an approach to predictive tumor growth modeling. Math. Model. Methods Appl. Sci. 2010, 20, 477–517. [Google Scholar] [CrossRef] [Green Version]
- Oden, J.T.; Lima, E.A.B.F.; Almeida, R.C.; Feng, Y.; Rylander, M.N.; Fuentes, D.; Faghihi, D.; Rahman, M.M.; DeWitt, M.; Gadde, M.; et al. Toward Predictive Multiscale Modeling of Vascular Tumor Growth. Arch. Comput. Methods Eng. 2016, 23, 735–779. [Google Scholar] [CrossRef]
- Goel, S.; Duda, D.G.; Xu, L.; Munn, L.L.; Boucher, Y.; Fukumura, D.; Jain, R.K. Normalization of the vasculature for treatment of cancer and other diseases. Physiol. Rev. 2011, 91, 1071–1121. [Google Scholar] [CrossRef]
- Benjamin, T.; Kevin, R.K.; Robert, J.; Titz, B.; Kozak, K.R.; Jeraj, R. Computational modelling of anti-angiogenic therapies based on multiparametric molecular imaging data. Phys. Med. Biol. 2012, 57, 6079. [Google Scholar] [CrossRef] [Green Version]
- Hormuth, D.A.; Jarrett, A.M.; Davis, T.; Yankeelov, T.E. Towards an Image-Informed Mathematical Model of In Vivo Response to Fractionated Radiation Therapy. Cancers 2021, 13, 1765. [Google Scholar] [CrossRef] [PubMed]
- Padhani, A.R.; Liu, G.; Mu-Koh, D.; Chenevert, T.L.; Thoeny, H.C.; Takahara, T.; Dzik-Jurasz, A.; Ross, B.D.; Van Cauteren, M.; Collins, D.; et al. Diffusion-Weighted Magnetic Resonance Imaging as a Cancer Biomarker: Consensus and Recommendations. Neoplasia 2009, 11, 102–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weis, J.A.; Miga, M.I.; Arlinghaus, L.R.; Li, X.; Chakravarthy, A.B.; Abramson, V.; Farley, J.; Yankeelov, T.E. A mechanically coupled reaction-diffusion model for predicting the response of breast tumors to neoadjuvant chemotherapy. Phys. Med. Biol. 2013, 58, 5851–5866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qutub, A.A.; Mac Gabhann, F.; Karagiannis, E.D.; Vempati, P.; Popel, A.S. Multiscale models of angiogenesis. Eng. Med. Biol. Mag. IEEE 2009, 28, 14–31. [Google Scholar] [CrossRef] [Green Version]
- Jackson, T.L. Modeling Tumor Vasculature: Molecular, Cellular, and Tissue Level Aspects and Implications; Springer: New York, NY, USA, 2013. [Google Scholar]
- Heck, T.A.M.; Vaeyens, M.M.; Van Oosterwyck, H. Computational models of sprouting angiogenesis and cell migration: Towards multiscale mechanochemical models of angiogenesis. Math. Model. Nat. Phenom. 2015, 10, 108–141. [Google Scholar] [CrossRef] [Green Version]
- Alarcón, T.; Byrne, H.M.; Maini, P.K. A multiple scale model for tumor growth. Multiscale Model Simul. 2005, 3, 440–475. [Google Scholar] [CrossRef] [Green Version]
- Kennel, P.; Dichamp, J.; Barreau, C.; Guissard, C.; Teyssedre, L.; Rouquette, J.; Colombelli, J.; Lorsignol, A.; Casteilla, L.; Plouraboué, F. From whole-organ imaging to in-silico blood flow modeling: A new multi-scale network analysis for revisiting tissue functional anatomy. PLoS Comput. Biol. 2020, 16, e1007322. [Google Scholar] [CrossRef] [Green Version]
- Kim, E.; Stamatelos, S.; Cebulla, J.; Bhujwalla, Z.M.; Popel, A.S.; Pathak, A.P. Multiscale imaging and computational modeling of blood flow in the tumor vasculature. Ann. Biomed. Eng. 2012, 40, 2425–2441. [Google Scholar] [CrossRef]
- Macklin, P.; McDougall, S.; Anderson, A.R.A.; Chaplain, M.A.; Cristini, V.; Lowengrub, J. Multiscale modelling and nonlinear simulation of vascular tumour growth. J. Math. Biol. 2009, 58, 765–798. [Google Scholar] [CrossRef] [Green Version]
- Deisboeck, T.S.; Wang, Z.; Macklin, P.; Cristini, V. Multiscale cancer modeling. Annu. Rev. Biomed. Eng. 2011, 13, 127–155. [Google Scholar] [CrossRef] [Green Version]
- Shipley, R.J.; Sweeney, P.W.; Chapman, S.J.; Roose, T. A four-compartment multiscale model of fluid and drug distribution in vascular tumours. Int. J. Numer. Method. Biomed. Eng. 2020, 36, e3315. [Google Scholar] [CrossRef] [Green Version]
- Billy, F.; Ribba, B.; Saut, O.; Morre-Trouilhet, H.; Colin, T.; Bresch, D.; Boissel, J.P.; Grenier, E.; Flandrois, J.P. A pharmacologically based multiscale mathematical model of angiogenesis and its use in investigating the efficacy of a new cancer treatment strategy. J. Theor. Biol. 2009, 260, 545–562. [Google Scholar] [CrossRef] [PubMed]
- Brady, R.; Enderling, H. Mathematical Models of Cancer: When to Predict Novel Therapies, and When Not to. Bull. Math. Biol. 2019, 81, 3722–3731. [Google Scholar] [CrossRef] [Green Version]
- Lima, E.A.B.F.; Oden, J.T.; Hormuth, D.A.; Yankeelov, T.E.; Almeida, R.C. Selection, calibration, and validation of models of tumor growth. Math. Model. Methods Appl. Sci. 2016, 26, 2341–2368. [Google Scholar] [CrossRef]
- Hormuth II, D.A.; Sorace, A.G.; Virostko, J.; Abramson, R.G.; Bhujwalla, Z.M.; Enriquez-Navas, P.; Gillies, R.; Hazle, J.D.; Mason, R.P.; Quarles, C.C.; et al. Translating preclinical MRI methods to clinical oncology. J. Magn. Reson. Imaging 2019, 50, 1377–1392. [Google Scholar] [CrossRef]
- O’Connor, J.P.B.; Aboagye, E.O.; Adams, J.E.; Aerts, H.J.W.L.; Barrington, S.F.; Beer, A.J.; Boellaard, R.; Bohndiek, S.E.; Brady, M.; Brown, G.; et al. Imaging biomarker roadmap for cancer studies. Nat. Rev. Clin. Oncol. 2017, 14, 169–186. [Google Scholar] [CrossRef]
- Whisenant, J.G.; Ayers, G.D.; Loveless, M.E.; Barnes, S.L.; Colvin, D.C.; Yankeelov, T.E. Assessing reproducibility of diffusion-weighted magnetic resonance imaging studies in a murine model of HER2+ breast cancer. Magn. Reson. Imaging 2014, 32, 245–249. [Google Scholar] [CrossRef] [Green Version]
- Barnes, S.L.; Whisenant, J.G.; Loveless, M.E.; Ayers, G.D.; Yankeelov, T.E. Assessing the reproducibility of dynamic contrast enhanced magnetic resonance imaging in a murine model of breast cancer. Magn. Reson. Med. 2012, 69, 1721–1734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Arlinghaus, L.R.; Ayers, G.D.; Chakravarthy, A.B.; Abramson, R.G.; Abramson, V.G.; Atuegwu, N.; Farley, J.; Mayer, I.A.; Kelley, M.C.; et al. DCE-MRI analysis methods for predicting the response of breast cancer to neoadjuvant chemotherapy: Pilot study findings. Magn. Reson. Med. 2014, 71, 1592–1602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galbán, C.J.; Ma, B.; Malyarenko, D.; Pickles, M.D.; Heist, K.; Henry, N.L.; Schott, A.F.; Neal, C.H.; Hylton, N.M.; Rehemtulla, A.; et al. Multi-Site Clinical Evaluation of DW-MRI as a Treatment Response Metric for Breast Cancer Patients Undergoing Neoadjuvant Chemotherapy. PLoS ONE 2015, 10, e0122151. [Google Scholar] [CrossRef] [Green Version]
- Malyarenko, D.; Galbán, C.J.; Londy, F.J.; Meyer, C.R.; Johnson, T.D.; Rehemtulla, A.; Ross, B.D.; Chenevert, T.L. Multi-system repeatability and reproducibility of apparent diffusion coefficient measurement using an ice-water phantom. J. Magn. Reson. Imaging 2013, 37, 1238–1246. [Google Scholar] [CrossRef] [Green Version]
- Ger, R.B.; Mohamed, A.S.R.; Awan, M.J.; Ding, Y.; Li, K.; Fave, X.J.; Beers, A.L.; Driscoll, B.; Elhalawani, H.; Hormuth, D.A.; et al. A Multi-Institutional Comparison of Dynamic Contrast-Enhanced Magnetic Resonance Imaging Parameter Calculations. Sci. Rep. 2017, 7, 11185. [Google Scholar] [CrossRef]
- Schmainda, K.M.; Prah, M.A.; Rand, S.D.; Liu, Y.; Logan, B.; Muzi, M.; Rane, S.D.; Da, X.; Yen, Y.F.; Kalpathy-Cramer, J.; et al. Multisite concordance of DSC-MRI analysis for brain tumors: Results of a National Cancer Institute Quantitative Imaging Network Collaborative Project. Am. J. Neuroradiol. 2018, 39, 1008–1016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaupel, P.; Mayer, A. Hypoxia in cancer: Significance and impact on clinical outcome. Cancer Metastasis Rev. 2007, 26, 225–239. [Google Scholar] [CrossRef] [PubMed]
- Jarrett, A.M.; Faghihi, D.; Hormuth, D.; Lima, E.; Virostko, J.; Biros, G.; Patt, D.; Yankeelov, T.E. Optimal Control Theory for Personalized Therapeutic Regimens in Oncology: Background, History, Challenges, and Opportunities. J. Clin. Med. 2020, 9, 1314. [Google Scholar] [CrossRef]
- Björnsson, B.; Borrebaeck, C.; Elander, N.; Gasslander, T.; Gawel, D.R.; Gustafsson, M.; Jörnsten, R.; Lee, E.J.; Li, X.; Lilja, S.; et al. Digital twins to personalize medicine. Genome Med. 2019, 12, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Niederer, S.A.; Sacks, M.S.; Girolami, M.; Willcox, K. Scaling digital twins from the artisanal to the industrial. Nat. Comput. Sci. 2021, 1, 313–320. [Google Scholar] [CrossRef]
- Jarrett, A.M.; Hormuth, D.A.; Adhikarla, V.; Sahoo, P.; Abler, D.; Tumyan, L.; Schmolze, D.; Mortimer, J.; Rockne, R.C.; Yankeelov, T.E. Towards integration of 64Cu-DOTA-Trasztusumab PET-CT and MRI with mathematical modeling to predict response to neoadjuvant therapy in HER2+ breast cancer. Sci. Rep. 2020, 10. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Hormuth, D.; Pineda, F.; Karczmar, G.; Yankeelov, T. Towards patient-specific optimization of neoadjuvant treatment protocols for breast cancer based on image-based fluid dynamics. Proc. AACR 2021 Annu. Meet. 2021, 222. Pending online. [Google Scholar]
- Almendro, V.; Cheng, Y.K.; Randles, A.; Itzkovitz, S.; Marusyk, A.; Ametller, E.; Gonzalez-Farre, X.; Muñoz, M.; Russnes, H.G.; Helland, Å.; et al. Inference of tumor evolution during chemotherapy by computational modeling and in situ analysis of genetic and phenotypic cellular diversity. Cell Rep. 2014, 6, 514–527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- West, J.; Robertson-Tessi, M.; Luddy, K.; Park, D.S.; Williamson, D.F.K.; Harmon, C.; Khong, H.T.; Brown, J.; Anderson, A.R.A. The Immune Checkpoint Kick Start: Optimization of Neoadjuvant Combination Therapy Using Game Theory. JCO Clin. Cancer Inform. 2019, 3, 1–12. [Google Scholar] [CrossRef]
- Owen, M.R.; Byrne, H.M.; Lewis, C.E. Mathematical modelling of the use of macrophages as vehicles for drug delivery to hypoxic tumour sites. J. Theor. Biol. 2004, 226, 377–391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Owen, M.R.; Stamper, I.J.; Muthana, M.; Richardson, G.W.; Dobson, J.; Lewis, C.E.; Byrne, H.M. Mathematical modeling predicts synergistic antitumor effects of combining a macrophage-based, hypoxia-targeted gene therapy with chemotherapy. Cancer Res. 2011, 71, 2826–2837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konstorum, A.; Vella, A.T.; Adler, A.J.; Laubenbacher, R.C. Addressing current challenges in cancer immunotherapy with mathematical and computational modelling. J. R. Soc. Interface 2017. [Google Scholar] [CrossRef] [Green Version]

| Paper | Modeling Approach | Scale | Use of Data |
|---|---|---|---|
| Perfahl 2011 [76] | Discrete | Cell-tissue | Microscopy used to initialize vasculature network |
| Xu 2020 [81] | Hybrid | Cell-tissue | Photoacoustic imaging was used to initialize vasculature network |
| Stepanova 2021 [77] | Hybrid | Cell | Agent-based model was calibrated against in vitro assays |
| Phillips 2019,2020 [18,79,100] | Discrete | Cell | Time-resolved microscopy was used to initialize and calibrate an agent-based model |
| Paper | Modeling Approach | Scale | Use of Data |
|---|---|---|---|
| d’Esposito 2018 [80] | Continuum | Tissue | Whole tumor imaging was used to initialize vasculature network, perfusion model validated against DCE-MRI |
| Stamatelos 2019 [48] | Continuum | Tissue | Whole tumor microscopy was used to initialize tumor vasculature |
| Adhikarla 2012, 2016 [83,84] | Discrete | Tissue | CT data was used to initialize vasculature network, model parameters were calibrated against PET measures of hypoxia |
| Wu 2020 [33] | Continuum | Tissue | DCE-MRI used to initialize breast vasculature |
| Titz 2012 [143] | Continuum | Cell-Tissue | PET estimates of oxygenation and proliferation were used to initialize tumor simulation and calibrate model parameters |
| Hormuth 2019,2020 [32,85] | Continuum | Tissue | Time-resolved DCE-MRI to calibrate and validate models |
| Jarrett 2018, 2020 [28,86] | Continuum | Tissue | Time-resolved DCE-MRI used to estimate drug delivery |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hormuth, D.A., II; Phillips, C.M.; Wu, C.; Lima, E.A.B.F.; Lorenzo, G.; Jha, P.K.; Jarrett, A.M.; Oden, J.T.; Yankeelov, T.E. Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data. Cancers 2021, 13, 3008. https://doi.org/10.3390/cancers13123008
Hormuth DA II, Phillips CM, Wu C, Lima EABF, Lorenzo G, Jha PK, Jarrett AM, Oden JT, Yankeelov TE. Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data. Cancers. 2021; 13(12):3008. https://doi.org/10.3390/cancers13123008
Chicago/Turabian StyleHormuth, David A., II, Caleb M. Phillips, Chengyue Wu, Ernesto A. B. F. Lima, Guillermo Lorenzo, Prashant K. Jha, Angela M. Jarrett, J. Tinsley Oden, and Thomas E. Yankeelov. 2021. "Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data" Cancers 13, no. 12: 3008. https://doi.org/10.3390/cancers13123008
APA StyleHormuth, D. A., II, Phillips, C. M., Wu, C., Lima, E. A. B. F., Lorenzo, G., Jha, P. K., Jarrett, A. M., Oden, J. T., & Yankeelov, T. E. (2021). Biologically-Based Mathematical Modeling of Tumor Vasculature and Angiogenesis via Time-Resolved Imaging Data. Cancers, 13(12), 3008. https://doi.org/10.3390/cancers13123008






