A Novel Framework for the Optimization of Simultaneous ThermoBrachyTherapy
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
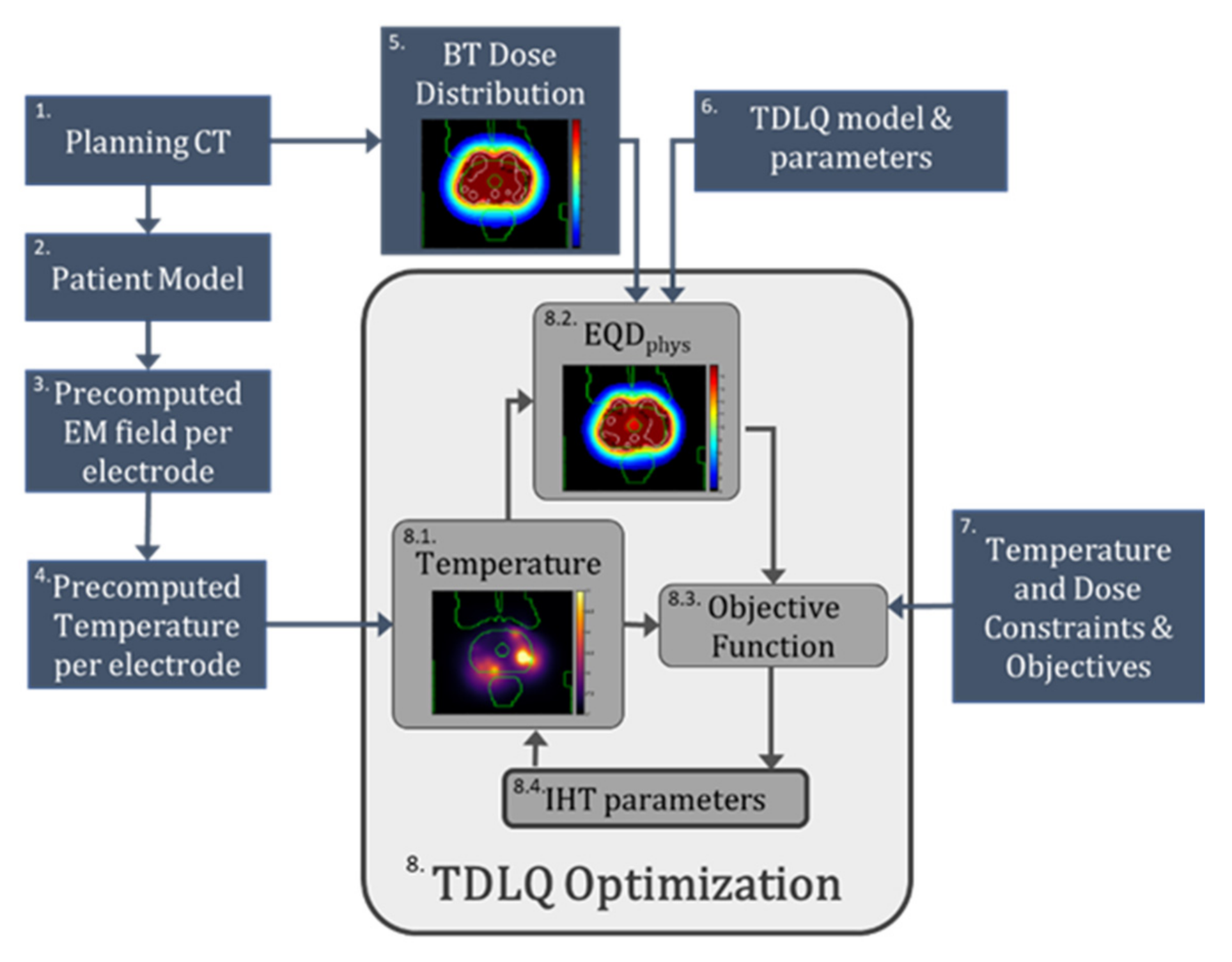
2.1. Overview of Optimization Framework
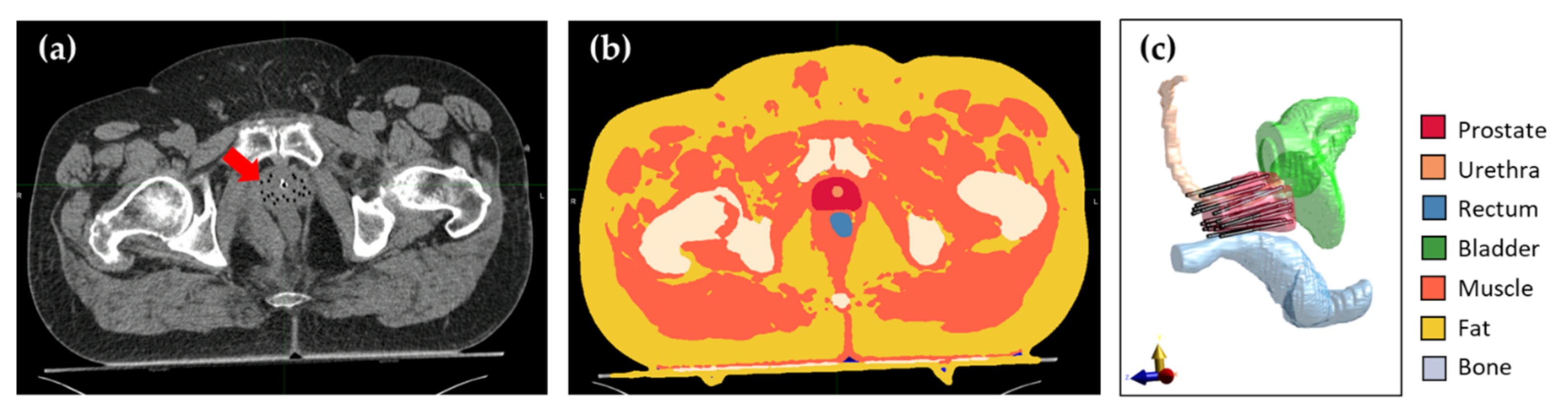
2.2. Patient Anatomy Modeling
2.3. TBT Applicator Modeling, Positioning, and E-Field Calculation
2.4. Temperature Calculation and Superpositioning
2.5. HDR-BT Treatment Plan and Dose Calculation
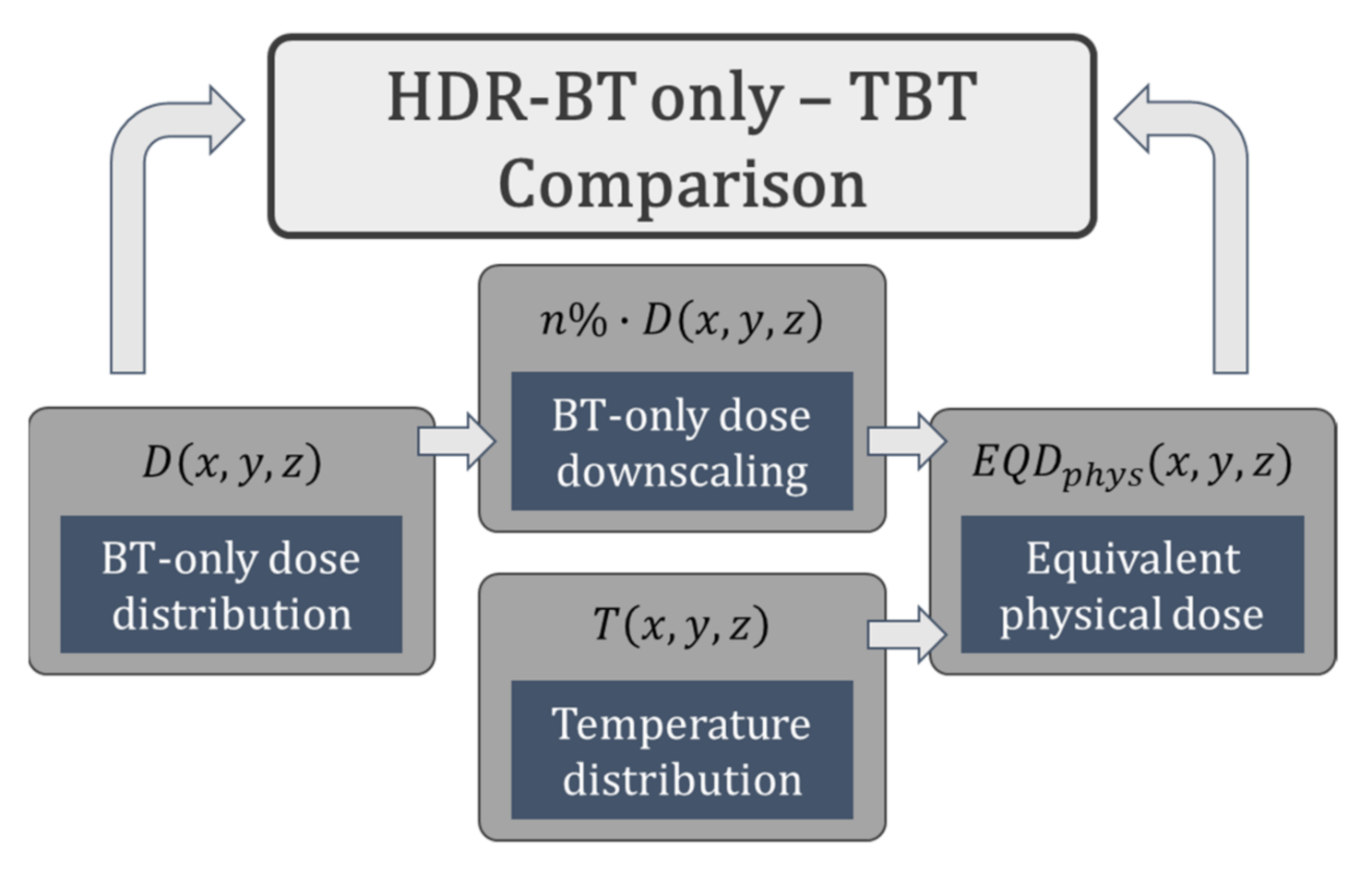
2.6. Thermoradiobiological Modeling
2.7. Thermoradiobiological Objective Function and Optimization Algorithm
2.8. Temperature Superpositioning Validation
2.9. Implementation on Patient Data
3. Results
3.1. Temperature Superpositioning Validation
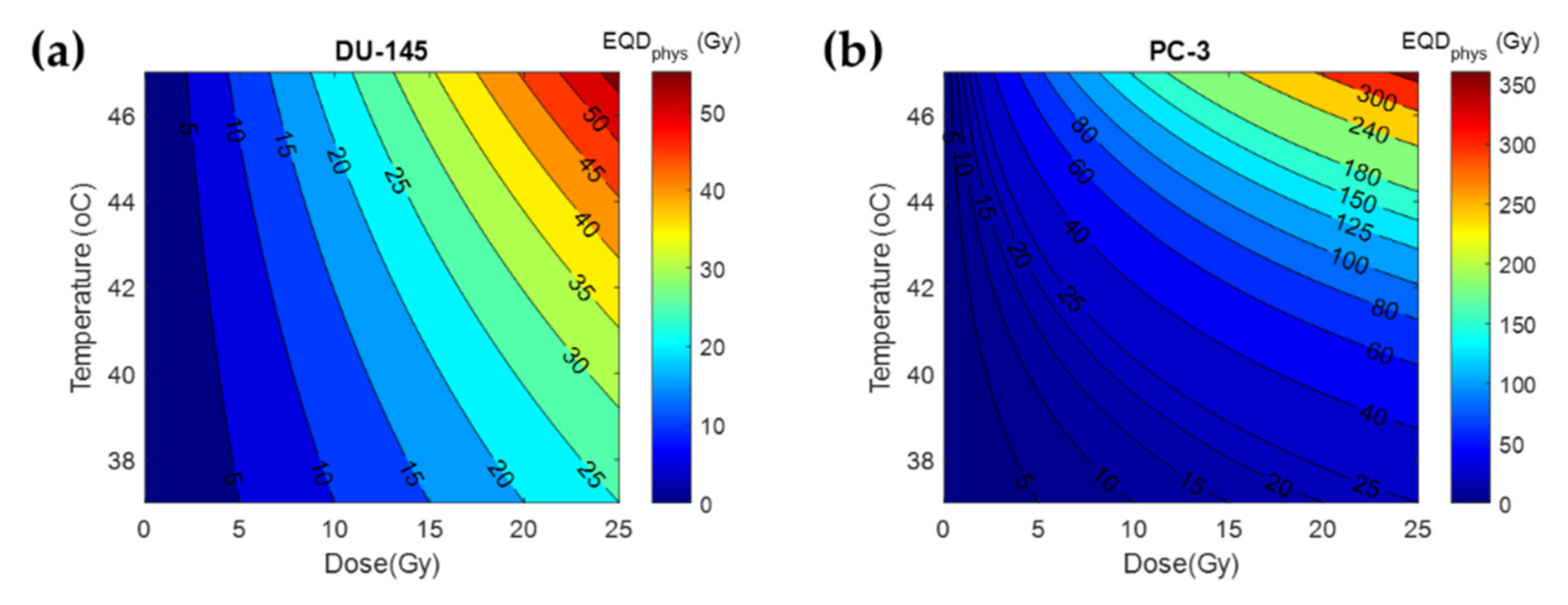
3.2. Thermal Radiosensitization
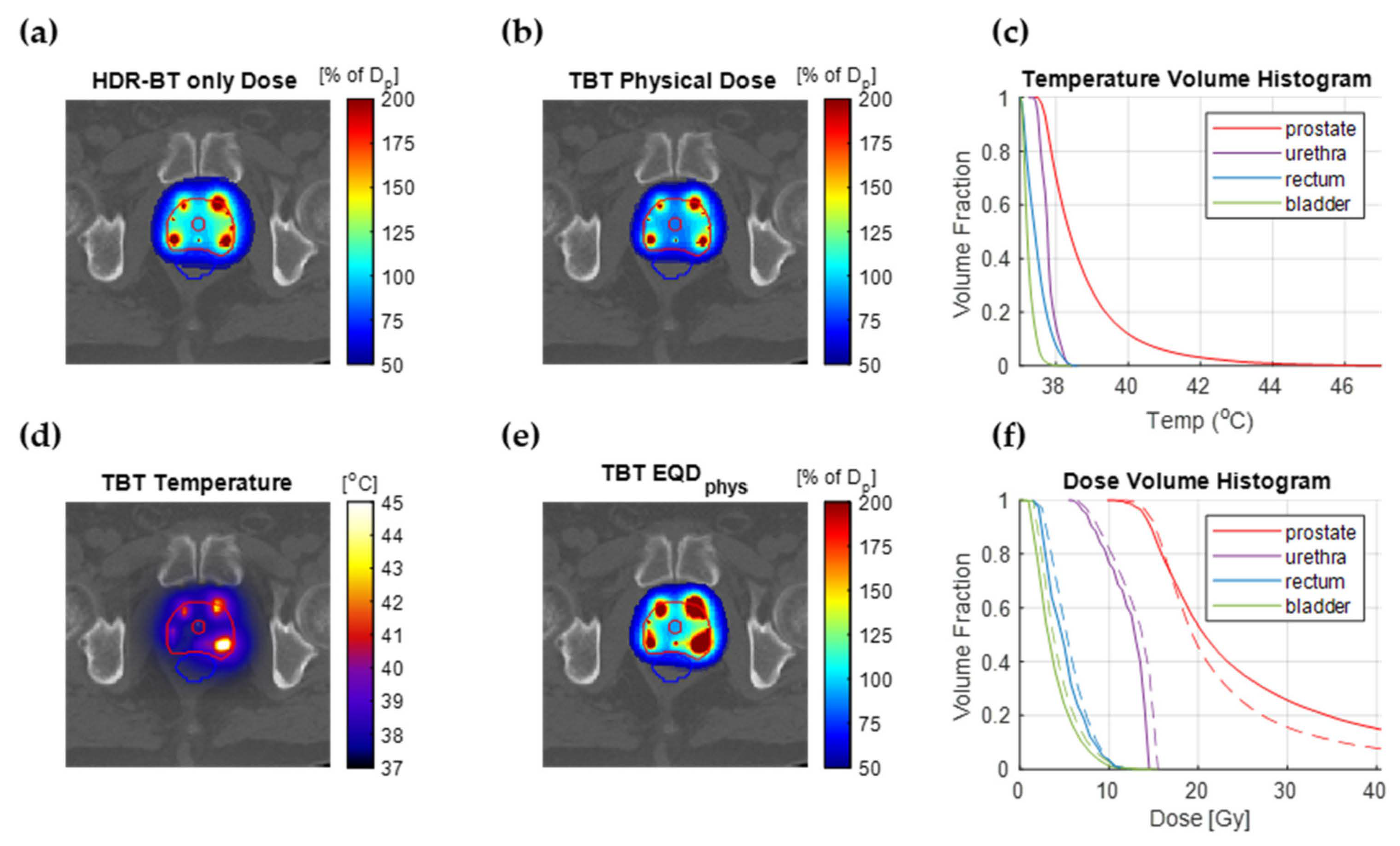
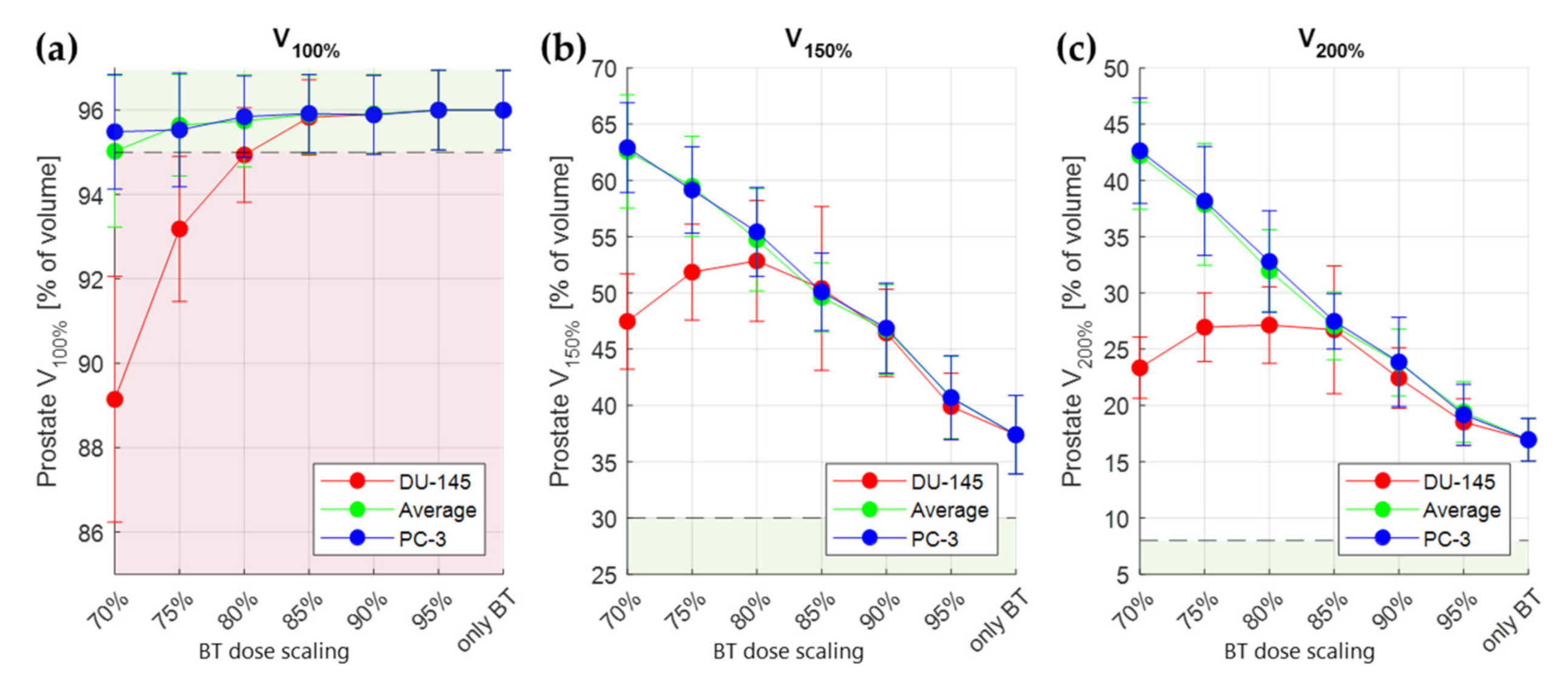
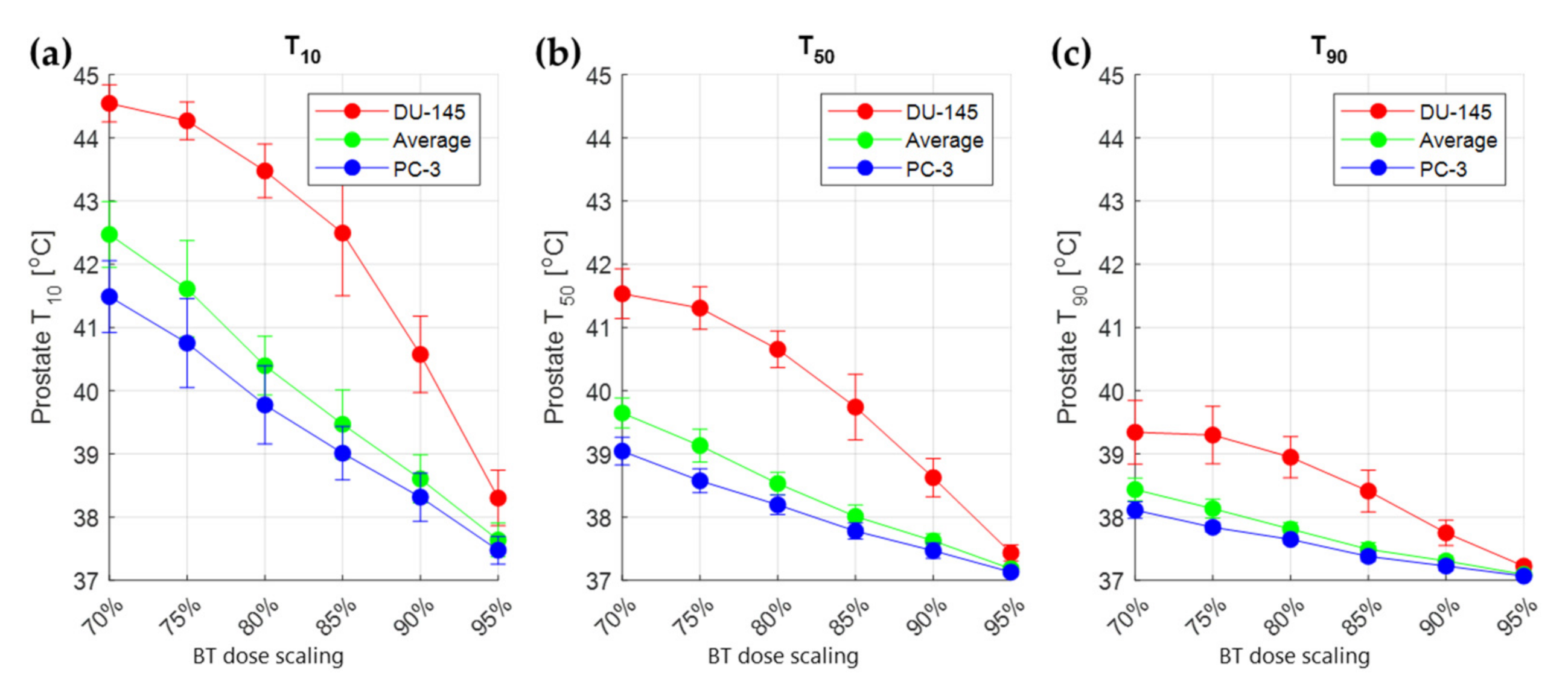
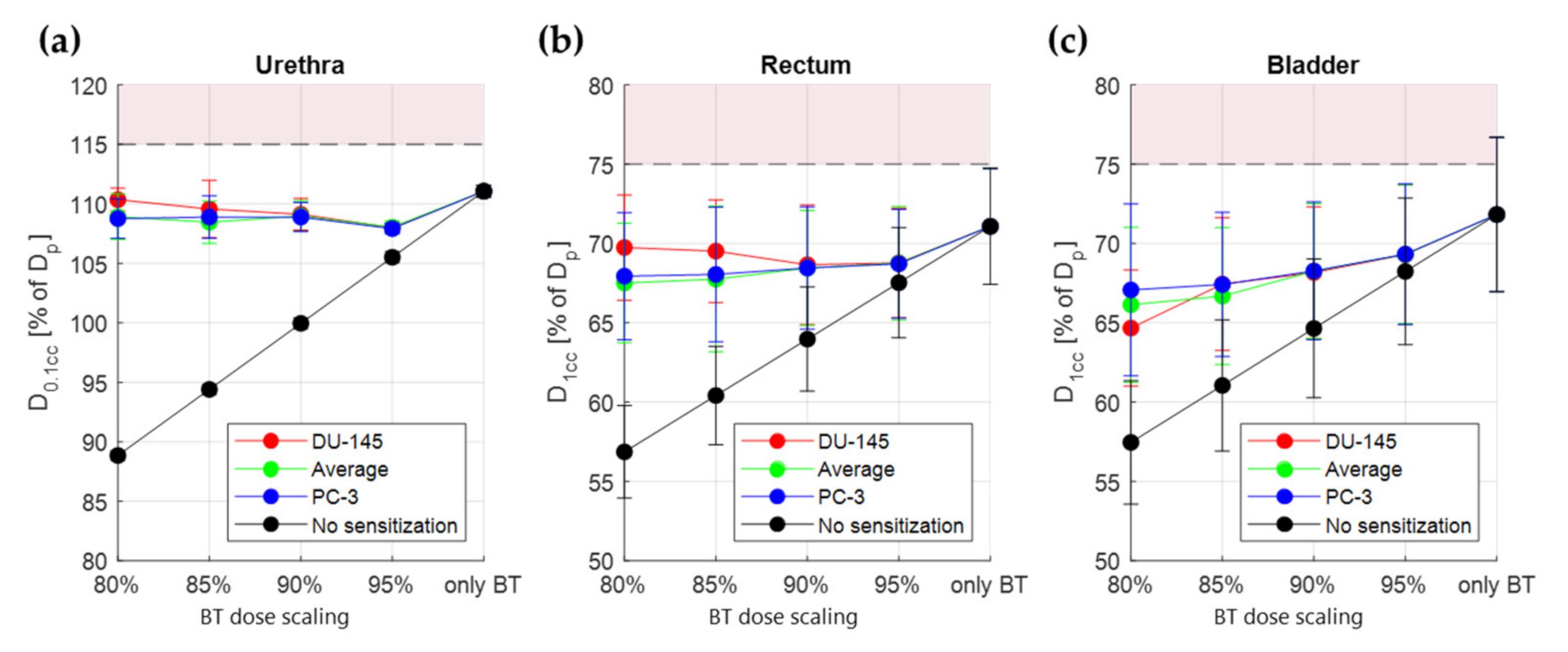
3.3. Treatment Planning Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Litwin, M.S.; Tan, H.-J. The Diagnosis and Treatment of Prostate Cancer: A Review. JAMA 2017, 317, 2532–2542. [Google Scholar] [CrossRef] [PubMed]
- Miralbell, R.; Roberts, S.A.; Zubizarreta, E.; Hendry, J.H. Dose-Fractionation Sensitivity of Prostate Cancer Deduced from Radiotherapy Outcomes of 5,969 Patients in Seven International Institutional Datasets: α/β = 1.4 (0.9–2.2) Gy. Int. J. Radiat. Oncol. Biol. Phys. 2012, 82, e17–e24. [Google Scholar] [CrossRef] [PubMed]
- Gocho, T.; Hori, M.; Fukushima, Y.; Someya, M.; Kitagawa, M.; Hasegawa, T.; Tsuchiya, T.; Hareyama, M.; Takagi, M.; Hashimoto, K. Evaluation of the Urethral α/β Ratio and Tissue Repair Half-Time for Iodine-125 Prostate Brachytherapy with or without Supplemental External Beam Radiotherapy. Brachytherapy 2020, 19, 290–297. [Google Scholar] [CrossRef] [PubMed]
- Brand, D.H.; Brüningk, S.C.; Wilkins, A.; Fernandez, K.; Naismith, O.; Gao, A.; Syndikus, I.; Dearnaley, D.P.; Tree, A.C.; van As, N. Estimates of Alpha/Beta (α/β) Ratios for Individual Late Rectal Toxicity Endpoints: An Analysis of the CHHiP Trial. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 596–608. [Google Scholar] [CrossRef] [PubMed]
- Morton, G.C. High-Dose-Rate Brachytherapy Boost for Prostate Cancer: Rationale and Technique. J. Contemp. Brachyther. 2014, 6, 323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tselis, N.; Hoskin, P.; Baltas, D.; Strnad, V.; Zamboglou, N.; Rödel, C.; Chatzikonstantinou, G. High Dose Rate Brachytherapy as Monotherapy for Localised Prostate Cancer: Review of the Current Status. Clin. Oncol. R. Coll. Radiol. 2017, 29, 401–411. [Google Scholar] [CrossRef] [PubMed]
- Hoskin, P.; Rojas, A.; Lowe, G.; Bryant, L.; Ostler, P.; Hughes, R.; Milner, J.; Cladd, H. High-Dose-Rate Brachytherapy Alone for Localized Prostate Cancer in Patients at Moderate or High Risk of Biochemical Recurrence. Int. J. Radiat. Oncol. 2012, 82, 1376–1384. [Google Scholar] [CrossRef]
- Nagore, G.; Guerra, J.L.L.; Krumina, E.; Lagos, M.; Ovalles, B.; Miró, A.; Beltran, L.; Gómez, E.; Praena-Fernandez, J.M.; del Campo, E.R.; et al. High Dose Rate Brachytherapy for Prostate Cancer: A Prospective Toxicity Evaluation of a One Day Schedule Including Two 13.5 Gy Fractions. Radiother. Oncol. 2018, 127, 219–224. [Google Scholar] [CrossRef]
- Aluwini, S.; Busser, W.M.; Alemayehu, W.G.; Boormans, J.L.; Kirkels, W.J.; Jansen, P.P.; Praag, J.O.; Bangma, C.H.; Kolkman-Deurloo, I.-K.K. Toxicity and Quality of Life after High-Dose-Rate Brachytherapy as Monotherapy for Low- and Intermediate-Risk Prostate Cancer. Radiother. Oncol. 2015, 117, 252–257. [Google Scholar] [CrossRef]
- Hoskin, P.; Colombo, A.; Henry, A.; Niehoff, P.; Hellebust, T.P.; Siebert, F.-A.; Kovacs, G. GEC/ESTRO Recommendations on High Dose Rate Afterloading Brachytherapy for Localised Prostate Cancer: An Update. Radiother. Oncol. 2013, 107, 325–332. [Google Scholar] [CrossRef] [Green Version]
- Yamada, Y.; Rogers, L.; Demanes, D.J.; Morton, G.; Prestidge, B.R.; Pouliot, J.; Cohen, G.; Zaider, M.; Ghilezan, M.; Hsu, I.-C. American Brachytherapy Society consensus guidelines for high-dose-rate prostate brachytherapy. Brachytherapy 2012, 11, 20–32. [Google Scholar] [CrossRef]
- Van Rhoon, G.C. Is CEM43 Still a Relevant Thermal Dose Parameter for Hyperthermia Treatment Monitoring? Int. J. Hyperth. 2016, 32, 50–62. [Google Scholar] [CrossRef]
- Horsman, M.R.; Overgaard, J. Hyperthermia: A Potent Enhancer of Radiotherapy. Clin. Oncol. 2007, 19, 418–426. [Google Scholar] [CrossRef]
- Datta, N.R.; Bodis, S. Hyperthermia with Radiotherapy Reduces Tumour Alpha/Beta: Insights from Trials of Thermoradiotherapy vs. Radiotherapy Alone. Radiother. Oncol. 2019, 138, 1–8. [Google Scholar] [CrossRef]
- Ryu, S.; Brown, S.L.; Kim, S.-H.; Khil, M.S.; Kim, J.H. Preferential Radiosensitization of Human Prostatic Carcinoma Cells by Mild Hyperthermia. Int. J. Radiat. Oncol. 1996, 34, 133–138. [Google Scholar] [CrossRef]
- Pajonk, F.; Van Ophoven, A.; McBride, W.H. Hyperthermia-Induced Proteasome Inhibition and Loss of Androgen Receptor Expression in Human Prostate Cancer Cells. Cancer Res. 2005, 65, 4836–4843. [Google Scholar] [CrossRef] [Green Version]
- Rajaee, Z.; Khoei, S.; Mahdavi, S.R.; Ebrahimi, M.; Shirvalilou, S.; Mahdavian, A. Evaluation of the Effect of Hyperthermia and Electron Radiation on Prostate Cancer Stem Cells. Radiat. Environ. Biophys. 2018, 57, 133–142. [Google Scholar] [CrossRef]
- Elming, P.B.; Sørensen, B.S.; Oei, A.L.; Franken, N.A.P.; Crezee, J.; Overgaard, J.; Horsman, M.R. Hyperthermia: The Optimal Treatment to Overcome Radiation Resistant Hypoxia. Cancers 2019, 11, 60. [Google Scholar] [CrossRef] [Green Version]
- Morton, G.C.; Hoskin, P.J. Single Fraction High-Dose-Rate Brachytherapy: Too good to Be True? Int. J. Radiat. Oncol. Biol. Phys. 2019, 104, 1054–1056. [Google Scholar] [CrossRef]
- Dobšíček Trefná, H.; Schmidt, M.; van Rhoon, G.C.; Kok, H.P.; Gordeyev, S.S.; Lamprecht, U.; Marder, D.; Nadobny, J.; Ghadjar, P.; Abdel-Rahman, S.; et al. Quality Assurance Guidelines for Interstitial Hyperthermia. Int. J. Hyperth. 2019, 36, 276–293. [Google Scholar] [CrossRef] [Green Version]
- Prionas, S.D.; Kapp, D.S.; Goffinet, D.R.; Ben-Yosef, R.; Fessenden, P.; Bagshaw, M.A. Thermometry of Interstitial Hyperthermia Given as an Adjuvant to Brachytherapy for the Treatment of Carcinoma of the Prostate. Int. J. Radiat. Oncol. 1994, 28, 151–162. [Google Scholar] [CrossRef]
- Williams, V.L.; Puthawala, A.; Phan, T.P.; Sharma, A.; Syed, A.N. Interstitial Hyperthermia during HDR Brachytherapy Monotherapy for Treatment of Early Stage Prostate Cancer with Benign Prostate Hyperplasia (BPH). Brachytherapy 2007, 6, 86. [Google Scholar] [CrossRef]
- Kukiełka, A.; Hetnał, M.; Dąbrowski, T.; Walasek, T.; Brandys, P.; Nahajowski, D.; Kudzia, R.; Dybek, D.; Reinfuss, M. Salvage Prostate HDR Brachytherapy Combined with Interstitial Hyperthermia for Local Recurrence after Radiation Therapy Failure. Strahlenther. Onkol. 2013, 190, 165–170. [Google Scholar] [CrossRef]
- Mei, X.; Ten Cate, R.; Van Leeuwen, C.M.; Rodermond, H.M.; De Leeuw, L.; Dimitrakopoulou, D.; Stalpers, L.J.A.; Crezee, J.; Kok, H.P.; Franken, N.A.P.; et al. Radiosensitization by Hyperthermia: The Effects of Temperature, Sequence, and Time Interval in Cervical Cell Lines. Cancers 2020, 12, 582. [Google Scholar] [CrossRef] [Green Version]
- Androulakis, I.; Mestrom, R.M.C.; Christianen, M.E.M.C.; Kolkman-Deurloo, I.-K.K.; van Rhoon, G.C. Design of the Novel ThermoBrachy Applicators Enabling Simultaneous Interstitial Hyperthermia and High Dose Rate Brachytherapy. Int. J. Hyperth. 2021, 38, 1660–1671. [Google Scholar] [CrossRef]
- Overgaard, J. Simultaneous and Sequential Hyperthermia and Radiation Treatment of an Experimental Tumor and Its Surrounding Normal Tissue in Vivo. Int. J. Radiat. Oncol. 1980, 6, 1507–1517. [Google Scholar] [CrossRef]
- Overgaard, J. The Heat Is (still) on—The Past and Future of Hyperthermic Radiation Oncology. Radiother. Oncol. 2013, 109, 185–187. [Google Scholar] [CrossRef]
- Kok, H.P.; Crezee, J.; Franken, N.; Stalpers, L.J.; Barendsen, G.W.; Bel, A. Quantifying the Combined Effect of Radiation Therapy and Hyperthermia in Terms of Equivalent Dose Distributions. Int. J. Radiat. Oncol. 2014, 88, 739–745. [Google Scholar] [CrossRef]
- Van Leeuwen, C.M.; Crezee, J.; Oei, A.L.; Franken, N.A.P.; Stalpers, L.J.A.; Bel, A.; Kok, H.P. 3D Radiobiological Evaluation of Combined Radiotherapy and Hyperthermia Treatments. Int. J. Hyperth. 2016, 33, 160–169. [Google Scholar] [CrossRef] [Green Version]
- Van Leeuwen, C.M.; Oei, A.L.; Cate, R.T.; Franken, N.A.P.; Bel, A.; Stalpers, L.J.A.; Crezee, J.; Kok, H.P. Measurement and Analysis of the Impact of Time-Interval, Temperature and Radiation Dose on Tumour Cell Survival and Its Application in Thermoradiotherapy Plan Evaluation. Int. J. Hyperth. 2017, 34, 30–38. [Google Scholar] [CrossRef] [Green Version]
- De Mendoza, A.M.; Michlíková, S.; Berger, J.; Karschau, J.; Kunz-Schughart, L.A.; McLeod, D.D. Mathematical Model for the Thermal Enhancement of Radiation Response: Thermodynamic Approach. Sci. Rep. 2021, 11, 5503. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Diederich, C.; Wootton, J.H.; Pouliot, J.; Hsu, I.-C. Optimisation-Based Thermal Treatment Planning for Catheter-Based Ultrasound Hyperthermia. Int. J. Hyperth. 2010, 26, 39–55. [Google Scholar] [CrossRef] [PubMed]
- Salgaonkar, V.A.; Prakash, P.; Diederich, C.J. Temperature Superposition for Fast Computation of 3D Temperature Distributions during Optimization and Planning of Interstitial Ultrasound Hyperthermia Treatments. Int. J. Hyperth. 2012, 28, 235–249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kok, H.P.; Kotte, A.N.T.J.; Crezee, J. Planning, Optimisation and Evaluation of Hyperthermia Treatments. Int. J. Hyperth. 2017, 33, 593–607. [Google Scholar] [CrossRef] [Green Version]
- Androulakis, I.; Mestrom, R.M.C.; Christianen, M.E.M.C.; Kolkman-Deurloo, I.-K.K.; van Rhoon, G.C. Simultaneous ThermoBrachytherapy: Electromagnetic Simulation Methods for Fast and Accurate Adaptive Treatment Planning. Sensors 2022, 22, 1328. [Google Scholar] [CrossRef]
- Haus, H.A.; Melcher, J.R. Electromagnetic Fields and Energy; Prentice Hall Englewood Cliffs: Hoboken, NJ, USA, 1989; Volume 107. [Google Scholar]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues; Version 4.0; IT’IS Foundation: Zürich, Switzerland, 2018. [Google Scholar]
- Khawaji, I.H.; Chindam, C.; Awadelkarim, O.O.; Lakhtakia, A. Dielectric Properties of and Charge Transport in Columnar Microfibrous Thin Films of Parylene C. IEEE Trans. Electron. Devices 2017, 64, 3360–3367. [Google Scholar] [CrossRef]
- Kahouli, A.; Sylvestre, A.; Jomni, F.; Yangui, B.; Legrand, J. Experimental and Theoretical Study of AC Electrical Conduction Mechanisms of Semicrystalline Parylene C Thin Films. J. Phys. Chem. A 2012, 116, 1051–1058. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Wissler, E.H. Pennes’ 1948 Paper Revisited. J. Appl. Physiol. 1998, 85, 35–41. [Google Scholar] [CrossRef]
- Das, S.K.; Clegg, S.T.; Samulski, T.V. Computational Techniques for Fast Hyperthermia Temperature Optimization. Med. Phys. 1999, 26, 319–328. [Google Scholar] [CrossRef]
- Lessard, E.; Pouliot, J. Inverse Planning Anatomy-Based Dose Optimization for HDR-Brachytherapy of the Prostate Using Fast Simulated Annealing Algorithm and Dedicated Objective Function. Med. Phys. 2001, 28, 773–779. [Google Scholar] [CrossRef]
- Perez-Calatayud, J.; Ballester, F.; Das, R.K.; DeWerd, L.A.; Ibbott, G.S.; Meigooni, A.S.; Ouhib, Z.; Rivard, M.J.; Sloboda, R.S.; Williamson, J.F. Dose Calculation for Photon-Emitting Brachytherapy Sources with Average Energy Higher than 50 keV: Report of the AAPM and ESTRO. Med. Phys. 2012, 39, 2904–2929. [Google Scholar] [CrossRef]
- Roos, M.; Kolkman-Deurloo, I.-K.; De Pan, C.; Aluwini, S. Single Fraction HDR Brachytherapy as Monotherapy in Patients with Prostate Cancer: What Is the Optimal Dose Level? Brachytherapy 2016, 15, S167–S168. [Google Scholar] [CrossRef]
- Low, D.A.; Harms, W.B.; Mutic, S.; Purdy, J.A. A Technique for the Quantitative Evaluation of Dose Distributions. Med. Phys. 1998, 25, 656–661. [Google Scholar] [CrossRef]
- De Bruijne, M.; Samaras, T.; Chavannes, N.; van Rhoon, G.C. Quantitative Validation of the 3D SAR Profile of Hyperthermia Applicators Using the Gamma Method. Phys. Med. Biol. 2007, 52, 3075. [Google Scholar] [CrossRef]
- Van Vulpen, M.; Raaymakers, B.W.; Lagendijk, J.J.W.; Crezee, J.; Leeuw, A.A.C.D.; Van Moorselaar, J.R.A.; Ligtvoet, C.M.; Battermann, J.J. Three-Dimensional Controlled Interstitial Hyperthermia Combined with Radiotherapy for Locally Advanced Prostate Carcinoma—A Feasibility Study. Int. J. Radiat. Oncol. 2002, 53, 116–126. [Google Scholar] [CrossRef]
- Christianen, M.; De Vries, K.; Jansen, P.; Luthart, L.; Kolkman-Deurloo, I.; Nout, R. PO-0244 HDR Brachytherapy Monotherapy with 2 × 13.5 Gy for Localized Prostate Cancer: Short Term Follow Up. Radiother. Oncol. 2021, 158, S203–S204. [Google Scholar] [CrossRef]
- Ling, C.; Roy, J.; Sahoo, N.; Wallner, K.; Anderson, L. Quantifying the Effect of Dose Inhomogeneity in Brachytherapy: Application to Permanent Prostatic Implant with 125I Seeds. Int. J. Radiat. Oncol. 1994, 28, 971–977. [Google Scholar] [CrossRef]
- Fatyga, M.; Williamson, J.F.; Dogan, N.; Todor, D.; Siebers, J.V.; George, R.; Barani, I.; Hagan, M. A Comparison of HDR BrachyTherapy and IMRT Techniques for Dose Escalation in Prostate Cancer: A Radiobiological Modeling Study. Med. Phys. 2009, 36, 3995–4006. [Google Scholar] [CrossRef] [Green Version]
- Datta, N.R.; Marder, D.; Datta, S.; Meister, A.; Puric, E.; Stutz, E.; Rogers, S.; Eberle, B.; Timm, O.; Staruch, M.; et al. Quantification of Thermal Dose in Moderate Clinical Hyperthermia with Radiotherapy: A Relook Using Temperature—Time Area under the Curve (AUC). Int. J. Hyperth. 2021, 38, 296–307. [Google Scholar] [CrossRef]

| Tissue | ρ (kg/m3) | σ @27 MHz (S/m) | εr @27 MHz | c (J/kg/K) | k (W/m/K) | ω (ml/kg/min) |
|---|---|---|---|---|---|---|
| Applicator Dielectric [38,39] | 1289 | 1 × 10−5 | 2.4 | 712 | 0.084 | - |
| Air [37] | 1.164 | 0 | 1.0 | 1004 | 0.0273 | - |
| Muscle [37] | 1090.4 | 0.654 | 95.8 | 3421 | 0.495 | 40 |
| Fat [37] | 911 | 0.061 | 17.9 | 2348 | 0.211 | 33 |
| Bone [37] | 1908 | 0.052 | 21.8 | 1313 | 0.320 | 10 |
| Prostate [37] | 1045 | 0.838 | 120.1 | 3760 | 0.512 | 394 |
| Rectum [37] | 1045 | 0.654 | 95.8 | 3801 | 0.557 | 0 |
| Urethra [37] | 1102 | 0.375 | 88.8 | 3306 | 0.462 | 394 |
| Bladder [37] | 1086 | 0.276 | 31.5 | 3581 | 0.522 | 78 |
| Tissue | Criterion | Aim | Type |
|---|---|---|---|
| Prostate | V100% | ≥95% | Objective |
| V150% | <30% | Soft Constraint | |
| V200% | <8% | Soft Constraint | |
| Urethra | D0.1cc | <115% | Hard Constraint |
| Rectum | D1cc | <75% | Hard Constraint |
| Bladder | D1cc | <75% | Soft Constraint |
| Tissue | α(37)/β(37) | α(43)/α(37) | β(43)/β(37) |
|---|---|---|---|
| Prostate | 3 | ||
| PC-3 [16] | 2.4 | 6.8 | |
| DU-145 [16] | 0.8 | 1.8 | |
| Normal Tissue | 3 |
| Constraints | Tissue | Criterion (Ci) | Limit (Li) | Type |
|---|---|---|---|---|
| Prostate | V100% | Value of BT-only | High pass | |
| Urethra | D0.1cc | Value of BT-only | Low pass | |
| Rectum | D1cc | Value of BT-only | Low pass | |
| Bladder | D1cc | Value of BT-only | Low pass | |
| All | Tmax | 47.5 °C | Low pass | |
| Objectives | Tissue | Criterion (Oj) | Goal (Gj) | Weight (wi) |
| Urethra | D0.1cc | 0 | 1 | |
| Rectum | D1cc | 0 | 1 | |
| Prostate | V150% | 30% of volume | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Androulakis, I.; Mestrom, R.M.C.; Christianen, M.E.M.C.; Kolkman-Deurloo, I.-K.K.; van Rhoon, G.C. A Novel Framework for the Optimization of Simultaneous ThermoBrachyTherapy. Cancers 2022, 14, 1425. https://doi.org/10.3390/cancers14061425
Androulakis I, Mestrom RMC, Christianen MEMC, Kolkman-Deurloo I-KK, van Rhoon GC. A Novel Framework for the Optimization of Simultaneous ThermoBrachyTherapy. Cancers. 2022; 14(6):1425. https://doi.org/10.3390/cancers14061425
Chicago/Turabian StyleAndroulakis, Ioannis, Rob M. C. Mestrom, Miranda E. M. C. Christianen, Inger-Karine K. Kolkman-Deurloo, and Gerard C. van Rhoon. 2022. "A Novel Framework for the Optimization of Simultaneous ThermoBrachyTherapy" Cancers 14, no. 6: 1425. https://doi.org/10.3390/cancers14061425
APA StyleAndroulakis, I., Mestrom, R. M. C., Christianen, M. E. M. C., Kolkman-Deurloo, I.-K. K., & van Rhoon, G. C. (2022). A Novel Framework for the Optimization of Simultaneous ThermoBrachyTherapy. Cancers, 14(6), 1425. https://doi.org/10.3390/cancers14061425







