Proposed Fuzzy-Stranded-Neural Network Model That Utilizes IoT Plant-Level Sensory Monitoring and Distributed Services for the Early Detection of Downy Mildew in Viticulture

Abstract

Novel monitoring architecture approaches are required to detect viticulture diseases early. Existing micro-climate decision support systems can only cope with late detection from empirical and semi-empirical models that provide less accurate results. Such models cannot alleviate precision viticulture planning and pesticide control actions, providing early reconnaissances that may trigger interventions. This paper presents a new plant-level monitoring architecture called thingsAI. The proposed system utilizes low-cost, autonomous, easy-to-install IoT sensors for vine-level monitoring, utilizing the low-power LoRaWAN protocol for sensory measurement acquisition. Facilitated by a distributed cloud architecture and open-source user interfaces, it provides state-of-the-art deep learning inference services and decision support interfaces. This paper also presents a new deep learning detection algorithm based on supervised fuzzy annotation processes, targeting downy mildew disease detection and, therefore, planning early interventions. The authors tested their proposed system and deep learning model on the grape variety of protected designation of origin called debina, cultivated in Zitsa, Greece. From their experimental results, the authors show that their proposed model can detect vine locations and timely breakpoints of mildew occurrences, which farmers can use as input for targeted intervention efforts.

1. Introduction

Plasmopara viticola (P. viticola), commonly known as downy mildew, is a North American origin fungus [1]. It invaded Europe at the end of the 18th century [1]. Downy mildew attacks vines mostly during spring when plants are in their most stressful developing stages. As a fungus, it has a two-stage-infection cycle of primary infections and repeated secondary ones [2,3,4]. The first signs of the fungus development from oomycete occurs in spring inflorescence growth, close to the 12th E-L vine stage [5], and its results are devastating if not detected and treated early [3,4,6]. Two significant environmental parameters influence P. viticola’s fungus growth. These are temperatures between 10 °C and 32 °C and increased humidity levels [3,7,8,9]. The spring oospores’ maturity succeeds the fungus oospores’ overwintering. Then spring environmental conditions lead to sporangia germinations, which in turn incubate zoospores that form germinations during wet periods, spread by wind or rain splashes to nearby leaves or berries [2,6,8].

Downy mildew oospore maturation starts with mild and rainy days in spring, usually with prolonged rainfall (e.g., at least 3–6 mm), temperatures between 12 and 26 °C, and relative humidity above 90% [2]. Then, the oospores form sporangia that, with the help of rain splashes and wind, reach the potential host tissue, typically wet young leaves near the soil. As a primary infection cycle, sporangia releases zoospores. The germinated zoospore infects young green tissues through open stomata and produces a mycelium that, by colonizing the intercellular spaces, leads to the appearance of oil spots on the leaves [2,6]. Germination mechanisms work faster when the temperature is between 20 and 24 °C and when there is rainfall or concentration of leaf litter [8,9].

According to [2,4,6], as a secondary infection cycle, the fungus initiates asexual reproduction, producing sporangiophores. Sporangia are released from the tip of the sporangiophores’ branches, and the released zoospores will emerge as secondary infections. In this cycle, the zoospores reach the berries, giving them a whitish appearance. The initial oil spot lesions usually appear as a brownish area spreading on the infected tissue at this stage. The cycle (up to sporangiophores’ production) typically lasts 5–7 up to 18 days [3,6,8].

According to Rossi et al. [4], sporangia incubation occurs at temperatures between 9.5 °C and 32 °C, and wet conditions or relative humidity above 65% ( [10]). On American varieties, the phenomenon occurs at temperatures ranging from 10 to 30 °C, with an optimum at 18–20 °C [11]; however, on Vitis vinifera Caffi pinpointed sporulating temperatures between 10.6 and 32.9 °C. Nevertheless, the authors consider Zacho’s observations for a minimum sporulating temperature of 13 °C for Vitis vinifera [12]. Furthermore, according to Caffi et al. [6], rainfall used by the majority of downy mildew models does not seem to be a triggering factor for secondary infections because the surface wetness for zoospore release and mobility can be generated by dew.

As modern Viticulture is continuously Industrialized and its practical appliances are automated, revolutionary viticulture technologies are incorporated into the vine fields [13,14]. Such technologies refer to sensors that monitor environmental conditions near the vine plants or vine plant clusters [2,15,16,17]. These data acquisition technologies bring forth elaborated processes, supported by machine learning or deep learning models, to improve agricultural practices in a more precise manner (proximal sensing) [14]. Focusing on the downy mildew fungus and the interventions that need to be accounted for the amelioration of this disease, the paper focuses in the following subsections on existing downy mildew (P. viticola) models applicable for viticulture use as well as Decision Support Systems that host such models for downy mildew forecasts at vine-plant level [15,16,18,19,20].

1.1. Related Work on Viticulture Downy Mildew Models

Several models have been proposed over the years, either of heuristic origin (empirical) or deterministic via experimentation (mechanistic), for P. viticola predictions [9,21]. Many of them have been incorporated into existing DSS systems [21]. The following models are presented in the literature as empirical models:

• Muller model is an empirical model based on temperature observations setting the infection occurrence when leaves are o 2 cm in diameter (E-L 9 development stage) and after heavy rain. According to this model, If the weather is dry (east wind), there is no risk of downy mildew, nor if the mean daily temperatures are below 12 °C or above 28 °C [10], the incubation period can be calculated in days. The actual daily add-ons to the sum based on the average daily temperature are provided by [22].
• Rule 3–10 is an empirical rule set by [23]. The rule states that infections initiate when the following conditions occur: Temperature, $T\ge$10 °C, vine shoots of 10 cm long, and at least 10mm of rainfall over the last 24–48 h.
• Goidanich model. This model assumes initiation of primary infections at E-L 12 development stage, based on Rule 3–10. After infection, the percentage of daily development of incubation is calculated as Infection Risk Cycles (IRC), using an index value (Goidanich Index-GI) based on the average daily relative humidity and temperature until it reaches 100% [24]. An appropriate table of Goidanich’s model infection percentages is used for both primary and secondary infections [19]. Above 25°, IRC is constant. Furthermore, according to Puelles et al. evaluation [25], this model on Vitis vinifera usually delivers over-prediction infection blocks with very few matches to field observations. Nevertheless, this differs from the research in northwestern Spain provided by [26].
• EPI model. This model, developed by Stryzik et al. [27], uses an EPI index metric that represents the pathogen potential infection energy $E_p$ for primary infections and the kinetic energy $E_c$ for secondary infections. For primary infections, it utilizes a set of equations that consider monthly rainfall and temperature, the number of days with rain per month, and the rainfall during the last ten days. For secondary infections, the model takes into account inputs of temperature, relative humidity, and relative humidity at night [9,28]. Potential infection energy $E_p$ is calculated using Equation (1) from October until January [27].

  $$E_p=2·\left[k(\sqrt{R_i}-\sqrt{0.95R_m})\right]+0.2·[\sqrt{R_i·T_i}-\left(\sqrt{0.95R_m{T}_m}\right)]-\left[\frac{1.5R{D}_m}{18}lo{g}_{10}\frac{Rd}{RDd}\right]$$

  (1)

  where the value k is 1.2 in October, 1 in November, and 0.8 for the rest of the months (until March), $R_i$ is the daily rainfall, $R_m$ is the mean monthly rainfall, $T_i$ the mean daily temperature, $T_m$ the mean monthly temperature, $Rd$ cumulative rainfall the last ten days, $R{D}_m$, number of monthly rainy days and $RDd$ number of rainy days the last ten days [27].
  Equation (2) gives the kinetic energy of the model calculated from April until September and corresponds to primary and secondary infections since the model assumes that oospore maturity is reached by the 31st of March [27].

  $$E_c=0.012·\frac{\frac{1}{4}{(5·R{H}_{m_{night}}+3·R{H}_{i_{10–18h}})}^2\sqrt{T_i}-R{H}_{i_{10–18h}}^2\sqrt{T_m}}{100}$$

  (2)

  where $R{H}_{m_{night}}$ is the average relative humidity at night, and $R{H}_{i_{10–18h}}$ is the average relative daily humidity, $T_i$ the average daily temperature, and $T_m$ the monthly average temperature. Finally, the EPI index value is calculated based on Equation (3) [27].

  $$EPI=\sum _{Oct}^{March}{E}_p+\sum _{Apr}^{Sept}{E}_c$$

  (3)
  From October until the end of March, the value of the EPI metric is an estimate of oospore maturation, where the first infection occurs when EPI > −10, while the EPI increases for three consecutive days [27].

Empirical models are easier to implement using sparse meteorological stations’ sensory data input, they require further evaluation and calibration to the applied viticulture environment. On the other hand, mechanistic models try to capture the infection mechanism in a holistic, more deterministic manner. Nevertheless, it requires the calculation of more elaborate metrics that cannot be easily inferred directly from environmental sensors. The following mechanistic models are presented in the literature.

• Downy Mildew foreCast is a model that tries to provide primary and secondary infection predictions. It uses a probabilistic normal distribution for primary infections using Equation (4) [29]

  $$P\left(d\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{\frac{-{(d-\mu )}^2}{2{\sigma }^2}},\mu =118-0.3R_a,\sigma =13.5+0.02R_a$$

  (4)

  where mean and standard deviation parameters are calculated by parameter $R_a$, which is the cumulative rainfall effect at the end of January according to Equation (5) [29].

  $$R_a=\sum _{21Sept}^{31Jan}{R}_m+\frac{std\left(R_m\right)}{R{D}_m}-2R_i$$

  (5)

  where $R_m$ is the mean monthly rainfall, $std\left(R_m\right)$ is the mean standard deviation of monthly rainfall, $R{D}_m$ are the total monthly rainy days and $R_i$ is the daily rainfall. Primary infections initiate when the daily probability $P\left(d\right)$ outcome reaches 3%. From this day forth, secondary infections are calculated as mentioned at [29]. It is considered that infections occur when rainfall is at least 2 mm and T ≤ 11 °C, while for seven up to 22 days after the beginning of oospore germinations [29].
• UCSC model was developed by Rossi et al. [8]. The model simulates, using a granularity time step of one hour, the entire process, starting from oospore maturation and germinations to zoospore discharge and dispersal and finally to secondary infection cycles [9]. The model uses sensory measurements of temperature, relative humidity, leaf wetness, and rainfall as inputs. Briefly, the model calculates the time when the first break of the oospore’s dormancy occurs (about the 1st of January), as well as the primary and secondary infection progress, by calculating the Relative Incidence of Infection (RII) metric value [2,4,8]. The metrics used by the model are shown in

  Table 1. UCSC model metrics and coefficients [8].

  Metric /Coef.	Equation	Description	Phys. Values	Stage
  Degree Days	$D{D}_i=\frac{{\sum }_{i=1}^m(\overline{T_i}-8)}{100},$ if $\overline{T_i}\ge 8$	cumulative sum of daily mean temperatures from Jan 1st	-	primary secondary infections
  Degree Hours	$D{H}_i=\frac{{\sum }_{i=1}^n(\overline{T_i}-10)}{1000},$ if $\overline{T_i}\ge 10$	cumulative sum ofhourly mean temperatures from Jan 1st	-	primary secondary infections
  Thermal Time	$T{T}_i={\sum }_{t=1}^n\left(\frac{1}{2.6256{\overline{T_i}}^2-116.19\overline{T_i}+1330.1)}\right),$ if $\overline{T_i}\ge 0$	cumulative hourly mean $\overline{T_i}$	-	-
  Hydro Thermal Time	$H{T}_i={\sum }_{i=1}^n(T{T}_i·M_i)$	cumulative hourly mean	-	oospore maturation germination
  Vapor Pressure Deficit	$VP{D}_i=(1-\frac{RH}{100})·6.11e^{(17.47·T)/(239+T)}$	The amount of waterin the air in termsof pressure (kPa)	min = 0 max = 12.5 norm = 0.6–0.8	-
  Moisture leaf litter	$M_i=\left\{\begin{array}{cc}1\hfill & VP{D}_i\le 4.5\hfill \\ 0\hfill & R_i=0andVP{D}_i>4.5\hfill \end{array}\right.$	cumulative hourly mean (hourly rainfall $R_i$ mm)	-	oospore maturation germination
  RII	$RII=e^{-\alpha ·e^{-\beta ·x}}$	Infection point of the Gompertz equationx = DD, DH, TT, HT	0.1	-
  Coef. $\alpha$	$\alpha =\left\{\begin{array}{cc}6.5\left(4.8–8.2\right)\hfill & forD{D}_i\hfill \\ 7.9\left(5.4–10.4\right)\hfill & forD{H}_i\hfill \\ 17.0\left(10.1–23.8\right)\hfill & forT{T}_i\hfill \\ 15.9\left(10.7–21\right)\hfill & forH{T}_i\hfill \end{array}\right.$	Coeficient $\alpha$ values	-	-
  Coef. $\beta$	$\beta =\left\{\begin{array}{cc}0.84\left(0.75–0.94\right)\hfill & forD{D}_i\hfill \\ 0.42\left(0.36–0.47\right)\hfill & forD{H}_i\hfill \\ 0.28\left(0.25–0.32\right)\hfill & forT{T}_i\hfill \\ 0.65\left(0.58–0.72\right)\hfill & forH{T}_i\hfill \end{array}\right.$	Coeficient $\beta$ values	-	-

  [8].
  Furthermore, Table 1 at [9], shows the model input parameters for oospore maturation and oospore-zoospore germination stages.
• UR model. This is a Goidanich-table-based model alternative that tries to address both primary and secondary infections [25]. According to this model, oospore maturation in winter is reached if the value of a cumulative temperatures sum reaches 140–160 °C. This sum $\sum T_m$ is calculated using mean daily temperatures ($T_m$), starting from the 1st of January, and using the following Equation (6) [30,31].

  $$\sum T_m=\sum \left\{\begin{array}{cc}\overline{T_m}-8\hfill & \overline{T_m}<8\hfill \\ \overline{T_m}\hfill & \overline{T_m}\ge 8\hfill \end{array}\right.$$

  (6)
  If oospore maturation is reached, then oospore germination occurs, providing primary sporangia either when mean relative humidity $R{H}_{8h}$ > 80 and mean temperature $T_{8h}$ > 8 for an 8-h window or when mean precipitation occurs more than 5 mm ($R{F}_m$ > 5) for the last 48 h. The first dispersion of zoospores is reached after oospore germination, when mean rainfall RF > 3 mm and $T_m$ > 8 for a 6 h interval (a modified 3–10 Rule). Then primary infections occur, if Degree hours Dh > 50, calculated based on Equation (7) [30,31].

  $$Dh=\sum _{i=1}^n\overline{T_i},ifR{H}_h\ge 90$$

  (7)

  where $T_i$ is the hourly temperature (hour $i=1\dots n$) and $R{H}_h$ is the hourly relative humidity. Secondary infections are calculated using the Goidanich table index. To achieve sporulation for secondary infections, two conditions needed to be met: $R{H}_h\ge 90$% or temperatures between 12 °C and 29 °C for at least 4 h at night [25]. Additionally, the model considers that exposure to more than 6 h above 30 °C results in the death of oospores, both for primary and secondary infections [32].
• Milvit Model. Developed by the French Plant Protection Service in the late 80s. It is a potato downy mildew simulated model, a pathogen with similar pathogen characteristics to P. viticola [33]. As mentioned by Magnien et al. [33], it uses temperature and relative humidity, four stages of the pathogen cycle. It is also supported by a DSS system. Nevertheless, this model is not taken into account since it is not targeting the phenological characteristics of V. vinifera and since, as mentioned by Puelles et al. experimentation [25], it has shown both over-prediction and under-prediction infection blocks compared to field observations.
• Vitimeteo—Plasmopara is a mechanistic model based on experimental observations, created by Bleyer et al. [34]. This model tries to predict both primary and secondary infections. The main model components are three stages: (1) Maturation oospores stage, (2) primary, and (3) secondary infections. Regarding (1) and (2) the UR model is used. However, secondary infections are calculated using mean temperature $T_m$ degree hours Dh > 50, if 3 < $T_m$ < 29, and if hourly relative humidity $R{H}_m$ > 95% [34].

The aspect of incorporating deterministic epidemiology models for precision viticulture planning is significant. Therefore, Savary et al. presented the critical factors and framework to develop dynamic epidemiology models for dual process epidemics [35]. That is, by calculating the disease x rate: $\frac{dx}{dt}=c·R_{c}p\left(x\right)f\left(x\right)·(1-p\left(x\right))h\left(x\right|y)$, as part of a model that takes into account an introductory infection rate as weight $R_c$, that compensates for the number of dispersed propagules per infectious lesion and its infectious efficiency. In contrast, $p\left(x\right)$ is the probability of the regression process of infected tissues, while $f\left(x\right)$ represents the disease rate x, considering disease multiplication, environmental parameters, latencies, and plant growth. $h\left(x\right)$ is the healthy issues growth parameter according to either infection rate x or plant growth parameter y.

Based on the previous paragraph mentioned framework, Bove et al. [3] developed a two-stage infection P. viticola simulation model taking into account environmental metrics of temperature, humidity, and variety that affect primary and secondary infections. According to Bove et al.’s elaborated model simulation scenarios, four major parameters can be considered catalytic on the rate of secondary infections: age, temperature, moisture, and grape variety [7]. Table 2 presents the simulation results of [7], under different temperature and humidity conditions, expressed as fuzzy sets, that downy mildew infestations depend on. Table 2 has been used as a piece of base information to implement the fuzzy logic annotation process of their deep learning model proposition.

Regarding vine aging, Reuveni has experimented with vine leaf aging and vine aging, showing increased resistance of both older leaves and older vine plants [36]. Variety also plays a significant role, as mentioned by [37]. Their paper examined 16 Italian grape varieties over four years and indicated the grape variety resistance variance towards downy mildew. The authors highlight here the results from the studies [36,37] that both grapes’ age and variety are discriminant factors for downy mildew. These factors can be considered uniform if a single grape variety is studied and cultivated in a specific designated area of origin, with slight aging variations in the examined area cultivation fields.

Table 2. P. viticola dependence on environmental parameters, according to [7], based on [11,38].

Environmental Description	Temperature (T °C)	Humidity (%$\mathit{RH}$)	Daily Rainfall (${\mathit{RF}}_{\mathit{mm}}$)	FGI (${\mathit{R}}_{\mathit{c}}\mathit{T}·{\mathit{R}}_{\mathit{c}}\mathit{W}$)
warm and wet	13 < T ≤ 28	70 < RH ≤ 100	RF ≥ 5	1
warm and partly wet	13 < T ≤ 28	70 < RH ≤ 95	0 < RF < 5	0.6
warm and dry	13 < T ≤ 28	70 ≤ RH ≤ 95	RF = 0	0.4
warm and very dry	13 < T ≤ 28	RH < 70	RF = 0	0.1
cold and wet	0 < T ≤ 13	RH < 70 < RH ≤ 100	RF ≥ 5	0.8
cold and partly wet	0 < T ≤ 13	70 < RH ≤ 95	0 < RF < 5	0.48
cold and dry	0 < T ≤ 13	70 ≤ RH ≤ 95	RF = 0	0.32
cold and very dry	0 < T ≤ 13	RH < 70	RF = 0	0.08

Table 2. P. viticola dependence on environmental parameters, according to [7], based on [11,38].

Environmental Description	Temperature (T °C)	Humidity (%$\mathit{RH}$)	Daily Rainfall (${\mathit{RF}}_{\mathit{mm}}$)	FGI (${\mathit{R}}_{\mathit{c}}\mathit{T}·{\mathit{R}}_{\mathit{c}}\mathit{W}$)
warm and wet	13 < T ≤ 28	70 < RH ≤ 100	RF ≥ 5	1
warm and partly wet	13 < T ≤ 28	70 < RH ≤ 95	0 < RF < 5	0.6
warm and dry	13 < T ≤ 28	70 ≤ RH ≤ 95	RF = 0	0.4
warm and very dry	13 < T ≤ 28	RH < 70	RF = 0	0.1
cold and wet	0 < T ≤ 13	RH < 70 < RH ≤ 100	RF ≥ 5	0.8
cold and partly wet	0 < T ≤ 13	70 < RH ≤ 95	0 < RF < 5	0.48
cold and dry	0 < T ≤ 13	70 ≤ RH ≤ 95	RF = 0	0.32
cold and very dry	0 < T ≤ 13	RH < 70	RF = 0	0.08

Since Millardet in 1882 who discovered the effects of copper against downy mildew, by observation, the Boareaux mixture was created using copper sulfate (CuSO₄) and lime (Ca(OH)₂) in water with a copper sulfate analogy of 2–3% up to 4%, the most suppressing competitive towards P. viticola. Another similar mixture is the Burgundy mixture that uses sodium carbonite (Na₂CO₃) instead of lime [39]. Therefore, the most successful protective treatment is using pesticide products based on the Bordeaux mixture solution before fungus development. Nevertheless, its uncontrolled use can threaten human health and soil [40], and therefore, precise treatment is required, applicable only at the early development stages before flowering and during berry formation. When environmental conditions favor fungus development, more active substance FRAC group 4 [41] fungicides are used [42]. In infection germination peaks, mixtures of copper protectants and phosphate-based fungicides can arrest the infection [43]. We also have to mention the use of microorganisms for the bio-control of plants as the alternative to chemical pesticides [39].

1.2. Conclusions of Downy Mildew Models Examination

Based on Section 1.1 presentation of existing models used for downy mildew, the following remarks are reached by the authors:

• Unlike the experimental varieties and conditions examined, all models fail to cope with the phenomenon’s evolution over attributes such as different environmental conditions, variety, and vine ages. No mechanistic model can be set as a catholic-holistic model due to the non-uniformity of the attributes described above, with the exception of some conservative empirical generic rules (for example, Rule 3–10).
• Mechanistic models trying to time the downy mildew disease process accurately can easily lead to erroneous calculations of significant offsets if the coefficients or variable parameters used do not match the examined environmental conditions that have been experimentally calculated (miscalibration). That is why, in several cases, empirical models can outperform mechanistic ones and can provide much more safe-ground predictions.
• Most mechanistic models target on-time evolution modeling of downy mildew and do not excerpt a decision suggestion required by Decision Support Systems. They are leaving such decisions to the non-expert’s eye. Such as precision viticulture practices (for example, vine leaves removal) or pesticide appliances and analogies (such as Bordeaux mixture products appliance).
• All models, specifically mechanistic ones (of higher sensory measurements, high granularity dependency), utilize meteorological station measurements. Such measurements are kept at best in hourly mean intervals. Furthermore, meteorological stations located at high elevation grounds, with 5–20 km radius coverage, servicing large areas of nonuniform terrestrial fields, cannot cope with the condition extrapolates. Due to this type of exploited input, they can provide only best-effort forecasts of significant field-level disease variations, thus leading to over-pesticide field uses in many cases.
• Downy mildew mechanistic models are trying to provide time-frames and thresholds for primary and secondary infections corresponding to large areas of different conditions. Because their inputs are in sparse hourly periods and are of single points of reference (single meteorological stations), without experimental calibrations of their coefficients, on field vine clusters, or on the monitored field areas, such models will consistently be outperformed by empirical ones.

Next-generation Agriculture 4.0 models should target mostly suggestions or phenomena evolution time-frame breakpoints. Their calculations should not be deterministically inferred by a single equation but by a machine learning process that has as input a time series of annotated measurements. To achieve better than best effort plant level forecasts, dense input real-time or close to real-time measurements of 1 min, 5 min, or at least 10 min periodic intervals are needed. Furthermore, more sensor nodes are required, installed in the viticulture fields of at least 0.5 Ha coverage areas per sensor node, providing measurements of wetness or soil moisture or evapotranspiration, vapor pressure deficit, or at least temperature and humidity. The next-generation models should consider a simplified approach regarding their data inputs, outputs, and trainable coefficients so that the training process is algorithmic and easy to program as a repetitive process that can provide a set of different trained models inferring different forecasts under different field conditions.

More data-driven machine-learning alternatives must be exploited to provide a holistic approach to cope with different environments. As mentioned by [44], ML algorithms, such as binomial LASSO regression, random forest, and gradient boosting, can infer better results and more accurate results than existing mechanistic models. Nevertheless, up to now, these models have yet to outperform mechanistic ones due to the lack of annotated measurements for model training purposes, thus degrading their accuracy and precision. Therefore, a more of a fuzzy logic annotation approach is fundamental to acquiring annotated data. Before presenting the authors’ deep learning implementation for P. viticola incident forecasting, a short subsection follows with the existing state-of-the-art Decision Support Systems implementing the described downy mildew detection models.

1.3. Downy Mildew Forecasting DSS Systems

Several Decision Support Systems that provide P. viticola predictions in the Mediterranean area have emerged over the last decade and are presented in literature [21]. One of the first DSS systems attempts for P. Viticola using meteorological station data inputs end empirical models is GrapeMilDeWS [45].

Rossi et al. [46], created a DSS system called vite.net utilizing meteorological station data inputs and from farmers’ meteorological sensors monitoring Vine Units (VUs) to provide decision support towards downy mildew using empirical models and mechanistic ones, specifically the UCSC model [4,8].

Agrometeo and Vitimeteo DSS systems also utilize weather stations to provide P. viticola primary infections and observe first oil spot alerts using a table-based Vitimeteo-Plasmopara model [47].

The authors of [26], created a custom system for dense micro-climate monitoring, collecting data from nearby meteorological stations, using average temperature, rainfall and pathogen concentration on the previous day and applying a linear regression prediction line, calculating the infection risk using the Goidanich algorithm [24]. Similarly, Decitrait DSS provides cultivation practices and forecasts using Goidanich and EPI models [48].

Finally, the authors of [49] presented a set of tools used for partitioning viticulture areas in Greece and post-processing data analysis of meteo station sensory measurements in the vicinity of these vine areas. In addition to precision viticulture treatments and DSS systems with inputs from sparsely located meteorological base stations, advancements in IoT and cloud technologies can provide new advanced Decision Support Systems (DSS) capable of better than micro-climate monitoring using dense monitoring stations for less than 2km sensory measurements acquisition [50]. Such systems can collect environmental data even at the plant-vine level using cheap IoT meteorological stations that aid farmers in making tactical and operational decisions.

Towards vine-plant sensory monitoring, Perez et al. [19] presented a DSS system (VineSens) that utilizes two types of monitoring end nodes using ARM MPUs that transmit temperature, humidity, and moisture sensory measurements. The measurements are transmitted over Wi-Fi to gateways, and then data is transmitted over 3G/4G(LTE) to the central DSS logging service using the appropriate ReST HTTP API. The system utilizes the Rule 3–10 and the Goidanich model for mildew predictions.

Furthermore, Trilles et al. [16] presented a cloud-based DSS system called SEnviro that includes edge IoT devices with temperature, humidity, and rainfall sensors. Using edge computing nodes, the Goidanich model cumulative index is calculated at the node level, and appropriate alerts are sent to the farmers via SMS. Other communication channels are also supported. SEnviro system can periodically collect measurements using GPRS transponders over long distances [16] and utilizing Wi-Fi transponders for short distances, as mentioned in [51]. The benefits of this platform are the use of open-source APIs, Non-relational sensory measurements data storage capabilities, and mainly its ability to perform end-node edge computing [16]. The authors express only a slight concern about how the selection and control tasks of different edge computational models can be performed at the SEnviro things edge nodes since relevant information is not provided in [16]; that is information regarding the control and orchestration of edge computational models or over-the-air SEnviro nodes forecasting model selections and updates via the SEnviro platform.

Mezei et al. implemented the Winet DSS, which uses NBIoT technology [52], to implement autonomous nodes spread on vine fields. Their DSS implementation transmits temperature, humidity, and soil moisture sensory measurements over UDP protocol streams to the Winet central service. For mildew predictions, a custom model that uses the 3–10 Rule for infection initiation and a polynomial equation: $f\left(t\right)=0.076t^2-3.454t+42.925$ fitted on the Muller model [10,18].

ZenAgro company [20] has implemented a DSS system using open-source ThingsBoard Application Service and sensory data acquisition SDK [53]. Their platform is capable of monitoring vine parameters of temperature, humidity, and leaf wetness via LoRa point-to-point transmissions, currently updated to LoRaWAN Dragino sensors capable of data transmissions using the LoRaWAN class A protocol [54]. Their DSS now provides only P. viticola forecasts using Rule 3–10 and a simplified Muller model [10].

Hnatiuc et al. have implemented a vine disease detection framework supported by a sensory measurement data collection service that implements clustering and classification algorithms using TensorFlow [55] and utilizing IoT devices that monitor plant level sensory parameters of temperature, leaf moisture, soil moisture, sap flow meters, solar radiation sensors and soil oxygen sensors [17].

Further technological achievements on plant-level monitoring for P. viticola in grapevines systems and services include the use of ground base LiDAR scanners for leaf area index estimations as mentioned in [56,57], as well as the use of static cameras modules that utilize deep learning Faster-RCNN, SSD and Yolo object detection models on real-time or close to real-time intervals using RGB image acquisition from grapevine fields [15,58]. Such RGB images can also be acquired for deep learning model training and inferences by mobile cameras or low-altitude flying drones (flying 3–5 m above vine clusters).

In addition, multispectral and specifically hyperspectral imaging (HSI), acquired from handheld cameras or methodologies for HSI image acquisition from drones [59], can provide more detailed color information than RGB images. The imaging spans at 400–800 nm bands are set for plant activity monitoring by calculating normalized vegetation coefficients, crucial in environmental remote sensing [60]. Reflectance differences between 470 nm and 700 nm frequency bands can easily distinguish and extract vine leaves contours [60]. Furthermore, reflectance differences combined with using Support Vector Machines (SVMs) can distinguish downy mildew spots on symptomatic leaves in the bands of 500–700 nm and 800–1000 nm, as mentioned at [61].

This paper focuses on sensory-measurement-driven DSS systems capable of issuing downy mildew forecasts and recommendations.

Table 3. Viticulture DSS systems capabilities.

DSS System	Meteo Station Data	IoT Plant Level Monitoring	Auto Location Tracking	Data Acquisition	Low-Cost Data Transmissions	ReST API	Interfaces	OpenSource Components	Installation-Maintenance Efforts
Agrometeo-Vitimeteo	Yes	No	Static Meteo-Station location-based	central DB, relational schema	-	-	Web-based	-	Low
Decitrait	Yes	No	Static - Meteo-Station location-based	-	-	Yes	Web Based, Mobile App	-	Low
vite.net	Yes	Vine Unit monitoring. Use of farmers meteo stations	VU meteo stations GPS	PSQL, relational schema	Annual Provider costs per VU	No	Web-based	Yes	VU stations maintenance
VineSens	No	Yes	No	MySQL, relational schema	Wi-Fi	No	Web-based	Yes	High, low coverage area transponders(100m)
SEnviro	No	Yes	Yes-GPS equipped nodes	Postgres-PostGISMongo Non-relational schema	Yes, GPRS, Annual Provider costs per node	Yes	Web-based, Mobile App	Yes	Medium
Winet	No	Yes	No-static node locations	Mysql relational schema	Yes, NBIoT, Annual Provider costs per node	No	Web-based, Mobile App	Yes	Low
ZenAgro	Yes	Yes	No-static node locations	PSQLNon-relational schema	LoRa P2P	Yes	Web-based	Yes	Low

presents each system mentioned in the literature and its corresponding capabilities. The authors set these capabilities as Key Performance Indicators (KPIs) required for vine-level monitoring, forecasting, and decision support. DSS systems presented in Table 3 have been examined based on the following KPIs set by the authors for plant-level monitoring and support:

• Meteo Station Data: Weather the DSS system also receives data inputs from meteorological stations via specifically designed protocols or interfaces. Meteorological stations.
• IoT Plant level Monitoring: Whether the DSS system acquires plant-level information using IoT sensors.
• Auto location tracking: Whether the DSS system can track its data input sources using GPS receivers (locality).
• data acquisition: The schema form that the DSS logging service stores the sensory data measurements, that can sustain big data records of different measurements-attributes over time as mentioned at [62].
• Low-cost data transmissions: Covers the low-power data transponder specifications of DSS systems that use nodes capable of plant-level monitoring. Such transponders are RF-based, NBIoT, LoRa, LoRaWAN, Wi-Fi, ZigBee, or BLE/Bluetooth, which maintain low energy footprints, in contrast to the power consumption of GSM GPRS/3G/4G-LTE transponders [63]. This performance characteristic also considers the required network provider costs per node, especially for technologies such as NBIoT and GSM/GPRS/3G/4G.
• ReST API: If the DSS system includes appropriate SDK API to fetch data measurements or forecasts by clients using HTTP/UDP/CoAP/MQTT or custom protocol requests [64].
• Interfaces: Type of accessible user interfaces offered by the DSS system (Web, Mobile App, Custom Application UI)
• OpenSource components: If the DSS utilizes open-source components SDKs or libraries
• Installation-Maintenance efforts: Whether the DSS system and its end vine-level nodes are easy to Install and scale, and the farmers’ minimum or no maintenance efforts are required.

As shown in Table 3, both SEnviro and ZenAgro DSS systems are the ones that fulfill all DSS system capabilities (KPIs), set as necessary DSS capabilities by the authors for vine-level monitoring. Medium installation efforts are set for SEnviro because custom User Interfaces and panels have to be made for the Open Geospatial Consortium (OGC) SensorThings API [65], or Sensor Observation Services (SOS) [66].

This paper presents a new DSS system architecture called thingsAI. The proposed system adopts ZenAgro’s DSS architecture regarding LoRaWAN sensory data transmissions and vine-level nodes for sensory measurements. ThingsAI utilizes long-range autonomous GPS-equipped devices called motes. These devices include sensors that use different profiles to monitor temperature and humidity, leaf wetness, and soil moisture [15]. ThingsAI also utilizes autonomous LoRaWAN meteorological stations. These stations include additional pressure, wind speed, direction, and rain gauge sensors.

ThingsAI measurements data storage engine utilizes the No-SQL capabilities of the Cassandra database [67,68], and ThingsBoard Web panels and alerts logic to provide messages via Twilio SMS, e-mail, and Slack interfaces [53]. ThingsAI also includes independent docker containers to implement, train, and infer deep-learning classifiers and detectors [69]. In such a dockerized container, the deep learning algorithm proposed by authors called the fuzzy-stranded-NN model is installed. The following section presents the author’s thingsAI implementation and their proposed fuzzy-stranded-NN algorithm, based on the stranded-NN implementation of [70], for detecting downy mildew.

2. Materials and Methods

This section provides information regarding the proposed thingsAI high-level system architecture, motes structure, and the authors’ deep learning algorithm proposition for detecting downy mildew events.

2.1. Proposed High-Level System Architecture

This paper proposes a new high-level architecture based on open-source libraries and tools comprising a system called thingsAI. Figure 1 illustrates the core structural parts of our proposition. These components can be categorized as field components and cloud components. Field components include IoT modes and devices that collect field measurements. In contrast, cloud components include the Virtual Machines and Dockerized services [69] that provide measurements storage, Deep Learning algorithms computational tools and services, and farmers’ monitoring and management User Interfaces. In detail, the thingsAI system architecture is comprised by the following components:

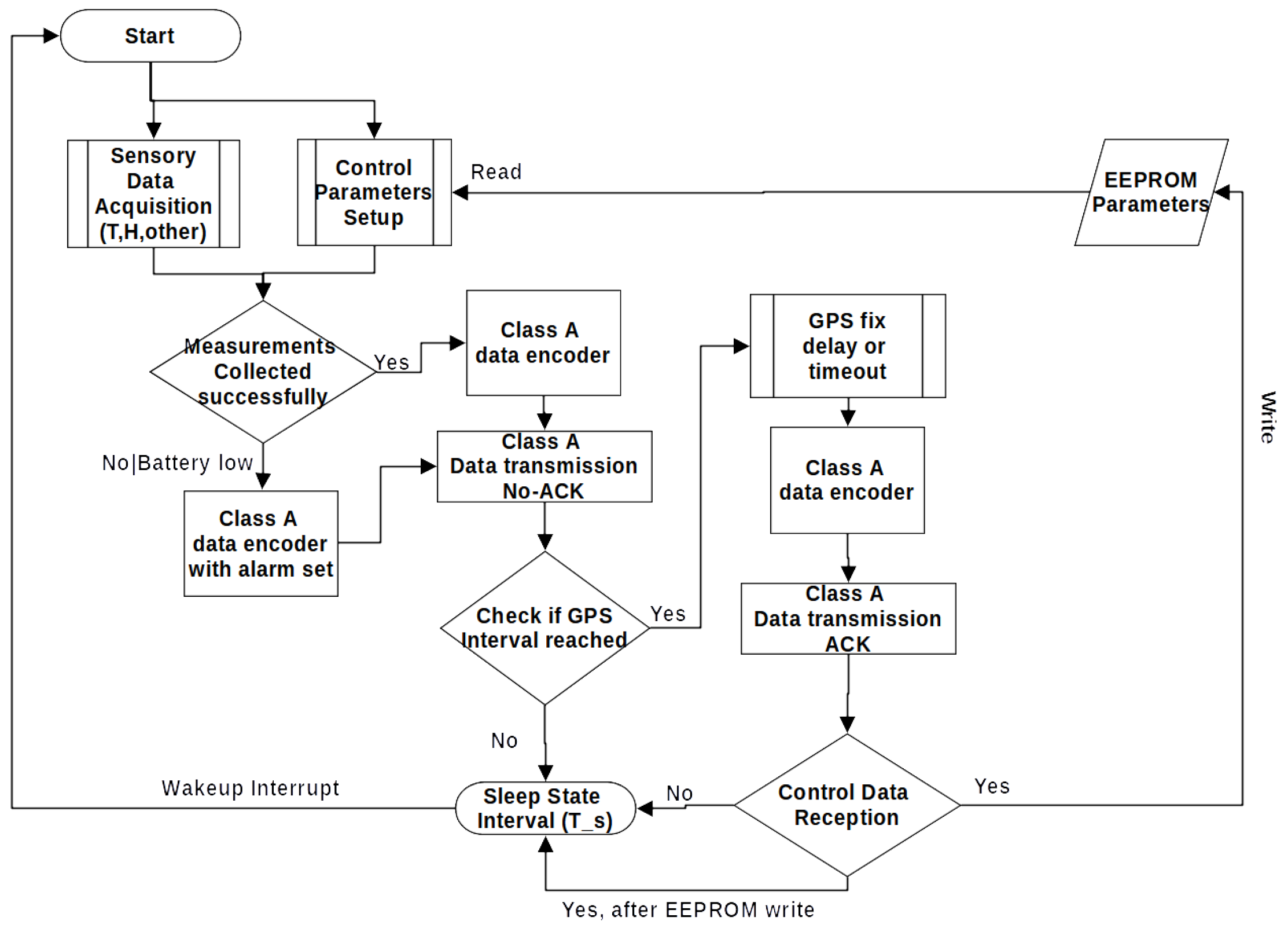
• Vine field device components: These include: 1. the IoT mote devices equipped with GPS receivers and a LoRaWAN transponder, acquiring field sensory measurements (see Figure 1, (1)), such as temperature, humidity, leaf wetness and soil moisture, and 2. the LoRaWAN meteorological stations (see Figure 1, (2)), which include a GPS receiver, LoRaWAN transponder, pressure, temperature, humidity, wind speed, direction sensors, and a rain gauge. In each viticulture field, the farmers place the IoT motes to measure plant-level sensory parameters of different mote profiles, for instance, temperature and humidity, according to our downy mildew experimentation. The suggested coverage area for an IoT mote is more of a regular hexagon with either height ($h=2acos({30}^{\circ }\approx 1.732a$) or width ($w=2a$), where a = 100 m. That is, a coverage area of $A=\frac{3s^2}{2·tan\left({30}^{\circ }\right)}\approx 2.598a^2$ per IoT mode device. The authors set the maximum coverage area for an IoT mode for vine-level monitoring up to 1 Ha. Usually, IoT motes are placed according to the following rules: (1) If there is a significant elevation difference between two points in a field more than 1 m, (2) If there is a slope of more than 20°, offering different soil drainage, and (3) if there is tree coverage near the field contributing to a significant reduction of at least 2 h of sun throughout the day concerning the rest of the viticulture field. LoRaWAN meteorological stations are usually installed in pinpointed locations based on the ground morphological characteristics, covering field areas of 70–80 Ha. The field components also include the LoRaWAN gateway, which acts as a sensory measurements concentration and thinsAI data forwarding point to the thingsAI LoRa Server [54].
  The sensory motes transmit measurements of temperature and humidity every $T_p$ period intervals. These intervals can be programmable over the air by the farmers via ThingsBoard panels (with a minimum value of every 1 min and a maximum value of 4 h), using Class A LoRaWAN data reception windows RX1, RX2 [71]. The motes also transmit GPS location LoRaWAN frames that can be set to every 8–48 h. The same applies to the LoRaWAN meteorological stations. The LoRaWAN meteorological station coverage area may extend more than 70–80 Ha and is used to capture meteorological measurements that accurately correspond to the included viticulture fields vine-clima. There is no need for vine-level measurements of wind speed, direction, or rain since their variations can be accurately captured using at least 1 km meteo-stations dense coverage. LoRaWAN meteorological stations are autonomous battery-operated devices with a mean power consumption of 1.8–3 W, transmitting measurements per-minute intervals via class A LoRaWAN protocol to the LoraWAN gateways. For the meteorological stations, different communication technologies can also be used, such as NBIoT UMTS(3G) or Wi-Fi, in order to transmit measurements to the thingsAI cloud infrastructure directly through the ThingsBoard container (see Figure 1, (7) ThingsBoard AS) bypassing the LoRaWAN application server (see Figure 1, (4) LoRaWAN AS).
  The thingsAI system field components utilize a dense grid of GPS-equipped IoT motes (see Figure 1, (1)) and a sparse grid of GPS-equipped LoRaWAN meteorological stations (see Figure 1, (2)) to provide sensory measurements at vine level. All motes (see Figure 1, (3)) transmit their GPS location using LoRaWAN frames via the gateway. The gateways use two communication technologies (NBIoT and LoRaWAN) deliberately made to minimize telecommunication provider costs. NBIoT transponders could have been used instead of LoRaWAN for end-device data transmissions (motes and meteorological stations). Nevertheless, such a technological alternative enforces a per mote SIM card annual communication fee for the farmers. Depending on the number of IoT motes used, the provider fees could reach up to 2–4€/device/month. Instead, the authors propose using the LoRaWAN communication as a free long-range narrow-band alternative of a single connection point with one cellular telecommunications link at the gateway bridge. Since the LoRaWAN coverage extends from 5–12 km, a single gateway may cover a significant portion of a huge cultivation area [72].
  LoRaWAN gateways (see Figure 1, (3) LoRaWAN gateways), are responsible for forwarding IoT mote measurement frames to the LoRaWAN network service and, therefore, to the application server (Figure 1, (4) LoRaWAN container) [69]. This is achieved by maintaining Internet connectivity via a cellular NBIoT network provider at the gateway level. The LoRaWAN gateways are autonomous devices of continuous operation, with a mean power consumption of 5–6 W, because they are operating simultaneously two different transponders: an NBIoT(GR-800MHz/B20) UART transponder of a 10 MHz/channel bandwidth and a LoRaWAN (EU:863–870 MHz) concentrator board of a 125 KHz/channel bandwidth. In areas where the B20 band is unavailable, the UMTS B21 band of 2100 MHz is used with higher channel bandwidths of 20 MHz/channel. All IoT motes and meteorological stations join the LoRa server using Over The Air Activation (OTAA). All IoT motes and meteorological stations have ADR LoRaWAN capabilities enabled. All motes transmit sensory data via the available LoRaWAN channels 1–8 and receive downlink windows RX1 via the data transmitting channel and RX2 at 869.5 MHz [71].
• Cloud Components: These are mainly docker containers that reside in a single or multiple cloud Virtual Machine instances [69]. The thingsAI cloud components as shown in Figure 1, include the: 4. LoRaWAN container of the chirpstack LoRa server [73], the 5. Cassandra No-SQL clustered database [74], for storing sensory measurements, the 6. AI containers running deep learning training and classification, prediction tasks, and the 7. ThingsBoard Application Server (AS), platform container capable of providing visualization outputs, motes control, and suggestions-alerts to the end users.
  The chirpstack LoRa server [73] (see Figure 1, (4)), is an open-source network and application server capable of receiving encrypted AES-128 data transmissions from the LoRaWAN gateways. Upon data validation and decryption, the data are pushed to the Chirpstack container mosquito Message Queue Telemetry Transport (MQTT) service [75]. Then, the appropriate data logging agent using MQTT subscribe mechanism acquires the sensory measurements and submits them as HTTP post-device telemetry requests, depending on the LoRaWAN mote device ID, to the ThingsBoard Application server [76].
  The ThingsBoard AS (see Figure 1, (7) ThingsBoard AS) is responsible for controlling all thingsAI devices (motes and meteorological stations) and device attributes at the application level, as well as storing the per-device sensory measurements and GPS locations at the Cassandra distributed Database cluster [74] (see Figure 1, (5)). In the ThingsBoard AS container reside the data logging service, the geo-location module, acquiring Google Map layers information (see Figure 1, (8)), the RPC motes control service, and notification services described in detail in Section 2.3.
  Finally, the thingsAI cluster (see Figure 1, (6)), described in Section 2.3, is a set of docker containers where the Deep Learning models, models’ training agents and inference services are instantiated, providing classifications and predictions.

The following subsection reveals technical characteristics of the IoT motes and LoRaWAN meteorological stations used by the thingsAI system.

2.2. ThingsAI IoT Motes and Stations

thingsAI end-devices have been implemented to provide a dense distributed grid of monitoring sensors. The implemented sensory devices called motes design is illustrated in Figure 2a. These devices operate autonomously and can be easily attached to striped viticulture fields’ viticulture iron corner stands. The end motes can be automatically spotted by the thingsAI system via their GPS receivers and are equipped with temperature and humidity sensors. Several other sensors, such as leaf wetness and soil moisture sensors, can be attached to these end devices, providing different profiles supported by the thingsAI data transmissions LoRaWAN protocol.

ThingsAI system IoT mote installations are performed using the following criteria:

• At least one sensory mote must exist in a rectangular area of 100 × 100 m (1 Hectare) called the maximum partitioning area
• If required due to elevation differences >0.8–2 m, the maximum partitioning area can be clustered into two or more areas where different motes are placed (vertical partitioning)
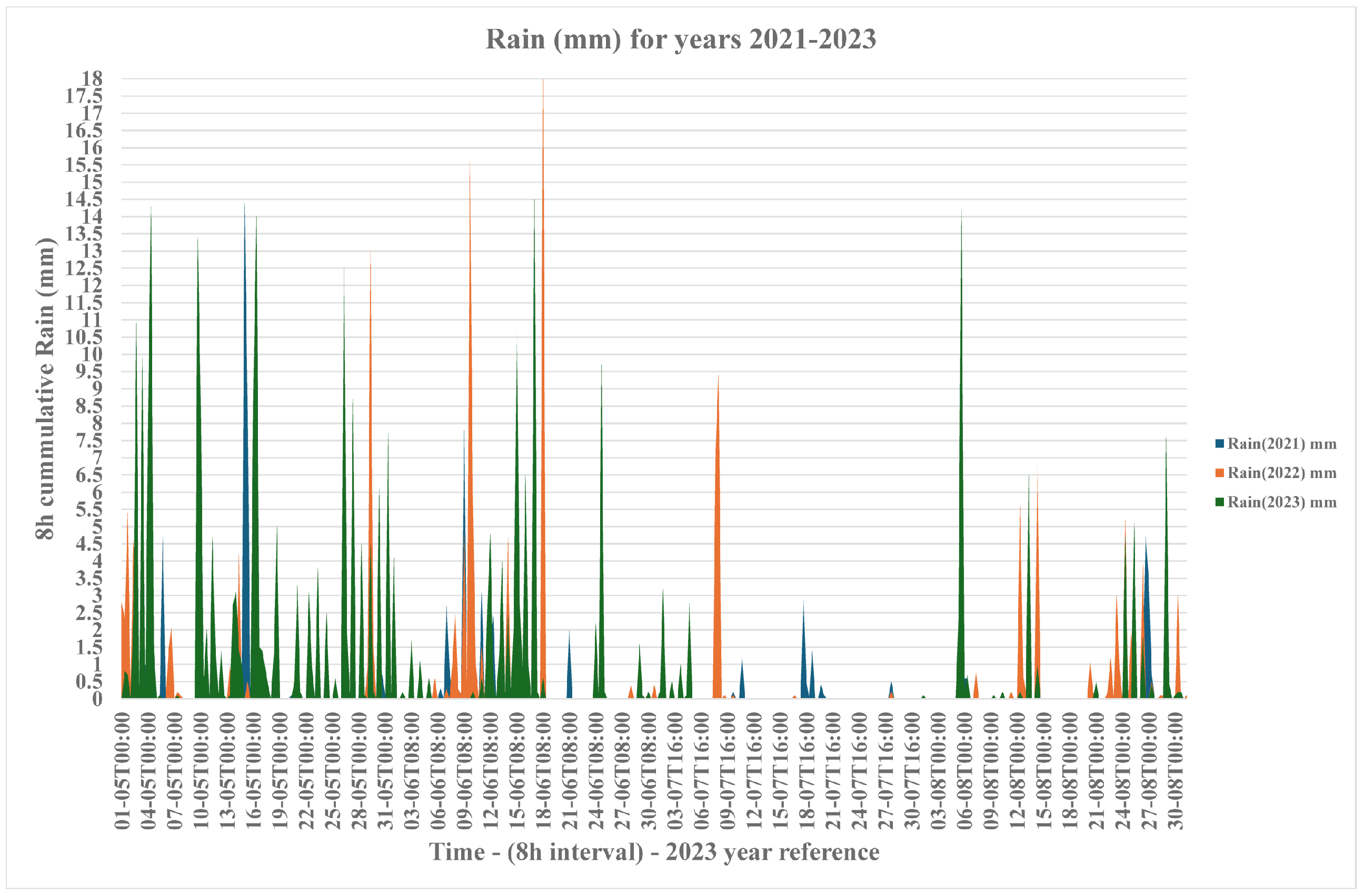
• If significant variances inside the maximum partitioning area occur with respect to direct hourly solar radiation measured daily at W/m due to shadowing caused by nearby tree clusters or other environmental factors, such as nearby water streams. Such calculations preferably take into account either monthly mean hourly differences of Vapor Pressure Deficit (VPD) in kPa for months May–Aug or reference evapotranspiration $E{T}_o$, in mm, based on PenMan-Monteith equations [77], as a cumulative sum for months May-August. At least one monthly variance of VPD $\ge 0.4$, or a yearly evapotranspiration difference of 30 mm/y, taking into account as a full year the months of May-Aug, denote an area partitioning into two different regular hexagon areas, whose centers are the two variation points of either VPD or $E{T}_o$.

The components included in the IoT plant-level motes (see Figure 2b,c, 1), are design-illustrated in Figure 2a, and are the following:

• Either a COTS 32 bit ESP32 cortex-M3 MPU 32 MHz, of 128 KB Flash, 16 KB or RAM and 4 KB of EEPROM and LoRaWAN onboard transponder that periodically collects and transmits sensory measurements using LoRaWAN frames [78], or Seeduino LoRaWAN RHF76-052AM board with the ATSAMD 48 MHz CPU and an onboard GPS receiver [79] can be used.
• DHT22 temperature and humidity sensor. Other sensors, such as leaf-wetness and soil moisture sensors, can also be attached.
• LoRaWAN 14 dBm, 868 MHz transponder supporting class A LoRaWAN protocol.
• a Ublox NEO-6M GPS on board UART receiver.
• 3.6 V, 8000 mA Lithium replaceable battery case connected with the board using a JST2.0 cable.
• External casing magnet for easy attachment to iron vineyard corners (see Figure 2a, 7, and Figure 2b, motes attached to iron corners). External tie wraps can be used for better grasping.
• Plastic IP67 casing.
• GPS antenna.
• LoRAWAN antenna.

thingsAI motes sensory data and GPS location transmissions are controlled by the LoRaWAN Application server per mote accordingly, using downlink LoRaWAN control frames. Usually, sensory measurements are transmitted every 1–4 h so as to conserve motes energy. Motes and meteorological stations’ GPS location frames are usually sent every 24 or 48 h or more. thingsAI IoT end-nodes data transmission application protocol uses two modes: (1) binary data mode and (2) stream data mode transmissions, controlled by the LoRaWAN Application Server. Binary data transmission’s advantage is the 1–3% less battery consumption by reducing the over-the-air data transmission time compared to stream transmissions. Nevertheless, external APIs and interfaces can manipulate stream transmissions much more easily, favoring the system’s scalability.

The thingsAI meteorological stations are illustrated in Figure 2d. Their processing unit and interface board are illustrated in Figure 2c, 2. It includes a Seeduino LoRaWAN RHF76-052AM board with the ATSAMD 48 MHz CPU and an onboard GPS receiver [79]. The Seeduino has an onboard GPS receiver, which is using a UART serial port where NMEA data are accumulated. It also has an onboard SPI connected, 14 dBM 868 MHz, LoRaWAN transponder. The sensors attached to the meteorological stations using the Seeduino digital interface pins are a DHT22 humidity sensor, a BMP280 pressure-temperature sensor connected to the I2C Seeduino digital pins, and via the Seeduino analog pins, an analog wind direction, speed sensor, and an open-type analog rain gauge.

The meteorological station’s field placements (see Figure 2d) usually follow a dense micro-climate grid monitoring approach of 1–1.5 km of coverage radius [50]. LoRaWAN meteorological stations also operate autonomously. Usually, data transmissions of meteorological stations are statically performed every 1 min, and their GPS location data transmissions every 24–48 h. Due to the per-minute granularity of sensory data transmissions and the number of sensors, meteorological stations are never in sleep mode. For this reason, a 12 V Pb 60 Ah battery and a pull-down 12–5 V converter are used to power those stations, including a 10–12 W/12 V PV panel directly connected to the battery using alligator clips.

Both IoT end motes and LoRaWAN meteorological stations use the Over The Air Activation OTAA mode and class A mode for LoRaWAN frame transmissions [54]. That is, prior to each transmitted frame, a LoRaWAN join process initiates according to the LoRaWAN protocol specification. The following subsection describes in detail the thingsAI cloud distributed services and LoRaWAN data transmission protocol used both by thingsAI motes and meteorological stations. Section 2.3 provides detailed information regarding the thingsAI system offered services and interfaces.

2.3. ThingsAI LoRaWAN Application Protocols and Cloud Services

The following services have been implemented in the thingsAI system: (1) the data logging service, (2) the geo-location module, (3) the distributed database architecture and interfaces, (4) the RPC motes control service, (5) the AI containers model training agent and inference service, and (6) the ThingsBoard data visualization and notification services.

The data logging service is on the ThingsBoard container. Its main functionality is to subscribe to the MQTT service of the open-source chirpstack LoRaWAN Application server for a specific application topic names and for every mote or meteorological station device ID in that area, as registered to the ThingsBoard Application Server (AS). The data logging service can store measurements in the Cassandra database cluster by performing ThingsBoard AS HTTP POST requests using each device’s unique token ID for authentication. ThingsBoard also has an MQTT broker installed, but it is not used for publishing requests directly since token authentication knowledge per device is required to publish data. Instead, the chirpstack MQTT broker is used as a central gathering point for all messages under a single application area topic. Henceforth, the data logging service is responsible for the per-device message classification and database sensory records submissions using per-device JSON HTTP POST requests. The devices’ Universally Unique Identifiers (DEV-UUIDs) and authentication tokens are maintained separately in the ThingsBoard PostgreSQL database. The data logging service uses this UUID-authentication token tuple information to listen for MQTT messages and forward HTTP POST measurement requests to the ThingsBoard AS, which in turn stores these measurements in the database cluster.

The geo-location module is instantiated in the ThingsBoard AS. It includes a map panel User Interface that can be added to a specific farmer’s monitoring dashboard and a set of notification rule chains that may notify the farmer using external ReST APIs (via e-mail, SMS, or Slack messages). The module keeps track of specific customer-farmer device nodes and updates the per-farmer map panel with the locations of the owned mote devices. The map panel can illustrate mote and meteorological station locations in real-time using the Google Maps API and satellite layer view. The panel can also illustrate the latest telemetry sensory data, recorded date, and battery status using the JavaScript marker popup balloons. Suppose a polygon-activated area is enabled (by drawing a default polygon at the map panel). In that case, the module can issue notifications if a node moves out of the polygon of interest (geofencing), the motes’ GPS coordinates have not been received for more than 48 h, or the mote battery is low.

The Cassandra No-SQL clustered database is a decentralized concept of database nodes that have the same responsibility, and data replication is performed by cloning data from one to the next. All mote records are parts of the same database with different cluster copies. This means that the ThingsBoard AS can directly access any mote stored data, thus enhancing data availability and speed in contrast to the MongoDB hierarchical clustered alternative. Data availability is, in fact, a more crucial parameter than speed for DSS systems offering forecasts since several agents from the AI containers may try to access data over time for model training and inference processes. However, as mentioned by [68], Cassandra outperforms MongoDB for large time ranges, while they have a comparable performance for shorter ones. For example, suppose statistical analysis trends are requested to plot mean temperatures on-demand over the last 20 years or when the requested data size is above 1 M records. In that case, some minor visualization latencies may occur, at most 5–10 s. Nevertheless, its direct any-node connect architecture makes it an ideal database for minimizing data loss and corruption compared to a hierarchical clustered model such as MongoDB [67].

The Remote Procedure Call (RPC) control service is instantiated on top of the ThingsBoard AS. It includes a set of control options that can be set per device entity as server attributes. Such attributes are the time interval, which specifies the mote telemetry transmission period, and the GPS time interval, which specifies the GPS latitude-longitude coordinates acquisition and transmission intervals. Other control options that can be specified are the device-enable attribute and the device-GPS-enabled device server attributes.

End motes and meteorological stations data transmissions are performed using class-A LoRaWAN protocol. In order to cope with different types of sensory motes having different types of sensors installed, different device profiles have been implemented. Profile S1 indicates a temperature-humidity mote. Profile S2 indicates a meteorological station with installed temperature, humidity, pressure, wind speed, direction sensors, and rain gauge (meteorological station profile). Profile S3 indicates a temperature-humidity and leaf wetness sensor, and profile S4 corresponds to a temperature-humidity and soil moisture sensor. Two different types of frames concerning sensory measurements or GPS location are also being transmitted (Type 1 and Type 2 accordingly).

Table 4. ThingsAI LoRaWAN frame data encoding for sensory measurements—Type 1 message. For profile S1, the maximum frame size for stream mode is 30 bytes, while for profile S2, the maximum frame size for stream mode is 50 bytes.

Field	Description	Binary Length (bytes)	Maximum Char Length (bytes)	Example Hex Value
Protocol Header	ThingsAI protocol header. 0 × 54 for binary encoding, 0 × 53 for string encoding	1	2	0 × 54|S
DevEUI	64 bit Device Unique ID in hex	8	-	0 × 0095690600003796
Device Profile	S1 (0 × 31-1) | S2(0 × 32-2) | S3 (0 × 33-3) | S4(0 × 34-4)	1	1	1
Frame Type	Type 1(A) (sensory data) or Type 2(B) (GPS data)	1	2	0 × 41|A
Sequence Number	Frame sequence number	2	5	1–65,535
Event	Event Code 0: Normal, 1: Battery low, 2–7 (bit|value): sensor measurement error	1	1	indicates all sensors with errors (1 bit/sensor)
Temperature	Temperature sensor value in °C	4	6 (−9.00–99.00)	10.00
Humidity	% relative air humidity	4	4 (0.0–99.0)	75.0
Pressure	Pressure in kPa (Profile S2 only)	4	6 (90.00–110.00)	93.09
Wind speed	Wind speed km/h (Profile S2 only)	4	5 (0.0–160.0)	12.3
Wind direction	Wind direction (N|NE|E|SE|S|SW|W|NW) (Profile S2 only)	4	2	0 × 02|NE
Rain Gauge	mm Rain (Profile S2 only)	4	5 (0.0–999.9)	34.5
Leaf wetness	0–1024 analog value (Profile S3 only)	4	4	Dry (230)
Soil moisture sensor	0–1024 analog value (Profile S4 only)	4	4	Wet (980)
Battery voltage	Current Battery Voltage (V)	4	3 (0.0–5.0)	3.5

shows Type 1 sensory measurements payload frame encoding for both binary and stream modes of motes operation.

Table 5. ThingsAI LoRaWAN frame data encoding for GPS measurements—Type 2 message. Maximum GPS measurements frame size for stream mode is 44 bytes.

Field	Description	Binary Length (bytes)	Maximum Char Length (bytes)	Example Hex Value
Protocol Header	ThingsAI protocol header. 0 × 54 for binary encoding, 0 × 53 for string encoding	1	2	0 × 54|S
DevEUI	64 bit Device Unique ID in hex	8	-	0 × 0095690600003796
Device Profile	S1(0 × 31-1) | S2(0 × 32-2) | S3(0 × 33-3) | S4(0 × 34-4)	1	1	1
Frame Type	Type 1(A) (sensory data) or Type 2(B) (GPS data)	1	2	0 × 42|B
Sequence Number	Frame sequence number	2	5	1–65,535
Event	Event Code 0: Normal, 1: Battery low, 2: location change	1	1	2
Longitude	Longitude value (double lng for binary, E0–E180/W0–W180 for stream)	8	13 (8 decimal places)	E21.03456871
Latitude	Latitude value (double lat for binary, N0–N90/S0–S90 for stream)	8	12 (8 decimal places)	N40.03556845
Time	UTC timestamp (long int for binary, none for stream- Use Lora-server time)	8	-	timestamp
Battery voltage	Current Battery Voltage (V)	4	3 (0.0–5.0)	3.5

shows Type 2 GPS location payload frame encoding for binary and stream modes accordingly. The end motes sensory transmission process flow is illustrated in Figure 3.

LoRaWAN mote data transmission process initiates with the sensory measurements data collection and set up of the control parameters, including parameters such as periods of sensory and GPS location data transmissions, GPS timeout, and transmission mode (binary or stream). Upon successful measurements collection, the device battery status is checked and using the appropriate alarm field, as indicated in Table 4. For sensory measurement transmissions, the data frame encoding process initiates (see Figure 3), and LoRaWAN class-A data transmission occurs without the data acknowledgment flag set. Then, the end device checks whether the GPS location transmission interval is reached. If so, a time interval of 500 s to 2 min to acquire NMEA GPS data from the GPS UART port is initiated as set by the GPS timeout control parameter. A LoRaWAN frame is constructed upon a successful GPS fix, and GPS data are payload-encoded using Table 5.

GPS LoRaWAN frame transmissions are followed with appropriate ACK (acknowledgment frame) reception from the network server during the class-A receive window intervals L1 and L2. During this mote frame receiving state, the LoRaWAN AS down-links the control data updates using explicit stream encoding of comma-delimited control streams. The end devices receive these control parameters and update their EEPROM or Flash control variables. After each data transmission, the motes sleep until the next measurement interval, as shown in Figure 3. The same measurement process applies to the meteorological stations with the difference that GPS measurements may be completely disabled (GPS turn off control command). If the meteorological station devices acquire measurements per minute intervals, due to the large number of sensors that need measurements to be acquired (which requires a mean data acquisition time of 25–30 s including a 5–15 s OTAA join process), the meteorological devices are never put to sleep mode. The following Section 2.4 describes the proposed authors’ deep learning model for the downy mildew events detection implemented by the authors in their thingsAI system implementation.

2.4. ThingsAI Downy Mildew Model

There are significant implications for using deep learning models regarding precision and decision making. Nevertheless, there are limited existing annotated datasets. That is because the need to annotate the sensory datasets properly requires efforts by experts, thus still leaving space for deterministic and empirical models to be used. Towards this direction, Fuzzy logic can offer an alternative utilizing fuzzy measurement sets and fuzzy operations that, if properly supervised, can lead to automated annotation processes. Moreover, the data annotation steps can be performed by auto-encoders to provide vine-level big-data collections as trainable datasets based on human fuzzy linguistic rules. Such datasets can, therefore, be exploited to train deep learning models for precise classification and prediction purposes rather than deterministic mechanistic models that are hard to implement or generalized empirical models.

Towards this automated annotation necessity, the authors propose a new Fuzzy-stranded-Neural Network (Fuzzy-stranded-NN) model for detecting downy mildew events. That is, using sets of Neural Networks of arbitrary depths so as to detect outliers or breakpoints more accurately in contrast to empirical or deterministic models with erroneously calibrated coefficients and parameters due to environmental diversities.

The authors first presented the proposed Stranded-NN model for detecting Industrial machinery outliers [70], now used for detecting downy mildew. The Fuzzy part of this model proposition deals with the automatic annotation tasks of measurements based on fuzzy logic observations, similar to the ones mentioned in Table 3. The model input is a batch of m number of time-series measurements such as $m\ge 8$ and $mmod\left(a\right)==0$, where a is the number of sensory attributes used, in our case temperature and humidity measurements $(a=2)$. These batches are given as input to the model with a specific order $(T,H)$. The model batch input series of: $T_0,H_0,\dots ,T_i,H_i,\dots ,T_m,H_m$ measurements, represent a 1D array of $(m,1)$, measurements taken from a specific thingsAI sensory mote: $s_l$, where $1<l\le k$. All measurements are entered in a chronological order stream of $t_0,\dots ,t_i,\dots t_{\frac{m}{a}}$ timed $(A_0,\dots ,A_n)$ sensory attributes. This 1D array is called model measurements input batch and corresponds to a specific time length that equals to $T_p={\sum }_{i=1}^{\frac{m}{a}}{t}_i-t_{i-1}$.

The fuzzy-stranded-NN algorithm includes different Neural Network sub-models, each capable of accepting a specific batch size input $(m,1)$ for training and inference processes. Our proposed model has been constructed using Python TensorFlow framework [55,80] and has been implemented in an AI container of the thingsAI system as a periodic inference service that predicts the criticality of the mildew events using three major classes: (1) Normal class that corresponds to the class when the downy mildew infections are in pause, mildew-1 when the downy mildew infections are linearly evolving or mildew-2 when the downy mildew infections are exponentially evolving. Two more classes are built in the model corresponding to extremely low and extremely high temperatures with declining infection phenomena.

The model can maintain different batch sizes of different time intervals $T_p$. This can be achieved by partitioning a specific time interval $dT$ using different m lengths for specific measured attributes a. The model acts as a prediction classifier presenting an output of the five classes: Cold stress, Mildew-1, Mildew-2, Normal and Hot stress. Cold and Hot stress classes correspond to the mildew decline phenomena classes due to very low and high temperatures that prevail; the normal class corresponds to the non-evolving phenomena class, while mildew-1 and mildew-2 classes correspond to the linear and exponential infections evolving classes accordingly. To provide classification vector outputs, all batch inputs need to be annotated (classified) to one of the above classes and rules based on either experimental results (taken from fungus traps) or simulation results as the ones presented in Table 2. Based on the input batch size $(m,1)$, the following Equation (8) determines each strand’s number of hidden layers q, where $q\ge 2$:

$${\displaystyle q=\left\{\begin{array}{cc}2\hfill & \mathit{9}\le \mathit{m}\le \mathit{32}\hfill \\ int\left(lo{g}_2\left(m\right)\right)-1\hfill & m>32\hfill \end{array}\right.}$$

(8)

If $5>q\ge 3$, two hidden layers instantiate for these strands of $nn=64$, 16 neurons per layer accordingly. The minimum value of batch input measurements is $m=9$. If the number of hidden layers $q>2$, then the total number of trainable parameters p per model strand as well as the number of neurons $n{n}_i$ per $ith$ hidden layer are calculated using Equations (9) and (10) accordingly.

$${\displaystyle p=2^q+\sum _{i=0}^{q-4}{2}^{int\left(lo{g}_2\left(m\right)\right)-i}}$$

(9)

$$n{n}_i=\left\{\begin{array}{cc}{2}^q\hfill & i=1,2\hfill \\ 2^{q-i}\hfill & i>2\hfill \end{array}\right.$$

(10)

where q is the total number of hidden layers calculated by Equation (8). For example, let us assume per-minute measurements of two attributes, temperature, and humidity $(T,H)$, acquired by a sensory mote $s_1$ in batches of m = 48 and m = 80 measurements. Each batch includes 24 and 40 periods $T_p$ of temperature and humidity measurements. For the input batch values of m = 48 and m = 80, the fuzzy-stranded-NN algorithm generates two fully connected neural network models of three $q=3$ and $q=4$ hidden layers accordingly. The neurons per hidden layer are $L_1^{32}-L_2^{32}-L_3^{16}$ for m=48 and $L_1^{64}-L_2^{64}-L_3^{32}-L_4^{16}$ for m = 80. If the measurements correspond to two attributes $(T,H)$, and each measurement is hourly measured, then the prediction time intervals $T_p$ = 24 h for m = 48 and $T_p$ = 40 h for m = 80. In order to eliminate degraded gradients, L1 regularization is also performed in each hidden layer, but the ability to introduce dropout layers per strand to avoid over-fitting has been disabled to improve accuracy results [70].

Table 6. Fuzzy-stranded-NN model hyperparameters and their default tuned values.

Hyperparameter	Description	Tuning Value Range	Default Value
$\lambda$	L1 regularization parameter	0.2–0.0001	0.005
$m_{max}$	Maximum number of input measurements (max batch size)	$2^{32}$	1024
${\lambda }_t$	Learning rate parameter	${10}^{-6}\ge {\lambda }_t\ge 0.01$	${10}^{-4}$
${\lambda }_d$	Learning rate decrease coefficient	0.00001–0.9	0.2
$n_s$	Number of model strands	$1\ge n_s\ge 128$	6
$C_{max}$	Maximum number of output detection classes	$2\ge C\ge 16$	5
$E_{pochs}$	Number of trained epochs	20–200	80
$Batc{h}_{size}$	Train Batch size	>16	64

presents the fuzzy-stranded-NN model hyperparameters that can be fine-tuned during the model training process.

A separate training process for each model strand must be performed for the model to provide multi-strand classification results. Therefore, an initial big annotated dataset of temperature and humidity measurements is needed. The training dataset has been acquired using a thingsAI meteorological station that the authors have placed in a viticulture field in Zitsa, Epirus, Greece. The meteorological station device could acquire temperature, pressure, humidity, wind direction, speed, and rain measurements per minute from 2018 to 2023. In order to obtain additional temperature and humidity measurements, the Open-Meteo API has been used [81], taking hourly measurements from 2010–2018. In order to expand these measurements to minute scale, a padding process has been implemented using a second-order polynomial kernel in the form of $a{x}^2+bx+c$ between two $i_{t}h$ interval hourly measurements, let $T_1,T_2$, $T_1\ne T_2$ and $H_1,H_2$, with $H_1\ne H_2$. If $T1=T2$, or $H_1=H_2$ then a random uniform padding process has been used starting from the base temperature $T_1$ or humidity $H_1$ in the $(min,max)$ range of $\pm 0.5$ for temperatures and $\pm 1$ for humidity measurements accordingly.

Each one of these measurement $T,H$ pairs have been annotated into the five different classes using an automated fuzzification process of semi-automated set rules. The fuzzy sets for temperature measurements include low temperatures (temp-cold set), of low temperatures up to 10 °C, where mildew infections do not occur according to the literature [12], mildew temperatures (temp-critical set) where primary and secondary infections occur (10–23 °C) [7], normal-class temperatures set (temp-normal) where secondary infections occur at a slower pace (23–32 °C) [7] and extremely hot temperatures where the infection cycle stops and diminishes over time (above 32 °C) [11]. The fuzzy sets used for humidity measurements include the dry set of humidity values up to 40%, the wet set of humidity values above 40% and up to 75% of incremental rate infections, and the moist set of humidity values above 75% of exponential rate infections [7]. Bounded sigmoid membership functions (MF) have been used for temp-cold and temp-hot sets according to the experimentally calculated using Equation (11).

$$f\left(x\right)=\frac{1}{1+e^{x·\frac{4log\left(3\right)}{low-high}·9e^{low·-\frac{4log\left(3\right)}{low-high}}}},1\ge f\left(x\right)\ge 0$$

(11)

where x corresponds to the $f\left(x\right)=1$ membership function (MF) center value and low and high are the arbitrary bounded sigmoid minimum and maximum values, where the corresponding confidence level values are zero. The same applies to dry and moist humidity sets. For all other sets of temperature and humidity domains, triangular sigmoid functions have been used. Each membership function (MF) output value is the fuzzy probability of confidence of a specific temperature or humidity value corresponding to a specified fuzzy state-set. Figure 4a,b illustrate the membership functions of temperature and humidity sets used for the sensory data automatic annotation process.

The fuzzy inference output set uses temperature as the base measure. It has five fuzzy states that correspond to the stranded-NN classifier outputs (1–5): Class-0 of cold abiotic temperature state, class-1, is the mildew-1 state for primary infections and low secondary infections, class-2, is the mildew-2 state for low primary infections and high secondary ones, class-3 is the normal state class for minimum secondary infections, or secondary infections at decline and the class-4 corresponds to hot abiotic stress conditions of high temperatures. Figure 4c shows the membership functions of the fuzzification output results corresponding to the fuzzy-stranded-NN classes (0–5). The fuzzy outputs are calculated from the fuzzy inputs according to the fuzzy rules presented in

Table 7. Fuzzy inference rules for the fuzzy inferred class annotation of the stranded-NN model. keyword plus.

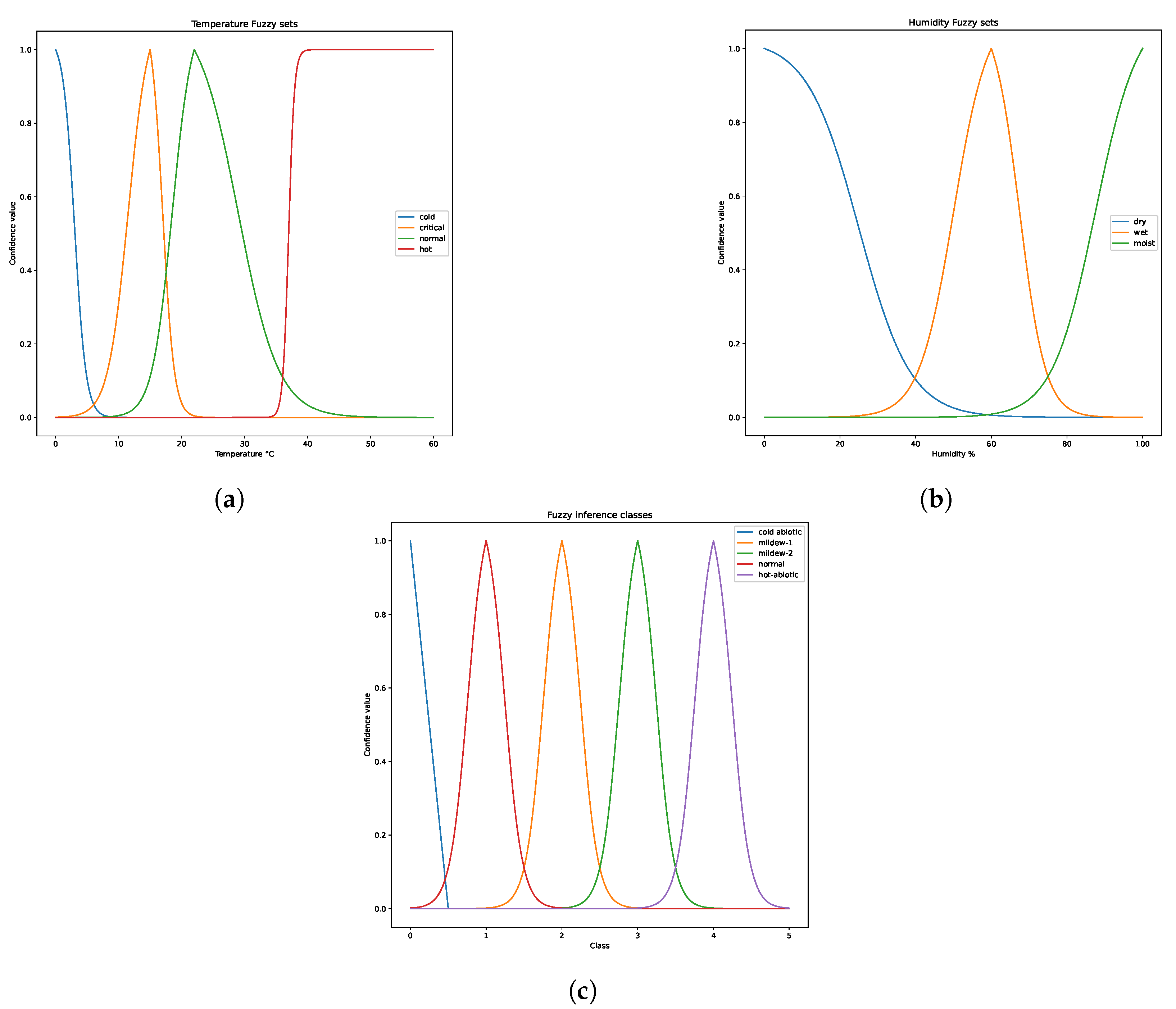
	Humidity (Dry)	Humidity (Wet)	Humidity (Moist)
Temperature (cold)	very (cold abiotic)	plus (cold abiotic)	cold abiotic
Temperature (critical)	very (mildew-1)	mildew-2	very (mildew-2)
Temperature (normal)	very (normal)	minus (normal)	mildew-1
Temperature (hot)	very (hot abiotic)	plus (hot abiotic)	minus (normal)

. These fuzzy rules are the non-automatic part of the fuzzy annotation process. The agriculturist experts can set them accordingly on the area of interest in a fuzzy manner.

Table 7 lingual hedges of plus, minus, and very modify the curves of the membership function values performed at the Mamdani-based fuzzy outputs as mentioned in [82]. The linguistic term very corresponds to the square of the output ($M{F}_v=M{F}_v^2$). The linguistic term plus equals $M{F}_v=1.2·M{F}_v$, while the minus hedge corresponds to $M{F}_v=0.75·M{F}_v$. With the use of the proposed fuzzy-stranded-NN model, the thingsAI platform can offer decision support regarding farmers’ intervention breakpoints starting from the 1st of May and focusing mainly on secondary infection cycles intervention events can be estimated from the model inference class outputs provided by Equation (12).

$$d{T}_{INT}=\left\{\begin{array}{cc}\frac{1}{k_c}{p}_{conf}·dT,\hfill & class=0\hfill \\ C_i{p}_{conf}·dT,\hfill & class=1,2\hfill \\ \frac{1}{k_n}(1-p_{conf})·dT,\hfill & class=3\hfill \\ 0,\hfill & class=4\hfill \end{array}\right.$$

(12)

where $d{T}_{INT}$ is the daily interval fraction that the disease is in progress. The $C_i$ values denote the model inference class value (For example, class 1 (mildew-1) and 2 (mildew-2)), and $p_{conf}$ is the confidence level that the predicted inference class result belongs to that specific class, as calculated by the model. Coefficients $k_c,k_n$ determine the contribution percentage of the disease as a weight parameter for cold abiotic and normal classes accordingly. Suppose the model inference output denotes a class 0 (cold abiotic) or class 3 (normal); parameter values in the range of $9\ge k_c,k_n\ge 3$ can be used. $dT$ is the corresponding periodic time interval that the model issues detections (inferences), as presented in

Table 8. Fuzzy-stranded-NN batch measurement sizes and inference intervals over number of $T,H$ measurements acquired by a single thingsAI mote.

	Hourly (2)	30 min (4)	15 min (8)	10 min (12)	1 min (120)
Inference Period (h)-dT	Batch_Size	Batch_Size	Batch_Size	Batch_Size	Batch_Size
6 h-$dT=0.25$	12	24	48	72	720
8 h-$dT=0.33$	16	32	64	96	960
12 h-$dT=0.5$	24	48	96	144	1440
24 h-$dT=1$	48	96	192	288	2880
48 h-$dT=2$	96	192	384	576	5760

, $dT$ value. The $d{T}_{INT}$ value is measured in daily intervals, using Equation (11). The total number of secondary infections progress $T_{INT}$ is expressed as a cumulative sum in days by Equation (13).

$$T_{INT}=\sum _{i=1}^{n}d{T}_{IN{T}_i}$$

(13)

where i is the model counted inference intervals cycles starting from the 1st of May. According to the bibliography, the initial oil spot lesions typically appear between 7 and 18 days. This means that an intervention breakpoint must be set when the $T_{INT}$ reaches this value, usually set to $T_{INT}$ = 7–12 days, in between the infection period intervals set by [3,6,8]. The system issues appropriate intervention alerts if such breakpoints are reached. When such a breakpoint elapses, the value of $T_{INT}$ is set to zero, i is set to 1, and the calculation is repeated for the following breakpoint interval.

In the following sections the authors present their experimentation with their proposed fuzzy-stranded-NN downy mildew classifier model.

3. Experimental Scenario

The author’s experimentation took place in a 0.7 Ha viticulture field of the Debina white grape variety in Zitsa, Epirus, Greece. The experimental setup included one LoRaWAN meteorological station set up in the middle of the field and three end motes (hkt_thp1–3) whose viticulture field placements were based on the elevation and VPD mote criteria of 2021. The end motes data transmissions have been set to hourly intervals. The meteorological station data transmissions have been set to every minute. Figure 5 shows the viticulture field and the installed temperature and humidity motes (motes htk_thp1–3), as illustrated on the ThingsBoard AS map-panel, over the satellite layer of the Google Maps API [83]. The motes used in this experimental scenario include temperature and humidity sensors. The installed meteorological station includes temperature, humidity, pressure, wind speed, wind direction sensors, and an open-type rain gauge.

The authors tested and validated their end-mote proposition by collecting temperature and humidity measurements per end-mote and presenting these results using the appropriate ThingsBoard AS dashboard User Interfaces. Moreover, appropriate dashboards have also been created for the LoRaWAN meteorological station that can illustrate measurements in real-time, hourly, weekly, monthly, and yearly. Measurements have been collected from the viticulture field motes for 2021–2023 and for the months of March until September for each year accordingly. At first, the fuzzification process was executed using the MF functions and fuzzy rules described in Section 2.4. The fuzzy inference class annotation outputs for different temperature and humidity values are illustrated in Figure 6.

The fuzzy-stranded-NN model has been trained using the collected temperature and humidity measurements. In order to circumvent model erroneous prediction for years 2021–2023 due to over-fitting, additional hourly temperature and humidity measurements have been acquired from years 2011–2023 from the Zitsa meteorological station using the OpenMeteo historical API [81] (acquiring Zitsa area historical data for months March until September each year (2011–2020)). Additionally, all OpenMeteo hourly measurement intervals have been padded to a minute scale as described in Section 2.4. From this training process, the author’s meteorological station collected data from the years 2021–2023, which have been kept and used by their model evaluation scenarios. The collected data set, upon data padding, included a total of 4.8 million temperature-humidity measurement pairs. These value pairs have been annotated and fed as input to the fuzzy-stranded-NN model using 80% of the dataset for training and 20% for testing. From the fuzzy stranded model, the strands of temperature-humidity batches of size n = 16, 48, 80, 160, 480, and 960 have been trained using the fuzzy annotated dataset as input.

Before different batch size model strand training, the input measurements data have been partitioned into batches of measurements. Since the fuzzy annotation process has been performed for each measurement of $T,H$ separately, the per batch aggregated annotated fuzzy output class and class confidence level (that expresses the probability that a set of measurements belongs to a class), have been calculated as a mean value of the class and confidence vectors per batch. According to the mentioned partitioning and batch annotation steps, different annotated batch input sets have been created for each strand to train. The per-strand training process used the default model hyperparameters as presented in Table 6. Section 3.1 presents the trained fuzzy-stranded-NN model evaluation results.

3.1. Training Model Evaluation

For the proposed fuzzy-stranded-NN model validation and evaluation, the technique that we use to minimize the loss is the Adaptive Momentum Estimation algorithm or Adam optimization, starting with an initial high learning rate parameter of 0.01 that is gradually reduced by a factor of $f={10}^{-2},ne{w}_{lr}=lr·f$. This adaptive callback monitors cross-entropy loss, and if no improvement is seen for three epochs (patience = 3), the learning rate is reduced until the value of $lr={10}^{-4}$. During epoch evaluation stages using the test dataset, both accuracy and the categorical cross-entropy loss function, which calculates loss between the actual labels and predictions for multi-class data, is used, based on Equation (14).

$$L_{to{t}_{CE}}=\sum _{j=1}^n-\sum _{i=0}^C{\widehat{y_j}}_{actua{l}_i}·log\left({\widehat{y_j}}_{pre{d}_i}\right)$$

(14)

where i = 0…C, the classifier classes, $j=1\dots n$, the testing set members, and ${\widehat{y}}_{actua{l}_i}$, ${\widehat{y}}_{pre{d}_i}$, the actual and predicted classification vectors, expressed as a cumulative value called total loss. Similarly, the accuracy metric is calculated for each epoch during testing as the percentage of the predicted classification values ($y_{Pred}$) that match actual values ($y_{True}$) over the total number of testing set members.

The confidence metric $Con{f}_j$, for each j predicted class output, expresses the distance between the maximum predicted value ($p{v}_i$) upon normalization of the classifier output vector and the actual ground truth class i (vector element position), expressed by Equation (15).

$$Con{f}_j=\left|max\left\{p{v}_i\right\}\right|,i=0\dots C$$

(15)

The metrics of accuracy and total loss($L_{to{t}_{CE}}$) have been used for each one of the model strands and different epoch values of 10, 20, 30, 40, 50, 60, 70, and 80 per strand accordingly. Figure 7 illustrates the accuracy results over batch size n for different epoch values, while Figure 8 illustrates the total loss values over batch size n for different epochs.

From Figure 7 accuracy results, the accuracy starts with the highest value of 95% for n = 16, and 92–93% for stranded models of n = 160, 80 and 48 batch sizes over 10–20 epochs. However, these high accuracy scores start decreasing above 20 epochs, achieving minimum accuracy scores of 85% at 40 epochs. The model accuracy stabilizes close to 90% for 60–70 epochs and close to 90.5% at 80 epochs.

Total loss for models n = 16, 48 remains constant for all epochs, while for n = 80, 160, the loss decreases starting from 10 to 20 epochs, and above 20 epochs, it also remains constant. This means that for small batch input size strands (up to 160 measurements batch), at least a number of 20 epochs is needed for the loss to minimize. Above 20 epochs, introducing more epoch cycles can contribute to improved accuracy results of 0–5% up until 80 epochs. This improvement is mainly caused by the adaptive learning rate mechanism of the Adam optimizer used by the model. Above 80 epochs, accuracy remains constant, offering no more than 0.5–1% improved accuracy results. The proposed fuzzy-stranded-NN model manages to maintain a mean accuracy result of 90.5% for stands of batch size less than 160 measurements. and mean accuracy of 90% for strands of batch size above 480. The number of measurements per batch size is presented in Table 6.

Large batch size strands of n = 480 and n = 960 present significant losses for low training epochs (less than 50 epochs) as shown in Figure 7. This is due to the excess size of their network and the large number of parameters that need to be trained, leading to categorical losses for a low number of epochs. However, above 70 epochs, the loss slowly decreases, presenting a minimum mean loss value of 0.7 at 80 epochs. Nevertheless, the pertained loss of high batch size strands is at least 100–120% more than their small batch size counterparts. This is not the case for the accuracy. As shown in Figure 7, for n = 480 and 80 epochs the accuracy of 91% has been achieved because of the adaptive learning rate is similar to the accuracy of small batch size strands.

Table 9. Fuzzy-stranded-NN model number of hidden layers and training parameters per input batch sizes.

Batch_Size	No. Hidden Layers	Per Layer Trainable Parameters
16	2	L16, L64
48	4	L48, L32, L32, L16
64	4	L64, L64, L32, L16
80	5	L80, L64, L64, L32, L16
96	5	L96, L64, L64, L32, L16
160	6	L160, L128, L128, L64, L32, L16
480	7	L480, L256, L256, L128, L64, L32, L16
960	8	L960, L512, L512, L256, L128, L64, L32, L16

presents the number of hidden layers and trainable parameters for the different strands according to their input measurements batch sizes.

The same accuracy results close to 90.5% can also be achieved for n = 960 for more than 80 epochs up to 120 trainning epochs. For 80 epochs though, the n = 960 strand presents the least accuracy of 89.5%. Concluding, the maximum accuracy difference for all stranded networks at 80 epochs is more or less 1% from the mean model strands accuracy of 90.4%. This means that for 80 training epochs, all strands present almost similar accuracy results close to 90% with a window of improvement of 0.8–1.2% for training up to 120epochs. This is not the case for total loss, where the loss of lower strands is at least two times lower than that of bigger strands. This, of course, mainly affects the confidence values of the classification outputs and not the output class values. The following Section 3.2 presents the author’s model experimentation on the debina white grape variety.

3.2. Trained Model Experimentation

In order to validate their model further, the authors performed the following experimentation in their viticulture field of reference for the years 2021–2023. The authors used their meteorological station measurements and their fuzzy-stranded-NN model to provide daily model classifications for their five-model output classes. Figure 9 shows their meteorological station rainfall measurements, and Figure 10 shows the vapor pressure deficit values for the years 2021 to 2023.

For 2021, the authors performed five protective treatments starting from the 15th of May using Bordeaux mixture every 15 days until the 15th of July. The same methodology has been repeated for 2022, with the difference that the fifth fungicide intervention has been replaced with leaf removal close to the fruit, leaving it exposed to sunlight. Both of these precision viticulture cases have been characterized as normal cases that led to mean productivity results of 680 kg/1000 m² for 2021 and 590 kg/1000 m² for 2022. The productivity difference between the years 2021 and 2022 is mostly due to other infections, specifically white mildew and specifically for botrytis cinerea, that have been treated on a separate intervention at the beginning of August each year, while the white mildew disease has been treated along with downy mildew fungicide interventions starting from the 1st of July. The experimental vineyard is a 40-year-old debina vineyard, and during the experimentation, no irrigation or fertilization plans have been performed. The authors also confirm that their intervention planning managed to prevent and eliminate completely even early downy mildew appearances for years 2021 and 2022.

For the year 2023, the authors performed no interventions, closely monitoring the progress of the disease, which started to appear with a minimum number of sporangia at the back of some leaves on the 1st of June. What followed was a catastrophic collapse. At least one oil spot/tree appeared until 12/6, the first signs of the disease at the fruit appeared until 20/6, and until 30/6, the whole fruit has been led to necrosis, with most of the leaves/tree having oil spots. The productivity results of the year 2023 were 0 kg/1000 m², thus characterizing this experiment as a mildew outburst case. Furthermore, the year 2023 has been characterized as a year of mildew outbursts in the area of Zitsa, where most of the nearby farmers did not manage to save their crops. A few that did were forced to perform 7–8 interventions from May until the end of August to save 70–80% of their production, while farmers that performed 5–7 interventions managed to save 30–50% of their production accordingly. Since most of the farmers in this viticulture area have in mind periodic planning of at most five interventions/year, usually applied after more than 5 mm/h of rainfall of more than 2 h, the fact that more than five interventions were needed for 2023 led to interventions misplanning and thus productivity losses.

Since the installed thingsAI meteorological station offers per-minute measurements, the strand of batch size n = 960, which offers 8 h interval predictions, has been used. Two main reasons led to the selection of this strand. First, it’s NN depth that makes it a deep learning representative concerning its similar accuracy results towards less deep strands, and second, its meteorological station measurements granularity.

Table 10. Average monthly rainfall and Vapor Pressure Deficit values for years 2021–2023.

Month_Year	Mean Rainfall (mm)	Mean VPD (kPa)
05_2021	0.85	0.35
05_2022	0.83	0.57
05_2023	0.49	1.9
06_2021	1.37	0.27
06_2022	1.38	0.7
06_2023	0.76	0.87
07_2021	1.99	0.07
07_2022	2.01	0.2
07_2023	1.79	0.08
08_2021	1.97	0.13
08_2022	1.52	0.39
08_2023	1.41	0.5

summarizes the mean VPD and rainfall results for the years 2021 to 2023.

As shown in Table 10, it is obvious that for 05/2023, there was an increase in monthly rainfall 5 and 3 times more compared to 2021 and 2022. For 06/2023 and 06/2022, there was also an increase in monthly rainfall three times more than in 2021. The same pattern applies for the 8/2022 and 8/2023 concerning 2021. Significant variations in rainfall appear for July. However, due to the small mean values (≤0.3) and high mean VPD values (>1.5), they are considered similar for all years in terms of downy mildew incubation time.

Regarding the mean VPD values between 2021 and 2023, the VPD differences are of value 0.36 for May, 0.61 for June, 0.2 for July, and 0.56 for August. These differences signify that monthly mean VPD reductions of more than 0.3 kPa over the years, especially for May and June, can lead to faster downy mildew growth and, thus, more frequent interventions to ameliorate it.

The authors experimented with the n = 960 strand of their model, which corresponds to a measurement time frame of 8 h ($dT=0.33$ day). The authors calibrated their model coefficients $k_c=\frac{1}{4}$ and $k_n=\frac{1}{6}$, derived from Equation (12), using the year 2021 as reference. Furthermore, they set a breakpoint for an imminent intervention $T_{INT}$ when the metric reaches the value of 12 infection cycle days. The following sections present the author’s intervention results over normal and mildew outbursts, as the model predicted.

3.3. Scenario I: Model Experimentation under Normal Conditions

The authors model experimental results for 2021 and 2022, characterized as normal conditions cases, are illustrated in Figure 11.

As shown in Figure 11, the $d{T}_{INT}$ infection cycle days are represented on the y-axis as a cumulative sum, calculated by Equation (12). Time of 8h intervals are shown on the x-axis, as denoted by the n = 960 model strand, starting from the 1st of May until the end of August. When the cumulative sum of $d{T}_{INT}$ infectious days reaches the value of 12 days, then an alert is triggered by the thingsAI system, indicating an intervention breakpoint, and the value of $d{T}_{INT}$ is set to zero for the cycle to repeat. Four intervention breakpoints have been triggered for 2021, while five breakpoints have been triggered for 2022. The first three breakpoints have been triggered almost at the same time intervals for both years, while there is a delayed offset of 10 days for the fourth breakpoint for 2021 with respect to 2022 and a fifth single breakpoint at 27/8 for 2022. From the farmer recorded interventions, only four interventions were required for the year 2021 instead of five performed and exactly five interventions for the year 2022 in order to disperse downy mildew infections.

3.4. Scenario II: Model Experimentation under Downy Mildew Outbursts

The author’s model experimental result for the year 2023, characterized as a downy mildew outburst case compared to the normal case of 2022, is illustrated in Figure 12.

The experimental results, illustrated in Figure 12 show an increase in the number of interventions required for 2023 concerning 2022 from 5 to 7 interventions and also pinpoint significant intervention offsets from 2 up to 10 days. This increased frequency and offsetting made it hard for the farmers to cope with such environmental changes compared to their previous years’ practices, thus leading to significant productivity losses or collapses due to downy mildew infections.

Additionally, the authors compared their model intervention outcomes for the year 2023 with the infection alerts provided by the Goidanich model, as adapted by [84]. The authors use a Goidanich index value of at least 100 to trigger an alert (resetting its value each time) and a cumulative rainfall RF > 10 mm for 72 h starting from the 1st of May for primary infections to occur. Figure 13 illustrates the fuzzy-stranded-NN n = 960 input batch size $T_{I}NT$ outputs compared to the Goidanich model alert results, using GI > 100, for imminent interventions during the 2023 mildew outburst in the Zitsa area.

The experimental results show that both the Goidanich and fuzzy-stranded-NN models detected the same number of seven seasonal interventions, as indicated by the number of triggered alerts issued by both models. Additionally, the fuzzy-stranded-NN model for May-July proposes earlier interventions with a mean offset of 5.3 days (from 1/5 until 6/8) concerning Goidanich alerts for interventions. This is indifferent for the rest of August, where the Goidanich model proposed one intervention 12 days prior to the one proposed by the fuzzy-stranded-NN model. These offsets are probably because the GI index starts increasing from the 8th of May due to the 72 h cumulative rainfall value > 10 mm threshold required for GI to start counting and the GI > 100 threshold value set. In conclusion, this validates the proposed model’s results compared to the most used model for alerts triggered by DSS systems. Nevertheless, further evaluation is required, set by the authors as future work.

4. Conclusions

This paper presents a new cloud-based Decision Support System architecture for the viticulture industry called thingsAI. It utilizes autonomous end-node devices called motes and meteorological stations to provide a dense plant-level measurement acquisition grid. Mote devices and meteorological stations use low-power, long-range LoRaWAN technology for their data transmissions. The thingsAI system includes a distributed Cassandra sensory data-collection entry-point and dockerized cloud-ready services hosting its deep learning models for classification and prediction inference tasks. Furthermore, the thingsAI system is equipped with the open-source ThingsBoard Application Server rule chains, alarms, and User Interfaces to deliver sensory measurement trends, suggestions, and decision results to the farmers.

Focusing on the downy mildew disease in viticulture and an extensive literature study on the methods used for the detection of downy mildew, the authors denote that existing ones are either too simplified or complex enough. Simplified in using measurements such as rainfall due to the lack of dense measurement grids. Complex, such as the mechanistic models of hard algorithmic processes for DSS systems to implement, rely on many parameters of extensive experimental calibration. Specifically, the mechanistic models focus mainly on the deterministic representation of the downy mildew development with minimum accountability on different varieties, environmental conditions, and climate change. That is, if applied, they do not provide useful feedback information for the farmers to use.

The authors implemented a deep learning model called fuzzy-stranded-NN to ameliorate the discrepancies between theory and application of the mechanistic models. The model utilizes an automated data annotation process based on semi-automated fuzzy rules. Using simplified lingual expressions, the farmer’s or agronomists’ experience can explicitly set these rules arbitrarily. The proposed model also utilizes several neural networks called strands, each of arbitrary layer depths based on the number of input measurements used, called input batches. This way, more precise predictions can be inferred based on the density of input measurements offering vine-level detections. Existing meteorological station grids may offer up to 15 min of sensory measurements and forecasts. The trained model strands can use these meteorological forecasts to provide 4–7 days of downy mildew forecasts and emerging and future interventions.

The authors experimented with their downy mildew model implementation on the debina white grape variety in its protected designation of origin cultivation area of Zitsa, Epirus, Greece, under normal cases and downy mildew outbursts. From their experimental scenario, the author’s fuzzy-stranded-NN model proposition trained on downy mildew fuzzy annotated datasets successfully issues accurate intervention breakpoints as indicated by the farmers, providing detection accuracies above 90% as indicated by model testing. The authors’ fuzzy-stranded-NN detection outputs have also been validated using the Goidanich model index under mildew outburst cases, where it successfully managed to provide the same number of monthly interventions as the Goidanich model.

Limitations of the presented thingsAI system are the LoRaWAN coverage required for the motes data transmissions to the cloud. This limitation can be easily surpassed with the use of a sparse grid of LoRaWAN gateways due to the 5–12 km coverage radius per gateway offered by the LoRa narrow-band chirp modulation. Another limitation is the mote’s autonomous operation. Motes transmitting measurements every hour may lead to the depletion of their included battery packs every 3–4 months. Thus, farmers’ efforts are required to monitor, replace, and recharge the mote’s battery packs. Regarding the fuzzy-stranded-NN algorithm as a generic algorithm for events classification, there are limitations on both the fuzzy and strand parts of the model. Focusing on the fuzzy part, the definition of the most accurate membership functions that represent a measurement or metric or a phenomenon and the expression of the most representative fuzzy rules for the auto-annotation process is critical and must be performed cautiously. Nevertheless, simulation and trial-and-error experimentation can easily surpass errors in this fuzzy semi-supervised process. Regarding the model NN strands, more than an adequate number of measurements due to limited input sources may lead to poorly trained narrow model strands of low accuracy results.

The authors set as future work the further experimentation of their proposed system and downy mildew model under different environments and vine varieties. The authors set future work to incorporate more models into their thingsAI system, focusing on deep learning irrigation planning models and other disease decision models specifically for botrytis cinerea and white mildew. The authors also set as future work the cross-comparison of their model proposition to existing mechanistic models for further improving their model toward the differentiation among primary and secondary downy mildew infection points, providing different valuable insights accordingly to the farmers.