Atomistic-Scale Simulations on Graphene Bending Near a Copper Surface
Abstract
:1. Introduction
2. Simulation Techniques and ReaxFF Force Field Descriptions
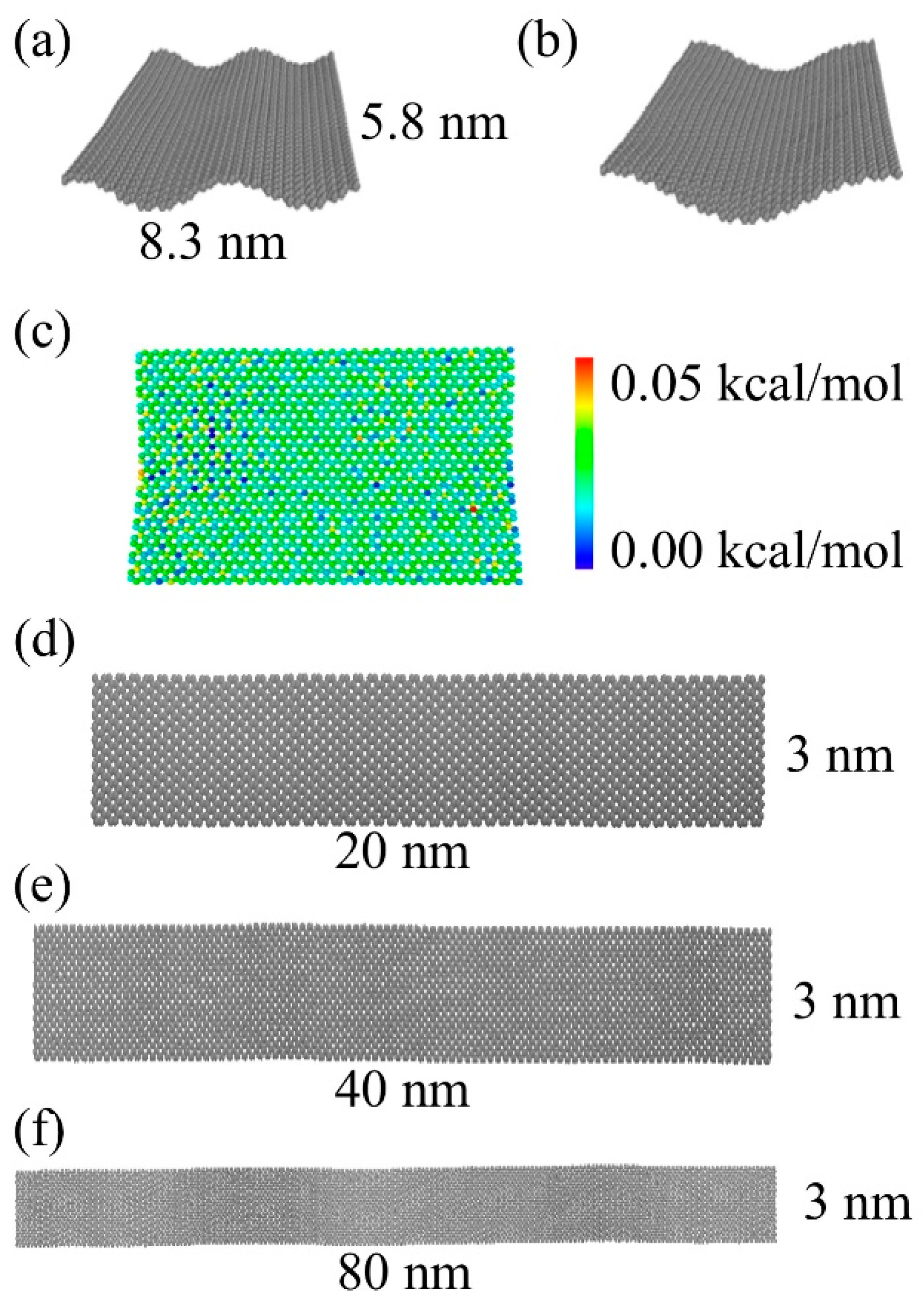
2.1. Bending in a Graphene Sheet
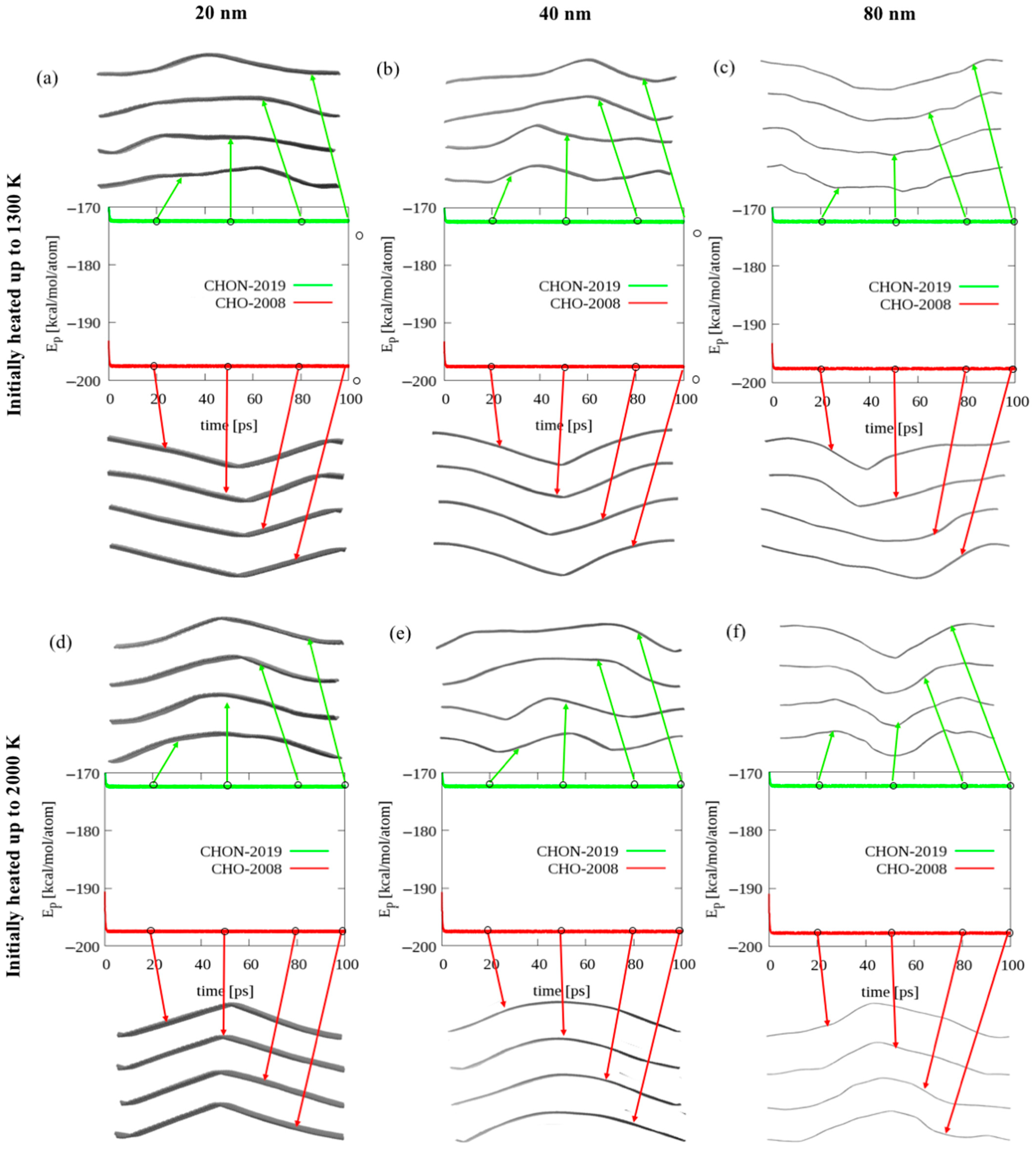
2.2. Bending of Long Graphene Ribbons
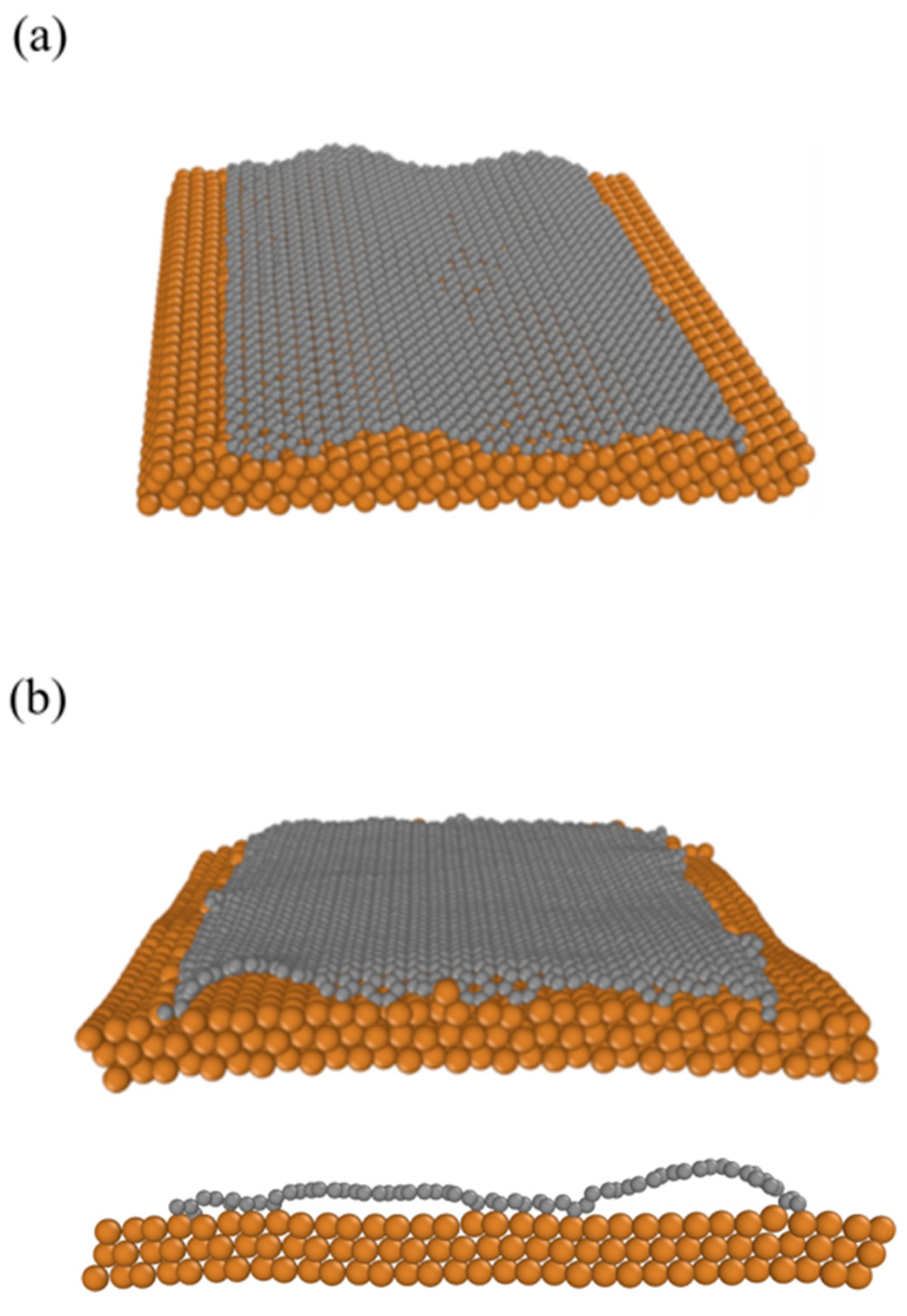
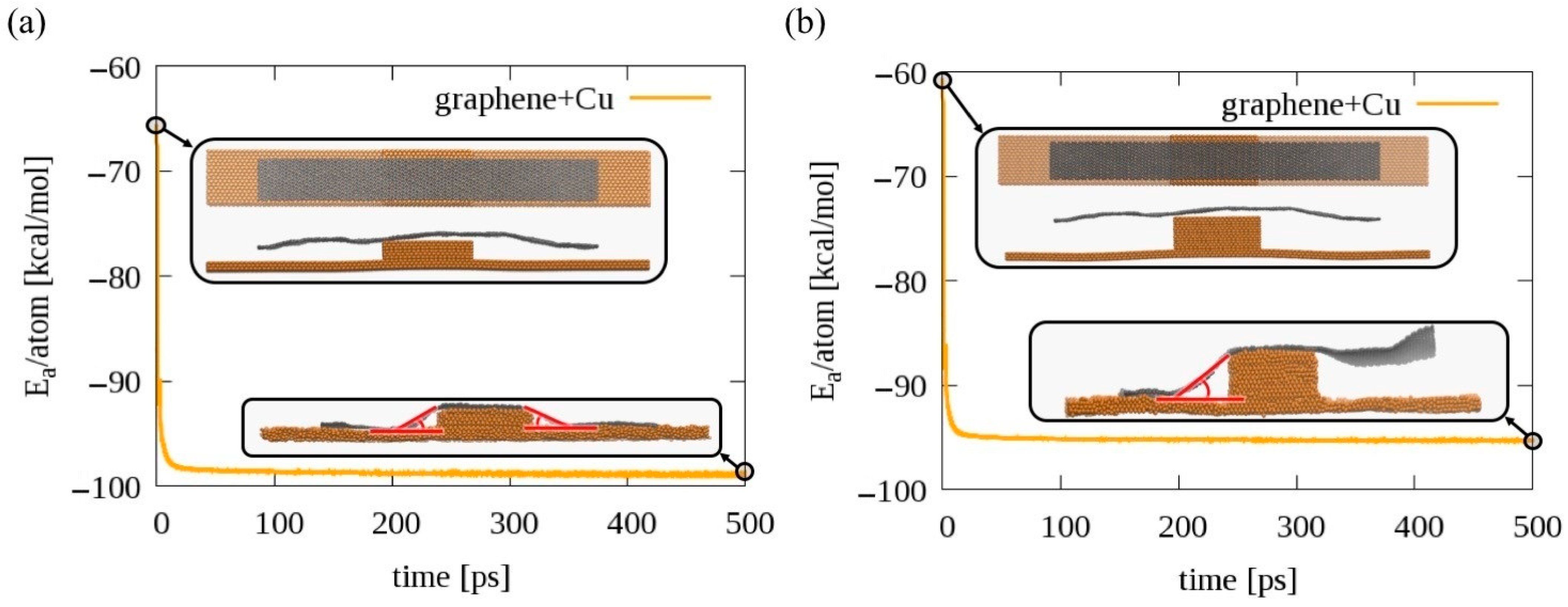
2.3. Graphene at Copper Surface
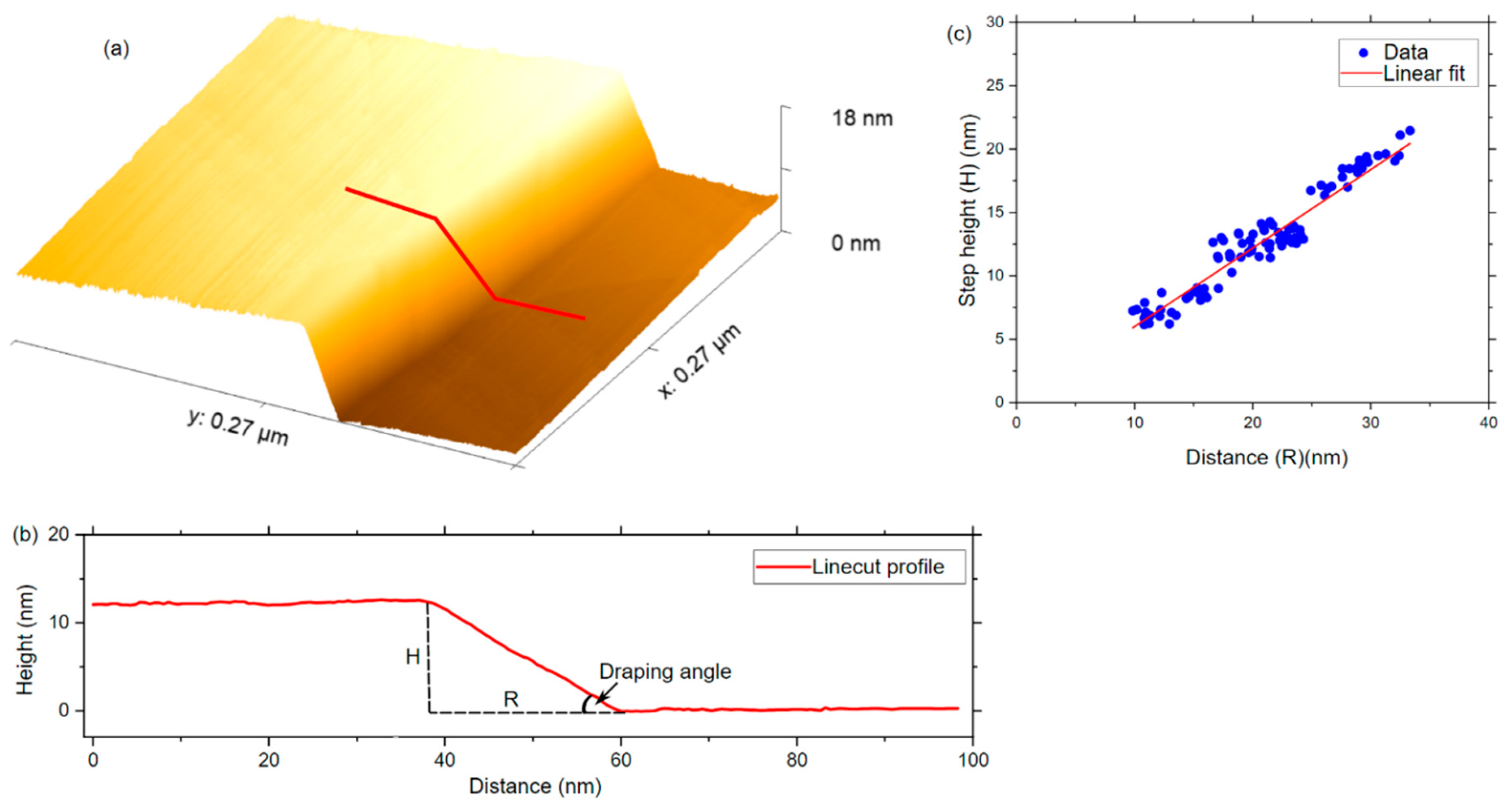
2.4. Determination of the Graphene Draping Angle
2.5. Reactivity of Rippled and Planar Graphene
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect In Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional Atomic Crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [Green Version]
- Lian, P.; Zhu, X.; Liang, S.; Li, Z.; Yang, W.; Wang, H. Large Reversible Capacity of High Quality Graphene Sheets as an Anode Material for Lithium-ion Batteries. Electrochim. Acta 2010, 55, 3909–3914. [Google Scholar] [CrossRef]
- Wu, Z.-S.; Ren, W.; Xu, L.; Li, F.; Cheng, H.-M. Doped Graphene Sheets as Anode Materials with Superhigh Rate and Large Capacity for Lithium Ion Batteries. ACS Nano 2011, 5, 5463–5471. [Google Scholar] [CrossRef]
- Hassoun, J.; Bonaccorso, F.; Agostini, M.; Angelucci, M.; Betti, M.G.; Cingolani, R.; Gemmi, M.; Mariani, C.; Panero, S.; Pellegrini, V.; et al. An Advanced Lithium-Ion Battery Based on a Graphene Anode and a Lithium Iron Phosphate Cathode. Nano Lett. 2014, 14, 4901–4906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Deng, S.; Berry, V. Wrinkled, Rippled and Crumpled Graphene: An Overview of Formation Mechanism, Electronic Properties, and Applications. Mater. Today 2016, 19, 197–212. [Google Scholar] [CrossRef]
- Levy, N.; Burke, S.A.; Meaker, K.L.; Panlasigui, M.; Zettl, A.; Guinea, F.; Neto, A.H.C.; Crommie, M.F. Strain-Induced Pseudo-Magnetic Fields Greater Than 300 Tesla in Graphene Nanobubbles. Science 2010, 329, 544–547. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, R.; Nguyen, V.-H.; Granzier-Nakajima, T.; Pabbi, L.; Lherbier, A.; Binion, A.R.; Charlier, J.-C.; Terrones, M.; Hudson, E.W. Strain Modulated Superlattices in Graphene. Nano Lett. 2020, 20, 3113–3121. [Google Scholar] [CrossRef]
- Dai, S.; Chen, J.; Ren, Y.; Liu, Z.; Chen, J.; Li, C.; Zhang, X.; Zhang, X.; Zeng, T. Electrochemical Corrosion Behavior of the Copper Current Collector in the Electrolyte of Lithium-ion Batteries. Int. J. Electrochem. Sci. 2017, 12, 10589–10598. [Google Scholar] [CrossRef]
- Kim, H.R.; Choi, W.M. Graphene Modified Copper Current Collector for Enhanced Electrochemical Performance of Li-ion Battery. Scr. Mater. 2018, 146, 100–104. [Google Scholar] [CrossRef]
- Lahiri, I.; Oh, S.-W.; Hwang, J.Y.; Cho, S.; Sun, Y.-K.; Banerjee, R.; Choi, W. High Capacity and Excellent Stability of Lithium Ion Battery Anode Using Interface-Controlled Binder-Free Multiwall Carbon Nanotubes Grown on Copper. ACS Nano 2010, 4, 3440–3446. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Zhang, B.; Luan, C.; Qin, T.; Zhang, W.; Wang, D.; Shi, X.; Deng, T.; Zheng, W.T. Vertical Graphene Nanowalls Coating of Copper Current Collector for Enhancing Rate Performance of Graphite Anode of Li Ion Battery: The Merit of Optimized Interface Architecture. Electrochim. Acta 2018, 268, 234–240. [Google Scholar] [CrossRef]
- Pang, Z.; Deng, B.; Liu, Z.; Peng, H.; Wei, Y. Defects Guided Wrinkling in Graphene on Copper Substrate. Carbon 2019, 143, 736–742. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.; Bryantsev, V.S.; van Duin, A.C.T. ReaxFF Reactive Force Field Simulations on the Influence of Teflon on Electrolyte Decomposition during Li/SWCNT Anode Discharge in Lithium-Sulfur Batteries. J. Electrochem. Soc. 2014, 161, E3009–E3014. [Google Scholar] [CrossRef] [Green Version]
- Bedrov, D.; Smith, G.D.; van Duin, A.C.T. Reactions of Singly-Reduced Ethylene Carbonate in Lithium Battery Electrolytes: A Molecular Dynamics Simulation Study Using the ReaxFF. J. Phys. Chem. A 2011, 116, 2978–2985. [Google Scholar] [CrossRef]
- Ong, M.T.; Verners, O.; Draeger, E.W.; van Duin, A.C.T.; Lordi, V.; Pask, J.E. Lithium Ion Solvation and Diffusion in Bulk Organic Electrolytes from First-Principles and Classical Reactive Molecular Dynamics. J. Phys. Chem. B 2015, 119, 1535–1545. [Google Scholar] [CrossRef] [Green Version]
- Hossain, J.; Pawar, G.; Liaw, B.; Gering, K.L.; Dufek, E.J.; van Duin, A.C.T. Lithium-electrolyte Solvation and Reaction in the Electrolyte of a Lithium Ion Battery: A ReaxFF Reactive Force Field Study. J. Chem. Phys. 2020, 152, 184301. [Google Scholar] [CrossRef] [PubMed]
- Van Duislamn, A.C.; Ostadhossein, A.; Borodin, O.; Yeates, A.T.; Tipton, W.W.; Hennig, R.G.; Kumar, N.; Van Duin, A.C. ReaxFF Molecular Dynamics Simulations on Lithiated Sulfur Cathode Materials. Phys. Chem. Chem. Phys. 2014, 17, 3383–3393. [Google Scholar] [CrossRef]
- Reddivari, S.; Lastoskie, C.; Wu, R.; Zhang, J. Chemical Composition and Formation Mechanisms in the Cathode-electrolyte Interface Layer of Lithium Manganese Oxide Batteries from Reactive Force Field (ReaxFF) Based Molecular Dynamics. Front. Energy 2017, 11, 365–373. [Google Scholar] [CrossRef]
- Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF Potential for Carbon Condensed Phases and Its Application to the Thermal Fragmentation of a Large Fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.; Kolesov, G.; Verstraelen, T.; Kaxiras, E.; van Duin, A.C.T. eReaxFF: A Pseudoclassical Treatment of Explicit Electrons within Reactive Force Field Simulations. J. Chem. Theory Comput. 2016, 12, 3463–3472. [Google Scholar] [CrossRef] [PubMed]
- Jensen, B.D.; Wise, K.E.; Odegard, G.M. Simulation of the Elastic and Ultimate Tensile Properties of Diamond, Graphene, Carbon Nanotubes, and Amorphous Carbon Using a Revised ReaxFF Parametrization. J. Phys. Chem. A 2015, 119, 9710–9721. [Google Scholar] [CrossRef] [PubMed]
- van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef] [Green Version]
- Chenoweth, K.; van Duin, A.C.T.; Goddard, W.A. ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Hydrocarbon Oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef] [Green Version]
- Kowalik, M.; Ashraf, C.; Damirchi, B.; Akbarian, D.; Rajabpour, S.; van Duin, A.C.T. Atomistic Scale Analysis of the Carbonization Process for C/H/O/N-Based Polymers with the ReaxFF Reactive Force Field. J. Phys. Chem. B 2019, 123, 5357–5367. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Gong, H.; Han, Y.; Zhang, M.; van Duin, A.C.T. Development of a Reactive Force Field for Simulations on the Catalytic Conversion of C/H/O Molecules on Cu-Metal and Cu-Oxide Surfaces and Application to Cu/CuO-Based Chemical Looping. J. Phys. Chem. C 2020, 124, 12512–12520. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Chemistry, S.T. ADF Modeling Suite; Vrije Universiteit: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Liu, X.; Wang, F.C.; Wu, H. Anomalous Twisting Strength of Tilt Grain Boundaries in Armchair Graphene Nanoribbons. Phys. Chem. Chem. Phys. 2015, 17, 31911–31916. [Google Scholar] [CrossRef]
- Kang, J.H.; Moon, J.; Kim, D.J.; Kim, Y.; Jo, I.; Jeon, C.; Lee, J.; Hong, B.H. Strain Relaxation of Graphene Layers by Cu Surface Roughening. Nano Lett. 2016, 16, 5993–5998. [Google Scholar] [CrossRef]
- Yi, D.; Luo, D.; Wang, Z.-J.; Dong, J.; Zhang, X.; Willinger, M.; Ruoff, R.S.; Ding, F. What Drives Metal-surface Step Bunching in Graphene Chemical Vapor Deposition? Phys. Rev. Lett. 2018, 120, 246101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of Image Analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, Z.; Soni, A.; Zhao, Y.; Xiong, Y.; Peng, B.; Wang, J.; Dresselhaus, M.S.; Xiong, Q. Raman Spectroscopy of Few-Quintuple Layer Topological Insulator Bi2Se3Nanoplatelets. Nano Lett. 2011, 11, 2407–2414. [Google Scholar] [CrossRef]
- Sofo, J.O.; Chaudhari, A.S.; Barber, G.D. Graphane: A Two-dimensional Hydrocarbon. Phys. Rev. B 2007, 75, 153401. [Google Scholar] [CrossRef] [Green Version]
- Yi, D.; Yang, L.; Xie, S.; Saxena, A.B. Stability of Hydrogenated Graphene: A First-principles Study. RSC Adv. 2015, 5, 20617–20622. [Google Scholar] [CrossRef]
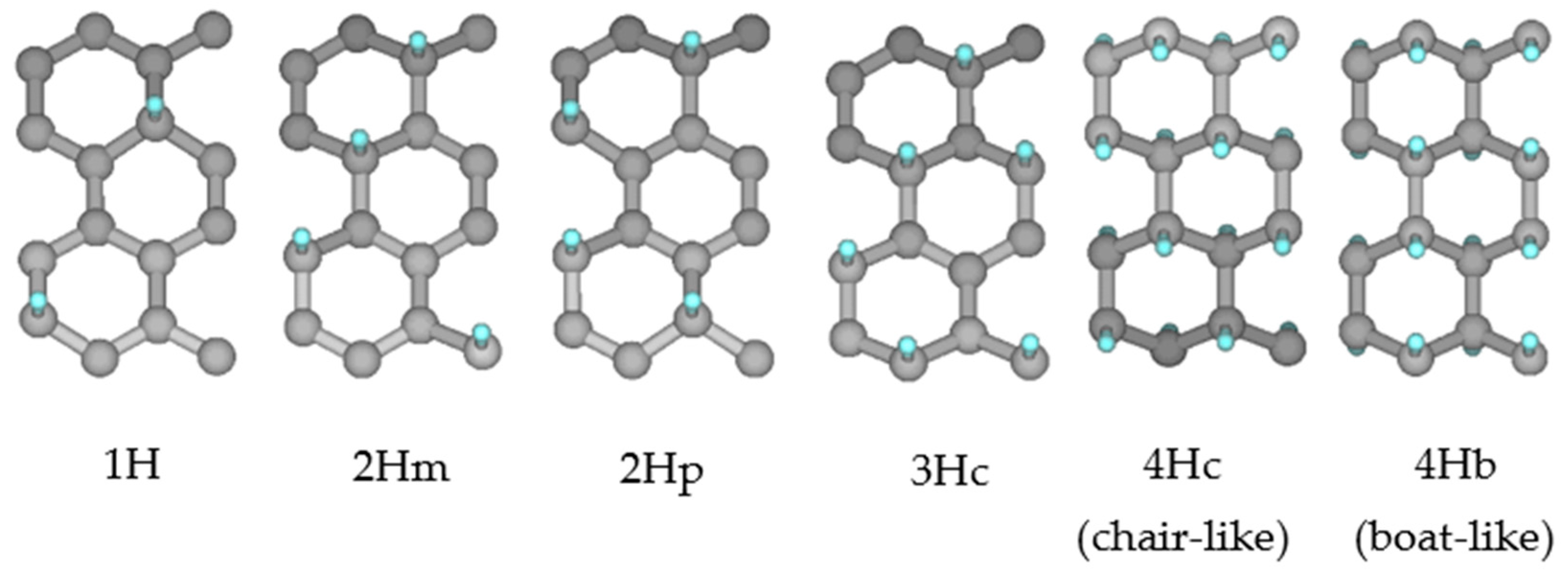
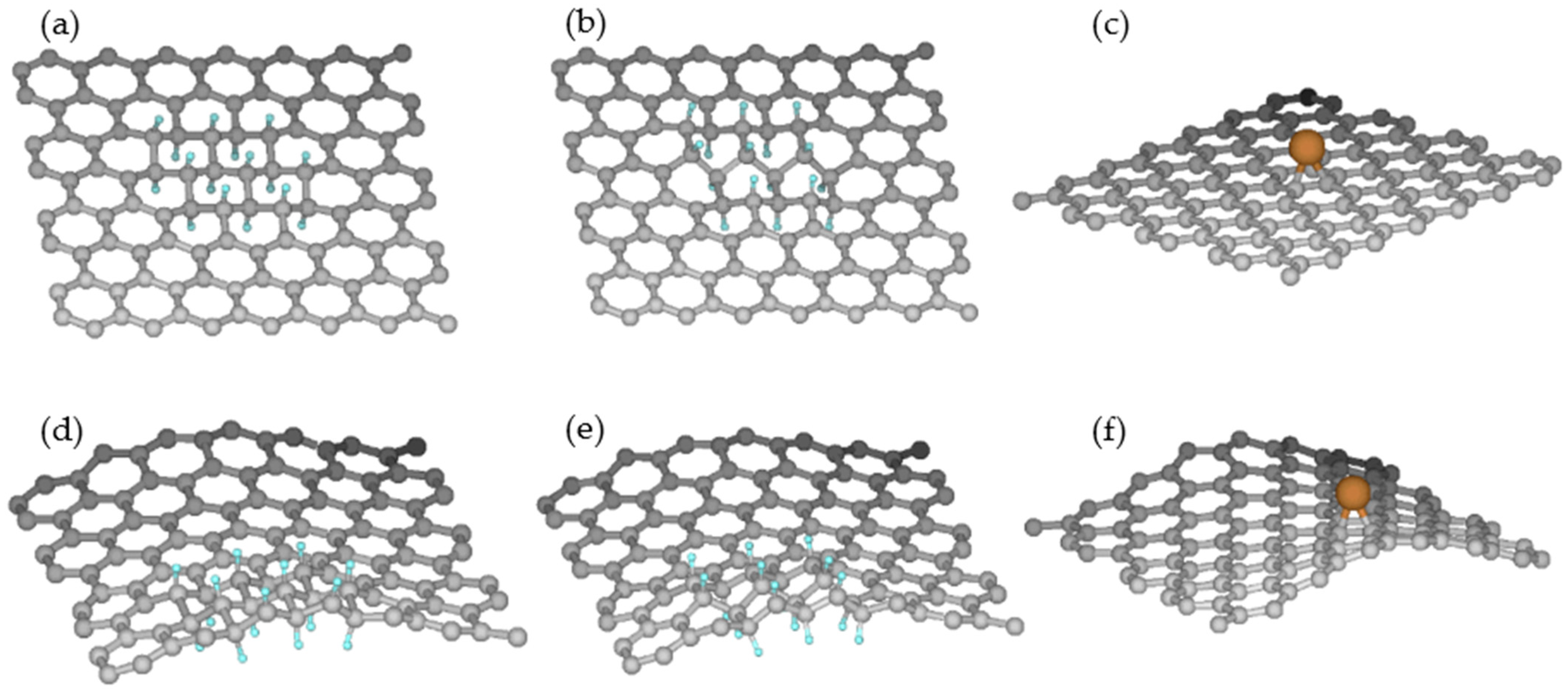
| Binding Energy with H Atom Reference | CHO-2008 (kcal/mol) | CHO-2019 (kcal/mol) | DFT Reference [38] (kcal/mol) |
| 1H | −80.82 | −27.63 | −25.37 |
| 2Hm | −62.55 | −21.75 | −21.91 |
| 2Hp | −64.60 | −35.84 | −46.12 |
| 3Hc | −49.67 | −16.96 | −20.75 |
| Binding Energy with H2 Molecule Reference | CHO-2008 (kcal/mol) | CHO-2019 (kcal/mol) | DFT Reference [38] (kcal/mol) |
| 1H | −26.04 | 24.89 | 27.67 |
| 2Hm | −7.77 | 30.77 | 29.98 |
| 2Hp | −9.82 | 16.69 | 5.77 |
| 3Hc | 5.12 | 35.57 | 31.13 |
| Binding Energy with H Atom Reference | CHO-2008 (kcal/mol) | CHO-2019 (kcal/mol) | DFT Reference [38] (kcal/mol) |
| 4Hc | −69.39 | −57.17 | −63.42 |
| 4Hb | −69.35 | −54.11 | −61.11 |
| Binding energy with H2 molecule reference | CHO-2008 (kcal/mol) | CHO-2019 (kcal/mol) | DFT Reference [38] (kcal/mol) |
| 4Hc | −14.61 | −4.64 | −11.53 |
| 4Hb | −14.56 | −1.58 | −9.22 |
| 4Hc | CHO-2008 | CHO-2019 | DFT Reference [38] |
| C–C bond | 1.557 Å | 1.529 Å | 1.539 Å |
| C–C–C angle | 104.6° | 107.2° | 111.4° |
| 4Hb | CHO-2008 | CHO-2019 | DFT Reference [38] |
| C–C bond | 1.570 Å | 1.539 Å | 1.539 Å |
| C–C–C angle | 108.2° | 109.9° | 111.8° |
| Binding Energy with H Atom Reference | Plane (kcal/mol) | Rippled (kcal/mol) |
| chair-like | −52.38 | −57.12 |
| boat-like | −50.04 | −54.59 |
| Binding Energy with H2 Molecule Reference | Plane (kcal/mol) | Ripple (kcal/mol) |
| chair-like | 0.15 | −4.60 |
| boat-like | 2.49 | −2.06 |
| Binding Energy with Cu Atom Reference | Cu-C Force Field (kcal/mol) |
| plane graphene | −37.32 |
| rippled graphene | −57.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowalik, M.; Hossain, M.J.; Lele, A.; Zhu, W.; Banerjee, R.; Granzier-Nakajima, T.; Terrones, M.; Hudson, E.W.; van Duin, A.C.T. Atomistic-Scale Simulations on Graphene Bending Near a Copper Surface. Catalysts 2021, 11, 208. https://doi.org/10.3390/catal11020208
Kowalik M, Hossain MJ, Lele A, Zhu W, Banerjee R, Granzier-Nakajima T, Terrones M, Hudson EW, van Duin ACT. Atomistic-Scale Simulations on Graphene Bending Near a Copper Surface. Catalysts. 2021; 11(2):208. https://doi.org/10.3390/catal11020208
Chicago/Turabian StyleKowalik, Malgorzata, Md Jamil Hossain, Aditya Lele, Wenbo Zhu, Riju Banerjee, Tomotaroh Granzier-Nakajima, Mauricio Terrones, Eric W. Hudson, and Adri C. T. van Duin. 2021. "Atomistic-Scale Simulations on Graphene Bending Near a Copper Surface" Catalysts 11, no. 2: 208. https://doi.org/10.3390/catal11020208
APA StyleKowalik, M., Hossain, M. J., Lele, A., Zhu, W., Banerjee, R., Granzier-Nakajima, T., Terrones, M., Hudson, E. W., & van Duin, A. C. T. (2021). Atomistic-Scale Simulations on Graphene Bending Near a Copper Surface. Catalysts, 11(2), 208. https://doi.org/10.3390/catal11020208









