A Computational Method to Predict Effects of Residue Mutations on the Catalytic Efficiency of Hydrolases
Abstract
:1. Introduction
2. Results
2.1. Data Set
2.2. Model Performance
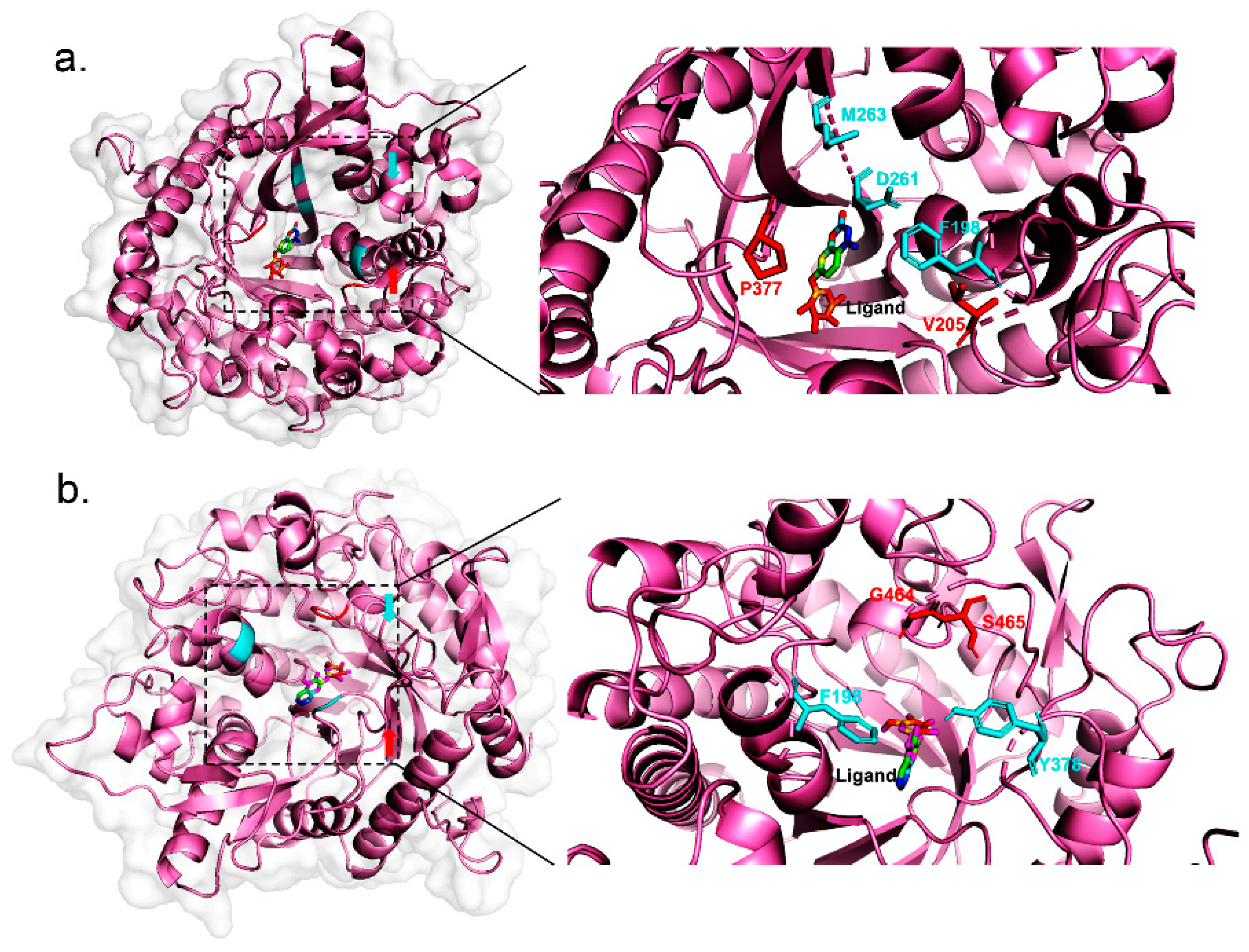
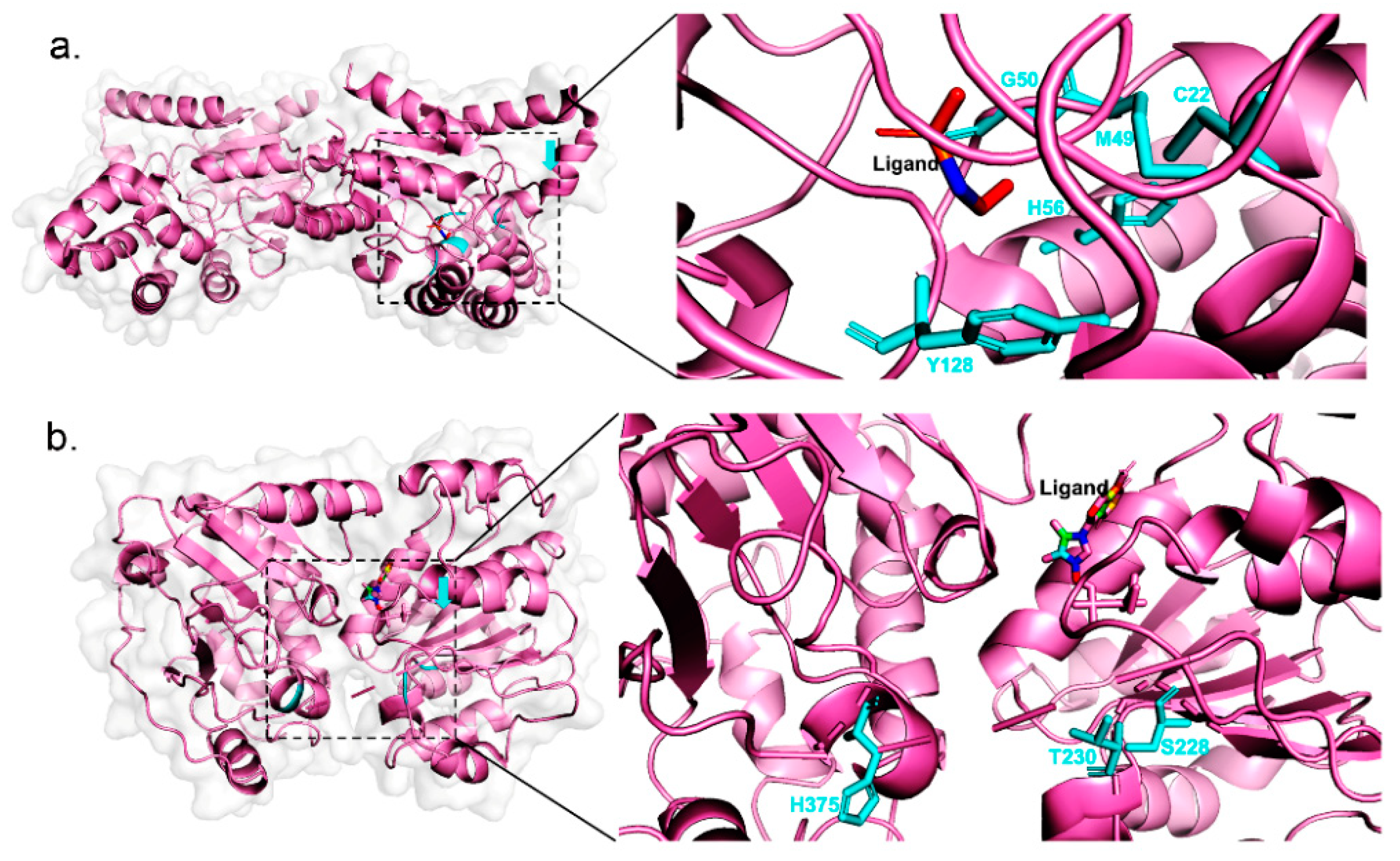
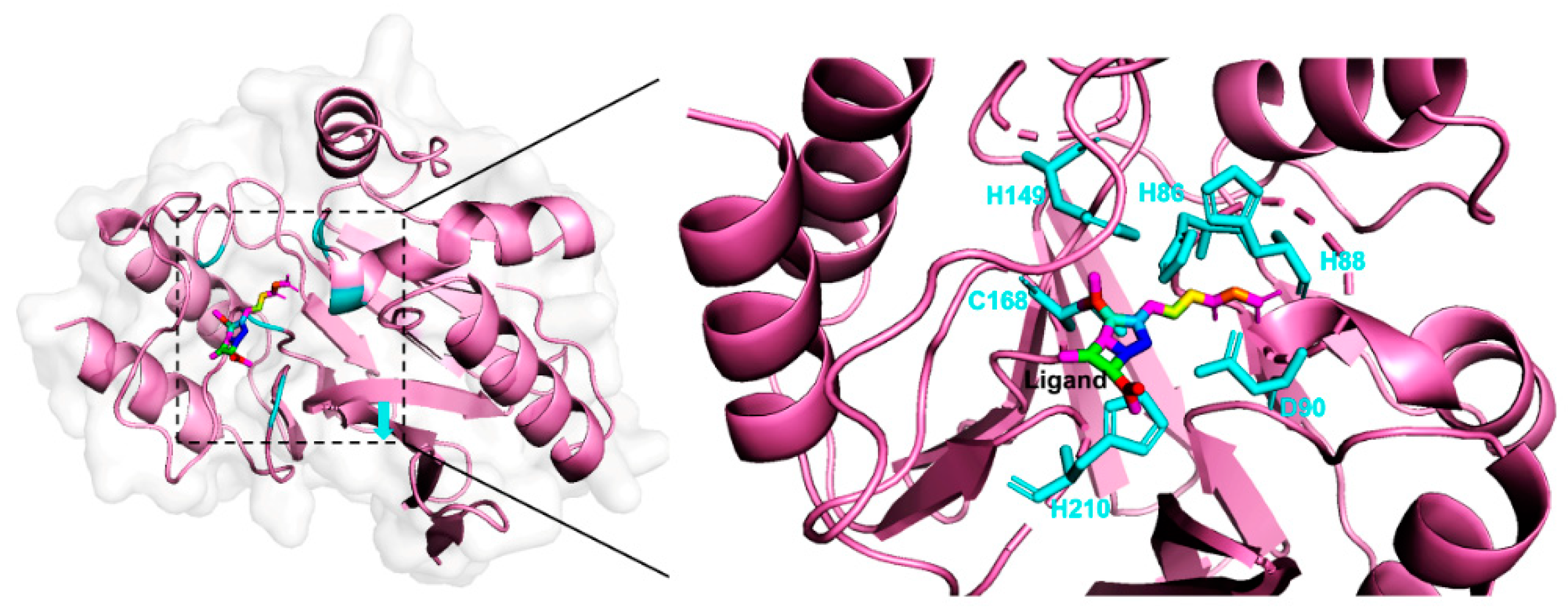
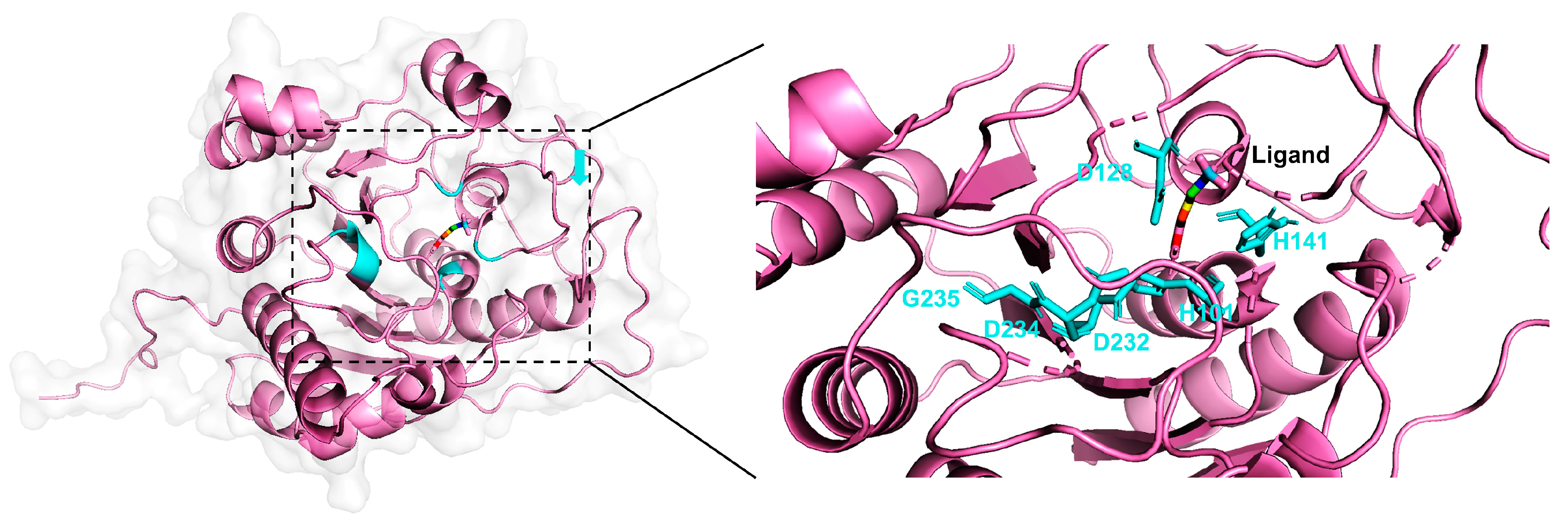
2.3. Case Study
3. Discussion
4. Materials and Methods
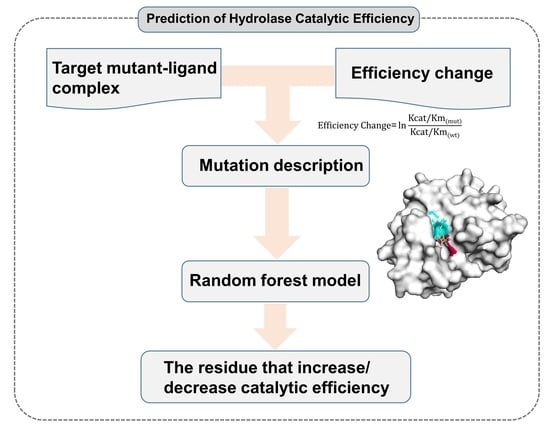
4.1. Method Workflow
4.2. Data Collection and Preparation
4.3. Feature Construction
4.4. Comparison of Different Classifiers
4.5. Model Evaluation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Garcia-Viloca, M.; Gao, J.; Karplus, M.; Truhlar, D.G. How enzymes work: Analysis by modern rate theory and computer simulations. Science 2004, 303, 186–195. [Google Scholar] [CrossRef]
- Zhou, X.X.; Fan, L.Z.; Li, P.; Shen, K.; Lin, M.Z. Optical control of cell signaling by single-chain photoswitchable kinases. Science 2017, 355, 836–842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feltcher, M.E.; Braunstein, M. Emerging themes in SecA2-mediated protein export. Nat. Rev. Microbiol. 2012, 10, 779–789. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Joachimiak, A.; Rosner, M.R.; Tang, W.J. Structures of human insulin-degrading enzyme reveal a new substrate recognition mechanism. Nature 2006, 443, 870–874. [Google Scholar] [CrossRef] [Green Version]
- King, J.V.; Liang, W.G.; Scherpelz, K.P.; Schilling, A.B.; Meredith, S.C.; Tang, W.J. Molecular basis of substrate recognition and degradation by human presequence protease. Structure 2014, 22, 996–1007. [Google Scholar] [CrossRef] [Green Version]
- Goyal, M.S.; Vlassenko, A.G.; Blazey, T.M.; Su, Y.; Couture, L.E.; Durbin, T.J.; Bateman, R.J.; Benzinger, T.L.; Morris, J.C.; Raichle, M.E. Loss of Brain Aerobic Glycolysis in Normal Human Aging. Cell Metab. 2017, 26, 353–360. [Google Scholar] [CrossRef]
- Greule, A.; Stok, J.E.; De Voss, J.J.; Cryle, M.J. Unrivalled diversity: The many roles and reactions of bacterial cytochromes P450 in secondary metabolism. Nat. Prod. Rep. 2018, 35, 757–791. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, D.; Eychmuller, A. Enzymatic Biofuel Cells on Porous Nanostructures. Small 2016, 12, 4649–4661. [Google Scholar] [CrossRef]
- Ji, C.; Hou, J.; Wang, K.; Ng, Y.H.; Chen, V. Single-Enzyme Biofuel Cells. Angew. Chem. Int. Ed. Engl. 2017, 56, 9762–9766. [Google Scholar] [CrossRef] [PubMed]
- Kirk, O.; Borchert, T.V.; Fuglsang, C.C. Industrial enzyme applications. Curr. Opin. Biotechnol. 2002, 13, 345–351. [Google Scholar] [CrossRef]
- Dulieu, C.; Moll, M.; Boudrant, J.; Poncelet, D. Improved performances and control of beer fermentation using encapsulated alpha-acetolactate decarboxylase and modeling. Biotechnol. Prog. 2000, 16, 958–965. [Google Scholar] [CrossRef]
- Boyce, A.; Walsh, G. Expression and characterisation of a thermophilic endo-1,4-beta-glucanase from Sulfolobus shibatae of potential industrial application. Mol. Biol. Rep. 2018, 45, 2201–2211. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Zhou, L.; Xu, Z.; Zhang, Y.; Liao, X. Enzyme inactivation in food processing using high pressure carbon dioxide technology. Crit. Rev. Food Sci. Nutr. 2013, 53, 145–161. [Google Scholar] [CrossRef] [PubMed]
- Pariza, M.W.; Johnson, E.A. Evaluating the safety of microbial enzyme preparations used in food processing: Update for a new century. Regul. Toxicol. Pharm. 2001, 33, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Anfinsen, C.B.; Haber, E.; Sela, M.; White, F.H., Jr. The kinetics of formation of native ribonuclease during oxidation of the reduced polypeptide chain. Proc. Natl. Acad. Sci. USA 1961, 47, 1309–1314. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Wei, J.; Wu, Z.; Gao, J. Effects of Substrate-Binding Site Residues on the Biochemical Properties of a Tau Class Glutathione S-Transferase from Oryza sativa. Genes 2019, 11, 25. [Google Scholar] [CrossRef] [Green Version]
- Cen, Y.; Singh, W.; Arkin, M.; Moody, T.S.; Huang, M.; Zhou, J.; Wu, Q.; Reetz, M.T. Artificial cysteine-lipases with high activity and altered catalytic mechanism created by laboratory evolution. Nat. Commun. 2019, 10, 3198. [Google Scholar] [CrossRef]
- Guan, L.-J.; Ohtsuka, J.; Okai, M.; Miyakawa, T.; Mase, T.; Zhi, Y.; Hou, F.; Ito, N.; Iwasaki, A.; Yasohara, Y.; et al. A new target region for changing the substrate specificity of amine transaminases. Sci. Rep. 2015, 5, 10753. [Google Scholar] [CrossRef] [Green Version]
- Marshall, S.A.; Lazar, G.A.; Chirino, A.J.; Desjarlais, J.R. Rational design and engineering of therapeutic proteins. Drug Discov. Today 2003, 8, 212–221. [Google Scholar] [CrossRef]
- Kostarelos, K. Rational design and engineering of delivery systems for therapeutics: Biomedical exercises in colloid and surface science. Adv. Colloid Interface Sci. 2003, 106, 147–168. [Google Scholar] [CrossRef]
- Carpenter, J.F.; Pikal, M.J.; Chang, B.S.; Randolph, T.W. Rational design of stable lyophilized protein formulations: Some practical advice. Pharm. Res. 1997, 14, 969–975. [Google Scholar] [CrossRef]
- Johnsson, K.; Allemann, R.K.; Widmer, H.; Benner, S.A. Synthesis, structure and activity of artificial, rationally designed catalytic polypeptides. Nature 1993, 365, 530–532. [Google Scholar] [CrossRef] [PubMed]
- Arnold, F.H. The nature of chemical innovation: New enzymes by evolution. Q. Rev. Biophys. 2015, 48, 404–410. [Google Scholar] [CrossRef]
- Jaeger, K.; Eggert, T. Enantioselective biocatalysis optimized by directed evolution. Curr. Opin. Biotechnol. 2004, 15, 305–313. [Google Scholar] [CrossRef] [PubMed]
- Turner, N.J. Directed evolution of enzymes for applied biocatalysis. Trends Biotechnol. 2003, 21, 474–478. [Google Scholar] [CrossRef]
- Lutz, S. Novel methods for directed evolution of enzymes: Quality, not quantity. Curr. Opin. Biotechnol. 2004, 15, 291–297. [Google Scholar] [CrossRef]
- Otten, L.G.; Quax, W.J. Directed evolution: Selecting today’s biocatalysts. Biomol. Eng. 2005, 22, 1–9. [Google Scholar] [CrossRef]
- Hibbert, E.G.; Dalby, P.A. Directed evolution strategies for improved enzymatic performance. Microb. Cell Factories 2005, 4, 29. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.Q.; Arnold, F.H. Enzyme engineering for nonaqueous solvents: Random mutagenesis to enhance activity of subtilisin E in polar organic media. Biotechnol. (N. Y.) 1991, 9, 1073–1077. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Cao, H.; Cai, H.; Jaeger, K.E.; Davari, M.D.; Schwaneberg, U. Computer-Assisted Recombination (CompassR) Teaches us How to Recombine Beneficial Substitutions from Directed Evolution Campaigns. Chemistry 2020, 26, 643–649. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pandurangan, A.P.; Ochoa-Montano, B.; Ascher, D.B.; Blundell, T.L. SDM: A server for predicting effects of mutations on protein stability. Nucleic. Acids Res. 2017, 45, W229–W235. [Google Scholar] [CrossRef] [Green Version]
- Fitter, J.; Heberle, J. Structural Equilibrium Fluctuations in Mesophilic and Thermophilic α-Amylase. Biophys. J. 2000, 79, 1629–1636. [Google Scholar] [CrossRef] [Green Version]
- Purmonen, M.; Valjakka, J.; Takkinen, K.; Laitinen, T.; Rouvinen, J. Molecular dynamics studies on the thermostability of family 11 xylanases. Protein Eng. Des. Sel. 2007, 20, 551–559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mazola, Y.; Guirola, O.; Palomares, S.; Chinea, G.; Menéndez, C.; Hernández, L.; Musacchio, A. A comparative molecular dynamics study of thermophilic and mesophilic β-fructosidase enzymes. J. Mol. Model. 2015, 21, 228. [Google Scholar] [CrossRef]
- Teng, S.; Srivastava, A.K.; Wang, L. Sequence feature-based prediction of protein stability changes upon amino acid substitutions. BMC Genom. 2010, 11, S5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laimer, J.; Hofer, H.; Fritz, M.; Wegenkittl, S.; Lackner, P. MAESTRO--multi agent stability prediction upon point mutations. BMC Bioinform. 2015, 16, 116. [Google Scholar] [CrossRef] [Green Version]
- Wainreb, G.; Ashkenazy, H.; Bromberg, Y.; Starovolsky-Shitrit, A.; Haliloglu, T.; Ruppin, E.; Avraham, K.B.; Rost, B.; Ben-Tal, N. MuD: An interactive web server for the prediction of non-neutral substitutions using protein structural data. Nucleic Acids Res. 2010, 38, W523–W528. [Google Scholar] [CrossRef] [Green Version]
- Koskinen, P.; Törönen, P.; Nokso-Koivisto, J.; Holm, L. PANNZER: High-throughput functional annotation of uncharacterized proteins in an error-prone environment. Bioinformatics 2015, 31, 1544–1552. [Google Scholar] [CrossRef]
- De Ferrari, L.; Mitchell, J.B. From sequence to enzyme mechanism using multi-label machine learning. BMC Bioinform. 2014, 15, 150. [Google Scholar] [CrossRef] [PubMed]
- Tournier, V.; Topham, C.M.; Gilles, A.; David, B.; Folgoas, C.; Moya-Leclair, E.; Kamionka, E.; Desrousseaux, M.L.; Texier, H.; Gavalda, S.; et al. engineered PET depolymerase to break down and recycle plastic bottles. Nature 2020, 580, 216–219. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Y.; Liu, X.; Dong, S.; Tian, Y.e.; Qiao, Y.; Mitra, R.; Han, J.; Li, C.; Han, X.; et al. Computational Redesign of a PETase for Plastic Biodegradation under Ambient Condition by the GRAPE Strategy. ACS Catal. 2021, 11, 1340–1350. [Google Scholar] [CrossRef]
- Kong, X.D.; Yuan, S.; Li, L.; Chen, S.; Xu, J.H.; Zhou, J. Engineering of an epoxide hydrolase for efficient bioresolution of bulky pharmaco substrates. Proc. Natl. Acad. Sci. USA 2014, 111, 15717–15722. [Google Scholar] [CrossRef] [Green Version]
- Lu, H.D.; Wheeldon, I.R.; Banta, S. Catalytic biomaterials: Engineering organophosphate hydrolase to form self-assembling enzymatic hydrogels. Protein Eng. Des. Sel. 2010, 23, 559–566. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Pang, Y.-P.; Lockridge, O.; Brimijoin, S. Re-engineering Butyrylcholinesterase as a Cocaine Hydrolase. Mol. Pharmacol. 2002, 62, 220–224. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Henrissat, B.; Davies, G.J. Glycoside Hydrolases and Glycosyltransferases. Families, Modules, and Implications for Genomics. Plant. Physiol. 2000, 124, 1515–1519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verdoucq, L.; Czjzek, M.; Moriniere, J.; Bevan, D.R.; Esen, A. Mutational and Structural Analysis of Aglycone Specificity in Maize and Sorghum β-Glucosidases. J. Biol. Chem. 2003, 278, 25055–25062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sue, M.; Yamazaki, K.; Yajima, S.; Nomura, T.; Matsukawa, T.; Iwamura, H.; Miyamoto, T. Molecular and structural characterization of hexameric beta-D-glucosidases in wheat and rye. Plant. Physiol 2006, 141, 1237–1247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Wilmanns, M.; Thornton, J.; Köhn, M. Elucidating human phosphatase-substrate networks. Sci. Signal. 2013, 6, rs10. [Google Scholar] [CrossRef] [PubMed]
- Morais, M.C.; Zhang, G.; Zhang, W.; Olsen, D.B.; Dunaway-Mariano, D.; Allen, K.N. X-ray crystallographic and site-directed mutagenesis analysis of the mechanism of Schiff-base formation in phosphonoacetaldehyde hydrolase catalysis. J. Biol. Chem. 2004, 279, 9353–9361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocak, S.; Emery, B.; Tanner, N.K.; Linder, P. Characterization of the ATPase and unwinding activities of the yeast DEAD-box protein Has1p and the analysis of the roles of the conserved motifs. Nucleic Acids. Res. 2005, 33, 999–1009. [Google Scholar] [CrossRef] [Green Version]
- De Seny, D.; Prosperi-Meys, C.; Bebrone, C.; Rossolini, G.M.; Page, M.I.; Noel, P.; Frère, J.M.; Galleni, M. Mutational analysis of the two zinc-binding sites of the Bacillus cereus 569/H/9 metallo-beta-lactamase. Biochem. J. 2002, 363, 687–696. [Google Scholar] [CrossRef]
- Llarrull, L.I.; Fabiane, S.M.; Kowalski, J.M.; Bennett, B.; Sutton, B.J.; Vila, A.J. Asp-120 locates Zn2 for optimal metallo-beta-lactamase activity. J. Biol. Chem. 2007, 282, 18276–18285. [Google Scholar] [CrossRef] [Green Version]
- Fries, M.; Ihrig, J.; Brocklehurst, K.; Shevchik, V.E.; Pickersgill, R.W. Molecular basis of the activity of the phytopathogen pectin methylesterase. Embo. J. 2007, 26, 3879–3887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cama, E.; Emig, F.A.; Ash, D.E.; Christianson, D.W. Structural and functional importance of first-shell metal ligands in the binuclear manganese cluster of arginase I. Biochemistry 2003, 42, 7748–7758. [Google Scholar] [CrossRef] [PubMed]
- Colleluori, D.M.; Reczkowski, R.S.; Emig, F.A.; Cama, E.; Cox, J.D.; Scolnick, L.R.; Compher, K.; Jude, K.; Han, S.; Viola, R.E.; et al. Probing the role of the hyper-reactive histidine residue of arginase. Arch. Biochem. Biophys. 2005, 444, 15–26. [Google Scholar] [CrossRef]
- Lavulo, L.T.; Emig, F.A.; Ash, D.E. Functional consequences of the G235R mutation in liver arginase leading to hyperargininemia. Arch. Biochem. Biophys. 2002, 399, 49–55. [Google Scholar] [CrossRef]
- Wells, J.A. Additivity of mutational effects in proteins. Biochemistry 1990, 29, 8509–8517. [Google Scholar] [CrossRef] [PubMed]
- Skinner, M.M.; Terwilliger, T.C. Potential use of additivity of mutational effects in simplifying protein engineering. Proc. Natl. Acad. Sci. USA 1996, 93, 10753–10757. [Google Scholar] [CrossRef] [Green Version]
- Fox, R.J.; Davis, S.C.; Mundorff, E.C.; Newman, L.M.; Gavrilovic, V.; Ma, S.K.; Chung, L.M.; Ching, C.; Tam, S.; Muley, S.; et al. Improving catalytic function by ProSAR-driven enzyme evolution. Nat. Biotechnol. 2007, 25, 338–344. [Google Scholar] [CrossRef] [PubMed]
- Pace, C.N. Energetics of protein hydrogen bonds. Nat. Struct. Mol. Biol. 2009, 16, 681–682. [Google Scholar] [CrossRef] [PubMed]
- Tanford, C. Contribution of Hydrophobic Interactions to the Stability of the Globular Conformation of Proteins. J. Am. Chem. Soc. 1962, 84, 4240–4247. [Google Scholar] [CrossRef]
- Kauzmann, W. Some Factors in the Interpretation of Protein Denaturation. In Advances in Protein Chemistry; Elsevier: Amsterdam, The Netherlands, 1959; pp. 1–63. [Google Scholar] [CrossRef]
- Rouhani, M.; Khodabakhsh, F.; Norouzian, D.; Cohan, R.A.; Valizadeh, V. Molecular dynamics simulation for rational protein engineering: Present and future prospectus. J. Mol. Graph. Model. 2018, 84, 43–53. [Google Scholar] [CrossRef]
- Braun, A.; Halwachs, B.; Geier, M.; Weinhandl, K.; Guggemos, M.; Marienhagen, J.; Ruff, A.J.; Schwaneberg, U.; Rabin, V.; Torres Pazmino, D.E.; et al. MuteinDB: The mutein database linking substrates, products and enzymatic reactions directly with genetic variants of enzymes. Database (Oxford) 2012, 2012, bas028. [Google Scholar] [CrossRef]
- Wittig, U.; Kania, R.; Golebiewski, M.; Rey, M.; Shi, L.; Jong, L.; Algaa, E.; Weidemann, A.; Sauer-Danzwith, H.; Mir, S.; et al. SABIO-RK--database for biochemical reaction kinetics. Nucleic. Acids Res. 2012, 40, D790–D796. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sussman, J.L.; Lin, D.; Jiang, J.; Manning, N.O.; Prilusky, J.; Ritter, O.; Abola, E.E. Protein Data Bank (PDB): Database of three-dimensional structural information of biological macromolecules. Acta. Cryst. D Biol. Cryst. 1998, 54, 1078–1084. [Google Scholar] [CrossRef] [Green Version]
- Koes, D.R.; Baumgartner, M.P.; Camacho, C.J. Lessons learned in empirical scoring with smina from the CSAR 2011 benchmarking exercise. J. Chem. Inf. Model. 2013, 53, 1893–1904. [Google Scholar] [CrossRef]
- Song, K.; Li, Q.; Gao, W.; Lu, S.; Shen, Q.; Liu, X.; Wu, Y.; Wang, B.; Lin, H.; Chen, G.; et al. AlloDriver: A method for the identification and analysis of cancer driver targets. Nucleic Acids Res. 2019, 47, W315–W321. [Google Scholar] [CrossRef] [PubMed]
- Bakan, A.; Meireles, L.M.; Bahar, I. ProDy: Protein dynamics inferred from theory and experiments. Bioinformatics 2011, 27, 1575–1577. [Google Scholar] [CrossRef] [Green Version]
- Cock, P.J.; Antao, T.; Chang, J.T.; Chapman, B.A.; Cox, C.J.; Dalke, A.; Friedberg, I.; Hamelryck, T.; Kauff, F.; Wilczynski, B.; et al. Biopython: Freely available Python tools for computational molecular biology and bioinformatics. Bioinformatics 2009, 25, 1422–1423. [Google Scholar] [CrossRef]
- Lassmann, T.; Sonnhammer, E.L. Kalign--an accurate and fast multiple sequence alignment algorithm. BMC Bioinform. 2005, 6, 298. [Google Scholar] [CrossRef] [Green Version]
- Kabsch, W.; Sander, C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-Bonded and Geometrical Features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Bailey, T.L.; Teasdale, R.D. Prediction of protein B-factor profiles. Proteins 2005, 58, 905–912. [Google Scholar] [CrossRef] [PubMed]
- Piovesan, D.; Minervini, G.; Tosatto, S.C. The RING 2.0 web server for high quality residue interaction networks. Nucleic Acids Res. 2016, 44, W367–W374. [Google Scholar] [CrossRef] [PubMed]
- Salentin, S.; Schreiber, S.; Haupt, V.J.; Adasme, M.F.; Schroeder, M. PLIP: Fully automated protein-ligand interaction profiler. Nucleic Acids Res. 2015, 43, W443–W447. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. et Biophys. Acta (BBA)-Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]

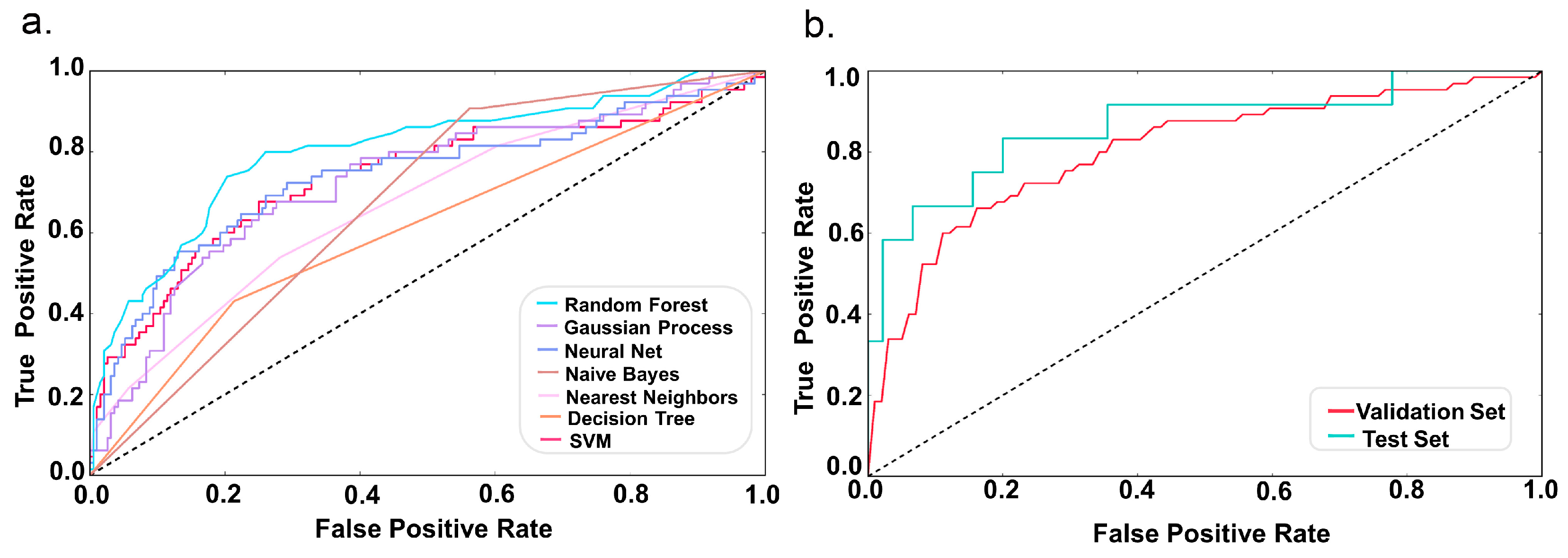


| Classifier. | Accuracy | Precision | Recall | AUC | MCC |
|---|---|---|---|---|---|
| Random Forest | 0.8 | 0.8 | 0.62 | 0.80 | 0.382 |
| Gaussian Process | 0.77 | 0.69 | 0.68 | 0.73 | 0.363 |
| Neural Net | 0.77 | 0.69 | 0.66 | 0.74 | 0.353 |
| Naive Bayes | 0.55 | 0.64 | 0.67 | 0.67 | 0.307 |
| Nearest Neighbors | 0.76 | 0.67 | 0.58 | 0.67 | 0.232 |
| Decision Tree | 0.7 | 0.60 | 0.61 | 0.61 | 0.213 |
| SVM | 0.75 | 0.88 | 0.52 | 0.74 | 0.152 |
| Data | Accuracy | Precision | Recall | AUC | MCC |
|---|---|---|---|---|---|
| Validation Set | 0.81 | 0.76 | 0.69 | 0.80 | 0.448 |
| Test Set | 0.89 | 0.89 | 0.78 | 0.86 | 0.659 |
| Mutation Type | Protein Name | Mutant | Kcat/Km(wt)/ s−1uM−1 | Kcat/Km(mut)/ s−1uM−1 | Increase/Decrease Fold |
|---|---|---|---|---|---|
| Increasing- Mutation | Beta-D-glucosidase(Maize) | V205L | 0.0819 | 0.0869 | 1.1 |
| P377A | 0.0819 | 0.105 | 1.3 | ||
| Beta-D-glucosidase(Rye) | G464F | 0.01247 | 0.015 | 1.2 | |
| S465L | 0.01247 | 0.03724 | 3.0 | ||
| Decreasing-Mutation | Beta-D-glucosidase(Maize) | F198V | 0.0819 | 0.0148 | 5.5 |
| D261N | 0.0461 | 0.00552 | 8.4 | ||
| M263F | 0.0461 | 0.02707 | 1.7 | ||
| Beta-D-glucosidase(Rye) | F198A | 0.1475 | 0.005283 | 27.9 | |
| Y378A | 0.1475 | 0.1374 | 1.1 | ||
| Phosphonoacetaldehyde hydrolase | C22A | 0.4546 | 0.00368 | 123.5 | |
| M49L | 0.4546 | 0.0000294 | 15,462.6 | ||
| G50A | 0.4546 | 0.0000391 | 11,626.6 | ||
| H56A | 0.4546 | 0.0005172 | 879.0 | ||
| Y128F | 0.4546 | 0.04911 | 9.3 | ||
| RNA helicase | S228A | 0.0002045 | 0.0000833 | 2.5 | |
| T230A | 0.0002045 | 0.00008024 | 2.5 | ||
| H375A | 0.0002045 | 0.00007609 | 2.7 | ||
| Beta-Lactamase | H86S | 1.353 | 0.08868 | 15.3 | |
| H88S | 1.353 | 0.01565 | 86.5 | ||
| C168S | 1.353 | 0.03158 | 42.8 | ||
| H149S | 1.353 | 0.001228 | 1101.8 | ||
| D90E | 1.386 | 0.02069 | 67.0 | ||
| H210S | 1.386 | 0.003562 | 389.1 | ||
| Pectin Esterase A | Q153A | 3.462 | 0.1055 | 32.8 | |
| Q177A | 3.462 | 0.1818 | 19.0 | ||
| V198A | 3.462 | 1.133 | 3.1 | ||
| T272A | 3.462 | 0.5519 | 6.3 | ||
| M306A | 3.462 | 0.1113 | 31.1 | ||
| Arginase | H101E | 0.1786 | 0.002655 | 67.3 | |
| D128E | 0.1786 | 0.00005 | 3572.0 | ||
| H141N | 0.1786 | 0.002333 | 76.6 | ||
| D232A | 0.1786 | 0.0000075 | 23,813.3 | ||
| D234E | 0.1786 | 0.00264 | 67.7 | ||
| G235A | 0.1175 | 0.08 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Song, K.; Zhang, J.; Lu, S. A Computational Method to Predict Effects of Residue Mutations on the Catalytic Efficiency of Hydrolases. Catalysts 2021, 11, 286. https://doi.org/10.3390/catal11020286
Li Y, Song K, Zhang J, Lu S. A Computational Method to Predict Effects of Residue Mutations on the Catalytic Efficiency of Hydrolases. Catalysts. 2021; 11(2):286. https://doi.org/10.3390/catal11020286
Chicago/Turabian StyleLi, Yun, Kun Song, Jian Zhang, and Shaoyong Lu. 2021. "A Computational Method to Predict Effects of Residue Mutations on the Catalytic Efficiency of Hydrolases" Catalysts 11, no. 2: 286. https://doi.org/10.3390/catal11020286
APA StyleLi, Y., Song, K., Zhang, J., & Lu, S. (2021). A Computational Method to Predict Effects of Residue Mutations on the Catalytic Efficiency of Hydrolases. Catalysts, 11(2), 286. https://doi.org/10.3390/catal11020286