Catalyst Heating Characteristics in the Traveling-Wave Microwave Reactor
Abstract
1. Introduction
2. Experimental System
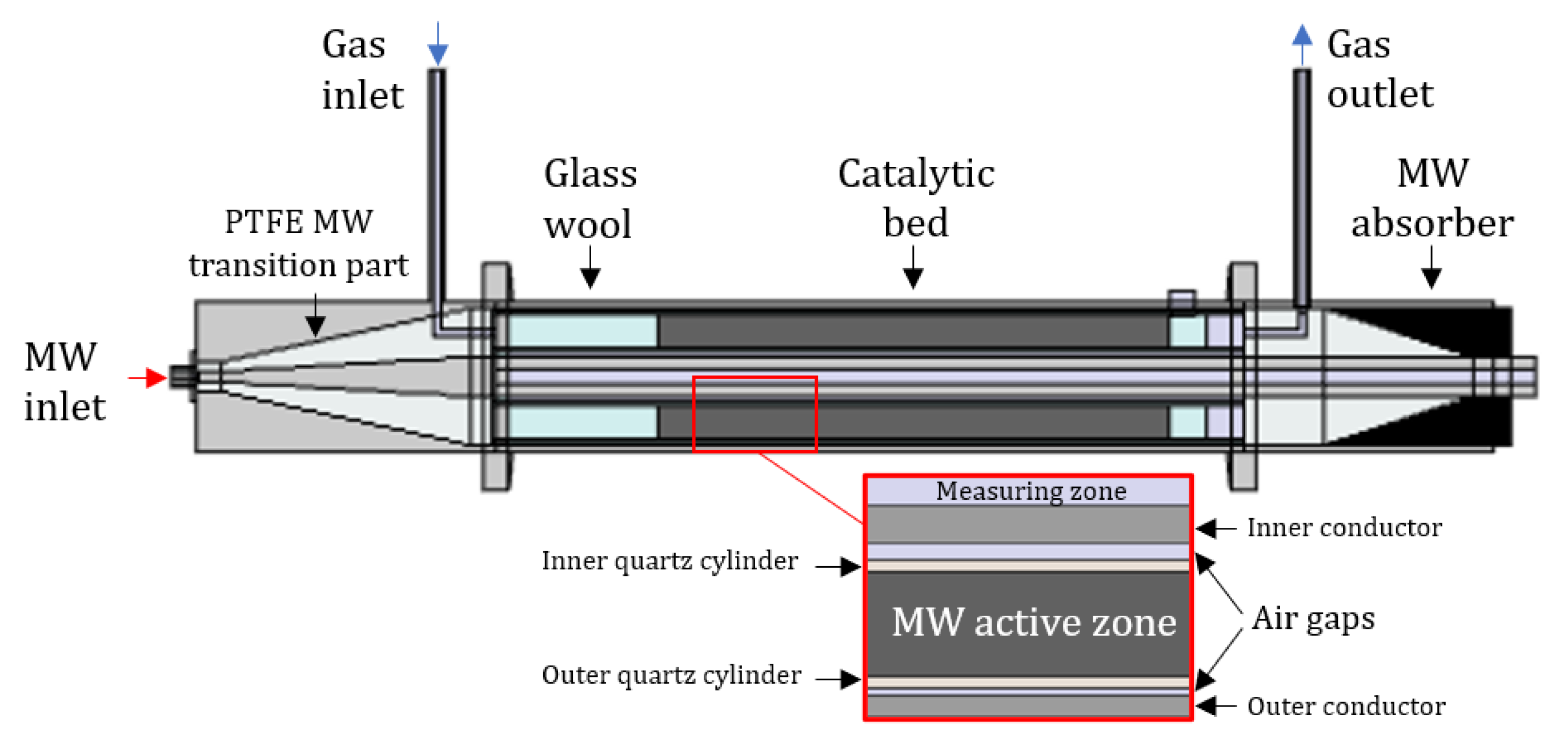
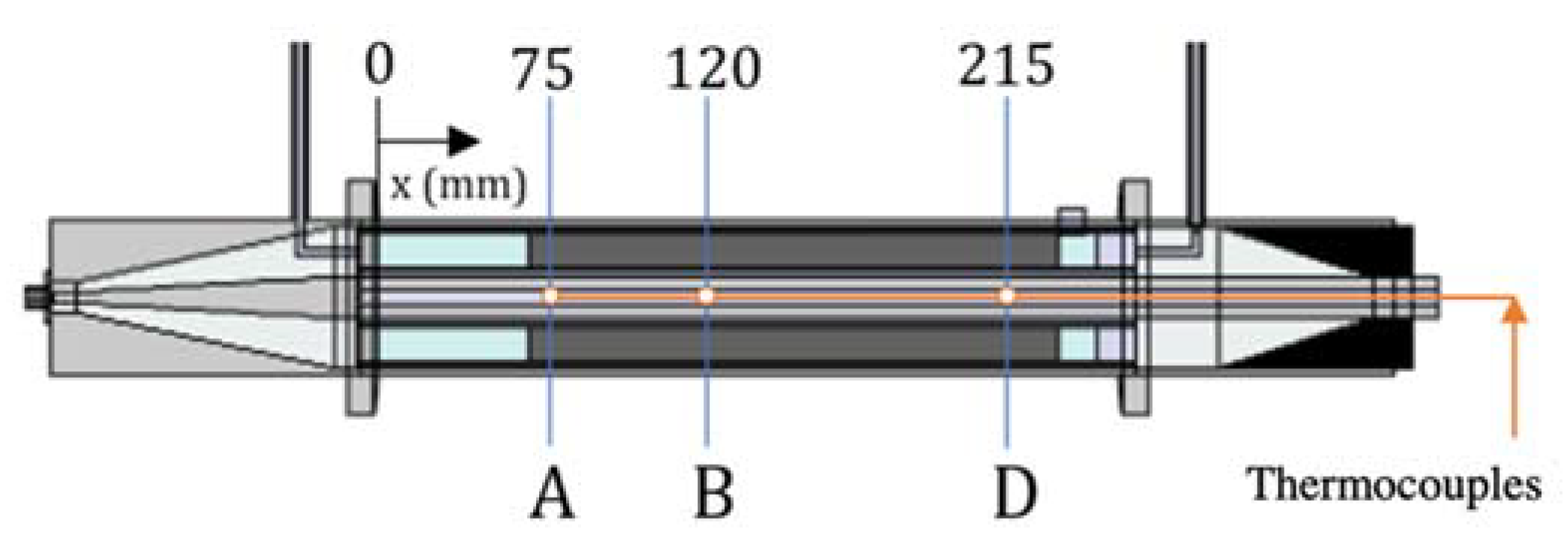
2.1. Traveling-Wave Microwave Reactor
2.2. Microwave Active Materials
3. Mathematical Model
3.1. Electromagnetic Waves
3.2. Heat Transfer
4. Results and Discussions
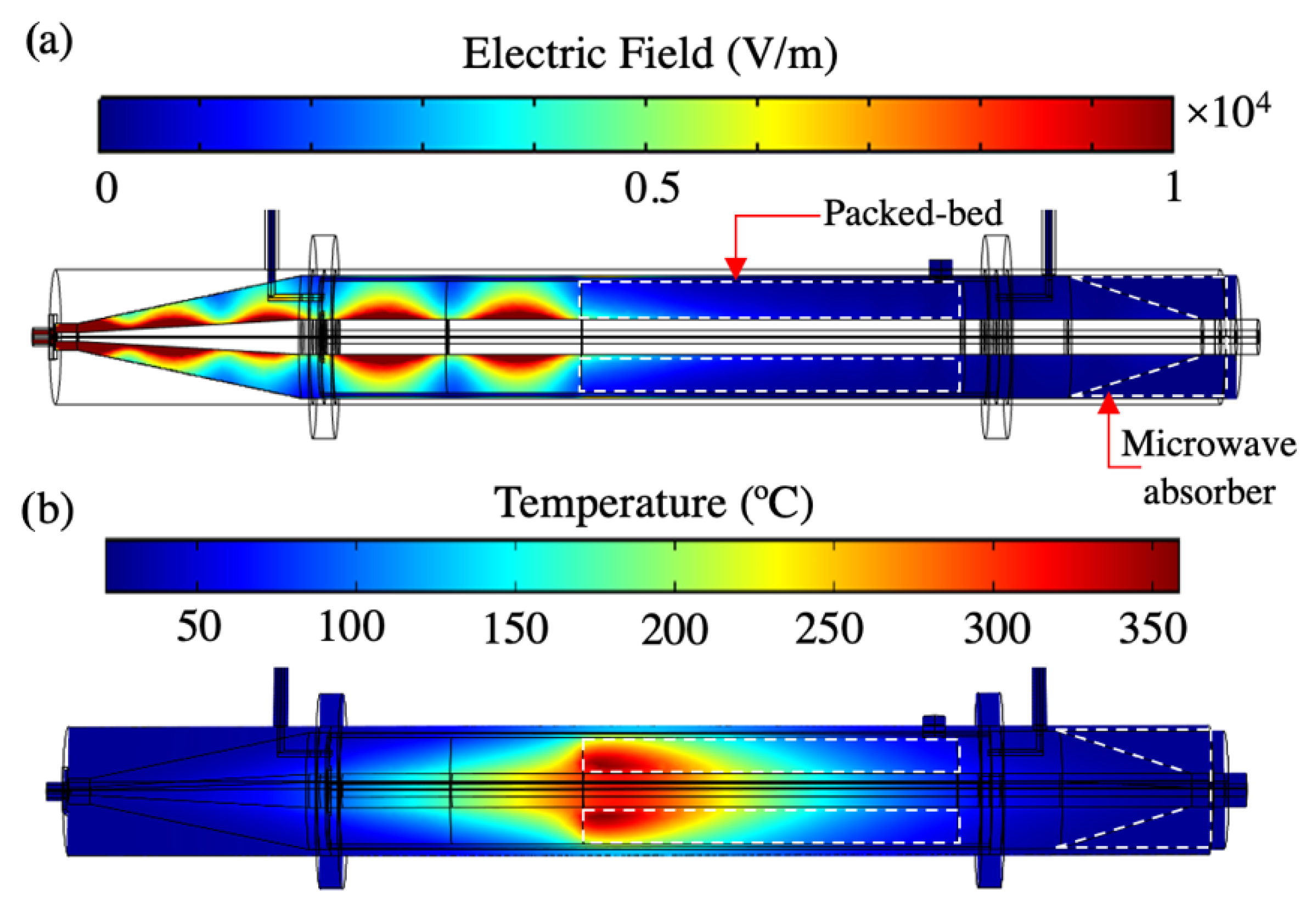
4.1. Validation of the Electromagnetic Model
- TMR without the microwave absorber or quartz tubes;
- TMR with external quartz tube, but no microwave absorber end (terminal part);
- TMR with microwave absorber and inner and outer quartz tubes.
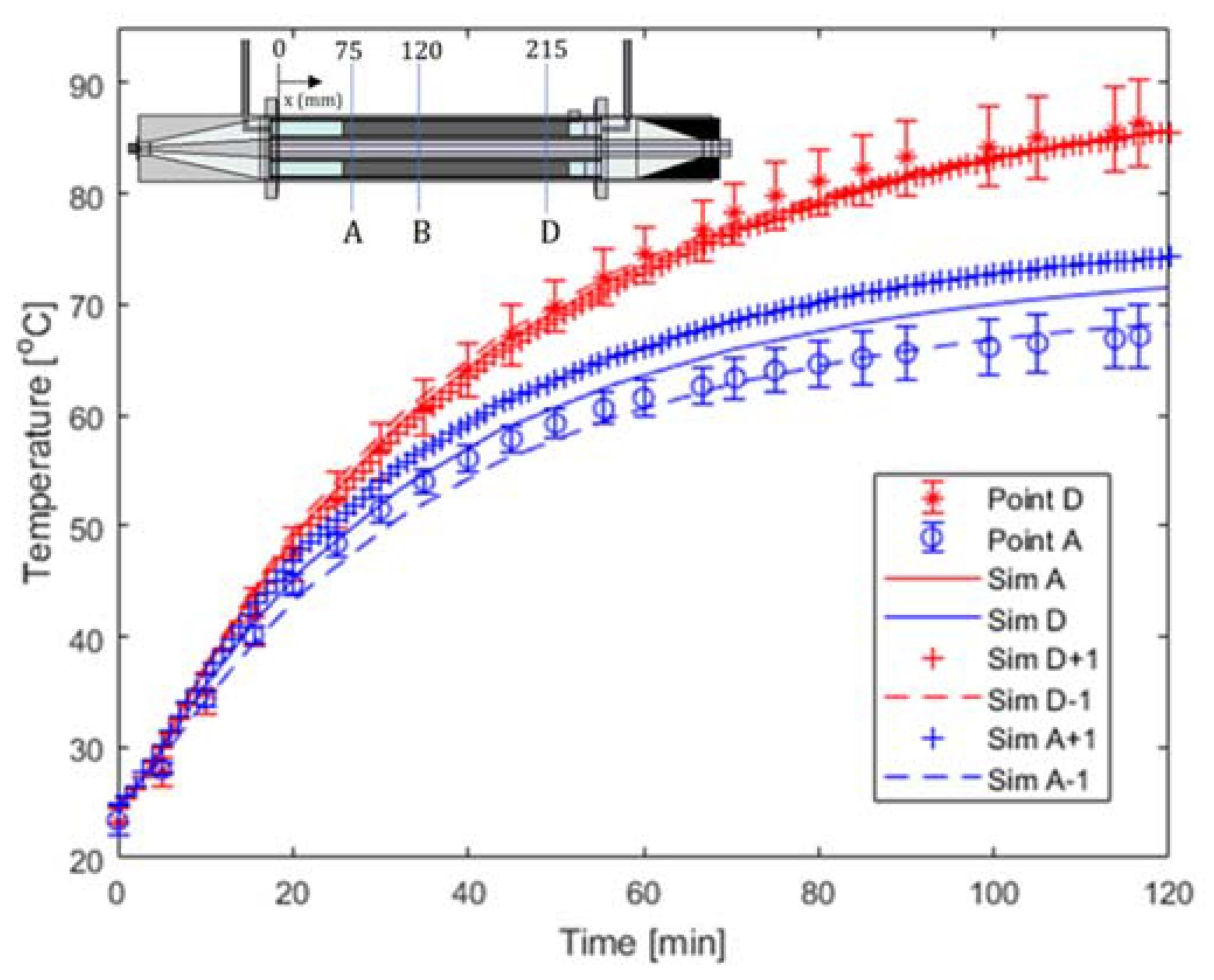
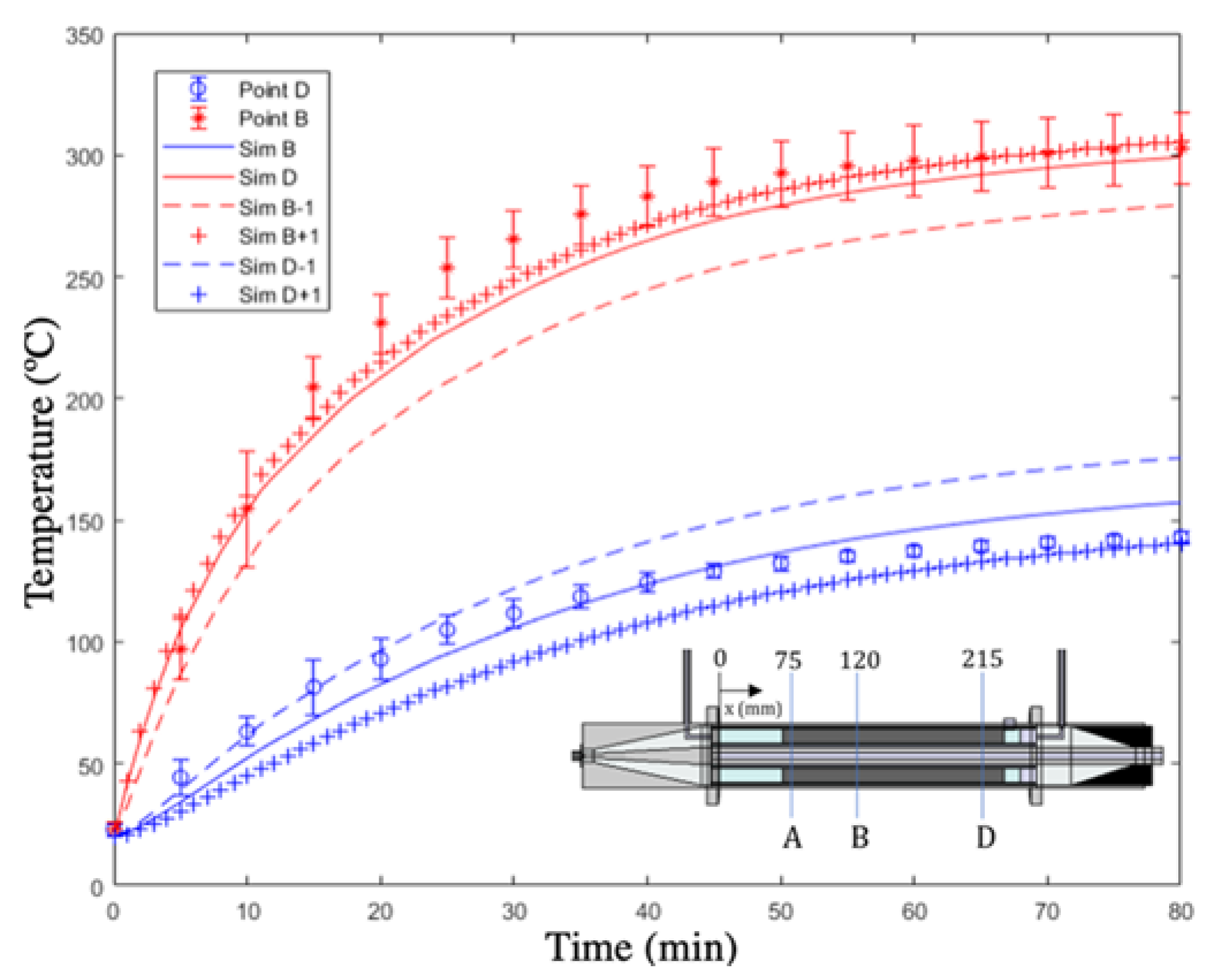
4.2. Validation of the Electromagnetic Heating Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Horváth, I.T. Introduction: Sustainable Chemistry. Chem. Rev. 2018, 118, 369–371. [Google Scholar] [CrossRef]
- Cséfalvay, E.; Horváth, I.T. Sustainability Assessment of Renewable Energy in the United States, Canada, the European Union, China, and the Russian Federation. ACS Sustain. Chem. Eng. 2018, 6, 8868–8874. [Google Scholar] [CrossRef]
- Náray-Szabó, G.; Mika, L.T. Conservative evolution and industrial metabolism in Green Chemistry. Green Chem. 2018, 20, 2171–2191. [Google Scholar] [CrossRef]
- Stankiewicz, A.I.; Nigar, H. Beyond electrolysis: Old challenges and new concepts of electricity-driven chemical reactors. React. Chem. Eng. 2020, 5, 1005–1016. [Google Scholar] [CrossRef]
- Tang, J.; Hong, Y.K.; Inanoglu, S.; Liu, F. Microwave pasteurization for ready-to-eat meals. Curr. Opin. Food Sci. 2018, 23, 133–141. [Google Scholar] [CrossRef]
- Feng, H.; Yin, Y.; Tang, J. Microwave Drying of Food and Agricultural Materials: Basics and Heat and Mass Transfer Modeling. Food Eng. Rev. 2012, 4, 89–106. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Abdan, K.; Janius, R.; Chen, G.; Kumar, C. Modelling of coupled heat and mass transfer for combined infrared and hot-air drying of sweet potato. J. Food Eng. 2018, 228, 12–24. [Google Scholar] [CrossRef]
- Palma, V.; Barba, D.; Cortese, M.; Martino, M.; Renda, S.; Meloni, E. Microwaves and Heterogeneous Catalysis: A Review on Selected Catalytic Processes. Catalysts 2020, 10, 246. [Google Scholar] [CrossRef]
- Julian, I.; Pedersen, C.M.; Achkasov, K.; Hueso, J.L.; Hellstern, H.L.; Silva, H.; Mallada, R.; Davis, Z.J.; Santamaria, J. Overcoming Stability Problems in Microwave-Assisted Heterogeneous Catalytic Processes Affected by Catalyst Coking. Catalysts 2019, 9, 867. [Google Scholar] [CrossRef]
- Zhang, F.; Song, Z.; Zhu, J.; Liu, L.; Sun, J.; Zhao, X.; Mao, Y.; Wang, W. Process of CH4-CO2 reforming over Fe/SiC catalyst under microwave irradiation. Sci. Total Environ. 2018, 639, 1148–1155. [Google Scholar] [CrossRef]
- Li, L.; Chen, J.; Yan, K.; Qin, X.; Feng, T.; Wang, J.; Wang, F.; Song, Z. Methane dry reforming with microwave heating over carbon-based catalyst obtained by agriculture residues pyrolysis. J. CO2 Util. 2018, 28, 41–49. [Google Scholar] [CrossRef]
- Li, L.; Yang, Z.; Chen, J.; Qin, X.; Jiang, X.; Wang, F.; Song, Z.; Ma, C. Performance of bio-char and energy analysis on CH4 combined reforming by CO2 and H2O into syngas production with assistance of microwave. Fuel 2018, 215, 655–664. [Google Scholar] [CrossRef]
- Durka, T. Microwave Effects in Heterogeneous Catalysis: Application to Gas-Solid Reactions for Hydrogen Production. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- de Dios García, I.; Stankiewicz, A.; Nigar, H. Syngas production via microwave-assisted dry reforming of methane. Catal. Today 2021, 362, 72–80. [Google Scholar] [CrossRef]
- Nigar, H.; Navascués, N.; De La Iglesia, O.; Mallada, R.; Santamaria, J. Removal of VOCs at trace concentration levels from humid air by Microwave Swing Adsorption, kinetics and proper sorbent selection. Sep. Purif. Technol. 2015, 151, 193–200. [Google Scholar] [CrossRef]
- Nigar, H.; Julián, I.; Mallada, R.; Santamaría, J. Microwave-Assisted Catalytic Combustion for the Efficient Continuous Cleaning of VOC-Containing Air Streams. Environ. Sci. Technol. 2018, 52, 5892–5901. [Google Scholar] [CrossRef]
- Julian, I.; Ramirez, H.; Hueso, J.L.; Mallada, R.; Santamaria, J. Non-oxidative methane conversion in microwave-assisted structured reactors. Chem. Eng. J. 2019, 377, 119764. [Google Scholar] [CrossRef]
- Korkakaki, E.; Walspurger, S.; Overwater, K.; Nigar, H.; Julian, I.; Stefanidis, G.D.; Tharakaraman, S.S.; Jurković, D.L. Adaptable Reactors for Resource- and Energy-Efficient Methane Valorisation (ADREM) benchmarking modular technologies. Johns. Matthey Technol. Rev. 2020, 64, 298–306. [Google Scholar] [CrossRef]
- Stankiewicz, A.; Sarabi, F.E.; Baubaid, A.; Yan, P.; Nigar, H. Perspectives of Microwaves-Enhanced Heterogeneous Catalytic Gas-Phase Processes in Flow Systems. Chem. Rec. 2019, 19, 40–50. [Google Scholar] [CrossRef]
- Sarabi, F.E.; Ghorbani, M.; Stankiewicz, A.; Nigar, H. Coaxial traveling-wave microwave reactors: Design challenges and solutions. Chem. Eng. Res. Des. 2020, 153, 677–683. [Google Scholar] [CrossRef]
- Muley, P.D.; Henkel, C.E.; Aguilar, G.; Klasson, K.T.; Boldor, D. Ex situ thermo-catalytic upgrading of biomass pyrolysis vapors using a traveling wave microwave reactor. Appl. Energy 2016, 183, 995–1004. [Google Scholar] [CrossRef]
- Mitani, T.; Hasegawa, N.; Nakajima, R.; Shinohara, N.; Nozaki, Y.; Chikata, T.; Watanabe, T. Development of a wideband microwave reactor with a coaxial cable structure. Chem. Eng. J. 2016, 299, 209–216. [Google Scholar] [CrossRef]
- Yan, P.; Stankiewicz, A.I.; Sarabi, F.E.; Nigar, H. Microwave heating in heterogeneous catalysis: Modelling and design of rectangular traveling-wave microwave reactor. Chem. Eng. Sci. 2021, 232, 116383. [Google Scholar] [CrossRef]
- Palma, V.; Meloni, E. Microwave susceptible catalytic diesel particulate filter. Chem. Eng. Trans. 2016, 52, 445–450. [Google Scholar]
- Sun, J.; Xia, G.; Yang, W.; Hu, Y.; Shen, W. Microwave-assisted method to degrade phenol using persulfate or hydrogen peroxide catalyzed by Cu-bearing silicon carbide. Water Sci. Technol. 2020, 82, 704–714. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Z.; Yan, Y.; Zhao, X.; Sun, J.; Mao, Y.; Wang, W. Performance of Fe/SiC catalysts for cracking of toluene under microwave irradiation. Int. J. Hydrogen Energy 2018, 43, 7227–7236. [Google Scholar] [CrossRef]
- Ledoux, M.J.; Pham-Huu, C.; Keller, N.; Nougayrede, J.B.; Savin-Poncet, S.; Bousquet, J. Silicon Carbide Supported NiS2 Catalyst for the Selective Oxidation of H2S in Claus Tail-Gas. In Studies in Surface Science and Catalysis; Elsevier: Amsterdam, The Netherlands, 2000; Volume 130 C, pp. 2891–2896. [Google Scholar]
- Díaz, J.A.; Calvo-Serrano, M.; De La Osa, A.R.; García-Minguillán, A.M.; Romero, A.; Giroir-Fendler, A.; Valverde, J.L. β-silicon carbide as a catalyst support in the Fischer–Tropsch synthesis: Influence of the modification of the support by a pore agent and acidic treatment. Appl. Catal. A Gen. 2014, 475, 82–89. [Google Scholar] [CrossRef]
- Ivanova, S.; Vanhaecke, E.; Louis, B.; Libs, S.; LeDoux, M.-J.; Rigolet, S.; Marichal, C.; Pham, C.; Luck, F.; Pham-Huu, C. Efficient Synthesis of Dimethyl Ether over HZSM-5 Supported on Medium-Surface-Area β-SiC Foam. ChemSusChem 2008, 1, 851–857. [Google Scholar] [CrossRef] [PubMed]
- COMSOL Multiphysics® v. 5.4. www.comsol.com; COMSOL AB: Stockholm, Sweden, 2018.
- RF Module User’s Guide; COMSOL Multiphysics® v. 5.4.; COMSOL AB: Stockholm, Sweden, 2018; pp. 84–92.
- Nigar, H.; Sturm, G.S.J.; Garcia-Baños, B.; Peñaranda-Foix, F.L.; Catalá-Civera, J.M.; Mallada, R.; Stankiewicz, A.; Santamaría, J. Numerical analysis of microwave heating cavity: Combining electromagnetic energy, heat transfer and fluid dynamics for a NaY zeolite fixed-bed. Appl. Therm. Eng. 2019, 155, 226–238. [Google Scholar] [CrossRef]
- Mohsen, A. On the impedance boundary condition. Appl. Math. Model. 1982, 6, 405–407. [Google Scholar] [CrossRef]
- Heat Transfer Module User’s Guide; COMSOL Multiphysics® v. 5.4.; COMSOL AB: Stockholm, Sweden, 2018; pp. 168–170.

| Catalyst | Reaction | Microwave Heated | Ref. |
|---|---|---|---|
| Fe | Dry reforming of methane | Yes | [10] |
| Ni | Dry reforming of methane | Yes | [14] |
| Mo-ZSM-5 | Non-oxidative methane conversion | Yes | [17] |
| CuFe2O4 | Catalytic oxidation of diesel soot | Yes | [24] |
| Cu | Phenol degradation | Yes | [25] |
| Fe | Cracking of toluene | Yes | [26] |
| NiS2 | H2S oxidation | No | [27] |
| Co | Fischer-Tropsch | No | [28] |
| HZSM-5 | Methanol dehydration | No | [29] |
| Model Number | Experimental (S11) | Simulated (S11) | ||
|---|---|---|---|---|
| dB | Power reflection (%) | dB | Power reflection (%) | |
| 1 | −8.17 | 15.24 | −6.78 | 20.99 |
| 2 | −3.93 | 40.46 | −2.74 | 53.21 |
| 3 | −18.46 | 1.43 | −14.45 | 3.59 |
| α-SiC | β-SiC | ||
|---|---|---|---|
| Simulated Point | APRD (%) | Simulated Point | APRD (%) |
| A | 2.02 | B | 4.52 |
| D | 2.34 | D | 8.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez González, A.; Stankiewicz, A.; Nigar, H. Catalyst Heating Characteristics in the Traveling-Wave Microwave Reactor. Catalysts 2021, 11, 369. https://doi.org/10.3390/catal11030369
Martínez González A, Stankiewicz A, Nigar H. Catalyst Heating Characteristics in the Traveling-Wave Microwave Reactor. Catalysts. 2021; 11(3):369. https://doi.org/10.3390/catal11030369
Chicago/Turabian StyleMartínez González, Alberto, Andrzej Stankiewicz, and Hakan Nigar. 2021. "Catalyst Heating Characteristics in the Traveling-Wave Microwave Reactor" Catalysts 11, no. 3: 369. https://doi.org/10.3390/catal11030369
APA StyleMartínez González, A., Stankiewicz, A., & Nigar, H. (2021). Catalyst Heating Characteristics in the Traveling-Wave Microwave Reactor. Catalysts, 11(3), 369. https://doi.org/10.3390/catal11030369






