Mechanical, Electrical, and Glass Transition Behavior of Copper–PMMA Composites
Abstract
:1. Introduction
2. Experimental
3. Results and Discussion
4. Conclusions
- In this article, the mechanical, electrical and glass transition behaviors of copper–PMMA composites were investigated. The hot compression molding method is an economic and feasible methodology to prepare a metallic copper particle-filled polymethylmethacrylate matrix. This method also allows to achieve a highly segregated distribution of mtal particles within the polymeric matrix. Using this method, it was possible to lower the percolation threshold reached by other authors in similar systems. The microstructural analysis carried out showed that the probability of forming a network is increased when restricting the volume that any metallic particle can occupy in a single interproximal contact or the interstices of the polymer particles. Considering the general behavior observed in the polymeric composites, it could be stated that when the polymer chains possess a strong affinity with the particles’ surface, the chain mobility is very restricted in the proximity of the particle surface. Even though chain mobility increased in proportion with the increase of the distance between particles, mobility cannot be reached in empty volumes of the polymeric matrix.
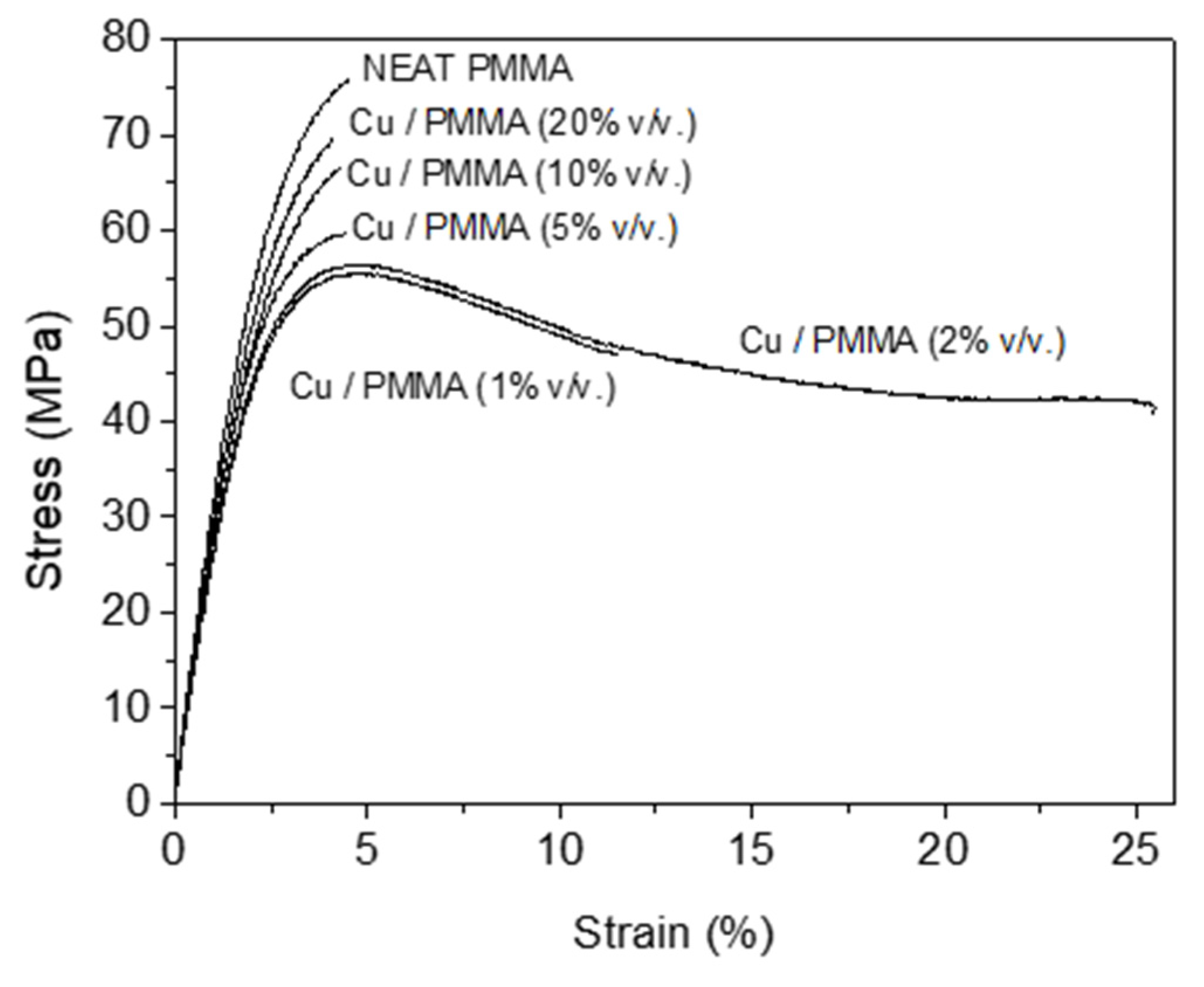
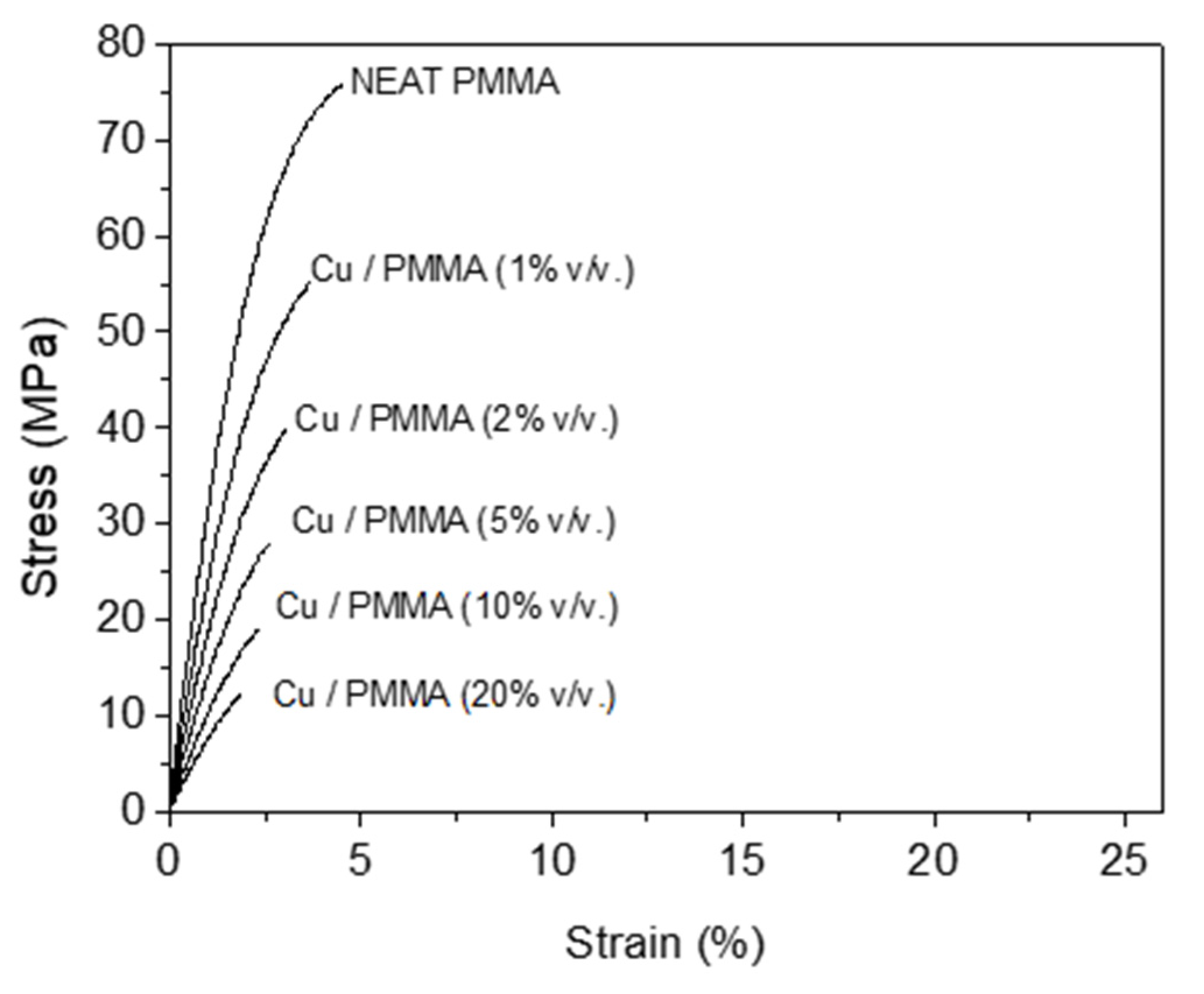
- The infiltration of low concentrations of nanometric-size metallic particles originates an important increase in the strain-to-failure percentage in the Cu/PMMA composites. In the case of nanometric-filled Cu/PMMA composites, a light descent of Young’s modulus was observed for low concentrations of filler material and a gradual increase as more metallic particles were incorporated into the polymeric matrix. Micrometric-size particles act as stress concentrators within the composite, diminishing the strain-to-failure percentage and Young’s modulus; then for these composites, the critical concentration of metal filler and the morphology are insufficient to obtain acceptable both mechanical and electrical properties. One of the best attributes of nanometric-size filler is its great contact surface in relation to volume. This area apparently plays a fundamental role in the properties observed for the conductive polymeric composites due to the extensive surrounding volume of polymer around the segregated, distributed metallic particles. The abovementioned corresponds to polymer chains that are in contact with the surface of metallic particles. If the polymer chains achieve a strong affinity with the surface of the particle, these chains lose part of their mobility, thus generating a region of reduced mobility around each filler particle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Gao, J.; Ma, Y.; Agarwal, U.S. Agarwal. Study on mechanical properties, thermal stability and crystallization behavior of PET/MMT nanocomposites. Compos. Part B Eng. 2006, 37, 399–407. [Google Scholar] [CrossRef]
- Rakowski, W.A.; Zimowski, S. Polyesterimide composites as a sensor material for sliding bearings. Compos. Part B Eng. 2005, 37, 81–88. [Google Scholar] [CrossRef]
- Luyt, A.; Molefi, J.; Krump, H. Thermal, mechanical, and electrical properties of copper powder filled low-density and linear low-density polyethylene composites. Polym. Degrad. Stab. 2006, 91, 1629–1636. [Google Scholar] [CrossRef]
- Weidenfeller, B.; Höfer, M.; Frank, R.S. Thermal conductivity, thermal diffusivity, and specific heat capacity of particle filled polypropylene. Compos. Part A Appl. Sci. Manuf. 2004, 35, 423–429. [Google Scholar] [CrossRef]
- Ash, B.J.; Schadler, L.; Siegel, R.W. Glass transition behavior of alumina/polymethylmethacrylate nanocomposites. Mater. Lett. 2002, 55, 83–87. [Google Scholar] [CrossRef]
- Wu, G.; Lin, J.; Zheng, Q.; Zhang, M. Correlation between percolation behavior of electricity and viscoelasticity for graphite filled high density polyethylene. Polymer 2006, 47, 2442–2447. [Google Scholar] [CrossRef]
- Mamunya, Y.P.; Davydenko, V.; Pissis, P.; Lebedev, E.V. Electrical and thermal conductivity of polymers filled with metal powders. Eur. Polym. J. 2002, 38, 1887–1897. [Google Scholar] [CrossRef]
- Zweifel, Y.; Christopher, J.G. Plummer and Hans-Henning Kausch. Current Transport in conducting particle filled epoxies. Polym. Bull. 1998, 40, 259–266. [Google Scholar] [CrossRef]
- Ou, R.; Gerhardt, R.A.; Marrett, C.; Moulart, A.; Colton, J.S. Assessment of percolation and homogeneity in ABS/carbon black composites by electrical measurements. Compos. Part B Eng. 2003, 34, 607–614. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Polymers, M.-F. (Eds.) Properties and Applications; Marcel Dekker, Inc.: New York, NY, USA, 1986. [Google Scholar]
- Marhoon, I.I.; Majeed, A.H.; Abdulrehman, M.A. Dielectric Behavior of Medical PMMA Polymer Filled With Copper Nanobud Particles. Adv. Electromagn. 2019, 8, 50–56. [Google Scholar] [CrossRef]
- Miola, M.; Cochis, A.; Kumar, A.; Arciola, C.R.; Rimondini, L.; Verne, E. Copper-Doped Bioactive Glass as Filler for PMMA-Based Bone Cements: Morphological, Mechanical, Reactivity, and Preliminary Antibacterial Characterization. Materials 2018, 11, 961. [Google Scholar] [CrossRef]
- Athar, N.; Akhtar, G.; Murtaza, M.; Shafique, A.; Ahmed; Haidyrah, S. Effect of Cu Ions Implantation on Structural, Electronic, Optical and Dielectric Properties of Polymethyl Methacrylate (PMMA). Polymers 2021, 13, 973. [Google Scholar]
- Wang, Z.; Wang, Y.; Cai, S.; Yang, J. Liquid Crystal Elastomers for Soft Actuators. Mater. Lab 2022, 1, 220030. [Google Scholar] [CrossRef]
- David, S.M.; Blaszkiewicz, M.; Robert, E. Newnham. Electrical Resistivity of Composites. J. Am. Ceram. Soc. 1990, 73, 2187. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction To Percolation Theory, 2nd ed.; Taylor and Francis: London, UK, 1992. [Google Scholar]
- Gungor, A. The physical and mechanical properties of polymer composites filled with Fepowder. J. Appl. Polym. Sci. 2005, 99, 2438–2442. [Google Scholar] [CrossRef]
- Benjamin, J.A.; Diana, F.R.; Christopher, J.W.; Linda, S.S.; Richard, W.S.; Brian, C.B.; Tom, A. Mechanical properties of Al2O3/polymethylmethacrylate nanocomposites. Polym. Compos. 2002, 23, 1014–1025. [Google Scholar]
- Levita, G.; Marchetti, A.; Lazzeri, A. Fracture of ultrafine calcium carbonate/polypropylene composites. Polym. Compos. 1989, 10, 39–43. [Google Scholar] [CrossRef]
- Gülsoy, H.; Taşdemır, M.; Taşdemir, M. Physical and Mechanical Properties of Polypropylene Reinforced with Fe Particles. Int. J. Polym. Mater. Polym. Biomater. 2006, 55, 619–626. [Google Scholar] [CrossRef]
- ZBartczak, Z.; Argon, A.; Cohen, R.; Weinberg, M. Toughness mechanism in semicrystalline polymer blends: II. High-density polyethylene toughened with calcium carbonate filler particles. Polymer 1999, 40, 2347–2365. [Google Scholar] [CrossRef]
- FBoydağ, F.; Özcanlı, Y.L.; Alekberov, V.; Hikmet, I. Temperature and time dependence of electrical and mechanical durability of LDPE/diamond composites. Compos. Part B Eng. 2005, 37, 249–254. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Lu, W.; Chen, G. The piezoresistive behaviors of polyethylene/foliated graphite nanocomposites. Eur. Polym. J. 2006, 42, 1015–1021. [Google Scholar] [CrossRef]
- Zhang, B.; Fu, R.; Zhang, M.; Dong, X.; Wang, L.; Pittman, C.U. Gas sensitive vapor grown carbon nanofiber/polystyrene sensors. Mater. Res. Bull. 2006, 41, 553–562. [Google Scholar] [CrossRef]
- Mahajan, D.; Desai, A.; Rafailovich, M.; Cui, M.-H.; Yang, N.-L. Synthesis and characterization of nanosized metals embedded in polystyrene matrix. Compos. Part B Eng. 2006, 37, 74–80. [Google Scholar] [CrossRef]
- Hergeth, W.-D.; Steinau, U.-J.; Bittrich, H.-J.; Simon, G.; Schmutzler, K. Polymerization in the presence of seeds. Part IV: Emulsion polymers containing inorganic filler particles. Polymer 1989, 30, 254–258. [Google Scholar] [CrossRef]
- Ash, B.; Stone, J.; Rogers, D.; Schadler, L.; Siegel, R.; Benicewicz, B.; Apple, T. Investigation into the Thermal and Mechanical Behavior of PMMA/Alumnia Nanocomposites. Mat. Res. Soc. Symp. Proc. 2001, 661. [Google Scholar] [CrossRef]
- Vollenberg, J.W.; de Haan, L.J.M.; van de Ven Heikens, D. Particle size dependence of the Young’s modulus of filled polymers: 2. Annealing and solid-state nuclear magnetic resonance experiments. Polymer 1989, 30, 1663–1668. [Google Scholar] [CrossRef]
- Nielsen, L.; Landel, R. Mechanical Properties of Polymers and Composites; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- Weir, C.E. temperature dependence of compression of linear high polymers at high pressures. J. Res. Natl. Bur. Stand. 1954, 53, 245. [Google Scholar] [CrossRef]
- Brandrup, J.; Immergut, E.H. (Eds.) Polymer Handbook, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1989. [Google Scholar]
- ASTM D792–66 (Reapproved 1975); Density of Plastics by Water Displacement. American Society for Testing and Materials: Philadelphia, PA, USA, 1966.
- ASTM D257–99; Standard Test Methods for DC Resistance or Conductance of Insulating Materials. American Society for Testing and Materials: Philadelphia, PA, USA, 1999.
- Ruschau Gregory Richard. Conductive Composites as Chemical Sensors. UMI Dissertation Services, The Pennsylvania State University, Order Number 9214261. 1991. Available online: https://www.proquest.com/openview/9a8b65e7483dc6de8023f7e0d41be172/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 26 January 2023).
- Broadbent, S.R.; Hammersley, J.M. Percolation Processes. Proc. Comb. Phil. Soc. 1957, 53, 629. [Google Scholar] [CrossRef]
- Ou, Y.; Yang, F.; Yu, Z.-Z. A new conception on the toughness of nylon 6/silica nanocomposite prepared via in situ polymerization. J. Polym. Sci. Part B Polym. Phys. 1998, 36, 789–795. [Google Scholar] [CrossRef]
- Sumita, M.; Tsukihi, H.; Miyasaka, K.; Ishikawa, K. Dynamic mechanical properties of polypropylene composites filled with ultrafine particles. J. Appl. Polym. Sci. 1984, 29, 1523–1530. [Google Scholar] [CrossRef]
- Kotsilkova, R.; Fragiadakis, D.; Pissis, P. Pissis. Reinforcement effect of carbon nanofillers in an epoxy resin system: Rheology, molecular dynamics, and mechanical studies. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 522–533. [Google Scholar] [CrossRef]
- Chisholm, N.; Mahfuz, H.; Vijaya; Rangari, K.; Ashfaq, A.; Jeelani, S. Fabrication and mechanical characterization of carbon/SiC-epoxy nanocomposites. Compos. Struct. 2005, 67, 115–124. [Google Scholar] [CrossRef]
- Unal, H.; Mimaroglu, A. Influence of Filler Addition on the Mechanical Properties of Nylon-6 Polymer. J. Reinf. Plast. Compos. 2004, 23, 461–469. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Pal, R. New Model for effective Young’s modulus of particulate composites. Compos. Part B Eng. 2005, 36, 513–523. [Google Scholar] [CrossRef]
- Wolock, I.; Kies, J.; Newman, S. Fracture: Proceedings of an International Conference on the Atomic Mechanisms of Fracture, 12–16 April 1959; Averbach, B.L., Felbeck, D.K., Eds.; MIT: Boston, MA, USA, 1959; Chapter 13. [Google Scholar]
- Young, R.J.; Lovell, P.A. Introduction to Polymers; Chapman and Hall: New York, NY, USA, 1991. [Google Scholar]
- Becker, K.H.; Schmidt, H. Tailoring of thermomechanical properties of thermoplastic nanocomposites by surface modification of nanoscale silica particles. Mat. Res. Soc.Symp. Proc. 1996, 435, 237. [Google Scholar] [CrossRef]
- Ng, C.; Ash, B.; Schadler, L.; Siegel, R. A Study of the Mechanical and Permeability Properties of Nano- and Micron- TiO2 Filled Epoxy Composites. Compos. Adv. Mater. 2001, 10. Available online: https://journals.sagepub.com/doi/full/10.1177/096369350101000301 (accessed on 26 January 2023). [CrossRef]
- Sternstein, S.S. Polymeric Materials: Relationships Between Structure and Mechanical Behavior; American Society for Metals: Metals Park, OH, USA, 1975; Chapter 7. [Google Scholar]
- Lazzeri, A.; Bucknall, C.B. Dilatational bands in rubber-toughened polymers. J. Mater. Sci. 1993, 28, 6799–6808. [Google Scholar] [CrossRef]
- Bucknall, C.B. Polymer Blends; Paul, D.R., Bucknall, C.B., Eds.; John Wiley & Sons Inc.: New York, NY, USA, 2000; Volume 2, Chapter 22. [Google Scholar]
- Pearson, R.; Yee, A. Influence of particle size and particle size distribution on toughening mechanisms in rubber-modified epoxies. J. Mater. Sci. 1991, 26, 3828–3844. [Google Scholar] [CrossRef]
- Wu, S. A generalized criterion for rubber toughening: The critical matrix ligament thickness. J. Appl. Polym. Sci. 1988, 35, 549–561. [Google Scholar] [CrossRef]
- Cousin, P.; Smith, P. Dynamic mechanical properties of sulfonated polystyrene/alumina composites. J. Polym. Sci. Part B Polym. Phys. 1994, 32, 459–468. [Google Scholar] [CrossRef]
- Kendall, K.; Sherliker, F.R. Colloidal reinforcement: The influence of bound polymer. Brit. Polym. J. 1980, 12, 85. [Google Scholar] [CrossRef]






| Time (min) to 400 °C | Molecular Weight (gr/mol) | Standard Deviation |
|---|---|---|
| 0 | 43,900 | 1287 |
| 5 | 43,900 | 1891 |
| 10 | 43,800 | 1436 |
| 15 | 43,500 | 1562 |
| 25 | 42,400 | 1583 |
| Cu (% v/v) | δc Teorica (g/cm3) | δc Residual (g/cm3) | Number of Samples | Standard Deviation |
|---|---|---|---|---|
| 2.5 | 1.385 | −0.0025 | 3 | 0.0035 |
| 5 | 1.579 | −0.0268 | 3 | 0.0423 |
| 10 | 1.967 | −0.0198 | 3 | 0.0389 |
| 15 | 2.356 | −0.0188 | 3 | 0.0443 |
| 20 | 2.744 | −0.0356 | 3 | 0.0479 |
| 25 | 3.133 | −0.0015 | 3 | 0.0047 |
| 30 | 3.521 | −0.0035 | 3 | 0.0123 |
| 35 | 3.909 | −0.0031 | 3 | 0.0122 |
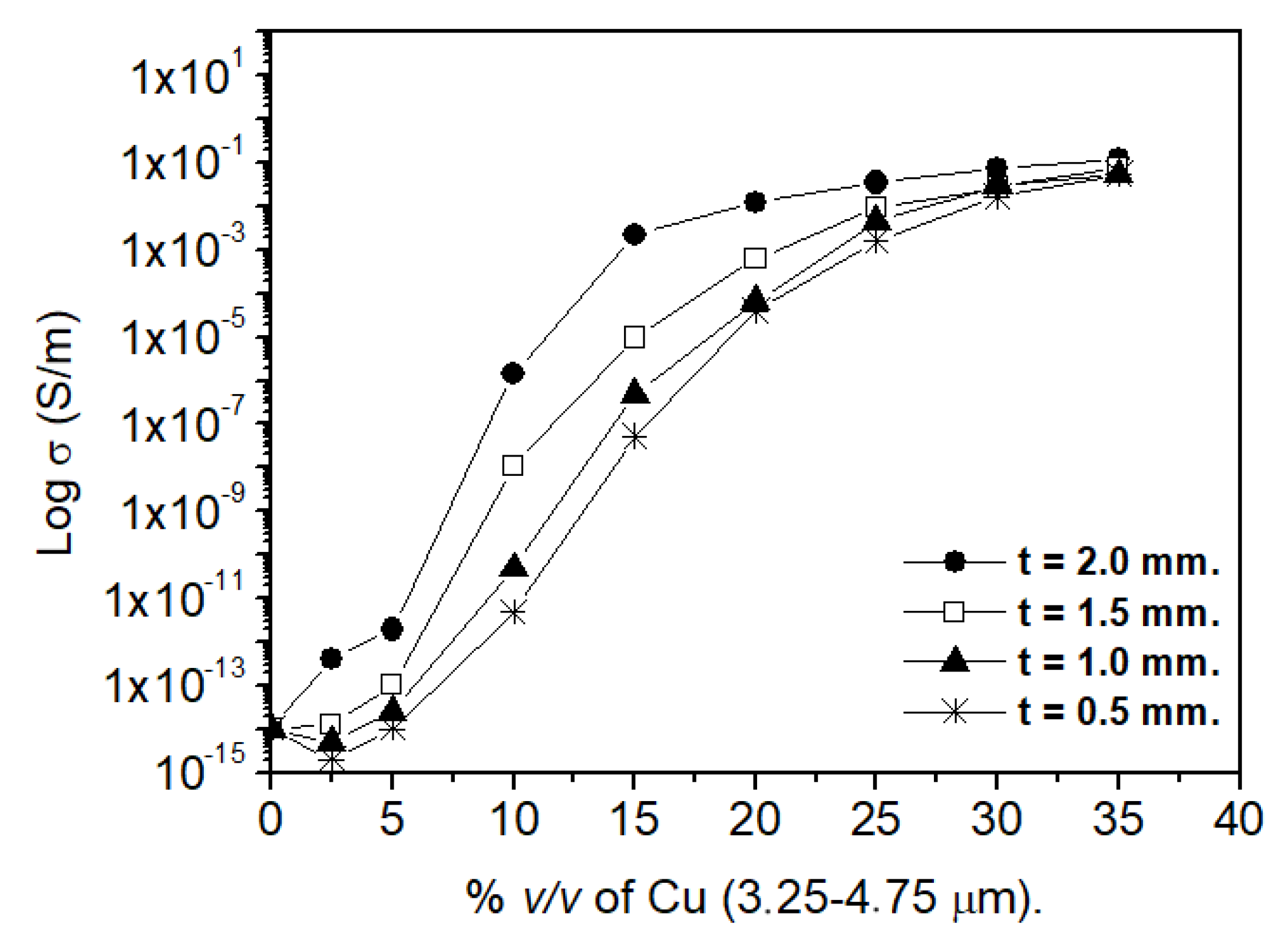
| Thickness Sample (mm) | Φc (% v/v) PMMA–Cu (3.25–4.75 μm) | Φc (% v/v) PMMA–Cu (78 nm) |
|---|---|---|
| 2.0 | 10.00 | 14.80 |
| 1.5 | 11.50 | 14.80 |
| 1.0 | 15.00 | 14.90 |
| 0.5 | 15.00 | 15.00 |
| Average Ultimate Strength | Strain to Failure | 1% Secant Modulus | ||||
|---|---|---|---|---|---|---|
| (MPa) | (% Strain) | (MPa) | ||||
| Cu (% v/v) | 78 nm | 3.25–4.75 µm | 78 nm | 3.25–4.75 µm | 78 nm | 3.25–4.75 µm |
| 0 | 75.88 | 75.88 | 4.52 | 4.52 | 31.80 | 31.80 |
| 1 | 55.25 | 55.20 | 11.45 | 3.70 | 26.60 | 24.28 |
| 2 | 56.14 | 39.82 | 25.03 | 3.04 | 27.03 | 18.82 |
| 5 | 59.67 | 28.15 | 4.48 | 2.51 | 28.66 | 14.26 |
| 10 | 66.69 | 19.13 | 4.33 | 2.30 | 28.21 | 10.33 |
| 20 | 69.60 | 12.15 | 4.13 | 1.89 | 29.74 | 7.65 |
| Composition | TMA—Tg (°C) | DSC—Tg (°C) | TMA—Tg (°C) | DSC—Tg (°C) |
|---|---|---|---|---|
| Copper/PMMA | 78 nm Copper/PMMA | 3.25–4.75 μm Copper/PMMA | ||
| Neat PMMA | 127 ± 1 | 129 ± 3 | 127 ± 1 | 129 ± 3 |
| 1 vol % | 103 ± 2 | 108 ± 2 | 122 ± 2 | 123 ± 2 |
| 2 vol % | 100 ± 2 | 100 ± 1 | 120 ± 1 | 120 ± 1 |
| 3 vol % | 103 ± 1 | 102 ± 2 | 120 ± 1 | 120 ± 2 |
| 5 vol % | 115 ± 1 | 109 ± 1 | 120 ± 1 | 121 ± 1 |
| 6 vol % | 117 ± 2 | 114 ± 2 | 121 ± 1 | 122 ± 2 |
| 7 vol % | 118 ± 2 | 117 ± 2 | 121 ± 2 | 122 ± 2 |
| 10 vol % | 118 ± 2 | 121 ± 3 | 122 ± 2 | 122 ± 3 |
| 15 vol % | 120 ± 3 | 121 ± 3 | 121 ± 1 | 123 ± 3 |
| 20 vol % | 120 ± 3 | 121 ± 2 | 122 ± 3 | 123 ± 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poblete, V.H.; Alvarez, M.P. Mechanical, Electrical, and Glass Transition Behavior of Copper–PMMA Composites. Crystals 2023, 13, 368. https://doi.org/10.3390/cryst13030368
Poblete VH, Alvarez MP. Mechanical, Electrical, and Glass Transition Behavior of Copper–PMMA Composites. Crystals. 2023; 13(3):368. https://doi.org/10.3390/cryst13030368
Chicago/Turabian StylePoblete, Victor H., and Mariela P. Alvarez. 2023. "Mechanical, Electrical, and Glass Transition Behavior of Copper–PMMA Composites" Crystals 13, no. 3: 368. https://doi.org/10.3390/cryst13030368
APA StylePoblete, V. H., & Alvarez, M. P. (2023). Mechanical, Electrical, and Glass Transition Behavior of Copper–PMMA Composites. Crystals, 13(3), 368. https://doi.org/10.3390/cryst13030368





