Enhancing the Predictive Modeling of n-Value Surfaces in Various High Temperature Superconducting Materials Using a Feed-Forward Deep Neural Network Technique
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Architecture of Deep Feed-Forward Neural Network
2.3. Performance Metrics
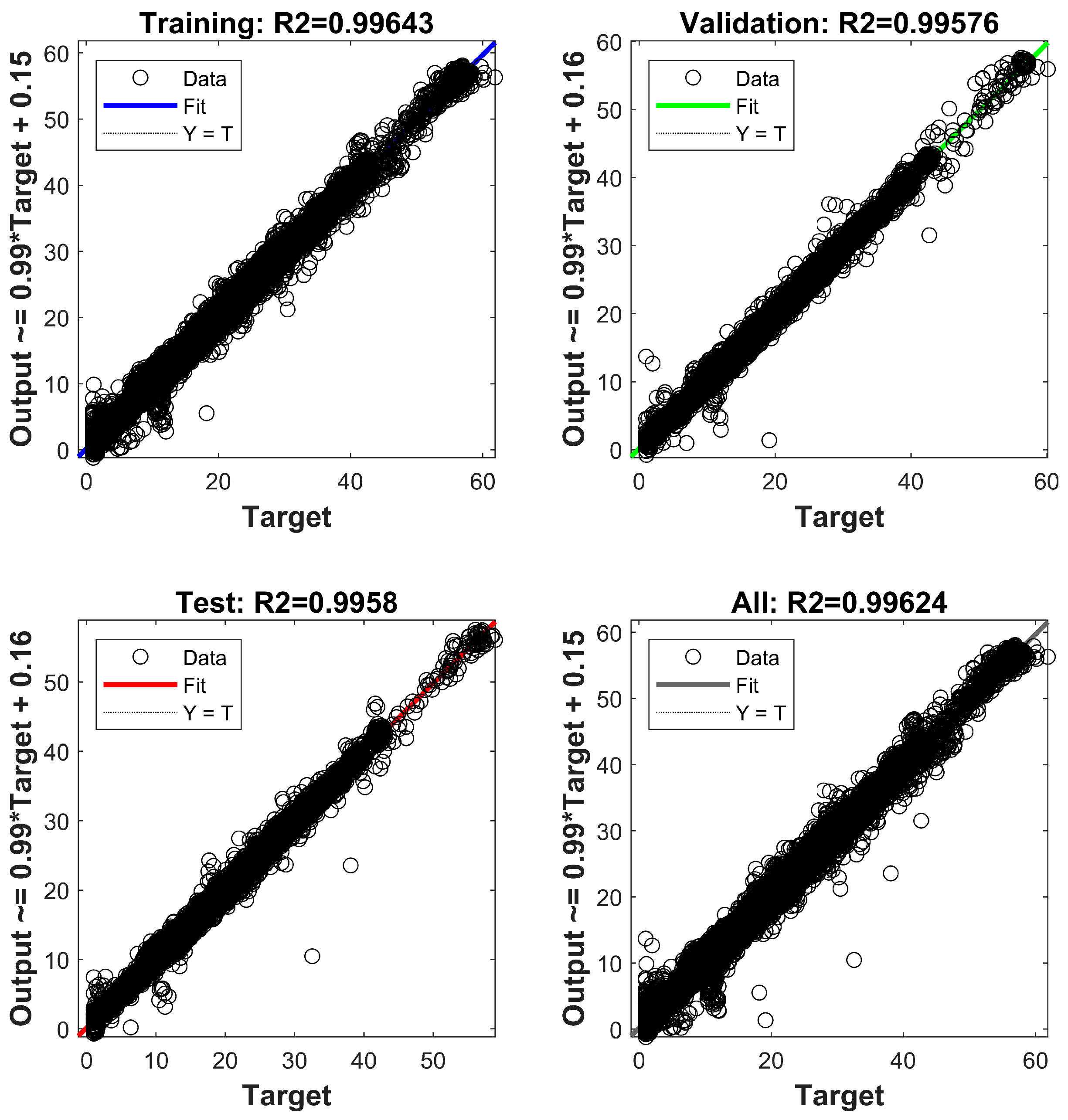
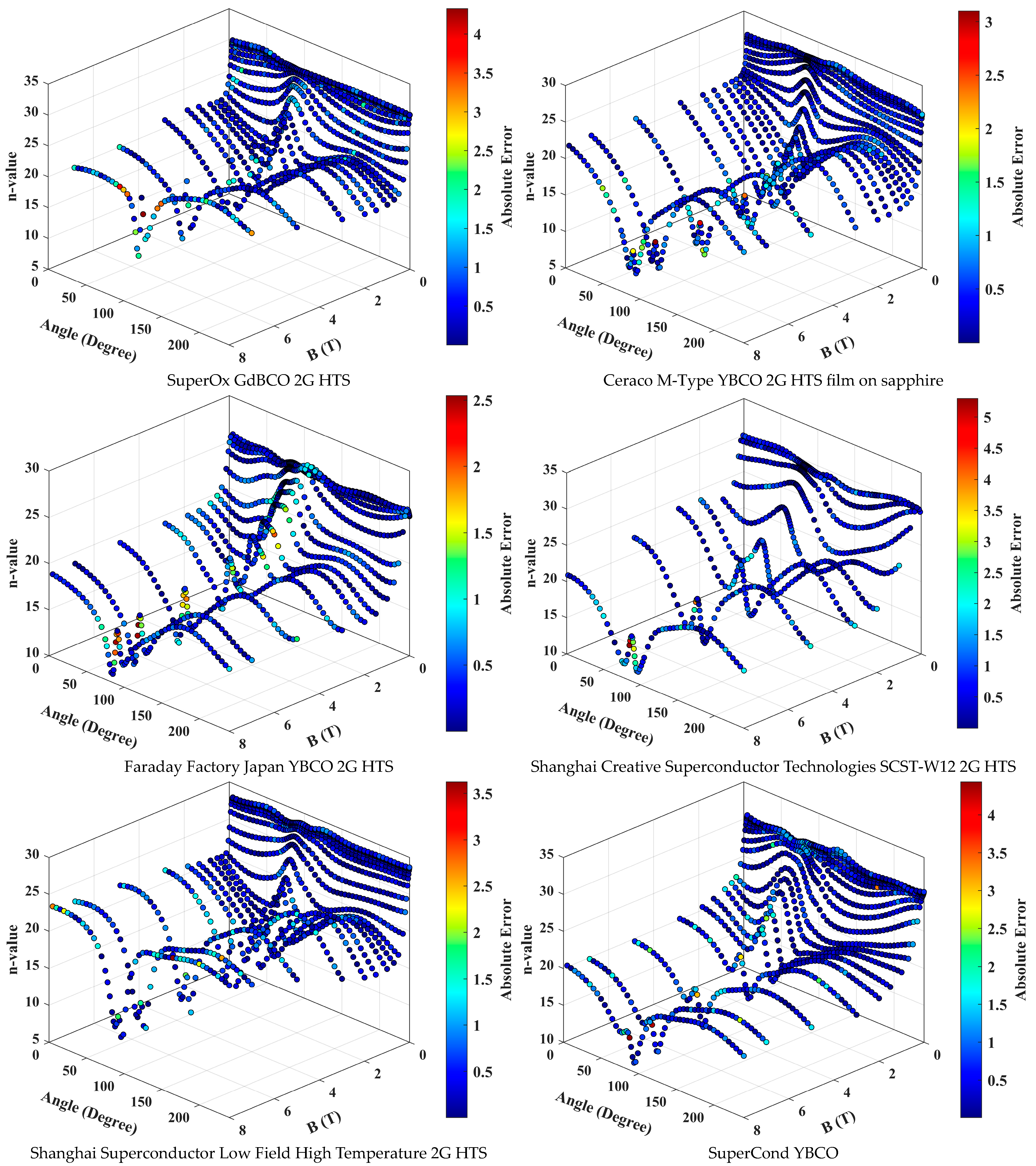
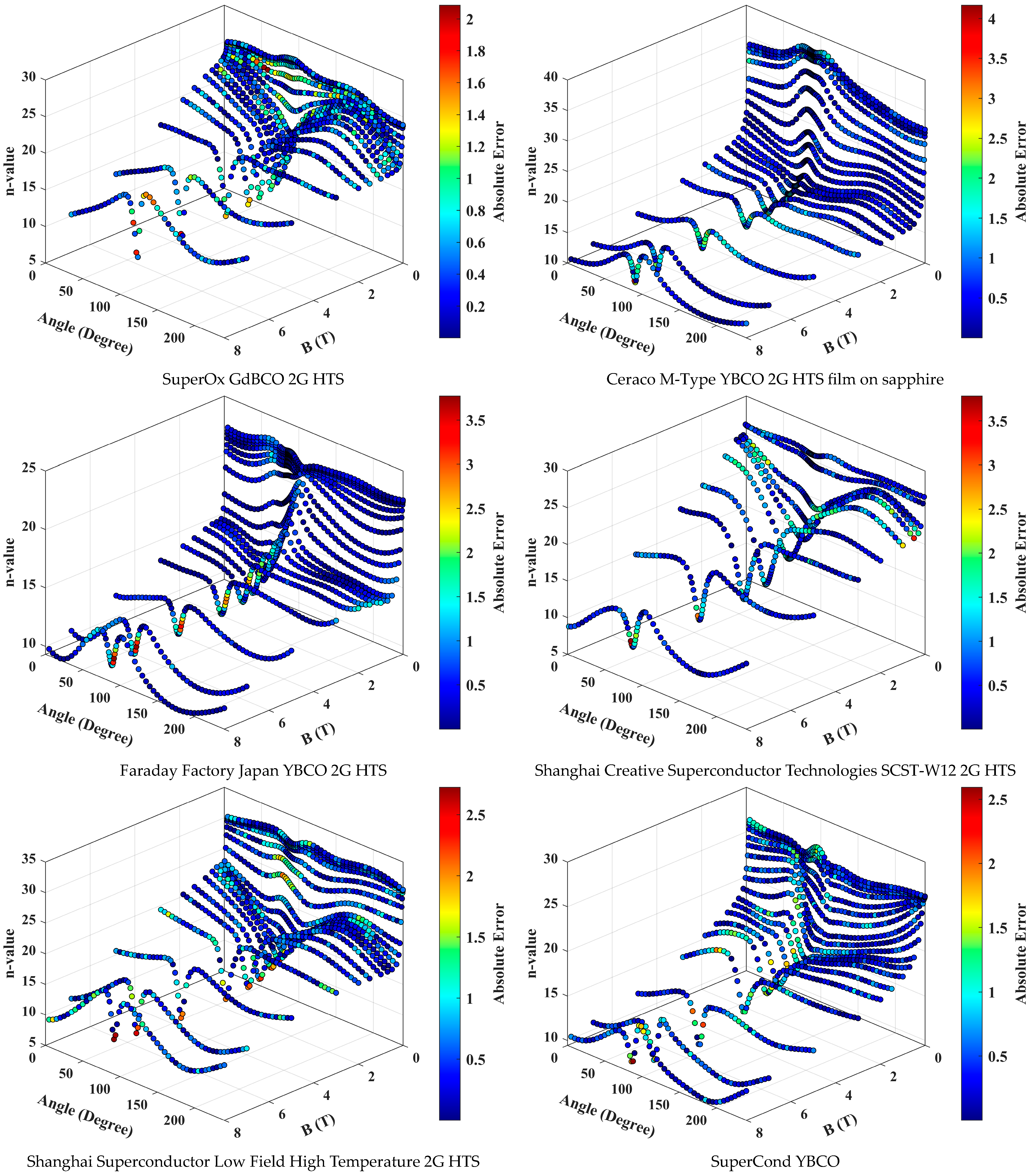
3. Results and Discussion
4. Conclusions
- The DFFNN model demonstrated excellent accuracy in predicting n-value surfaces for various HTS materials, achieving an R-squared value of 0.9962.
- It achieved a mean absolute error of 0.4921 and a mean relative error of 3.33%, indicating high precision in predictions.
- The model provides ultra-fast predictions, with testing times of mere milliseconds for over 15,000 data points.
- The model is capable of generalizing across different HTS samples, eliminating the need for separate models for individual samples.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Godeke, A. High temperature superconductors for commercial magnets. Supercond. Sci. Technol. 2023, 36, 113001. [Google Scholar] [CrossRef]
- Taylor, D.; Keys, S.; Hampshire, D. E–J characteristics and n-values of a niobium–tin superconducting wire as a function of magnetic field, temperature and strain. Phys. C Supercond. 2002, 372-376, 1291–1294. [Google Scholar] [CrossRef]
- Bruzzone, P.; Fietz, W.H.; Minervini, J.V.; Novikov, M.; Yanagi, N.; Zhai, Y.; Zheng, J. High temperature superconductors for fusion magnets. Nucl. Fusion 2018, 58, 103001. [Google Scholar] [CrossRef]
- Matsushita, T.; Matsuda, A.; Yanagi, K. Irreversibility line and flux pinning properties in high-temperature superconductors. Phys. C Supercond. 1993, 213, 477–482. [Google Scholar] [CrossRef]
- Ishida, K.; Byun, I.; Nagaoka, I.; Fukumitsu, K.; Tanaka, M.; Kawakami, S.; Tanimoto, T.; Ono, T.; Kim, J.; Inoue, K. Superconductor Computing for Neural Networks. IEEE Micro 2021, 41, 19–26. [Google Scholar] [CrossRef]
- Bonab, S.A.; Xing, Y.; Russo, G.; Fabbri, M.; Morandi, A.; Bernstein, P.; Noudem, J.; Yazdani-Asrami, M. Estimation of magnetic levitation and lateral forces in MgB2 superconducting bulks with various dimensional sizes using artificial intelligence techniques. Supercond. Sci. Technol. 2024, 37, 075008. [Google Scholar] [CrossRef]
- Li, G.Z.; Yang, Y.; A Susner, M.; Sumption, M.D.; Collings, E.W. Critical current densities and n-values of MgB2 strands over a wide range of temperatures and fields. Supercond. Sci. Technol. 2011, 25, 025001. [Google Scholar] [CrossRef]
- Martinez, E.; Martinez-Lopez, M.; Millan, A.; Mikheenko, P.; Bevan, A.; Abell, J.S. Temperature and Magnetic Field Dependence of the n-Values of MgB2 Superconductors. IEEE Trans. Appl. Supercond. 2007, 17, 2738–2741. [Google Scholar] [CrossRef]
- Sadeghi, A.; Bonab, S.A.; Song, W.; Yazdani-Asrami, M. Intelligent estimation of critical current degradation in HTS tapes under repetitive overcurrent cycling for cryo-electric transportation applications. Mater. Today Phys. 2024, 42, 101365. [Google Scholar] [CrossRef]
- Wu, G.; Yong, H. Estimation of critical current density of bulk superconductor with artificial neural network. Superconductivity 2023, 7, 100055. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, Z.; Geng, J.; Shen, B.; Ma, J.; Li, C.; Zhang, H.; Dong, Q.; Coombs, T.A. Study of Critical Current and n-Values of 2G HTS Tapes: Their Magnetic Field-Angular Dependence. J. Supercond. Nov. Magn. 2018, 31, 3847–3854. [Google Scholar] [CrossRef]
- Goodrich, L.; Srivastava, A.; Yuyama, M.; Wada, H. n-value and second derivative of the superconductor voltage-current characteristic. IEEE Trans. Appl. Supercond. 1993, 3, 1265–1268. [Google Scholar] [CrossRef]
- Shen, B.; Grilli, F.; Coombs, T. Review of the AC loss computation for HTS using H formulation. Supercond. Sci. Technol. 2020, 33, 033002. [Google Scholar] [CrossRef]
- Kim, J.; Dou, S.; Matsumoto, A.; Choi, S.; Kiyoshi, T.; Kumakura, H. Correlation between critical current density and n-value in MgB2/Nb/Monel superconductor wires. Phys. C Supercond. 2010, 470, 1207–1210. [Google Scholar] [CrossRef]
- Romanovskii, V.; Watanabe, K.; Ozhogina, V. Thermal peculiarities of the electric mode formation of high temperature superconductors with the temperature-decreasing n-value. Cryogenics 2009, 49, 360–365. [Google Scholar] [CrossRef]
- Douine, B.; Bonnard, C.-H.; Sirois, F.; Berger, K.; Kameni, A.; Leveque, J. Determination of Jc and n-Value of HTS Pellets by Measurement and Simulation of Magnetic Field Penetration. IEEE Trans. Appl. Supercond. 2015, 25, 1–8. [Google Scholar] [CrossRef]
- Taylor, D.M.J.; Hampshire, D.P. Relationship between the n-value and critical current in Nb3Sn superconducting wires exhibiting intrinsic and extrinsic behaviour. Supercond. Sci. Technol. 2005, 18, S297–S302. [Google Scholar] [CrossRef]
- Liu, Q.; Kim, S. Temperature-field-angle dependent critical current estimation of commercial second generation high temperature superconducting conductor using double hidden layer Bayesian regularized neural network. Supercond. Sci. Technol. 2022, 35, 035001. [Google Scholar] [CrossRef]
- Amemiya, N.; Miyamoto, K.; Banno, N.; Tsukamoto, O. Numerical analysis of AC losses in high Tc superconductors based on E-j characteristics represented with n-value. IEEE Trans. Appl. Supercond. 1997, 7, 2110–2113. [Google Scholar] [CrossRef]
- Russo, G.; Yazdani-Asrami, M.; Scheda, R.; Morandi, A.; Diciotti, S. Artificial intelligence-based models for reconstructing the critical current and index-value surfaces of HTS tapes. Supercond. Sci. Technol. 2022, 35, 124002. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Song, W.; Madureira, A.; Murta-Pina, J.; Morandi, A.; Parizh, M. Artificial intelligence methods for applied superconductivity: Material, design, manufacturing, testing, operation, and condition monitoring. Supercond. Sci. Technol. 2022, 35, 123001. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Seyyedbarzegar, S.; Song, W. DC Electro-Magneto-Mechanical Characterization of 2G HTS Tapes for Superconducting Cable in Magnet System Using Artificial Neural Networks. IEEE Trans. Appl. Supercond. 2022, 32, 1–10. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Sadeghi, A.; Seyyedbarzegar, S.M.; Saadat, A. Advanced experimental-based data-driven model for the electromechanical behavior of twisted YBCO tapes considering thermomagnetic constraints. Supercond. Sci. Technol. 2022, 35, 054004. [Google Scholar] [CrossRef]
- Suresh, N.V.U.; Sadeghi, A.; Yazdani-Asrami, M. Critical current parameterization of high temperature Superconducting Tapes: A novel approach based on fuzzy logic. Superconductivity 2023, 5, 100036. [Google Scholar] [CrossRef]
- Bonab, S.A.; Russo, G.; Morandi, A.; Yazdani-Asrami, M. A comprehensive machine learning-based investigation for the index-value prediction of 2G HTS coated conductor tapes. Mach. Learn. Sci. Technol. 2024, 5, 025040. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, Y.; Meng, Z.; Wang, T. Critical current and n-value prediction of second-generation high temperature superconducting conductors considering the temperature-field dependence based on the back propagation neural network with encoder. Supercond. Sci. Technol. 2022, 35, 104002. [Google Scholar] [CrossRef]
- Ke, Z.; Deng, Z.; Chen, Y.; Yi, H.; Liu, X.; Wang, L.; Zhang, P.; Ren, T. Vibration States Detection of HTS Pinning Maglev System Based on Deep Learning Algorithm. IEEE Trans. Appl. Supercond. 2022, 32, 1–6. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M. Artificial intelligence, machine learning, deep learning, and big data techniques for the advancements of superconducting technology: A road to smarter and intelligent superconductivity. Supercond. Sci. Technol. 2023, 36, 084001. [Google Scholar] [CrossRef]
- Ke, Z.; Liu, X.; Chen, Y.; Shi, H.; Deng, Z. Prediction models establishment and comparison for guiding force of high-temperature superconducting maglev based on deep learning algorithms. Supercond. Sci. Technol. 2022, 35, 024005. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Song, W.; Morandi, A.; De Carne, G.; Murta-Pina, J.; Pronto, A.; Oliveira, R.; Grilli, F.; Pardo, E.; Parizh, M.; et al. Roadmap on artificial intelligence and big data techniques for superconductivity. Supercond. Sci. Technol. 2023, 36, 043501. [Google Scholar] [CrossRef]
- Robinson HTS Wire Critical Current Database. Available online: https://htsdb.wimbush.eu/ (accessed on 27 October 2023).
- Wimbush, S.C.; Strickland, N.M. A Public Database of High-Temperature Superconductor Critical Current Data. IEEE Trans. Appl. Supercond. 2016, 27, 1–5. [Google Scholar] [CrossRef]
- Sumayli, A. Development of advanced machine learning models for optimization of methyl ester biofuel production from papaya oil: Gaussian process regression (GPR), multilayer perceptron (MLP), and K-nearest neighbor (KNN) regression models. Arab. J. Chem. 2023, 16, 104833. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef]
- Xia, J.; Khabaz, M.K.; Patra, I.; Khalid, I.; Alvarez, J.R.N.; Rahmanian, A.; Eftekhari, S.A.; Toghraie, D. Using feed-forward perceptron Artificial Neural Network (ANN) model to determine the rolling force, power and slip of the tandem cold rolling. ISA Trans. 2023, 132, 353–363. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Ekonomou, L.; Fotis, G.; Maris, T.; Liatsis, P. Estimation of the electromagnetic field radiating by electrostatic discharges using artificial neural networks. Simul. Model. Pract. Theory 2007, 15, 1089–1102. [Google Scholar] [CrossRef]
- Le, T.D.; Noumeir, R.; Quach, H.L.; Kim, J.H.; Kim, J.H.; Kim, H.M. Critical Temperature Prediction for a Superconductor: A Variational Bayesian Neural Network Approach. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications. 1994. Available online: https://books.google.co.uk/books?id=ONylQgAACAAJ (accessed on 10 January 2024).
- Mohanasundaram, R.; Malhotra, A.S.; Arun, R.; Periasamy, P.S. Deep Learning and Semi-Supervised and Transfer Learning Algorithms for Medical Imaging. In Deep Learning and Parallel Computing Environment for Bioengineering Systems; Academic Press: Cambridge, MA, USA, 2019; pp. 139–151. [Google Scholar] [CrossRef]
- Al-Ruqaishi, Z.; Ooi, C.R. Multilayer neural network models for critical temperature of cuprate superconductors. Comput. Mater. Sci. 2024, 241, 113018. [Google Scholar] [CrossRef]
- Kamran, M.; Haider, S.; Akram, T.; Naqvi, S.; He, S. Prediction of IV curves for a superconducting thin film using artificial neural networks. Superlattices Microstruct. 2016, 95, 88–94. [Google Scholar] [CrossRef]
- Moseley, B.; Markham, A.; Nissen-Meyer, T. Finite basis physics-informed neural networks (FBPINNs): A scalable domain decomposition approach for solving differential equations. Adv. Comput. Math. 2023, 49, 62. [Google Scholar] [CrossRef]
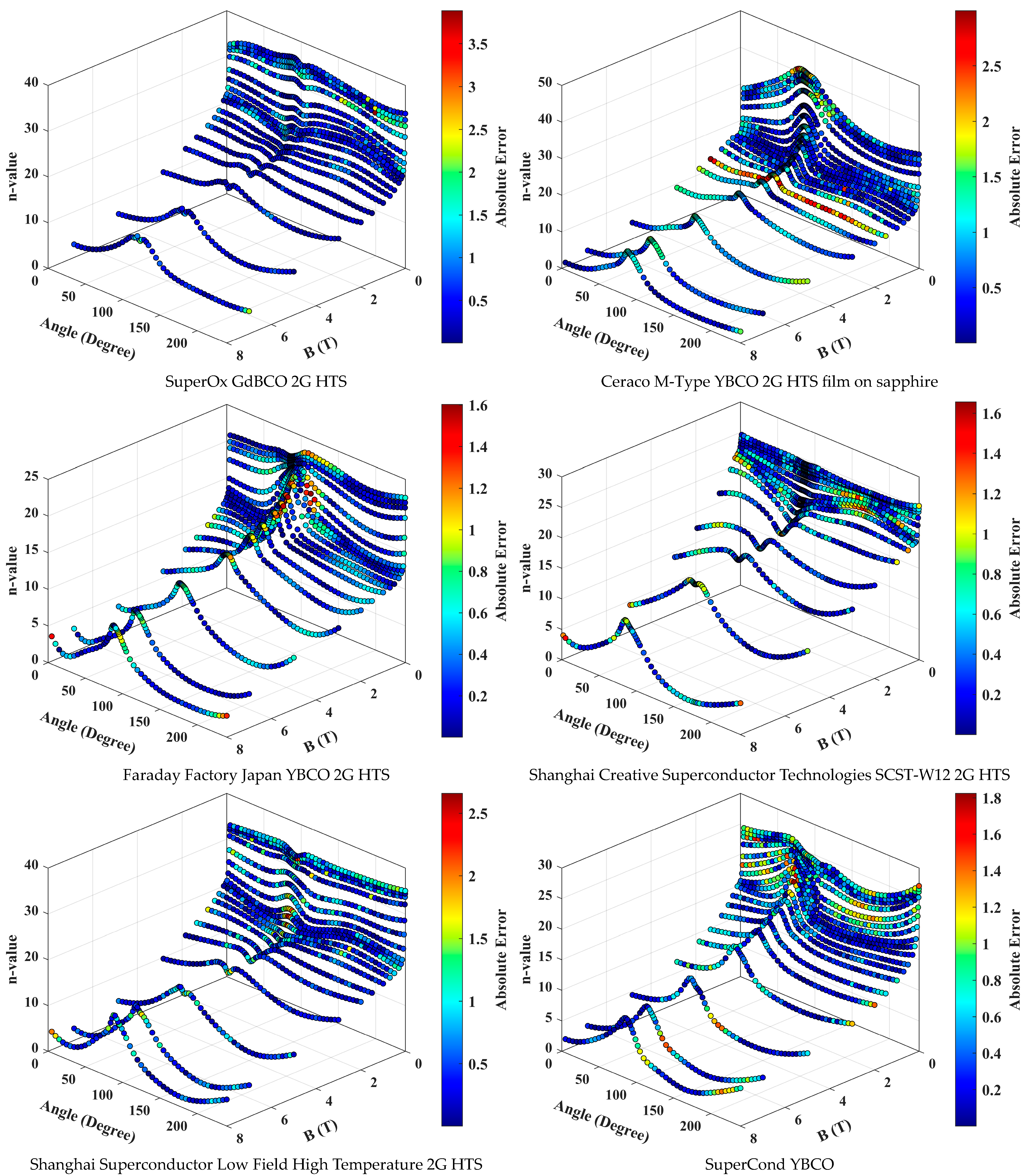
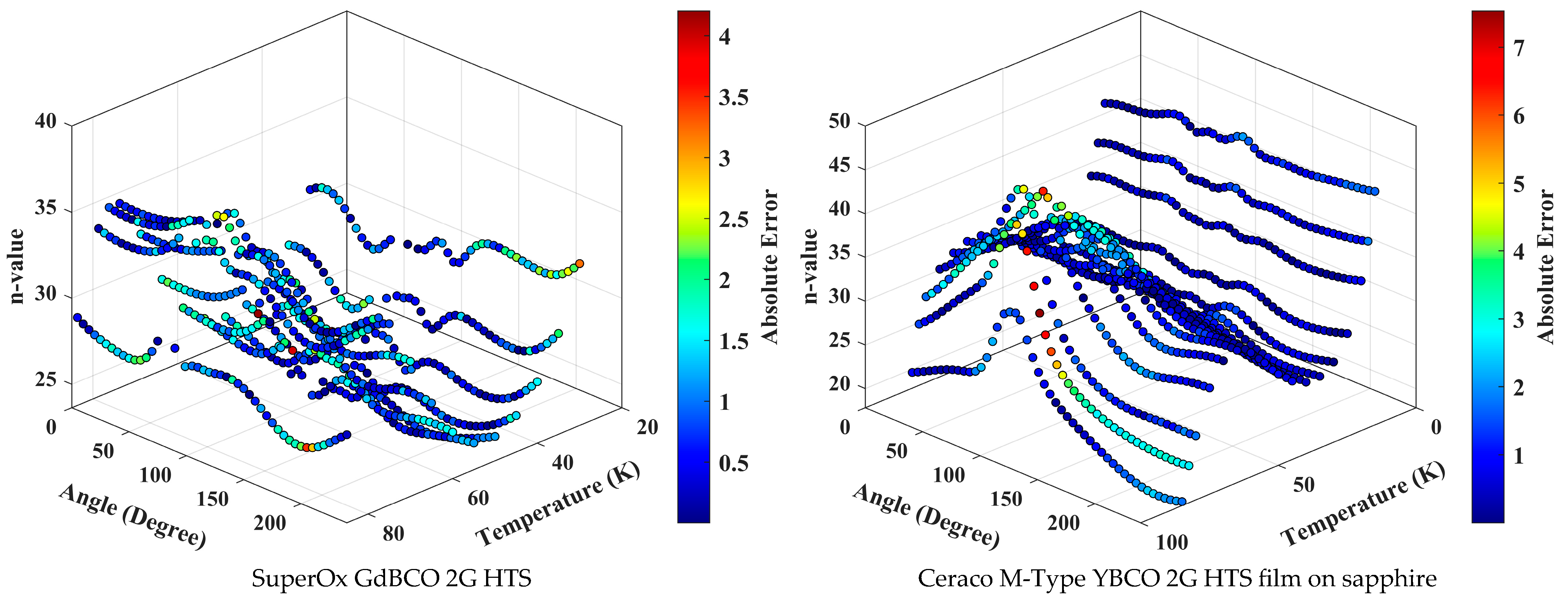
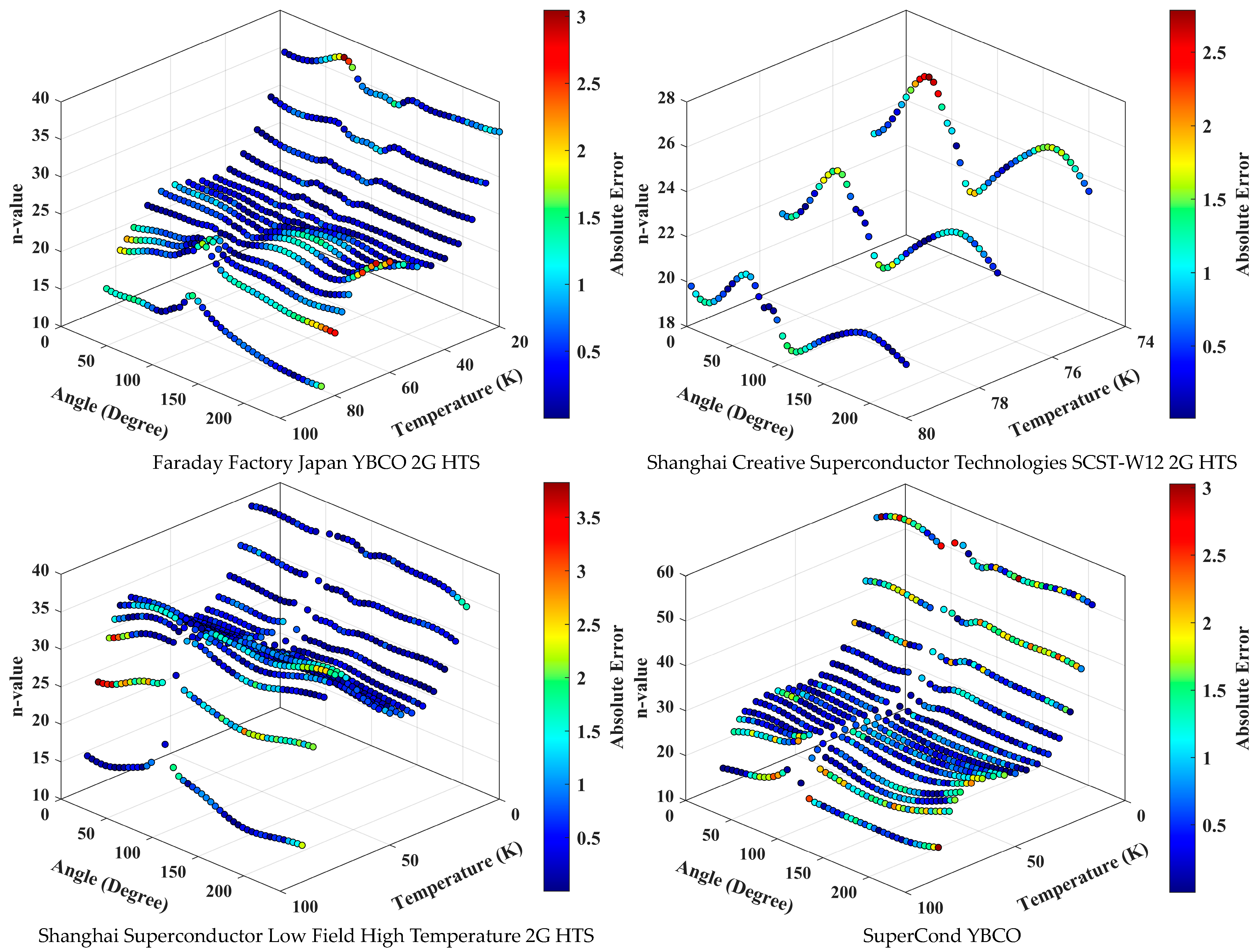
| Number of Fold(s) | R-Squared | RMSE |
|---|---|---|
| 1 | 0.99521 | 0.82374 |
| 2 | 0.99496 | 0.85219 |
| 3 | 0.99516 | 0.81372 |
| Mean | 0.99511 | 0.82988 |
| RMSE | R-Squared | MAE | MRE [%] | Testing Time [s] |
|---|---|---|---|---|
| 0.744591657 | 0.996244289 | 0.492103476 | 3.328049383 | 0.6135193 |
| RMSE | R-Squared | MAE | MRE [%] | Testing Time [s] |
|---|---|---|---|---|
| 1.058721 | 0.973809126 | 0.76842511 | 2.7668185 | 0.259087 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alipour Bonab, S.; Song, W.; Yazdani-Asrami, M. Enhancing the Predictive Modeling of n-Value Surfaces in Various High Temperature Superconducting Materials Using a Feed-Forward Deep Neural Network Technique. Crystals 2024, 14, 619. https://doi.org/10.3390/cryst14070619
Alipour Bonab S, Song W, Yazdani-Asrami M. Enhancing the Predictive Modeling of n-Value Surfaces in Various High Temperature Superconducting Materials Using a Feed-Forward Deep Neural Network Technique. Crystals. 2024; 14(7):619. https://doi.org/10.3390/cryst14070619
Chicago/Turabian StyleAlipour Bonab, Shahin, Wenjuan Song, and Mohammad Yazdani-Asrami. 2024. "Enhancing the Predictive Modeling of n-Value Surfaces in Various High Temperature Superconducting Materials Using a Feed-Forward Deep Neural Network Technique" Crystals 14, no. 7: 619. https://doi.org/10.3390/cryst14070619
APA StyleAlipour Bonab, S., Song, W., & Yazdani-Asrami, M. (2024). Enhancing the Predictive Modeling of n-Value Surfaces in Various High Temperature Superconducting Materials Using a Feed-Forward Deep Neural Network Technique. Crystals, 14(7), 619. https://doi.org/10.3390/cryst14070619










