Polymerization Kinetics of Cyanate Ester Confined to Hydrophilic Nanopores of Silica Colloidal Crystals with Different Surface-Grafted Groups
Abstract
1. Introduction
2. Materials and Methods
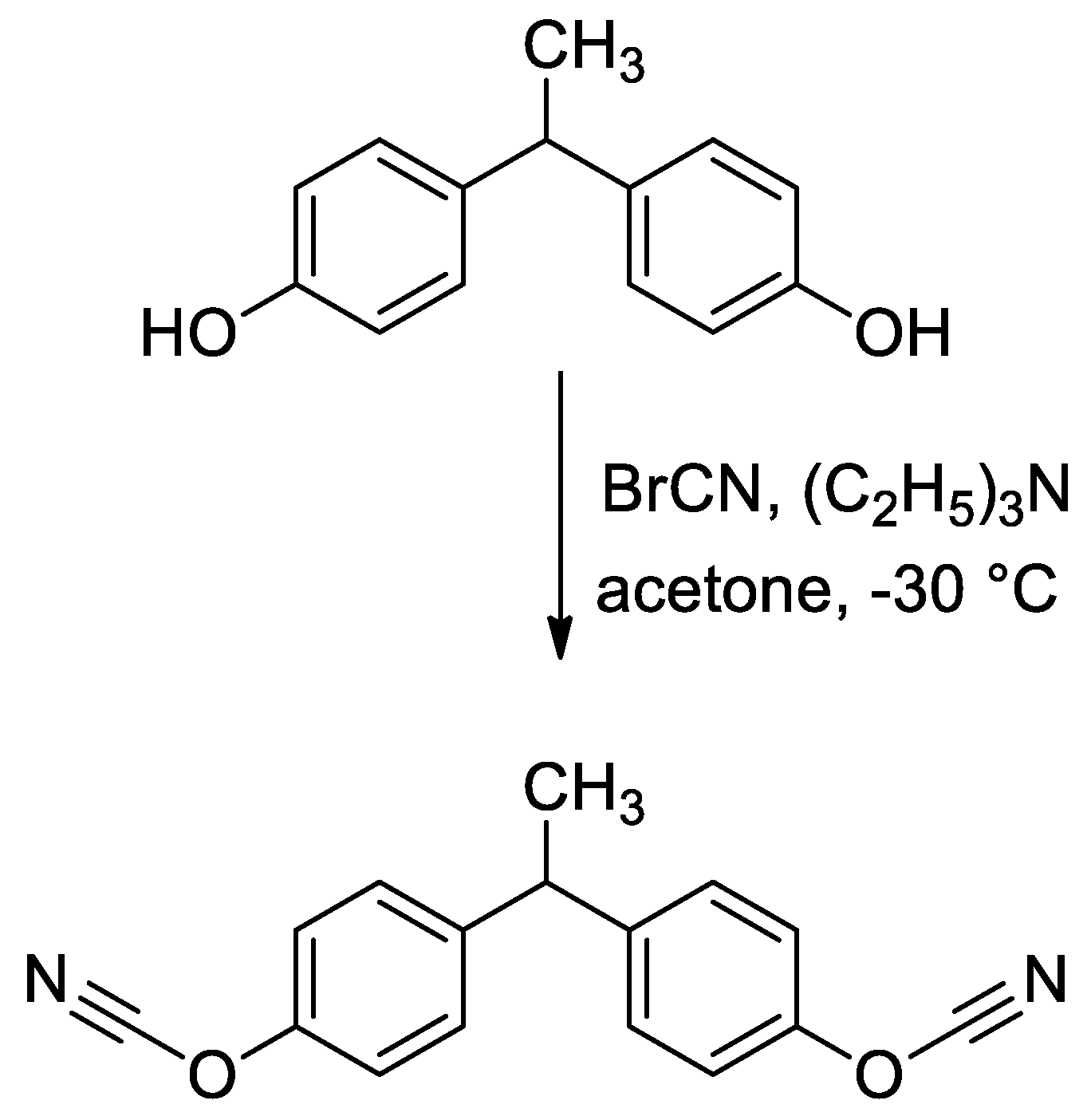
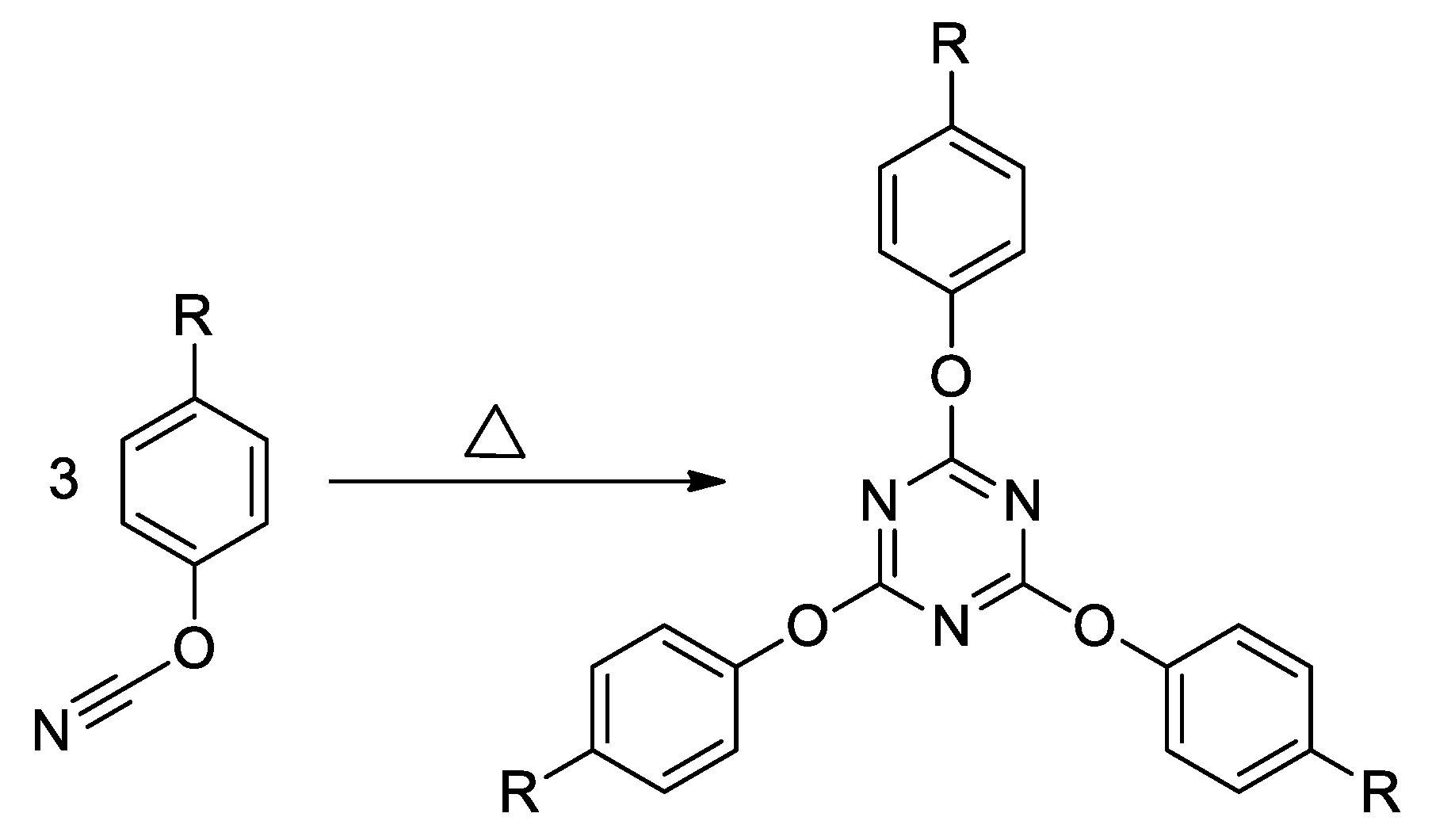
2.1. Materials
2.2. Methods
3. Computations
4. Results and Discussion
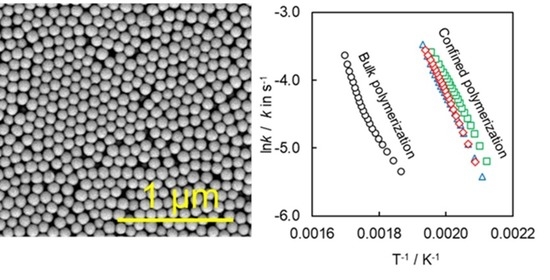
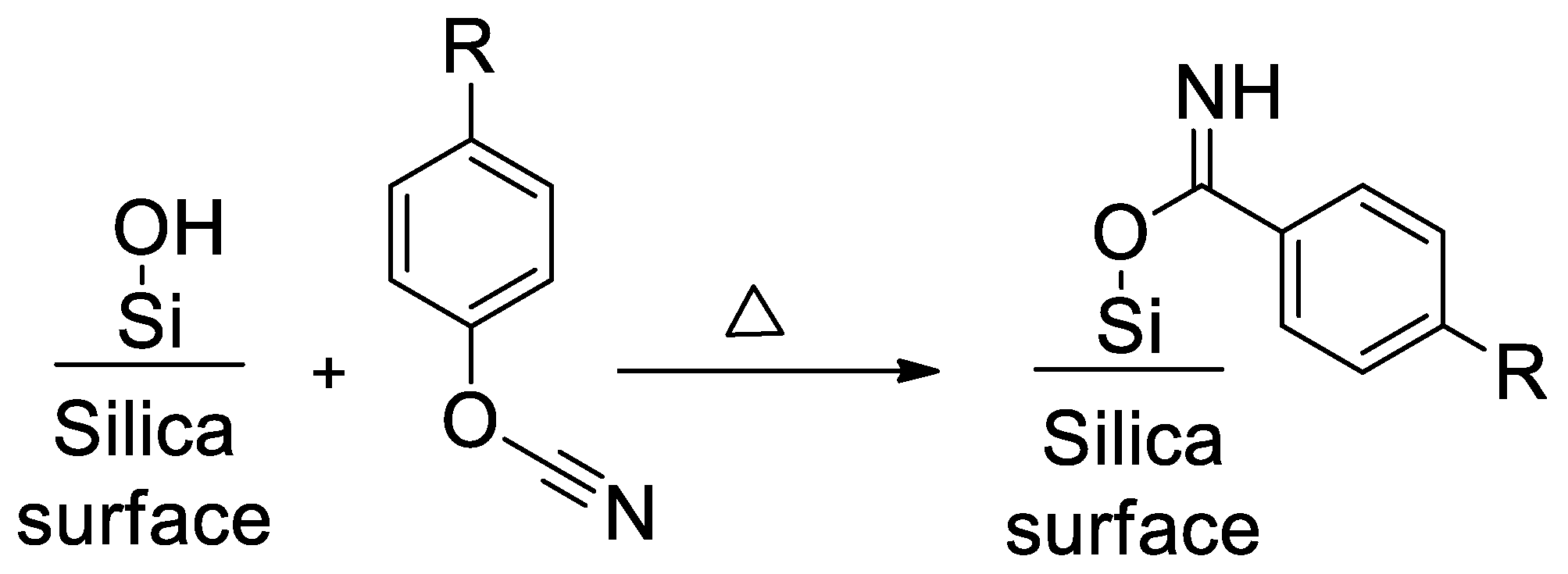
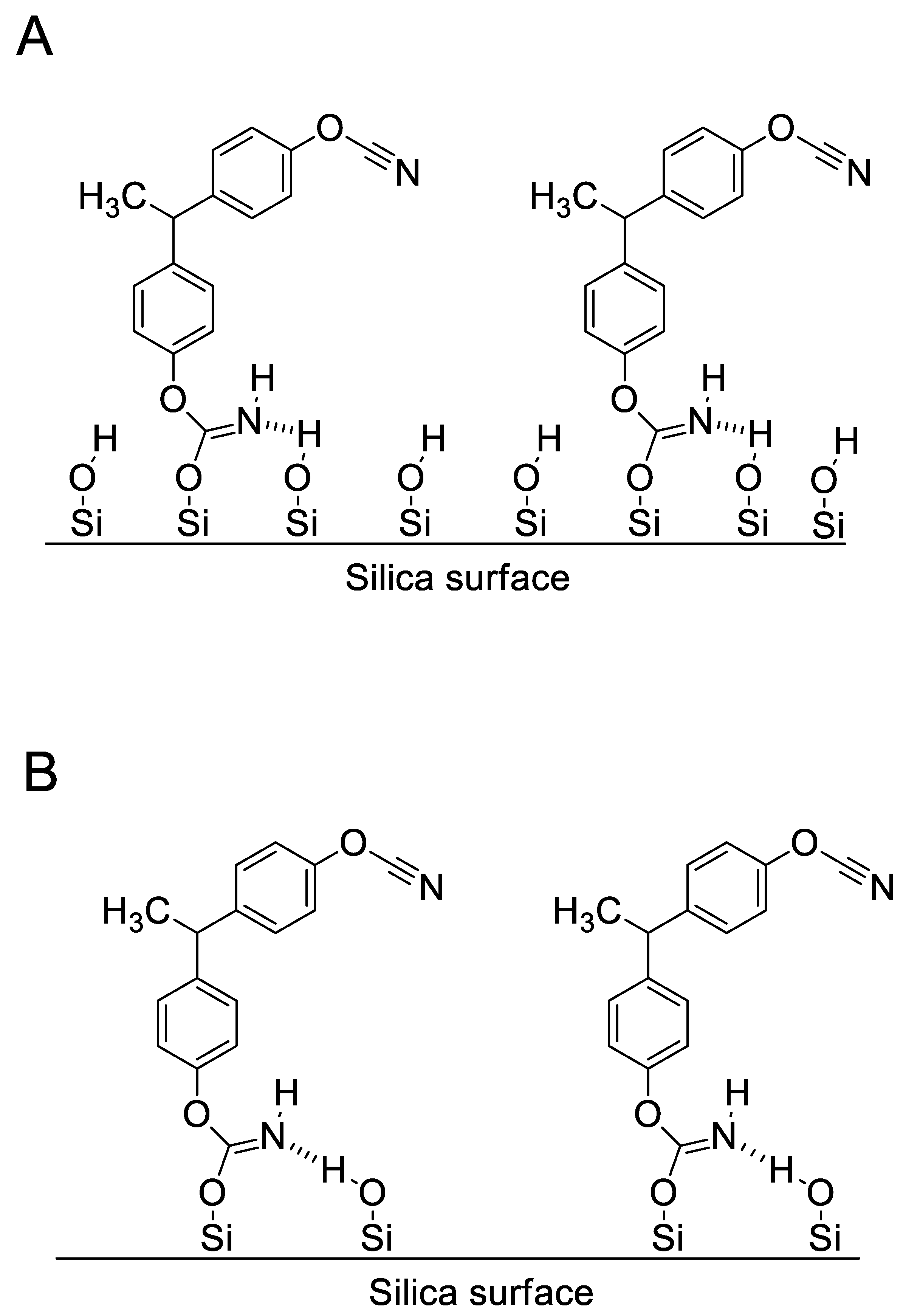
4.1. Synthesis and Characterization of SCCs Having Different Surface Chemistry
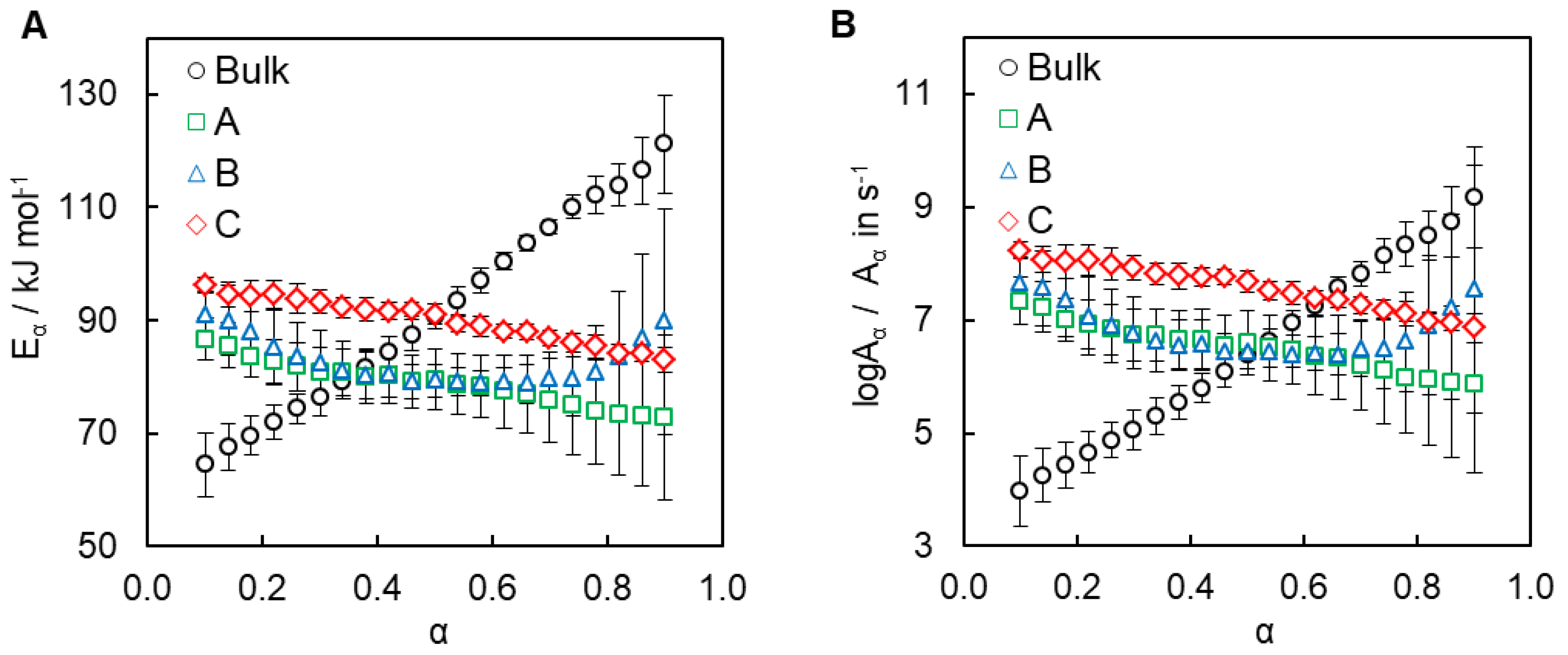
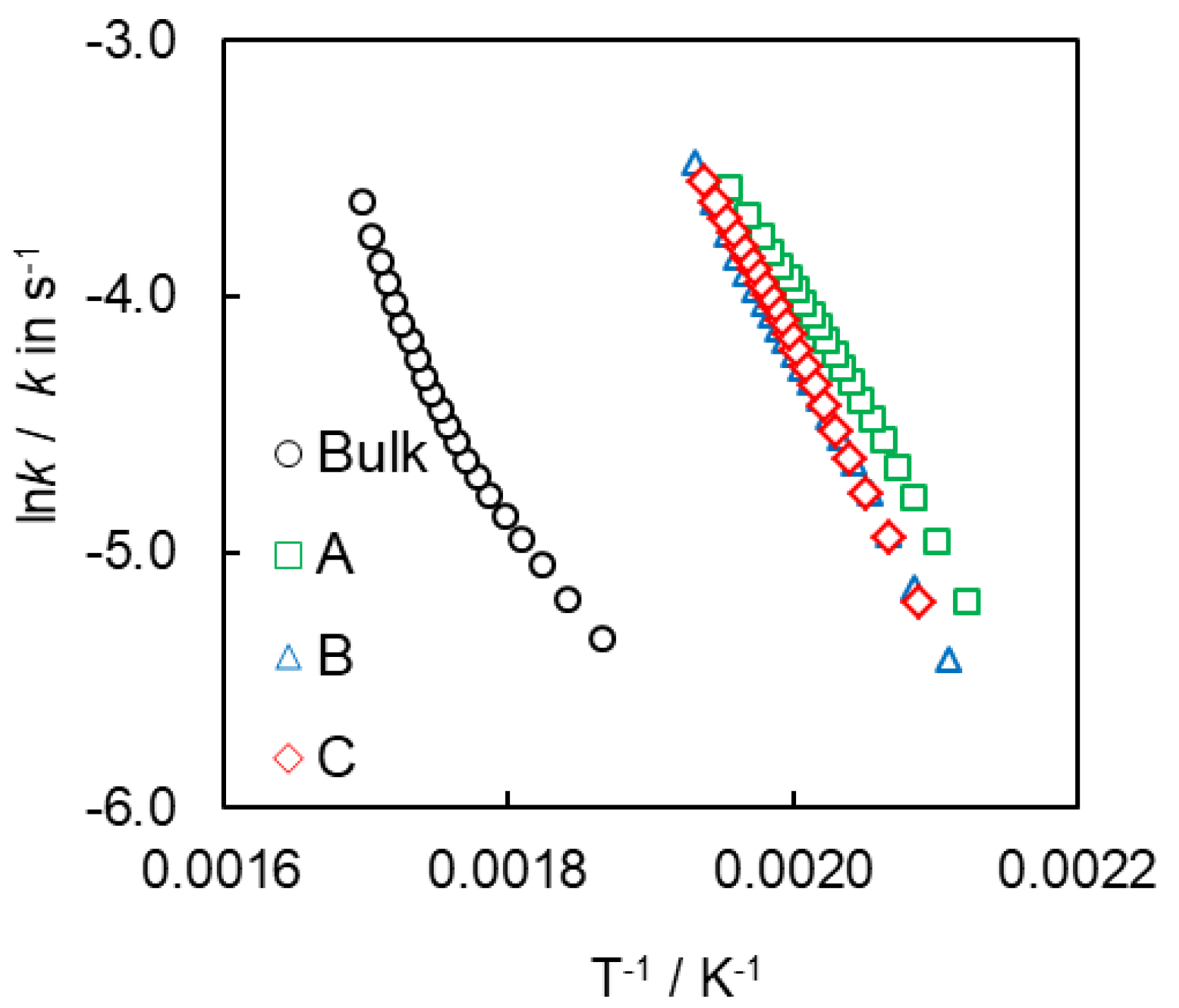
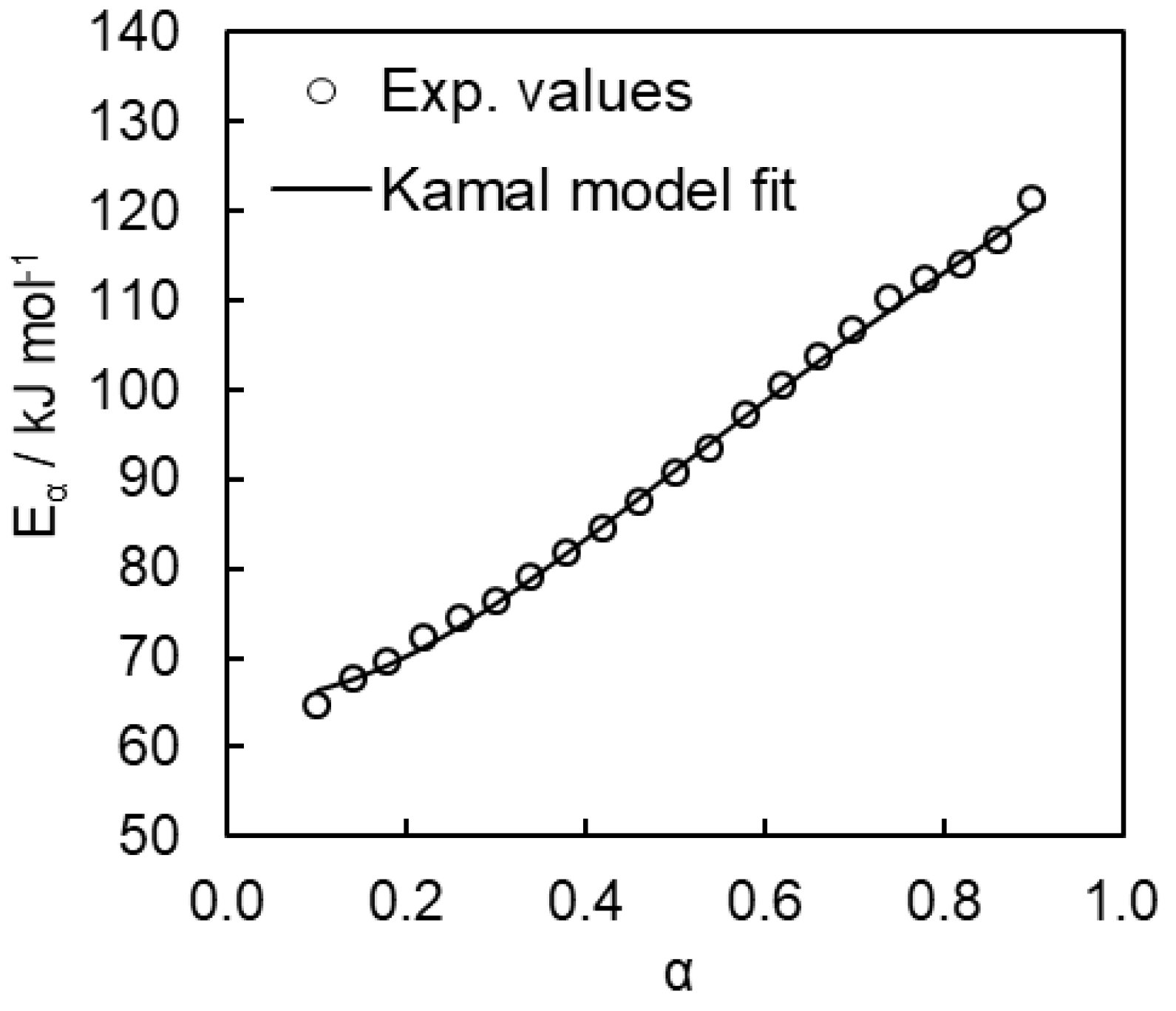
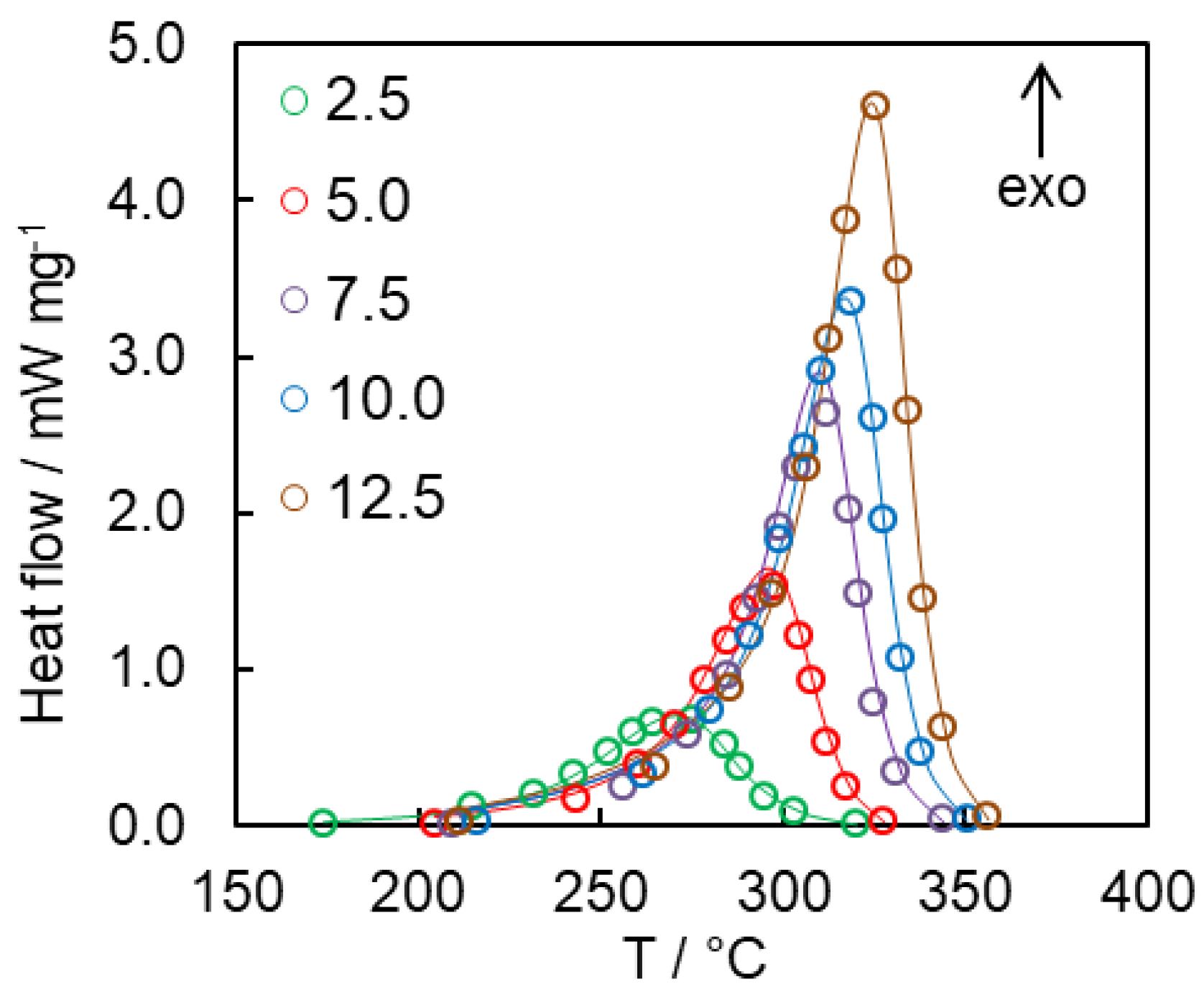
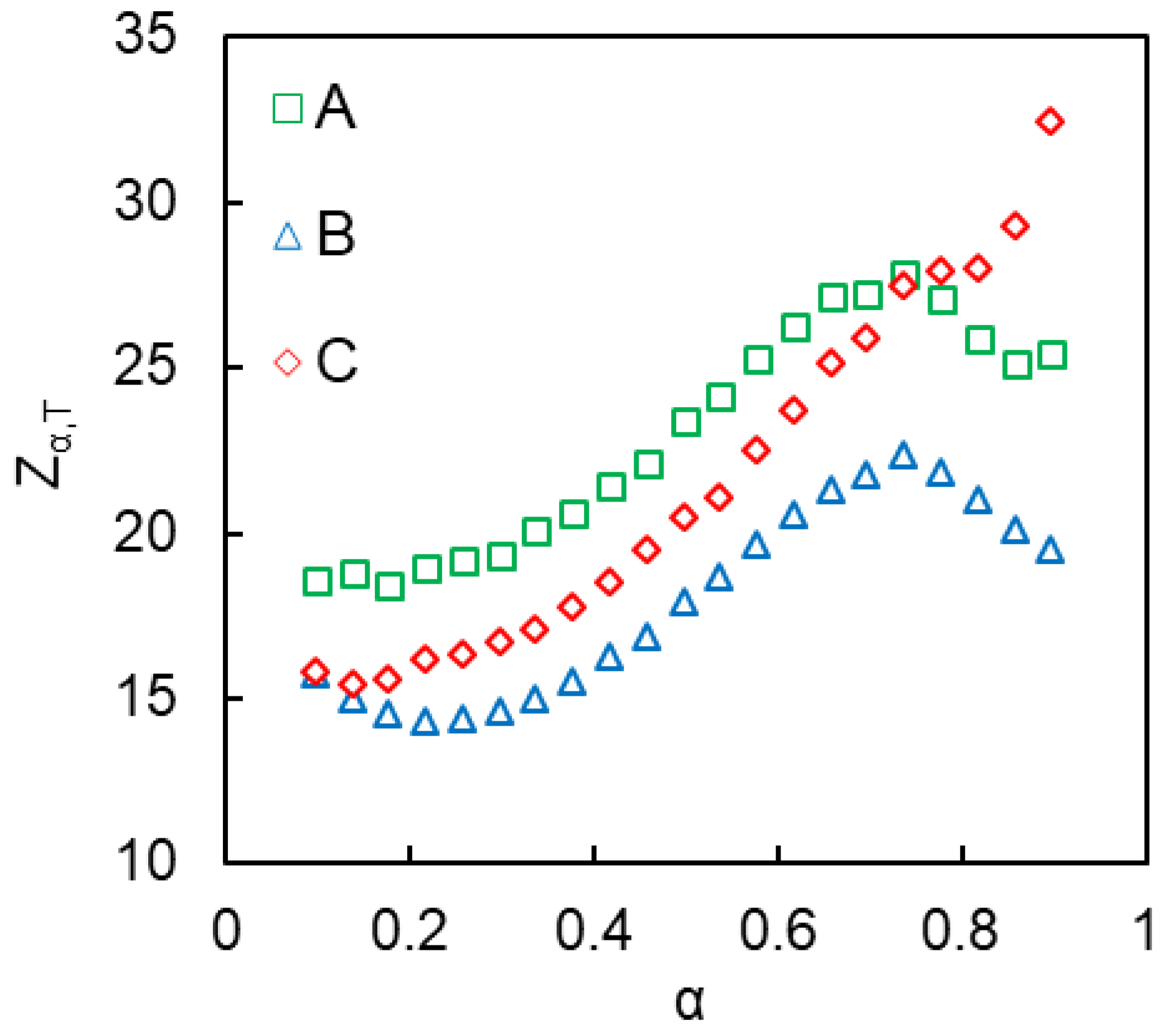
4.2. Kinetics of Polymerization Studied by DSC
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ania, C.O.; Gomis-Berenguer, A.; Dentzer, J.; Vix-Guterl, C. Nanoconfinement of glucose oxidase on mesoporous carbon electrodes with tunable pore sizes. J. Electroanal. Chem. 2018, 808, 372–379. [Google Scholar] [CrossRef]
- Yancey, B.; Vyazovkin, S. The kinetics and mechanism of nanoconfined molten salt reactions: Trimerization of potassium and rubidium dicyanamide. Phys. Chem. Chem. Phys. 2015, 17, 10209–10217. [Google Scholar] [CrossRef]
- Yancey, B.; Vyazovkin, S. Venturing into kinetics and mechanism of nanoconfined solid-state reactions: Trimerization of sodium dicyanamide in nanopores. Phys. Chem. Chem. Phys. 2014, 16, 11409–11416. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Susner, M.A.; Vyazovkin, S. Effect of the Brush Structure on the Degradation Mechanism of Polystyrene–Clay Nanocomposites. Macromol. Rapid Commun. 2005, 26, 690–695. [Google Scholar] [CrossRef]
- Wang, J.; Kenseth, J.R.; Jones, V.W.; Green, J.-B.D.; McDermott, M.T.; Porter, M.D. SFM Tip-Assisted Hydrolysis of a Dithiobis(succinimido undecanoate) Monolayer Chemisorbed on a Au(111) Surface. J. Am. Chem. Soc. 1997, 119, 12796–12799. [Google Scholar] [CrossRef]
- Sullivan, T.P.; Huck, W.T.S. Reactions on Monolayers: Organic Synthesis in Two Dimensions. Eur. J. Org. Chem. 2003, 2003, 17–29. [Google Scholar] [CrossRef]
- Chechik, V.; Stirling, C.J.M. Reactivity in Self-Assembled Monolayers: Effect of the Distance from the Reaction Center to the Monolayer−Solution Interface. Langmuir 1998, 14, 99–105. [Google Scholar] [CrossRef]
- Chechik, V.; Crooks, R.M.; Stirling, C.J.M. Reactions and Reactivity in Self-Assembled Monolayers. Adv. Mater. 2000, 12, 1161–1171. [Google Scholar] [CrossRef]
- Küchler, A.; Yoshimoto, M.; Luginbühl, S.; Mavelli, F.; Walde, P. Enzymatic reactions in confined environments. Nat. Nanotechnol. 2016, 11, 409–420. [Google Scholar] [CrossRef]
- Huck, W.T.S. Effects of nanoconfinement on the morphology and reactivity of organic materials. Chem. Commun. 2005, 4143–4148. [Google Scholar] [CrossRef]
- Sanz, B.; Ballard, N.; Asua, J.M.; Mijangos, C. Effect of Confinement on the Synthesis of PMMA in AAO Templates and Modeling of Free Radical Polymerization. Macromolecules 2017, 50, 811–821. [Google Scholar] [CrossRef]
- Ng, S.M.; Ogino, S.-I.; Aida, T.; Koyano, K.A.; Tatsumi, T. Free radical polymerization within mesoporous zeolite channels. Macromol. Rapid Commun. 1997, 18, 991–996. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Yu, Z.N.; Begum, F.; Hedden, R.C.; Simon, S.L. The effect of nanoconfinement on methyl methacrylate polymerization: Tg, molecular weight, and tacticity. Polymer 2014, 55, 4959–4965. [Google Scholar] [CrossRef]
- Guan, Y.; Liu, G.; Gao, P.; Li, L.; Ding, G.; Wang, D. Manipulating Crystal Orientation of Poly(ethylene oxide) by Nanopores. ACS Macro Lett. 2013, 2, 181–184. [Google Scholar] [CrossRef]
- Serghei, A.; Zhao, W.; Miranda, D.; Russell, T.P. Curie Transitions for Attograms of Ferroelectric Polymers. Nano Lett. 2013, 13, 577–580. [Google Scholar] [CrossRef]
- Suzuki, Y.; Duran, H.; Steinhart, M.; Butt, H.-J.; Floudas, G. Homogeneous crystallization and local dynamics of poly(ethylene oxide) (PEO) confined to nanoporous alumina. Soft Matter 2013, 9, 2621–2628. [Google Scholar] [CrossRef]
- Uemura, T.; Ono, Y.; Kitagawa, K.; Kitagawa, S. Radical Polymerization of Vinyl Monomers in Porous Coordination Polymers: Nanochannel Size Effects on Reactivity, Molecular Weight, and Stereostructure. Macromolecules 2008, 41, 87–94. [Google Scholar] [CrossRef]
- Uemura, T.; Ono, Y.; Hijikata, Y.; Kitagawa, S. Functionalization of Coordination Nanochannels for Controlling Tacticity in Radical Vinyl Polymerization. J. Am. Chem. Soc. 2010, 132, 4917–4924. [Google Scholar] [CrossRef]
- Moller, K.; Bein, T.; Fischer, R.X. Entrapment of PMMA Polymer Strands in Micro- and Mesoporous Materials. Chem. Mater. 1998, 10, 1841–1852. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, Y.; Priestley, R.D. Glass Transition Temperature of Polymer Nanoparticles under Soft and Hard Confinement. Macromolecules 2011, 44, 4001–4006. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Dranca, I.; Fan, X.; Advincula, R. Degradation and Relaxation Kinetics of Polystyrene−Clay Nanocomposite Prepared by Surface Initiated Polymerization. J. Phys. Chem. B 2004, 108, 11672–11679. [Google Scholar] [CrossRef]
- Salsamendi, M.; Ballard, N.; Sanz, B.; Asua, J.M.; Mijangos, C. Polymerization kinetics of a fluorinated monomer under confinement in AAO nanocavities. RSC Adv. 2015, 5, 19220–19228. [Google Scholar] [CrossRef]
- Li; Simon, S.L. Curing of Bisphenol M Dicyanate Ester under Nanoscale Constraint. Macromolecules 2008, 41, 1310–1317. [Google Scholar] [CrossRef]
- Li, Q.; Simon, S.L. Surface Chemistry Effects on the Reactivity and Properties of Nanoconfined Bisphenol M Dicyanate Ester in Controlled Pore Glass. Macromolecules 2009, 42, 3573–3579. [Google Scholar] [CrossRef]
- Koh, Y.P.; Simon, S.L. Trimerization of Monocyanate Ester in Nanopores. J. Phys. Chem. B 2010, 114, 7727–7734. [Google Scholar] [CrossRef]
- Koh, Y.P.; Simon, S.L. Kinetic Study of Trimerization of Monocyanate Ester in Nanopores. J. Phys. Chem. B 2011, 115, 925–932. [Google Scholar] [CrossRef]
- Koh, Y.P.; Simon, S.L. Crystallization and Vitrification of a Cyanurate Trimer in Nanopores. J. Phys. Chem. B 2012, 116, 7754–7761. [Google Scholar] [CrossRef]
- Lopez, E.; Simon, S.L. Trimerization Reaction Kinetics and Tg Depression of Polycyanurate under Nanoconfinement. Macromolecules 2015, 48, 4692–4701. [Google Scholar] [CrossRef]
- Liang, K.; Li, G.; Toghiani, H.; Koo, J.H.; Pittman, C.U. Cyanate Ester/Polyhedral Oligomeric Silsesquioxane (POSS) Nanocomposites: Synthesis and Characterization. Chem. Mater. 2006, 18, 301–312. [Google Scholar] [CrossRef]
- Sheng, X.; Akinc, M.; Kessler, M.R. The effects of alumina and silica nanoparticles on the cure kinetics of bisphenol E cyanate ester. Polym. Eng. Sci. 2010, 50, 1075–1084. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer International Publishing: Basel, Switzerland, 2015; p. 239. [Google Scholar] [CrossRef]
- Galukhin, A.; Liavitskaya, T.; Vyazovkin, S. Kinetic and Mechanistic Insights into Thermally Initiated Polymerization of Cyanate Esters with Different Bridging Groups. Macromol. Chem. Phys. 2019, 220, 1900141. [Google Scholar] [CrossRef]
- Galukhin, A.; Nikolaev, I.; Nosov, R.; Vyazovkin, S. Solid-state polymerization of a novel cyanate ester based on 4-tert-butylcalix[6]arene. Polym. Chem. 2020, 11, 4115–4123. [Google Scholar] [CrossRef]
- Matthias, T.; Katsumi, K.; Alexander, V.N.; James, P.O.; Francisco, R.-R.; Jean, R.; Kenneth, S.W.S. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Giesche, H. Synthesis of monodispersed silica powders II. Controlled growth reaction and continuous production process. J. Eur. Ceram. Soc. 1994, 14, 205–214. [Google Scholar] [CrossRef]
- Galukhin, A.; Bolmatenkov, D.; Emelianova, A.; Zharov, I.; Gor, G.Y. Porous Structure of Silica Colloidal Crystals. Langmuir 2019, 35, 2230–2235. [Google Scholar] [CrossRef] [PubMed]
- Wong, S.; Kitaev, V.; Ozin, G.A. Colloidal Crystal Films: Advances in Universality and Perfection. J. Am. Chem. Soc. 2003, 125, 15589–15598. [Google Scholar] [CrossRef] [PubMed]
- Bohaty, A.K.; Smith, J.J.; Zharov, I. Free-Standing Silica Colloidal Nanoporous Membranes. Langmuir 2009, 25, 3096–3101. [Google Scholar] [CrossRef] [PubMed]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Wight, C.A. Estimating Realistic Confidence Intervals for the Activation Energy Determined from Thermoanalytical Measurements. Anal. Chem. 2000, 72, 3171–3175. [Google Scholar] [CrossRef]
- Fang, T.; Shimp, D.A. Polycyanate esters: Science and applications. Prog. Polym. Sci. 1995, 20, 61–118. [Google Scholar] [CrossRef]
- Kamal, M.R. Thermoset characterization for moldability analysis. Polym. Eng. Sci. 1974, 14, 231–239. [Google Scholar] [CrossRef]
- Chen, C.-C.; Don, T.-M.; Lin, T.-H.; Cheng, L.-P. A kinetic study on the autocatalytic cure reaction of a cyanate ester resin. J. Appl. Polym. Sci. 2004, 92, 3067–3079. [Google Scholar] [CrossRef]
- Liavitskaya, T.; Birx, L.; Vyazovkin, S. Thermal Stability of Malonic Acid Dissolved in Poly(vinylpyrrolidone) and Other Polymeric Matrices. Ind. Eng. Chem. Res. 2018, 57, 5228–5233. [Google Scholar] [CrossRef]
- Maximov, M.A.; Galukhin, A.V.; Gor, G.Y. Pore-Size Distribution of Silica Colloidal Crystals from Nitrogen Adsorption Isotherms. Langmuir 2019, 35, 14975–14982. [Google Scholar] [CrossRef]
- Zhuravlev, L.T. The surface chemistry of amorphous silica. Zhuravlev model. Colloids Surf. A 2000, 173, 1–38. [Google Scholar] [CrossRef]
- Smith, J.J.; Zharov, I. Ion Transport in Sulfonated Nanoporous Opal Films. In Nanoparticles: Synthesis, Stabilization, Passivation, and Functionalization; American Chemical Society: Washington, DC, USA, 2008; Volume 996, pp. 248–255. [Google Scholar]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Grenier-Loustalot, M.-F.; Lartigau, C.; Metras, F.; Grenier, P. Mechanism of thermal polymerization of cyanate ester systems: Chromatographic and spectroscopic studies. J. Polym. Sci. Part A Polym. Chem. 1996, 34, 2955–2966. [Google Scholar] [CrossRef]
- Lin, R.H.; Su, A.C.; Hong, J.L. Kinetics of polycyclotrimerization of aromatic dicyanates. J. Polym. Res. 1997, 4, 191–202. [Google Scholar] [CrossRef]
- Simon, S.L.; Gillham, J.K. Cure kinetics of a thermosetting liquid dicyanate ester monomer/high-Tg polycyanurate material. J. Appl. Polym. Sci. 1993, 47, 461–485. [Google Scholar] [CrossRef]
- Vyazovkin, S. A time to search: Finding the meaning of variable activation energy. Phys. Chem. Chem. Phys. 2016, 18, 18643–18656. [Google Scholar] [CrossRef] [PubMed]
- Alzina, C.; Sbirrazzuoli, N.; Mija, A. Hybrid Nanocomposites: Advanced Nonlinear Method for Calculating Key Kinetic Parameters of Complex Cure Kinetics. J. Phys. Chem. B 2010, 114, 12480–12487. [Google Scholar] [CrossRef] [PubMed]
- Sheng, X.; Akinc, M.; Kessler, M.R. Cure kinetics of thermosetting bisphenol E cyanate ester. J. Therm. Anal. Calorim. 2008, 93, 77–85. [Google Scholar] [CrossRef]
- Bonetskaya, A.K.; Ivanov, V.V.; Kravchenko, M.A.; Pankratov, V.A.; Frenkel, T.M.; Korshak, V.V.; Vinogradova, S.V. Polycyclotrimerization of aryldicyanates in the presence of Cr3+ acetylacetonate. Polym. Sci. U.S.S.R. 1980, 22, 845–862. [Google Scholar] [CrossRef]
- Bauer, M.; Bauer, J.; Kühn, G. Kinetics and modelling of thermal polycyclotrimerization of aromatic dicyanates. Acta Polym. 1986, 37, 715–719. [Google Scholar] [CrossRef]
- Gómez, C.M.; Recalde, I.B.; Mondragon, I. Kinetic parameters of a cyanate ester resin catalyzed with different proportions of nonylphenol and cobalt acetylacetonate catalyst. Eur. Polym. J. 2005, 41, 2734–2741. [Google Scholar] [CrossRef]







| SBET, m2 g−1 | Pore Volume, cm3 g−1 | CBET | |
|---|---|---|---|
| A | 34 ± 1 | 0.26 ± 0.01 | 103 ± 15 |
| B | 33 ± 1 | 0.26 ± 0.01 | 182 ± 53 |
| C | 34 ± 1 | 0.25 ± 0.01 | 135 ± 33 |
| E1/kJ mol−1 | logA1/A in s−1 | E2/kJ mol−1 | logA2/A in s−1 | m | n | |
|---|---|---|---|---|---|---|
| Bulk | 65 ± 1 | 3.1 ± 0.1 | 154 ± 3 | 12.0 ± 0.1 | 0.9 ± 0.3 | 1.2 ± 0.1 |
| A | - | - | 79 ± 6 | 6.6 ± 0.1 | 1.0 ± 0.1 | 1.4 ± 0.1 |
| B | - | - | 83 ± 6 | 6.9 ± 0.1 | 1.0 ± 0.1 | 1.4 ± 0.1 |
| C | - | - | 90 ± 4 | 7.5 ± 0.1 | 0.9 ± 0.1 | 1.1 ± 0.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galukhin, A.; Taimova, G.; Nosov, R.; Liavitskaya, T.; Vyazovkin, S. Polymerization Kinetics of Cyanate Ester Confined to Hydrophilic Nanopores of Silica Colloidal Crystals with Different Surface-Grafted Groups. Polymers 2020, 12, 2329. https://doi.org/10.3390/polym12102329
Galukhin A, Taimova G, Nosov R, Liavitskaya T, Vyazovkin S. Polymerization Kinetics of Cyanate Ester Confined to Hydrophilic Nanopores of Silica Colloidal Crystals with Different Surface-Grafted Groups. Polymers. 2020; 12(10):2329. https://doi.org/10.3390/polym12102329
Chicago/Turabian StyleGalukhin, Andrey, Guzel Taimova, Roman Nosov, Tatsiana Liavitskaya, and Sergey Vyazovkin. 2020. "Polymerization Kinetics of Cyanate Ester Confined to Hydrophilic Nanopores of Silica Colloidal Crystals with Different Surface-Grafted Groups" Polymers 12, no. 10: 2329. https://doi.org/10.3390/polym12102329
APA StyleGalukhin, A., Taimova, G., Nosov, R., Liavitskaya, T., & Vyazovkin, S. (2020). Polymerization Kinetics of Cyanate Ester Confined to Hydrophilic Nanopores of Silica Colloidal Crystals with Different Surface-Grafted Groups. Polymers, 12(10), 2329. https://doi.org/10.3390/polym12102329