Aberration-Based Quality Metrics in Holographic Lenses
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Composition
2.2. Holographic Process
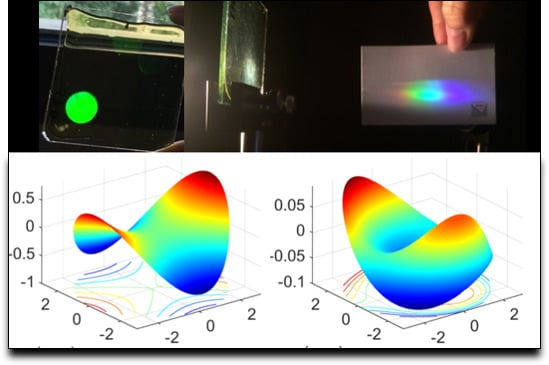
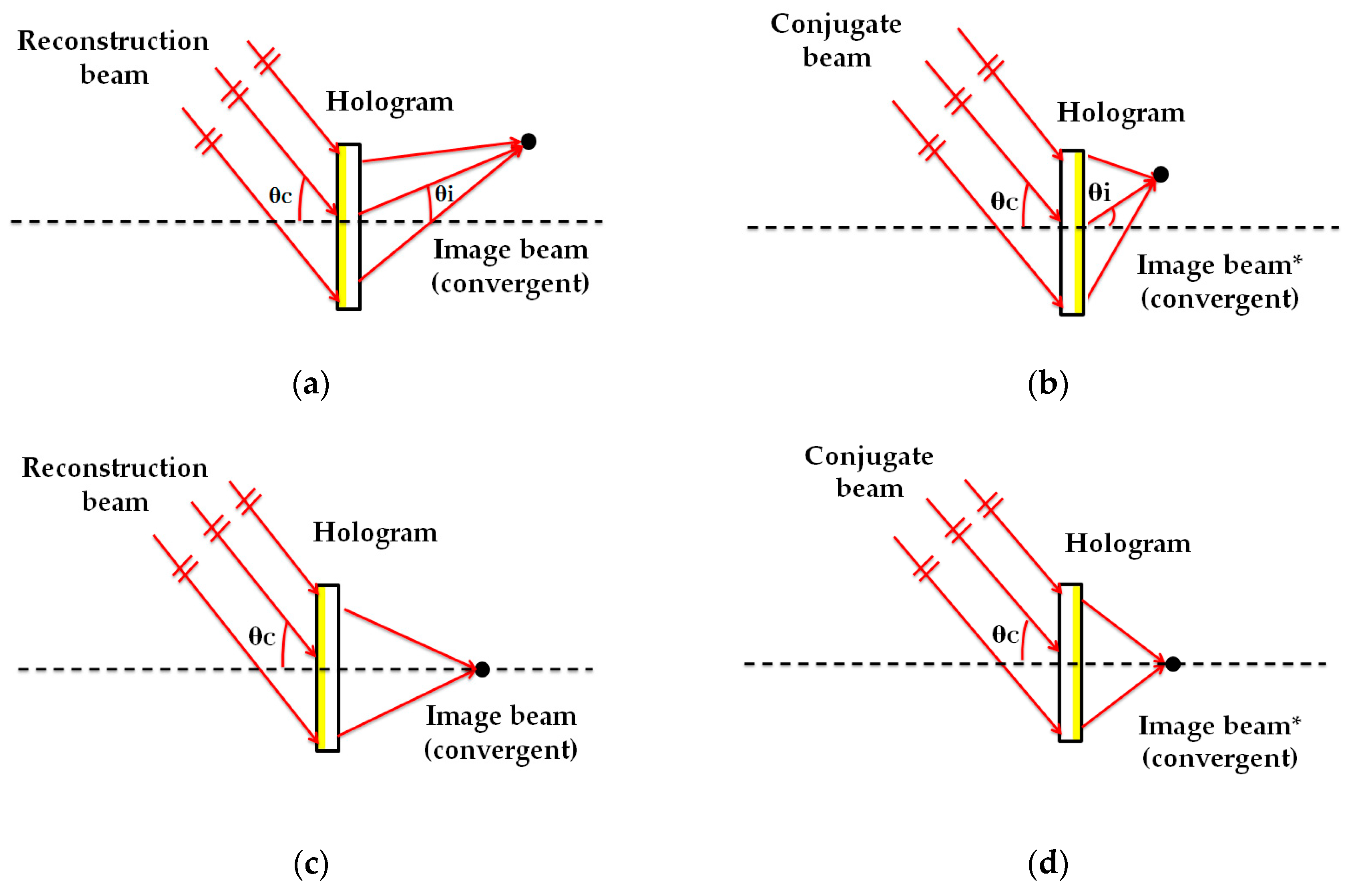
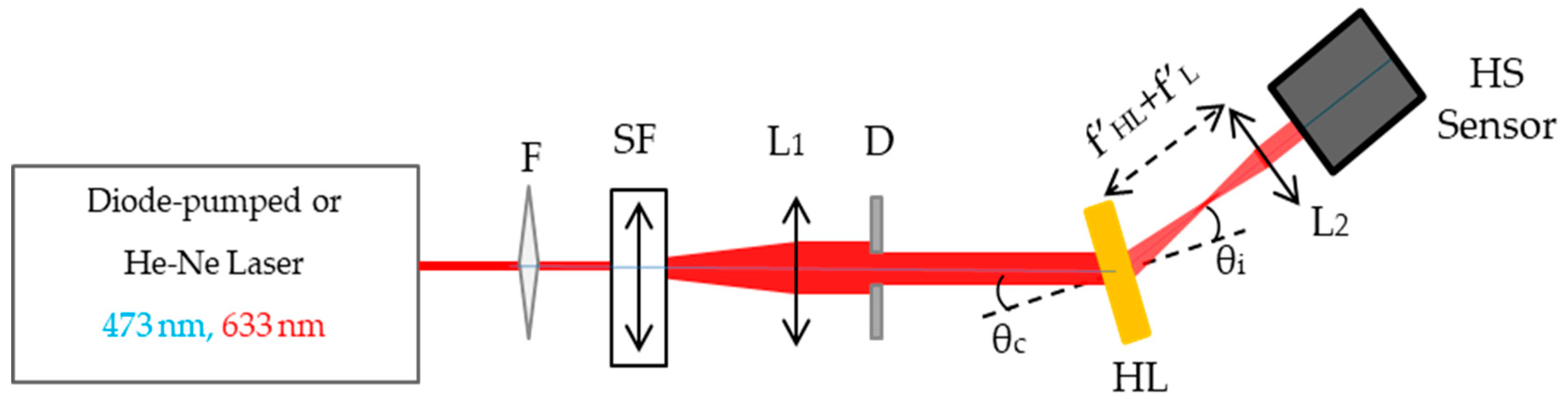
2.3. Evaluation of the Aberrated Wavefront of HLs
2.4. Optical Quality Metrics Based on Aberrations
2.4.1. Wave Aberration Function
2.4.2. Seidel Coefficients (Theoretical and Experimental)
2.4.3. Marechal Tolerances
2.4.4. Root Mean Square
2.4.5. Critical Pupil Fraction
2.4.6. Peak to Valley
2.5. Image Quality Based on Impulse Response
2.5.1. Strehl Ratio
2.5.2. Entropy
2.6. Image Quality Based on the Fourier Domain
2.6.1. Cutoff Frequency
2.6.2. Modulation Transfer Function (MTF) and Area under the MTF
3. Results and Discussion
3.1. Wavefront Aberration
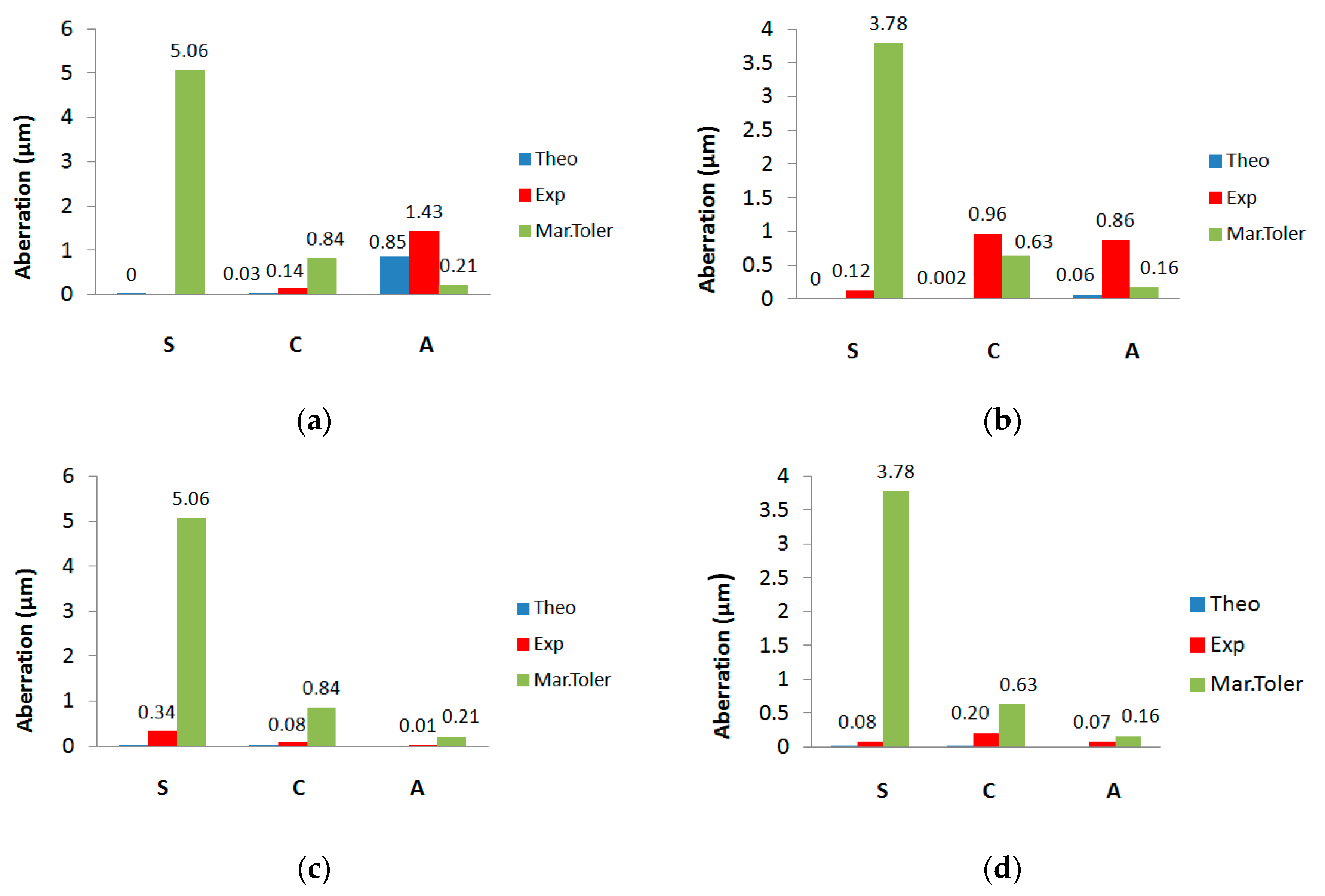
3.2. Seidel Coefficients and Marechal Tolerances
3.3. Optical Quality Metrics Based on Aberrations
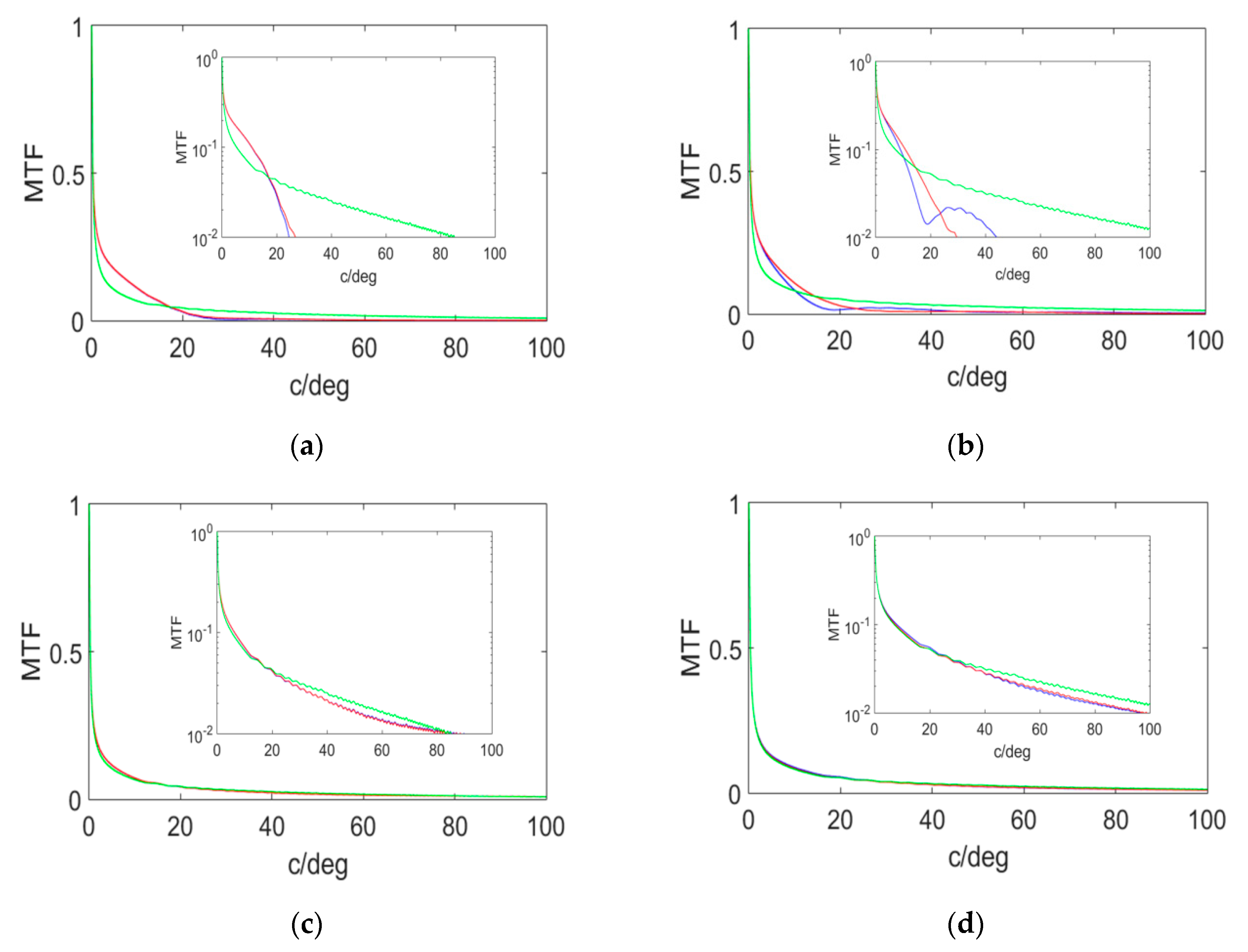
3.4. Image Quality Based on Impulse Response and Fourier Domain
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hariharan, P. Basics of Holography; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Barachevsky, V.A. The Current Status of the Development of Light-Sensitive Media for Holography (a Review). Opt. Spectroc. 2018, 124, 373–407. [Google Scholar] [CrossRef]
- Schwar, M.J.R.; Pandya, T.P.; Weinberg, F.J. Point holograms as optical elements. Nature 1967, 215, 239–241. [Google Scholar] [CrossRef]
- Store, T.W.; Thompson, B.J. Holographic and diffractive lenses and mirrors. SPIE Milestore Ser. 1991, 34, 3–668. [Google Scholar]
- Kostuk, R.K. Holography Principles and Applications; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Fernández, E.; Ortuño, M.; Gallego, S.; García, C.; Beléndez, A.; Pascual, I. Comparison of peristrophic multiplexing and a combination of angular and peristrophic holographic multiplexing in a thick PVA/acrylamide photopolymer for data storage. Appl. Opt. 2007, 46, 5368–5373. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Fuster, V.; Ortuño, M.; Fernández, R.; Gallego, S.; Marquez, A.; Beléndez, A.; Pascual, I. Peristrophic multiplexed holograms recorded in a low toxicity photopolymer. Opt. Mater. Express 2017, 7, 133–147. [Google Scholar] [CrossRef]
- Piao, M.L.; Kim, N.; Park, J.H. Phase contrast projection display using photopolymer. J. Opt. Soc. Korea 2008, 12, 319–325. [Google Scholar] [CrossRef][Green Version]
- Lee, K.Y.; Jeung, S.H.; Cho, B.M.; Kim, N. Photopolymer-based surface-normal input/output volume holographic grating coupler for 1550-nm optical wavelength. J. Opt. Soc. Korea 2012, 16, 17–21. [Google Scholar] [CrossRef][Green Version]
- Fernández, E.; Márquez, A.; Gallego, S.; Fuentes, R.; García, C.; Pascual, I. Hybrid ternary modulation applied to multiplexing holograms in photopolymers for data page storage. J. Light. Technol. 2010, 28, 776–783. [Google Scholar] [CrossRef]
- Gunter, P.; Huignard, J.P. Photorefractive Materials and Their Applications 3; Buse, K., Havermeyer, F., Liu, W., Moser, C., Psaltis, D., Eds.; Springer: New York, NY, USA, 2007; pp. 295–317. [Google Scholar]
- Stevenson, S.H.; Armstrong, M.L.; O’Connor, P.J.; Tipton, D.F. Advances in Photopolymer Films for Display Holography. In Proceedings of the SPIE Display Holography: Fifth International Symposium, Lake Forest, IL, USA, 18–22 July 1994; pp. 60–70. [Google Scholar]
- Yeom, H.-J.; Kim, H.-J.; Kim, S.-B.; Zhang, H.; Li, B.; Ji, Y.-M.; Kim, S.-H.; Park, J.-H. 3D holographic head mounted display using holographic optical elements with astigmatism aberration compensation. Opt. Express 2015, 23, 32025–32034. [Google Scholar] [CrossRef]
- Chen, Z.; Sang, X.; Lin, Q.; Li, J.; Yu, X.; Gao, X.; Yan, B.; Wang, K.; Yu, C.; Xie, S. A see-through holographic head-mounted display with the large viewing angle. Opt. Commun. 2017, 384, 125–129. [Google Scholar] [CrossRef]
- Kim, N.; Piao, Y.-L.; Wu, H.-Y. Holographic Material and Optical Systems. In Holographic Optical Elements and Applications; Naydenova, I., Nazarova, D., Babeva, T., Eds.; InTech: Rijeka, Croatia, 2017; pp. 99–131. [Google Scholar]
- Lee, S.; Lee, B.; Cho, J.; Jang, C.; Kim, J.; Lee, B. Analysis and Implementation of Hologram Lenses for See-Through Head-Mounted Display. IEEE Photonics Technol. Lett. 2017, 29, 82–85. [Google Scholar] [CrossRef]
- Lin, W.-K.; Matoba, O.; Lin, B.-S.; Su, W.-C. Astigmatism and deformation correction for a holographic head-mounted display with a wedge-shaped holographic waveguide. Appl. Opt. 2018, 57, 7094–7101. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Nirala, A.K. Design and fabrication of different types of holographic lenses, with analysis of their imagery and aberration. Meas. Sci. Technol. 2017, 28, 125402–125427. [Google Scholar] [CrossRef]
- Meier, R.W. Magnification and third-order aberrations in holography. J. Opt. Soc. Am. 1965, 55, 987–992. [Google Scholar] [CrossRef]
- Latta, J.N. Computer-Based Analysis of Hologram Imagery and Aberrations II: Aberrations Induced by a Wavelength Shift. Appl. Opt. 1971, 10, 609–618. [Google Scholar] [CrossRef] [PubMed]
- Dubik, B.; Masajada, J.; Nowak, J.; Zajac, M. Aberrations of holographic lenses in image quality evaluation. Opt. Eng. 1992, 31, 478–490. [Google Scholar] [CrossRef]
- Tripathy, S.K.; Rao, S.A. Expressions for third-order aberration theory for holographic images. Pramana J Phys. 2003, 60, 151–157. [Google Scholar] [CrossRef]
- García, C.; Rodriguez, J.D.; Fernandez, E.; Camps, V.; Fuentes, R.; Pascual, I. Holographic lens recorded on photopolymers: Fabrication and study of the image quality. J. Mod. Opt. 2009, 56, 1288–1295. [Google Scholar] [CrossRef]
- Lloret, T.; Navarro-Fuster, V.; Ramírez, M.G.; Ortuño, M.; Neipp, C.; Beléndez, A.; Pascual, I. Holographic Lenses in an Environment-Friendly Photopolymer. Polymers 2018, 10, 302. [Google Scholar] [CrossRef]
- Cheng, J. The principles of Astronomical Telescope Design; Springer: New York, NY, USA, 2009. [Google Scholar]
- Prieto, P.M.; Vargas-Martín, F.; Goelz, S.; Artal, P. Analysis of the performance of the Hartmann-Shack sensor of the human eye. J. Opt. Soc. Am. A 2000, 17, 1388–1398. [Google Scholar] [CrossRef]
- Mompeán, J.; Aragón, J.L.; Prieto, P.M.; Artal, P. GPU-based processing of Hartmann-Shack images for accurate and high-speed ocular wavefront sensing. Future Gener. Comput. Syst. 2019, 91, 177–190. [Google Scholar] [CrossRef]
- Platt, B.C.; Shack, R. History and principles of Hartmann-Shack wavefront sensing. J. Refract. Surg. 2001, 17, S573–S577. [Google Scholar] [CrossRef] [PubMed]
- Gong, H.; Soloviev, O.; Wilding, D.; Pozzi, P.; Verhaegen, M.; Vdovin, G. Holographic imaging with a Shack-Hartmann wavefront sensor. Opt. Express 2016, 24, 13729–13737. [Google Scholar] [CrossRef] [PubMed]
- Kubota, T.; Ose, T. Lippmann color holograms recorded in methylene-blue sensitized dichromated gelatin. Opt. Lett. 1979, 1, 8–9. [Google Scholar] [CrossRef] [PubMed]
- Oliva, J.; Boj, P.G.; Pardo, M. Dichromated gelatin holograms derivated from agfa 8E75 HD plates. Appl. Opt. 1984, 23, 196–197. [Google Scholar] [CrossRef]
- Beléndez, A.; Neipp, C.; Flores, M.; Pascual, I. High-efficiency silver-halide sensitized gelatin holograms with low absorption and scatter. J. Mod. Opt. 1998, 45, 1985–1992. [Google Scholar] [CrossRef][Green Version]
- Kim, J.M.; Choi, B.S.; Choi, Y.S.; Kim, J.M.; Bjelkhagen, H.I.; Phillips, N.J. Holographic optical elements recorded in silver halide sensitized gelatin emulsions Part 2 Reflection holographic optical elements. Appl. Opt. 2002, 41, 1522. [Google Scholar] [CrossRef]
- Berneth, H.; Bruder, F.K.; Fäcke, T.; Hagon, T.; Hönel, D.; Jurbergs, D.; Rölle, T.; Weiser, M.S. Holographic Recording Aspects of High Resolution Bayfol HX Photopolymer. In Proceedings of the SPIE OPTO, San Francisco, CA, USA, 22–27 January 2011. [Google Scholar]
- Kozma, A. Effects of film-grain noise in holography. J. Opt. Soc. Am. 1968, 58, 436–438. [Google Scholar] [CrossRef]
- Close, D.H.; Jacobson, A.D.; Margerum, J.D.; Brault, R.G.; McClung, F.J. Hologram recording on photopolymer materials. Appl. Phys. Lett. 1969, 14, 159–160. [Google Scholar] [CrossRef]
- Guo, J.; Gleeson, M.R.; Sheridan, J.T. A review of the optimisation of photopolymer materials for holographic data storage. Phys. Res. Int. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Bianco, G.; Ferrara, M.A.; Borbone, F.; Roviello, A.; Striano, V.; Coppola, G. Photopolymer-based volume holographic optical elements: Design and possible applications. J. Eur. Opt. Soc. Rapid Publ. 2015, 10, 15057–15060. [Google Scholar] [CrossRef]
- Malallah, R.; Li, H.; Kelly, D.P.; Healy, J.J.; Sheridan, J.T. A review of hologram storage and self-written waveguides formation in photopolymer media. Polymers 2017, 9, 337. [Google Scholar] [CrossRef] [PubMed]
- Gallego, S.; Ortuño, M.; Neipp, C.; Márquez, A.; Beléndez, A.; Pascual, I. Characterization of polyvinyl alcohol/acrylamide holographic memories with a first-harmonic diffusion model. Appl. Opt. 2005, 44, 6205–6210. [Google Scholar] [CrossRef] [PubMed]
- Gallego, S.; Márquez, A.; Méndez, D.; Neipp, C.; Ortuño, M.; Beléndez, A.; Fernández, E.; Pascual, I. Direct analysis of monomer diffusion times in polyvinyl/acrylamide materials. Appl. Phys. Lett. 2008, 92, 73306. [Google Scholar] [CrossRef]
- Weiss, V.; Millul, E.; Friesem, A.A. Photopolymeric holographic recording media: In-situ and real-time characterization. In Proceedings of the SPIE PHOTONICS WEST ’96, San Jose, CA, USA, 27 January–2 February 1996; Volume 2688, pp. 11–21. [Google Scholar]
- Zhu, J.; Wang, G.; Hao, Y.; Xie, B.; Cheng, A.Y.S. Highly sensitive and spatially resolved polyvinyl alcohol/acrylamide photopolymer for real-time holographic applications. Opt. Express 2010, 18, 18106–18112. [Google Scholar] [CrossRef]
- Olivares-Perez, A.; Fuentes-Tapia, I.F.; Hernández-Garay, M.P.; Ibarra-Torres, C.J. Holograms in polyvinyl alcohol photosensitized with CuCl2(2H2O). Opt. Eng. 2011, 50, 65801–65807. [Google Scholar]
- Cody, D.; Naydenova, I.; Mihaylova, E. New non-toxic holographic photopolymer material. J. Opt. 2012, 14, 15601. [Google Scholar] [CrossRef]
- Cody, D.; Gribbin, S.; Mihaylova, E.; Naydenova, I. Low-Toxicity Photopolymer for Reflection Holography. ACS Appl. Mater. Interfaces 2016, 8, 18481–18487. [Google Scholar] [CrossRef]
- Alim, M.D.; Glugla, D.J.; Mavila, S.; Wang, C.; Nystrom, P.D.; Sullivan, A.C.; McLeod, R.R.; Bowman, C.N. High Dynamic Range (Dn) Two-Stage Photopolymers via Enhanced Solubility of a High Refractive Index AcrylateWriting Monomer. ACS Appl. Mater. Interfaces 2018, 10, 1217–1224. [Google Scholar] [CrossRef]
- Peng, H.; Nair, D.P.; Kowalski, B.A.; Xi, W.; Gong, T.; Wang, C.; Cole, M.; Cramer, N.B.; Xie, X.; McLeod, R.R.; et al. High performance graded rainbow holograms via two-stage sequential orthogonal thiol-click chemistry. Macromolecules 2014, 47, 2306–2315. [Google Scholar] [CrossRef]
- Ortuño, M.; Gallego, S.; Márquez, A.; Neipp, C.; Pascual, I.; Beléndez, A. Biophotopol: A Sustainable Photopolymer for Holographic Data Storage Applications. Materials 2012, 5, 772–783. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Fuster, V.; Ortuño, M.; Gallego, S.; Márquez, A.; Beléndez, A.; Pascual, I. Biophotopol’s energetic sensitivity improved in 300 μm layers by tuning the recording wavelength. Opt. Mater. 2016, 52, 111–115. [Google Scholar] [CrossRef]
- Ortuño, M.; Fernández, E.; Gallego, S.; Beléndez, A.; Pascual, I. New photopolymer holographic recording material with sustainable design. Opt. Express 2007, 15, 12425–12435. [Google Scholar] [CrossRef] [PubMed]
- Guirao, A. Optics and Visual Metrics. In Handbook of Visual Optics; Artal, P., Ed.; CRC Press: London, UK, 2017; Volume II, pp. 276–297. ISBN 9781482237924. [Google Scholar]
- Smith, W.J. Modern Optical Engineering; McGraw Hill Professional: New York, NY, USA, 2000; ISBN 0071363602. [Google Scholar]
- Michael, K. Giles, Aberration tolerances for visual optical systems*†. J. Opt. Soc. Am. 1977, 67, 634–643. [Google Scholar]
- Hecht, E. Optics, 5th ed.; Pearson Education: London, England, 2016. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics; Roberts Company Publishers: Greenwood Village, CO, USA, 2005. [Google Scholar]
- Fernandez-Oliveras, A.; Molina, A.M.; López, M.R. Comparision of spectacle-lens optical quality by modulation transfer function measurements based on random-dot patterns. Opt. Eng. 2010, 49, 083603. [Google Scholar] [CrossRef]
- Comastri, S.A.; Simon, J.M.; Martin, G.; Colombo, E.M.; Issolio, L.A.; Santillán, J.E.; Aguirre, R.C. Definition and use of spatial frequencies in Fourier Optics and in Physiological Optics. Óptica Pura Apl. 2007, 40, 119–128. [Google Scholar]
- Mejía Barbosa, Y. The wavefront and its representation with Zernike polynomials. Cienc. Tecnol. Para Salud Vis. Ocul. 2011, 9, 145–166. [Google Scholar]
- Vidal Olarte, R. Understanding and interpreting optical aberrations. Cienc. Tecnol. Para Salud Vis. Ocul. 2011, 9, 105–122. [Google Scholar]
- Navarro, R.; Rivera, R.; Aporta, J. Representation of wavefronts in free-form transmission pupils with complex Zernike polynomials. J. Optom. 2011, 4, 41–48. [Google Scholar] [CrossRef]
- Marechal, A.; Françon, M. Diffraction: Structure des Images: Influence de la Cohérence de la Lumière; Masson: Paris, France, 1970. [Google Scholar]



| Recording Geometry at 488 nm | Positive HL | Negative HL |
|---|---|---|
| Symmetrical | mm | mm |
| Asymmetrical | mm | mm |
| Reconstruction Geometry | 473 nm | 633 nm |
|---|---|---|
| Symmetrical | mm | mm |
| Asymmetrical | mm | mm |
| HL | RMSTheo (10−4) (μm) | RMSExp (μm) | PF | P–V (μm) |
|---|---|---|---|---|
| Sym (+) 633 nm | 1.61 | 0.29 | 0.0625 1 | 1.4788 |
| Sym (+) 473 nm | 0.114 | 0.21 | 0.0625 1 | 1.3269 |
| Asym (−) 633 nm | 0.002 | 0.05 | 0.25 | 0.2902 |
| Asym (−) 473 nm | 0.0002 | 0.03 | 0.25 | 0.1776 |
| HL | SR (%) | Normalized Entropy | Fcut MTF Dif. Lim (Green) (cycle/deg) | Fcut MTF Cut in x (Red) (cycle/deg) | Fcut MTF Cut in y (Blue) (cycle/deg) |
|---|---|---|---|---|---|
| Sym (+) 633 nm | 4 | 18 | 82.7 | 27 | 24 |
| Sym (+) 473 nm | 12 | 7.7 | 110.7 | 29 | 29 |
| Asym (−) 633 nm | 80 | 1.8 | 82.7 | 79 | 79 |
| Asym (−) 473 nm | 86 | 1.7 | 110.7 | 99 | 99 |
| HL | Area under MTF Cut in x (Red) (arb. units) | Area under MTF Cut in y (Blue) (arb. units) | Area under MTF Dif. Lim (Green) (arb. units) |
|---|---|---|---|
| Sym (+) 633 nm | 6.2299 | 6.0090 | 7.4053 |
| Sym (+) 473 nm | 7.0814 | 7.0878 | 9.9103 |
| Asym (−) 633 nm | 7.2467 | 7.2208 | 7.4053 |
| Asym (−) 473 nm | 9.2002 | 9.4010 | 9.9103 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lloret, T.; Navarro-Fuster, V.; Ramírez, M.G.; Morales-Vidal, M.; Beléndez, A.; Pascual, I. Aberration-Based Quality Metrics in Holographic Lenses. Polymers 2020, 12, 993. https://doi.org/10.3390/polym12040993
Lloret T, Navarro-Fuster V, Ramírez MG, Morales-Vidal M, Beléndez A, Pascual I. Aberration-Based Quality Metrics in Holographic Lenses. Polymers. 2020; 12(4):993. https://doi.org/10.3390/polym12040993
Chicago/Turabian StyleLloret, Tomás, Víctor Navarro-Fuster, Manuel G. Ramírez, Marta Morales-Vidal, Augusto Beléndez, and Inmaculada Pascual. 2020. "Aberration-Based Quality Metrics in Holographic Lenses" Polymers 12, no. 4: 993. https://doi.org/10.3390/polym12040993
APA StyleLloret, T., Navarro-Fuster, V., Ramírez, M. G., Morales-Vidal, M., Beléndez, A., & Pascual, I. (2020). Aberration-Based Quality Metrics in Holographic Lenses. Polymers, 12(4), 993. https://doi.org/10.3390/polym12040993