Numerical Study Using Microstructure Based Finite Element Modeling of the Onset of Convective Heat Transfer in Closed-Cell Polymeric Foam
Abstract
:1. Introduction
2. Finite Element Analysis of Closed-Cell Foam
2.1. Computational Domain
2.2. Structural Parameters in PVC Microstructure
2.3. Conjugate Heat Transfer
2.4. Thermal Computational Homogenization
3. Results and Discussion
3.1. Model Verification
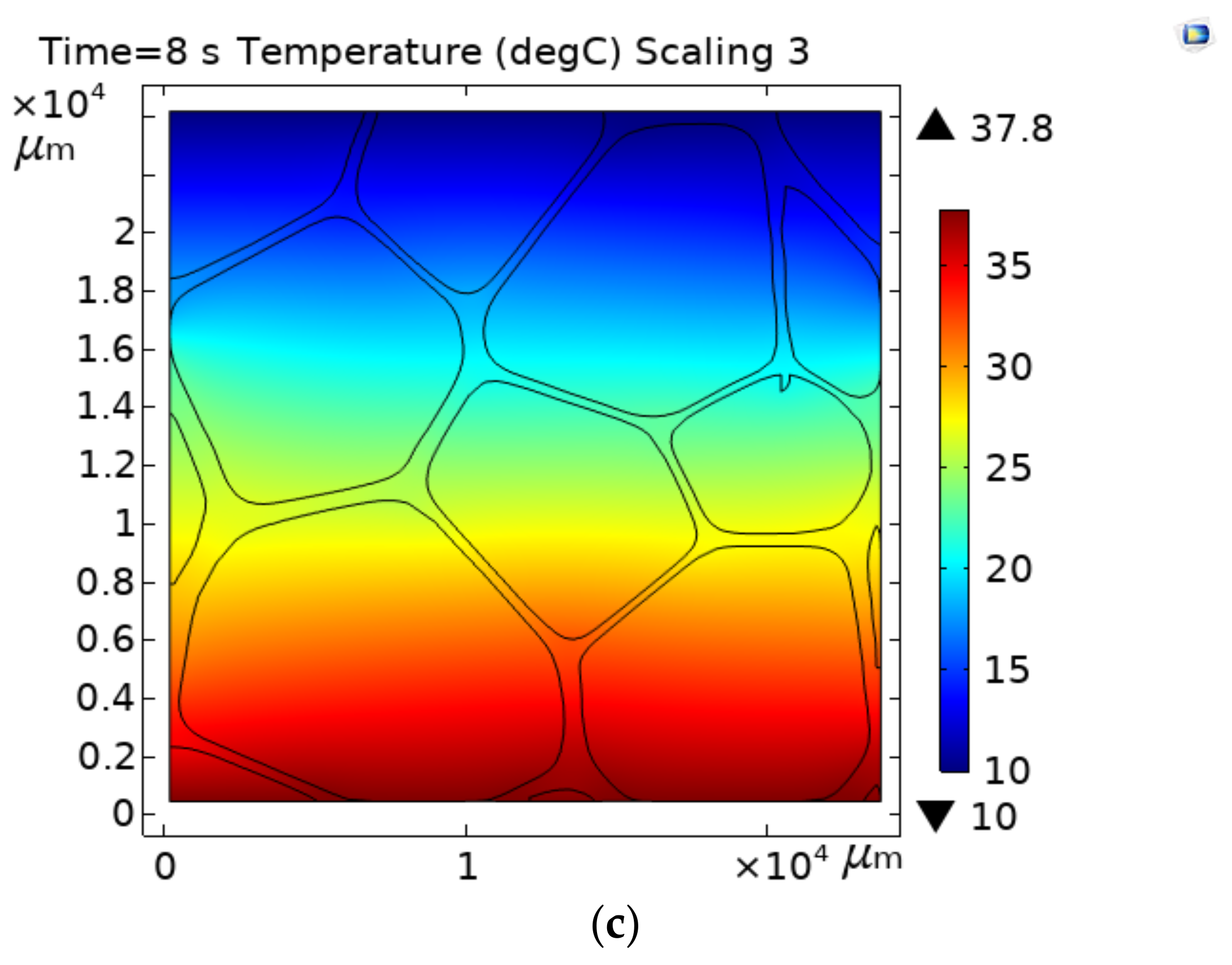
3.2. Temperature Distribution across the PVC Foam
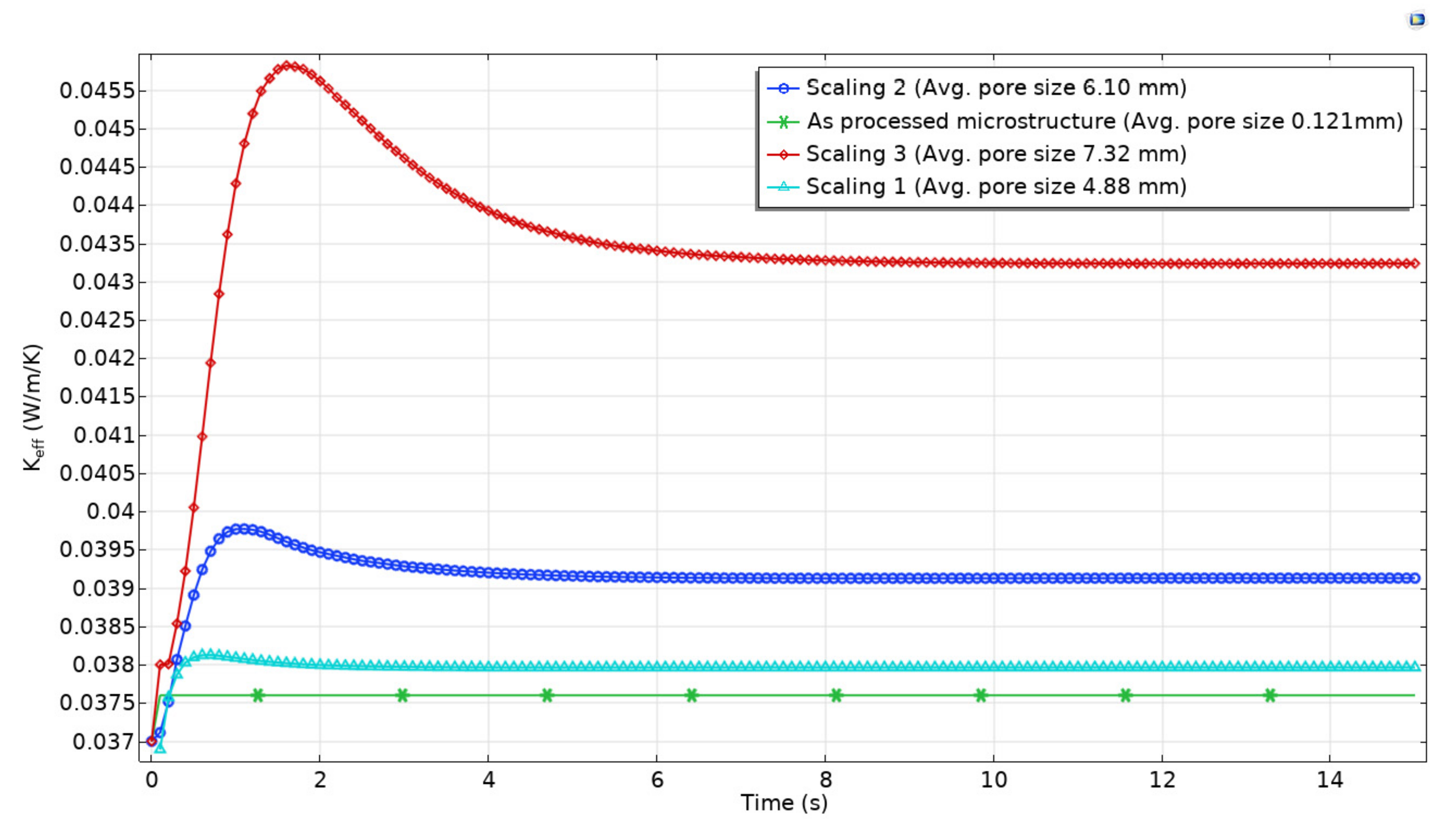
3.3. Effective Thermal Conductivity ()
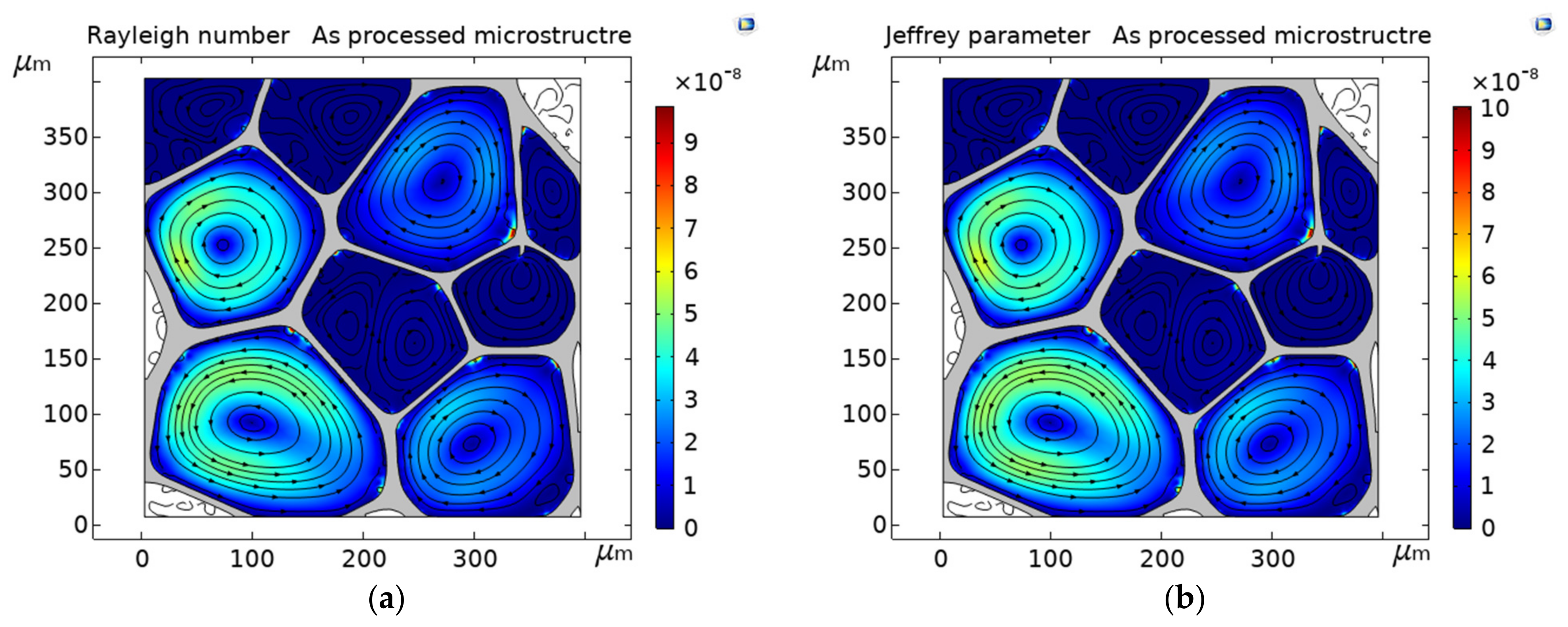
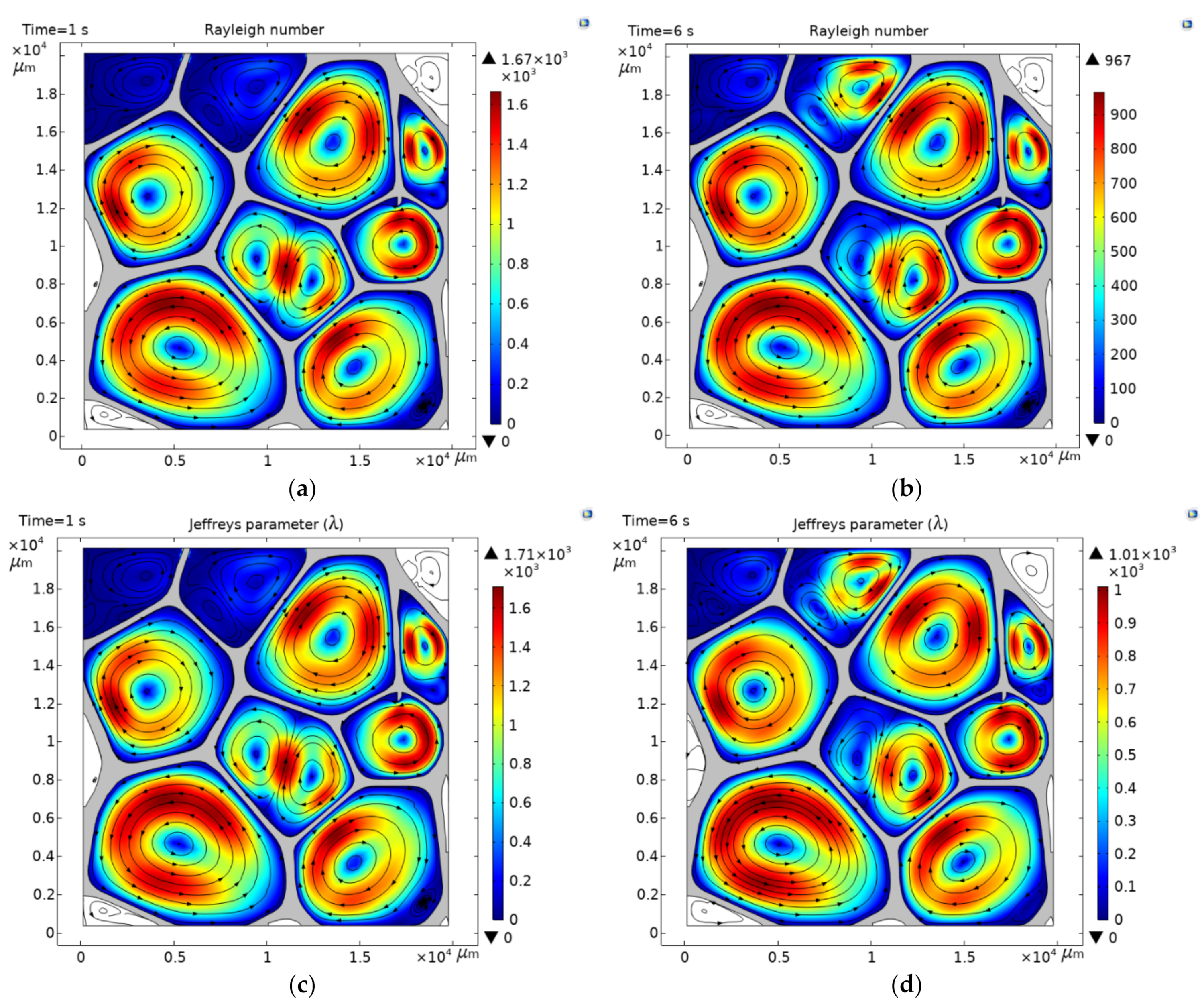
3.4. Onset of Convective Heat Transfer
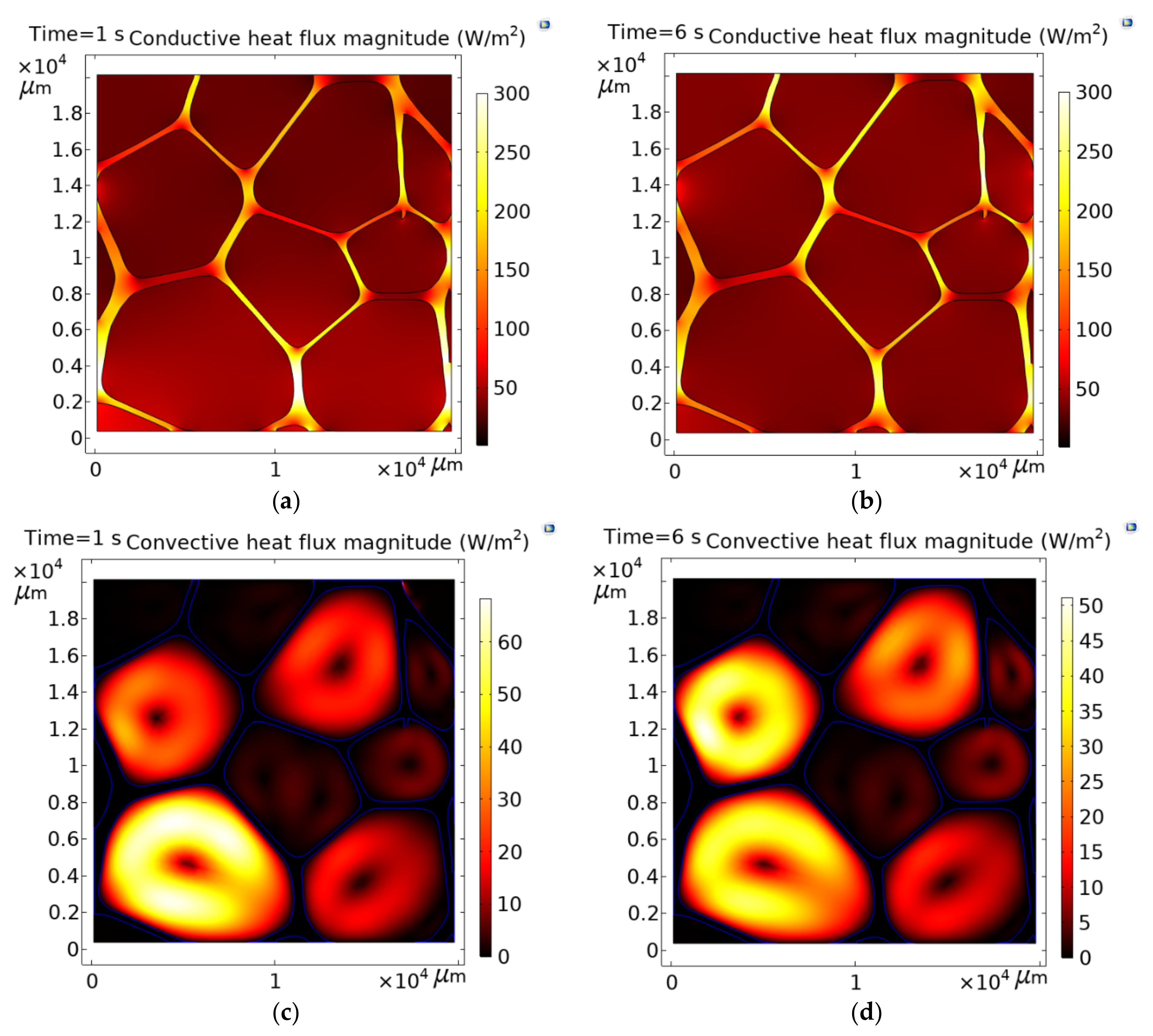
3.5. Conductive and Convective Heat Flux Magnitudes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koru, M. Determination of thermal conductivity of closed-cell insulation materials that depend on temperature and density. Arab. J. Sci. Eng. 2016, 41, 4337–4346. [Google Scholar] [CrossRef]
- Wang, C.; Mobedi, M.; Kuwahara, F. Simulation of heat transfer in a closed-cell porous media under local thermal non-equilibrium condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2478–2500. [Google Scholar] [CrossRef]
- Sun, Z.; Lu, C.; Fan, J.; Yuan, F. Porous silica ceramics with closed-cell structure prepared by inactive hollow spheres for heat insulation. J. Alloys Compd. 2016, 662, 157–164. [Google Scholar] [CrossRef]
- Yang, X.; Lu, T.; Kim, T. Effective Thermal Conductivity Modelling for Closed-Cell Porous Media with Analytical Shape Factors. Transp. Porous Media 2013, 100, 211–224. [Google Scholar] [CrossRef]
- Progelhof, R.C.; Throne, J.L.; Ruetsch, R.R. Methods for predicting the thermal conductivity of composite systems: A review. Polym. Eng. Sci. 1976, 16, 615–625. [Google Scholar] [CrossRef]
- Coquard, R.; Baillis, D. Numerical investigation of conductive heat transfer in high-porosity foams. Acta Mater. 2009, 57, 5466–5479. [Google Scholar] [CrossRef]
- Randrianalisoa, J.; Baillis, D. Thermal conductive and radiative properties of solid foams: Traditional and recent advanced modelling approaches. C. R. Phys. 2014, 15, 683–695. [Google Scholar] [CrossRef]
- Ranut, P.; Nobile, E. On the effective thermal conductivity of metal foams. J. Phys. Conf. Ser. 2014, 547, 012021. [Google Scholar] [CrossRef]
- Hu, Y.; Fang, Q.-Z.; Yu, H.; Hu, Q. Numerical simulation on thermal properties of closed-cell metal foams with different cell size distributions and cell shapes. Mater. Today Commun. 2020, 24, 100968. [Google Scholar] [CrossRef]
- Rivera-Salinas, J.E.; Gregorio-Jáuregui, K.M.; Romero-Serrano, J.A.; Cruz-Ramírez, A.; Hernández-Hernández, E.; Miranda-Pérez, A.; Gutierréz-Pérez, V.H. Simulation on the effect of porosity in the elastic modulus of sic particle reinforced al matrix composites. Metals 2020, 10, 391. [Google Scholar] [CrossRef] [Green Version]
- Collishaw, P.G.; Evans, J.R.G. An assessment of expressions for the apparent thermal conductivity of cellular materials. J. Mater. Sci. 1994, 29, 486–498. [Google Scholar] [CrossRef]
- Liang, J.; Li, F. Simulation of heat transfer in hollow-glass-bead-filled polypropylene composites by finite element method. Polym. Test. 2007, 26, 419–424. [Google Scholar] [CrossRef]
- Qin, Z.; Li, G.; Tian, Y.; Ma, Y.; Shen, P. Numerical simulation of thermal conductivity of foam glass based on the steady-state method. Materials 2018, 12, 54. [Google Scholar] [CrossRef] [Green Version]
- Coquard, R.; Baillis, D.; Maire, E. Numerical investigation of the radiative properties of polymeric foams from tomographic images. J. Heat Transf. 2010, 24, 647–658. [Google Scholar] [CrossRef]
- Coquard, R.; Randrianalisoa, J.; Baillis, D.D. Computational prediction of radiative properties of polymer closed-cell foams with random structure. J. Porous Media 2013, 16, 137–154. [Google Scholar] [CrossRef]
- Baillis, D.D.; Coquard, R.; Randrianalisoa, J.; Dombrovsky, L.A.; Viskanta, R. Thermal radiation properties of highly porous cellular foams. Spéc. Top. Rev. Porous Media Int. J. 2013, 4, 111–136. [Google Scholar] [CrossRef]
- Vesenjak, M.; Žunič, Z.; Öchsner, A.; Hriberšek, M.; Ren, Z. Heat conduction in closed-cell cellular metals. Mater. Werkst. 2005, 36, 608–612. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Karimipour, A.; Afrand, M.; Goodarzi, M. Investigation of free convection heat transfer and entropy generation of nanofluid flow inside a cavity affected by magnetic field and thermal radiation. J. Anal. Calorim. 2019, 137, 997–1019. [Google Scholar] [CrossRef]
- Jeffreys, H. Some cases of instability in fluid motion. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1928, 118, 195–208. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, T.; Hodson, H.; Jackson, J. The temperature dependence of effective thermal conductivity of open-celled steel alloy foams. Mater. Sci. Eng. A 2004, 367, 123–131. [Google Scholar] [CrossRef]
- Berardi, U. The impact of aging and environmental conditions on the effective thermal conductivity of several foam materials. Energy 2019, 182, 777–794. [Google Scholar] [CrossRef]
- Charters, W.; Peterson, L. Free convection suppression using honeycomb cellular materials. Sol. Energy 1972, 13, 353–361. [Google Scholar] [CrossRef]
- Arreola-Herrera, R.; Cruz-Ramírez, A.; Rivera-Salinas, J.E.; Romero-Serrano, J.A.; Sánchez-Alvarado, R.G. The effect of non-metallic inclusions on the mechanical properties of 32 CDV 13 steel and their mechanical stress analysis by numerical simulation. Appl. Fract. Mech. 2018, 94, 134–146. [Google Scholar] [CrossRef]
- Zhang, P.; Li, F.-G. Effect of particle characteristics on deformation of particle reinforced metal matrix composites. Trans. Nonferrous Met. Soc. China 2010, 20, 655–661. [Google Scholar] [CrossRef]
- Rivera-Salinas, J.E.; Gregorio-Jáuregui, K.M.; Cruz-Ramírez, A.; Gutierréz-Pérez, V.H.; Romero-Serrano, J.A.; Olvera-Vazquez, S.L.; Fonseca-Florido, H.A.; Ávila-Orta, C.A. Computational study in bottom gas injection using the conservative level set method. Processes 2020, 8, 1643. [Google Scholar] [CrossRef]
- Rivera-Salinas, J.E.; Gregorio-Jáuregui, K.M.; Cruz-Ramírez, A.; Romero-Serrano, J.A.; Ramírez-Vargas, E.; Gutierréz-Pérez, V.H.; Hernández-Quintanar, L.F.J. Determination of Threshold Pressure for Infiltration of NaCl Preforms by a Zinc Base Alloy and Its Effect on Young´s Modulus by Numerical Simulation. Met. Mater. Trans. A 2021, 52, 826–839. [Google Scholar] [CrossRef]
- Yáñez-Macías, R.; Rivera-Salinas, J.E.; Solís-Rosales, S.; Orduña-Altamirano, D.; Ruíz-Mendoza, D.; Herrera-Guerrero, A.; Lara-Sanchez, J.; González-Morones, P.; García-Hernández, Z.; Hernández-Hernández, E. Mechanical behavior of glass fiber-reinforced Nylon-6 syntactic foams and its Young’s modulus numerical study. J. Appl. Polym. Sci. 2021, 138, 50648. [Google Scholar] [CrossRef]
- Berardi, U. The impact of temperature dependency of the building insulation thermal conductivity in the Canadian climate. Energy Procedia 2017, 132, 237–242. [Google Scholar] [CrossRef]
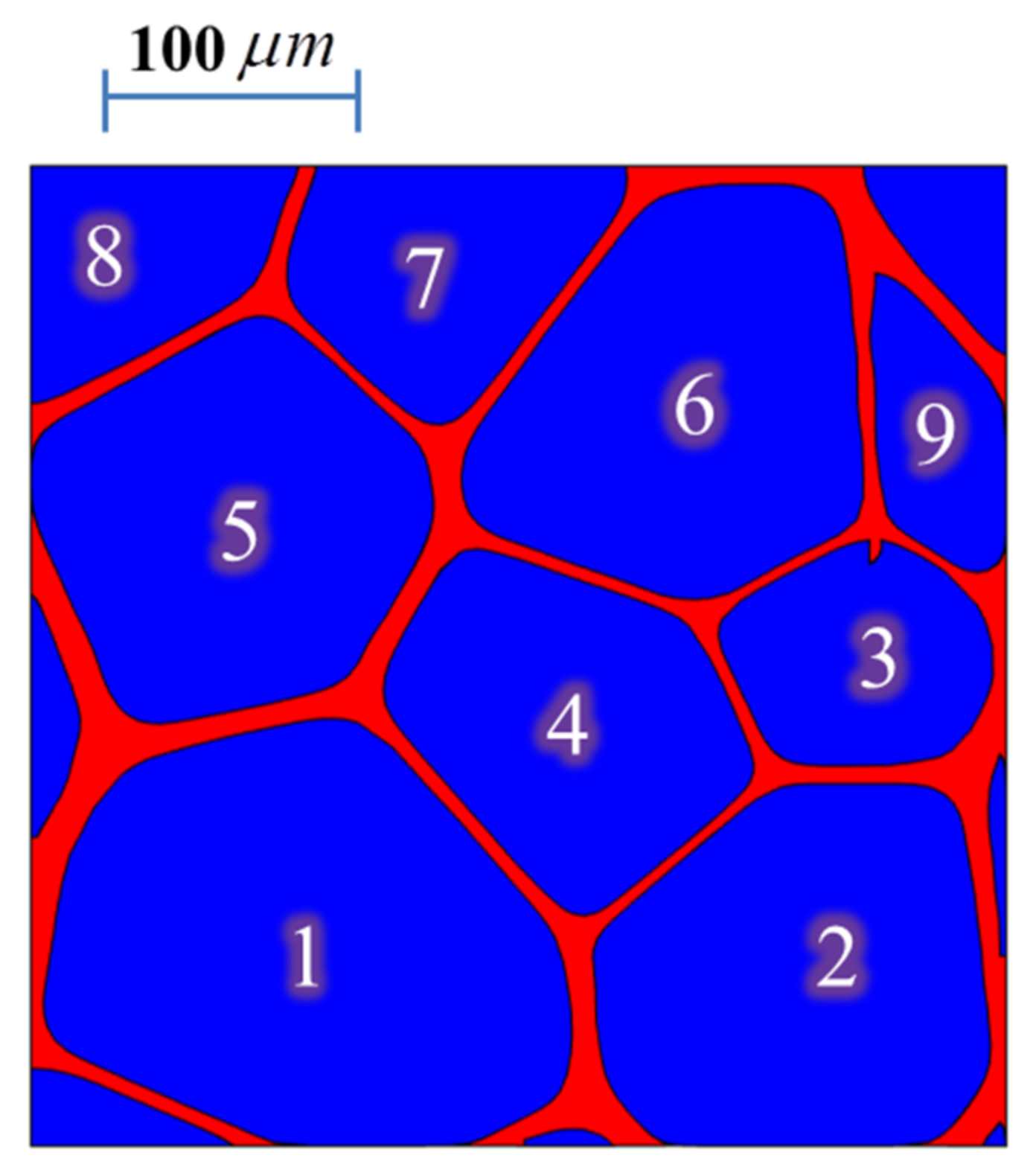



| Pore Shape | Shape Factor | Pore Shape | Shape Factor |
|---|---|---|---|
| Roundness | 1.00 | Ellipse (1:4) | 1.89 |
| Square | 1.27 | Rectangle (1:2) | 1.43 |
| Ellipse (1:2) | 1.19 | Rectangle (1:3) | 1.69 |
| Ellipse (1:3) | 1.51 | Rectangle (1:4) | 2.29 |
| Pore Number | Equivalent Diameter | Shape Factor | Pore Shape |
|---|---|---|---|
| 1 | 0.181 | 1.08 | Circular |
| 2 | 0.151 | 1.08 | Circular |
| 3 | 0.091 | 1.16 | Ellipse (1:2) |
| 4 | 0.127 | 1.11 | Ellipse (1:2) |
| 5 | 0.150 | 1.06 | Circular |
| 6 | 0.150 | 1.12 | Ellipse (1:2) |
| 7 | 0.098 | 1.26 | Square |
| 8 | 0.081 | 1.39 | Circular * |
| 9 | 0.064 | 1.43 | Rectangle (1:2) |
| Equivalent Diameter | ||||
|---|---|---|---|---|
| Pore Number | As Processed Microstructure | Scaling 1 (40×) | Scaling 2 (50×) | Scaling 3 (60×) |
| 1 | 0.181 | 7.25 | 9.06 | 10.9 |
| 2 | 0.151 | 6.08 | 7.6 | 9.11 |
| 3 | 0.091 | 3.66 | 4.58 | 5.49 |
| 4 | 0.127 | 5.1 | 6.37 | 7.65 |
| 5 | 0.150 | 6.03 | 7.54 | 9.04 |
| 6 | 0.150 | 6.02 | 7.53 | 9.04 |
| 7 | 0.098 | 3.95 | 4.94 | 5.93 |
| 8 | 0.081 | 3.25 | 4.07 | 4.88 |
| 9 | 0.064 | 2.59 | 3.24 | 3.88 |
| Avg. | 0.121 | 4.88 | 6.10 | 7.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivera-Salinas, J.-E.; Gregorio-Jáuregui, K.-M.; Fonseca-Florido, H.-A.; Ávila-Orta, C.-A.; Ramírez-Vargas, E.; Romero-Serrano, J.-A.; Cruz-Ramírez, A.; Gutierréz-Pérez, V.-H.; Olvera-Vazquez, S.-L.; Rosales-Marines, L. Numerical Study Using Microstructure Based Finite Element Modeling of the Onset of Convective Heat Transfer in Closed-Cell Polymeric Foam. Polymers 2021, 13, 1769. https://doi.org/10.3390/polym13111769
Rivera-Salinas J-E, Gregorio-Jáuregui K-M, Fonseca-Florido H-A, Ávila-Orta C-A, Ramírez-Vargas E, Romero-Serrano J-A, Cruz-Ramírez A, Gutierréz-Pérez V-H, Olvera-Vazquez S-L, Rosales-Marines L. Numerical Study Using Microstructure Based Finite Element Modeling of the Onset of Convective Heat Transfer in Closed-Cell Polymeric Foam. Polymers. 2021; 13(11):1769. https://doi.org/10.3390/polym13111769
Chicago/Turabian StyleRivera-Salinas, Jorge-Enrique, Karla-Monzerratt Gregorio-Jáuregui, Heidi-Andrea Fonseca-Florido, Carlos-Alberto Ávila-Orta, Eduardo Ramírez-Vargas, José-Antonio Romero-Serrano, Alejandro Cruz-Ramírez, Víctor-Hugo Gutierréz-Pérez, Seydy-Lizbeth Olvera-Vazquez, and Lucero Rosales-Marines. 2021. "Numerical Study Using Microstructure Based Finite Element Modeling of the Onset of Convective Heat Transfer in Closed-Cell Polymeric Foam" Polymers 13, no. 11: 1769. https://doi.org/10.3390/polym13111769
APA StyleRivera-Salinas, J.-E., Gregorio-Jáuregui, K.-M., Fonseca-Florido, H.-A., Ávila-Orta, C.-A., Ramírez-Vargas, E., Romero-Serrano, J.-A., Cruz-Ramírez, A., Gutierréz-Pérez, V.-H., Olvera-Vazquez, S.-L., & Rosales-Marines, L. (2021). Numerical Study Using Microstructure Based Finite Element Modeling of the Onset of Convective Heat Transfer in Closed-Cell Polymeric Foam. Polymers, 13(11), 1769. https://doi.org/10.3390/polym13111769






