Experimental Evaluation of Tensile Performance of Aluminate Cement Composite Reinforced with Weft Knitted Fabrics as a Function of Curing Temperature
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methodology
2.2.1. Yarns and 3D Fabrics Tensile Test
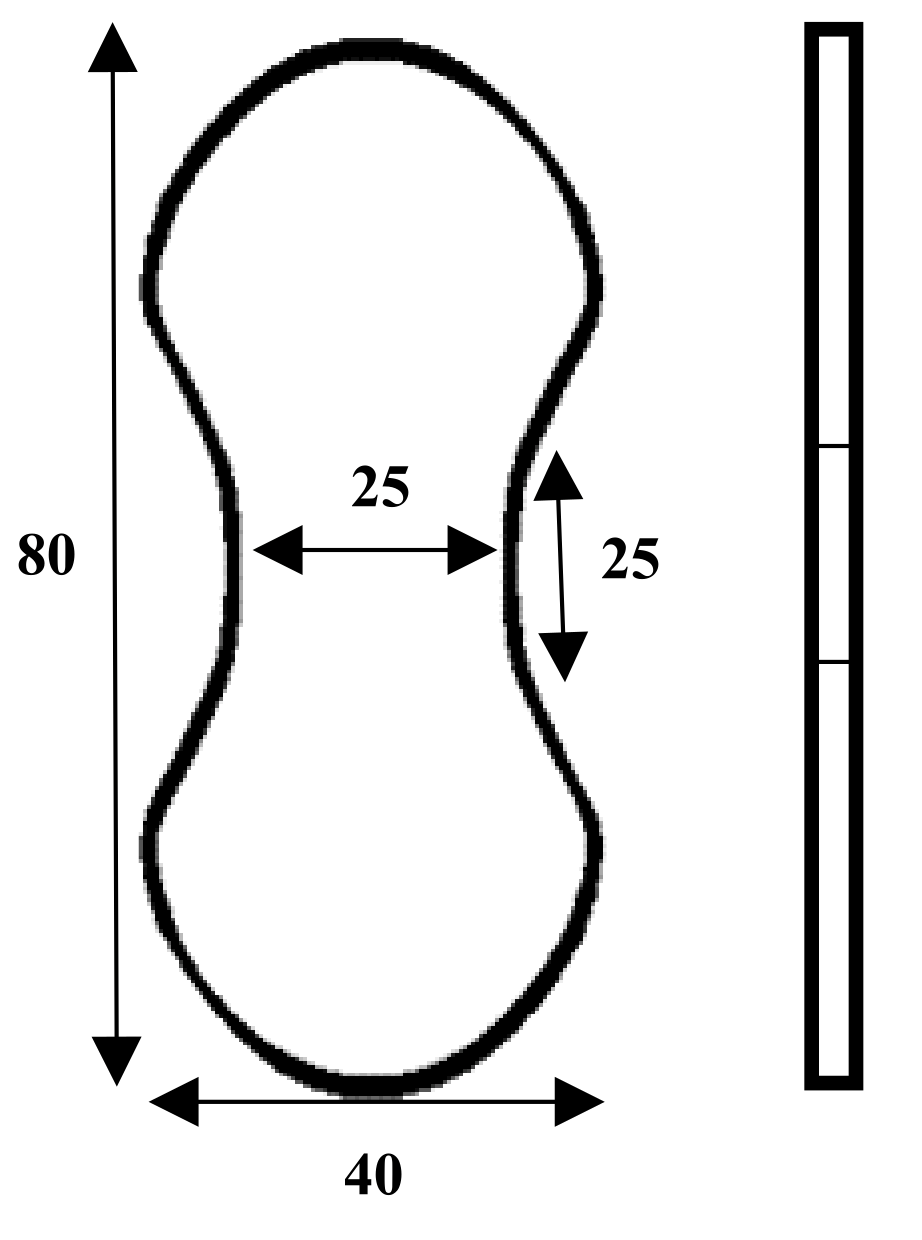
2.2.2. Reinforced Cementitious Composites Tensile Test
3. Results and Discussion
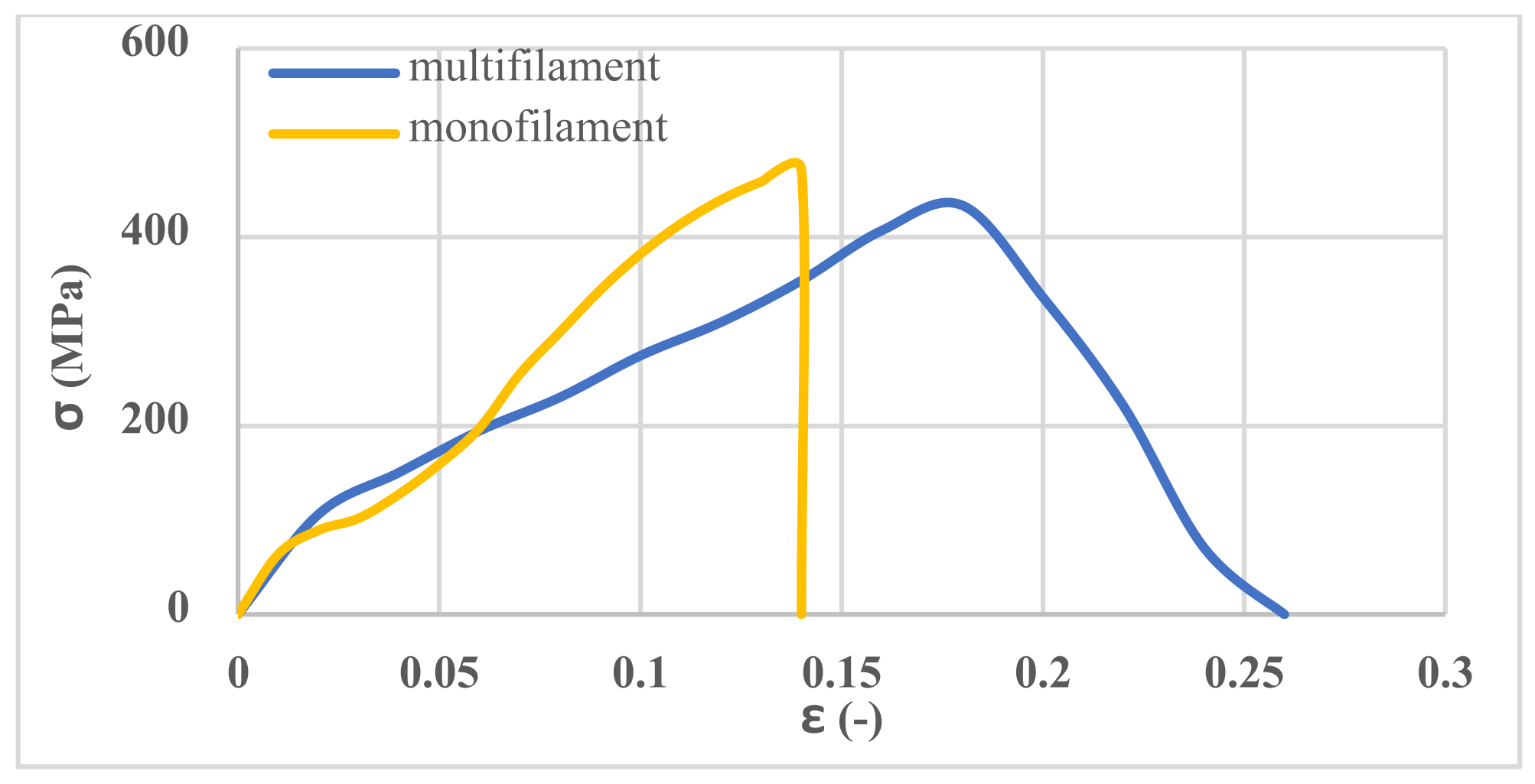
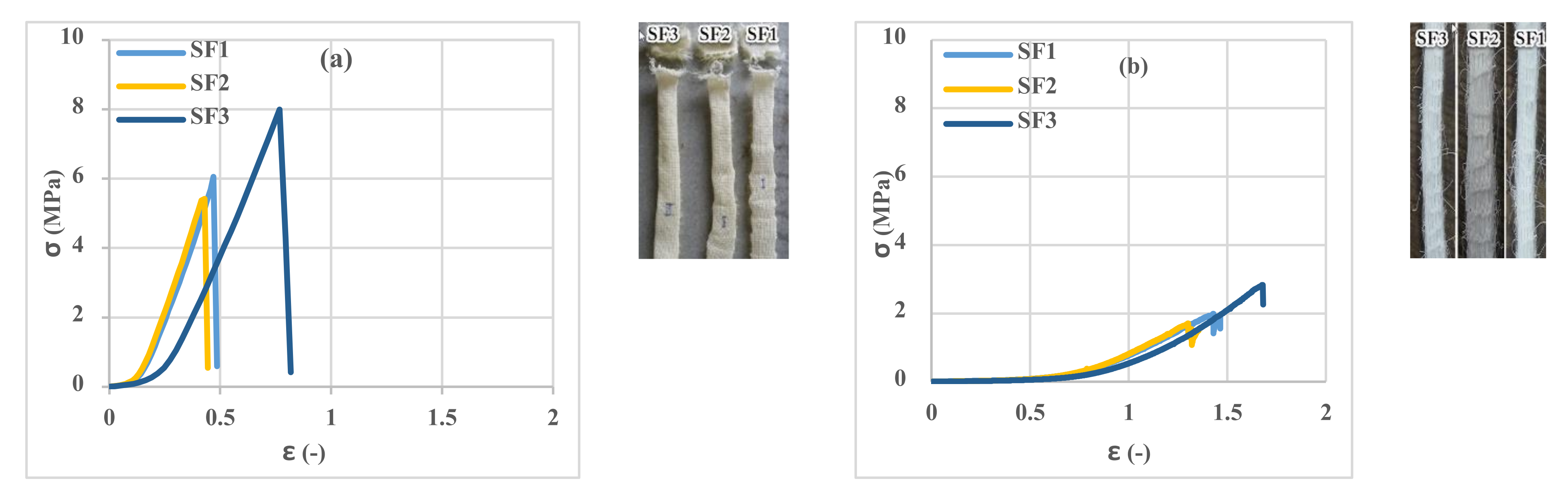
3.1. Tensile Properties of Yarn
3.2. Tensile Properties of 3D Fabrics
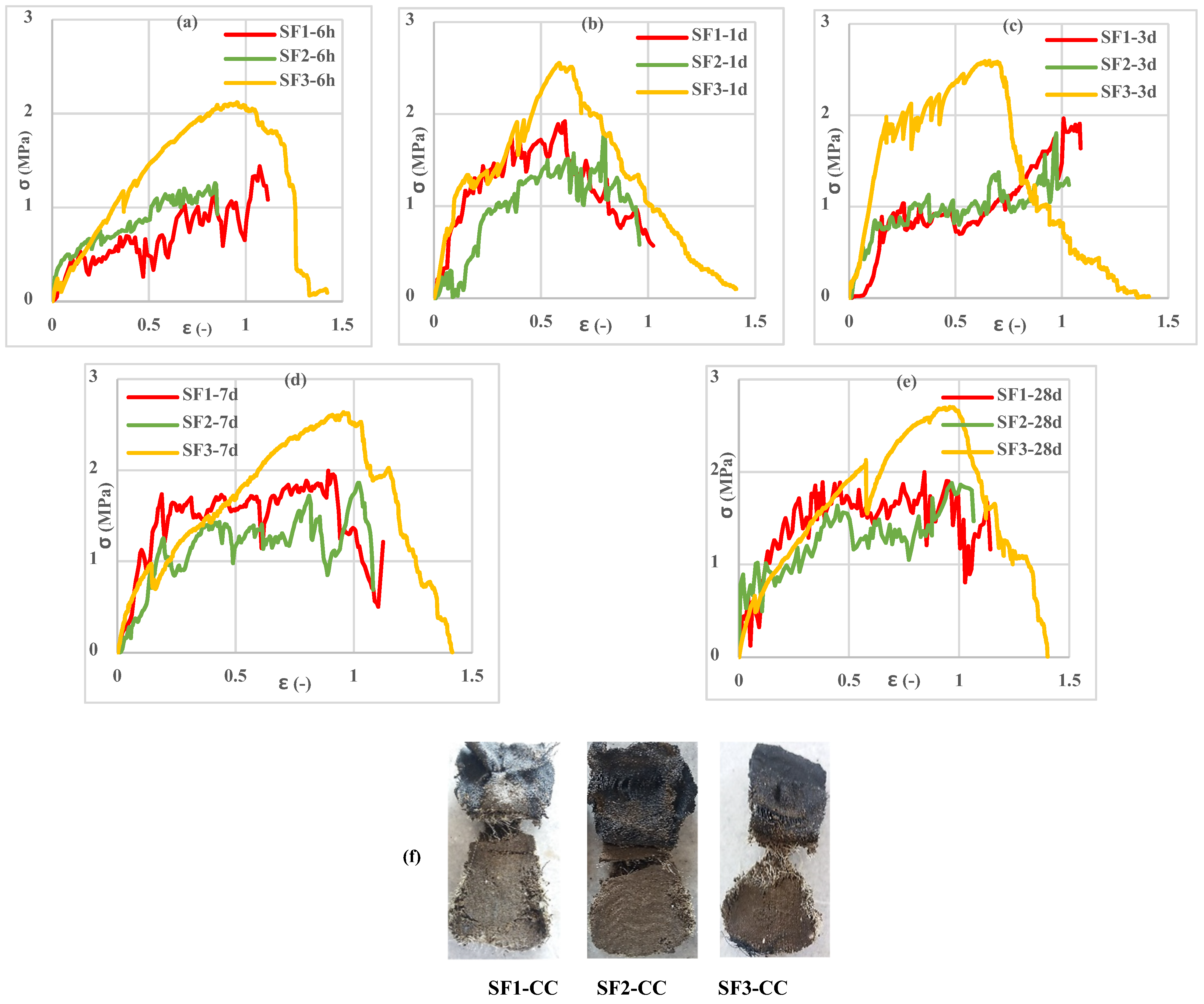
3.3. Investigation of Cement Phase Properties in Tension
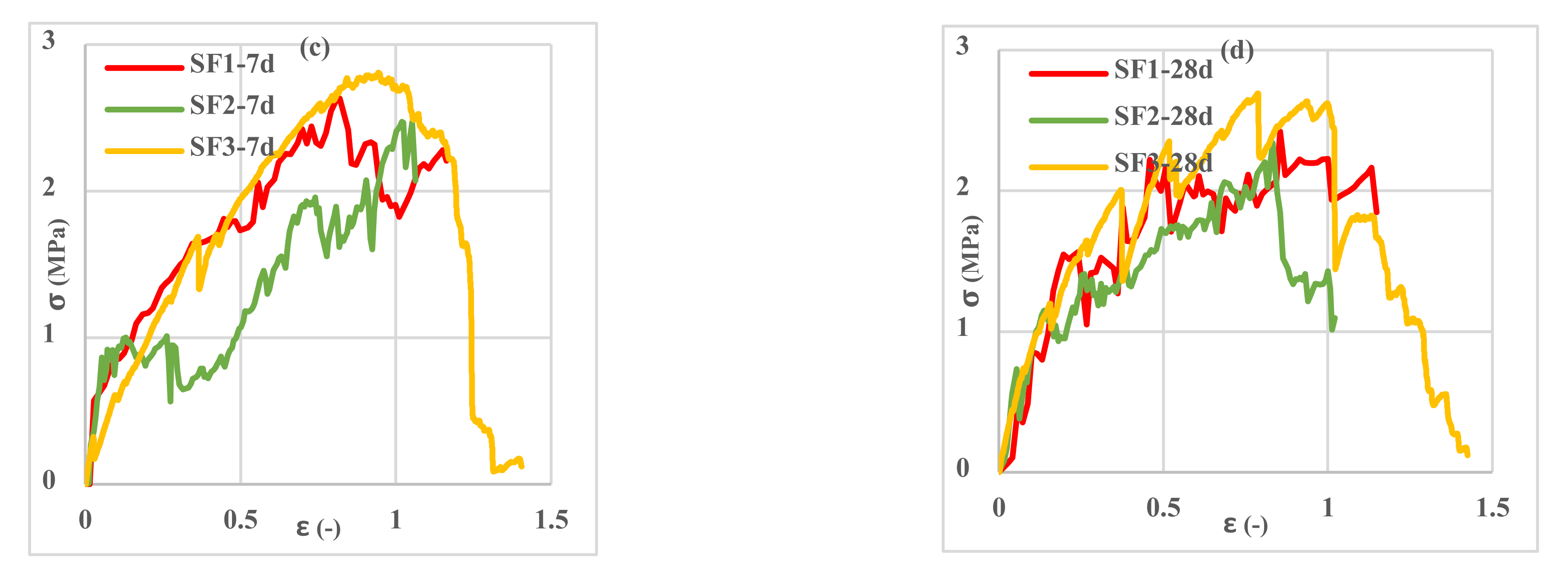
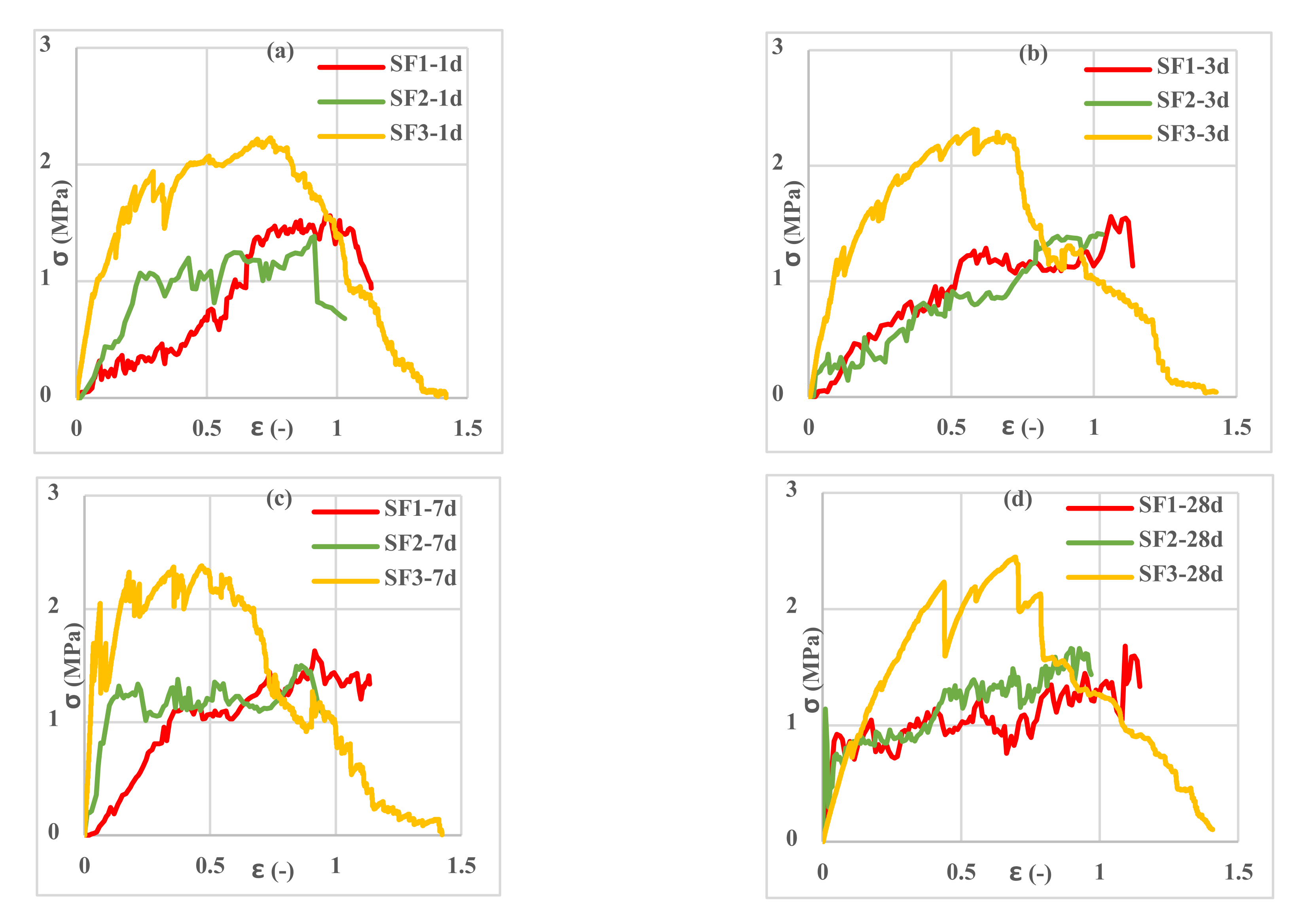
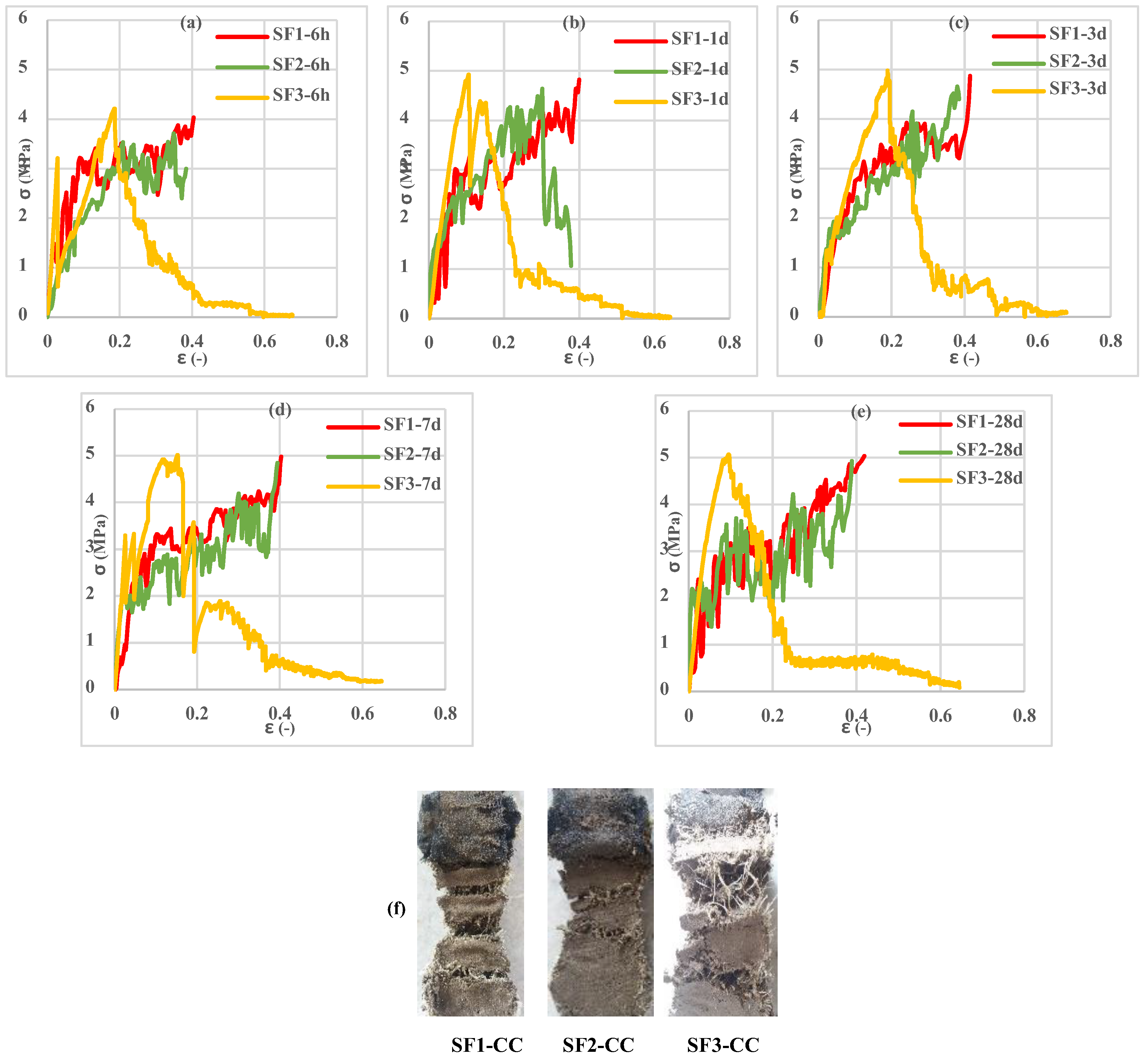
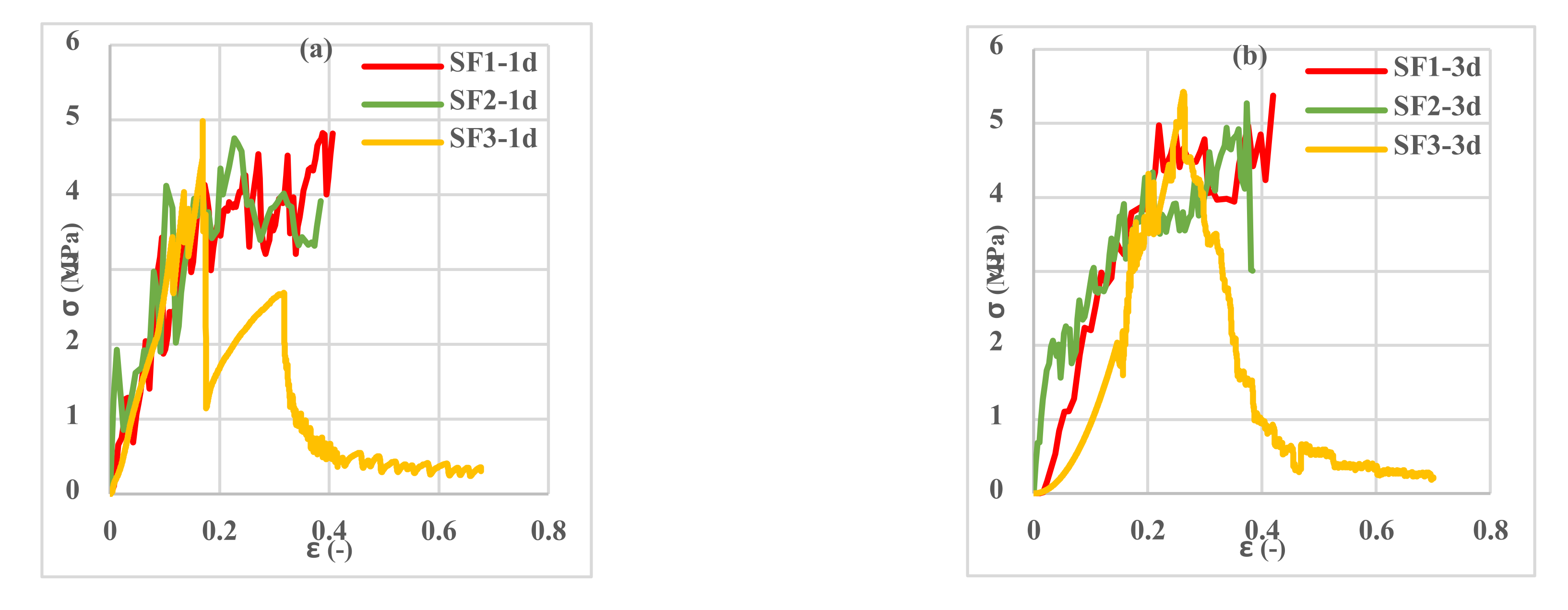
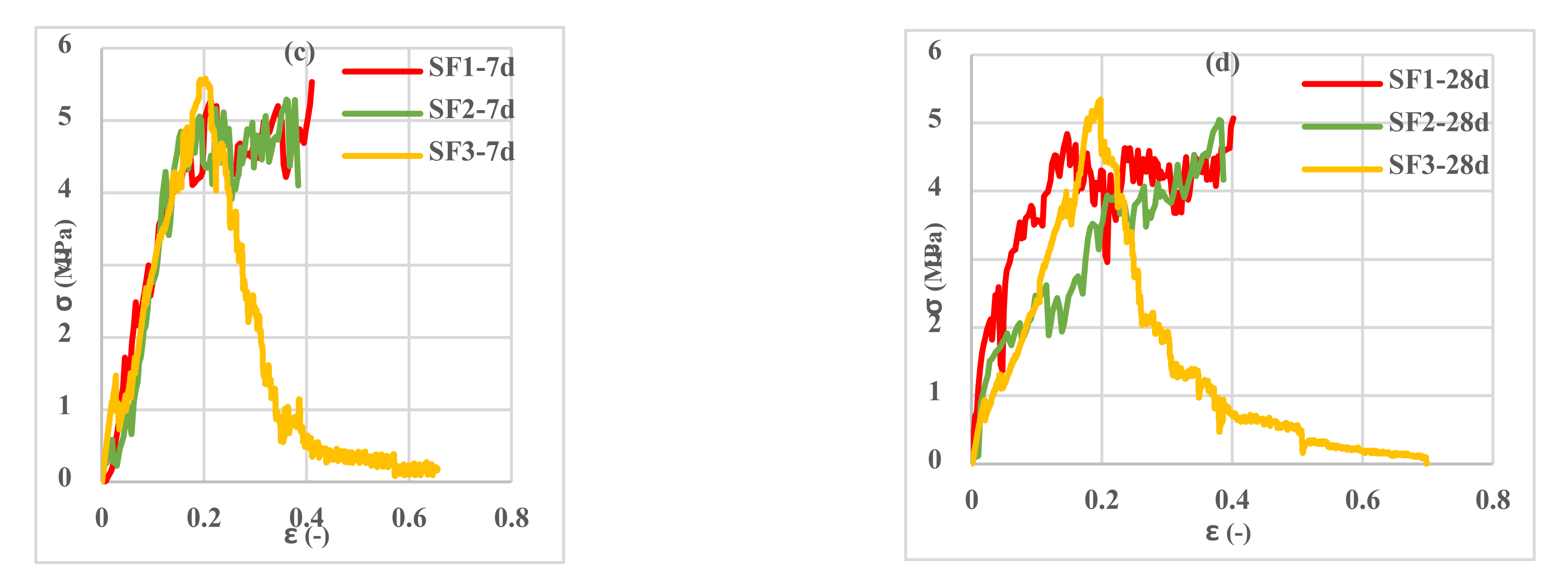
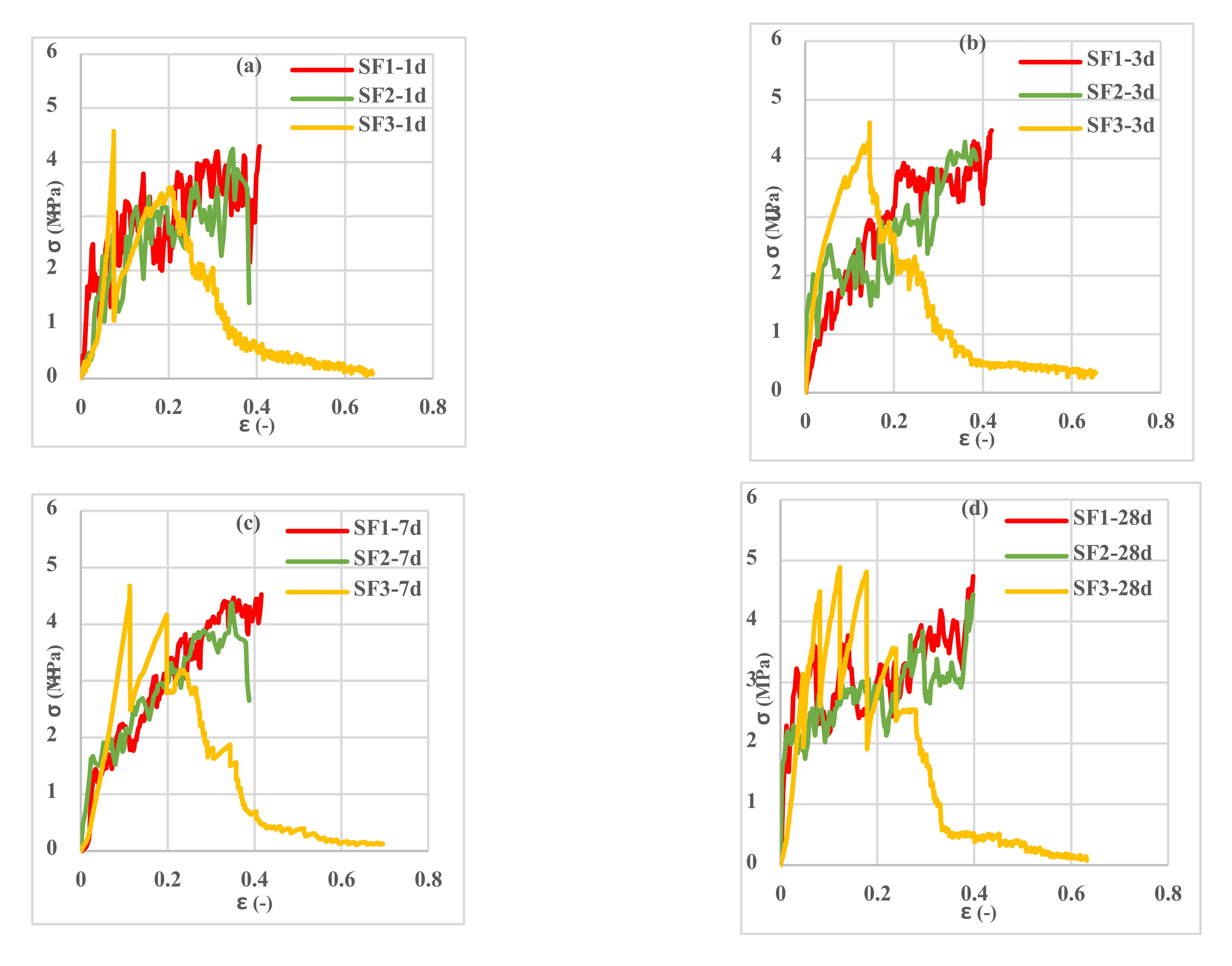
3.4. Tensile Behavior of Reinforced Cementitious Composites
4. Conclusions
- Three types of 3D fabric (SF1-SF2-SF3) with three different types of loop textures in the bottom layer of the fabric in terms of length and width were stretched, and the SF3 fabric had the highest tensile capacity and ductility compared to the other 3D fabrics. The SF1 had the least amount of stress and strain.
- By examining the amount of stress and strain in fabrics in both warp and weft directions, it was observed that reinforced CCs had higher tensile strength and lower strain in the weft direction than in the warp direction. This trend was observed in all three types of fabrics.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hegger, J.; Voss, S. Investigations on the bearing behavior and application potential of textile reinforced concrete. Eng. Struct. 2008, 30, 2050–2056. [Google Scholar] [CrossRef]
- Colombo, G.; Magri, A.; Zani, G.; Colombo, M.; di Prisco, M. Textile Reinforced Concrete: Experimental investigation on design parameters. Mater. Struct. Constr. 2013, 46, 1933–1951. [Google Scholar] [CrossRef]
- Halvaei, M.; Jamshidi, M.; Latifi, M. Strength properties of fine aggregate concretes reinforced by polyamide fibers. J. Ind. Text. 2016, 46, 684–697. [Google Scholar] [CrossRef]
- Halvaei, M.; Jamshidi, M.; Latifi, M. Effect of fiber geometry and tenacity on the mechanical properties of fine aggregates concrete. J. Ind. Text. 2016, 45, 1083–1099. [Google Scholar] [CrossRef]
- Contamine, R.; Larbi, A.S. Development of a textile reinforced concrete (TRC) to retrofit reinforced concrete structures. Eur. J. Environ. Civ. Eng. 2016, 20, 626–642. [Google Scholar] [CrossRef]
- el Messiry, M.; Mito, A.B.; Al-Oufy, A.; El-Tahan, E. Effect of fabric material and tightness on the mechanical properties of fabric-cement composites. Alexandria Eng. J. 2014, 53, 795–801. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.G.; Park, J.K.; Kim, D.J. Direct tensile responses of aramid fiber reinforced cementitious composites and textile reinforced cementitious composites with 3D spacer fabric at high strain rates. Constr. Build. Mater. 2018, 168, 232–243. [Google Scholar] [CrossRef]
- Ghorbani, V.; Jeddi, A.A.A.; Dabiryan, H.; Ramezanianpour, A.A. Investigation of the flexural behavior of self-consolidating mortars reinforced with net warp-knitted spacer fabrics. Constr. Build. Mater. 2020, 232, 117270. [Google Scholar] [CrossRef]
- Armakan, D.M.; Roye, A. A study on the compression behavior of spacer fabrics designed for concrete applications. Fibers Polym. 2009, 10, 116–123. [Google Scholar] [CrossRef]
- De Munck, M.; El Kadi, M.; Tsangouri, E.; Vervloet, J.; Verbruggen, S.; Wastiels, J.; Tysmans, T.; Remy, O. Influence of environmental loading on the tensile and cracking behavior of textile reinforced cementitious composites. Constr. Build. Mater. 2018, 181, 325–334. [Google Scholar] [CrossRef]
- Li, H.; Chen, H.; Li, X.; Zhang, F. Design and construction application of concrete canvas for slope protection. Powder Technol. 2019, 344, 937–946. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, H.; Li, X.; Li, H.; Lv, T.; Zhang, W.; Yang, Y. Experimental study of the mechanical behavior of FRP-reinforced concrete canvas panels. Compos. Struct. 2017, 176, 608–616. [Google Scholar] [CrossRef]
- Haik, R.; Sasi, E.A.; Peled, A. Influence of three-dimensional (3D) fabric orientation on flexural properties of cement-based composites. Cem. Concr. Compos. 2017, 80, 1–9. [Google Scholar] [CrossRef]
- Amzaleg, E.; Peled, A.; Janetzko, S.; Gries, T. Flexural behavior of cement-based element reinforced with 3D fabric. In Proceedings of the VIII International Conference on Fracture Mechanics of Concrete and Concrete Structures, Toledo, Spain, 10–14 March 2013; pp. 1080–1088. [Google Scholar]
- Li, H.; Chen, H.; Liu, L.; Zhang, F.; Han, F.; Lv, T. Application design of concrete canvas (CC) in soil reinforced structure. Geotext. Geomembranes 2016, 44, 557–567. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Slowik, V.; Kabele, P. (Eds.) Strain-Hardening Cement-Based Composites: SHCC4; RILEM Bookseries; Springer: Berlin/Heidelberg, Germany, 2018; Volume 15. [Google Scholar] [CrossRef]
- Barnes, J.B.P. Structure and Performance of Cements, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Scrivener, K.L.; Cabiron, J.L.; Letourneux, R. High-performance concretes from calcium aluminate cements. Cem. Concr. Res. 1999, 29, 1215–1223. [Google Scholar] [CrossRef]
- Adams, J.H.I.M.P. Volume Stability of Calcium Aluminate Cement and Calcium Sulfoaluminate Cement Systems. Factors Influencing Conversion and Volume Stability in Calcium Aluminate Cement Systems. 2014. Available online: http://library1.nida.ac.th/termpaper6/sd/2554/19755.pdf (accessed on 27 December 2020).
- Scrivener, K.L.; Capmas, A. Calcium Aluminate Cement. In Lea’s Chemistry of Cement and Concrete; Hewlett, P.C., Ed.; Elsevier Ltd: Oxford, UK, 1998; pp. 713–782. [Google Scholar]
- Juenger, M.C.G.; Winnefeld, F.; Provis, J.L.; Ideker, J.H. Advances in alternative cementitious binders. Cem. Concr. Res. 2011, 41, 1232–1243. [Google Scholar] [CrossRef]
- Ukrainczyk, N.; Matusinović, T. Thermal properties of hydrating calcium aluminate cement pastes. Cem. Concr. Res. 2010, 40, 128–136. [Google Scholar] [CrossRef]
- Paulo, J.M. Concrete: Monteiro, Microstructure, Properties, and Materials; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Abounaim, M.; Hoffmann, G.; Diestel, O.; Cherif, C. Development of Flat Knitted Spacer Fabrics for Composites using Hybrid Yarns and Investigation of Two-dimensional Mechanical Properties. Text. Res. J. 2009, 79, 596–610. [Google Scholar] [CrossRef]
- Gosselin, C. Microstructural Development of Calcium Aluminate Cement Based Systems with and without Supplementary Cementitious Materials; EPFL: Lausanne, Switzerland, 2009; Volume 4443, p. 234. [Google Scholar]
- Odler, I. Special Inorganic Cements; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Lothenbach, B. Thermodynamic modelling of effect of time and silica on the conversion process. In Calcium Aluminates, Proceedings of the International Conference; Whittles Publishing: Dunbeath, UK, 2014; pp. 153–164. [Google Scholar]
- Adams, M.P.; Lute, R.D.; Moffatt, E.G.; Ideker, J.H. Evaluation of a Procedure for Determining the Converted Strength of Calcium Aluminate Cement Concrete. J. Test. Eval. 2018, 46, 20160277. [Google Scholar] [CrossRef]
- Nowacka, M.; Pacewska, B. Effect of structurally different aluminosilicates on early-age hydration of calcium aluminate cement depending on temperature. Constr. Build. Mater. 2020, 235, 117404. [Google Scholar] [CrossRef]
- Şengül, K.; Erdoğan, S.T. Influence of ground perlite on the hydration and strength development of calcium aluminate cement mortars. Constr. Build. Mater. 2021, 266, 120943. [Google Scholar] [CrossRef]
- Zhutovsky, S.; Kovler, K. Influence of water to cement ratio on the efficiency of internal curing of high-performance concrete. Constr. Build. Mater. 2017, 144, 311–316. [Google Scholar] [CrossRef]
- Dowell, A.; Cramer, S. Field Measurement of Water-Cement Ratio Portland Cement Concrete. In Phase II, Field Evaluation and Development; Wisconsin Highway Research Program, University of Wisconsin: Madison, WI, USA, 2002; pp. 1–50. [Google Scholar]
- Petersson, P.E. Crack growth and development of fracture zone in plain concrete and similar materials, Report No, TVBM-1006. Div. Build. Mater. Lund Inst. Technol. Lun. 1981, 18, 84–85. [Google Scholar] [CrossRef] [Green Version]
- Phillips, D.V.; Binsheng, Z. Direct tension tests on notched and un-notched plain concrete specimens. Mag. Concr. Res. 1993, 45, 25–35. [Google Scholar] [CrossRef]
- Popvics, S. Method for Developing Relationships between Mechanical Properties of Hardened Concrete. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/7138 (accessed on 27 December 2020).
- Chen, X.; Wu, S.; Zhou, J. Influence of porosity on compressive and tensile strength of cement mortar. Constr. Build. Mater. 2013, 40, 869–874. [Google Scholar] [CrossRef]
- Peled, A.; Cohen, Z.; Pasder, Y.; Roye, A.; Gries, T. Influences of textile characteristics on the tensile properties of warp knitted cement-based composites. Cem. Concr. Compos. 2008, 30, 174–183. [Google Scholar] [CrossRef]
- Han, F.; Chen, H.; Jiang, K.; Zhang, W.; Lv, T.; Yang, Y. Influences of geometric patterns of 3D spacer fabric on tensile behavior of concrete canvas. Constr. Build. Mater. 2014, 65, 620–629. [Google Scholar] [CrossRef]
- Abdellahi, S.B.; Hejazi, S.M.; Hasani, H. Investigation of flexural behavior of 3D textile reinforced concrete using both experimental tests and finite element method. J. Sandw. Struct. Mater. 2018, 20, 578–594. [Google Scholar] [CrossRef]
- Sun, F.; Ma, M.; Pan, X.; Liu, G.; Yang, S.; Zheng, D.; Li, M.; Du, Z. Simulation of plate compression behavior of warp-knitted spacer fabrics based on geometry and property parameters. Text. Res. J. 2019, 89, 1051–1064. [Google Scholar] [CrossRef]
- López-Alba, E.; Schmeer, S.; Díaz, F. Capacity, Energy Absorption Composite, Reinforced. Text. Sci. Technol. 2012, 2, 65–70. [Google Scholar]
- NF EN ISO 5084. Textile- Determination of Thickness of Textile and Textile Products; ICS: 59.080.30; Textile Fabrics, Technical Committee; ISO/ TC 38 Textile; International Organization for Standardization: Geneva, Switzerland, 1996.
- EN 196-2. Methods of Testing Cement-Part2: Chemical Analysis of Cement; ICS Code: 91.100.10; International Organization for Standardization: Geneva, Switzerland, 26 June 1995.
- EN BSI 14647. Calcium Aluminate Cement Composition, Specifications and Conformity Criteria; ICS Code: 91.100.10; British Standards Institution: London, UK, 29 August 2005.
- ISIRI INSO 29. Textile-Determination of Breaking Force and Elongation at Break Using CRE Tester; ICS: 59.080.30 Textile Fabrics; Iran National Standards Organization, 29 August 2013.
- ISO 13934-1. Textile-Tensile Properties of Fabric—Part 1: Determination of Maximum Force and Elongation at Maximum Force Using the Strip Method.; ICS Code: 59.080.30 Textile Fabrics, Technical Committee: ISO/ TC38/ SC 24; International Organization for Standardization: Geneva, Switzerland, 29 August 2013.
- ASTM. Standard Test Method for Tensile Strength of Chemical-Resistant Mortar. In Grouts, and Monolithic Surfacings; ASTM C307; ASTM: West Conshohocken, PA, USA, 2012. [Google Scholar] [CrossRef]
- Babak, F.; Abolfazl, H.; Alimorad, R.; Parviz, G. Preparation and Mechanical Properties of Graphene Oxide: Cement Nanocomposites. Sci. World J. 2014, 2014, 276323. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.M.; Moon, J.; Kim, J.J. Microstructure and Mechanical Properties of Hardened Cement Paste Including Nylon 66 Nanofibers. Construct. Build. Mater. 2020, 232, 117134. [Google Scholar] [CrossRef]
- Mirjalili, S.A. Mechanism of Weft Knitted Fabrics; Mesbah Energy: Arak, Iran, 2003. [Google Scholar]
- Shao, B.; Fang, Y.; Chen, B.; Shen, J.; Xu, S.; Ou, R.; Wang, Q. Statistical distribution of mechanical properties and energy absorption of laminated cotton fabric reinforced epoxy composites. Polym. Compos. 2020, 41, 2829–2840. [Google Scholar] [CrossRef]
- Arifin, M.T.; Abdullah, S.; Rafiquzzaman, M.; Zulkifli, R.; Wahab, D.A.; Arifin, A.K. Investigation of the behavior of a chopped strand mat/woven roving/foam-Klegecell composite lamination structure during Charpy testing. Mater. Des. 2014, 59, 475–485. [Google Scholar] [CrossRef]
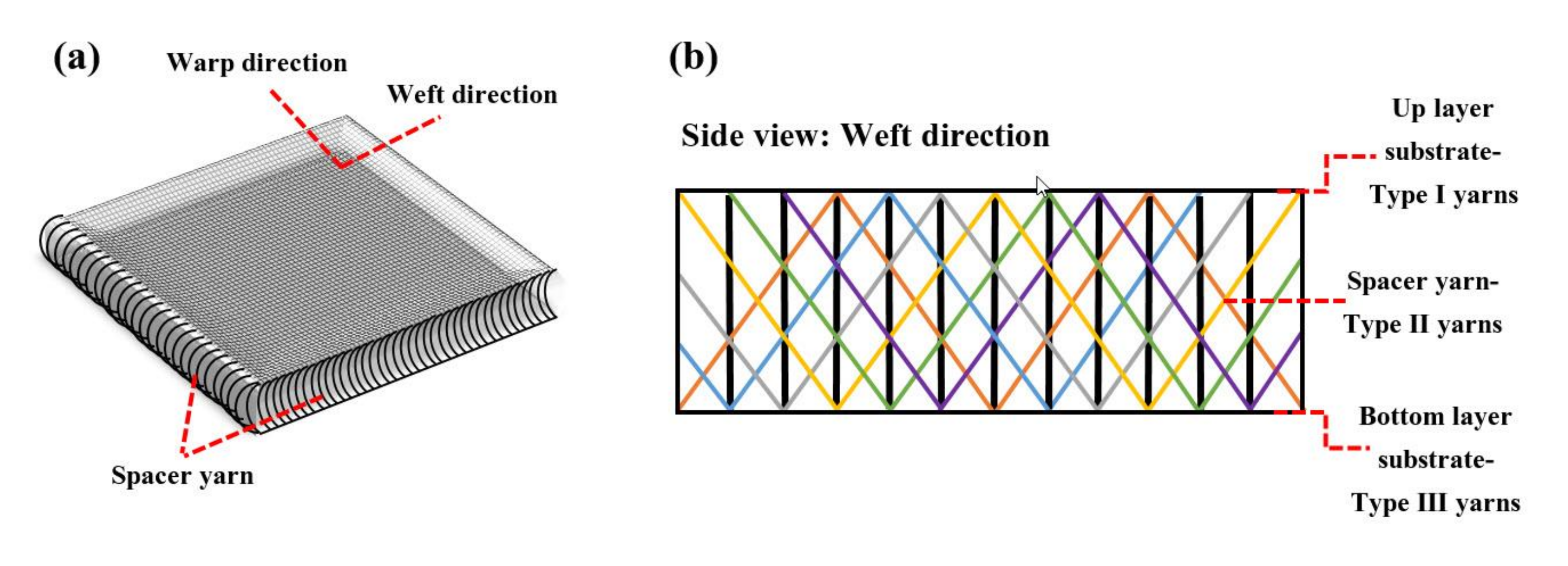
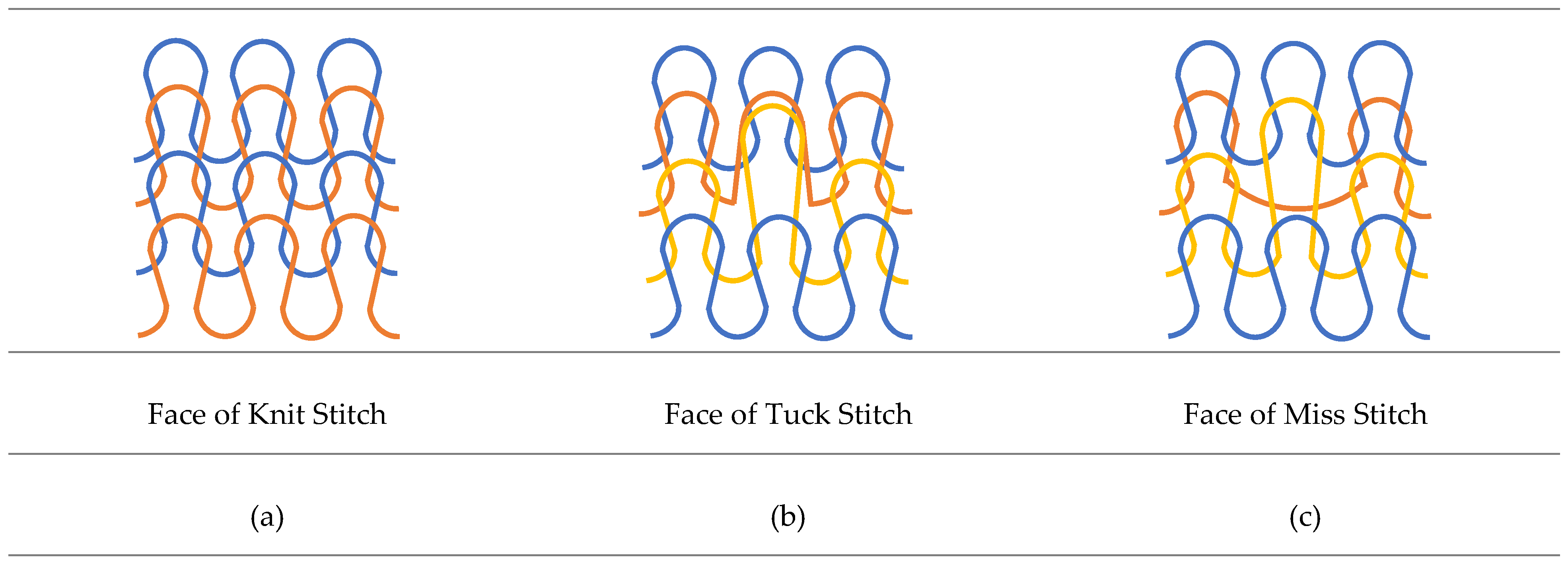





| 3D Spacer Fabric | Density (kg/m3) | Amount of Spacer Yarn (Spacer Yarns/cm2) | Bottom Layer of Outer Textile Substrate | The Knit Repeat of Layers of Spacer Fabrics | Top Layer of Outer Textile Substrate | |
|---|---|---|---|---|---|---|
| Top Layer | Bottom Layer | |||||
| SF1 | 104.687 | 63 |  |  |  |  |
| SF2 | 102.864 | 80 |  |  |  |  |
| SF3 | 97.1354 | 54 |  |  |  |  |
| Chemical Composition | Cement (%) | Sand (%) |
|---|---|---|
| Al2O3 | 37 | 0.29 |
| Si2O | 4 | 98.63 |
| CaO | 37 | 0.3 |
| Fe2O3 | 15 | 0.041 |
| Ti2O | 5 | - |
| MgO | 2 | 0.05 |
| Na2O | - | 0.02 |
| K2O | - | 0.07 |
| L.O.I | - | 0.5 |
| Mixing Proportions and Tests Set Up | |
|---|---|
| sand | 1500 kg/m3 |
| cement | 500 kg/m3 |
| cement-to-sand ratio | 1:3 |
| water-to-cement ratio | 0.366 |
| curing temperature conditions | 7 °C, 23 °C, and 50 °C |
| curing age conditions | 6 h, 1,3,7, and 28 days |
| stitch structures | SF1, SF2, and SF3 |
| tensile test directions | warp and weft |
| 3D Spacer Fabric | Component | Young’s Modulus (GPa) | Tensile Strength (MPa) | Ultimate Elongation (%) | Fineness (den) | Diameter (mm) |
|---|---|---|---|---|---|---|
| SF1–SF2–SF3 | Warp/Weft Yarn | 1.712 | 426.194 | 25.2 | 150 | 0.12 |
| Spacer Yarn | 3.328 | 475.831 | 14.2 | 80 | 0.1 |
| SF1/Weft | SF1/Warp | SF2/Weft | SF2/Warp | SF3/Weft | SF3/Warp | |
|---|---|---|---|---|---|---|
| Tensile stress max (MPa) | 5.53 | 2.6 | 5.29 | 2.47 | 5.57 | 2.8 |
| Fracture tensile strain (εf) | 0.41 | 0.81 | 0.36 | 1.01 | 0.2 | 0.94 |
| Ultimate tensile stress (MPa) | 5.53 | 2.2 | 4.1 | 2.07 | 0.18 | 0.12 |
| Ultimate tensile strain (εu) | 0.41 | 1.16 | 0.38 | 1.06 | 0.65 | 1.4 |
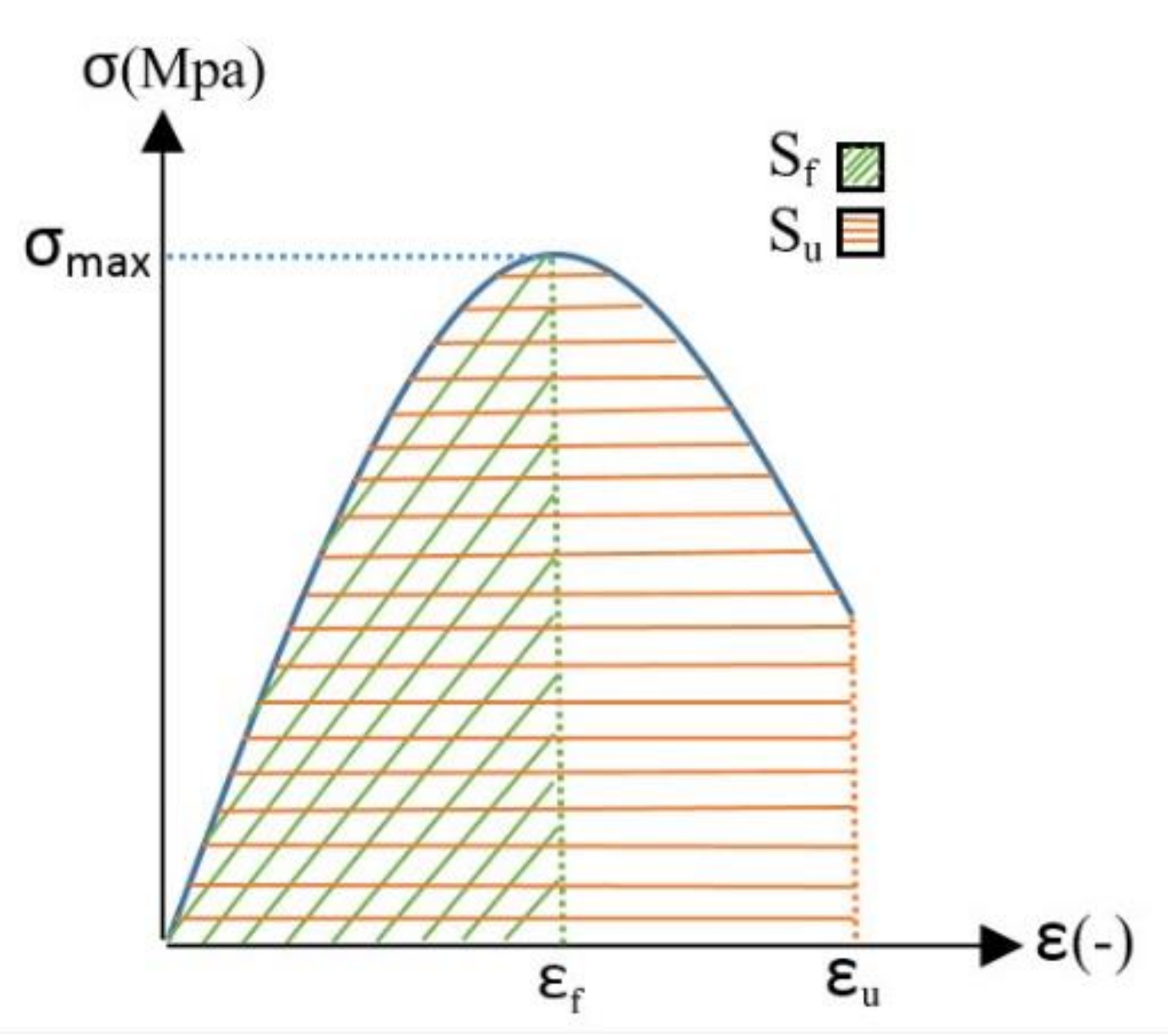
| Weft Direction | εf | εu | εf/εu | Sf | Su | Warp Direction | εf | εu | εf/εu | Sf | Su |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7C-6h-w SF1 | 0.404 | 0.404 | 1.000 | 1.175 | 1.175 | 7C-6h-C SF1 | 1.072 | 1.115 | 0.962 | 0.715 | 0.769 |
| 7C-6h-w SF2 | 0.349 | 0.383 | 0.910 | 0.822 | 0.920 | 7C-6h-C SF2 | 0.841 | 0.853 | 0.986 | 0.694 | 0.708 |
| 7C-6h-w SF3 | 0.186 | 0.677 | 0.275 | 0.444 | 0.833 | 7C-6h-C SF3 | 0.955 | 1.421 | 0.672 | 1.229 | 1.801 |
| 7C-1d-w SF1 | 0.400 | 0.400 | 1.000 | 1.196 | 1.196 | 7C-1d-C SF1 | 0.612 | 1.024 | 0.597 | 0.787 | 1.223 |
| 7C-1d-w SF2 | 0.302 | 0.379 | 0.798 | 0.900 | 1.071 | 7C-1d-C SF2 | 0.795 | 0.960 | 0.828 | 0.763 | 0.946 |
| 7C-1d-w SF3 | 0.106 | 0.642 | 0.165 | 0.297 | 0.858 | 7C-1d-C SF3 | 0.586 | 1.412 | 0.415 | 1.275 | 1.840 |
| 7C-3d-w SF1 | 0.415 | 0.415 | 1.000 | 1.219 | 1.219 | 7C-3d-C SF1 | 1.007 | 1.088 | 0.926 | 0.917 | 1.317 |
| 7C-3d-w SF2 | 0.380 | 0.385 | 0.987 | 1.049 | 1.072 | 7C-3d-C SF2 | 0.973 | 1.033 | 0.942 | 0.821 | 0.994 |
| 7C-3d-w SF3 | 0.189 | 0.679 | 0.279 | 0.452 | 0.981 | 7C-3d-C SF3 | 0.659 | 1.409 | 0.468 | 1.300 | 1.855 |
| 7C-7d-w SF1 | 0.403 | 0.403 | 1.000 | 1.285 | 1.285 | 7C-7d-C SF1 | 0.892 | 1.124 | 0.794 | 1.312 | 1.591 |
| 7C-7d-w SF2 | 0.394 | 0.394 | 1.000 | 1.108 | 1.108 | 7C-7d-C SF2 | 1.018 | 1.082 | 0.941 | 1.149 | 1.243 |
| 7C-7d-w SF3 | 0.153 | 0.646 | 0.237 | 0.534 | 1.024 | 7C-7d-C SF3 | 0.957 | 1.416 | 0.676 | 1.581 | 2.254 |
| 7C-28d-w SF1 | 0.419 | 0.419 | 1.000 | 1.322 | 1.322 | 7C-28d-C SF1 | 0.842 | 1.142 | 0.738 | 1.319 | 1.640 |
| 7C-28d-w SF2 | 0.389 | 0.389 | 1.000 | 1.115 | 1.115 | 7C-28d-C SF2 | 0.966 | 1.065 | 0.906 | 1.180 | 1.360 |
| 7C-28d-w SF3 | 0.095 | 0.646 | 0.148 | 0.408 | 1.035 | 7C-28d-C SF3 | 0.958 | 1.401 | 0.684 | 1.621 | 2.114 |
| 23C-1d-w SF1 | 0.388 | 0.406 | 0.955 | 1.200 | 1.280 | 23C-1d-C SF1 | 0.982 | 1.153 | 0.851 | 1.003 | 1.323 |
| 23C-1d-w SF2 | 0.227 | 0.384 | 0.591 | 1.024 | 1.230 | 23C-1d-C SF2 | 0.923 | 1.035 | 0.892 | 0.822 | 0.979 |
| 23C-1d-w SF3 | 0.169 | 0.677 | 0.250 | 0.365 | 0.875 | 23C-1d-C SF3 | 0.488 | 1.472 | 0.331 | 1.280 | 1.867 |
| 23C-3d-w SF1 | 0.420 | 0.420 | 1.000 | 1.399 | 1.399 | 23C-3d-C SF1 | 0.778 | 1.195 | 0.651 | 1.008 | 1.885 |
| 23C-3d-w SF2 | 0.373 | 0.383 | 0.973 | 1.235 | 1.275 | 23C-3d-C SF2 | 0.670 | 0.907 | 0.739 | 0.832 | 1.225 |
| 23C-3d-w SF3 | 0.263 | 0.700 | 0.375 | 0.533 | 1.042 | 23C-3d-C SF3 | 0.594 | 1.416 | 0.420 | 1.373 | 2.026 |
| 23C-7d-w SF1 | 0.410 | 0.410 | 1.000 | 1.540 | 1.540 | 23C-7d-C SF1 | 0.819 | 1.162 | 0.705 | 1.327 | 2.064 |
| 23C-7d-w SF2 | 0.360 | 0.384 | 0.939 | 1.276 | 1.388 | 23C-7d-C SF2 | 1.019 | 1.063 | 0.959 | 1.307 | 1.409 |
| 23C-7d-w SF3 | 0.203 | 0.656 | 0.309 | 0.586 | 1.151 | 23C-7d-C SF3 | 0.944 | 1.404 | 0.672 | 1.652 | 2.400 |
| 23C-28d-w SF1 | 0.402 | 0.402 | 1.000 | 1.523 | 1.523 | 23C-28d-C SF1 | 0.855 | 1.148 | 0.745 | 1.321 | 1.941 |
| 23C-28d-w SF2 | 0.380 | 0.387 | 0.983 | 1.148 | 1.180 | 23C-28d-C SF2 | 0.833 | 1.021 | 0.815 | 1.186 | 1.390 |
| 23C-28d-w SF3 | 0.198 | 0.968 | 0.205 | 0.513 | 1.049 | 23C-28d-C SF3 | 0.788 | 1.425 | 0.553 | 1.638 | 2.396 |
| 50C-1d-w SF1 | 0.406 | 0.406 | 1.000 | 1.184 | 1.184 | 50C-1d-C SF1 | 0.973 | 1.131 | 0.860 | 0.743 | 0.950 |
| 50C-1d-w SF2 | 0.345 | 0.382 | 0.902 | 0.840 | 0.973 | 50C-1d-C SF2 | 0.913 | 1.029 | 0.887 | 0.710 | 0.939 |
| 50C-1d-w SF3 | 0.075 | 0.663 | 0.113 | 0.098 | 0.844 | 50C-1d-C SF3 | 0.745 | 1.418 | 0.525 | 1.265 | 1.810 |
| 50C-3d-w SF1 | 0.420 | 0.420 | 1.000 | 1.194 | 1.194 | 50C-3d-C SF1 | 1.060 | 1.136 | 0.933 | 0.914 | 1.026 |
| 50C-3d-w SF2 | 0.359 | 0.385 | 0.934 | 0.918 | 1.021 | 50C-3d-C SF2 | 1.013 | 1.030 | 0.984 | 0.794 | 0.952 |
| 50C-3d-w SF3 | 0.145 | 0.654 | 0.221 | 0.427 | 0.965 | 50C-3d-C SF3 | 0.581 | 1.428 | 0.406 | 1.270 | 1.589 |
| 50C-7d-w SF1 | 0.416 | 0.416 | 1.000 | 1.205 | 1.220 | 50C-7d-C SF1 | 0.917 | 1.135 | 0.807 | 1.074 | 1.140 |
| 50C-7d-w SF2 | 0.348 | 0.387 | 0.899 | 1.088 | 1.085 | 50C-7d-C SF2 | 0.862 | 0.960 | 0.898 | 0.812 | 1.099 |
| 50C-7d-w SF3 | 0.113 | 0.695 | 0.162 | 0.215 | 0.991 | 50C-7d-C SF3 | 0.467 | 1.422 | 0.328 | 1.318 | 1.612 |
| 50C-28d-w SF1 | 0.398 | 0.398 | 1.000 | 1.237 | 1.237 | 50C-28d-C SF1 | 1.092 | 1.144 | 0.955 | 1.117 | 1.195 |
| 50C-28d-w SF2 | 0.397 | 0.397 | 1.000 | 1.103 | 1.103 | 50C-28d-C SF2 | 0.926 | 0.969 | 0.956 | 1.019 | 1.110 |
| 50C-28d-w SF3 | 0.123 | 0.632 | 0.194 | 0.342 | 1.024 | 50C-28d-C SF3 | 0.696 | 1.408 | 0.495 | 1.369 | 1.921 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adosi, B.; Mirjalili, S.A.; Adresi, M.; Tulliani, J.-M.; Antonaci, P. Experimental Evaluation of Tensile Performance of Aluminate Cement Composite Reinforced with Weft Knitted Fabrics as a Function of Curing Temperature. Polymers 2021, 13, 4385. https://doi.org/10.3390/polym13244385
Adosi B, Mirjalili SA, Adresi M, Tulliani J-M, Antonaci P. Experimental Evaluation of Tensile Performance of Aluminate Cement Composite Reinforced with Weft Knitted Fabrics as a Function of Curing Temperature. Polymers. 2021; 13(24):4385. https://doi.org/10.3390/polym13244385
Chicago/Turabian StyleAdosi, Bentolhoda, Seyed Abbas Mirjalili, Mostafa Adresi, Jean-Marc Tulliani, and Paola Antonaci. 2021. "Experimental Evaluation of Tensile Performance of Aluminate Cement Composite Reinforced with Weft Knitted Fabrics as a Function of Curing Temperature" Polymers 13, no. 24: 4385. https://doi.org/10.3390/polym13244385
APA StyleAdosi, B., Mirjalili, S. A., Adresi, M., Tulliani, J.-M., & Antonaci, P. (2021). Experimental Evaluation of Tensile Performance of Aluminate Cement Composite Reinforced with Weft Knitted Fabrics as a Function of Curing Temperature. Polymers, 13(24), 4385. https://doi.org/10.3390/polym13244385






