Improvement of the Centrifugal Force in Gravity Driven Method for the Fabrication of Highly Ordered and Submillimeter-Thick Colloidal Crystal
Abstract
:1. Introduction
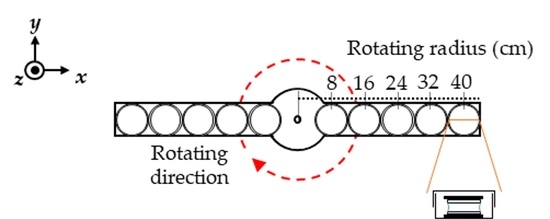
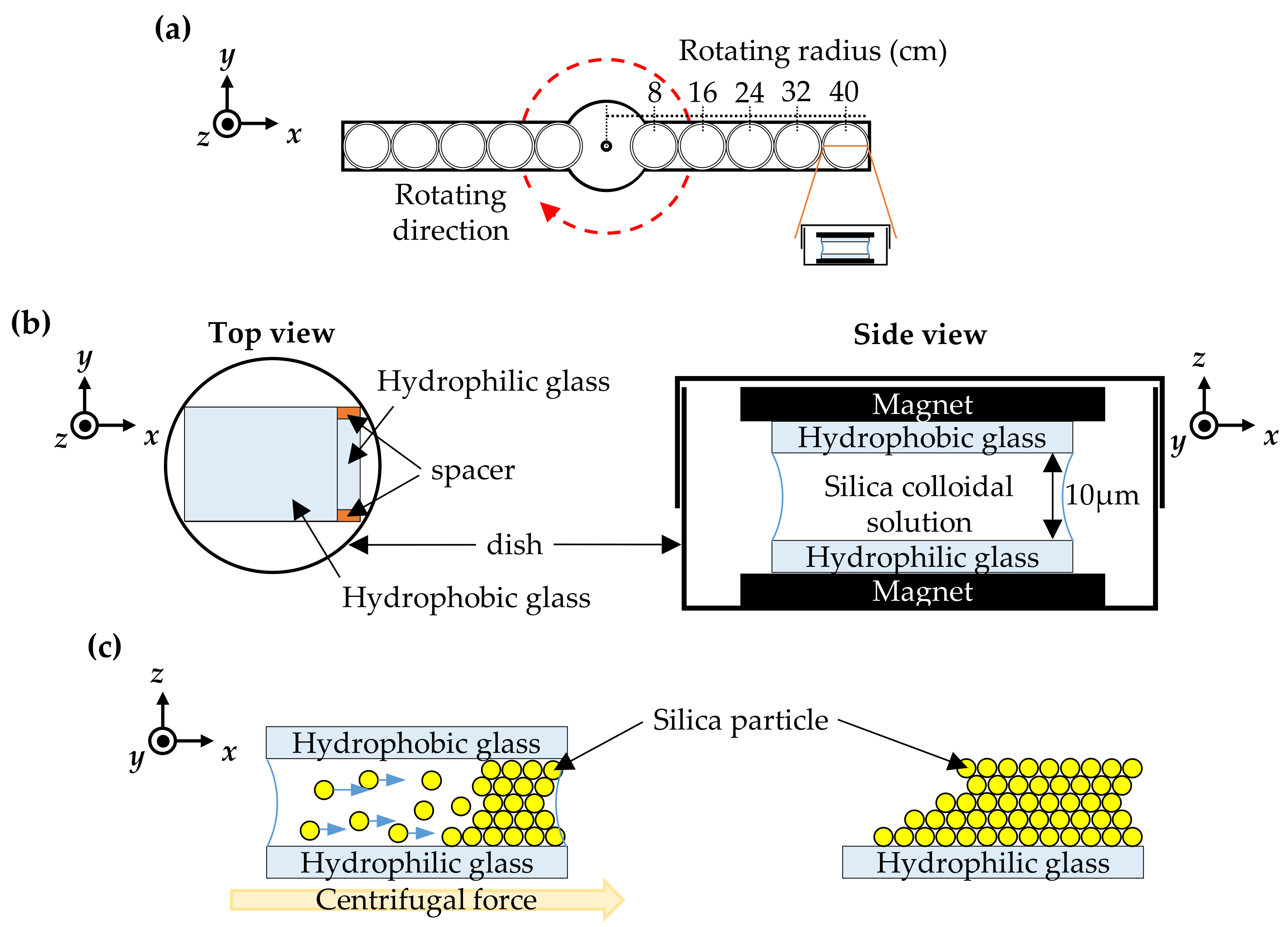
2. Materials and Methods
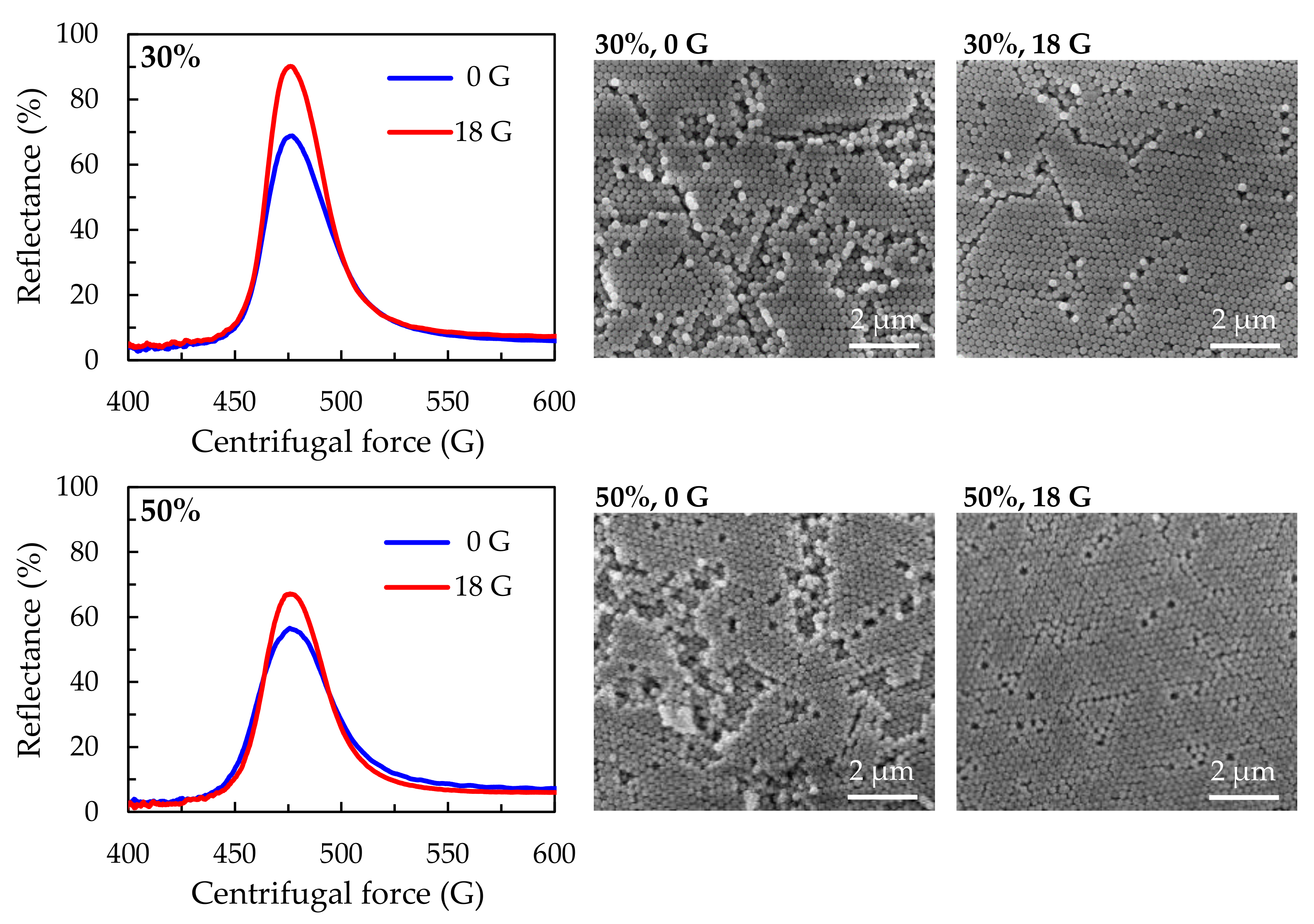
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yamada, H.; Nakamura, T.; Yamada, Y.; Yano, K. Colloidal-Crystal Laser Using Monodispersed Mesoporous Silica Spheres. Adv. Mater. 2009, 21, 4134–4138. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, K.; Chen, Q.; Cheddah, S.; Shen, L.; Xiao, H.; Wang, Y.; Yan, C. Preparation of silica colloidal crystal column and its application in pressurized capillary electrochromatography. J. Chromatogr. A 2019, 1587, 172–179. [Google Scholar] [CrossRef] [PubMed]
- Salcedo-Reyes, J.C.; Vásquez-Rojas, J.R.; Jiménez-Borrego, L.C.; Castañeda-Uribe, O.A.; Méndez-Pinzón, H.A. Improving extraction efficiency of OLEDs by a luminescent polymer embedded in a colloidal crystal matrix. Semicond. Sci. Technol. 2019, 34, 115016. [Google Scholar] [CrossRef]
- Yang, D.; Ye, S.; Ge, J. From Metastable Colloidal Crystalline Arrays to Fast Responsive Mechanochromic Photonic Gels: An Organic Gel for Deformation-Based Display Panels. Adv. Funct. Mater. 2014, 24, 3197–3205. [Google Scholar] [CrossRef]
- Aguirre, C.I.; Reguera, E.; Stein, A. Tunable Colors in Opals and Inverse Opal Photonic Crystals. Adv. Funct. Mater. 2010, 20, 2565–2578. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, M.; Zhang, J.; Tong, Y.L.; Wang, C.F.; Wiederrecht, G.P.; Chen, S. Highly enhanced luminescence performance of LEDs via controllable layer-structured 3D photonic crystals and photonic crystal beads. Small Methods 2018, 2, 1800104. [Google Scholar] [CrossRef]
- Galukhin, A.; Bolmatenkov, D.; Emelianova, A.; Zharov, I.; Gor, G.Y. Porous Structure of Silica Colloidal Crystals. Langmuir 2019, 35, 2230–2235. [Google Scholar] [CrossRef]
- Ye, R.; Ye, Y.-H.; Zhou, Z.; Xu, H. Gravity-Assisted Convective Assembly of Centimeter-Sized Uniform Two-Dimensional Colloidal Crystals. Langmuir 2013, 29, 1796–1801. [Google Scholar] [CrossRef] [PubMed]
- Trau, M.; Saville, D.A.; Aksay, I.A. Field-Induced Layering of Colloidal Crystals. Science 1996, 272, 706–709. [Google Scholar] [CrossRef]
- Solomentsev, Y.; Böhmer, M.; Anderson, J.L. Particle Clustering and Pattern Formation during Electrophoretic Deposition: A Hydrodynamic Model. Langmuir 1997, 13, 6058–6068. [Google Scholar] [CrossRef]
- Hung, P.S.; Liao, C.H.; Chou, Y.S.; Wang, G.R.; Wang, C.J.; Chung, W.A.; Wu, P.W. High throughput fabrication of large-area colloidal crystals via a two-stage electrophoretic deposition method. Electrochim. Acta 2019, 317, 52–60. [Google Scholar] [CrossRef]
- He, Y.; Zhu, B.; Zeng, X.; Yang, R.; Lv, X.; Yuan, W. Fabrication of large-area, close-packed, monolayer colloidal crystals via a hybrid method of spin coating and peeling–draining. Thin Solid Films 2017, 639, 98–106. [Google Scholar] [CrossRef]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Capillary flow as the cause of ring stains from dried liquid drops. Nature 1997, 389, 827–829. [Google Scholar] [CrossRef]
- Celio, H.; Barton, E.; Stevenson, K.J. Patterned Assembly of Colloidal Particles by Confined Dewetting Lithography. Langmuir 2006, 22, 11426–11435. [Google Scholar] [CrossRef]
- Wong, S.; Kitaev, V.; Ozin, G.A. Colloidal Crystal Films: Advances in Universality and Perfection. J. Am. Chem. Soc. 2003, 125, 15589–15598. [Google Scholar] [CrossRef] [PubMed]
- Phillips, K.R.; Zhang, C.T.; Yang, T.; Kay, T.; Gao, C.; Brandt, S.; Liu, L.; Yang, H.; Li, Y.; Aizenberg, J.; et al. Fabrication of Photonic Microbricks via Crack Engineering of Colloidal Crystals. Adv. Funct. Mater. 2019, 30, 1908242. [Google Scholar] [CrossRef]
- Jiang, P.; Bertone, J.F.; Hwang, K.S.; Colvin, V.L. Single-Crystal Colloidal Multilayers of Controlled Thickness. Chem. Mater. 1999, 11, 2132–2140. [Google Scholar] [CrossRef]
- Sandu, I.; Dumitru, M.; Fleaca, C.T.; Dumitrache, F. Hanging colloidal drop: A new photonic crystal synthesis route. Photonics Nanostruct. 2018, 29, 42–48. [Google Scholar] [CrossRef]
- Ye, Y.-H.; LeBlanc, F.; Haché, A.; Truong, V.-V. Self-assembling three-dimensional colloidal photonic crystal structure with high crystalline quality. Appl. Phys. Lett. 2001, 78, 52–54. [Google Scholar] [CrossRef]
- Zeng, F.; Sun, Z.; Wang, C.; Ren, B.; Liu, X.; Tong, Z. Fabrication of Inverse Opal via Ordered Highly Charged Colloidal Spheres. Langmuir 2002, 18, 9116–9120. [Google Scholar] [CrossRef]
- Maury, P.; Escalante, M.; Reinhoudt, D.N.; Huskens, J. Directed Assembly of Nanoparticles onto Polymer-Imprinted or Chemically Patterned Templates Fabricated by Nanoimprint Lithography. Adv. Mater. 2005, 17, 2718–2723. [Google Scholar] [CrossRef]
- Wu, Y.; Yuan, J.; Li, M.; Liu, C.; Wu, P.; Lu, J.; Wang, X. Rapid fabrication and characterization of SiO2-Fe2O3 heterogeneous metamaterial via one-step self-assembly process. Mater. Res. Bull. 2019, 114, 68–73. [Google Scholar] [CrossRef]
- Stöber, W.; Fink, A.; Bohn, E. Controlled growth of monodisperse silica spheres in the micron size range. J. Colloid Interf. Sci. 1968, 26, 62–69. [Google Scholar] [CrossRef]
- Bogush, G.H.; Tracy, M.A.; Zukoski IV, C.F. Preparation of monodisperse silica particles: Control of size and mass fraction. J. Non Cryst. Solids 1988, 104, 95–106. [Google Scholar] [CrossRef]
- Watanabe, R.; Yokoi, T.; Kobayashi, E.; Otsuka, Y.; Shimojima, A.; Okubo, T.; Tatsumi, T. Extension of size of monodisperse silica nanospheres and their well-ordered assembly. J. Colloid Interf. Sci. 2011, 360, 1–7. [Google Scholar] [CrossRef]
- Masuda, Y.; Itoh, M.; Yonezawa, T.; Koumoto, K. Low-Dimensional Arrangement of SiO2 Particles. Langmuir 2002, 18, 4155–4159. [Google Scholar] [CrossRef]
- Szekeres, M.; Kamalin, O.; Grobet, P.G.; Schoonheydt, R.A.; Wostyn, K.; Clays, K.; Persoons, A.; Dékány, I. Two-dimensional ordering of Stöber silica particles at the air/water interface. Colloids Surf. A Physicochem. Eng. Asp. 2003, 227, 77–83. [Google Scholar] [CrossRef]
- Choi, K.-M.; Kuroda, K. Double function of tris(hydroxymethyl)aminomethane (THAM) for the preparation of colloidal silica nanospheres and the conversion to ordered mesoporous carbon. Chem. Commun. 2011, 47, 10933–10935. [Google Scholar] [CrossRef]
- Yokoi, T.; Wakabayashi, J.; Otsuka, Y.; Fan, W.; Iwama, M.; Watanabe, R.; Aramaki, K.; Shimojima, A.; Tatsumi, T.; Okubo, T. Mechanism of Formation of Uniform-Sized Silica Nanospheres Catalyzed by Basic Amino Acids. Chem. Mater. 2009, 21, 3719–3729. [Google Scholar] [CrossRef]
- Yokoi, T.; Sakamoto, Y.; Terasaki, O.; Kubota, Y.; Okubo, T.; Tatsumi, T. Periodic Arrangement of Silica Nanospheres Assisted by Amino Acids. J. Am. Chem. Soc. 2006, 128, 13664–13665. [Google Scholar] [CrossRef]
- Yan, Q.; Zhou, Z.; Zhao, X.S. Inward-Growing Self-Assembly of Colloidal Crystal Films on Horizontal Substrates. Langmuir 2005, 21, 3158–3164. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.-H.; Huang, S.-Y.; Huang, S.-Y.; Lin, J.-D.; Huang, B.-Y.; Kuo, C.-T. Improvement of the Centrifugal Force in Gravity Driven Method for the Fabrication of Highly Ordered and Submillimeter-Thick Colloidal Crystal. Polymers 2021, 13, 692. https://doi.org/10.3390/polym13050692
Chen T-H, Huang S-Y, Huang S-Y, Lin J-D, Huang B-Y, Kuo C-T. Improvement of the Centrifugal Force in Gravity Driven Method for the Fabrication of Highly Ordered and Submillimeter-Thick Colloidal Crystal. Polymers. 2021; 13(5):692. https://doi.org/10.3390/polym13050692
Chicago/Turabian StyleChen, Ting-Hui, Shuan-Yu Huang, Syuan-Yi Huang, Jia-De Lin, Bing-Yau Huang, and Chie-Tong Kuo. 2021. "Improvement of the Centrifugal Force in Gravity Driven Method for the Fabrication of Highly Ordered and Submillimeter-Thick Colloidal Crystal" Polymers 13, no. 5: 692. https://doi.org/10.3390/polym13050692
APA StyleChen, T.-H., Huang, S.-Y., Huang, S.-Y., Lin, J.-D., Huang, B.-Y., & Kuo, C.-T. (2021). Improvement of the Centrifugal Force in Gravity Driven Method for the Fabrication of Highly Ordered and Submillimeter-Thick Colloidal Crystal. Polymers, 13(5), 692. https://doi.org/10.3390/polym13050692