Design and Analysis of Solid Rocket Composite Motor Case Connector Using Finite Element Method
Abstract
:1. Introduction
2. Experimental Analysis
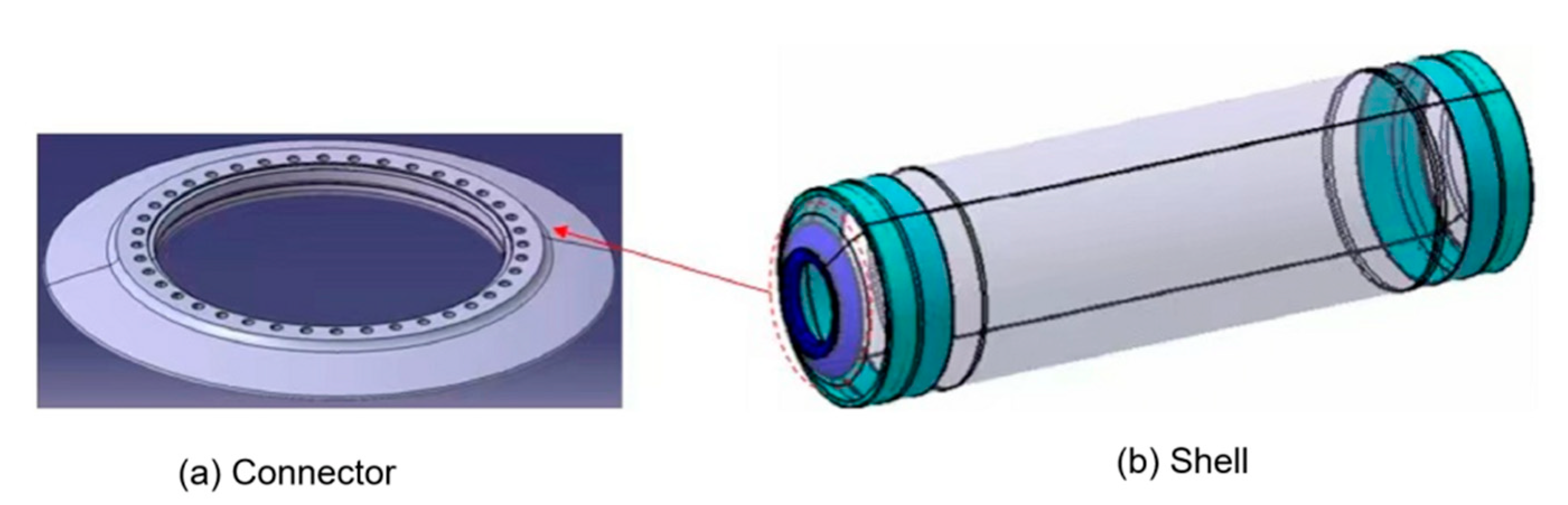
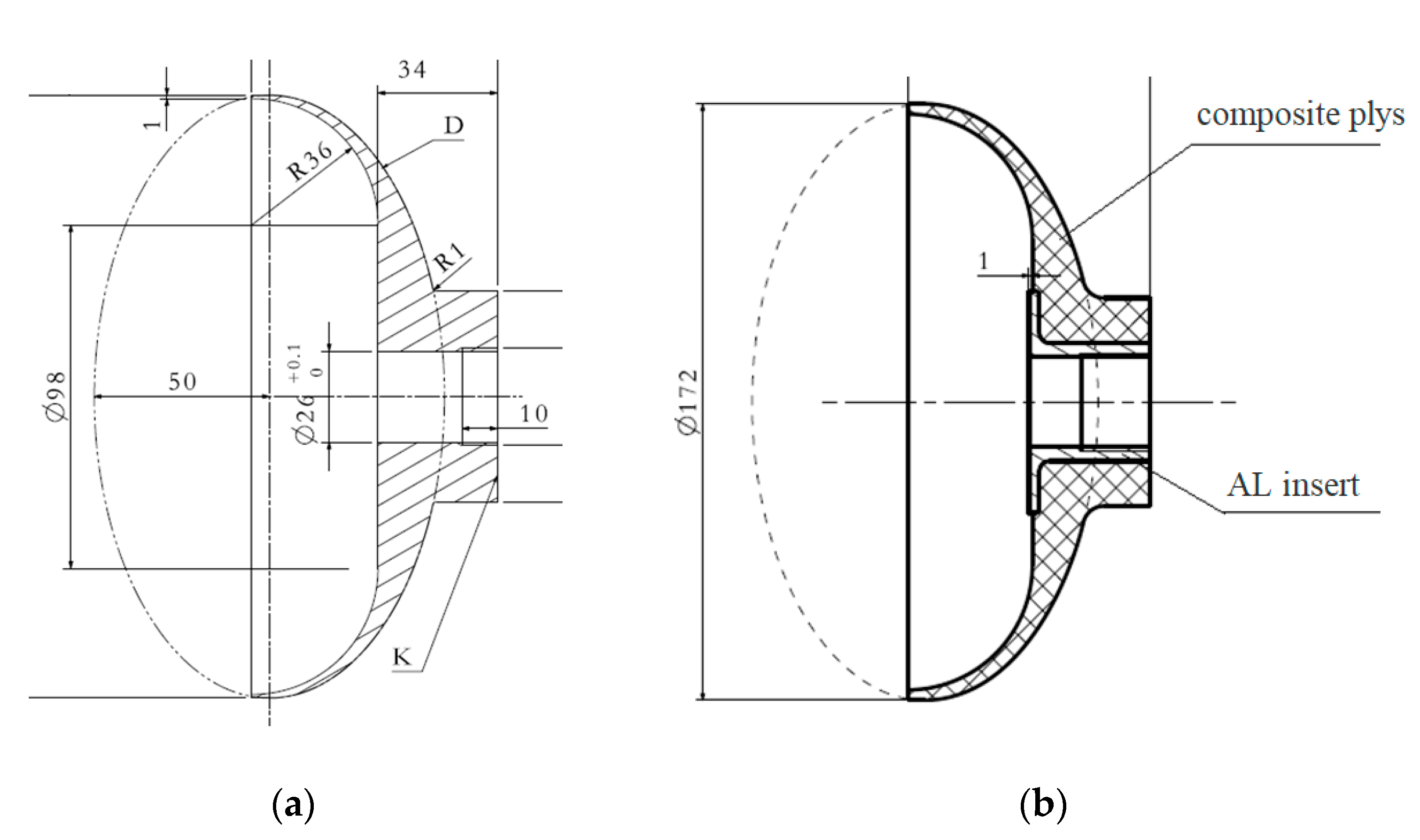
3. Structural Design
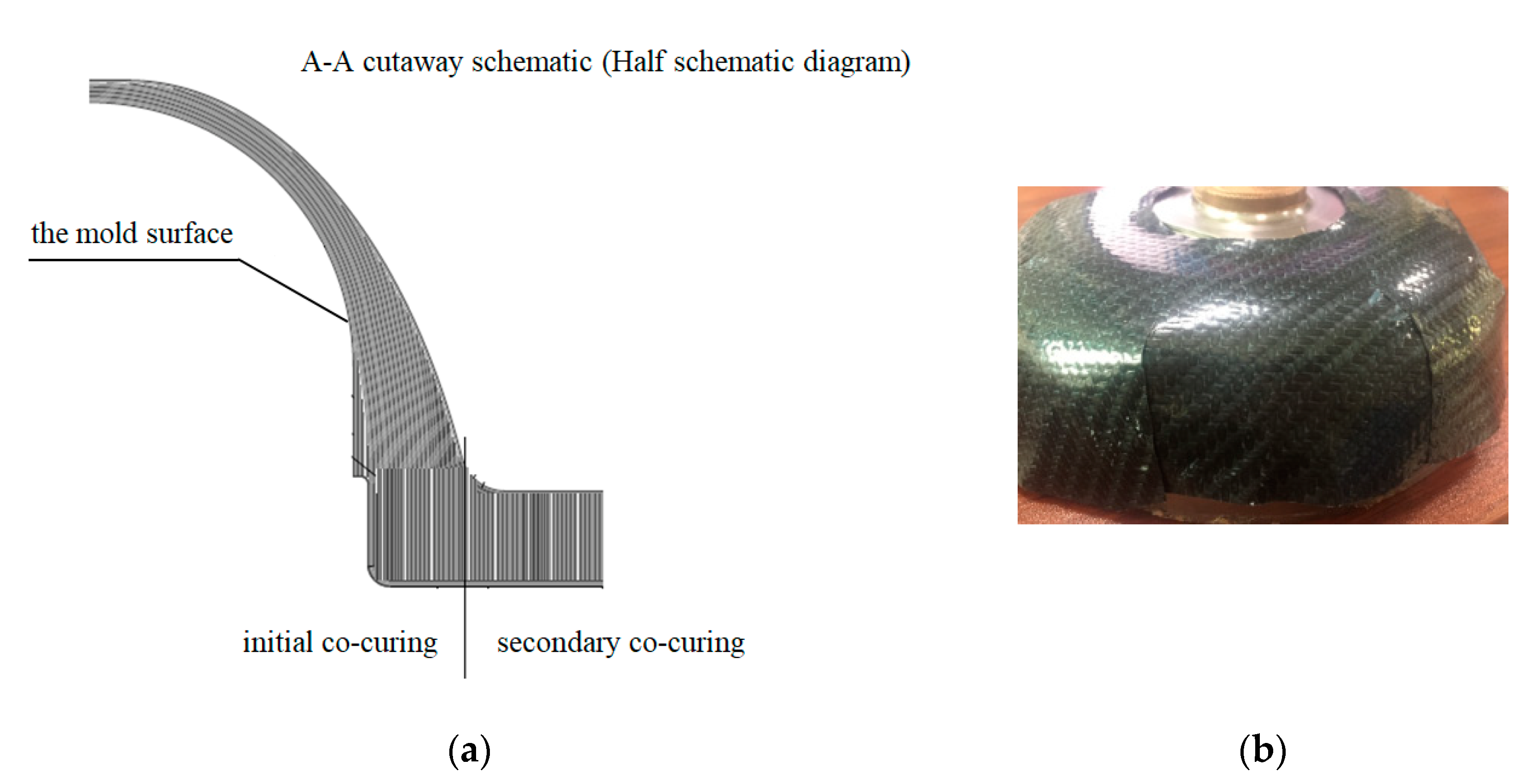
4. RS05A Lay-Up Mode
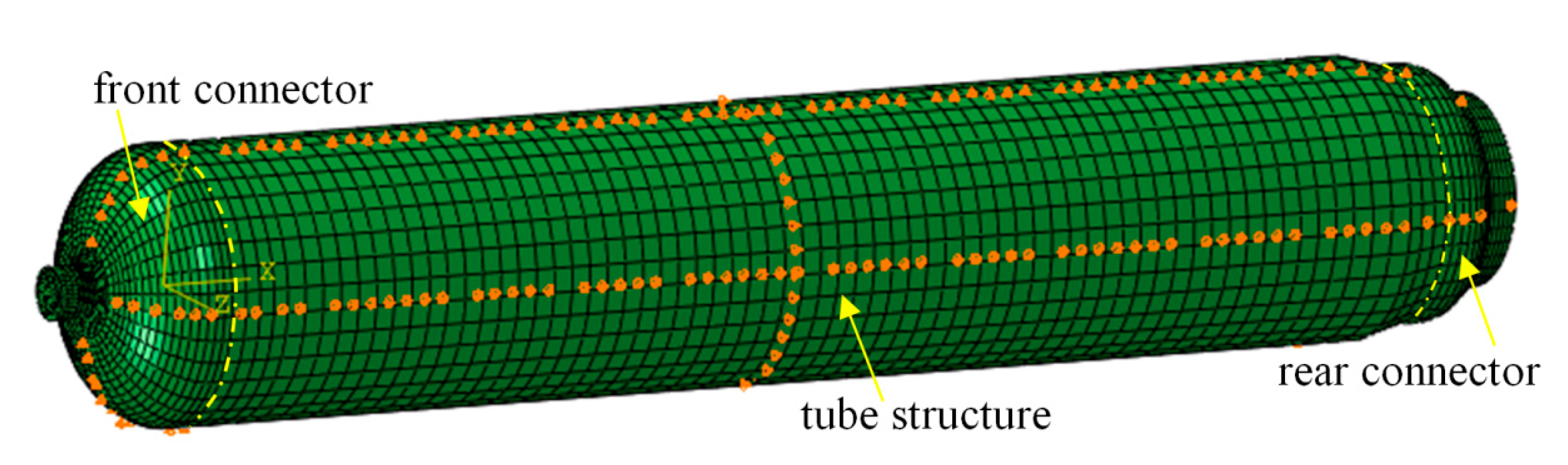
5. Finite Element Model
5.1. Lay-Up Information Table
5.2. Loading and Constraints
6. Results and Discussion
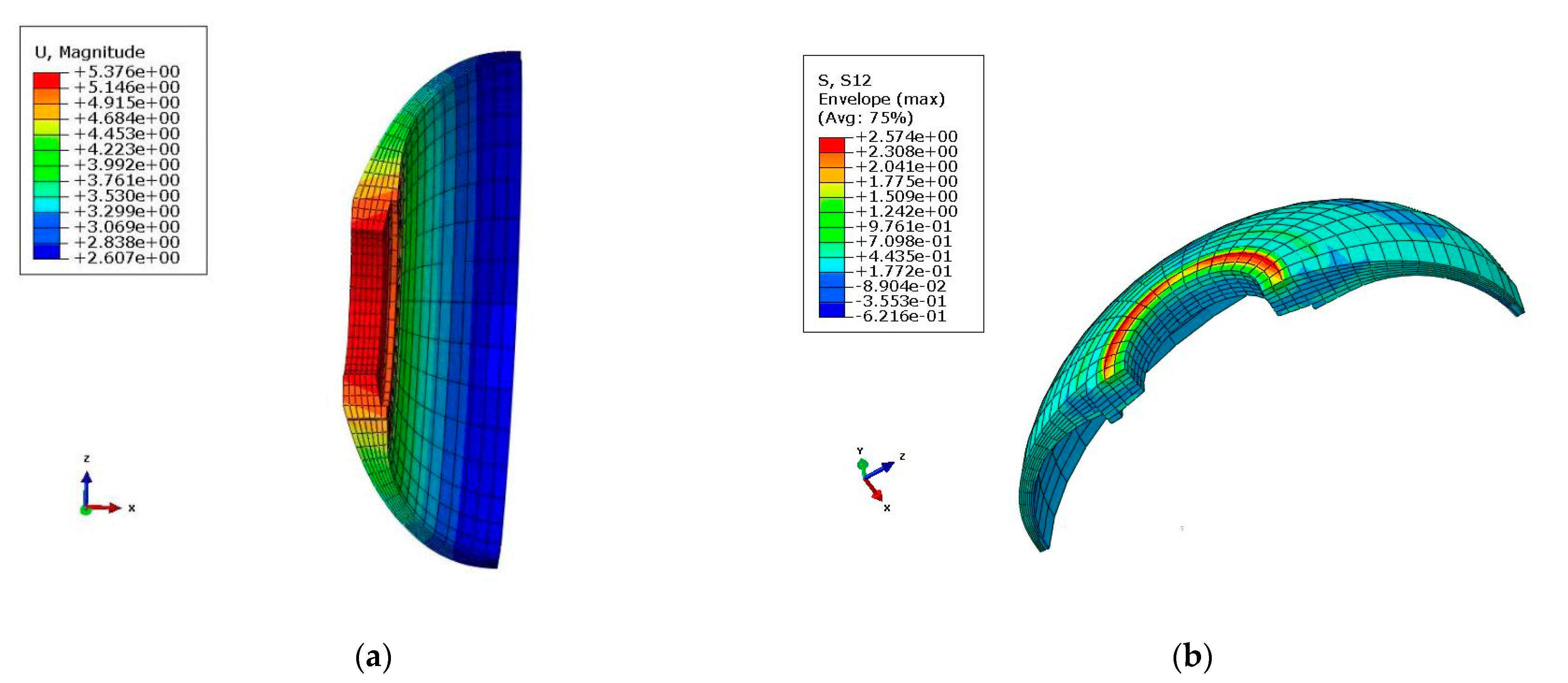
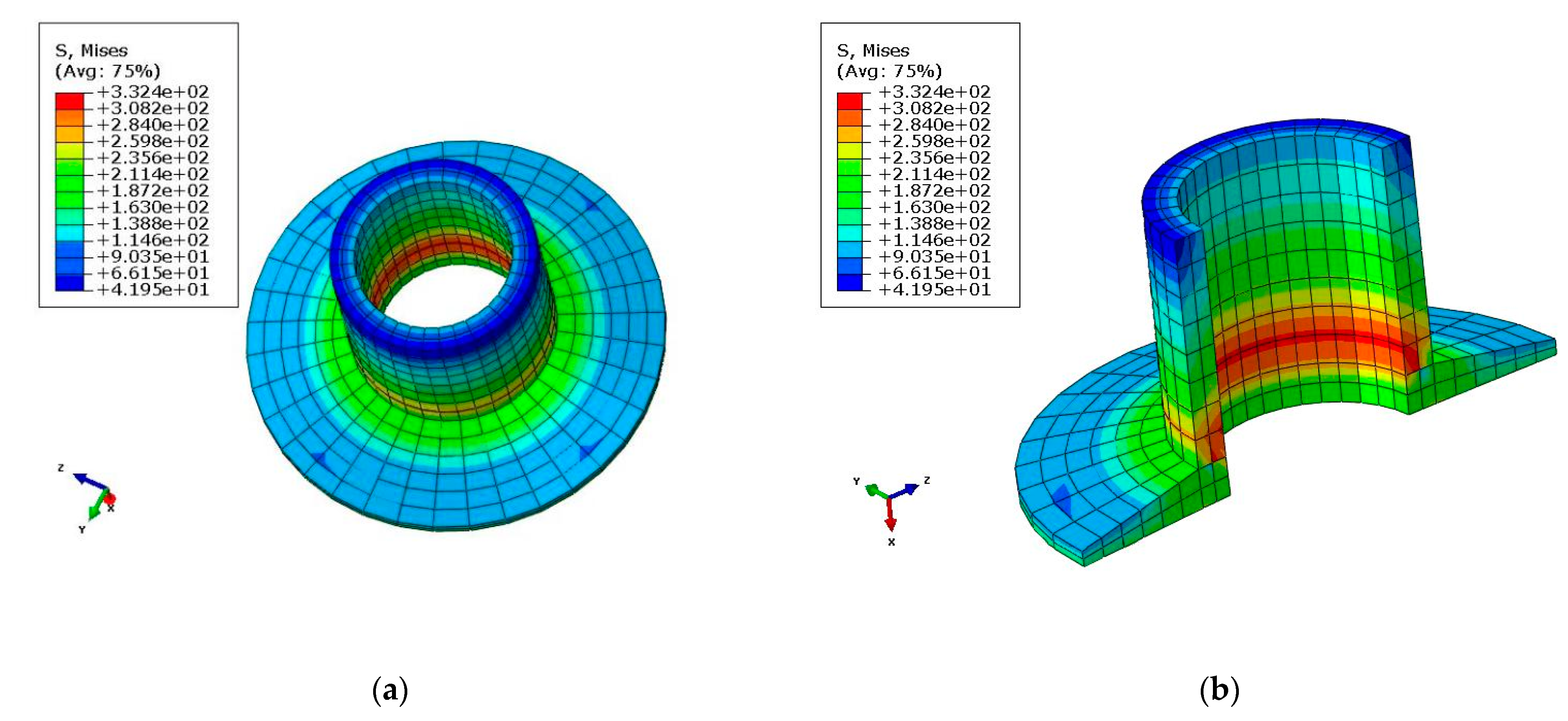
6.1. Analysis Results of the RS05A Front Connector
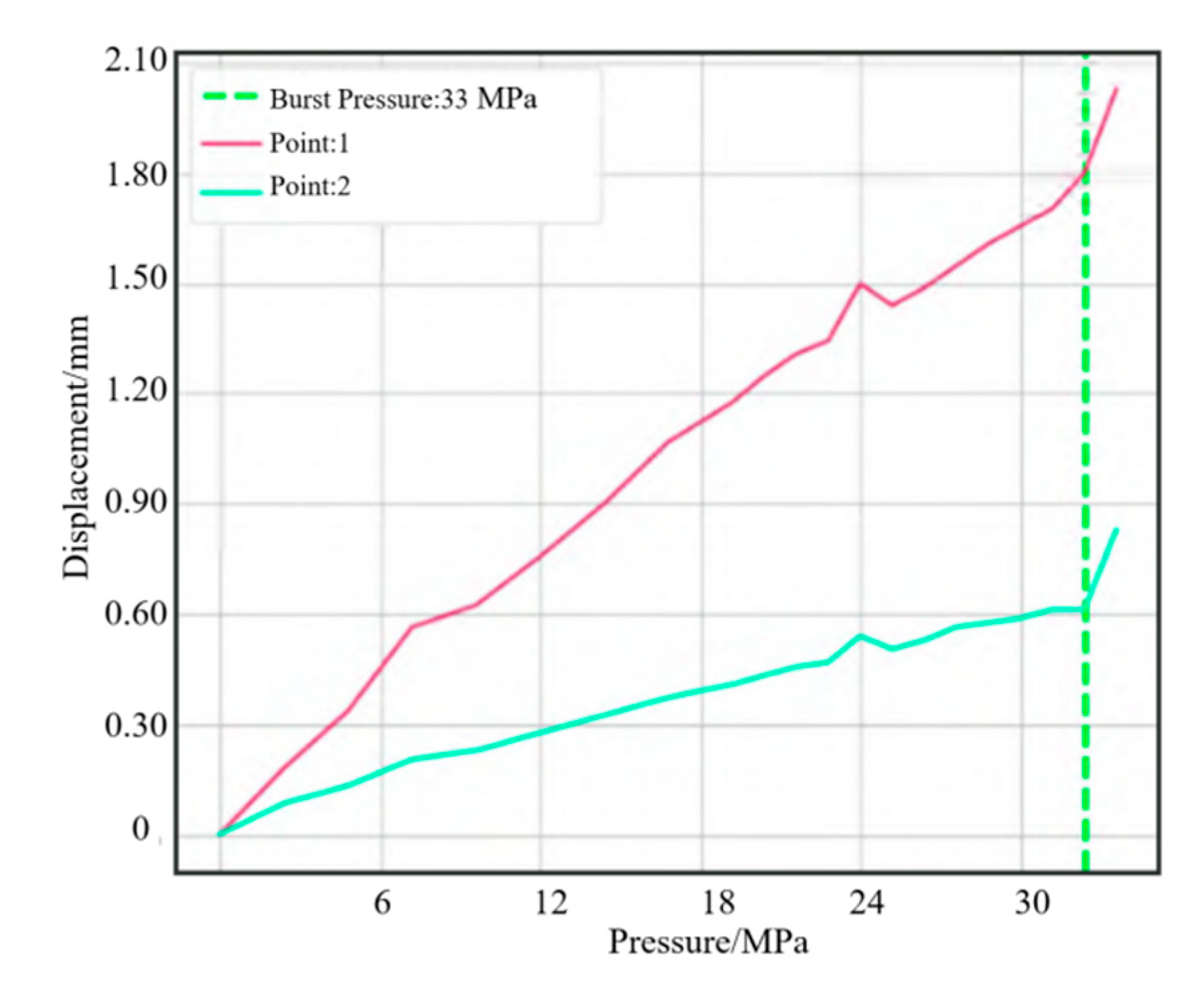
6.2. Experimental Results
7. Conclusions
- In this study, finite element analysis of the SRMC connector was performed. The lay-up and optimum structure designs of the connector were investigated. An experimental design was established, and the FEM simulation value was calculated. Loading and constrains were implemented in the FEM model. The actual experimental measurements were studied for a comparison. A blasting experiment was conducted to verify the simulation results.
- The maximum shear stress in the XY-direction was 2.57 MPa, the maximal tensile and compressive stress calculated using FEM was 492 MPa and −537 MPa, respectively, and the Von Mises stress of the AL insert was 332.4 MPa. The stress–strain values obtained from the simulations were all within the permissible limits obtained from the experiments.
- The accuracy of the modeling method was verified by analyzing the displacement and blasting pressure of the finite element simulation results. The comparison results showed that the FME result of blasting was 15 MPa, while the actual blasting was 33 MPa, suggesting that the simulated shell could meet the internal pressure in working conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hou, X.; Qin, Y.; Ding, W.H. Load-bearing Capacity Analysis of Composite Case Structure of Solid Rocket Motor, Acta Materiae Compositae. Acta Mater. Compos. Sin. 2014, 31, 1343–1349. [Google Scholar]
- Yang, M.; Chen, X.H.; Wu, C.B. Numerical Simulation for Burst Progressive Failure of Filament-Wound Composite Case in Solid Rocket Motor. Mater. Mech. Eng. 2012, 36, 92–96. [Google Scholar] [CrossRef]
- Jiang, A.M.; Li, G.C.; Huang, W.D. Finite Element computation and parametric analysis on mechanical property of solid rocket motor bondline. Chin. J. Explos. Propellants 2012, 35, 54–59. [Google Scholar]
- Ramanjaneyulu, V.; Murchy, V.B.; Mohan, R.C. Analysis of composite rocket motor case using finite element method. Mater. Today Proc. 2018, 5, 4920–4929. [Google Scholar] [CrossRef]
- Özaslan, E.; Acar, B.; Yetgin, A. Design and validation of a filament wound composite rocket motor case. In Proceedings of the ASME 2018 Pressure Vessels and Piping Conference, Prague, Czech Republic, 15–20 July 2018; Volume 3A, pp. 1–7. [Google Scholar]
- Niharika, B.; Varma, B.B. Design and analysis of composite rocket motor casing. Mater. Sci. Eng. 2018, 455, 1–8. [Google Scholar] [CrossRef]
- Hossam, I.; Saleh, S.; Hamel, H. Review of challenges of the design of rocket motor case structures. In Proceedings of the 18th International Conference on Aerospace Sciences & Aviation Technology, Cairo, Egypt, 9–11 August 2021; pp. 1–13. [Google Scholar]
- Shaheen, S.; Gupta, G.S. Design and analysis of carbon-epoxy composite rocket motor casing. Int. J. Adv. Res. Innov. Ideas Educ. 2015, 1, 859–871. [Google Scholar]
- Prakash, D.; Murthy, V.B.; Mohan, R.C. Effect of material mismatch on static behavior of flex seal. Mater. Today Proc. 2017, 4, 2290–2297. [Google Scholar] [CrossRef]
- Juan, P.B.R. 700 Bar Type IV High Pressure Hydrogen Storage Vessel Burst-Simulation and Experimental Validation. Int. J. Hydrogen Energy 2015, 40, 13183–13192. [Google Scholar]
- Johansen, B.S.; Lystrup, A.; Jensen, M.T. CAD Path: A Complete Program for the CAD, CAE and CAM-winding of Advanced fibre composites. J. Mater. Process. Technol. 1998, 77, 194–200. [Google Scholar] [CrossRef]
- Amach, M.F. Fibre Composite Strengthening of Thin Steel Passenger Vehicle Roof Structures. Thin-Walled Struct. 2014, 74, 1–11. [Google Scholar]
- Wang, R.B.; Cheng, L.Q.; Lu, J.T.; Jin, R.Q.; He, M.Z.; Yan, S.H.; Jiang, D.M.; Deng, S.J.; Chu, X.C. Preparation and Properties of Carbon Fiber Reinforced BT-HA Composites. Bull. Am. Ceram. Soc. 2022, 41, 994–1001. [Google Scholar]
- Liang, Y.; Chen, L.; Yang, J.Y.; Lyu, C.X.; Jia, H.L.; Wang, Y.S. Application of Carbon Fiber Composite Polymer on Urban Rail Transit Vehicle Bogy. Urban Mass Transit. 2020, 23, 5. [Google Scholar]
- Kovarskii, A.L.; Kasparov, V.V.; Krivandin, A.V.; Shatalova, O.V.; Korokhin, R.A.; Kuperman, A.M. EPR spectroscopic and X-Ray diffraction studies of carbon fibers with different mechanical properties. Russ. J. Phys. Chem. 2017, 11, 233–241. [Google Scholar] [CrossRef]
- Teja, P.S.; Sudhakar, B.; Dhass, A.D. Numerical and experimental analysis of hydroxyl-terminated poly-butadiene solid rocket motor by using ANSYS. Mater. Today Proc. 2020, 33, 308–314. [Google Scholar] [CrossRef]
- Faber, J.; Schmidt-Eisenlohr, C.; Dickhut, T.; Ortmann, P. Concept study on optimized auxiliary material designs and application techniques for vacuum bagging of full-scale CFRP rocket boosters. In Proceedings of the 8th European Conference on Composite Materials, Athens, Greece, 25–28 June 2018; pp. 1–8. [Google Scholar]
- Babu, P.M.; Krishna, G.B.; Prasad, B.S. Design & analysis of solid rocket motor casing for aerospace applications. Int. J. Curr. Eng. Technol. 2015, 5, 1947–1954. [Google Scholar]
- Mohmmed, R.; Zhang, F.; Sun, B.Z.; Gu, B.H. Finite element analyses of low-velocity impact damage of foam sandwiched composites with different ply angles face sheets. Mater. Des. 2013, 47, 189–199. [Google Scholar] [CrossRef]
- Chen, R.X. Netting analysis method for the filament-wound case design. J. Solid Rocket. Technol. 2003, 26, 30–32. [Google Scholar]
- Gao, J.L.; Yu, J.S. Application of composite motor case in space carrier rocket. Fiber Compos. 2005, 22, 53–54. [Google Scholar]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- GB 150-98; Steel Presure Vessel. National Standardization Technical Committee on Pressure Vessels. Bejing China Standards Press: Beijing, China, 1998; pp. 26–51.
- American Society of Mechanical Engineers. Boiler and Pressure Vessel Code: Section V Division 1 and Division 2S; Ju, D.Y., Translator; Chinese Mechanical Engineering Society, Pressure Vessel Society: Hefei, China, 1992; pp. 15–34. [Google Scholar]



| Property Items | Lamina Property | Resin | AL7075-T6 | |
|---|---|---|---|---|
| Tensile strength (MPa) | 0° | 665 | 70 | 570 |
| 90° | 552 | |||
| Tensile modulus (GPa) | 0° | 55.7 | 3.6 | 72 |
| 90° | 56.3 | |||
| Compression strength (MPa) | 0° | 500 | ||
| 90° | 500 | |||
| Compression modulus (GPa) | 0° | 55.7 | ||
| 90° | 56.3 | |||
| Serial Number | Lay Up | Thickness (mm) | Angle (°) | Layer Number |
|---|---|---|---|---|
| 1 | Twill weaves of carbon fiber T300 | 0.225 | 0/90 | 1001 |
| 2 | Twill weaves of carbon fiber T300 | 0.225 | 45/−45 | 1002 |
| 3 | Twill weaves of carbon fiber T300 | 0.225 | 0/90 | 1003 |
| 4 | Twill weaves of carbon fiber T300 | 0.225 | 45/−45 | 1004 |
| 5 | Twill weaves of carbon fiber T300 | 0.225 | 0/90 | 1005 |
| 6 | Twill weaves of carbon fiber T300 | 0.225 | 45/−45 | 1006 |
| … | … | … | … | … |
| 163 | Twill weaves of carbon fiber T300 | 0.225 | 0/90 | 1163 |
| 164 | Twill weaves of carbon fiber T300 | 0.225 | 45/−45 | 1164 |
| 165 | Prepreg of carbon fiber T300 | 0.145 | 0 | 2001 |
| 166 | Prepreg of carbon fiber T300 | 0.145 | 45 | 2002 |
| 167 | Prepreg of carbon fiber T300 | 0.145 | −45 | 2003 |
| 168 | Prepreg of carbon fiber T300 | 0.145 | 90 | 2004 |
| 169 | Prepreg of carbon fiber T300 | 0.145 | 0 | 2005 |
| 170 | Prepreg of carbon fiber T300 | 0.145 | 45 | 2006 |
| 171 | Prepreg of carbon fiber T300 | 0.145 | −45 | 2007 |
| 172 | Prepreg of carbon fiber T300 | 0.145 | 90 | 2008 |
| … | … | … | … | … |
| 285 | Prepreg of carbon fiber T300 | 0.145 | 0 | 2021 |
| 286 | Prepreg of carbon fiber T300 | 0.145 | 45 | 2122 |
| 287 | Prepreg of carbon fiber T300 | 0.145 | −45 | 2123 |
| 288 | Prepreg of carbon fiber T300 | 0.145 | 90 | 2124 |
| 289 | Prepreg of carbon fiber T300 | 0.145 | 0 | 2125 |
| Total thickness | 55.025 mm | |||
| Location | AL Front Connector Scheme | The Initial Configuration | Optimized Scheme | Experimental Measurements |
|---|---|---|---|---|
| Front connector weight (kg) | 0.68 | 0.41 | 0.408 | 0.411 |
| AL insert weight (kg) | - | 0.056 | 0.0613 | 0.0613 |
| Total weight (kg) | 0.68 | 0.466 | 0.469 | 0.472 |
| Percentage weight loss (%) | - | 31.4% | 31.0% | 30.6% |
| Final Preferred Solution | Experimental Measurements | |||
|---|---|---|---|---|
| Allowable Value [23,24] | Calculated Value | Safety Factor | Experimental Value | |
| Front connector deformation (mm) | - | 1.92 | - | 1.98 |
| Tensile stress in X-direction (MPa) | 500 | 492.0 | 1.24 | 496.4 |
| Compressive stress in X-direction (MPa) | −665 | −158.9 | 1.02 | −172.8 |
| Tensile stress in Y-direction (MPa) | 552 | 450.2 | 1.23 | 463.6 |
| Compressive stress in Y-direction (MPa) | −500 | −212.6 | 3.16 | −235.8 |
| Shear stress in XY-plane (MPa) | 118 | 2.574 | 45.91 | 6.431 |
| Von Mises stress of AL inserts (MPa) | 505 | 332.4 | 1.52 | 362.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Wang, J.; Shen, W.; Chen, L.; Zhu, C. Design and Analysis of Solid Rocket Composite Motor Case Connector Using Finite Element Method. Polymers 2022, 14, 2596. https://doi.org/10.3390/polym14132596
Zhu L, Wang J, Shen W, Chen L, Zhu C. Design and Analysis of Solid Rocket Composite Motor Case Connector Using Finite Element Method. Polymers. 2022; 14(13):2596. https://doi.org/10.3390/polym14132596
Chicago/Turabian StyleZhu, Lvtao, Jiayi Wang, Wei Shen, Lifeng Chen, and Chengyan Zhu. 2022. "Design and Analysis of Solid Rocket Composite Motor Case Connector Using Finite Element Method" Polymers 14, no. 13: 2596. https://doi.org/10.3390/polym14132596






