Research on the Mechanical Behavior of Buried Double-Wall Corrugated Pipes
Abstract
:1. Introduction
2. Materials of FA/HDPE Double-Wall Corrugated Pipes
3. Finite Element Model
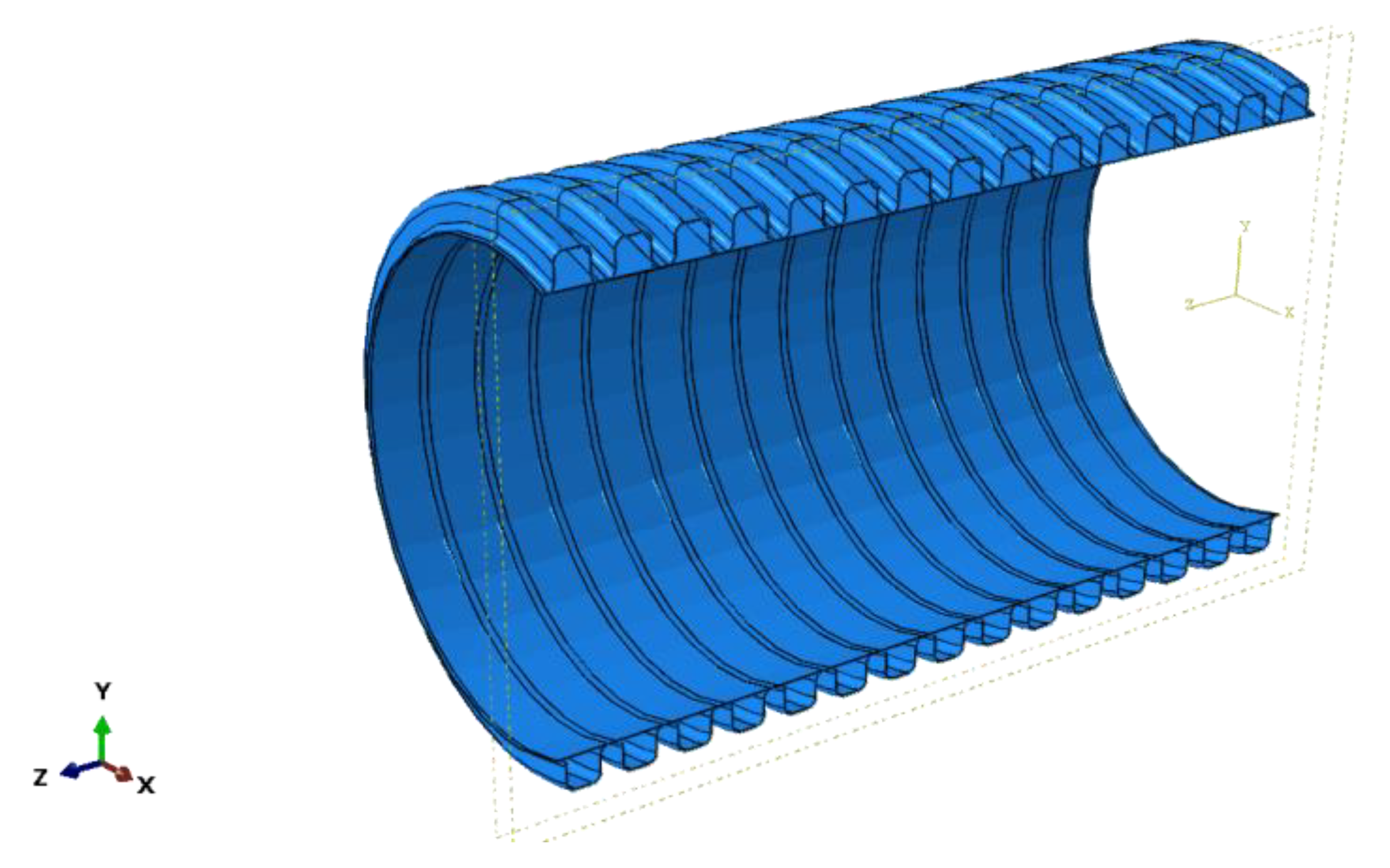
3.1. Models of Pipes and Soils
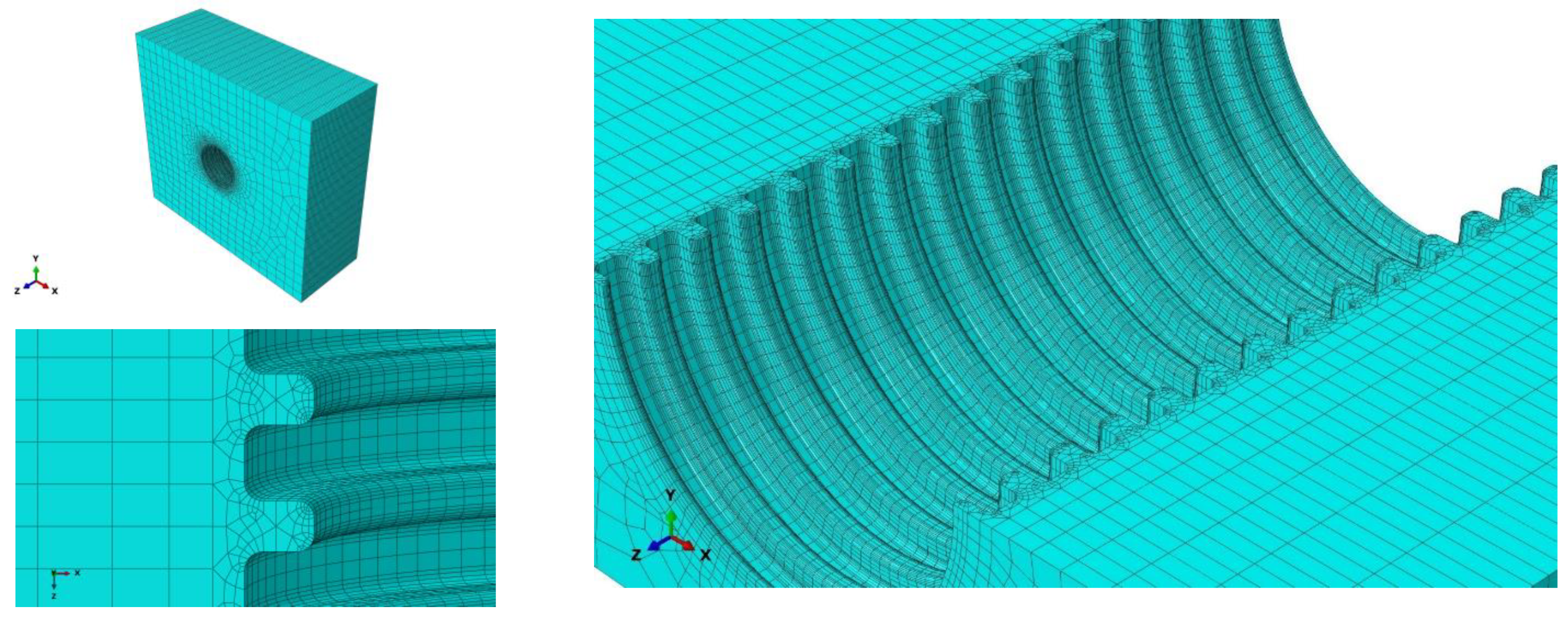
3.2. Meshing of Pipes and Soils
3.3. Calculation Conditions for Simulation
- (1)
- It is assumed that the pipes and soil are always in the elastic deformation during the stress stage. Through the study of semi-crystalline polymer yield behavior and macroscopic phenomena, Jin Tao found that although the semi-crystalline polymer material produces nonlinear changes at the end of the elastic stage [6], a linear elastic model can still be used to simulate the elastic stage of the semi-crystalline polymer. Under quasi-static conditions of polyethylene materials, when the stress and deformation of the material is within the yield point, the linear elastic model agrees well with the experimental results [5]. The maximum strains calculated in this paper are smaller than the yield point of the material, so the actual elastic strain value of the pipe does not reach the limit of ultimate elastic strain value. At this deformation stage, the deformation of the pipeline is always in an approximately linear elastic stage, so it is credible to use the linear elastic model to simulate the pipe deformation in this paper.
- (2)
- The sum of the thickness of the interior and exterior walls of the pipe is 5 mm, and is equal to the thickness of the valley between the corrugations. The production cost of double-wall corrugated pipes is affected by the distribution of interior and exterior wall thicknesses, and proper ratio of interior and exterior wall thicknesses can maximize structural performance and reduce costs. The strain and deformation characteristics of the pipe are studied under different wall thickness ratios by keeping the sum of wall thickness unchanged and adjusting the ratio of the interior and exterior wall thicknesses. The geometric parameters of the pipes are shown in Table 3.
- (3)
- Consider the friction between the pipe and soil, and that the friction coefficient is 0.4. According to specification [28], the friction coefficient between the high-density polyethylene pipes and the medium sand layer ranges from 0.2 to 0.4. According to the research of Wang, Fei and others [31], the friction coefficient between the buried high density polyethylene pipe and the surrounding soil is affected by the working temperature of the pipe. The friction coefficient between the pipes and soil increases with the increase of the difference between the working temperature and the installation temperature. When the working temperature is too high, the friction coefficient between the pipes and soil is even greater than 0.4. This paper comprehensive consideration of pipes’ work environment, the friction coefficient between the double-wall corrugated pipes and the confining soil layer is considered to be 0.4 in this paper.
- (4)
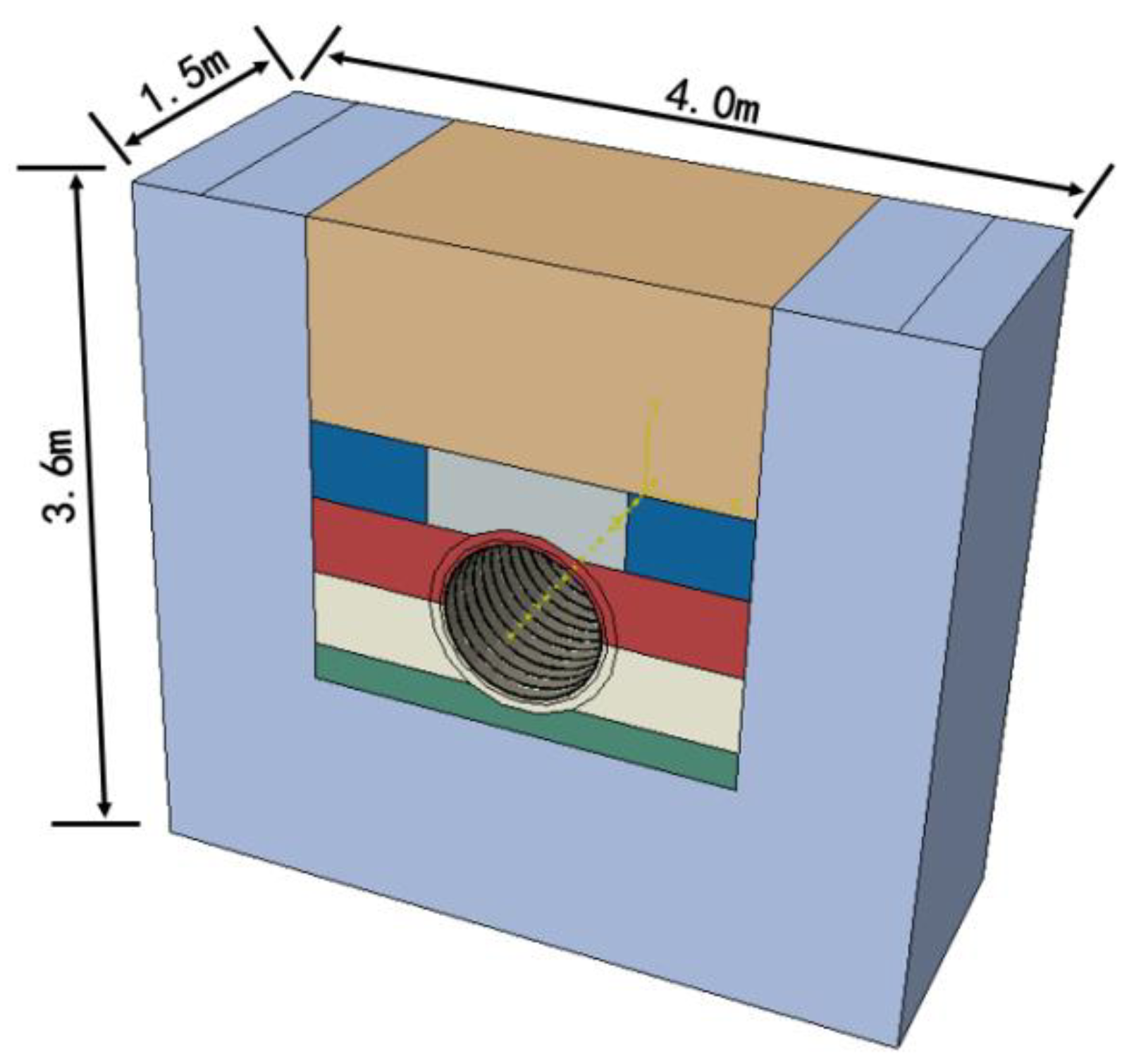
- Gravity and ground load are considered in load calculations, and ground load is set to 0.4 Mpa. The boundaries of the pipe-soil model are constrained as follows: on the side and bottom of the pipe, the soil is fixed completely. The upper surface of the soil does not impose any constraints. Both the front and rear sides of the pipe are perpendicular to the bottom surface, only the normal direction are constrained. Based on the static equivalent principle, the road load is transformed into a 40 kPa uniform load applied directly above the soil, acting on the foundation soil at a position of 3.28 m × 1.5 m. The three-dimension model of the pipe and surrounding soils is shown in Figure 6.
- (5)
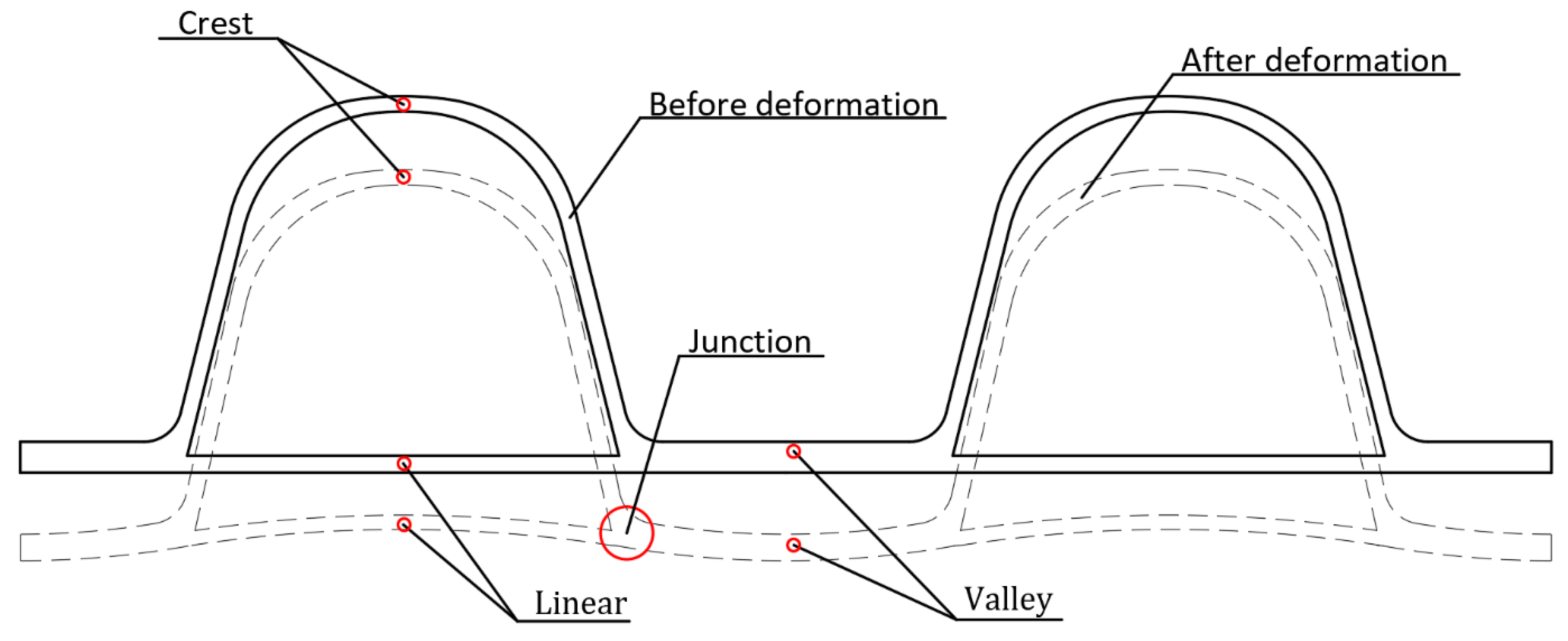
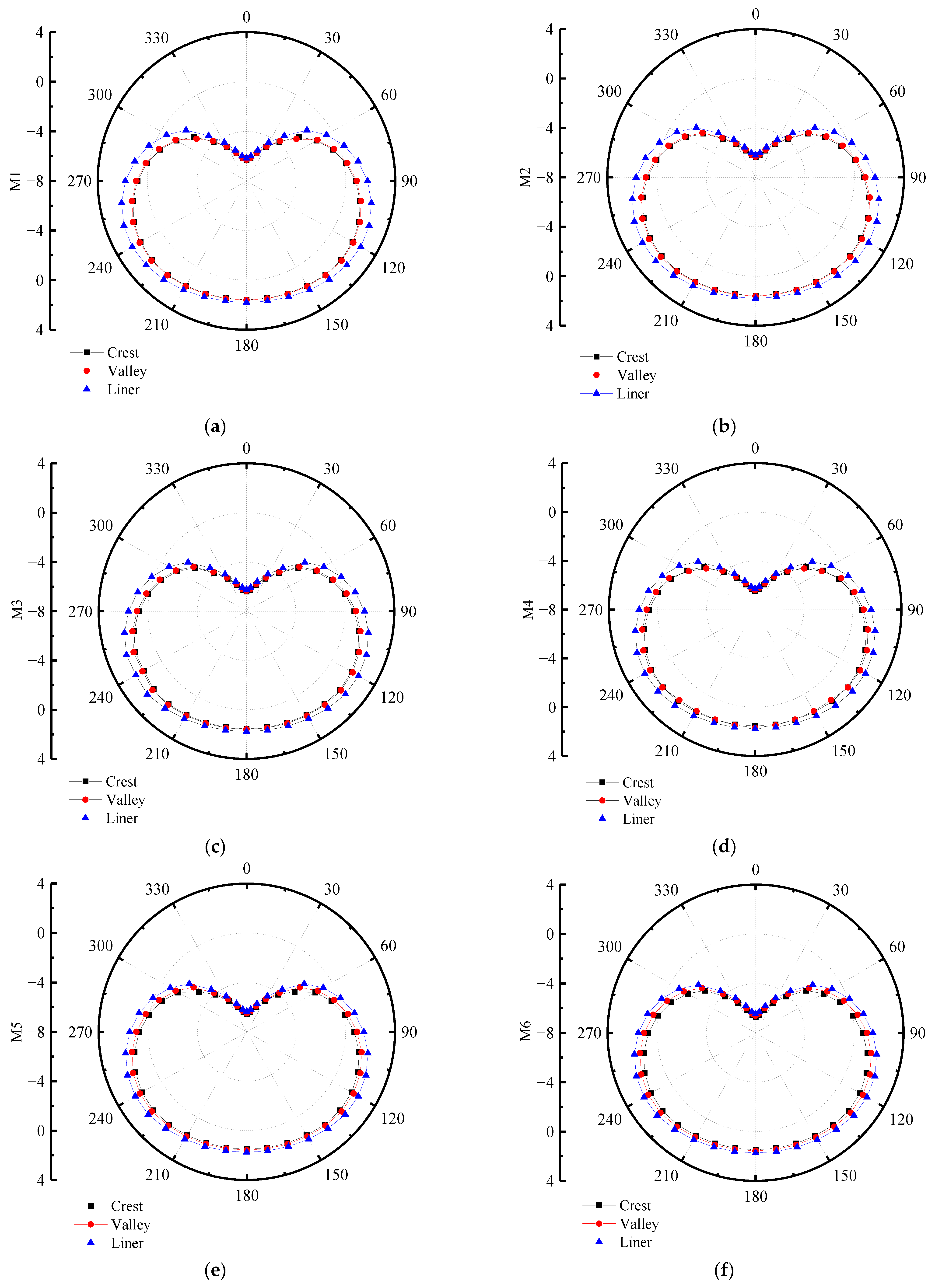
- The detection section of pipes can be seen from Figure 7. According to its deformation characteristics, this paper selects crest, valley, and liner of the pipe as monitoring points, and compares and analyzes its displacement and strain under the action of the surrounding soil. Based on the structural characteristics of the double-wall corrugated pipes, this paper studies the strain and deformation of the double-wall corrugated pipes about various interior and exterior wall thickness structures. The mechanical characteristics of double-wall corrugated pipes with various interior and exterior wall thicknesses are summarized. These results can provide some reference for the structural design of double-wall corrugated pipes.
4. In-Situ Measurement
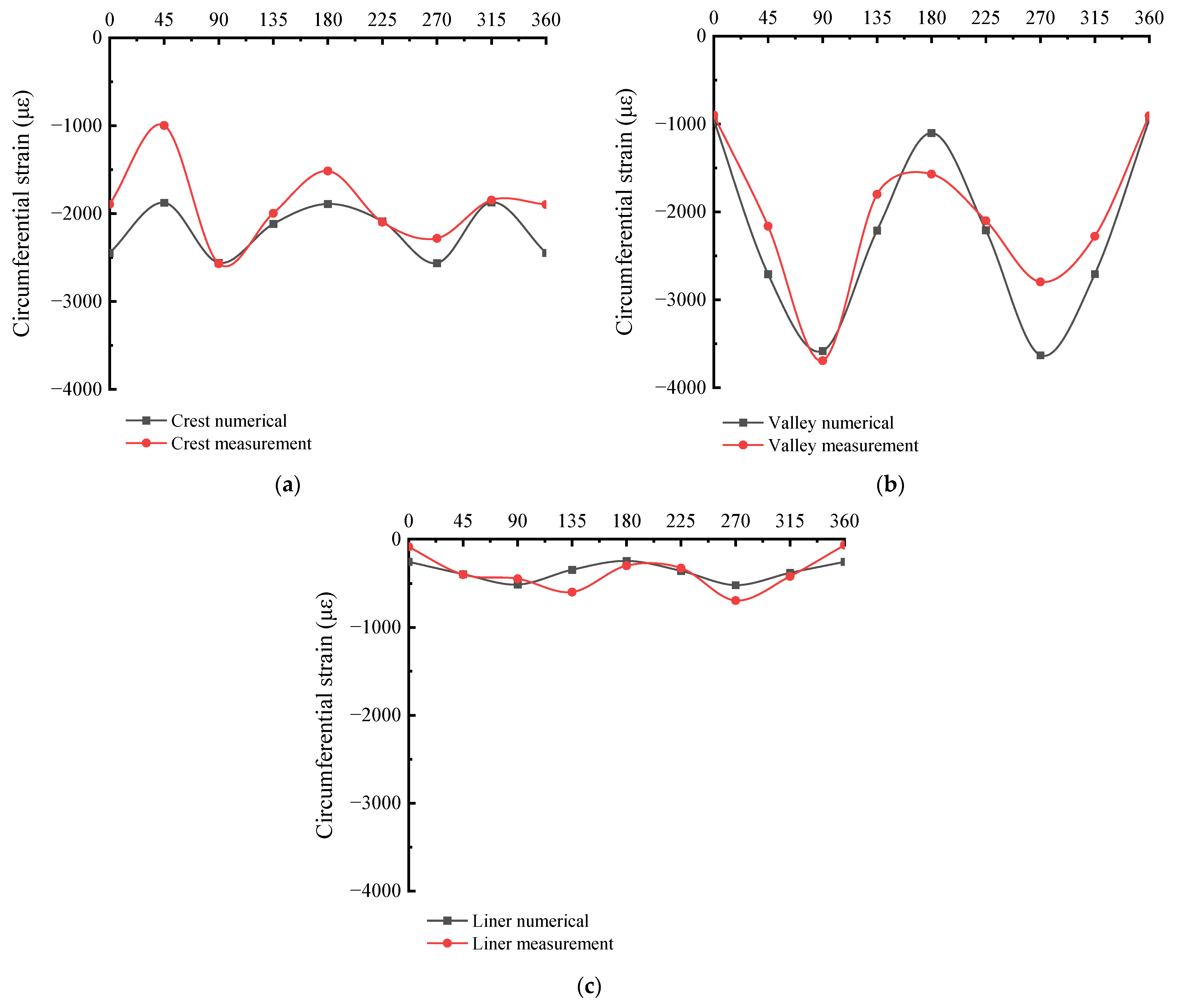
5. Verification of Number Models
6. FA/HDPE Double-Wall Corrugated Pipes
7. Analysis of Numerical Simulations
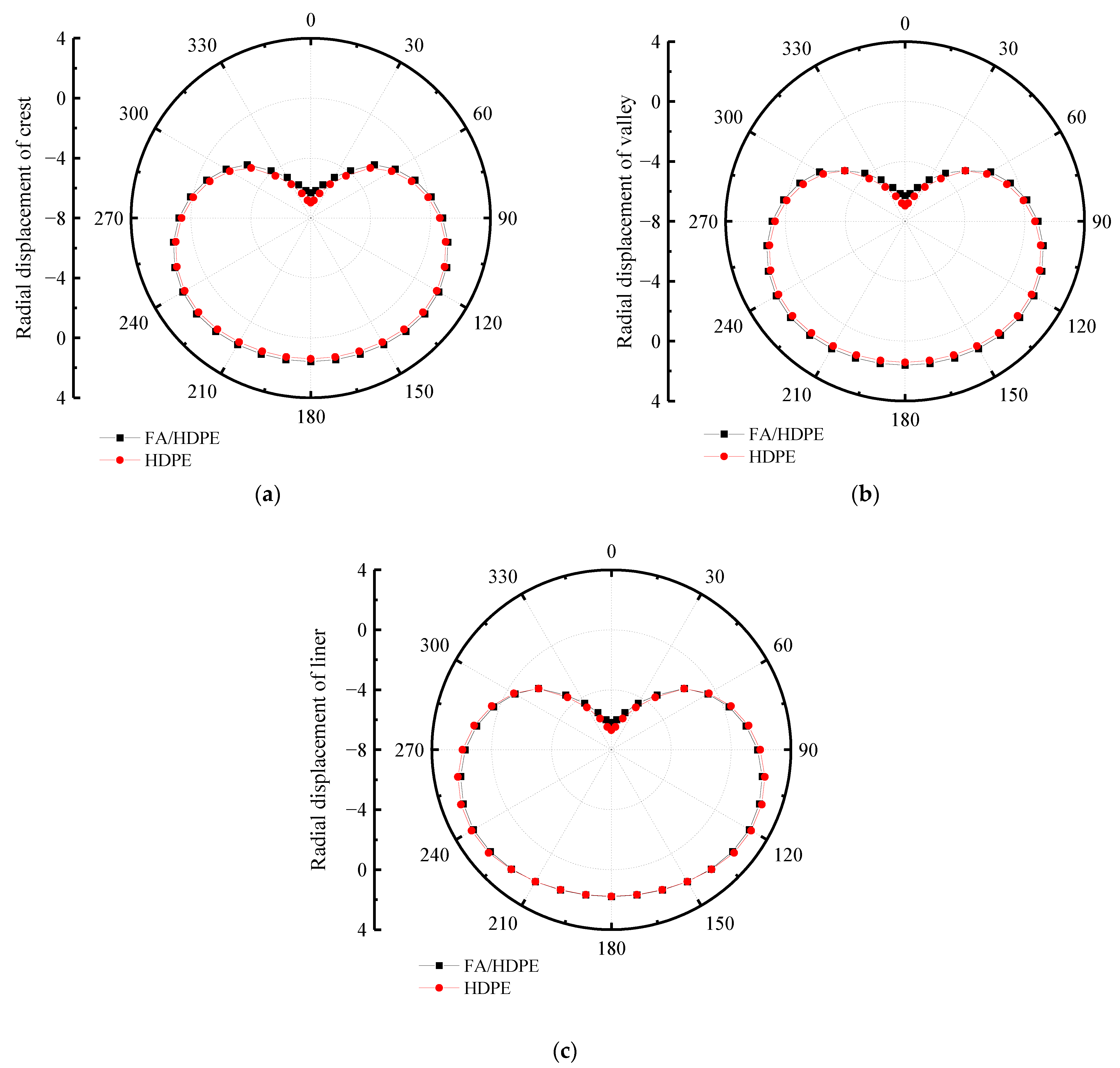
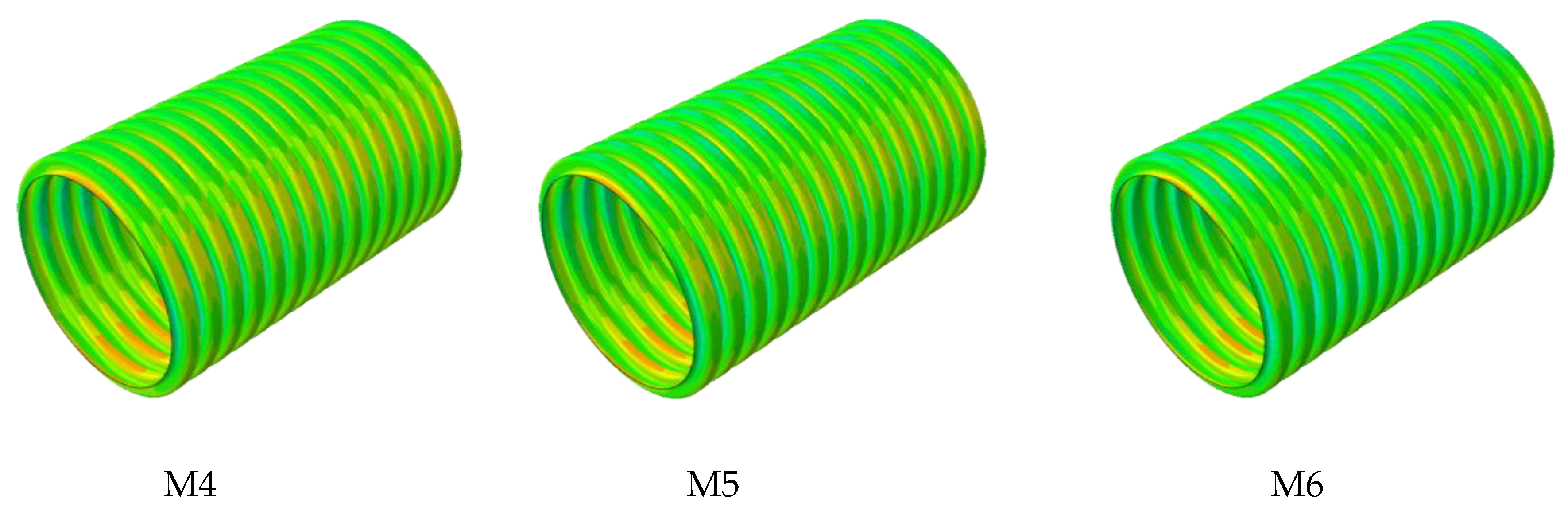
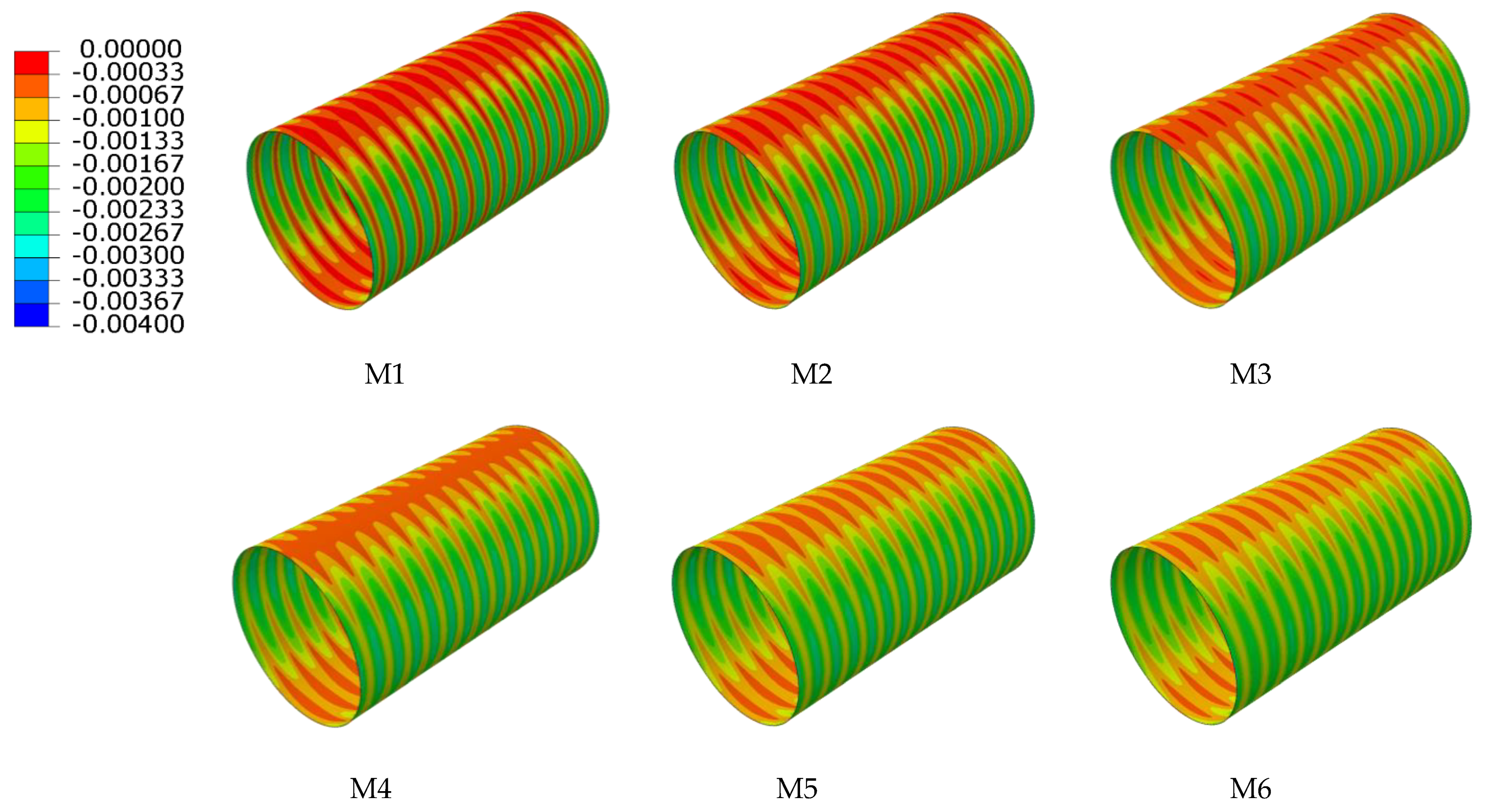
7.1. Radial Displacement of Various Interior and Exterior Wall Thicknesses
7.2. Circumferential Strain with Various Interior and Exterior Wall Thicknesses
7.3. Comprehensive Evaluation of Various Interior and Exterior Wall Thicknesses
7.4. Comprehensive Indicators of Interior and Exterior Wall Thickness Ratio
8. Conclusions
- (1)
- When the surrounding soil load acts directly on the wall of the double-wall corrugated pipes, the direction of the depression at the valley is the same as the direction of the force, and the depression direction of the liner is opposite to the valley.
- (2)
- FA/HDPE double-wall corrugated pipes have smaller strain and displacement than HDPE double-wall corrugated pipes in the same condition. The maximum strain of FA/HDPE double wall corrugated pipes is about 30% smaller than with HDPE.
- (3)
- The strain distribution of double-wall corrugated pipe is significantly affected by the ratio of interior and exterior wall thickness, and different ratios may have different dangerous areas under the action of surrounding soil.
- (4)
- When the thickness of the interior and exterior walls changes, the strain changes at the valley are much smaller than the crest and liner.
- (5)
- From the perspective of economy and mechanics, when the thickness ratio of the interior wall and the exterior wall is controlled to be from 1.3 to 1.8, this can give a better structural performance for the double-wall corrugated pipes and reduce production cost.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zaghloul, M.Y.M.; Zaghloul, M.M.Y.; Zaghloul, M.M.Y. Developments in polyester composite materials—An in-depth review on natural fibres and nano filler. Compos. Struct. 2021, 278, 114698. [Google Scholar] [CrossRef]
- Zaghloul, M.Y.; Zaghloul, M.M.Y.; Zaghloul, M.M.Y. Influence of Stress Level and Fibre Volume Fraction on Fatigue Performance of Glass Fibre-Reinforced Polyester Composites. Polymers 2022, 14, 2662. [Google Scholar] [CrossRef] [PubMed]
- Zaghloul, M.M.Y.; Zaghloul, M.Y.M.; Zaghloul, M.M.Y. Experimental and modeling analysis of mechanical-electrical behaviors of polypropylene composites filled with graphite and MWCNT fillers. Polym. Test. 2017, 63, 467–474. [Google Scholar] [CrossRef]
- Zaghloul, M.M.Y.M. Mechanical properties of linear low-density polyethylene fire-retarded with melamine polyphosphate. J. Appl. Polym. Sci. 2018, 135, 46. [Google Scholar] [CrossRef]
- Xu, L.; Gao, G.; Zhao, Z.; Wang, J.; Cheng, C.; Du, Z. Compressive mechanical properties of polyethylene at different strain rates. Explos. Shock Waves. Nanjing China 2019, 39, 55–62. [Google Scholar]
- Jin, T.; Zhou, Z.; Shu, X.; Wang, Z.; Wu, G.; Zhao, L. Investigation on the yield behaviour and macroscopic phenomenological constitutive law of PA66. Polym. Test. 2018, 69, 563–582. [Google Scholar] [CrossRef]
- Fuseini, M.; Zaghloul, M.M.Y. Investigation of Electrophoretic Deposition of PANI Nano Fibers as a Manufacturing Technology for Corrosion Protection. Prog. Org. Coat. 2022, 171, 107015. [Google Scholar] [CrossRef]
- Fuseini, M.; Zaghloul, M.M.Y. Statistical and qualitative analyses of the kinetic models using electrophoretic deposition of polyaniline. J. Ind. Eng. Chem. 2022, 113, 475–487. [Google Scholar] [CrossRef]
- General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; Standardization Administration of the People’s Repub. GB/T 1040.2-2006 Plastic―Determination of Tensile Properties―Part 2: Test Conditions for Moulding and Extrusion Plastics; Standards Press of China: Beijing, China, 2006.
- Wu, A.; Jia, L.; Yu, W.; Zhu, F.; Liu, F.; Wang, Y.; Lu, G.; Qin, S.; Gao, D.; Wang, H.; et al. Preparation and Finite Element Analysis of Fly Ash/HDPE Composites for Large Diameter Bellows. Polymers 2022, 13, 4204. [Google Scholar] [CrossRef]
- Fang, H.; Tan, P.; Du, X.; Li, B.; Yang, K.; Zhang, Y. Numerical and Experimental Investigation of the Effect of Traffic Load on the Mechanical Characteristics of HDPE Double-Wall Corrugated Pipe. Appl. Sci. 2021, 10, 627. [Google Scholar] [CrossRef]
- Fang, H.; Li, B.; Wang, F.; Wang, Y.; Cui, C. The mechanical behaviour of drainage pipeline under traffic load before and after polymer grouting trenchless repairing. Tunn. Undergr. Space Technol. 2018, 74, 185–194. [Google Scholar] [CrossRef]
- An, Z.T.; Tang, Q.; Li, H.; Zhang, P. Experimental and numerical study of shallow-buried high-density polyethylene pipeline under collapse touchdown impact. Energy Sci. Eng. 2020, 10, 355–373. [Google Scholar] [CrossRef]
- Trickey, S.A.; Moore, I.D. Three-dimensional response of buried pipes under circular surface loading. J. Geotech. Geoenviron. Eng. 2007, 133, 219–223. [Google Scholar] [CrossRef]
- Alzabeebee, S. Seismic Seismic response and design of buried concrete pipes subjected to soil loads. Tunn. Undergr. Space Technol. 2019, 93, 103084. [Google Scholar] [CrossRef]
- Xie, X.; Symans, M.D.; O’Rourke, M.J.; Abdoun, T.H.; O’Rourke, T.D.; Palmer, M.C.; Stewart, H.E. Numerical Modeling of Buried HDPE Pipelines Subjected to Normal Faulting: A Case Study. Earthq. Spectra 2013, 29, 609–632. [Google Scholar] [CrossRef]
- Mahdavi, H.; Kenny, S.; Phillips, R.; Popescu, R. Significance of geotechnical loads on local buckling response of buried pipelines with respect to conventional practice. Can. Geotechnol. J. 2013, 50, 68–80. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, F.; Du, Y.; Liu, M. Laboratory evaluation of buried high-density polyethylene pipes subjected to localized ground subsidence. Acta Geotechnol. 2019, 14, 1081–1099. [Google Scholar] [CrossRef]
- Zhou, M.; Du, Y.; Wang, F.; You, Q.; Dong, D. Mechanical response of buried HDPE pipes subjected to localized land subsidence. Chin. J. Rock Mech. Eng. Nanjing China 2017, 36, 4177–4187. [Google Scholar]
- Roy, K.; Hawlader, B.; Kenny, S.; Moore, I. Finite element modeling of lateral pipeline-soil interactions in dense sand. Can. Geotechnol. J. 2016, 53, 490–540. [Google Scholar] [CrossRef]
- Kunert, H.G.; Otegui, J.L.; Marquez, A. Nonlinear FEM strategies for modeling pipe-soil interaction. Eng. Fail. Anal. 2012, 24, 46–56. [Google Scholar] [CrossRef]
- Naeini, S.A.; Mahmoudi, E.; Shojaedin, M.M.; Misaghian, M. Mechanical response of buried High-Density Polyethylene pipes under normal fault motions. KSCE J. Civ. Eng. 2016, 20, 2253–2261. [Google Scholar] [CrossRef]
- Das, S.; Dhar, A.S. Modeling time-dependent behavior of medium-density polyethylene pipes. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021049. [Google Scholar] [CrossRef]
- Bilgin, O.; Stewart, H.E. Design Guidelines for Polyethylene Pipe Interface Shear Resistance. Geotext. Geomembr. 2009, 135, 809–818. [Google Scholar] [CrossRef]
- Hao, W.; Xie, J.; Wang, F.; Liu, Z.; Wang, Z. Analytical model of thin-walled corrugated tubes with sinusoidal patterns under axial impacting. Int. J. Mech. Sci. 2017, 128, 1–16. [Google Scholar] [CrossRef]
- GB/T20801; Pressure Piping Code-Industrial Piping State. Administration for Market Regulation; Standardization Administration of the People’s Republic of China. China Standard Press: Beijing, China, 2020.
- Ministry of Housing and Urban-Rural Development and General Administration of Supervision. CJJ143-2010 Technical Specification for Buried Plastic Drainage Pipe Engineering; China Architecture & Building Press: Beijing, China, 2010.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. CJJ/T81-2013 Technical Specification for Directly Buried Hot-Water Heating Pipeline in city; China Building Industry Press: Beijing, China, 2013.
- Ministry of Construction People’s Republic of China; State General Administration of the People’s Republic of China for Quality Supervision and Inspection and Quarantine. GB/50332--2002 Structure Design Code for Pipelines of Water Supply and Waste Water Engineering; China Planning Press: Beijing, China, 2002.
- Ministry of Transport of the People’s Republic of China. JTG D50-2017 Specifications for Design of Highway Asphalt Pavement; China Communications Press: Beijing, China, 2017.
- Wang, F.; Zhang, J. Study on the Changing Regulation of Friction Factor of Large Diameter Precast Buried Heating Pipes; Building Energy & Environment: Taiyuan, China, 2007; Volume 1, pp. 81–85. [Google Scholar]
- Shan, Y.; Shi, G.; Hu, Q.; Zhang, Y.; Wang, F. Numerical Investigation of the Short-Term Mechanical Response of Buried Profiled Thermoplastic Pipes with Different Diameters to External Loads. Math. Probl. Eng. 2021, 2021, 8853959. [Google Scholar] [CrossRef]
- Fang, H.; Tan, P.; Li, B.; Yang, K.; Zhang, Y. Influence of Backfill Compaction on Mechanical Characteristics of High-Density Polyethylene Double-Wall Corrugated Pipelines. Math. Probl. Eng. 2019, 2019, 3960864. [Google Scholar] [CrossRef]
- Robert, D.J. A Modified Mohr-Coulomb Model to Simulate the Behavior of Pipelines in Unsaturated Soils. Comput. Geotechnol. 2017, 97, 146–160. [Google Scholar] [CrossRef]
- Moradi, G.; Abbasnejad, A. Experimental and numerical investigation of arching effect in sand using modified Mohr Coulomb. Geomech. Eng. 2015, 8, 829–844. [Google Scholar] [CrossRef]
- Kianian, M.; Shiri, H. The effect of backfilling stiffness on lateral response of the shallowly trenched-backfilled pipelines in clay. Mar. Georesour. Geotechnol. 2020, 39, 610–622. [Google Scholar] [CrossRef]









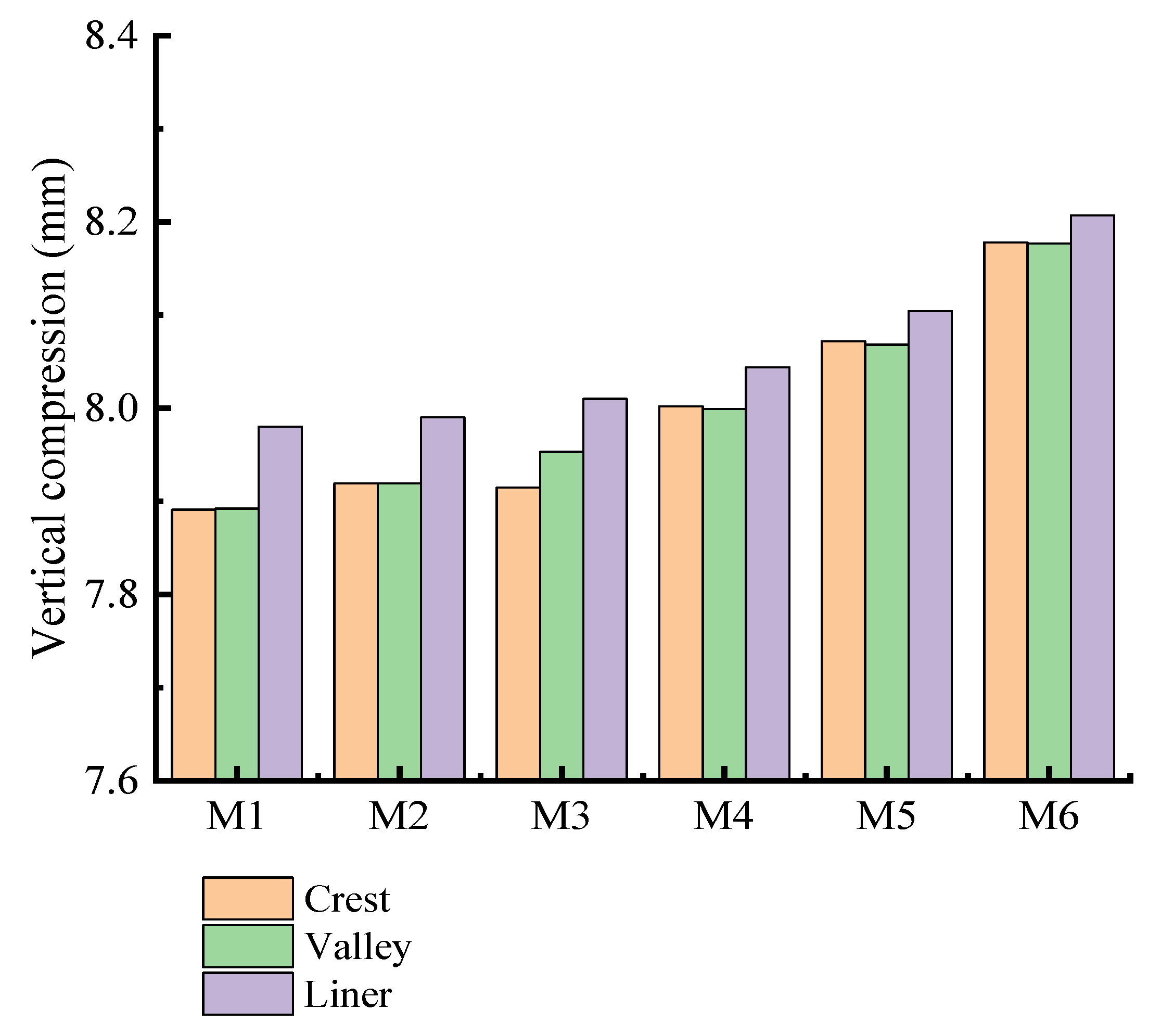




| Blend Composition | Tensile Strength at Yield (Mpa) | Tensile Strength at Break (Mpa) | Young’s Modulus (Mpa) | Elongation at Break (Mpa) |
|---|---|---|---|---|
| Pure HDPE | 22.13 ± 2.23 | 16.54 ± 1.57 | 500.00% ± 0% | |
| 5%FA masterbatch/95% HDPE | 25.60 ± 1.09 | 19.63 ± 0.01 | 1495.0 ± 35.4 | 252.85% ± 56.56% |
| 10%FA masterbatch /90% HDPE | 27.55 ± 1.25 | 21.62 ± 1.01 | 1477.2 ± 49.9 | 325.55% ± 51.97% |
| 15%FA masterbatch/85% HDPE | 26.06 ± 1.03 | 20.93 ± 0.60 | 1370.1 ± 23.2 | 344.20% ± 22.56% |
| 20%FA masterbatch/80% HDPE | 27.13 ± 1.15 | 22.03 ± 1.47 | 1327.5 ± 92.3 | 399.61% ± 40.10% |
| 10%FA masterbatch/5% compatibilizer/85% HDPE | 28.82 ± 2.54 | 23.23 ± 2.80 | 1451.1 ± 10.8 | 355.15% ± 9.05% |
| 10%FA masterbatch/10% compatibilizer/80% HDPE | 27.22 ± 1.16 | 22.62 ± 1.01 | 1360.8 ± 18.8 | 411.28% ± 51.33% |
| 10%FA masterbatch/15% compatibilizer/75% HDPE | 25.56 ± 0.74 | 21.35 ± 0.36 | 1297.1 ± 17.1 | 420.33% ± 61.47% |
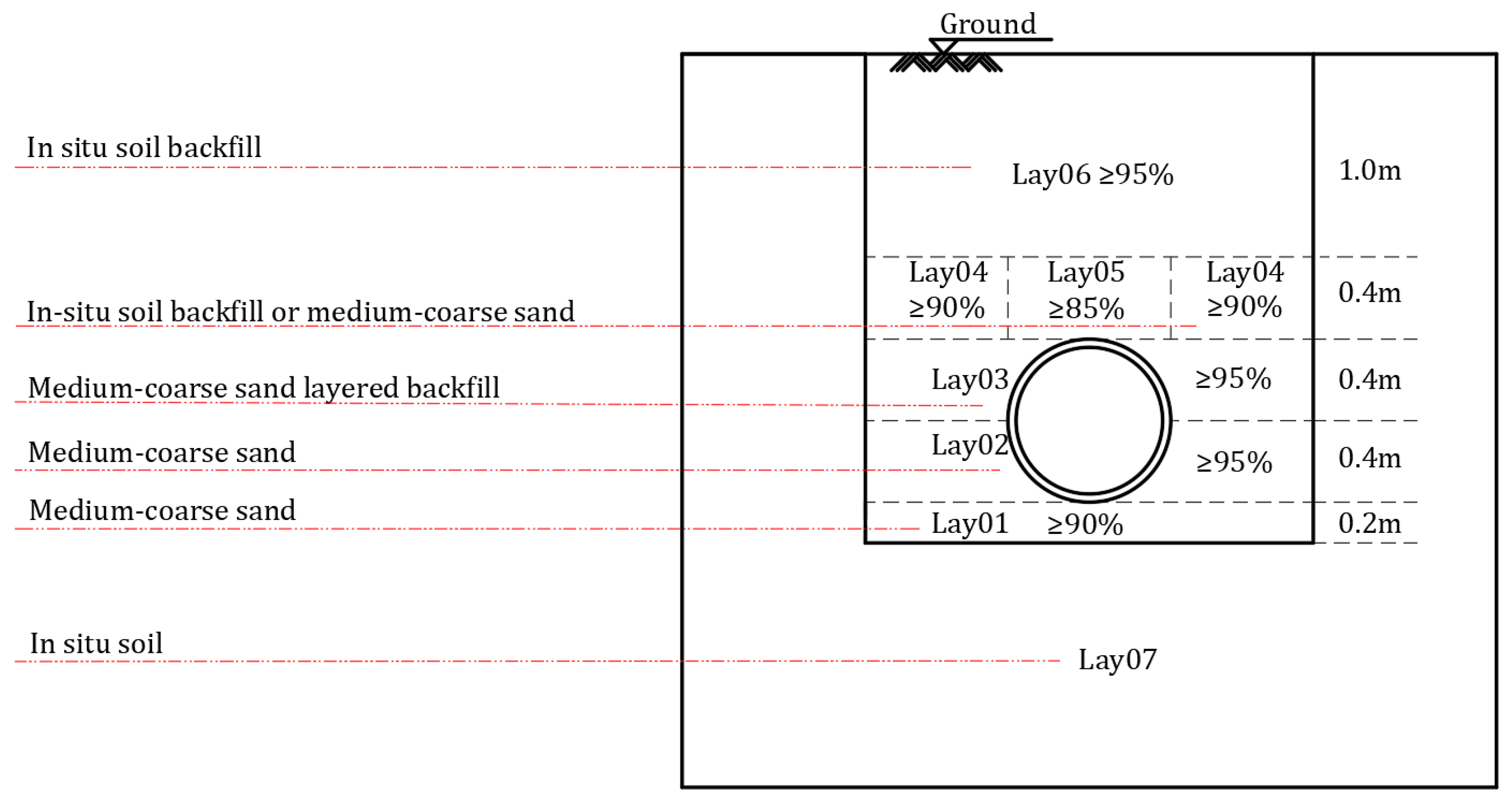
| Properties | Lay01 | Lay02 | Lay03 | Lay04 | Lay05 | Lay06 | Lay07 |
|---|---|---|---|---|---|---|---|
| Density (kg/m3) | 1800 | 1750 | 1740 | 1600 | 1600 | 1650 | 1500 |
| Elastic modulus (MPa) | 10 | 15 | 15 | 7 | 9 | 9 | 30 |
| Friction angle (°) | 35 | 31 | 25 | 28 | 30 | 27 | 30 |
| Cohesive (kPa) | 12 | 10 | 10 | 15 | 15 | 10 | 20 |
| Poisson’s ratio | 0.3 | 0.26 | 0.26 | 0.23 | 0.3 | 0.32 | 0.35 |
| Compaction degree (%) | 90 | 95 | 95 | 90 | 85 | 90 |
| Properties | Value | |
|---|---|---|
| Nominal diameter (mm) | 800 | |
| Corrugate height (mm) | 55 | |
| Corrugate length (mm) | 60 | |
| Corrugate spacing (mm) | 40 | |
| Pipe number | Interior thickness (mm) | Exterior wall thickness (mm) |
| M1 | 2.0 | 3.0 |
| M2 | 2.3 | 2.7 |
| M3 | 2.6 | 2.4 |
| M4 | 2.9 | 2.1 |
| M5 | 3.2 | 1.8 |
| M6 | 3.5 | 1.5 |
| Properties | HDPE Corrugated Pipes | FA/HDPE Corrugated Pipes |
|---|---|---|
| Density (kg/m3) | 950 | 970 |
| Young’s modulus (Mpa) | 800 | 1451.1 |
| Poisson ratio | 0.4 | 0.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, D.; Yang, H.; Yu, W.; Wu, X.; Wu, A.; Lu, G.; Zheng, Q. Research on the Mechanical Behavior of Buried Double-Wall Corrugated Pipes. Polymers 2022, 14, 4000. https://doi.org/10.3390/polym14194000
Gao D, Yang H, Yu W, Wu X, Wu A, Lu G, Zheng Q. Research on the Mechanical Behavior of Buried Double-Wall Corrugated Pipes. Polymers. 2022; 14(19):4000. https://doi.org/10.3390/polym14194000
Chicago/Turabian StyleGao, Dongyang, Huiwei Yang, Wenwen Yu, Xiaogang Wu, Angxuan Wu, Guoyun Lu, and Qiang Zheng. 2022. "Research on the Mechanical Behavior of Buried Double-Wall Corrugated Pipes" Polymers 14, no. 19: 4000. https://doi.org/10.3390/polym14194000
APA StyleGao, D., Yang, H., Yu, W., Wu, X., Wu, A., Lu, G., & Zheng, Q. (2022). Research on the Mechanical Behavior of Buried Double-Wall Corrugated Pipes. Polymers, 14(19), 4000. https://doi.org/10.3390/polym14194000






