Thermal Percolation Behavior in Thermal Conductivity of Polymer Nanocomposite with Lateral Size of Graphene Nanoplatelet
Abstract
:1. Introduction
2. Experimental Methods
2.1. Materials
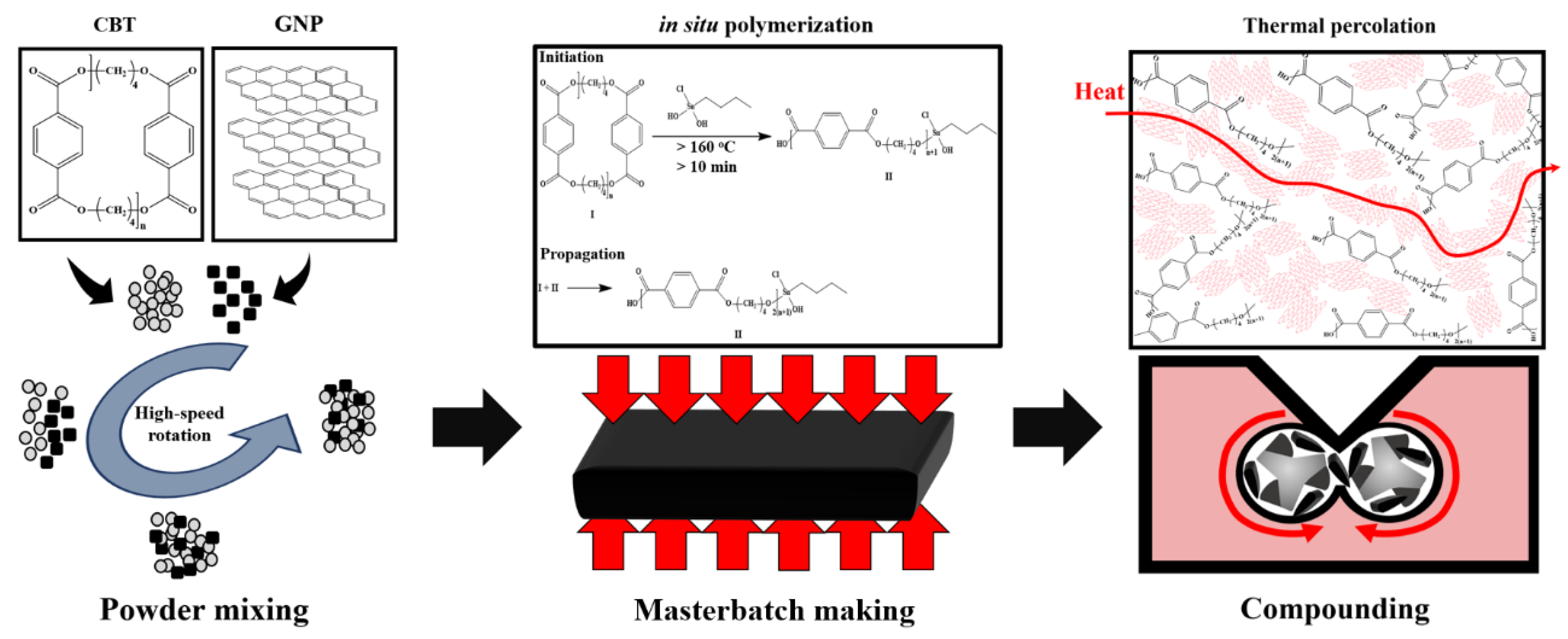
2.2. Fabrication
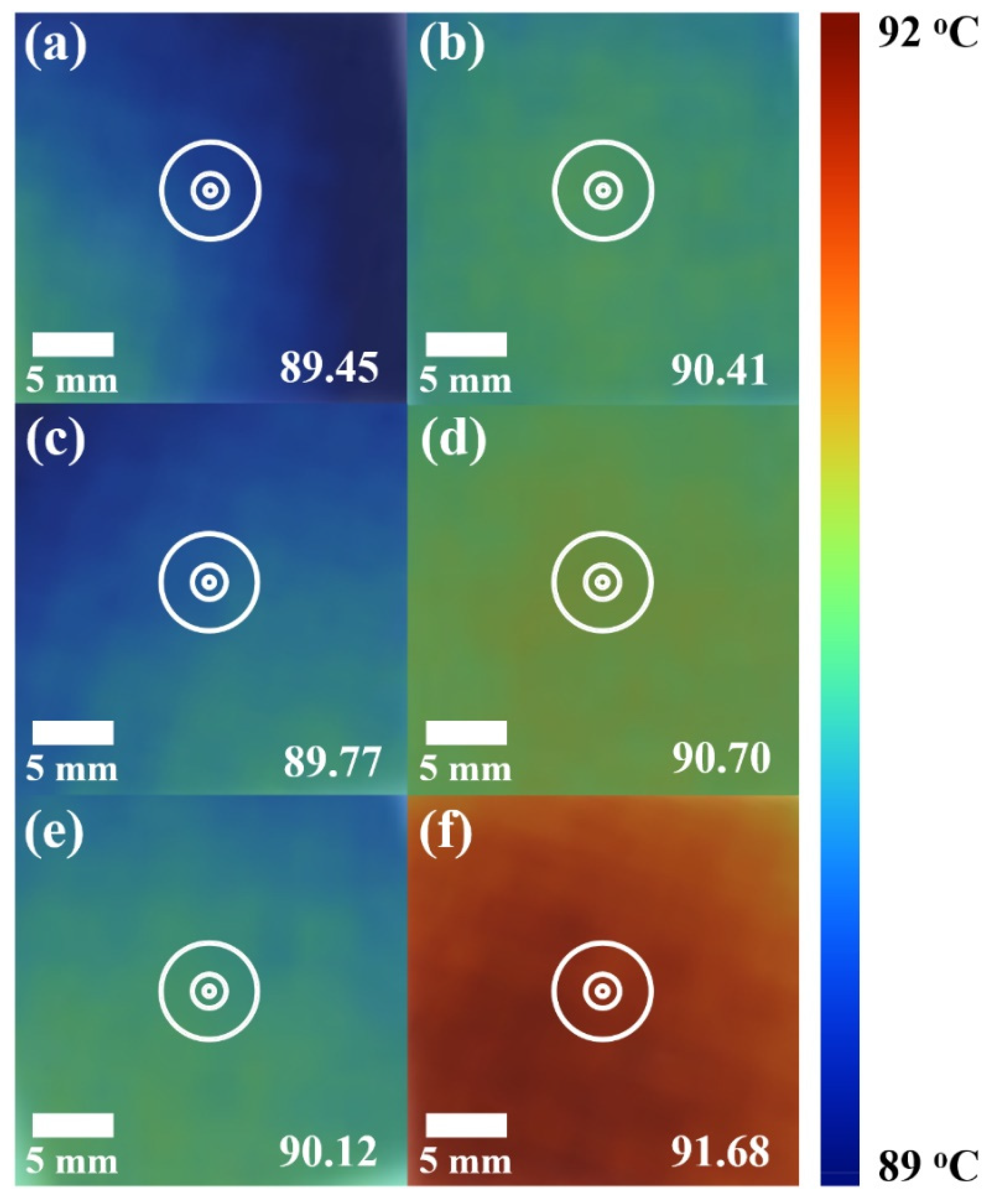
2.3. Characterization
2.4. Theoretical Calculations
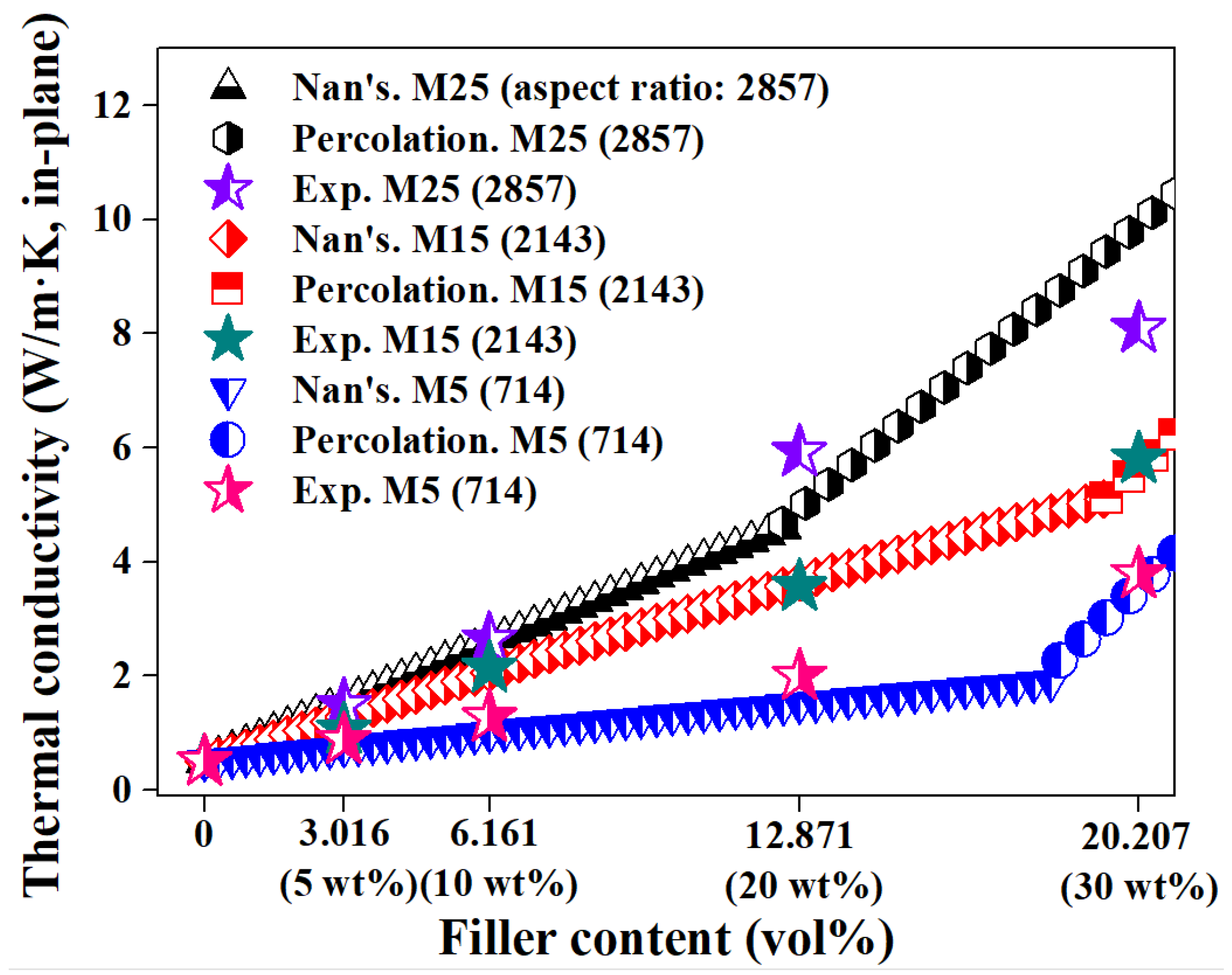
2.4.1. Nan’s Model
2.4.2. Percolation Equation
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 51–58. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Subramoney, S. Novel Nanocarbons—Structure, Properties, and Potential Applications. Adv. Mater. 1998, 10, 1157–1171. [Google Scholar] [CrossRef]
- Kinloch, I.A.; Suhr, J.; Lou, J.; Young, R.J.; Ajayan, P.M. Composites with carbon nanotubes and graphene: An outlook. Science 2018, 362, 6414. [Google Scholar] [CrossRef] [Green Version]
- Kim, P.; Shi, L.; Majumdar, A.; EcEuen, P.L. Thermal Transport Measurements of Individual Multiwalled Nanotubes. Phys. Rev. Lett. 2001, 87, 215502. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 2001, 92, 151911. [Google Scholar] [CrossRef]
- Han, Z.; Fina, A. Thermal conductivity of carbon nanotubes and their polymer nanocomposites: A review. Prog. Polym. Sci. 2011, 36, 914–944. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Y.F.; Cao, X.Y.; Zhang, J.N.; Ma, Y.Y.; Shang, X.X.; Lu, J.X.; Yang, S.L.; Zheng, K.; Ma, Y.M. Monomer casting nylon/graphene nanocomposite with both improved thermal conductivity and mechanical performance. Compos. Part A-Appl. Sci. Manuf. 2019, 120, 49–55. [Google Scholar] [CrossRef]
- Jang, J.-u.; Lee, H.S.; Kim, J.W.; Kim, S.Y.; Kim, S.H.; Hwang, I.; Kang, B.J.; Kang, M.K. Facile and cost-effective strategy for fabrication of polyamide 6 wrapped multi-walled carbon nanotube via anionic melt polymerization of ε-caprolactam. Chem. Eng. J. 2019, 373, 251–258. [Google Scholar] [CrossRef]
- Song, N.; Cao, D.; Luo, X.; Wang, Q.; Ding, P.; Shi, L. Highly thermally conductive polypropylene/graphene composites for thermal management. Compos. Part A-Appl. Sci. Manuf. 2020, 135, 105912. [Google Scholar] [CrossRef]
- He, G.; Wang, P.; Dai, Y.; Sun, Y.; Zhang, J.; Yang, Z. Carbon nanofillers repair strategy for high-efficiency thermal conductivity enhancement of PBX composites at ultralow mass fraction. Compos. Part A-Appl. Sci. Manuf. 2021, 148, 106492. [Google Scholar] [CrossRef]
- Kim, H.S.; Jang, J.-u.; Yu, J.; Kim, S.Y. Thermal conductivity of polymer composites based on the length of multi-walled carbon nanotubes. Compos. Part B-Eng. 2015, 79, 505–512. [Google Scholar] [CrossRef]
- Kim, H.S.; Bae, H.S.; Yu, J.; Kim, S.Y. Thermal conductivity of polymer composites with the geometrical characteristics of graphene nanoplatelets. Sci. Rep. 2016, 6, 26825. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.; Seveno, D.; Gorbatikh, L. Multiscale modeling and maximizing the thermal conductivity of Polyamide-6 reinforced by highly entangled graphene flakes. Compos. Part A-Appl. Sci. Manuf. 2021, 151, 106632. [Google Scholar] [CrossRef]
- Jia, C.; Zhang, P.; Seraji, S.M.; Xie, R.; Chen, L.; Liu, D.; Xiong, Y.; Chen, H.; Fu, Y.; Xu, H.; et al. Effects of BN/GO on the recyclable, healable and thermal conductivity properties of ENR/PLA thermoplastic vulcanizates. Compos. Part A-Appl. Sci. Manuf. 2022, 152, 106686. [Google Scholar] [CrossRef]
- Shtein, M.; Nadiv, R.; Buzaglo, M.; Kahil, K.; Regev, O. Thermally Conductive Graphene-Polymer Composites: Size, Percolation, and Synergy Effects. Chem. Mater. 2015, 27, 2100–2106. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, J.H.; Kim, W.Y.; Lee, H.S.; Kim, S.Y.; Khil, M.-S. Volume control of expanded graphite based on inductively coupled plasma and enhanced thermal conductivity of epoxy composite by formation of the filler network. Carbon 2017, 119, 40–46. [Google Scholar] [CrossRef]
- Barani, Z.; Mohammadzadeh, A.; Geremew, A.; Huang, C.-Y.; Coleman, D.; Mangolini, L.; Kargar, F.; Balandin, A.A. Thermal Properties of the Binary-Filler Hybrid Composites with Graphene and Copper Nanoparticles. Adv. Funct. Mater. 2020, 30, 1904008. [Google Scholar] [CrossRef]
- Jang, J.-u.; Lee, S.H.; Kim, J.; Kim, S.Y.; Kim, S.H. Nano-bridge effect on thermal conductivity of hybrid polymer composites incorporating 1D and 2D nanocarbon fillers. Compos. Part B-Eng. 2021, 222, 109072. [Google Scholar] [CrossRef]
- Prolongo, S.G.; Printz, A.D.; Rolston, N.; Watson, B.L.; Dauskardt, R.H. Poly(triarylamine) composites with carbon nanomaterials for highly transparent and conductive coatings. Thin Solid Films 2018, 646, 61–66. [Google Scholar] [CrossRef]
- Abt, T.; Sánchez-Soto, M. A Review of the Recent Advances in Cyclic Butylene Terephthalate Technology and its Composites. Crit. Rev. Solid State Mater. Sci. 2017, 42, 173–217. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.Y.; Noh, Y.J.; Yu, J. Thermal conductivity of graphene nanoplatelets filled composites fabricated by solvent-free processing for the excellent filler dispersion and a theoretical approach for the composites containing the geometrized fillers. Compos. Part A-Appl. Sci. Manuf. 2015, 69, 219–225. [Google Scholar] [CrossRef]
- Nan, C.-W.; Liu, G.; Lin, Y.; Li, M. Interface effect on thermal conductivity of carbon nanotube composites. Appl. Phys. Lett. 2004, 85, 3549. [Google Scholar] [CrossRef]
- Huxtable, S.T.; Cahill, D.G.; Shenogin, S.; Xue, L.; Ozisik, R.; Barone, P.; Usrey, M.; Strano, M.S.; Siddons, G.; Shim, M.; et al. Interfacial heat flow in carbon nanotube suspensions. Nat. Mater. 2003, 2, 731–734. [Google Scholar] [CrossRef]
- Yu, J.; Cha, J.E.; Kim, S.Y. Thermally conductive composite film filled with highly dispersed graphene nanoplatelets via solvent-free one-step fabrication. Compos. Part B-Eng. 2017, 110, 171–177. [Google Scholar] [CrossRef]
- Noh, Y.J.; Kim, S.Y. Synergistic improvement of thermal conductivity in polymer composites filled with pitch based carbon fiber and graphene nanoplatelets. Polym. Test. 2015, 45, 132–138. [Google Scholar] [CrossRef]
- Zheng, X.; Wen, B. Practical PBT/PC/GNP composites with anisotropic thermal conductivity. RSC Adv. 2019, 9, 36316. [Google Scholar] [CrossRef] [Green Version]
- Seki, Y.; Avci, B.; Uzun, S.; Kaya, N.; Atagur, M.; Sever, K.; Sarikanat, M. The Using of Graphene Nano-Platelets for a Better through-Plane Thermal Conductivity for Polypropylene. Polym. Compos. 2019, 40, E1320–E1328. [Google Scholar] [CrossRef]


| Sample | GNP | pCBT (wt.%) | ||
|---|---|---|---|---|
| M5 (wt.%) | M15 (wt.%) | M25 (wt.%) | ||
| pCBT | - | - | - | 100 |
| M5-pCBT-5 | 5 | - | - | 95 |
| M5-pCBT-10 | 10 | - | - | 90 |
| M5-pCBT-20 | 20 | - | - | 80 |
| M5-pCBT-30 | 30 | - | - | 70 |
| M15-pCBT-5 | - | 5 | - | 95 |
| M15-pCBT-10 | - | 10 | - | 90 |
| M15-pCBT-20 | - | 20 | - | 80 |
| M15-pCBT-30 | - | 30 | - | 70 |
| M25-pCBT-5 | - | - | 5 | 95 |
| M25-pCBT-10 | - | - | 10 | 90 |
| M25-pCBT-20 | - | - | 20 | 80 |
| M25-pCBT-30 | - | - | 30 | 70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, J.-u.; Nam, H.E.; So, S.O.; Lee, H.; Kim, G.S.; Kim, S.Y.; Kim, S.H. Thermal Percolation Behavior in Thermal Conductivity of Polymer Nanocomposite with Lateral Size of Graphene Nanoplatelet. Polymers 2022, 14, 323. https://doi.org/10.3390/polym14020323
Jang J-u, Nam HE, So SO, Lee H, Kim GS, Kim SY, Kim SH. Thermal Percolation Behavior in Thermal Conductivity of Polymer Nanocomposite with Lateral Size of Graphene Nanoplatelet. Polymers. 2022; 14(2):323. https://doi.org/10.3390/polym14020323
Chicago/Turabian StyleJang, Ji-un, Hae Eun Nam, Soon Oh So, Hyeseong Lee, Geon Su Kim, Seong Yun Kim, and Seong Hun Kim. 2022. "Thermal Percolation Behavior in Thermal Conductivity of Polymer Nanocomposite with Lateral Size of Graphene Nanoplatelet" Polymers 14, no. 2: 323. https://doi.org/10.3390/polym14020323
APA StyleJang, J.-u., Nam, H. E., So, S. O., Lee, H., Kim, G. S., Kim, S. Y., & Kim, S. H. (2022). Thermal Percolation Behavior in Thermal Conductivity of Polymer Nanocomposite with Lateral Size of Graphene Nanoplatelet. Polymers, 14(2), 323. https://doi.org/10.3390/polym14020323








