Elastomer-Based Visuotactile Sensor for Normality of Robotic Manufacturing Systems
Abstract
:1. Introduction
2. Methodology
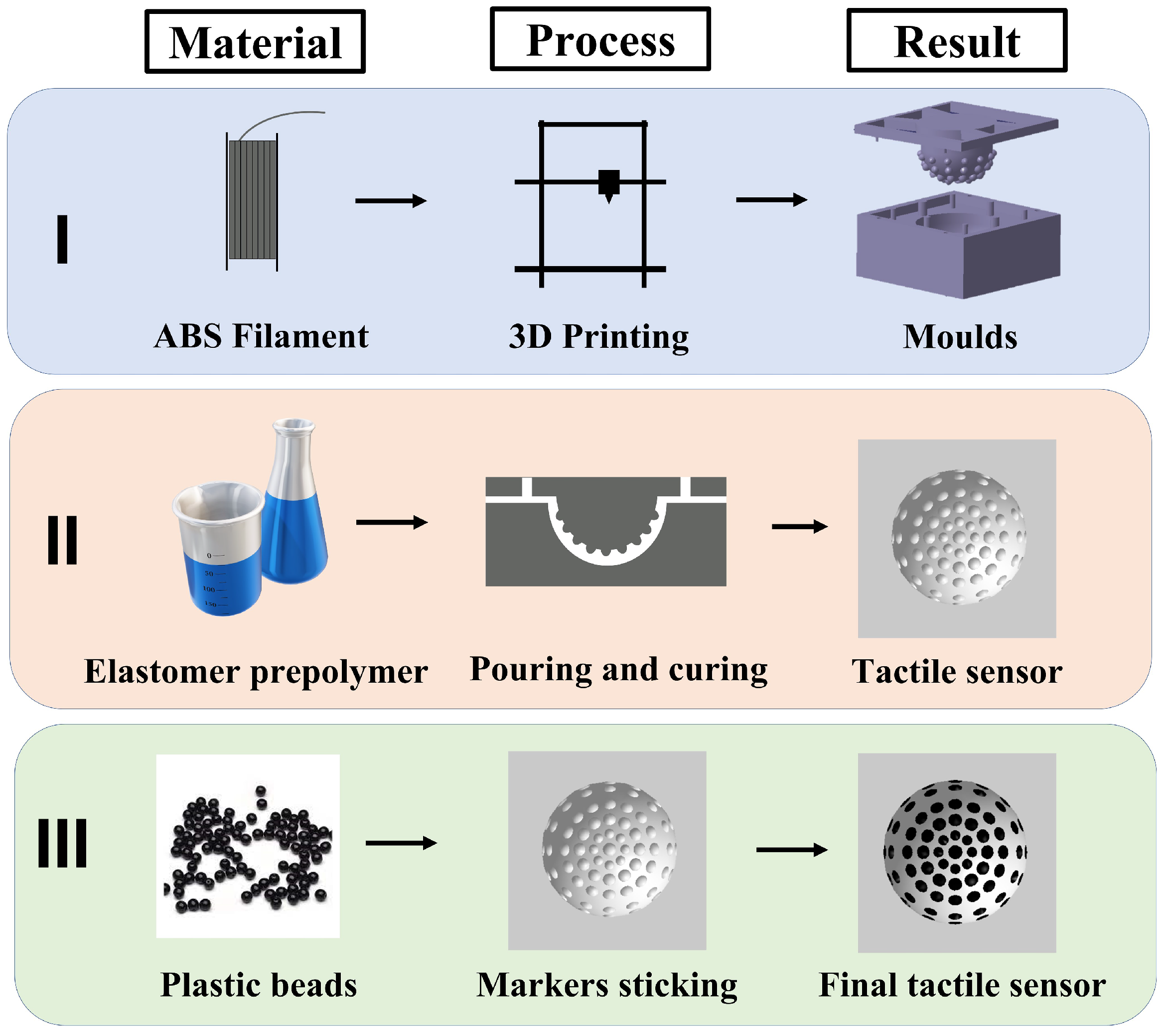
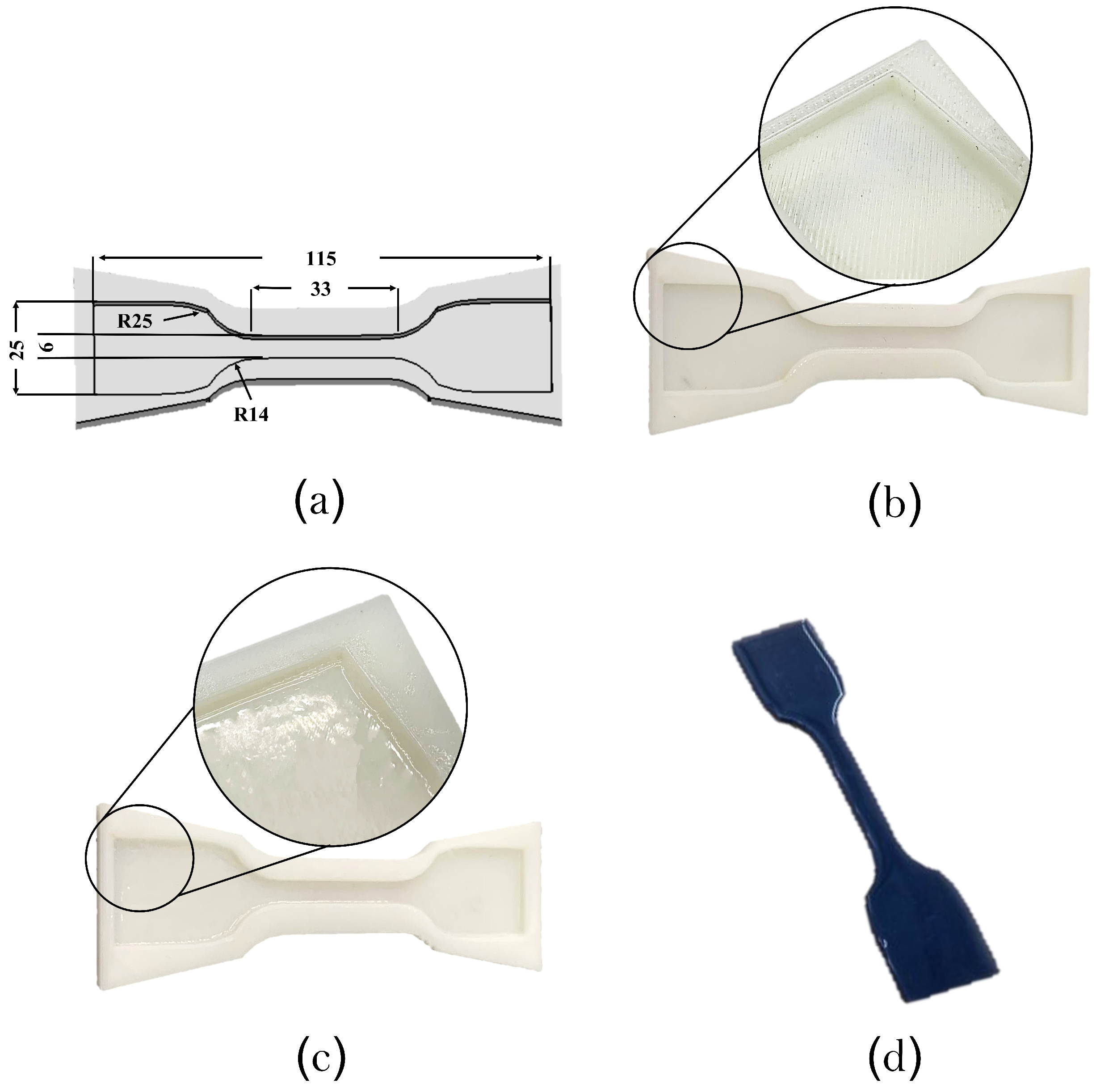
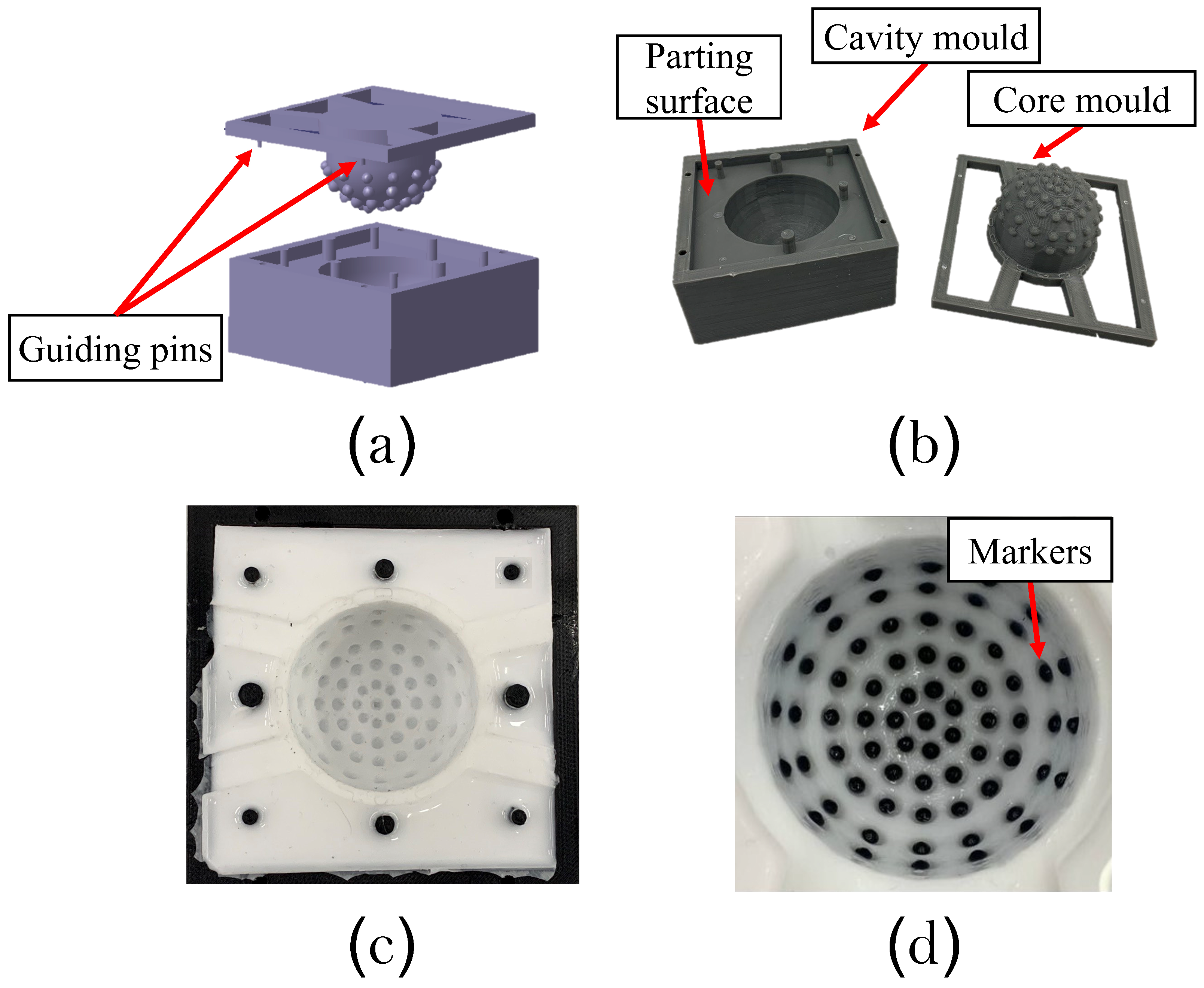
2.1. Sensor Materials and Fabrication
2.2. Experimental Setup
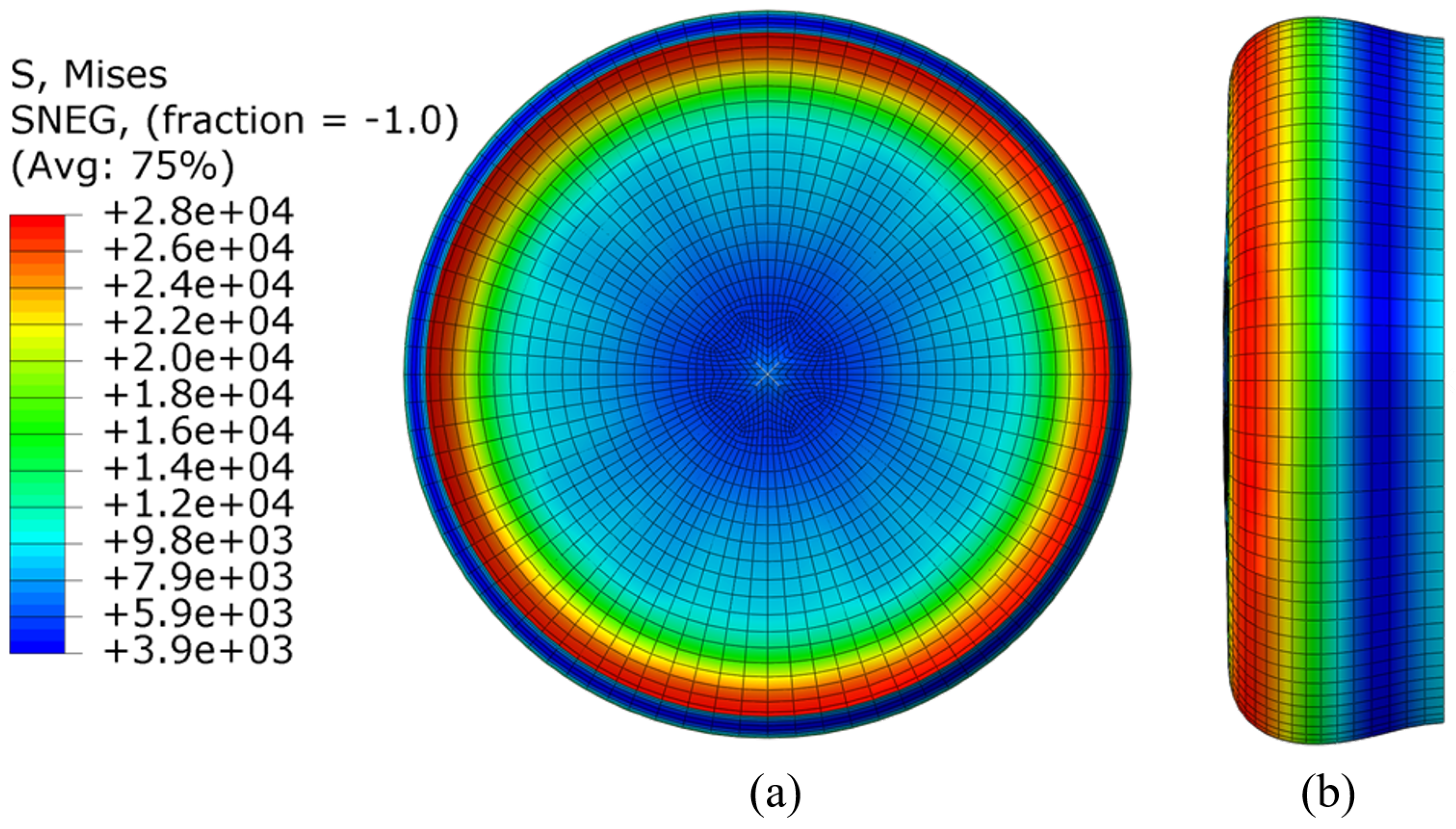
2.3. Finite Element Modelling
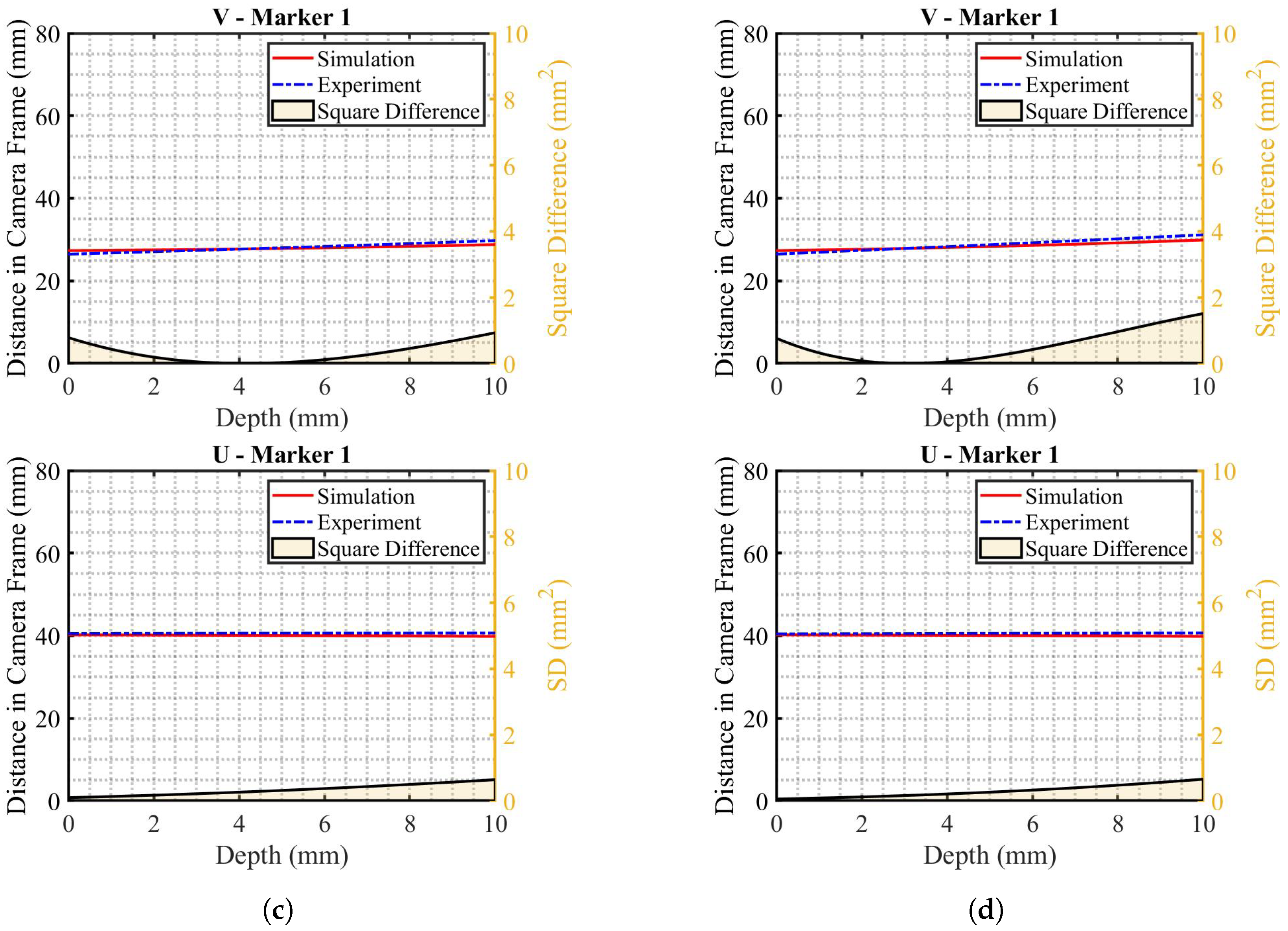
3. Results and Discussion
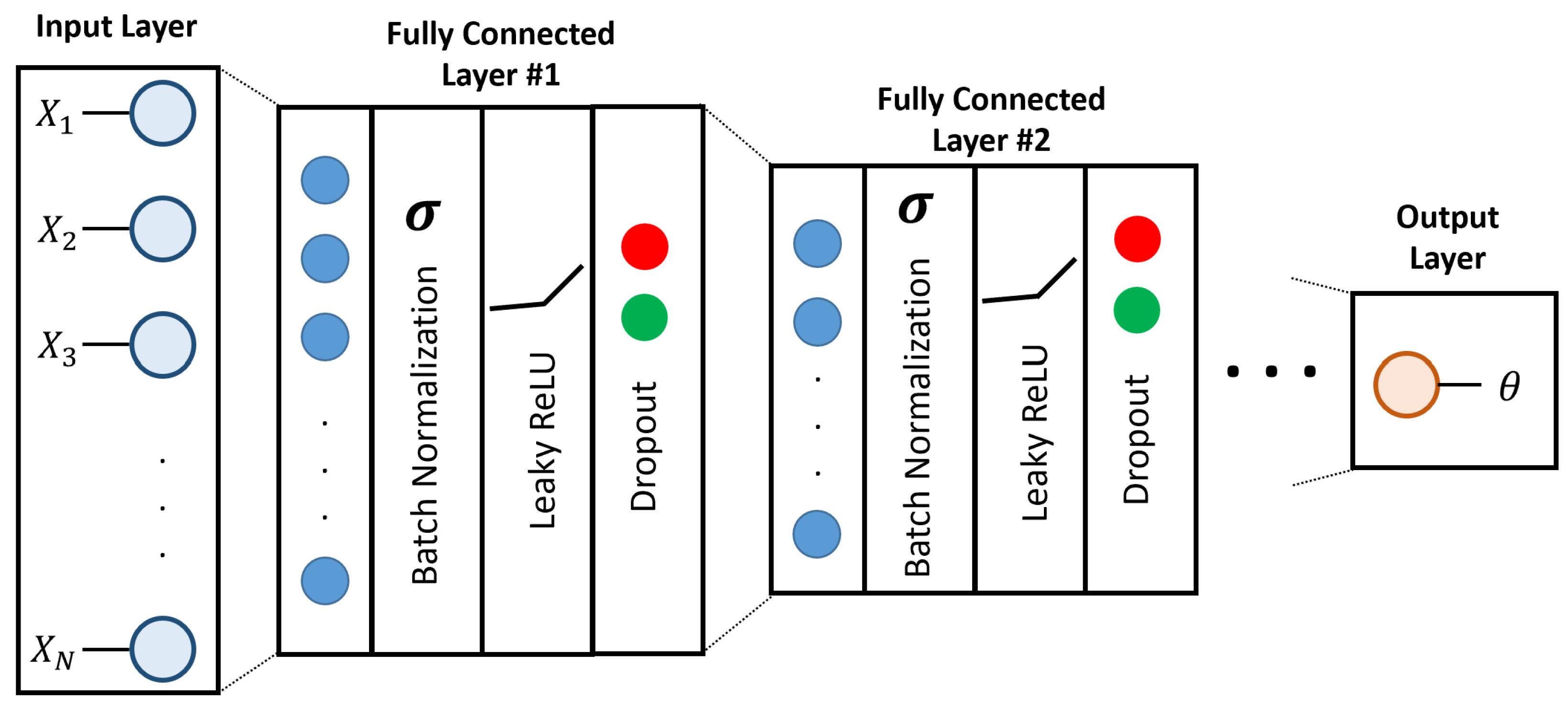
Deep Learning for Sim2Real
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tables and Figures
| Node Number | Error (mm) | |||||||
|---|---|---|---|---|---|---|---|---|
| U | V | U | V | U | V | U | V | |
| 1 | 1.509 | 1.749 | 1.509 | 1.361 | 1.767 | 1.507 | 1.629 | 1.945 |
| 2 | 2.939 | 1.294 | 2.971 | 1.271 | 3.1 | 1.43 | 2.876 | 1.618 |
| 3 | 2.61 | 1.311 | 2.538 | 1.209 | 2.714 | 1.422 | 2.501 | 1.439 |
| 4 | 2.718 | 2.146 | 2.561 | 1.34 | 2.493 | 1.393 | 2.314 | 1.556 |
| 5 | 2.092 | 1.84 | 2.154 | 1.395 | 2.296 | 1.47 | 2.12 | 1.587 |
| 6 | 1.578 | 1.933 | 1.502 | 1.602 | 1.711 | 1.758 | 1.67 | 2.168 |
| 7 | 0.957 | 1.326 | 1.078 | 1.376 | 1.26 | 1.562 | 1.014 | 1.97 |
| 8 | 1.634 | 1.161 | 1.742 | 1.25 | 1.866 | 1.456 | 2.034 | 1.848 |
| 9 | 2.754 | 1.169 | 2.815 | 1.224 | 3.061 | 1.462 | 2.953 | 1.718 |
| 10 | 3.148 | 1.085 | 3.176 | 1.314 | 3.367 | 1.594 | 3.197 | 1.567 |
| 11 | 2.769 | 1.087 | 2.682 | 1.186 | 2.885 | 1.435 | 2.689 | 1.309 |
| 12 | 3.43 | 1.146 | 3.309 | 1.032 | 3.487 | 1.35 | 3.229 | 1.151 |
| 13 | 3.037 | 1.939 | 2.925 | 1.153 | 3.059 | 1.167 | 2.819 | 1.2 |
| 14 | 3.124 | 2.614 | 3.062 | 1.579 | 3.247 | 1.493 | 2.972 | 1.784 |
| 15 | 1.842 | 2.653 | 1.952 | 1.85 | 2.125 | 1.873 | 1.965 | 2.293 |
| 16 | 0.426 | 2.42 | 0.718 | 1.965 | 0.862 | 2.043 | 0.748 | 2.795 |
| 17 | 0.739 | 1.82 | 0.781 | 1.83 | 0.852 | 2.104 | 0.831 | 2.836 |
| 18 | 0.521 | 1.338 | 0.652 | 1.656 | 0.703 | 1.855 | 0.692 | 2.305 |
| 19 | 0.849 | 1.26 | 1.157 | 1.555 | 1.389 | 1.769 | 1.503 | 1.989 |
| 20 | 1.724 | 1.387 | 2.008 | 1.679 | 2.358 | 1.735 | 2.394 | 1.796 |
| 21 | 2.811 | 1.123 | 3.019 | 1.482 | 3.316 | 1.686 | 3.326 | 1.704 |
| 22 | 3.524 | 0.905 | 3.564 | 1.559 | 3.919 | 1.951 | 3.909 | 1.49 |
| 23 | 3.763 | 0.77 | 3.607 | 1.023 | 3.858 | 1.51 | 3.71 | 1.124 |
| 24 | 3.087 | 0.925 | 2.851 | 1.104 | 2.996 | 1.673 | 2.825 | 1.103 |
| 25 | 3.749 | 1.334 | 3.566 | 0.914 | 3.777 | 1.093 | 3.465 | 0.93 |
| 26 | 3.95 | 1.869 | 3.807 | 0.998 | 3.932 | 1.016 | 3.667 | 0.993 |
| 27 | 3.498 | 3.185 | 3.452 | 1.684 | 3.635 | 1.175 | 3.32 | 1.424 |
| 28 | 2.142 | 3.392 | 2.141 | 2.126 | 2.394 | 1.671 | 2.168 | 2.022 |
| 29 | 0.567 | 4.167 | 0.644 | 3.169 | 1.012 | 2.729 | 0.892 | 3.376 |
| 30 | 0.957 | 2.541 | 0.887 | 2.024 | 0.79 | 2.216 | 0.989 | 3.162 |
| 31 | 1.315 | 1.138 | 1.279 | 1.556 | 1.183 | 2.074 | 1.328 | 3.111 |
| 32 | 0.831 | 1.006 | 0.844 | 1.593 | 0.682 | 2.112 | 0.783 | 3.024 |
| 33 | 1.26 | 1.574 | 1.137 | 2.009 | 0.906 | 2.157 | 0.924 | 2.548 |
| 34 | 0.709 | 1.965 | 0.995 | 2.426 | 1.448 | 2.227 | 1.521 | 2.15 |
| 35 | 1.756 | 2.141 | 2.057 | 2.609 | 2.577 | 2.44 | 2.864 | 2.185 |
| 36 | 2.502 | 1.784 | 2.836 | 2.377 | 3.371 | 2.386 | 3.677 | 2.024 |
| 37 | 3.108 | 1.117 | 3.345 | 1.816 | 3.824 | 2.127 | 3.96 | 1.742 |
| sum | 79.931 | 63.615 | 81.322 | 59.295 | 88.222 | 64.119 | 85.475 | 70.987 |
| min | 0.426 | 0.77 | 0.644 | 0.914 | 0.682 | 1.016 | 0.692 | 0.93 |
| max | 3.95 | 4.167 | 3.807 | 3.169 | 3.932 | 2.729 | 3.96 | 3.376 |
| avg | 2.16 | 1.719 | 2.198 | 1.603 | 2.384 | 1.733 | 2.31 | 1.919 |

References
- Phanden, R.K.; Sharma, P.; Dubey, A. A review on simulation in digital twin for aerospace, manufacturing and robotics. Mater. Today Proc. 2021, 38, 174–178. [Google Scholar] [CrossRef]
- Onstein, I.F.; Semeniuta, O.; Bjerkeng, M. Deburring using robot manipulators: A review. In Proceedings of the 2020 3rd International Symposium on Small-scale Intelligent Manufacturing Systems (SIMS), Gjøvik, Norway, 10–12 June 2020; pp. 1–7. [Google Scholar]
- Alvares, A.J.; Rodriguez, E.; Jaimes, C.I.R.; Toquica, J.S.; Ferreira, J.C. STEP-NC Architectures for Industrial Robotic Machining: Review, Implementation and Validation. IEEE Access 2020, 8, 152592–152610. [Google Scholar] [CrossRef]
- Luo, H.; Zhang, D.; Luo, M. Tool Wear and Remaining Useful Life Estimation of Difficult-to-machine Aerospace Alloys: A Review. China Mech. Eng. 2021, 32, 2647. [Google Scholar]
- Sun, D.; Lemoine, P.; Keys, D.; Doyle, P.; Malinov, S.; Zhao, Q.; Qin, X.; Jin, Y. Hole-making processes and their impacts on the microstructure and fatigue response of aircraft alloys. Int. J. Adv. Manuf. Technol. 2018, 94, 1719–1726. [Google Scholar] [CrossRef] [Green Version]
- Akula, S.; Nayak, S.N.; Bolar, G.; Managuli, V. Comparison of conventional drilling and helical milling for hole making in Ti6Al4V titanium alloy under sustainable dry condition. Manuf. Rev. 2021, 8, 12. [Google Scholar] [CrossRef]
- Yuan, C.G.; Pramanik, A.; Basak, A.; Prakash, C.; Shankar, S. Drilling of titanium alloy (Ti6Al4V)—A review. Mach. Sci. Technol. 2021, 25, 637–702. [Google Scholar] [CrossRef]
- Abdelhafeez, A.; Soo, S.; Aspinwall, D.; Dowson, A.; Arnold, D. Burr formation and hole quality when drilling titanium and aluminium alloys. Procedia Cirp 2015, 37, 230–235. [Google Scholar] [CrossRef]
- Aamir, M.; Giasin, K.; Tolouei-Rad, M.; Vafadar, A. A review: Drilling performance and hole quality of aluminium alloys for aerospace applications. J. Mater. Res. Technol. 2020, 9, 12484–12500. [Google Scholar] [CrossRef]
- da Silva Santos, K.R.; de Carvalho, G.M.; Tricarico, R.T.; Ferreira, L.F.L.R.; Villani, E.; Sutério, R. Evaluation of perpendicularity methods for a robotic end effector from aircraft industry. In Proceedings of the 2018 13th IEEE International Conference on Industry Applications (INDUSCON), Sao Paulo, Brazil, 12–14 November 2018; pp. 1373–1380. [Google Scholar]
- Yu, L.; Zhang, Y.; Bi, Q.; Wang, Y. Research on surface normal measurement and adjustment in aircraft assembly. Precis. Eng. 2017, 50, 482–493. [Google Scholar] [CrossRef]
- Zhang, Y.; Bi, Q.; Yu, L.; Wang, Y. Online adaptive measurement and adjustment for flexible part during high precision drilling process. Int. J. Adv. Manuf. Technol. 2017, 89, 3579–3599. [Google Scholar] [CrossRef]
- Hassanin, H.; Abena, A.; Elsayed, M.A.; Essa, K. 4D printing of NiTi auxetic structure with improved ballistic performance. Micromachines 2020, 11, 745. [Google Scholar] [CrossRef] [PubMed]
- Brambilla, C.R.; Okafor-Muo, O.L.; Hassanin, H.; ElShaer, A. 3DP printing of oral solid formulations: A systematic review. Pharmaceutics 2021, 13, 358. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Reinicke, T. On the environmental impacts of 3D printing technology. Appl. Mater. Today 2020, 20, 100689. [Google Scholar] [CrossRef]
- Shah, U.H.; Muthusamy, R.; Gan, D.; Zweiri, Y.; Seneviratne, L. On the Design and Development of Vision-based Tactile Sensors. J. Intell. Robot. Syst. 2021, 102, 82. [Google Scholar] [CrossRef]
- Lambeta, M.; Chou, P.W.; Tian, S.; Yang, B.; Maloon, B.; Most, V.R.; Stroud, D.; Santos, R.; Byagowi, A.; Kammerer, G.; et al. DIGIT: A Novel Design for a Low-Cost Compact High-Resolution Tactile Sensor with Application to In-Hand Manipulation. IEEE Robot. Autom. Lett. 2020, 5, 3838–3845. [Google Scholar] [CrossRef]
- hyun Choi, S.; Tahara, K. Dexterous object manipulation by a multi-fingered robotic hand with visual-tactile fingertip sensors. Robomech. J. 2020, 7. [Google Scholar] [CrossRef]
- Kumagai, K.; Shimonomura, K. Event-based Tactile Image Sensor for Detecting Spatio-Temporal Fast Phenomena in Contacts. In Proceedings of the 2019 IEEE World Haptics Conference, WHC 2019, Tokyo, Japan, 9–12 July 2019; Institute of Electrical and Electronics Engineers Inc.: Interlaken, Switzerland, 2019; pp. 343–348. [Google Scholar] [CrossRef]
- Muthusamy, R.; Huang, X.; Zweiri, Y.; Seneviratne, L.; Gan, D.; Muthusamy, R. Neuromorphic Event-Based Slip Detection and Suppression in Robotic Grasping and Manipulation. IEEE Access 2020, 8, 153364–153384. [Google Scholar] [CrossRef]
- Rigi, A.; Baghaei Naeini, F.; Makris, D.; Zweiri, Y. A Novel Event-Based Incipient Slip Detection Using Dynamic Active-Pixel Vision Sensor (DAVIS). Sensors 2018, 18, 333. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Kuchenbecker, K.J.; Martius, G. A soft thumb-sized vision-based sensor with accurate all-round force perception. Nat. Mach. Intell. 2022, 4, 135–145. [Google Scholar] [CrossRef]
- Baghaei Naeini, F.; Alali, A.M.; Al-Husari, R.; Rigi, A.; Al-Sharman, M.K.; Makris, D.; Zweiri, Y. A Novel Dynamic-Vision-Based Approach for Tactile Sensing Applications. IEEE Trans. Instrum. Meas. 2020, 69. [Google Scholar] [CrossRef]
- Naeini, F.B.; Makris, D.; Gan, D.; Zweiri, Y. Dynamic-vision-based force measurements using convolutional recurrent neural networks. Sensors 2020, 20, 4469. [Google Scholar] [CrossRef] [PubMed]
- Lepora, N.F.; Lloyd, J. Optimal Deep Learning for Robot Touch: Training Accurate Pose Models of 3D Surfaces and Edges. IEEE Robot. Autom. Mag. 2020, 27, 66–77. [Google Scholar] [CrossRef]
- Ward-Cherrier, B.; Pestell, N.; Lepora, N.F. NeuroTac: A Neuromorphic Optical Tactile Sensor applied to Texture Recognition. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation, Paris, France, 31 May–31 August 2020; pp. 2654–2660. [Google Scholar] [CrossRef]
- Fang, B.; Sun, F.; Yang, C.; Xue, H.; Chen, W.; Zhang, C.; Guo, D.; Liu, H. A dual-modal vision-based tactile sensor for robotic hand grasping. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4740–4745. [Google Scholar]
- Hu, C.B.; Zhang, C.; Xie, X.; He, J.Y.; Xie, W.A. Real-time Marker Recognition Using Vision-based Tactile Sensor. In Proceedings of the 2018 14th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Qingdao, China, 1 October–3 November 2018; pp. 1–3. [Google Scholar]
- Kamiyama, K.; Vlack, K.; Mizota, T.; Kajimoto, H.; Kawakami, K.; Tachi, S. Vision-based sensor for real-time measuring of surface traction fields. IEEE Comput. Graph. Appl. 2005, 25, 68–75. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Zhou, Z.; Zeng, J.; Liu, H. An Enhanced FingerVision for Contact Spatial Surface Sensing. IEEE Sens. J. 2021, 21, 16492–16502. [Google Scholar] [CrossRef]
- Sui, R.; Zhang, L.; Li, T.; Jiang, Y. Incipient Slip Detection Method With Vision-Based Tactile Sensor Based on Distribution Force and Deformation. IEEE Sens. J. 2021, 21, 25973–25985. [Google Scholar] [CrossRef]
- Gomes, D.F.; Paoletti, P.; Luo, S. Generation of gelsight tactile images for sim2real learning. IEEE Robot. Autom. Lett. 2021, 6, 4177–4184. [Google Scholar] [CrossRef]
- Sferrazza, C.; D’Andrea, R. Sim-to-real for high-resolution optical tactile sensing: From images to 3D contact force distributions. arXiv 2020, arXiv:2012.11295. [Google Scholar]
- Wang, S.; Lambeta, M.; Chou, P.W.; Calandra, R. TACTO: A Fast, Flexible, and Open-Source Simulator for High-Resolution Vision-Based Tactile Sensors. IEEE Robot. Autom. Lett. 2022, 7, 3930–3937. [Google Scholar] [CrossRef]
- Hassanin, H.; Jiang, K. Net shape manufacturing of ceramic micro parts with tailored graded layers. J. Micromech. Microeng. 2013, 24, 015018. [Google Scholar] [CrossRef]
- Hassanin, H.; Jiang, K. Fabrication and characterization of stabilised zirconia micro parts via slip casting and soft moulding. Scr. Mater. 2013, 69, 433–436. [Google Scholar] [CrossRef]
- Hassanin, H.; Jiang, K. Multiple replication of thick PDMS micropatterns using surfactants as release agents. Microelectron. Eng. 2011, 88, 3275–3277. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, X.; Chu, K.; Wang, X.; Hu, Z.; Su, H. Carbon Black/PDMS Based Flexible Capacitive Tactile Sensor for Multi-Directional Force Sensing. Sensors 2022, 22, 628. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Peng, H.; Wang, X.; Chen, X.; Yang, C.; Yang, B.; Liu, J. PDMS/MWCNT-based tactile sensor array with coplanar electrodes for crosstalk suppression. Microsyst. Nanoeng. 2016, 2, 16065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, X.; Sun, J.; Li, T.; Zheng, S.; Wang, C.; Tan, W.; Zhang, J.; Liu, C.; Ma, T.; Qi, Z.; et al. Flexible tactile electronic skin sensor with 3D force detection based on porous CNTs/PDMS nanocomposites. Nano-Micro Lett. 2019, 11, 57. [Google Scholar] [CrossRef] [Green Version]
- Sferrazza, C.; D’Andrea, R. Design, Motivation and Evaluation of a Full-Resolution Optical Tactile Sensor. Sensors 2019, 19, 928. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Zhang, L.; Li, T.; Jiang, Y. Continuous Marker Patterns for Representing Contact Information in Vision-Based Tactile Sensor: Principle, Algorithm, and Verification. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Duran, O.; Zweiri, Y.; Smith, M. Hybrid spectral unmixing: Using artificial neural networks for linear/non-linear switching. Remote Sens. 2017, 9, 775. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Andrew, L.; Maas, A.Y.; Hannun, A.Y.N. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ge, G.; Wang, Q.; Zhang, Y.Z.; Alshareef, H.N.; Dong, X. 3D printing of hydrogels for stretchable ionotronic devices. Adv. Funct. Mater. 2021, 31, 2107437. [Google Scholar] [CrossRef]

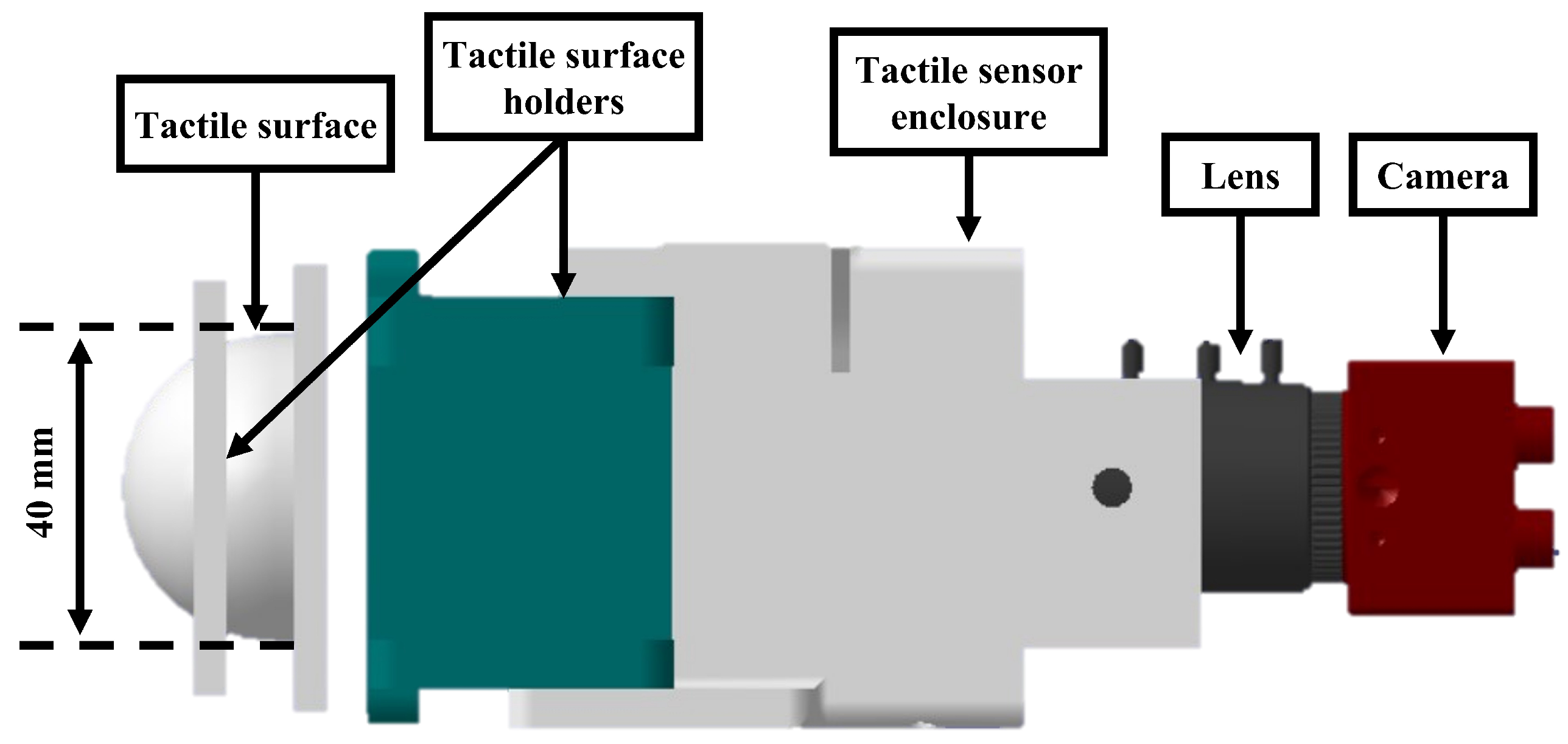
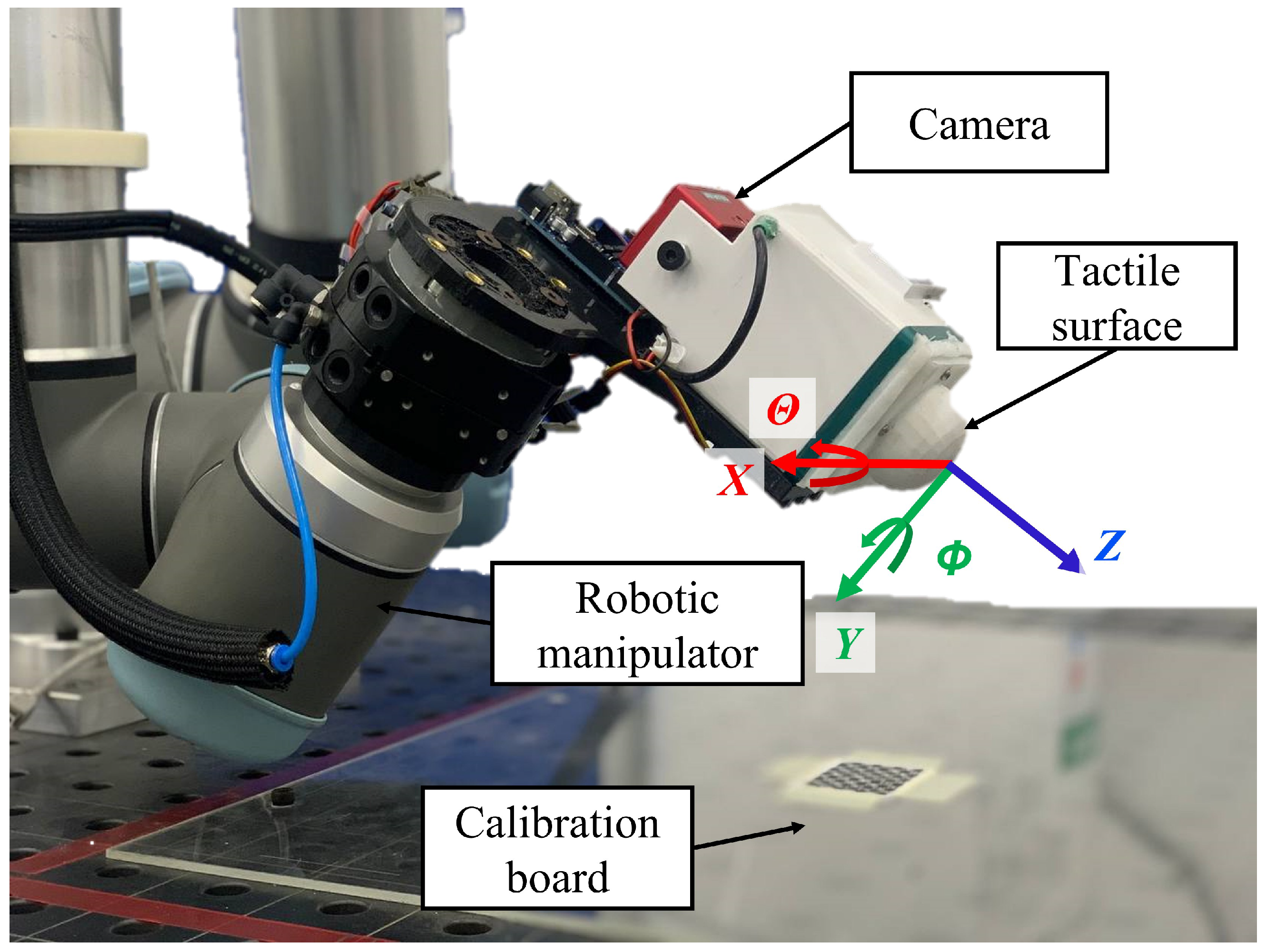
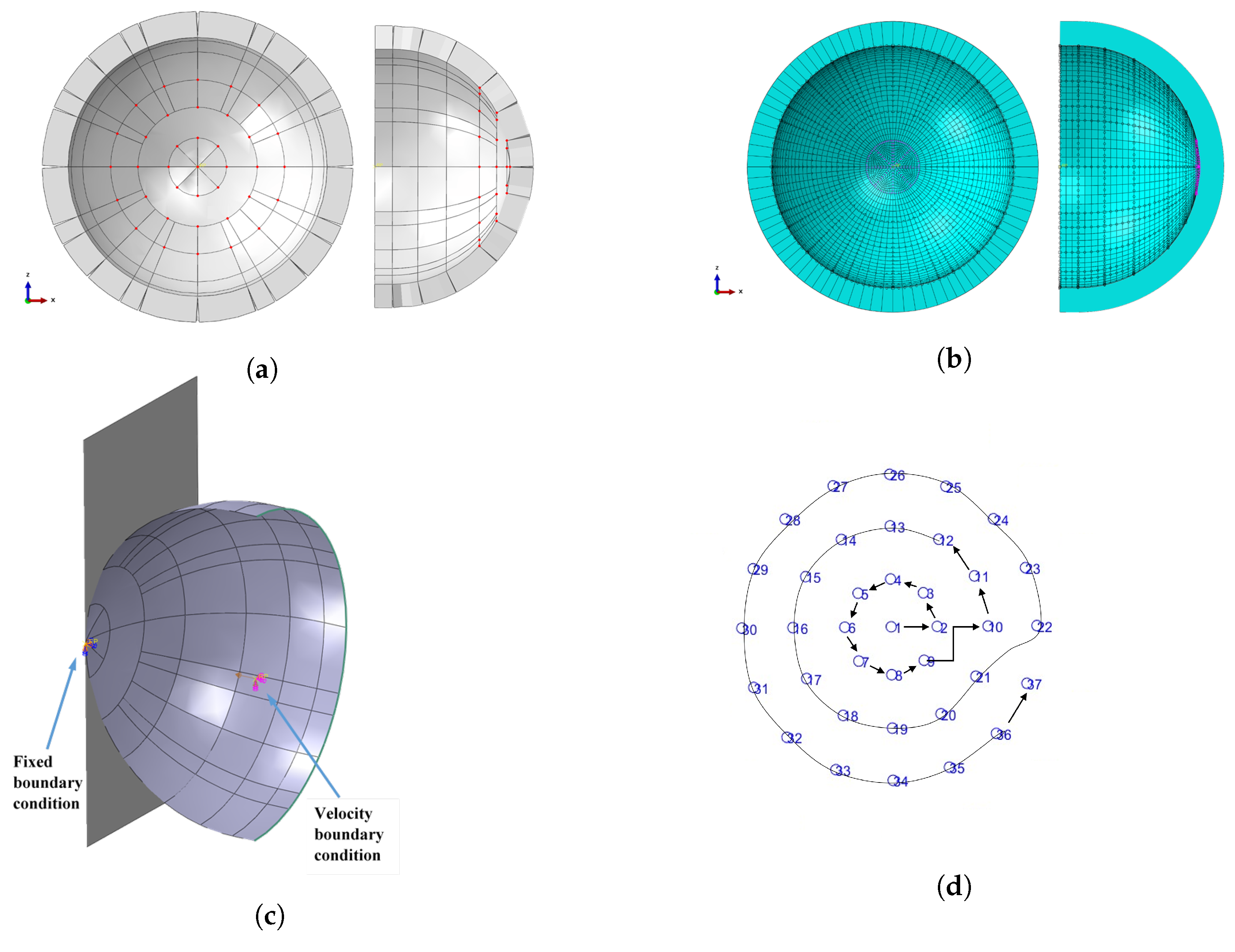
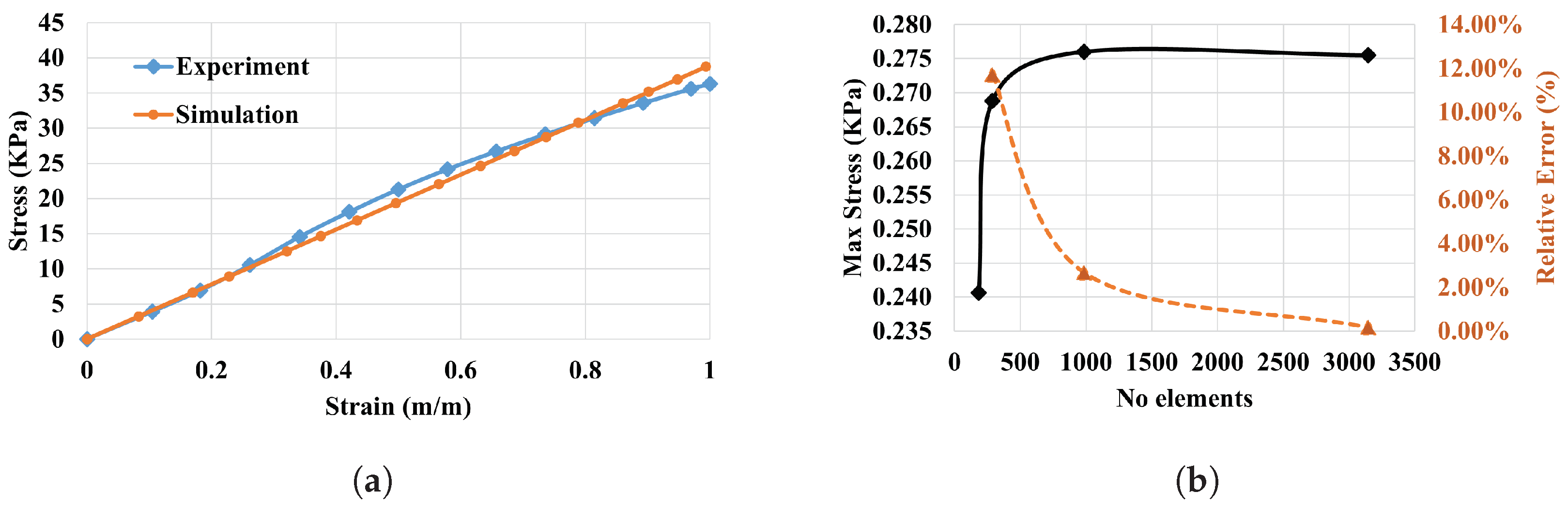
| Elastomer | Ultimate Strength (MPa) | Young’s Modulus (MPa) | Ductility (Strain %) |
|---|---|---|---|
| Dragon Skin™30 | 3.118 | 0.907 | 490 |
| Ecoflex™00-30 | 1.115 | 0.039 | 1290 |
| Ecoflex™00-50 | 1.480 | 0.099 | 1250 |
| Parameter | Value |
|---|---|
| Tactile surface material | Ecoflex™00-30 (E = 0.039 MPa) (rubber (Hardness: Shore 00-30)) |
| Tactile surface size | 40 mm diameter |
| Markers’ material | plastic |
| No. of markers | 37 |
| The diameter of markers | 2.5 mm |
| Size of the sensor enclosure (L × H × W) | 20 cm × 12 cm ×10 cm |
| Sensors’ 3D-printed enclosure material | ABS |
| Node Number | Error (mm) | Node Number | Error (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.297 | 0.279 | 0.297 | 0.311 | 21 | 0.326 | 0.349 | 0.368 | 0.369 |
| 2 | 0.338 | 0.339 | 0.35 | 0.348 | 22 | 0.346 | 0.372 | 0.398 | 0.382 |
| 3 | 0.326 | 0.318 | 0.334 | 0.326 | 23 | 0.35 | 0.354 | 0.381 | 0.361 |
| 4 | 0.363 | 0.325 | 0.324 | 0.323 | 24 | 0.329 | 0.327 | 0.355 | 0.326 |
| 5 | 0.326 | 0.31 | 0.319 | 0.317 | 25 | 0.371 | 0.348 | 0.363 | 0.345 |
| 6 | 0.308 | 0.29 | 0.306 | 0.322 | 26 | 0.397 | 0.36 | 0.366 | 0.355 |
| 7 | 0.248 | 0.258 | 0.276 | 0.284 | 27 | 0.425 | 0.373 | 0.361 | 0.358 |
| 8 | 0.275 | 0.284 | 0.3 | 0.324 | 28 | 0.387 | 0.34 | 0.331 | 0.336 |
| 9 | 0.326 | 0.33 | 0.35 | 0.355 | 29 | 0.358 | 0.321 | 0.318 | 0.34 |
| 10 | 0.338 | 0.348 | 0.366 | 0.359 | 30 | 0.308 | 0.28 | 0.285 | 0.335 |
| 11 | 0.323 | 0.323 | 0.342 | 0.329 | 31 | 0.257 | 0.277 | 0.297 | 0.346 |
| 12 | 0.352 | 0.343 | 0.362 | 0.344 | 32 | 0.223 | 0.257 | 0.275 | 0.321 |
| 13 | 0.367 | 0.332 | 0.338 | 0.33 | 33 | 0.277 | 0.292 | 0.288 | 0.306 |
| 14 | 0.394 | 0.354 | 0.358 | 0.359 | 34 | 0.269 | 0.304 | 0.315 | 0.315 |
| 15 | 0.349 | 0.321 | 0.329 | 0.339 | 35 | 0.325 | 0.355 | 0.368 | 0.369 |
| 16 | 0.277 | 0.269 | 0.28 | 0.309 | 36 | 0.34 | 0.375 | 0.394 | 0.393 |
| 17 | 0.263 | 0.266 | 0.283 | 0.315 | 37 | 0.338 | 0.373 | 0.401 | 0.393 |
| 18 | 0.224 | 0.25 | 0.263 | 0.285 | min | 0.223 | 0.25 | 0.263 | 0.284 |
| 19 | 0.239 | 0.271 | 0.292 | 0.307 | max | 0.425 | 0.375 | 0.401 | 0.393 |
| 20 | 0.29 | 0.316 | 0.333 | 0.337 | avg | 0.32 | 0.318 | 0.331 | 0.337 |
| Parameter | Parameter Range | Optimal Value |
|---|---|---|
| Number of hidden layers | 5 | |
| Width of hidden layers | ||
| Dropout coefficient | 0.5 | |
| Batch size | 256 | |
| Number of epochs | 128 | |
| Base learning rate | 0.01 |
| Dataset | MAE | Standard Deviation | Max Error |
|---|---|---|---|
| Simulation | 0.41° | 0.37° | 1.65° |
| Experimental | 0.34° | 0.31° | 1.33° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaid, I.M.; Halwani, M.; Ayyad, A.; Imam, A.; Almaskari, F.; Hassanin, H.; Zweiri, Y. Elastomer-Based Visuotactile Sensor for Normality of Robotic Manufacturing Systems. Polymers 2022, 14, 5097. https://doi.org/10.3390/polym14235097
Zaid IM, Halwani M, Ayyad A, Imam A, Almaskari F, Hassanin H, Zweiri Y. Elastomer-Based Visuotactile Sensor for Normality of Robotic Manufacturing Systems. Polymers. 2022; 14(23):5097. https://doi.org/10.3390/polym14235097
Chicago/Turabian StyleZaid, Islam Mohamed, Mohamad Halwani, Abdulla Ayyad, Adil Imam, Fahad Almaskari, Hany Hassanin, and Yahya Zweiri. 2022. "Elastomer-Based Visuotactile Sensor for Normality of Robotic Manufacturing Systems" Polymers 14, no. 23: 5097. https://doi.org/10.3390/polym14235097








