Flexural Properties of Textile-Reinforced Concrete with Nonorthogonal Grids
Abstract
:1. Introduction
2. Experiment Program
2.1. Material Properties
2.1.1. Matrix
2.1.2. Basalt Textile
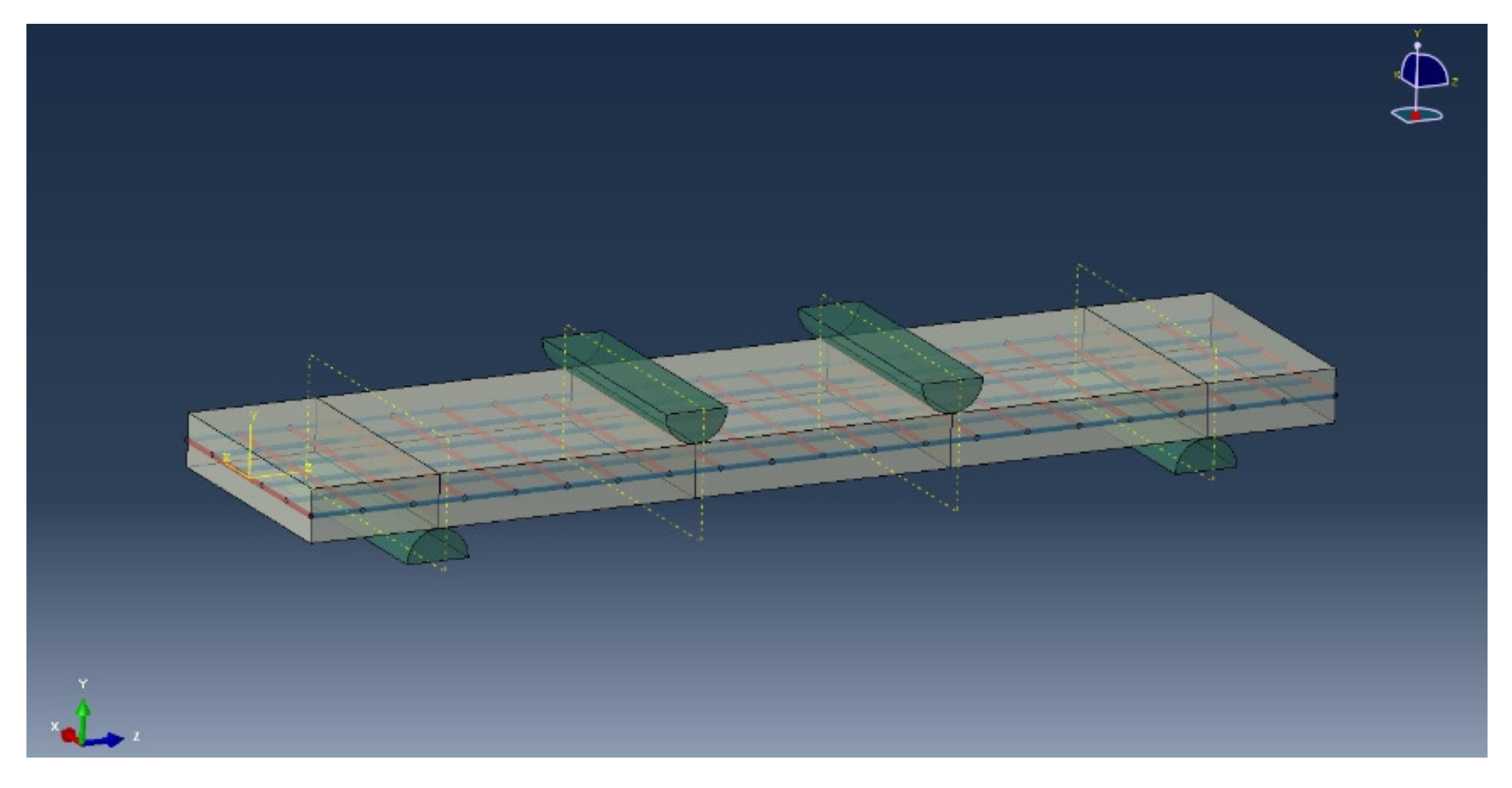
2.2. Test Specimens
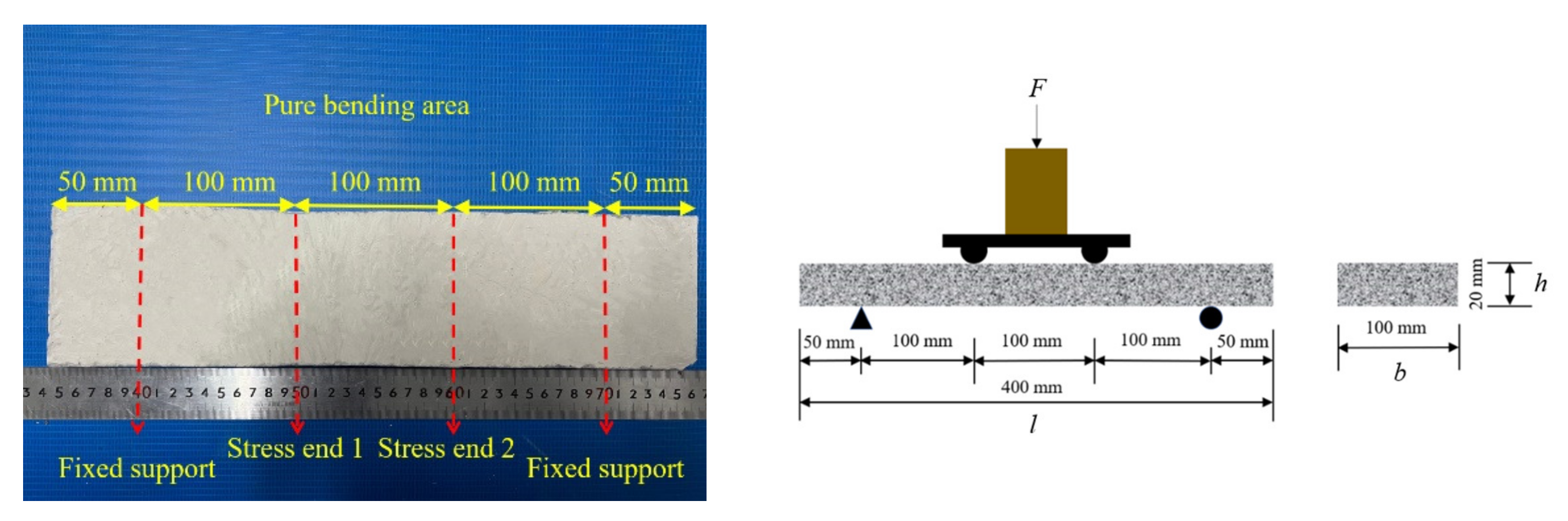
2.3. Four-Point Bending Test
3. Experimental Results
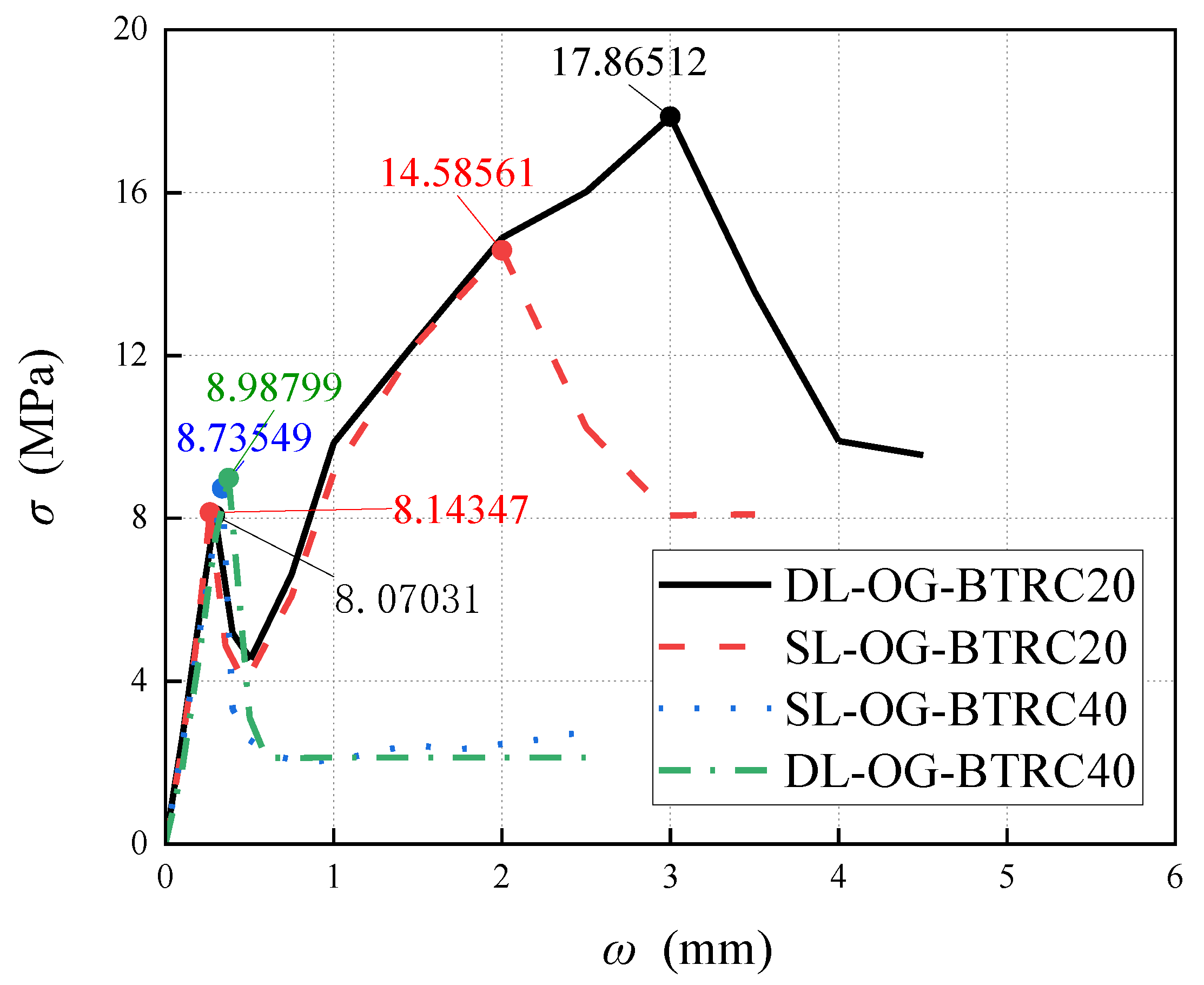
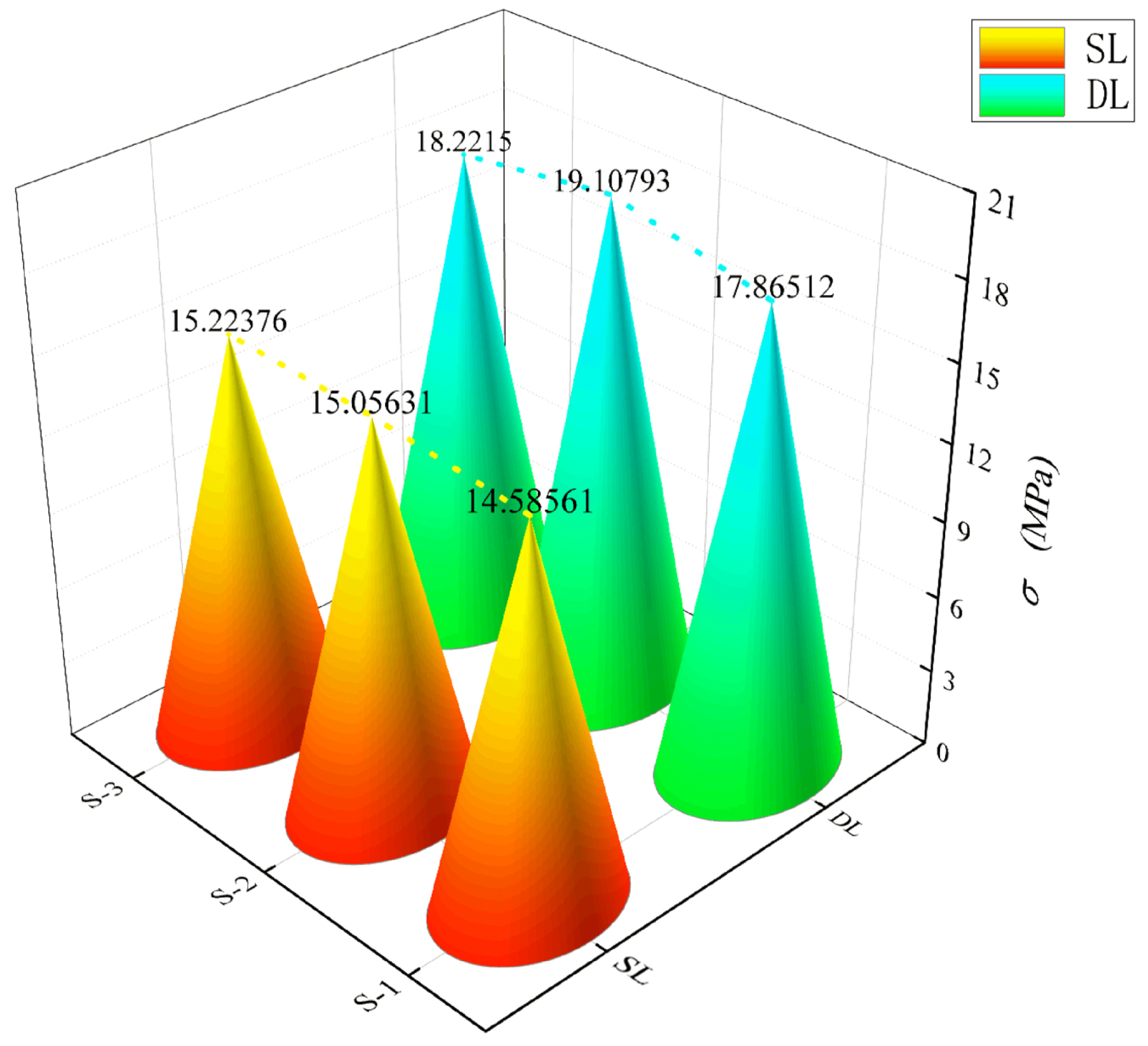
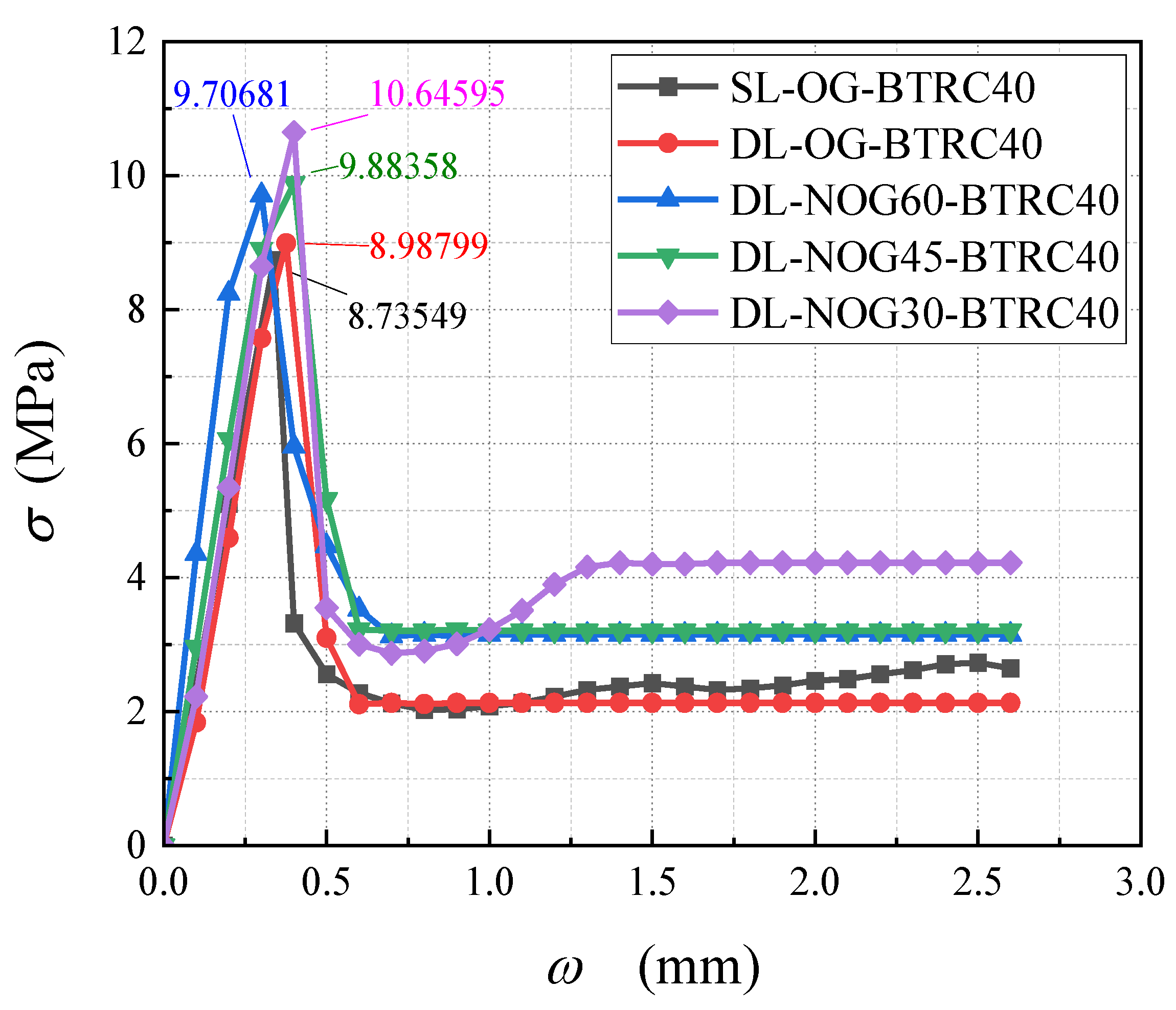
3.1. Influence of Different Laying Methods on the Bending Properties of BTRC Plates
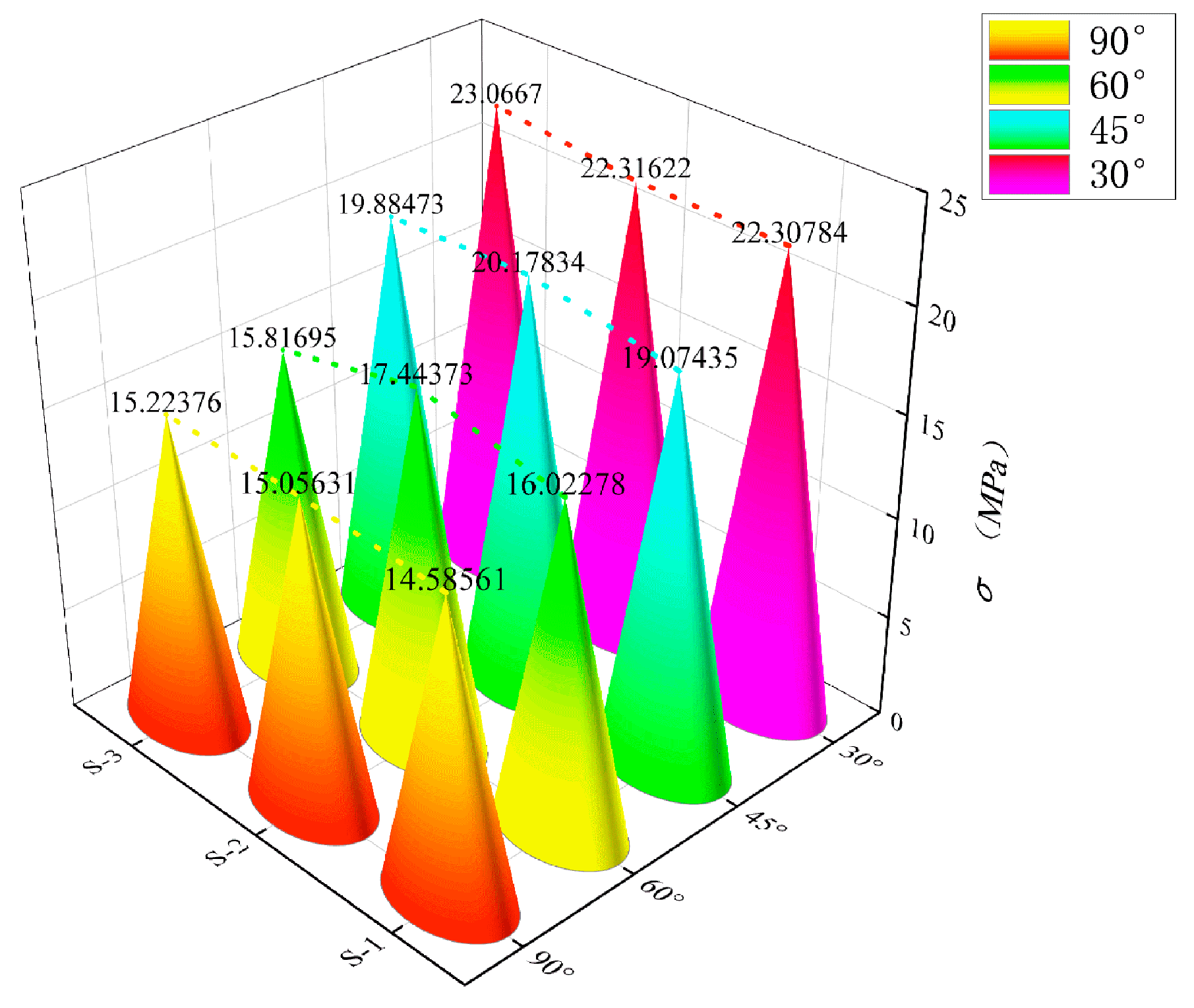
3.2. Effects of Different Grid Angles on the Bending Properties of BTRC Plates
3.3. Effects of Different Grid Sizes on the Bending Properties of BTRC Plates
3.4. Analysis of Failure Modes and Constitutive Relationship of Four-Point Bending Tests
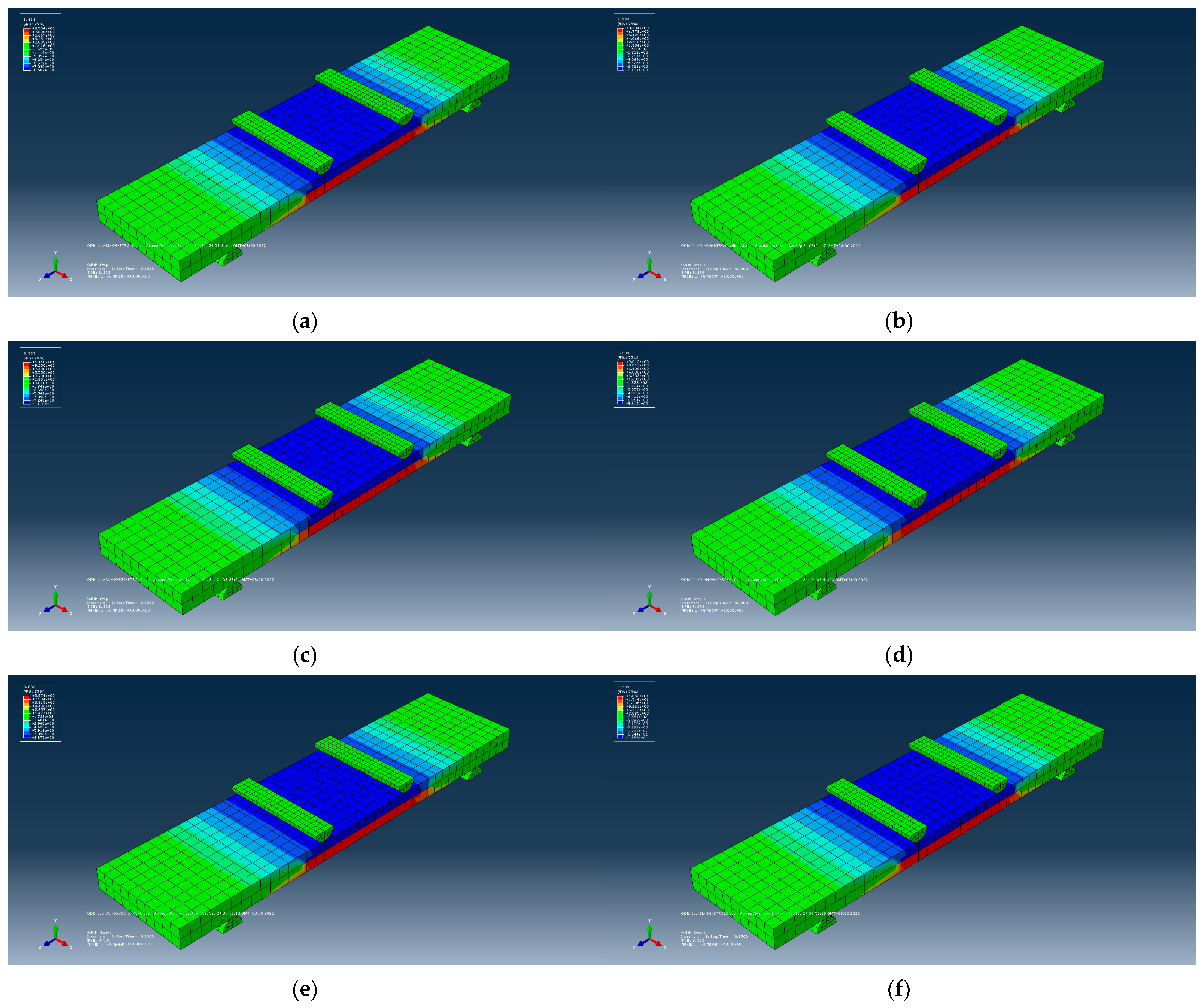
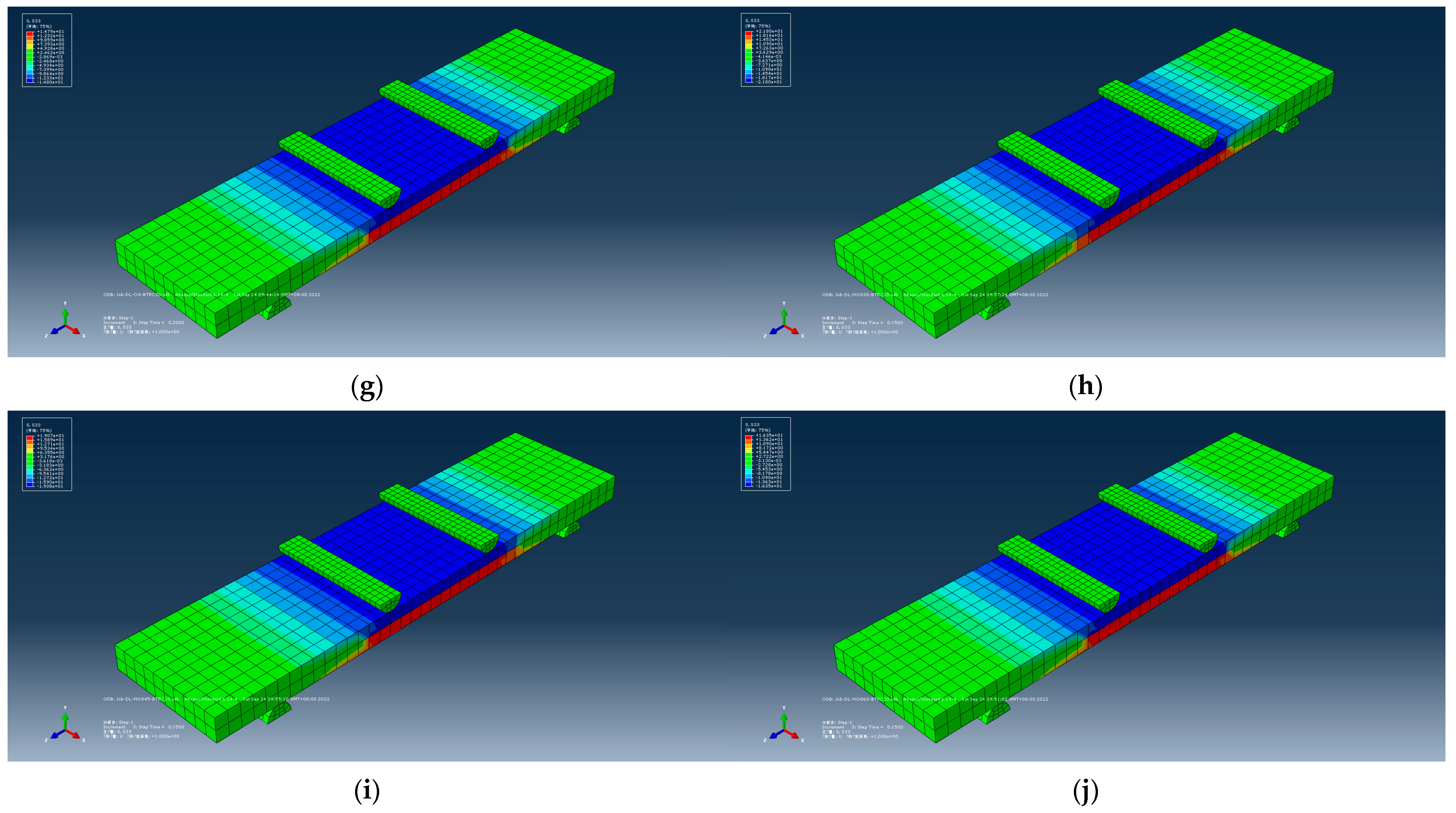
4. Analysis of Numerical Model
5. Conclusions
- (1)
- As the grid angle decreased, the BTRC specimen exhibited excellent flexural bearing capacity, good ductility, and high toughness, and the total number of cracks in the pure bending section of the specimen increased, the crack spacing decreased, and the crack morphology appeared as fine and uniform features.
- (2)
- The toughness of the specimen with a small grid angle and a DL laying method was greater than that with a SL laying method.
- (3)
- As the grid size decreased, the ultimate bending stress and ultimate deflection of the specimen increased greatly. The change in grid size hardly affected the cracking stress and cracking deflection of the specimen.
- (4)
- The simulation results verified the reinforcing effect of the textile on concrete and the retarding effect on cracks in the tests. The simulation value obtained by the finite element software had a high degree of agreement with the test data results. Thus, the four-point bending test results were reliable.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alva, P.; Arnon, B.; Barzin, M. Textile Reinforced Concrete; Taylor & Francis Group: Abingdon, UK; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Volkova, A.; Paykov, A.; Semenov, S.; Stolyarov, O.; Melnikov, B. Flexural Behavior of Textile-Reinforced Concrete. In Proceedings of the International Scientific Conference Week of Science in SPbPU—Civil Engineering (SPbWOSCE), Saint Petersburg, Russia, 3–4 December 2015. [Google Scholar]
- Al-Shalif, S.A.H.; Akin, A.; Aksoylu, C.; Arslan, M.H. Strengthening of shear-critical reinforced concrete T-beams with anchored and non-anchored GFRP fabrics applications. Structures 2022, 44, 809–827. [Google Scholar] [CrossRef]
- Ozkilic, Y.O.; Aksoylu, C.; Yazman, S.; Gemi, L.; Arslan, M.H. Behavior of CFRP-strengthened RC beams with circular web openings in shear zones: Numerical study. Structures 2022, 41, 1369–1389. [Google Scholar] [CrossRef]
- Yazman, S.; Aksoylu, C.; Gemi, L.; Arslan, M.H.; Hamad, A.A.; Ozkilic, Y.O. Shear strengthening of reinforced concrete T-beams with anchored and non-anchored CFRP fabrics. Structures 2022, 39, 527–542. [Google Scholar]
- Gemi, L.; Alsdudi, M.; Aksoylu, C.; Yazman, S.; Ozkilic, Y.O.; Arslan, M.H. Optimum amount of CFRP for strengthening shear deficient reinforced concrete beams. Steel Compos. Struct. 2022, 43, 735–757. [Google Scholar]
- Aksoylu, C. Experimental analysis of shear deficient reinforced concrete beams strengthened by glass fiber strip composites and mechanical stitches. Steel Compos. Struct. 2021, 40, 267–285. [Google Scholar]
- Ozkilic, Y.O.; Yazman, S.; Aksoylu, C.; Arslan, M.H.; Gemi, L. Numerical investigation of the parameters influencing the behavior of dapped end prefabricated concrete purlins with and without CFRP strengthening. Constr. Build. Mater. 2021, 275, 122173. [Google Scholar] [CrossRef]
- Aksoylu, C.; Yazman, S.; Ozkilic, Y.O.; Gemi, L.; Arslan, M.H. Experimental analysis of reinforced concrete shear deficient beams with circular web openings strengthened by CFRP composite. Compos. Struct. 2020, 249, 112561. [Google Scholar] [CrossRef]
- Gemi, L.; Aksoylu, C.; Yazman, S.; Ozkilic, Y.O.; Arslan, M.H. Experimental investigation of shear capacity and damage analysis of thinned end prefabricated concrete purlins strengthened by CFRP composite. Compos. Struct. 2019, 229, 111399. [Google Scholar] [CrossRef]
- Aksoylu, C. Shear strengthening of reinforced concrete beams with minimum CFRP and GFRP strips using different wrapping technics without anchoring application. Steel Compos. Struct. 2022, 44, 831–851. [Google Scholar]
- Yin, S.P.; Xu, S.L.; Li, H.D. Improved mechanical properties of textile reinforced concrete thin plate. J. Wuhan Univ. Technol. -Mater. Sci. Ed. 2013, 28, 92–98. [Google Scholar] [CrossRef]
- Yin, S.P.; Xu, S.L.; Wang, F. Investigation on the flexural behavior of concrete members reinforced with epoxy resin-impregnated textiles. Mater. Struct. 2015, 48, 153–166. [Google Scholar] [CrossRef]
- Wang, B.; Jin, H.; Man, T. Study on the bending behaviour of textile reinforced self-stressing concrete sheets. Mater. Res. Innov. 2015, 19, 227–233. [Google Scholar] [CrossRef]
- Wang, B.X.; Jin, H.N.; Man, T.; Wang, Q. Study on the mechanical property of textile reinforced self-stressing concrete sheets. Constr. Build. Mater. 2016, 107, 1–10. [Google Scholar] [CrossRef]
- Lior, N.; Alva, P.; Erez, G. The flexural performance of structural concrete beams reinforced with carbon textile fabrics. Compos. Struct. 2020, 239, 111917. [Google Scholar]
- Kurban, M.; Babaarslan, O.; Cagatay, I.H. Investigation of the flexural behavior of textile reinforced concrete with braiding yarn structure. Constr. Build. Mater. 2022, 334, 127434. [Google Scholar] [CrossRef]
- Kim, H.Y.; You, Y.J.; Ryu, G.S. Reinforced Concrete Slabs Strengthened with Lap-Spliced Carbon TRC System. Materials 2021, 14, 3340. [Google Scholar] [CrossRef]
- Murcia, D.H.; Comak, B.; Soliman, E.; Taha, M.R.M. Flexural Behavior of a Novel Textile-Reinforced Polymer Concrete. Polymers 2022, 14, 176. [Google Scholar] [CrossRef]
- Li, S.C.; Yin, S.P.; Wang, C.C.; Yang, Y.H. Research on the bonding performance of TRC permanent formwork and cast-in-place concrete. Eng. Struct. 2021, 235, 112021. [Google Scholar] [CrossRef]
- Yin, S.P.; Yu, Y.L.; Xi, Y.P. Flexural performance of TRC-strengthened RC beam under chloride environment. Anti-Corros. Methods Mater. 2018, 65, 444–450. [Google Scholar]
- Yin, S.P.; Cong, X.; Wang, C.Y.; Wang, C.C. Research on flexural performance of composited RC beams with different forms of TRC permanent formwork. Structures 2021, 29, 1424–1434. [Google Scholar] [CrossRef]
- Yu, Y.L.; Yin, S.P.; Na, M.W. Bending performance of TRC-strengthened RC beams with secondary load under chloride erosion. J. Cent. South Univ. 2019, 26, 196–206. [Google Scholar] [CrossRef]
- Yin, S.P.; Sheng, J.; Wang, X.X.; Li, S.G. Experimental Investigations of the Bending Fatigue Performance of TRC-Strengthened RC Beams in Conventional and Aggressive Chlorate Environments. J. Compos. Constr. 2016, 20, 04015051. [Google Scholar] [CrossRef]
- Yin, S.P.; Yu, Y.L.; Na, M.W. Flexural properties of load-holding reinforced concrete beams strengthened with textile-reinforced concrete under a chloride dry-wet cycle. J. Eng. Fibers Fabr. 2019, 14, 1–9. [Google Scholar] [CrossRef]
- Yin, S.P.; Lu, H.L.; Xu, S.L. Properties and calculation of normal section bearing capacity of RC flexural beam with skin textile reinforcement. J. Cent. South Univ. 2013, 20, 1731–1741. [Google Scholar] [CrossRef]
- Yin, S.P.; Na, M.W.; Yu, Y.L.; Wu, J. Research on the flexural performance of RC beams strengthened with TRC under the coupling action of load and marine environment. Constr. Build. Mater. 2017, 132, 251–261. [Google Scholar] [CrossRef]
- Mobasher, B.; Jain, N.; Aldea, C.M.; Soranakom, C. Mechanical Properties of Alkali Resistant Glass Fabric Composites for Retrofitting Unreinforced Masonry Walls; SP-244-8; American Concrete Institute: New York, NY, USA, 2007; pp. 124–140. [Google Scholar]
- ISO 10618:2004; Carbon Fibre—Determination of Tensile Properties of Resin-Impregnated Yarn. ISO: Geneva, Switzerland, 2004.
- EN 1170-5; Precast Concrete Products—Test Method for Glass-Fiber Reinforced Cement (Part 5): Measuring Bending Strength, Complete Bending Test Method. European Committee for Standardization: London, UK, 1997.
- ASTM C947-03; Standard Test Method for Flexural Properties of Thin-Section Glass-Fiber-Reinforced Concrete (Using Simple Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2009.







| Water | Cement | Sand | Limestone Gravel | Superplasticizer |
|---|---|---|---|---|
| 206 | 458 | 961 | 641 | 1.87 |
| Fiber Type | Number of Filaments Per Bundle/k | Tensile Strength/MPa | Fiber Bundle Density g/cm3 | Elastic Modulus/GPa | Fiber Bundle Linear Density g/1000 m |
|---|---|---|---|---|---|
| Basalt fiber | 3.6 | 2100 | 2.63 | 98.7 | 2400 |
| Specimen Number | Destruction Form | Mean Ultimate Load/kN | Mean Debonding Load/kN | Deformation |
|---|---|---|---|---|
| BT20-SL90 | Debonding of warp and weft fiber bundles | 0.788 | 0.330 | 0.2675% |
| BT40-SL90 | Debonding of warp and weft fiber bundles | 0.303 | 0.166 | 0.2933% |
| BT20-DL90 | Debonding of basalt textile and fixture | 0. 765 | 0.328 | 0.2665% |
| BT40-DL90 | Debonding of basalt textile and fixture | 0.199 | 0.053 | 0.6250% |
| BT20-DL60 | Debonding of basalt textile and fixture | 0.923 | 0.412 | 0.1732% |
| BT40-DL60 | Debonding of basalt textile and fixture | 0.400 | 0.201 | 0.4156% |
| BT20-DL45 | Debonding of basalt textile and fixture | 1.055 | 0.443 | 0.1283% |
| BT40-DL45 | Debonding of basalt textile and fixture | 0.654 | 0.296 | 0.3030% |
| BT20-DL30 | Debonding of basalt textile and fixture | 1.150 | 0.490 | 0.0855% |
| BT40-DL30 | Debonding of basalt textile and fixture | 0.923 | 0.412 | 0.2083% |
| Grid Size | Grid Type | Grid Angle | Laying Method | Group |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | PC |
| 20 mm × 20 mm | OG | 90° | SL | SL-OG-BTRC20 |
| DL | DL-OG-BTRC20 | |||
| NOG | 30° | DL | DL-NOG30-BTRC20 | |
| 45° | DL | DL-NOG45-BTRC20 | ||
| 60° | DL | DL-NOG60-BTRC20 | ||
| 40 mm × 40 mm | OG | 90° | SL | SL-OG-BTRC40 |
| DL | DL-OG-BTRC40 | |||
| NOG | 30° | DL | DL-NOG30-BTRC20 | |
| 45° | DL | DL-NOG45-BTRC20 | ||
| 60° | DL | DL-NOG60-BTRC20 |
| Group | Cracking Stress/MPa | Cracking Deflection/mm | Ultimate Stress/MPa | Ultimate Deflection/mm | Toughness/N·mm | Total Number of Cracks in Pure Bending Section | |
|---|---|---|---|---|---|---|---|
| DL-NOG30-BTRC20 | S-1 | 8.25 | 0.34 | 20.88 | 5.93 | 12,381.84 | 2 |
| S-2 | 8.32 | 0.40 | 21.65 | 6.22 | 13,466.30 | 2 | |
| S-3 | 8.26 | 0.34 | 22.32 | 6.51 | 14,530.32 | 4 | |
| DL-NOG45-BTRC20 | S-1 | 8.20 | 0.30 | 17.95 | 2.97 | 5331.15 | 1 |
| S-2 | 8.22 | 0.33 | 18.57 | 3.00 | 5571.00 | 1 | |
| S-3 | 8.30 | 0.42 | 19.07 | 3.05 | 5816.35 | 2 | |
| DL-NOG60-BTRC20 | S-1 | 8.22 | 0.25 | 15.94 | 2.53 | 4032.82 | 1 |
| S-2 | 8.29 | 0.31 | 16.35 | 2.58 | 4218.30 | 1 | |
| S-3 | 8.18 | 0.28 | 16.02 | 2.55 | 4085.10 | 1 | |
| DL-OG-BTRC20 | S-1 | 8.14 | 0.30 | 14.59 | 2.05 | 2990.95 | 1 |
| S-2 | 8.22 | 0.35 | 15.06 | 2.08 | 3132.48 | 1 | |
| S-3 | 8.20 | 0.33 | 15.22 | 2.10 | 3196.20 | 1 | |
| DL-NOG30-BTRC40 | S-1 | 8.33 | 0.31 | 10.78 | 0.46 | 495.88 | 1 |
| S-2 | 8.25 | 0.25 | 10.34 | 0.37 | 382.58 | 1 | |
| S-3 | 8.34 | 0.30 | 10.65 | 0.44 | 468.60 | 1 | |
| DL-NOG45-BTRC40 | S-1 | 8.21 | 0.20 | 9.75 | 0.38 | 370.50 | 1 |
| S-2 | 8.33 | 0.25 | 9.60 | 0.35 | 336.00 | 1 | |
| S-3 | 8.38 | 0.29 | 9.89 | 0.39 | 385.71 | 1 | |
| DL-NOG60-BTRC40 | S-1 | 8.10 | 0.26 | 9.21 | 0.33 | 303.93 | 1 |
| S-2 | 8.17 | 0.28 | 9.48 | 0.35 | 331.80 | 1 | |
| S-3 | 8.24 | 0.29 | 9.71 | 0.37 | 359.27 | 1 | |
| DL-OG-BTRC40 | S-1 | 8.10 | 0.37 | 8.10 | 0.37 | 302.13 | 1 |
| S-2 | 8.26 | 0.38 | 8.26 | 0.38 | 315.53 | 1 | |
| S-3 | 8.44 | 0.39 | 8.44 | 0.39 | 329.16 | 1 | |
| Group | Simulated Value/MPa | Experimental Value/MPa | Relative Deviation/% |
|---|---|---|---|
| SL-OG-BTRC20 | 18.50 | 18.40 | 0.54 |
| SL-OG-BTRC40 | 8.51 | 8.31 | 2.35 |
| DL-OG-BTRC20 | 14.80 | 14.96 | 1.08 |
| DL-OG-BTRC40 | 8.14 | 8.27 | 1.60 |
| DL-NOG30-BTRC20 | 21.80 | 21.62 | 0.83 |
| DL-NOG45-BTRC20 | 19.10 | 18.53 | 2.98 |
| DL-NOG60-BTRC20 | 16.37 | 16.10 | 1.65 |
| DL-NOG30-BTRC40 | 11.10 | 10.60 | 4.50 |
| DL-NOG45-BTRC40 | 9.62 | 9.74 | 1.25 |
| DL-NOG60-BTRC40 | 8.87 | 9.46 | 6.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Wang, B.; Lu, X.; Guo, J. Flexural Properties of Textile-Reinforced Concrete with Nonorthogonal Grids. Polymers 2022, 14, 5185. https://doi.org/10.3390/polym14235185
Zhang T, Wang B, Lu X, Guo J. Flexural Properties of Textile-Reinforced Concrete with Nonorthogonal Grids. Polymers. 2022; 14(23):5185. https://doi.org/10.3390/polym14235185
Chicago/Turabian StyleZhang, Tianqi, Boxin Wang, Xinyu Lu, and Jiahuan Guo. 2022. "Flexural Properties of Textile-Reinforced Concrete with Nonorthogonal Grids" Polymers 14, no. 23: 5185. https://doi.org/10.3390/polym14235185
APA StyleZhang, T., Wang, B., Lu, X., & Guo, J. (2022). Flexural Properties of Textile-Reinforced Concrete with Nonorthogonal Grids. Polymers, 14(23), 5185. https://doi.org/10.3390/polym14235185






