Shape-Memory Composites Based on Ionic Elastomers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Rubber Compounds
2.3. Characterization Methods
3. Results and Discussion
3.1. Formation of Rubber Networks
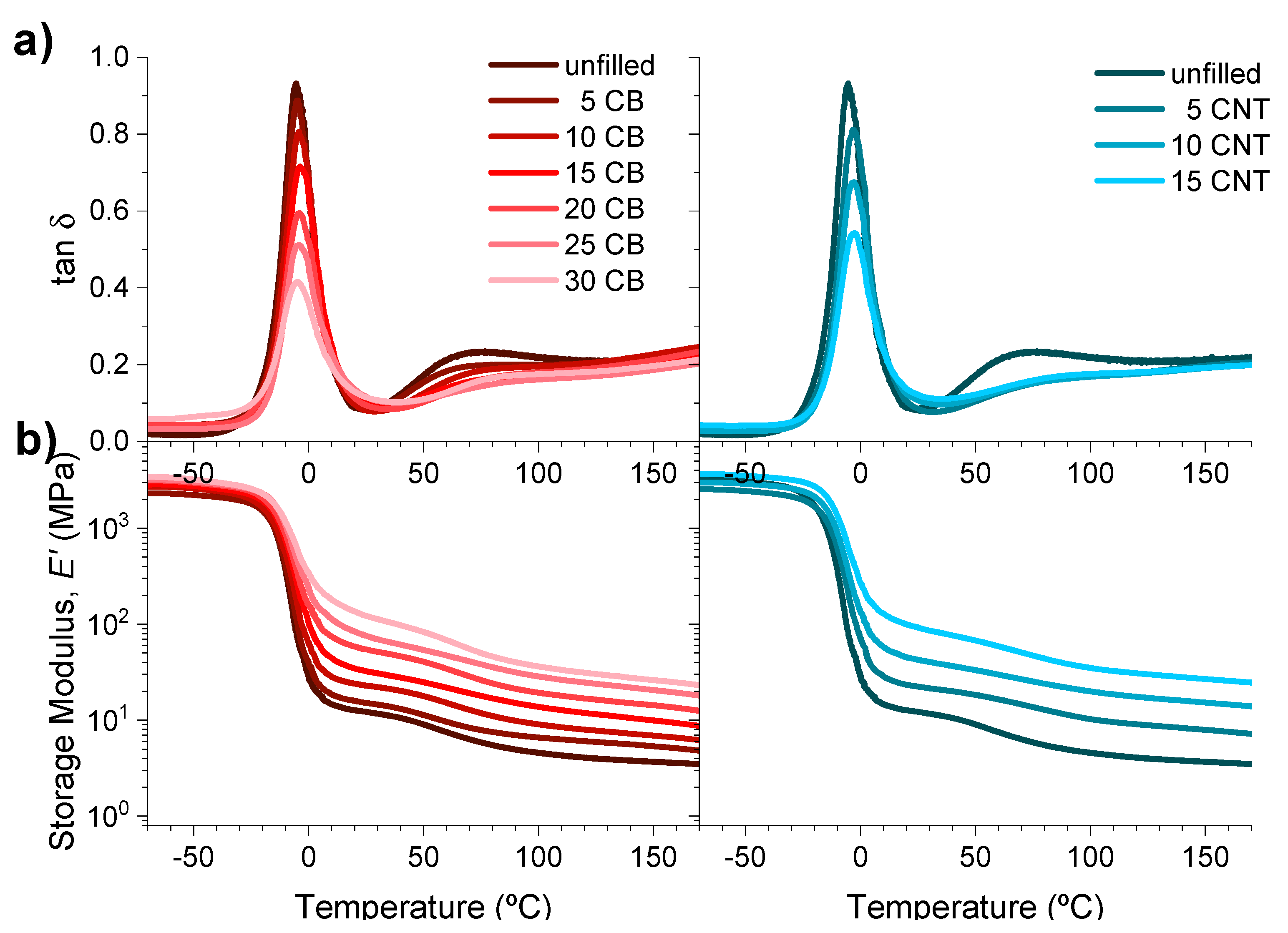
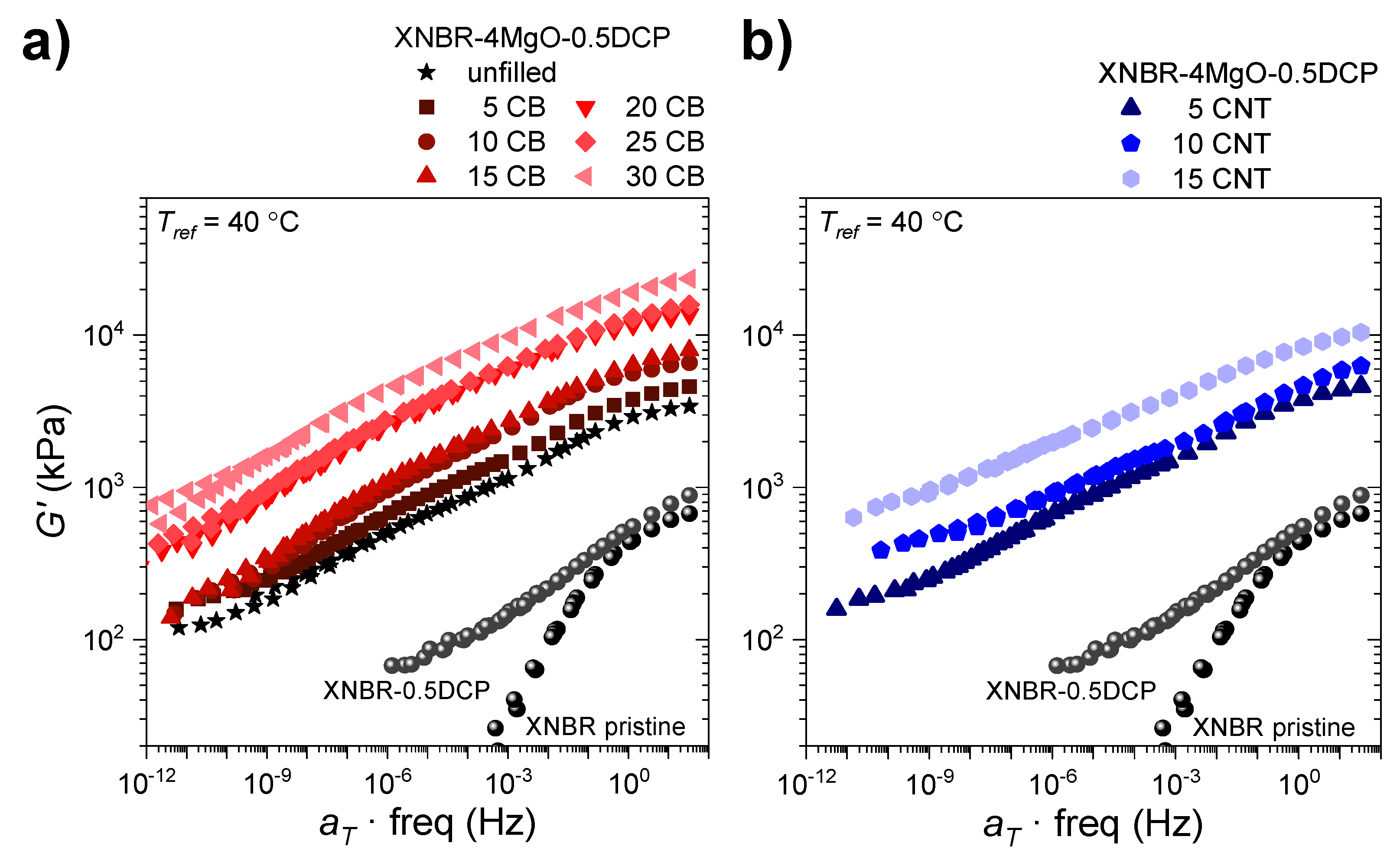
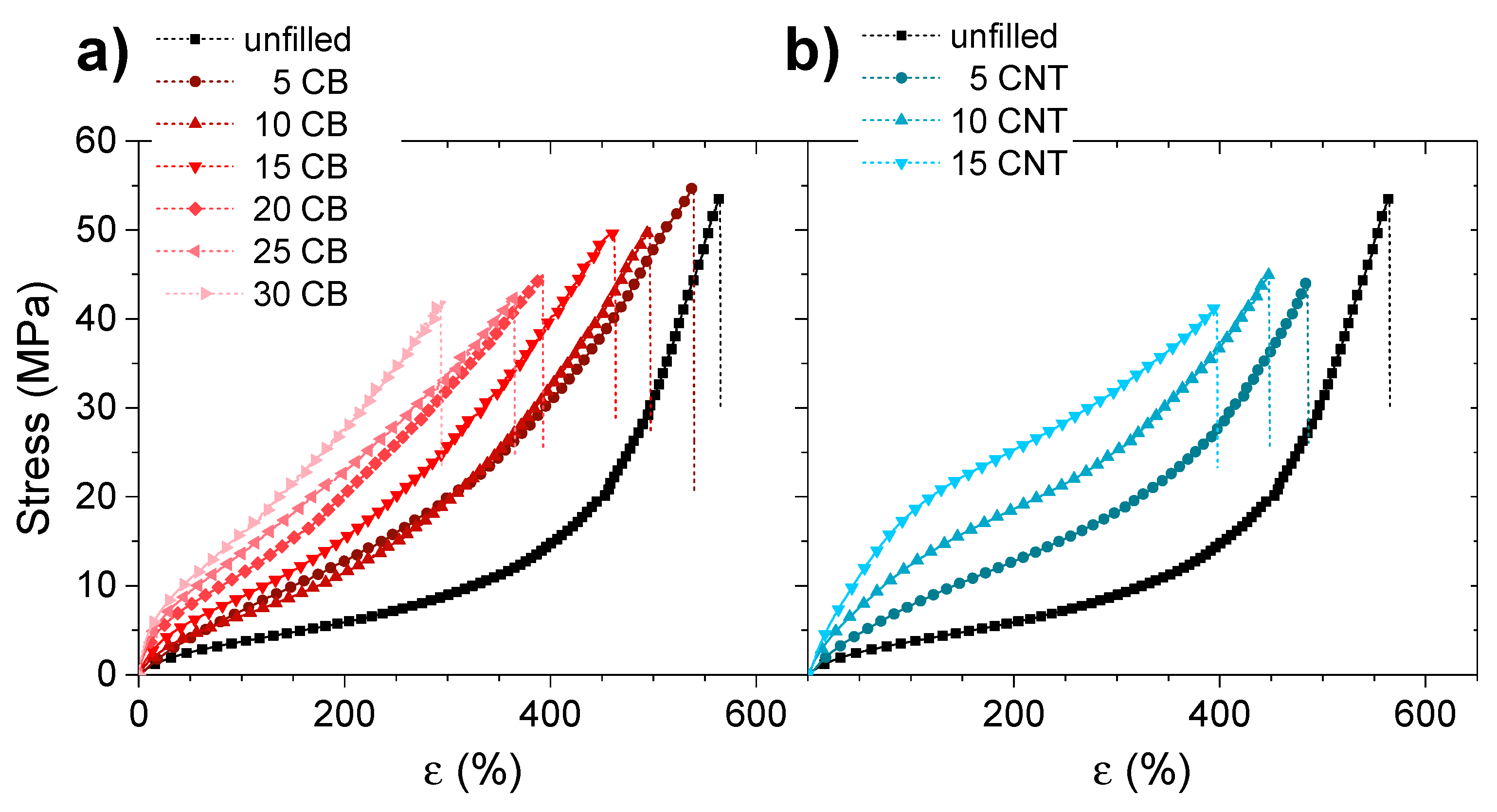
3.2. Physical Properties
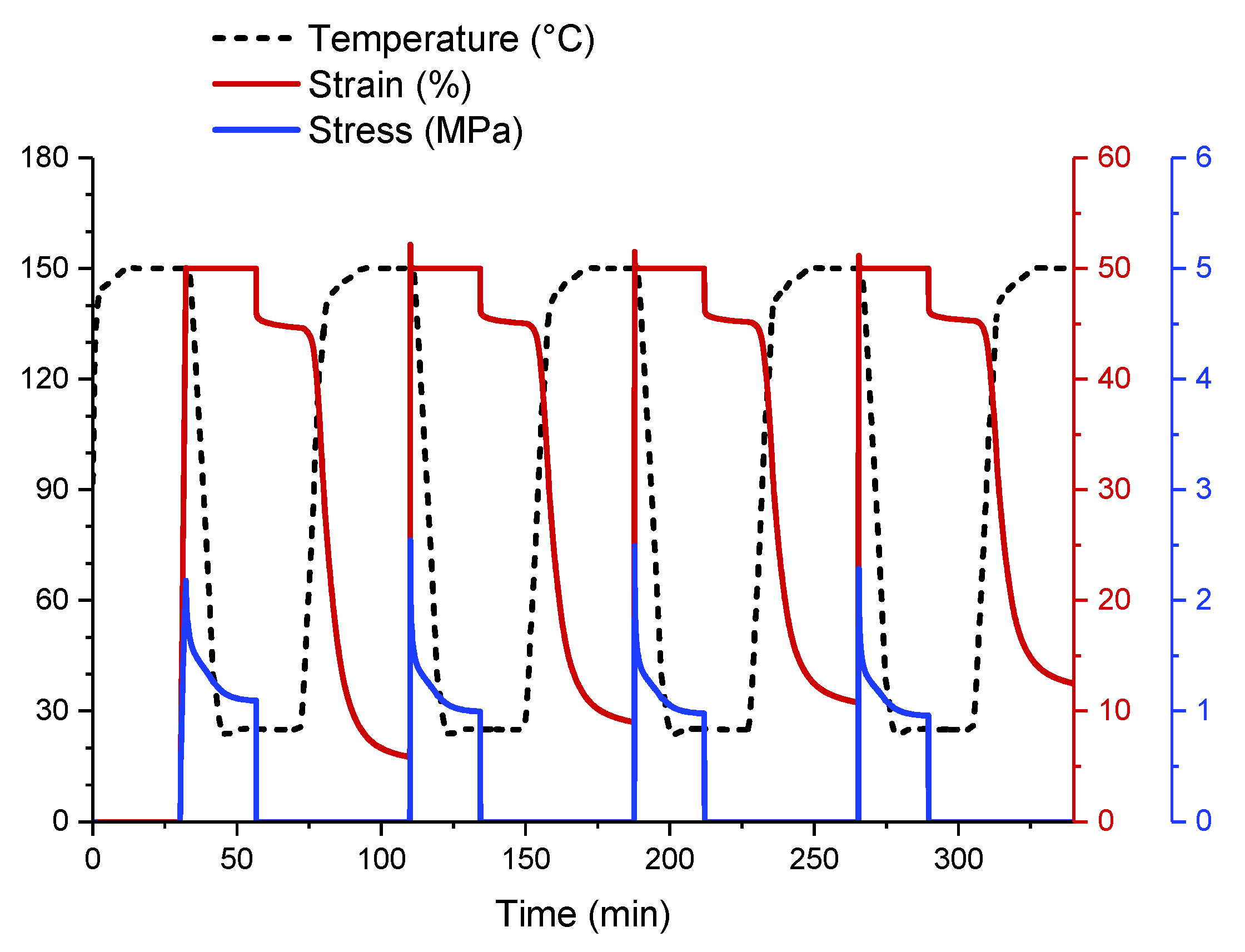
3.3. Shape-Memory Properties of Elastomeric Composites
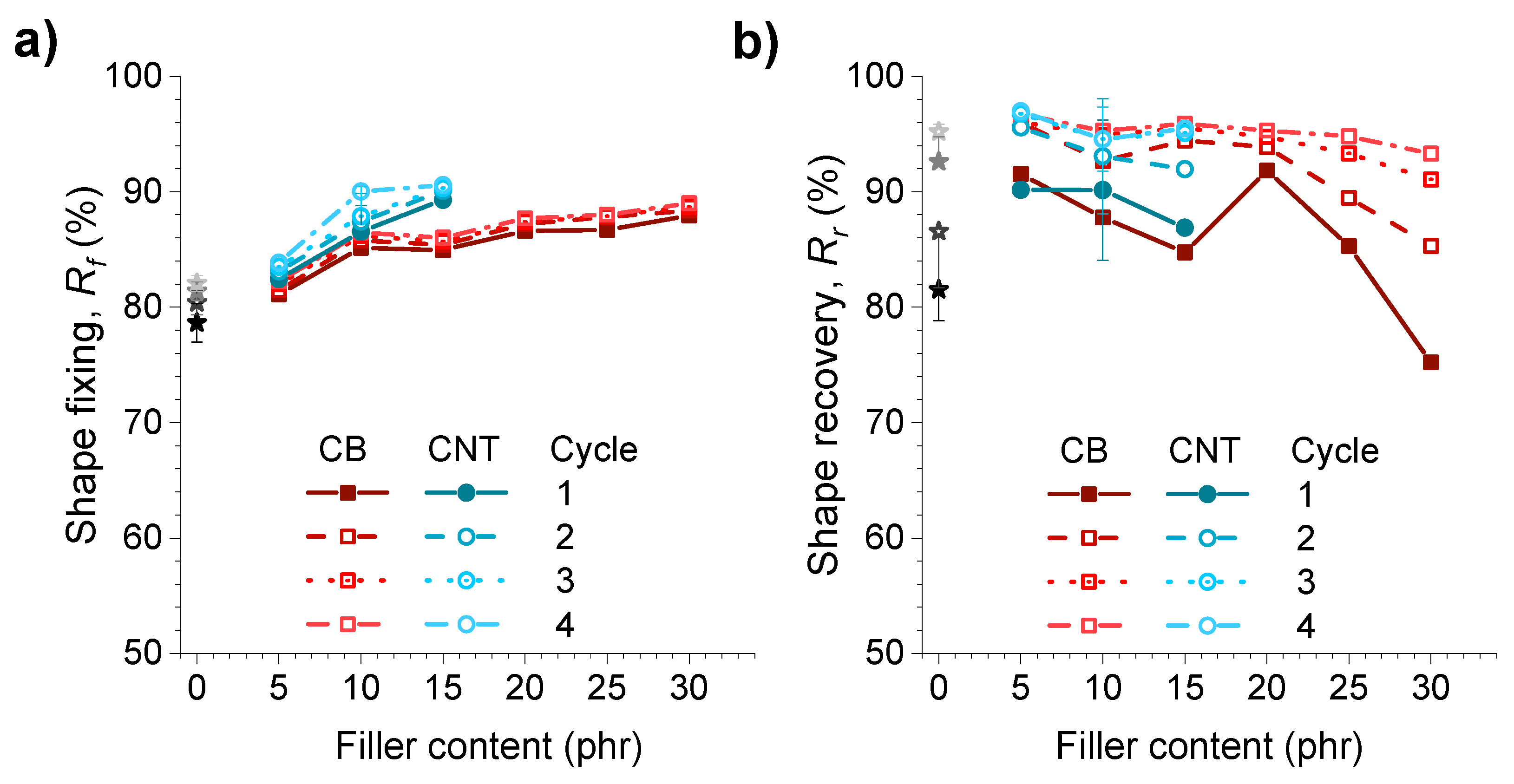
3.3.1. Effect of the Incorporation of Reinforcing Fillers on the Shape-Memory Properties of Elastomers
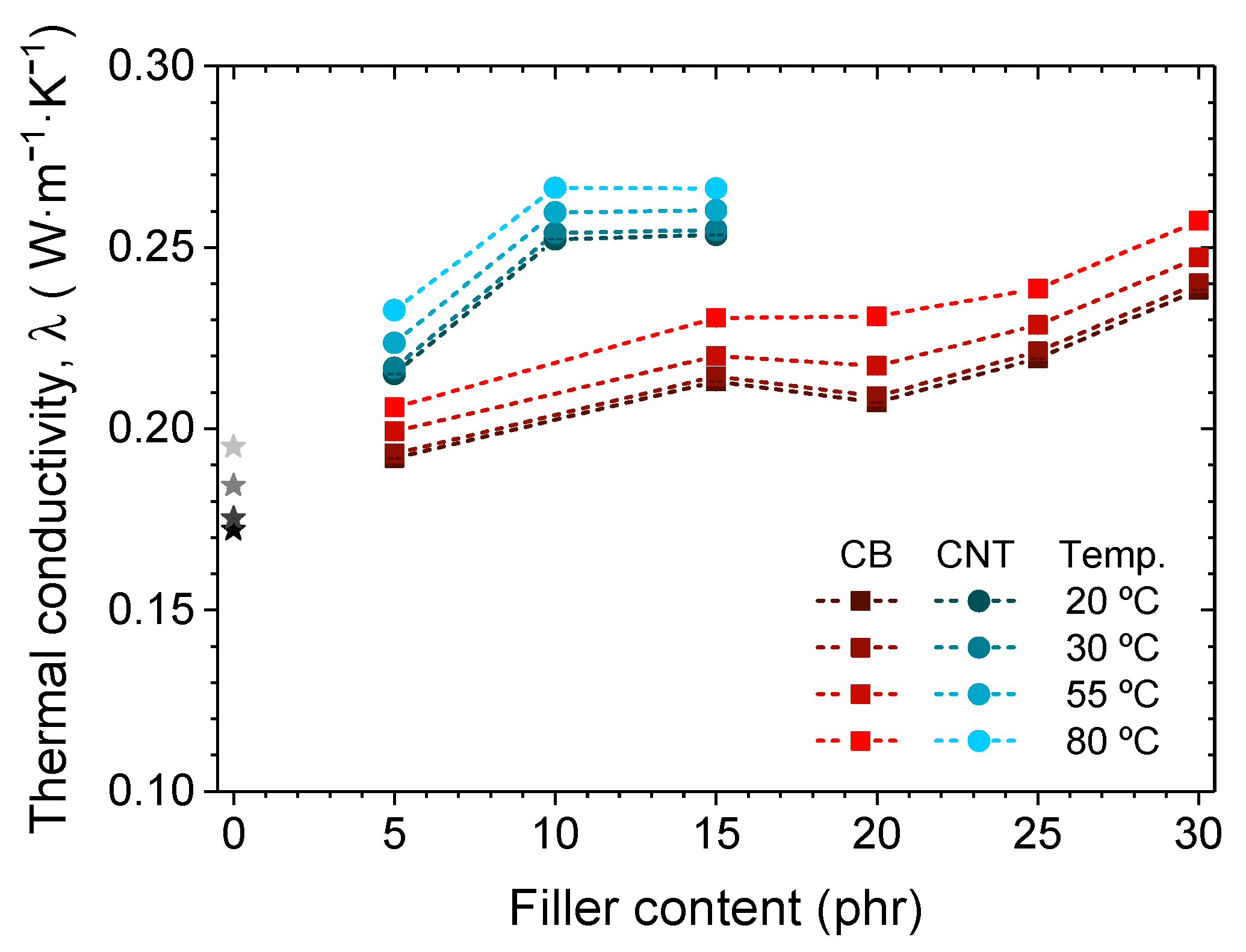
3.3.2. Effect of the Incorporation of Fillers on the Thermal Conductivity of Elastomeric Nanocomposites
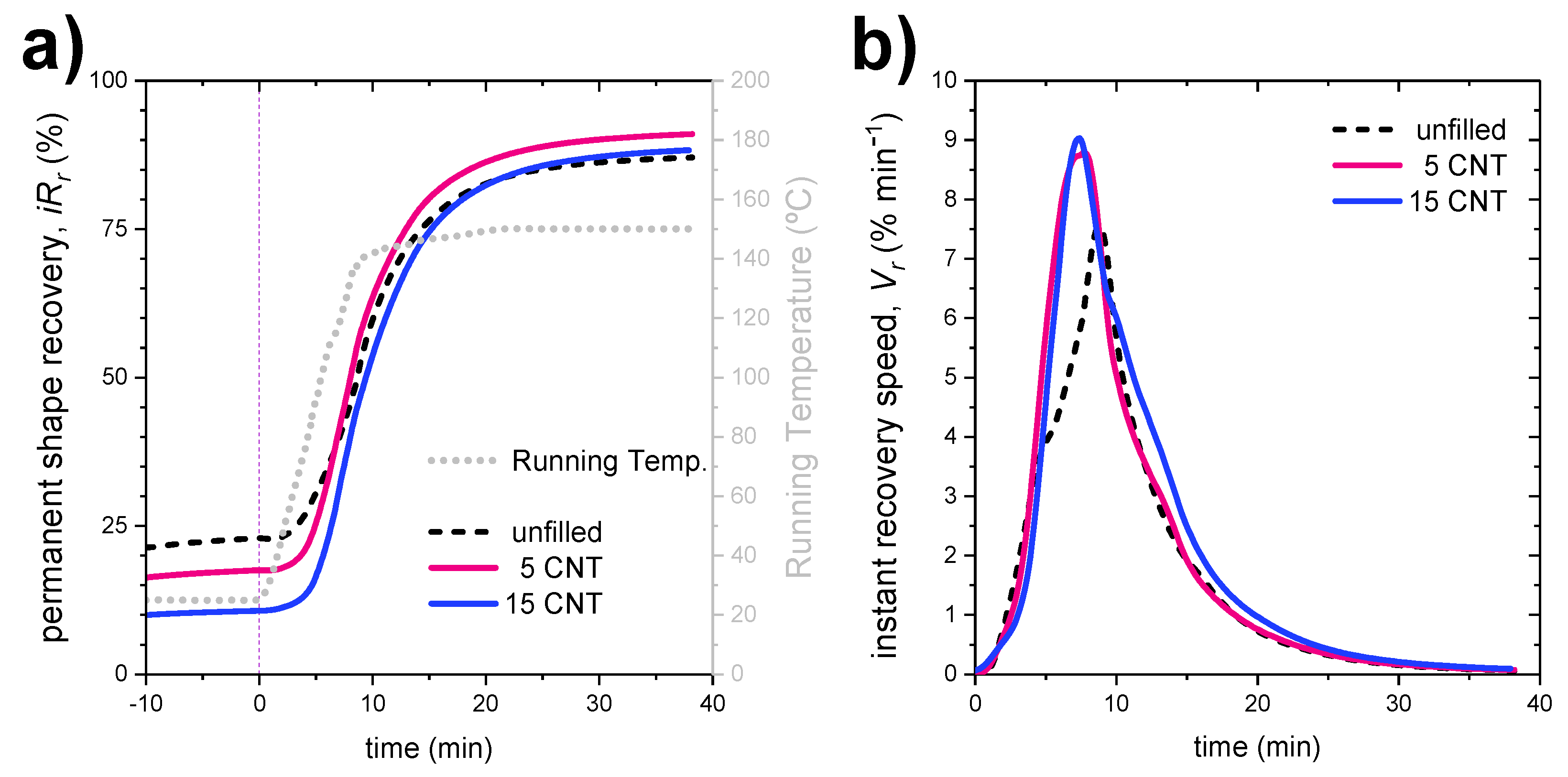
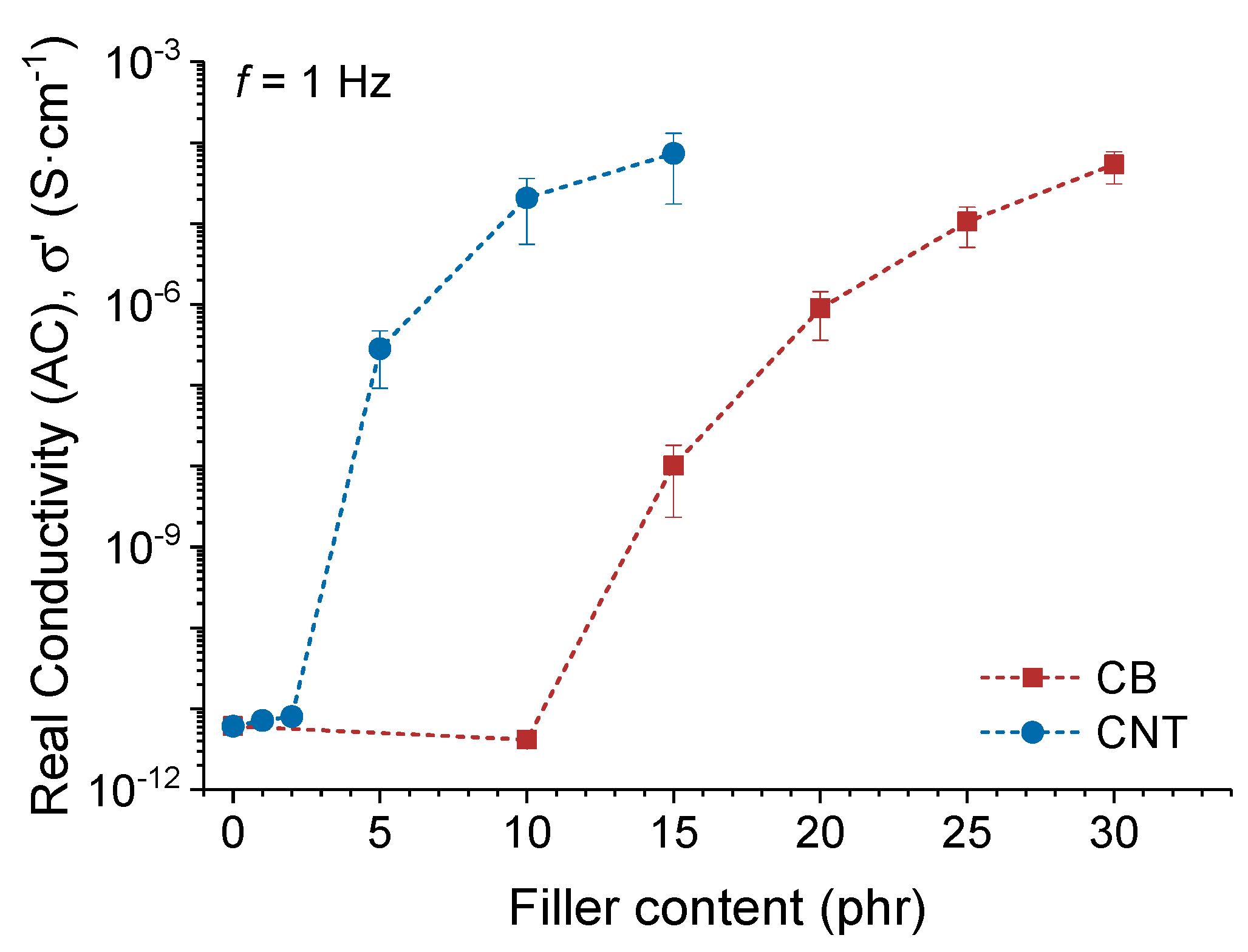
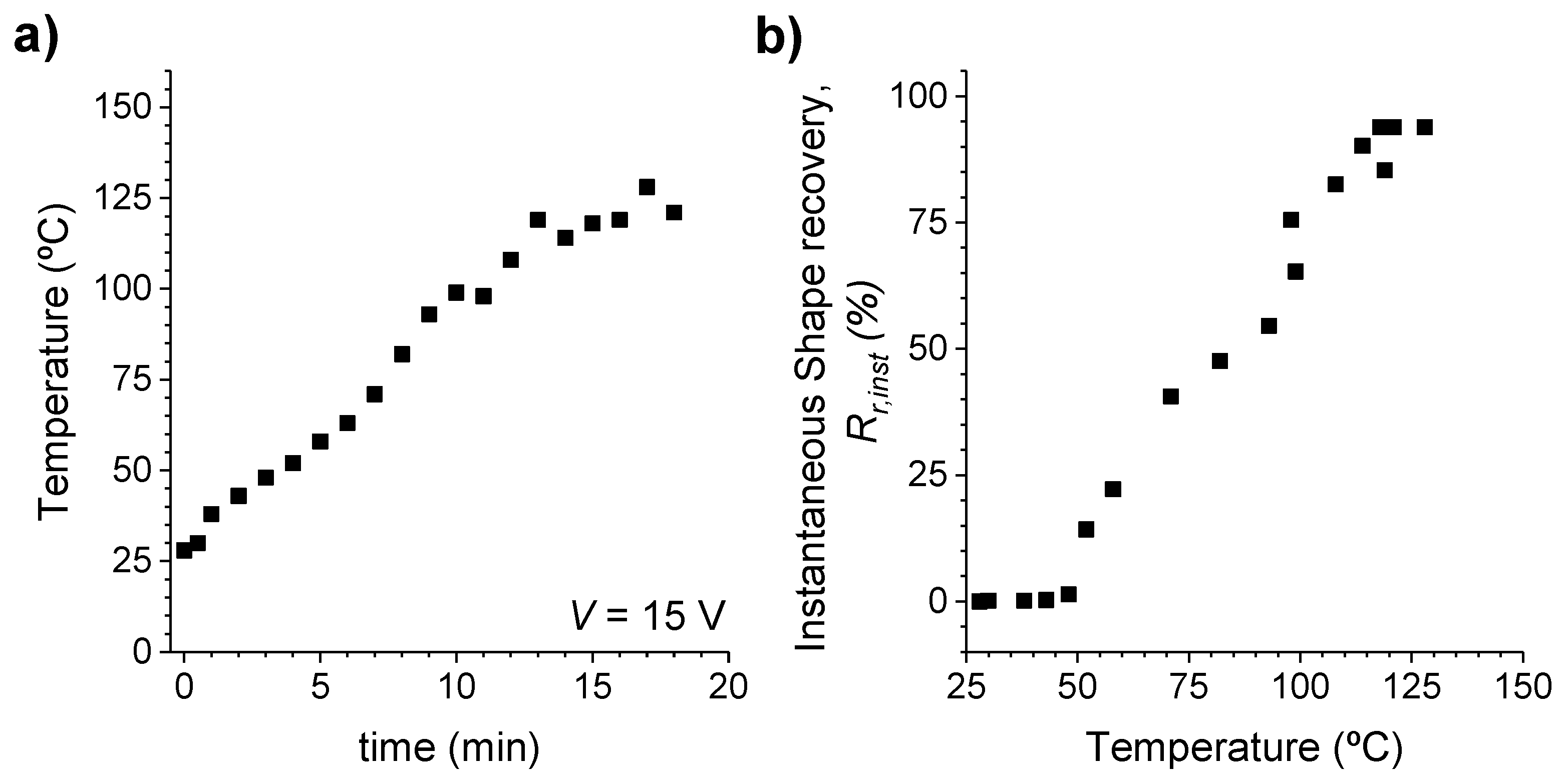
3.3.3. Electroactivation of the Shape-Memory Effect in Elastomeric Nanocomposites
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stuart, M.A.C.; Huck, W.T.S.; Genzer, J.; Müller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.V.; Urban, M.; et al. Emerging Applications of Stimuli-Responsive Polymer Materials. Nat. Mater. 2010, 9, 101–113. [Google Scholar] [CrossRef]
- Lendlein, A.; Kelch, S. Shape-Memory Polymers. Angew. Chem. 2002, 41, 2034–2057. [Google Scholar] [CrossRef]
- Chung, T.; Romo-Uribe, A.; Mather, P.T. Two-Way Reversible Shape Memory in a Semicrystalline Network. Macromolecules 2008, 41, 184–192. [Google Scholar] [CrossRef]
- Li, J.; Rodgers, W.R.; Xie, T. Semi-Crystalline Two-Way Shape Memory Elastomer. Polymer 2011, 52, 5320–5325. [Google Scholar] [CrossRef]
- Heo, M.S.; Kim, T.H.; Chang, Y.W.; Jang, K.S. Near-Infrared Light-Responsive Shape Memory Polymer Fabricated from Reactive Melt Blending of Semicrystalline Maleated Polyolefin Elastomer and Polyaniline. Polymers 2021, 13, 3984. [Google Scholar] [CrossRef] [PubMed]
- Pringpromsuk, S.; Xia, H.; Ni, Q.Q. Multifunctional Stimuli-Responsive Shape Memory Polyurethane Gels for Soft Actuators. Sens. Actuators A 2020, 313, 112207. [Google Scholar] [CrossRef]
- Li, M.; Chen, J.; Shi, M.; Zhang, H.; Ma, P.X.; Guo, B. Electroactive Anti-Oxidant Polyurethane Elastomers with Shape Memory Property as Non-Adherent Wound Dressing to Enhance Wound Healing. Chem. Eng. J. 2019, 375, 121999. [Google Scholar] [CrossRef]
- Gong, X.; Tan, K.; Deng, Q.; Shen, S. Athermal Shape Memory Effect in Magnetoactive Elastomers. ACS Appl. Mater. Interfaces 2020, 12, 16930–16936. [Google Scholar] [CrossRef] [PubMed]
- Testa, P.; Style, R.W.; Cui, J.; Donnelly, C.; Borisova, E.; Derlet, P.M.; Dufresne, E.R.; Heyderman, L.J. Magnetically Addressable Shape-Memory and Stiffening in a Composite Elastomer. Adv. Mater. 2019, 31, 1900561. [Google Scholar] [CrossRef]
- Wang, X.; Yang, X.; Xu, C.; Lin, B.; Fu, L. Enhanced, Hydrophobic, Initial-Shape Programmable Shape-Memory Composites with a Bio-Based Nano-Framework via Gradient Metal-Ligand Cross-Linking. Compos. Sci. Technol. 2022, 220, 109255. [Google Scholar] [CrossRef]
- Panda, P.K.; Yang, J.M.; Chang, Y.H. Water-Induced Shape Memory Behavior of Poly (Vinyl Alcohol) and p-Coumaric Acid-Modified Water-Soluble Chitosan Blended Membrane. Carbohydr. Polym. 2021, 257, 117633. [Google Scholar] [CrossRef] [PubMed]
- Lai, S.M.; Guo, G.L.; Xie, Y.C.; Chen, J.M.; Xu, D.Y.; Wei, Y.E.; Cao, Z.R. A Novel Multi-Triggered Natural Rubber (NR)/Beeswax (BW)/Carbon Nanotube (CNT) Shape Memory Bio-Nanocomposite. J. Polym. Res. 2020, 27, 283. [Google Scholar] [CrossRef]
- Mather, P.T. Soft Answers for Hard Problems. Nat. Mater. 2006, 6, 93–94. [Google Scholar] [CrossRef] [PubMed]
- Miriyev, A.; Stack, K.; Lipson, H. Soft Material for Soft Actuators. Nat. Commun. 2017, 8, 596. [Google Scholar] [CrossRef]
- Luo, X.; Mather, P.T. Preparation and Characterization of Shape Memory Elastomeric Composites. Macromolecules 2009, 42, 7251–7253. [Google Scholar] [CrossRef]
- Rousseau, I.A.; Mather, P.T. Shape Memory Effect Exhibited by Smectic-C Liquid Crystalline Elastomers. J. Am. Chem. Soc. 2003, 125, 15300–15301. [Google Scholar] [CrossRef]
- Cavicchi, K.A. Shape Memory Polymers from Blends of Elastomers and Small Molecule Additives. Macromol. Symp. 2015, 358, 194–201. [Google Scholar] [CrossRef]
- Xie, T.; Rousseau, I.A. Facile Tailoring of Thermal Transition Temperatures of Epoxy Shape Memory Polymers. Polymer 2009, 50, 1852–1856. [Google Scholar] [CrossRef]
- Heuwers, B.; Beckel, A.; Krieger, A.; Katzenberg, F.; Tiller, J.C. Shape-Memory Natural Rubber: An Exceptional Material for Strain and Energy Storage. Macromol. Chem. Phys. 2013, 214, 912–923. [Google Scholar] [CrossRef]
- Heuwers, B.; Quitmann, D.; Hoeher, R.; Reinders, F.M.; Tiemeyer, S.; Sternemann, C.; Tolan, M.; Katzenberg, F.; Tiller, J.C. Stress-Induced Stabilization of Crystals in Shape Memory Natural Rubber. Macromol. Rapid Commun. 2013, 34, 180–184. [Google Scholar] [CrossRef]
- Pantoja, M.; Lin, Z.; Cakmak, M.; Cavicchi, K.A. Structure-Property Relationships of Fatty Acid Swollen, Crosslinked Natural Rubber Shape Memory Polymers. J. Polym. Sci. Part B Polym. Phys. 2018, 56, 673–688. [Google Scholar] [CrossRef]
- Mehrbakhsh, E.; Rezaei, M.; Babaie, A.; Mohammadi, A.; Mayan Sofla, R.L. Physical and Thermo-Mechanical Properties of Shape Memory Polyurethane Containing Reversible Chemical Cross-Links. J. Mech. Behav. Biomed. Mater. 2021, 116, 104336. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; He, Y.; Li, Q.; Wu, C. SBS Thermoplastic Elastomer Based on Dynamic Metal-Ligand Bond: Structure, Mechanical Properties, and Shape Memory Behavior. Macromol. Mater. Eng. 2021, 306, 2000737. [Google Scholar] [CrossRef]
- Yan, X.; Wang, F.; Zheng, B.; Huang, F. Stimuli-Responsive Supramolecular Polymeric Materials. Chem. Soc. Rev. 2012, 41, 6042. [Google Scholar] [CrossRef]
- Cavicchi, K.A.; Pantoja, M.; Cakmak, M. Shape Memory Ionomers. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1389–1396. [Google Scholar] [CrossRef] [Green Version]
- Weiss, R.A.; Izzo, E.; Mandelbaum, S. New Design of Shape Memory Polymers: Mixtures of an Elastomeric Ionomer and Low Molar Mass Fatty Acids and Their Salts. Macromolecules 2008, 41, 2978–2980. [Google Scholar] [CrossRef]
- Dong, J.; Weiss, R.A. Shape Memory Behavior of Zinc Oleate-Filled Elastomeric Ionomers. Macromolecules 2011, 44, 8871–8879. [Google Scholar] [CrossRef]
- Xie, T. Tunable Polymer Multi-Shape Memory Effect. Nature 2010, 464, 267–270. [Google Scholar] [CrossRef]
- Li, J.; Xie, T. Significant Impact of Thermo-Mechanical Conditions on Polymer Triple-Shape Memory Effect. Macromolecules 2011, 44, 175–180. [Google Scholar] [CrossRef]
- Zheng, Z.; Xu, C.; Wu, W.; Shen, Q.; Lin, B.; Fu, L. Structure and Performance of Carboxylic Styrene Butadiene Rubber/Citric Acid Composite Films. Ind. Eng. Chem. Res. 2020, 59, 13613–13622. [Google Scholar] [CrossRef]
- Salaeh, S.; Das, A.; Wießner, S. Design and Fabrication of Thermoplastic Elastomer with Ionic Network: A Strategy for Good Performance and Shape Memory Capability. Polymer 2021, 223, 123699. [Google Scholar] [CrossRef]
- González-Jiménez, A.; Malmierca, M.A.; Bernal-Ortega, P.; Posadas, P.; Pérez-Aparicio, R.; Marcos-Fernández, Á.; Mather, P.T.; Valentín, J.L. The Shape-Memory Effect in Ionic Elastomers: Fixation through Ionic Interactions. Soft Matter 2017, 13, 2983–2994. [Google Scholar] [CrossRef] [PubMed]
- Malmierca, M.A.; González-Jiménez, A.; Mora-Barrantes, I.; Posadas, P.; Rodríguez, A.; Ibarra, L.; Nogales, A.; Saalwächter, K.; Valentín, J.L. Characterization of Network Structure and Chain Dynamics of Elastomeric Ionomers by Means of 1H Low-Field NMR. Macromolecules 2014, 47, 5655–5667. [Google Scholar] [CrossRef]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gun’ko, Y.K. Small but Strong: A Review of the Mechanical Properties of Carbon Nanotube–Polymer Composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Meng, H.; Li, G. A Review of Stimuli-Responsive Shape Memory Polymer Composites. Polymer 2013, 54, 2199–2221. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Cui, X.; Sui, K.; Zhu, Y.; Jiang, W. Balance the Electrical Properties and Mechanical Properties of Carbon Black Filled Immiscible Polymer Blends with a Double Percolation Structure. Compos. Sci. Technol. 2017, 140, 99–105. [Google Scholar] [CrossRef]
- Han, Z.; Fina, A. Thermal Conductivity of Carbon Nanotubes and Their Polymer Nanocomposites: A Review. Prog. Polym. Sci. 2011, 36, 914–944. [Google Scholar] [CrossRef] [Green Version]
- Mondal, T.; Bhowmick, A.K.; Ghosal, R.; Mukhopadhyay, R. Graphene-Based Elastomer Nanocomposites: Functionalization Techniques, Morphology, and Physical Properties; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 267–318. [Google Scholar]
- Yang, Z.; Liu, J.; Liao, R.; Yang, G.; Wu, X.; Tang, Z.; Guo, B.; Zhang, L.; Ma, Y.; Nie, Q.; et al. Rational Design of Covalent Interfaces for Graphene/Elastomer Nanocomposites. Compos. Sci. Technol. 2016, 132, 68–75. [Google Scholar] [CrossRef]
- Araby, S.; Meng, Q.; Zhang, L.; Kang, H.; Majewski, P.; Tang, Y.; Ma, J. Electrically and Thermally Conductive Elastomer/Graphene Nanocomposites by Solution Mixing. Polymer 2014, 55, 201–210. [Google Scholar] [CrossRef]
- Shan, W.; Lu, T.; Majidi, C. Soft-Matter Composites with Electrically Tunable Elastic Rigidity. Smart Mater. Struct. 2013, 22, 085005. [Google Scholar] [CrossRef]
- Pang, H.; Xu, L.; Yan, D.-X.; Li, Z.-M. Conductive Polymer Composites with Segregated Structures. Prog. Polym. Sci. 2014, 39, 1908–1933. [Google Scholar] [CrossRef]
- O’Halloran, A.; O’Malley, F.; McHugh, P. A Review on Dielectric Elastomer Actuators, Technology, Applications, and Challenges. J. Appl. Phys. 2008, 104, 071101. [Google Scholar] [CrossRef]
- Al-Saleh, M.H.; Sundararaj, U. A Review of Vapor Grown Carbon Nanofiber/Polymer Conductive Composites. Carbon 2009, 47, 2–22. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.M.; Ding, Z.; Zhao, Y.; Wang, C.C.; Purnawali, H.; Tang, C. Stimulus-Responsive Shape Memory Materials: A Review. Mater. Des. 2012, 33, 577–640. [Google Scholar] [CrossRef]
- Bokobza, L. Multiwall Carbon Nanotube Elastomeric Composites: A Review. Polymer 2007, 48, 4907–4920. [Google Scholar] [CrossRef] [Green Version]
- Pérez, L.D.; Giraldo, L.F.; Brostow, W.; López, B.L. Poly(Methyl Acrylate) plus Mesoporous Silica Nanohybrids: Mechanical and Thermophysical Properties. e-Polymers 2007, 7, 324–334. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.-W.; Zhu, Y.-F.; Liang, J. Preparation and Properties of Powder Styrene–Butadiene Rubber Composites Filled with Carbon Black and Carbon Nanotubes. Mater. Res. Bull. 2007, 42, 456–464. [Google Scholar] [CrossRef]
- Choudhury, A.; Bhowmick, A.K.; Ong, C.; Soddemann, M. Effect of Various Nanofillers on Thermal Stability and Degradation Kinetics of Polymer Nanocomposites. J. Nanosci. Nanotechnol. 2010, 10, 5056–5071. [Google Scholar] [CrossRef]
- Meyyappan, M. Carbon Nanotubes: Science and Applications; CRC Press: Boca Raton, FL, USA, 2005; ISBN 9780849321115. [Google Scholar]
- Iijima, S. Helical Microtubules of Graphitic Carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Das, N.C.; Maiti, S. Electromagnetic Interference Shielding of Carbon Nanotube/Ethylene Vinyl Acetate Composites. J. Mater. Sci. 2008, 43, 1920–1925. [Google Scholar] [CrossRef]
- Raja, M.; Ryu, S.H.; Shanmugharaj, A.M. Thermal, Mechanical and Electroactive Shape Memory Properties of Polyurethane (PU)/Poly (Lactic Acid) (PLA)/CNT Nanocomposites. Eur. Polym. J. 2013, 49, 3492–3500. [Google Scholar] [CrossRef]
- Costa, P.; Silva, J.; Sencadas, V.; Simoes, R.; Viana, J.C.; Lanceros-Méndez, S. Mechanical, Electrical and Electro-Mechanical Properties of Thermoplastic Elastomer Styrene–Butadiene–Styrene/Multiwall Carbon Nanotubes Composites. J. Mater. Sci. 2013, 48, 1172–1179. [Google Scholar] [CrossRef] [Green Version]
- Kurup, S.N.; Ellingford, C.; Wan, C. Shape Memory Properties of Polyethylene/Ethylene Vinyl Acetate /Carbon Nanotube Composites. Polym. Test. 2020, 81, 106227. [Google Scholar] [CrossRef]
- Hohimer, C.J.; Petrossian, G.; Ameli, A.; Mo, C.; Pötschke, P. 3D printed conductive thermoplastic polyurethane/carbon nanotube composites for capacitive and piezoresistive sensing in soft pneumatic actuators. Addit. Manuf. 2020, 34, 101281. [Google Scholar] [CrossRef]
- Mirvakili, S.M.; Hunter, I.W. Artificial Muscles: Mechanisms, Applications, and Challenges. Adv. Mater. 2018, 30, 1704407. [Google Scholar] [CrossRef] [PubMed]
- Bernal-Ortega, P.; Bernal, M.M.; González-Jiménez, A.; Posadas, P.; Navarro, R.; Valentín, J.L. New Insight into Structure-Property Relationships of Natural Rubber and Styrene-Butadiene Rubber Nanocomposites Filled with MWCNT. Polymer 2020, 201, 122604. [Google Scholar] [CrossRef]
- Sasikumar, K.; Manoj, N.R.; Mukundan, T.; Khastgir, D. Design of XNBR Nanocomposites for Underwater Acoustic Sensor Applications: Effect of MWNT on Dynamic Mechanical Properties and Morphology. J. Appl. Polym. Sci. 2014, 131, 40752. [Google Scholar] [CrossRef]
- Xu, C.; Cao, L.; Lin, B.; Liang, X.; Chen, Y. Design of Self-Healing Supramolecular Rubbers by Introducing Ionic Cross-Links into Natural Rubber via a Controlled Vulcanization. ACS Appl. Mater. Interfaces 2016, 8, 17728–17737. [Google Scholar] [CrossRef]
- Tian, M.; Zhang, J.; Zhang, L.; Liu, S.; Zan, X.; Nishi, T.; Ning, N. Graphene Encapsulated Rubber Latex Composites with High Dielectric Constant, Low Dielectric Loss and Low Percolation Threshold. J. Colloid Interface Sci. 2014, 430, 249–256. [Google Scholar] [CrossRef]
- Liu, X.; Sun, D.; Wang, L.; Guo, B. Sodium Humate Functionalized Graphene and Its Unique Reinforcement Effects for Rubber. Ind. Eng. Chem. Res. 2013, 52, 14592–14600. [Google Scholar] [CrossRef]
- Wang, J.; Jia, H.; Tang, Y.; Ji, D.; Sun, Y.; Gong, X.; Ding, L. Enhancements of the Mechanical Properties and Thermal Conductivity of Carboxylated Acrylonitrile Butadiene Rubber with the Addition of Graphene Oxide. J. Mater. Sci. 2012, 48, 1571–1577. [Google Scholar] [CrossRef]
- Nair, K.P.; Thomas, P.; Joseph, R. Technical Report. Mater. Des. 2012, 41, 23–30. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1980; ISBN 9780471048947. [Google Scholar]
- Rousseau, I.A. Challenges of Shape Memory Polymers: A Review of the Progress toward Overcoming SMP’s Limitations. Polym. Eng. Sci. 2008, 48, 2075–2089. [Google Scholar] [CrossRef]
- Mora-Barrantes, I.; Malmierca, M.A.A.; Valentin, J.L.; Rodriguez, A.; Ibarra, L. Effect of Covalent Cross-Links on the Network Structure of Thermo-Reversible Ionic Elastomers. Soft Matter 2012, 8, 5201. [Google Scholar] [CrossRef]
- Rodríguez, A.; Ibarra, L.; Mora, I. Effect of Low-Load Reinforcing Nanofillers on Rheological Behavior and Physical Properties of Ionic Elastomers Based on XNBR and MgO. J. Appl. Polym. Sci. 2007, 106, 973–980. [Google Scholar] [CrossRef]
- González, A.E. Viscosity of Ionomer Gels. Polymer 1983, 24, 77–80. [Google Scholar] [CrossRef]
- González, A.E. Viscoelasticity of Ionomer Gels: 2. The Elastic Moduli. Polymer 1984, 25, 1469–1474. [Google Scholar] [CrossRef]
- Leibler, L.; Rubinstein, M.; Colby, R.H. Dynamics of Reversible Networks. Macromolecules 1991, 24, 4701–4707. [Google Scholar] [CrossRef]
- Tanaka, F.; Edwards, S.F. Viscoelastic Properties of Physically Crosslinked Networks. 1. Transient Network Theory. Macromolecules 1992, 25, 1516–1523. [Google Scholar] [CrossRef]
- Rubinstein, M.; Semenov, A.N. Dynamics of Entangled Solutions of Associating Polymers. Macromolecules 2001, 34, 1058–1068. [Google Scholar] [CrossRef]
- Lu, H.; Yin, J.; Xu, B.; Gou, J.; Hui, D.; Fu, Y. Synergistic Effects of Carboxylic Acid-Functionalized Carbon Nanotube and Nafion/Silica Nanofiber on Electrical Actuation Efficiency of Shape Memory Polymer Nanocomposite. Compos. Part B 2016, 100, 146–151. [Google Scholar] [CrossRef]
- Le, H.H.; Kolesov, I.; Ali, Z.; Uthardt, M.; Osazuwa, O.; Ilisch, S.; Radusch, H.-J. Effect of Filler Dispersion Degree on the Joule Heating Stimulated Recovery Behaviour of Nanocomposites. J. Mater. Sci. 2010, 45, 5851–5859. [Google Scholar] [CrossRef]
- Leng, J.; Lan, X.; Liu, Y.; Du, S. Shape-Memory Polymers and Their Composites: Stimulus Methods and Applications. Prog. Mater. Sci. 2011, 56, 1077–1135. [Google Scholar] [CrossRef]




| Sample | XNBR | MgO | DCP | Stearic Acid | Filler | |
|---|---|---|---|---|---|---|
| phr | phr | phr | phr | phr | Type | |
| XNBR-4MgO-0.5DCP (unfilled) | 100 | 4 | 0.5 | 1 | ||
| 5CB | 100 | 4 | 0.5 | 1 | 5 | CB |
| 10CB | 100 | 4 | 0.5 | 1 | 10 | CB |
| 15CB | 100 | 4 | 0.5 | 1 | 15 | CB |
| 20CB | 100 | 4 | 0.5 | 1 | 20 | CB |
| 25CB | 100 | 4 | 0.5 | 1 | 25 | CB |
| 30CB | 100 | 4 | 0.5 | 1 | 30 | CB |
| 5CNT | 100 | 4 | 0.5 | 1 | 5 | CNT |
| 10CNT | 100 | 4 | 0.5 | 1 | 10 | CNT |
| 15CNT | 100 | 4 | 0.5 | 1 | 15 | CNT |
| Sample | Tensile Strength | Elongation at Break | ||
|---|---|---|---|---|
| MPa | % | |||
| Unfilled | 51 | ±3 | 560 | ±10 |
| 5CB | 52 | ±5 | 506 | ±37 |
| 10CB | 49 | ±6 | 493 | ±10 |
| 15CB | 50 | ±2 | 462 | ±17 |
| 20CB | 45 | ±2 | 399 | ±35 |
| 25CB | 44 | ±1 | 353 | ±39 |
| 30CB | 42 | ±2 | 308 | ±23 |
| 5CNT | 45 | ±3 | 493 | ±34 |
| 10CNT | 44 | ±4 | 453 | ±27 |
| 15CNT | 42 | ±2 | 389 | ±18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Jiménez, A.; Bernal-Ortega, P.; Salamanca, F.M.; Valentin, J.L. Shape-Memory Composites Based on Ionic Elastomers. Polymers 2022, 14, 1230. https://doi.org/10.3390/polym14061230
González-Jiménez A, Bernal-Ortega P, Salamanca FM, Valentin JL. Shape-Memory Composites Based on Ionic Elastomers. Polymers. 2022; 14(6):1230. https://doi.org/10.3390/polym14061230
Chicago/Turabian StyleGonzález-Jiménez, Antonio, Pilar Bernal-Ortega, Fernando M. Salamanca, and Juan L. Valentin. 2022. "Shape-Memory Composites Based on Ionic Elastomers" Polymers 14, no. 6: 1230. https://doi.org/10.3390/polym14061230
APA StyleGonzález-Jiménez, A., Bernal-Ortega, P., Salamanca, F. M., & Valentin, J. L. (2022). Shape-Memory Composites Based on Ionic Elastomers. Polymers, 14(6), 1230. https://doi.org/10.3390/polym14061230









