Bead–Spring Simulation of Ionomer Melts—Studying the Effects of Chain-Length and Associating Group Fraction on Equilibrium Structure and Extensional Flow Behavior
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
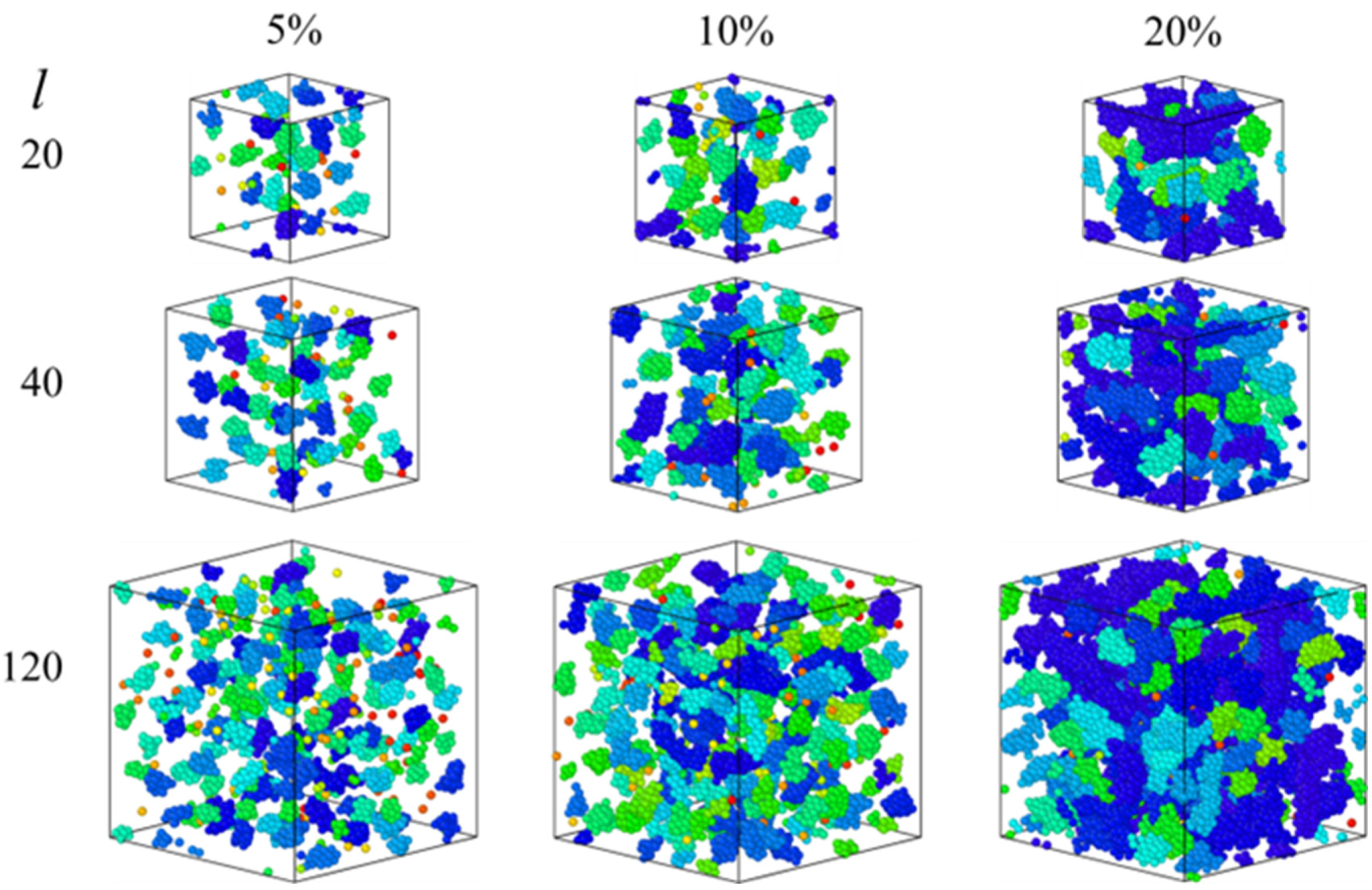
3.1. Equilibrium Study
3.2. Ionomers under Extensional Flow
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Janietz, S.; Brening, T.; Schiestel, T.; Götz, T. Block copoly (phenylquinoxaline) s as potential ionomers for proton exchange membranes. Polymer 2023, 271, 125794. [Google Scholar] [CrossRef]
- Cha, J.-E.; Jang, S.; Seo, D.-J.; Hwang, J.; Seo, M.H.; Choi, Y.-W.; Kim, W.B. A reinforced composite membrane of two-layered asymmetric structure with Nafion ionomer and polyethylene substrate for improving proton exchange membrane fuel cell performance. Chem. Eng. J. 2023, 454, 140091. [Google Scholar] [CrossRef]
- Khan, Z.U.; Moronshing, M.; Shestakova, M.; Al-Othman, A.; Sillanpää, M.; Zhan, Z.; Song, B.; Lei, Y. Electro-deionization (EDI) technology for enhanced water treatment and desalination: A review. Desalination 2023, 548, 116254. [Google Scholar] [CrossRef]
- Verma, A.; Parashar, A.; Van Duin, A.C. Graphene-Reinforced Polymeric Membranes for Water Desalination and Gas Separation/Barrier Applications, Innovations in Graphene-Based Polymer Composites; Elsevier: Amsterdam, The Netherlands, 2022; pp. 133–165. [Google Scholar]
- Braaten, J.P.; Kariuki, N.N.; Myers, D.J.; Blackburn, S.; Brown, G.; Park, A.; Litster, S. Integration of a high oxygen permeability ionomer into polymer electrolyte membrane fuel cell cathodes for high efficiency and power density. J. Power Sources 2022, 522, 230821. [Google Scholar] [CrossRef]
- Soleymani, A.P.; Reid, M.; Jankovic, J. An Epoxy-Free Sample Preparation Approach to Enable Imaging of Ionomer and Carbon in Polymer Electrolyte Membrane Fuel Cells. Adv. Funct. Mater. 2023, 33, 2209733. [Google Scholar] [CrossRef]
- Cánovas, R.; Blondeau, P.; Andrade, F.J. Modulating the mixed potential for developing biosensors: Direct potentiometric determination of glucose in whole, undiluted blood. Biosens. Bioelectron. 2020, 163, 112302. [Google Scholar] [CrossRef] [PubMed]
- Komkova, M.A.; Eliseev, A.A.; Poyarkov, A.A.; Daboss, E.V.; Evdokimov, P.V.; Eliseev, A.A.; Karyakin, A.A. Simultaneous monitoring of sweat lactate content and sweat secretion rate by wearable remote biosensors. Biosens. Bioelectron. 2022, 202, 113970. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Q.; So, S.; Kim, H.-T.; Choi, S.Q. Highly ordered ultrathin perfluorinated sulfonic acid ionomer membranes for vanadium redox flow battery. ACS Energy Lett. 2020, 6, 184–192. [Google Scholar] [CrossRef]
- Yang, S.-H.; Yang, D.-S.; Yoon, S.J.; So, S.; Hong, S.-K.; Yu, D.M.; Hong, Y.T. TEMPO radical-embedded perfluorinated sulfonic acid ionomer composites for vanadium redox flow batteries. Energy Fuels 2020, 34, 7631–7638. [Google Scholar] [CrossRef]
- Zhong, H.; He, Y.; Yang, E.; Bi, Y.; Yang, T. Modeling of microflow during viscoelastic polymer flooding in heterogenous reservoirs of Daqing Oilfield. J. Pet. Sci. Eng. 2022, 210, 110091. [Google Scholar] [CrossRef]
- Zhong, H.; Li, Y.; Zhang, W.; Yin, H.; Lu, J.; Guo, D. Microflow mechanism of oil displacement by viscoelastic hydrophobically associating water-soluble polymers in enhanced oil recovery. Polymers 2018, 10, 628. [Google Scholar] [CrossRef] [PubMed]
- Roels, E.; Terryn, S.; Iida, F.; Bosman, A.W.; Norvez, S.; Clemens, F.; Van Assche, G.; Vanderborght, B.; Brancart, J. Processing of Self-Healing Polymers for Soft Robotics. Adv. Mater. 2022, 34, 2104798. [Google Scholar] [CrossRef] [PubMed]
- Banshiwal, J.K.; Tripathi, D.N. Self-healing polymer composites for structural application. In Functional Materials; Sahn, D., Ed.; IntechOpen: London, UK, 2019; Volume 10, pp. 1–13. [Google Scholar]
- Eisenberg, A.; Kim, J.-S. Introduction to Ionomers; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Eisenberg, A. Clustering of ions in organic polymers. A theoretical approach. Macromolecules 1970, 3, 147–154. [Google Scholar] [CrossRef]
- Eisenberg, A.; Hird, B.; Moore, R. A new multiplet-cluster model for the morphology of random ionomers. Macromolecules 1990, 23, 4098–4107. [Google Scholar] [CrossRef]
- Dreyfus, B. Model for the clustering of multiplets in ionomers. Macromolecules 1985, 18, 284–292. [Google Scholar] [CrossRef]
- Kirkmeyer, B.P.; Weiss, R.A.; Winey, K.I. Spherical and vesicular ionic aggregates in Zn-neutralized sulfonated polystyrene ionomers. J. Polym. Sci. B Polym. Phys. 2001, 39, 477–483. [Google Scholar] [CrossRef]
- Winey, K.I.; Laurer, J.H.; Kirkmeyer, B.P. Ionic Aggregates in Partially Zn-Neutralized Poly (ethylene-r an-methacrylic acid) Ionomers: Shape, Size, and Size Distribution. Macromolecules 2000, 33, 507–513. [Google Scholar] [CrossRef]
- Lu, X.; Steckle, W.; Weiss, R. Ionic aggregation in a block copolymer ionomer. Macromolecules 1993, 26, 5876–5884. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Q.; Weiss, R. Nonlinear rheology of random sulfonated polystyrene ionomers: The role of the sol–gel transition. Macromolecules 2016, 49, 9203–9214. [Google Scholar] [CrossRef]
- Fitzgerald, J.; Weiss, R. Synthesis, properties, and structure of sulfonate ionomers. Polym. Rev. 1988, 28, 99–185. [Google Scholar] [CrossRef]
- Pregi, E.; Kun, D.; Wacha, A.; Pukánszky, B. The role of ionic clusters in the determination of the properties of partially neutralized ethylene-acrylic acid ionomers. Eur. Polym. J. 2021, 142, 110110. [Google Scholar] [CrossRef]
- Agrawal, A.; Perahia, D.; Grest, G.S. Clustering effects in ionic polymers: Molecular dynamics simulations. Phys. Rev. E 2015, 92, 022601. [Google Scholar] [CrossRef] [PubMed]
- Mohottalalage, S.S.; Aryal, D.; Thurston, B.A.; Grest, G.S.; Perahia, D. Effects of Ionic Group Distribution on the Structure and Dynamics of Amorphous Polymer Melts. Macromolecules 2022, 55, 217–223. [Google Scholar] [CrossRef]
- Hall, L.M.; Stevens, M.J.; Frischknecht, A.L. Effect of polymer architecture and ionic aggregation on the scattering peak in model ionomers. Phys. Rev. Lett. 2011, 106, 127801. [Google Scholar] [CrossRef] [PubMed]
- Frischknecht, A.L.; Winey, K.I. The evolution of acidic and ionic aggregates in ionomers during microsecond simulations. J. Chem. Phys. 2019, 150, 064901. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Perahia, D.; Grest, G.S. Cluster morphology-polymer dynamics correlations in sulfonated polystyrene melts: Computational study. Phys. Rev. Lett. 2016, 116, 158001. [Google Scholar] [CrossRef] [PubMed]
- Mohottalalage, S.S.; Clemmer, J.T.; Perahia, D.; Grest, G.S.; O’Connor, T. Nonlinear Elongation Flows in Associating Polymer Melts: From Homogeneous to Heterogeneous Flow. Phys. Rev. X 2022, 12, 021024. [Google Scholar] [CrossRef]
- Senanayake, M.; Perahia, D.; Grest, G.S. Effects of interaction strength of associating groups on linear and star polymer dynamics. J. Chem. Phys. 2021, 154, 074903. [Google Scholar] [CrossRef]
- Qiao, X.; Weiss, R. Nonlinear rheology of lightly sulfonated polystyrene ionomers. Macromolecules 2013, 46, 2417–2424. [Google Scholar] [CrossRef]
- Weiss, R.; Yu, W.-C. Viscoelastic behavior of very lightly sulfonated polystyrene ionomers. Macromolecules 2007, 40, 3640–3643. [Google Scholar] [CrossRef]
- Weiss, R.; Zhao, H. Rheological behavior of oligomeric ionomers. J. Rheol. 2009, 53, 191–213. [Google Scholar] [CrossRef]
- GLing, H.; Wang, Y.; Weiss, R. Linear viscoelastic and uniaxial extensional rheology of alkali metal neutralized sulfonated oligostyrene ionomer melts. Macromolecules 2012, 45, 481–490. [Google Scholar]
- Mohottalalage, S.S.; Kosgallana, C.; Meedin, S.; O’Connor, T.C.; Grest, G.S.; Perahia, D. Response of Sulfonated Polystyrene Melts to Nonlinear Elongation Flows. Macromolecules 2023, 56, 947–953. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D. LAMMPS-A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2021, 271, 108171. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Auhl, R.; Everaers, R.; Grest, G.S.; Kremer, K.; Plimpton, S.J. Equilibration of long chain polymer melts in computer simulations. J. Chem. Phys. 2003, 119, 12718–12728. [Google Scholar] [CrossRef]
- Dobson, M. Periodic boundary conditions for long-time non-equilibrium molecular dynamics simulations of incompressible flows. J. Chem. Phys. 2014, 141, 184103. [Google Scholar] [CrossRef]
- Nicholson, D.A.; Rutledge, G.C. Molecular simulation of flow-enhanced nucleation in n-eicosane melts under steady shear and uniaxial extension. J. Chem. Phys. 2016, 145, 244903. [Google Scholar] [CrossRef]
- O’Connor, T.C.; Hopkins, A.; Robbins, M.O. Stress relaxation in highly oriented melts of entangled polymers. Macromolecules 2019, 52, 8540–8550. [Google Scholar] [CrossRef]
- Evans, D.J.; Morriss, G. Nonlinear-response theory for steady planar Couette flow. Phys. Rev. A 1984, 30, 1528. [Google Scholar] [CrossRef]
- Daivis, P.J.; Todd, B. A simple, direct derivation and proof of the validity of the SLLOD equations of motion for generalized homogeneous flows. J. Chem. Phys. 2006, 124, 194103. [Google Scholar] [CrossRef] [PubMed]
- Subbotin, A.V.; Malkin, A.Y.; Kulichikhin, V.G. The Elasticity of Polymer Melts and Solutions in Shear and Extension Flows. Polymers 2023, 15, 1051. [Google Scholar] [CrossRef] [PubMed]
- Wen, Y.-H.; Wang, C.-C.; Cyue, G.-S.; Kuo, R.-H.; Hsu, C.-H.; Chang, R.-Y. Extensional rheology of linear and branched polymer melts in fast converging flows. Rheol. Acta 2023, 62, 183–204. [Google Scholar] [CrossRef]
- O’Connor, T.C.; Alvarez, N.J.; Robbins, M.O. Relating chain conformations to extensional stress in entangled polymer melts. Phys. Rev. Lett. 2018, 121, 047801. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, T.C.; Ge, T.; Rubinstein, M.; Grest, G.S. Topological linking drives anomalous thickening of ring polymers in weak extensional flows. Phys. Rev. Lett. 2020, 124, 027801. [Google Scholar] [CrossRef]
- Borger, A.; Wang, W.; O’Connor, T.C.; Ge, T.; Grest, G.S.; Jensen, G.V.; Ahn, J.; Chang, T.; Hassager, O.; Mortensen, K. Threading–unthreading transition of linear-ring polymer blends in extensional flow. ACS Macro Lett. 2020, 9, 1452–1457. [Google Scholar] [CrossRef]
- Sukumaran, S.K.; Grest, G.S.; Kremer, K.; Everaers, R. Identifying the primitive path mesh in entangled polymer liquids. J. Polym. Sci. B Polym. Phys. 2005, 43, 917–933. [Google Scholar] [CrossRef]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803. [Google Scholar] [CrossRef]
- Ge, T.; Robbins, M.O.; Perahia, D.; Grest, G.S. Healing of polymer interfaces: Interfacial dynamics, entanglements, and strength. Phys. Rev. E 2014, 90, 012602. [Google Scholar] [CrossRef]
- Bolintineanu, D.S.; Stevens, M.J.; Frischknecht, A.L. Atomistic simulations predict a surprising variety of morphologies in precise ionomers. ACS Macro Lett. 2013, 2, 206–210. [Google Scholar] [CrossRef]
- Hall, L.M.; Seitz, M.E.; Winey, K.I.; Opper, K.L.; Wagener, K.B.; Stevens, M.J.; Frischknecht, A.L. Ionic aggregate structure in ionomer melts: Effect of molecular architecture on aggregates and the ionomer peak. J. Am. Chem. Soc. 2012, 134, 574–587. [Google Scholar] [CrossRef] [PubMed]
- Yarusso, D.J.; Cooper, S.L. Microstructure of ionomers: Interpretation of small-angle x-ray scattering data. Macromolecules 1983, 16, 1871–1880. [Google Scholar] [CrossRef]
- Zhou, N.C.; Chan, C.D.; Winey, K.I. Reconciling STEM and X-ray scattering data to determine the nanoscale ionic aggregate morphology in sulfonated polystyrene ionomers. Macromolecules 2008, 41, 6134–6140. [Google Scholar] [CrossRef]
- Forsman, W.C. Effect of segment-segment association on chain dimensions. Macromolecules 1982, 15, 1032–1040. [Google Scholar] [CrossRef]
- Squires, E.; Painter, P.; Howe, S. Cluster formation and chain extension in ionomers. Macromolecules 1987, 20, 1740–1744. [Google Scholar] [CrossRef]
- Visser, S.A.; Pruckmayr, G.; Cooper, S.L. Small-angle neutron scattering analysis of model polyurethane ionomers. Macromolecules 1991, 24, 6769–6775. [Google Scholar] [CrossRef]
- Kröger, M.; Dietz, J.D.; Hoy, R.S.; Luap, C. The Z1+ package: Shortest multiple disconnected path for the analysis of entanglements in macromolecular systems. Comput. Phys. Commun. 2023, 283, 108567. [Google Scholar] [CrossRef]
- Hinton, Z.R.; Alvarez, N.J. The Trade-Off between Processability and Performance in Commercial Ionomers. Rheol. Acta 2019, 58, 499. [Google Scholar] [CrossRef]
- Hinton, Z.R.; Shabbir, A.; Alvarez, N.J. Dynamics of Supramolecular Self-Healing Recovery in Extension. Macromolecules 2019, 52, 2231. [Google Scholar] [CrossRef]
- Shabbir, A.; Huang, Q.; Chen, Q.; Colby, R.H.; Alvarez, N.J.; Hassager, O. Brittle Fracture in Associative Polymers: The Case of Ionomer Melts. Soft Matter. 2016, 12, 7606. [Google Scholar] [CrossRef] [PubMed]
- Shabbir, A.; Huang, Q.; Baeza, G.P.; Vlassopoulos, D.; Chen, Q.; Colby, R.H.; Alvarez, N.J.; Hassager, O. Nonlinear Shear and Uniaxial Extensional Rheology of Polyether-Ester-Sulfonate Copolymer Ionomer Melts. J. Rheol. 2017, 61, 1279. [Google Scholar] [CrossRef]
- Schaefer, C.; Laity, P.R.; Holland, C.; McLeish, T.C. Stretching of Bombyx mori Silk Protein in Flow. Molecules 2021, 26, 1663. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Madsen, J.; Genina, N.; Hassager, O.; Skov, A.L.; Huang, Q. Toward a Design for Flowable and Extensible Ionomers: An Example of Diamine-Neutralized Entangled Poly (styrene-co-4-vinylbenzoic acid) Ionomer Melts. Macromolecules 2021, 54, 2306–2315. [Google Scholar] [CrossRef]
- Liu, S.; Cao, X.; Huang, C.; Weiss, R.A.; Zhang, Z.; Chen, Q. Brittle-to-ductile transition of sulfonated polystyrene ionomers. ACS Macro Lett. 2021, 10, 503–509. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohottalalage, S.S.; Saab, A.P.; Maiti, A. Bead–Spring Simulation of Ionomer Melts—Studying the Effects of Chain-Length and Associating Group Fraction on Equilibrium Structure and Extensional Flow Behavior. Polymers 2023, 15, 4560. https://doi.org/10.3390/polym15234560
Mohottalalage SS, Saab AP, Maiti A. Bead–Spring Simulation of Ionomer Melts—Studying the Effects of Chain-Length and Associating Group Fraction on Equilibrium Structure and Extensional Flow Behavior. Polymers. 2023; 15(23):4560. https://doi.org/10.3390/polym15234560
Chicago/Turabian StyleMohottalalage, Supun S., Andrew P. Saab, and Amitesh Maiti. 2023. "Bead–Spring Simulation of Ionomer Melts—Studying the Effects of Chain-Length and Associating Group Fraction on Equilibrium Structure and Extensional Flow Behavior" Polymers 15, no. 23: 4560. https://doi.org/10.3390/polym15234560
APA StyleMohottalalage, S. S., Saab, A. P., & Maiti, A. (2023). Bead–Spring Simulation of Ionomer Melts—Studying the Effects of Chain-Length and Associating Group Fraction on Equilibrium Structure and Extensional Flow Behavior. Polymers, 15(23), 4560. https://doi.org/10.3390/polym15234560






