Dielectric and Viscoelastic Behavior of Polyvinyl Butyral Films
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Polyvinyl Butyral Films
2.2. Thermal, Viscoelastic, and Dielectric Characterization
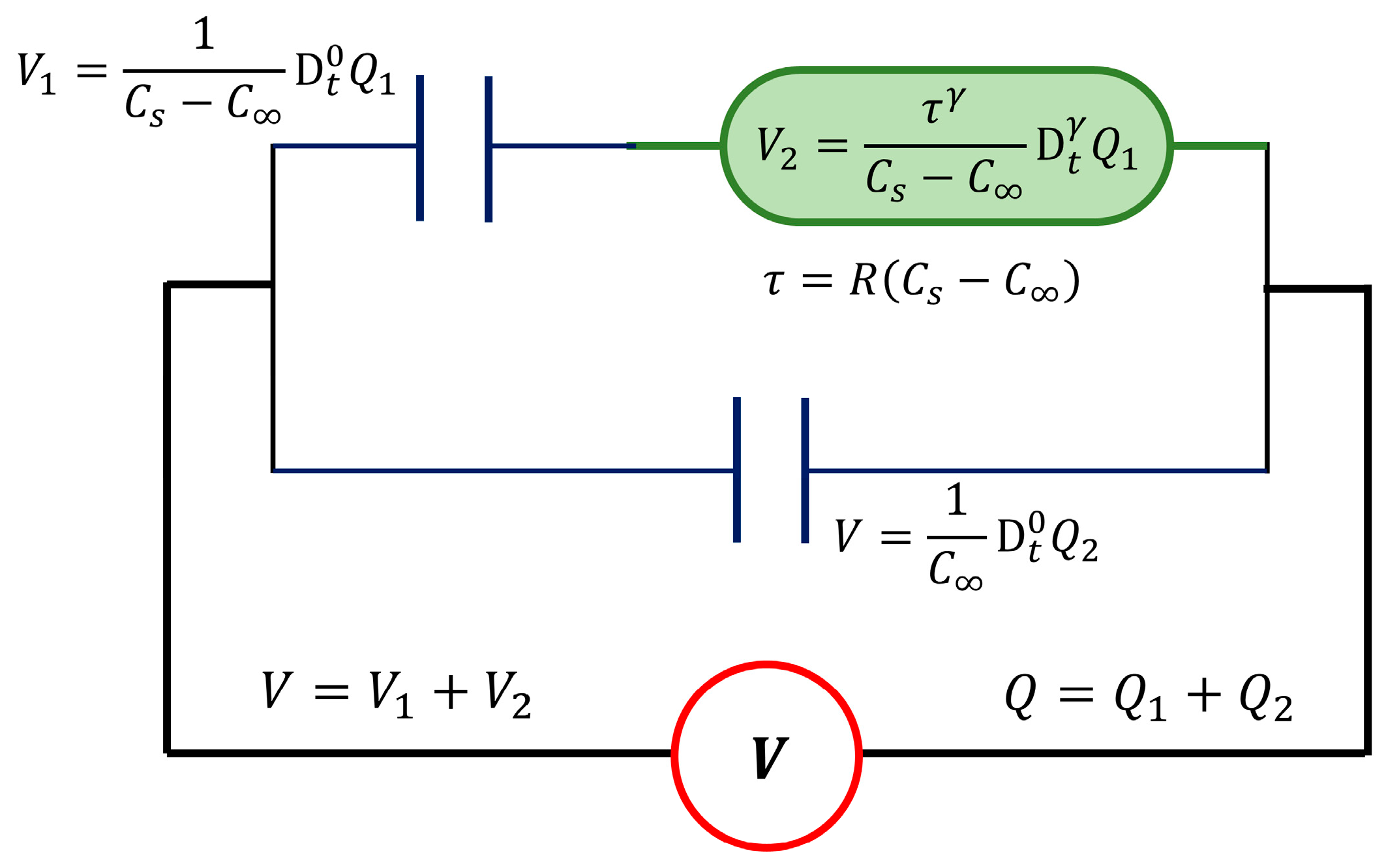
2.3. The Fractional Debye Model and the Cap-Resistor
3. Results and Discussion
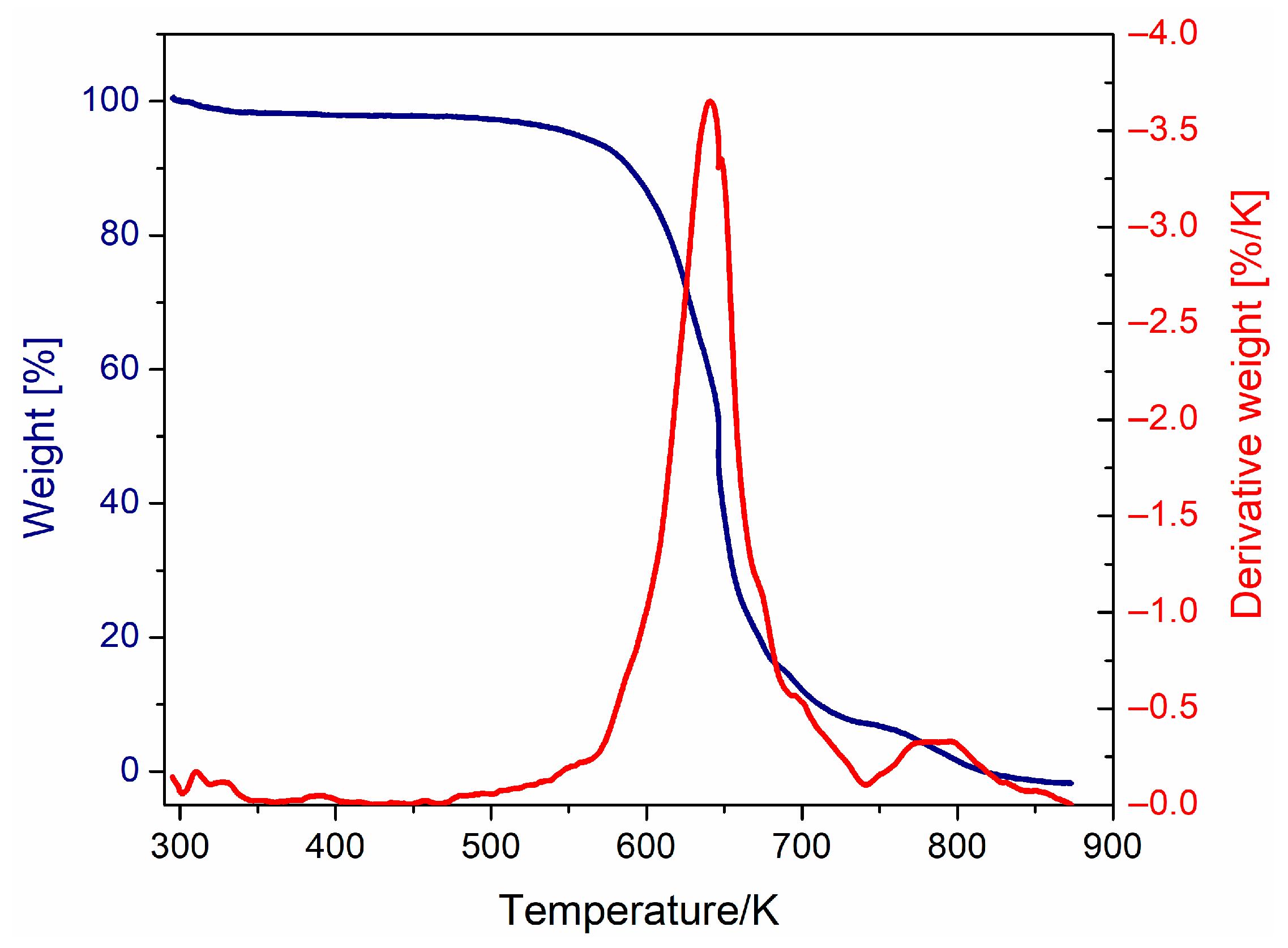
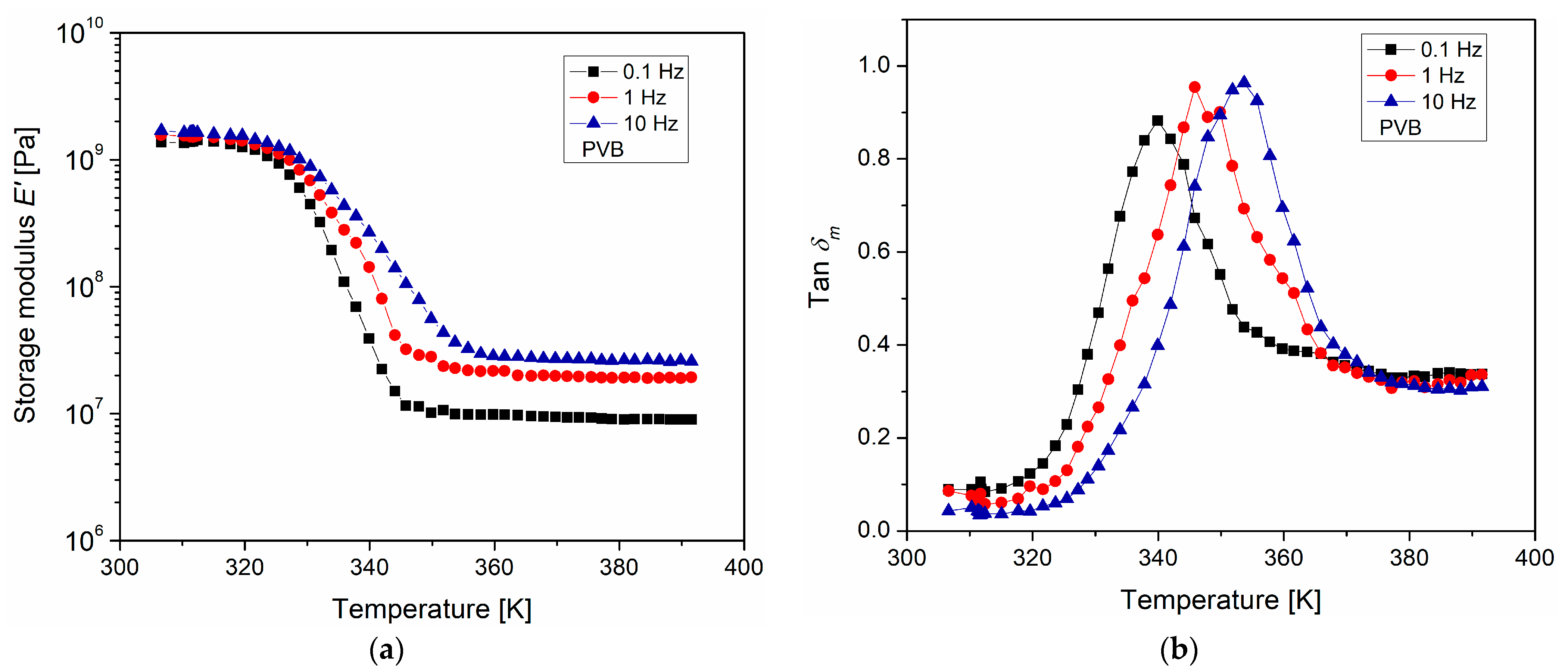
3.1. Thermal and Viscoelastic Analysis
3.2. Dynamic Dielectric Analysis DEA
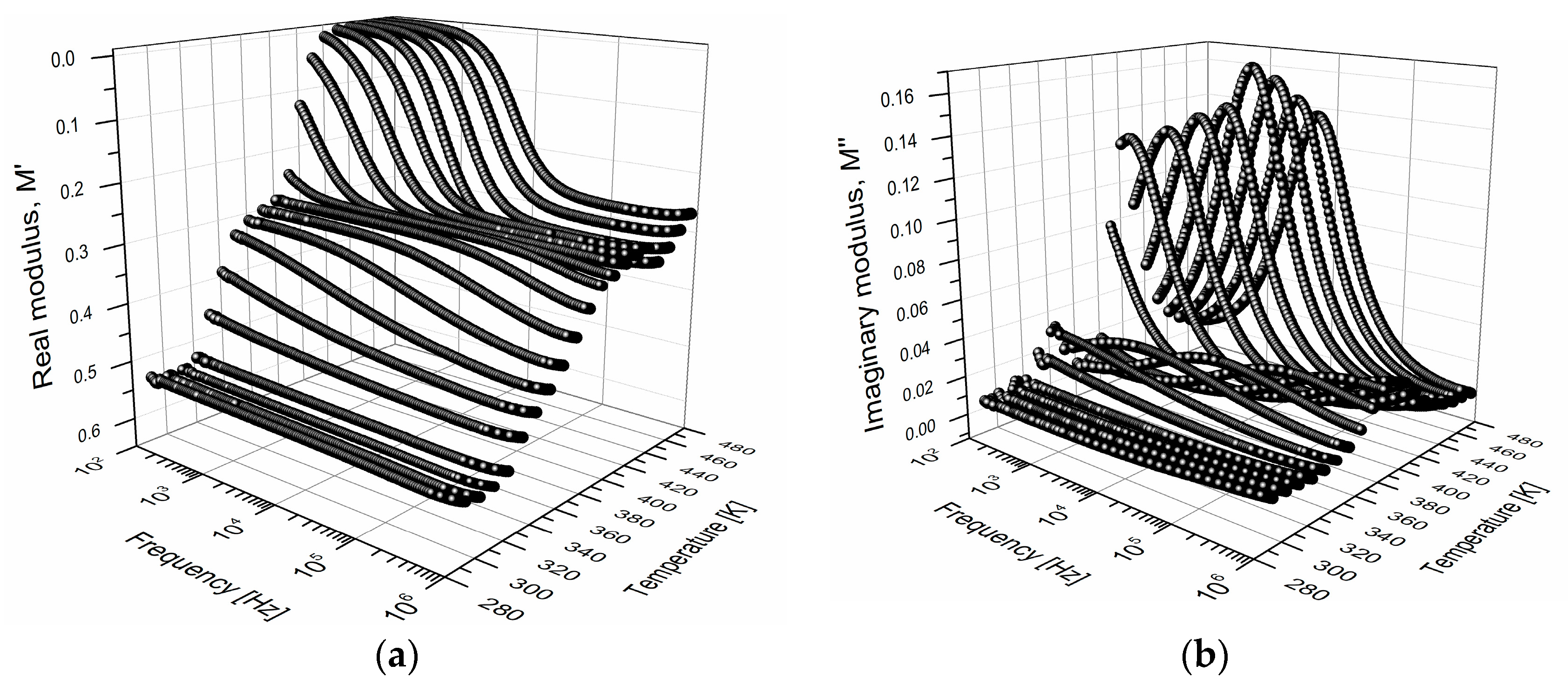
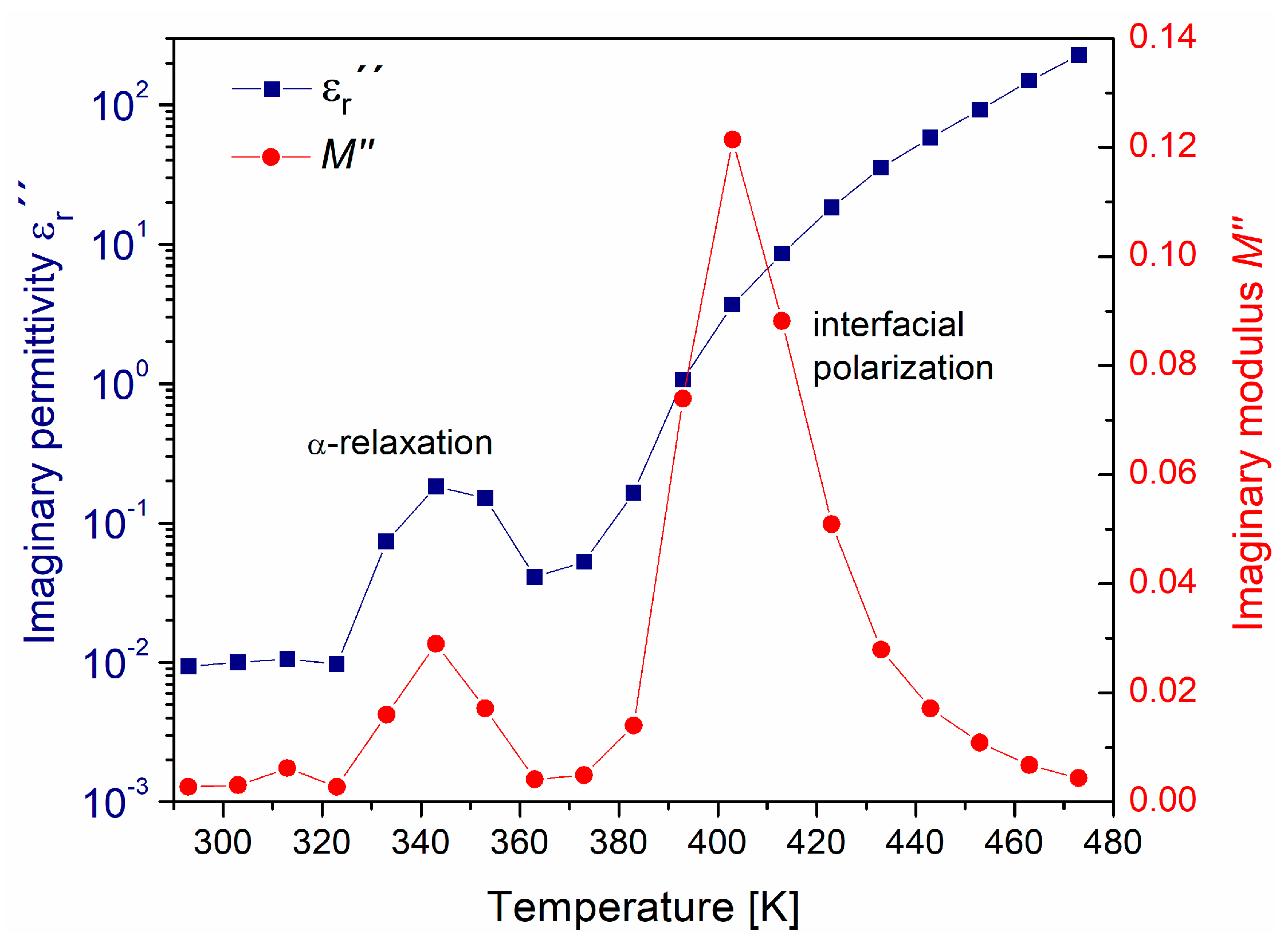
3.3. Electric Modulus Approach
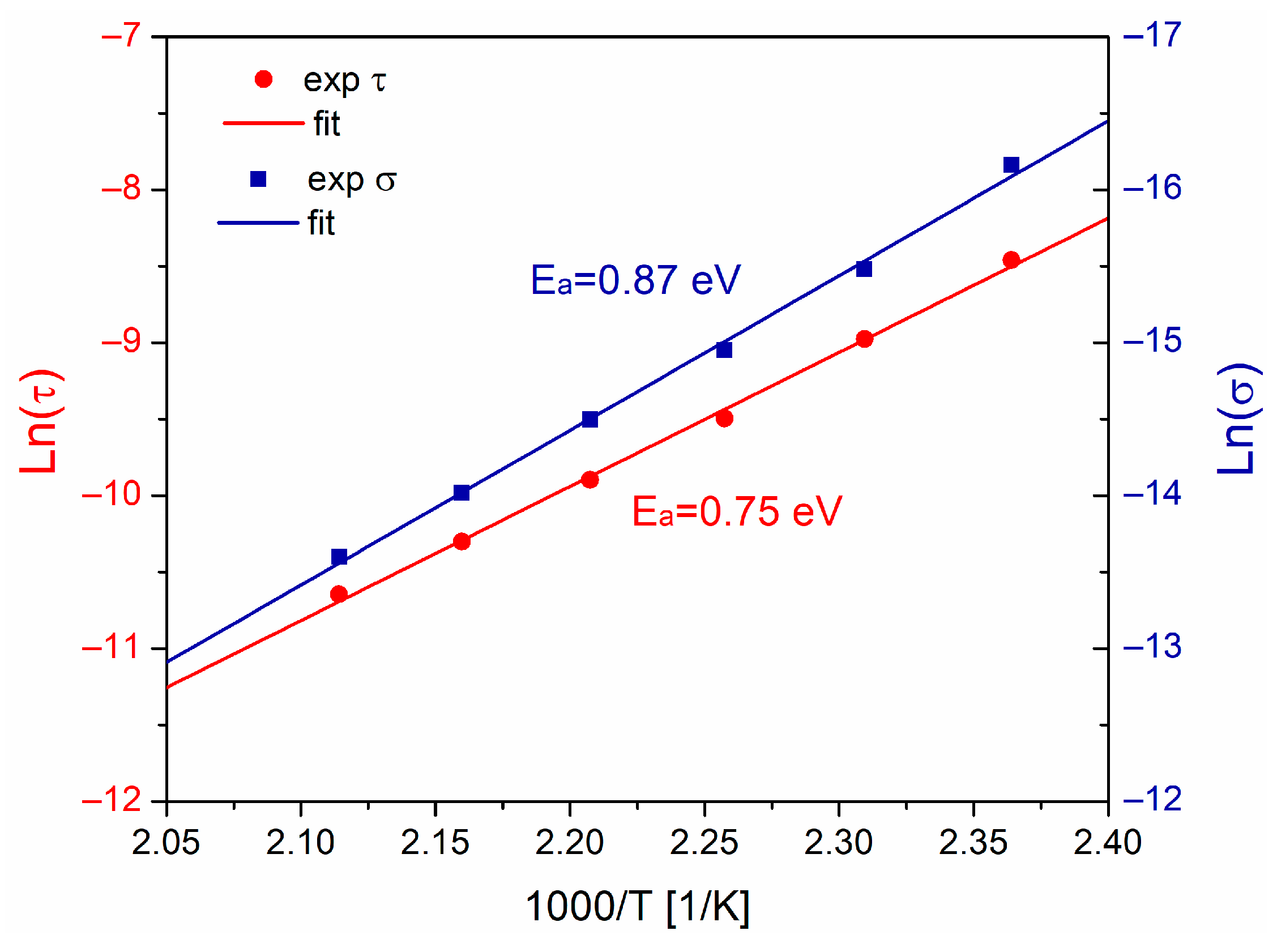
3.4. Comparison between Experimental Data and Theoretical Predictions from the Fractional Debye Model
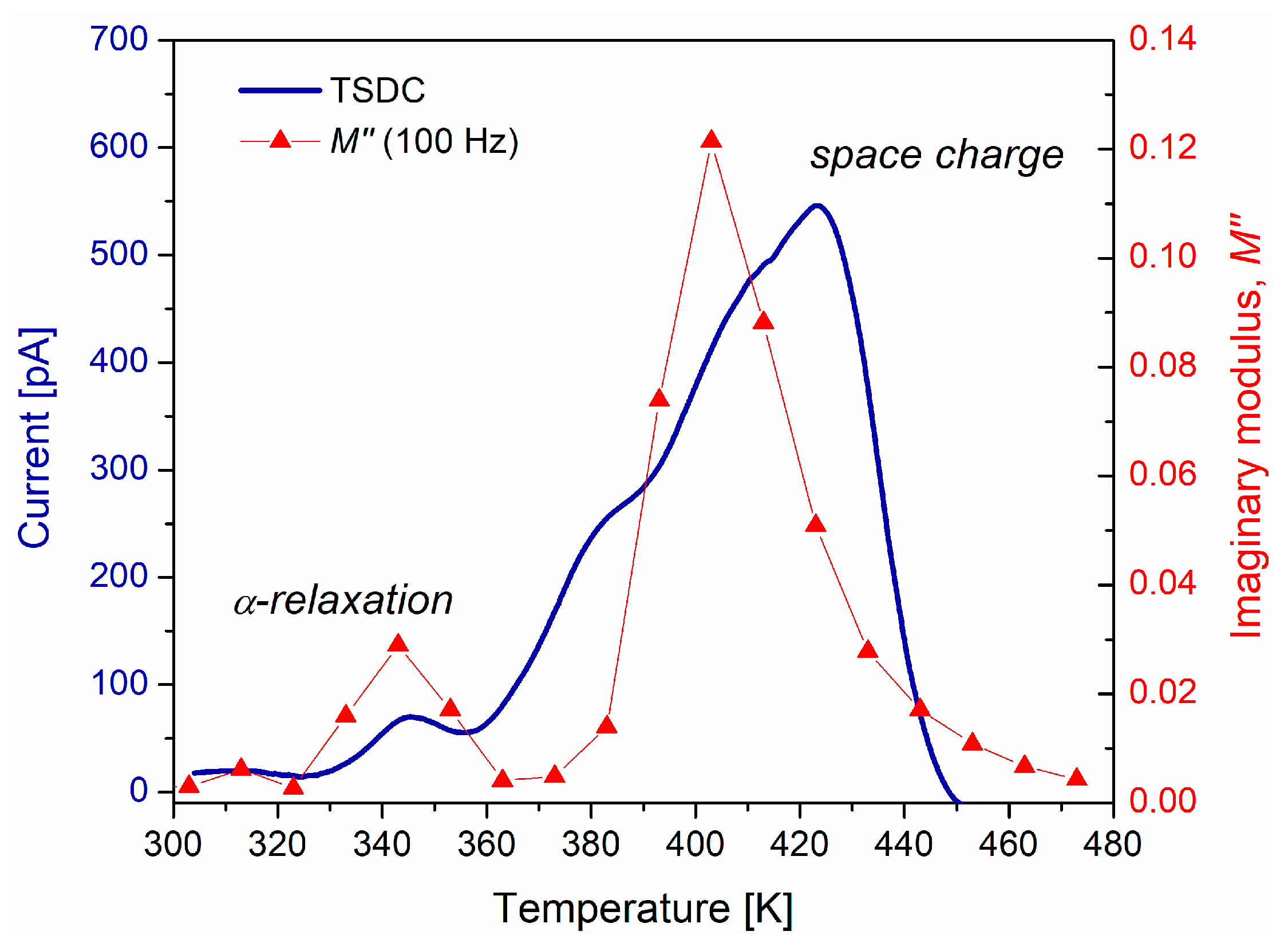
3.5. Thermally Stimulated Discharge Current (TSDC)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Zhu, Y.; Huang, J.; Zhang, J.; Pan, D.; Zhou, J.; Ryu, J.E.; Umar, A.; Guo, Z. Advances in Responsively Conductive Polymer Composites and Sensing Applications. Polym. Rev. 2021, 61, 157–193. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, A.; Han, Y.; Li, T. Sensors Based on Conductive Polymers and Their Composites: A Review. Polym. Int. 2020, 69, 7–17. [Google Scholar] [CrossRef]
- Kumar, D.; Sharma, R.C. Advances in Conductive Polymers. Eur. Polym. J. 1998, 34, 1053–1060. [Google Scholar] [CrossRef]
- Merrick, M.M.; Sujanani, R.; Freeman, B.D. Glassy Polymers: Historical Findings, Membrane Applications, and Unresolved Questions Regarding Physical Aging. Polymer 2020, 211, 123176. [Google Scholar] [CrossRef]
- Mandal, S.; Dasmahapatra, A.K. Effect of Aging on the Microstructure and Physical Properties of Poly(Vinyl Alcohol) Hydrogel. J. Polym. Res. 2021, 28, 269. [Google Scholar] [CrossRef]
- McKenzie, R.; Zurawsky, W.; Mijovic, J. A Molecular Interpretation of Maxwell-Wagner-Sillars Processes. J. Non. Cryst. Solids 2014, 406, 11–21. [Google Scholar] [CrossRef]
- Samet, M.; Levchenko, V.; Boiteux, G.; Seytre, G.; Kallel, A.; Serghei, A. Electrode Polarization vs. Maxwell-Wagner-Sillars Interfacial Polarization in Dielectric Spectra of Materials: Characteristic Frequencies and Scaling Laws. J. Chem. Phys. 2015, 142, 194703. [Google Scholar] [CrossRef]
- Mudarra, M.; Belana, J.; Cañadas, J.C.; Diego, J.A.; Sellarès, J.; Díaz-Calleja, R.; Sanchís, M.J. Space Charge Relaxation in Polyetherimides by the Electric Modulus Formalism. J. Appl. Phys. 2000, 88, 4807–4812. [Google Scholar] [CrossRef]
- Mudarra, M.; Sellarès, J.; Canãdas, J.C.; Diego, J.A. Sublinear Dispersive Conductivity in Polyetherimides by the Electric Modulus Formalism. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3327–3333. [Google Scholar] [CrossRef]
- Arous, M.; Karray, F.; Hammami, H.; Perrier, G. Study of the Space Charge Relaxation in Poly Ether Ether Ketone (PEEK). Phys. Chem. News 2003, 10, 5–7. [Google Scholar]
- Hasegawa, Y.; Ohki, Y.; Fukunaga, K.; Mizuno, M.; Sasaki, K. Complex Permittivity Spectra of Various Insulating Polymers at Ultrawide-Band Frequencies. Electr. Eng. Jpn. 2017, 198, 11–18. [Google Scholar] [CrossRef]
- Mudarra, M.; Díaz-Calleja, R.; Belana, J.; Cañadas, J.C.; Diego, J.A.; Sellarès, J.; Sanchís, M.J. Study of Space Charge Relaxation in PMMA at High Temperatures by Dynamic Electrical Analysis. Polymer 2001, 42, 1647–1651. [Google Scholar] [CrossRef]
- Tian, F.; Ohki, Y. Electric Modulus Powerful Tool for Analyzing Dielectric Behavior. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 929–931. [Google Scholar] [CrossRef]
- Tsangaris, G.M.; Psarras, G.C.; Kouloumbi, N. Electric Modulus and Interfacial Polarization in Composite Polymeric Systems. J. Mater. Sci. 1998, 33, 2027–2037. [Google Scholar] [CrossRef]
- Richert, R.; Wagner, H. The Dielectric Modulus: Relaxation versus Retardation. Solid State Ion. 1998, 105, 167–173. [Google Scholar] [CrossRef]
- Reyes-Melo, M.E.; Miranda-Valdez, I.Y.; Puente-Córdova, J.G.; Camarillo-Hernández, C.A.; López-Walle, B. Fabrication and Characterization of a Biocompatible Hybrid Film Based on Silver Nanoparticle/Ethyl Cellulose Polymer. Cellulose 2021, 28, 9227–9240. [Google Scholar] [CrossRef]
- Rentería-Baltiérrez, F.Y.; Reyes-Melo, M.E.; Puente-Córdova, J.G.; López-Walle, B. Application of Fractional Calculus in the Mechanical and Dielectric Correlation Model of Hybrid Polymer Films with Different Average Molecular Weight Matrices. Polym. Bull. 2023, 80, 6327–6347. [Google Scholar] [CrossRef]
- Puente-Córdova, J.G.; Reyes-Melo, M.E.; López-Walle, B.; Miranda-Valdez, I.Y.; Torres-Castro, A. Characterization of a Magnetic Hybrid Film Fabricated by the In-Situ Synthesis of Iron Oxide Nanoparticles into Ethyl Cellulose Polymer. Cellulose 2022, 29, 3845–3857. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Pawar, S.J. Experimental and Simulation Studies on Fatigue Behavior of Laminated Glass Having Polyvinyl Butyral and Ethyl Vinyl Acetate Interlayers. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1437–1446. [Google Scholar] [CrossRef]
- Iwasaki, R.; Sato, C.; Latailladeand, J.L.; Viot, P. Experimental Study on the Interface Fracture Toughness of PVB (Polyvinyl Butyral)/Glass at High Strain Rates. Int. J. Crashworthiness 2007, 12, 293–298. [Google Scholar] [CrossRef]
- Hoepfner, J.C.; Loos, M.R.; Pezzin, S.H. Role of the Degree of Acetalization on Dynamic Mechanical Properties of Polyvinyl Butyral/Carbon Nanotube Composites. J. Appl. Polym. Sci. 2019, 136, 48146. [Google Scholar] [CrossRef]
- Bartolotta, A.; Marco, G.D.I.; Federico, M.; Carini, G. Rising the Molecular Mobility of Polyvinyl Butyral by Plasticizers: Towards Energy Storage Applications. Atti Della Accad. Peloritana Dei Pericolanti-Cl. Di Sci. Fis. Mat. E Nat. 2020, 98, 1–11. [Google Scholar] [CrossRef]
- Jain, K.; Kumar, N.; Mehendru, P.C. Electrical and Dielectric Properties of Polyvinyl Butyral: I. Studies of Charge Storage Mechanism. J. Electrochem. Soc. 1979, 126, 1958–1963. [Google Scholar] [CrossRef]
- Funt, B.L. Dielectric Dispersion in Solid Polyvinyl Butyral. Can. J. Chem. 1952, 30, 84–91. [Google Scholar] [CrossRef]
- Saad, G.R.; El-Shafee, E.; Sabaa, M.W. Dielectric and Mechanical Properties in the Photodegradation of Poly(Vinyl Butyral) Films. Polym. Degrad. Stab. 1995, 47, 209–215. [Google Scholar] [CrossRef]
- Mehendru, P.C.; Kumar, N.; Arora, V.P.; Gupta, N.P. Dielectric Relaxation Studies in Polyvinyl Butyral. J. Chem. Phys. 1982, 77, 4232–4235. [Google Scholar] [CrossRef]
- Carini, G.; Bartolotta, A.; Carini, G.; D’Angelo, G.; Federico, M.; Di Marco, G. Water-Driven Segmental Cooperativity in Polyvinyl Butyral. Eur. Polym. J. 2018, 98, 172–176. [Google Scholar] [CrossRef]
- Ortigueira, M.; Machado, J. Which Derivative? Fractal Fract. 2017, 1, 3. [Google Scholar] [CrossRef]
- Rentería-Baltiérrez, F.Y.; Reyes-Melo, M.E.; Puente-Córdova, J.G.; López-Walle, B. Correlation between the Mechanical and Dielectric Responses in Polymer Films by a Fractional Calculus Approach. J. Appl. Polym. Sci. 2021, 138, 49853. [Google Scholar] [CrossRef]
- Reyes-Melo, E.; Martinez-Vega, J.; Guerrero-Salazar, C.; Ortiz-Mendez, U. Application of Fractional Calculus to the Modeling of Dielectric Relaxation Phenomena in Polymeric Materials. J. Appl. Polym. Sci. 2005, 98, 923–935. [Google Scholar] [CrossRef]
- Reyes-Melo, M.E.; Martínez-Vega, J.J.; Guerrero-Salazar, C.A.; Ortiz-Méndez, U. Mechanical and Dielectric Relaxation Phenomena of Poly(Ethylene-2,6- Napthalene Dicarboxylate) by Fractional Calculus Approach. J. Appl. Polym. Sci. 2006, 102, 3354–3368. [Google Scholar] [CrossRef]
- Meng, R. Application of Fractional Calculus to Modeling the Nonlinear Behaviors of Ferroelectric Polymer Composites: Viscoelasticity and Dielectricity. Membranes 2021, 11, 409. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Chen, H.S. A New Generalized Fractional Maxwell Model of Dielectric Relaxation. Chin. J. Phys. 2017, 55, 1998–2004. [Google Scholar] [CrossRef]
- Ivanov, V.B.; Zavodchikova, A.A.; Popova, E.I.; Lazareva, O.L.; Belova, O.A.; Kryuchkov, I.A.; Bykov, E.V. Accelerated Testing of Thermo-Oxidative Degradation of Polyvinyl Butyral. Thermochim. Acta 2014, 589, 70–75. [Google Scholar] [CrossRef]
- Hajian, M.; Reisi, M.R.; Koohmareh, G.A.; Jam, A.R.Z. Preparation and Characterization of Polyvinylbutyral/Graphene Nanocomposite. J. Polym. Res. 2012, 19, 409. [Google Scholar] [CrossRef]
- Calucci, L.; Pizzanelli, S.; Mandoli, A.; Birczyński, A.; Lalowicz, Z.T.; De Monte, C.; Ricci, L.; Bronco, S. Unravelling Main- and Side-Chain Motions in Polymers with NMR Spectroscopy and Relaxometry: The Case of Polyvinyl Butyral. Polymers 2021, 13, 2686. [Google Scholar] [CrossRef]
- Kirchberg, S.; Rudolph, M.; Ziegmann, G.; Peuker, U.A. Nanocomposites Based on Technical Polymers and Sterically Functionalized Soft Magnetic Magnetite Nanoparticles: Synthesis, Processing, and Characterization. J. Nanomater. 2012, 2012, 670531. [Google Scholar] [CrossRef]
- Carini, G.; Carini, G.; D’Angelo, G.; Federico, M.; Di Marco, G.; Bartolotta, A. Enhancing the Molecular Cooperativity of Polyvinyl Butyral Using Liquid Additives. J. Polym. Sci. Part B Polym. Phys. 2018, 56, 340–346. [Google Scholar] [CrossRef]
- Hoang, M.Q.; Boudou, L.; Le Roy, S.; Teyssedre, G. Dissociating Space Charge Processes from Orientation Polarization in Poly(Ethylene Naphthalate) Films. J. Phys. D. Appl. Phys. 2014, 47, 455306. [Google Scholar] [CrossRef]
- Mazzanti, G.; Montanari, G.C.; Dissado, L.A. Electrical Aging and Life Models: The Role of Space Charge. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 876–890. [Google Scholar] [CrossRef]
- Montanari, G.C.; Seri, P.; Dissado, L.A. Aging Mechanisms of Polymeric Materials under DC Electrical Stress: A New Approach and Similarities to Mechanical Aging. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 634–641. [Google Scholar] [CrossRef]
- Marín-Genescà, M.; Mujal-Rosas, R.; García-Amorós, J.; Mudarra, M.; Juan, X.R.; Fajula, X.C. Study Analysis of Thermal, Dielectric and Functional Characteristics of an Ethylene Polyethylene Diene Monomer Blended with End-of-Life Tire Microparticles Amounts. Polymers 2021, 13, 509. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Liu, S.; Zhang, H.; Lu, J. A Flexible Temperature Sensor Array with Polyaniline/Graphene–Polyvinyl Butyral Thin Film. Sensors 2019, 19, 4105. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Y.; Shi, P.; Lei, Y.; Weng, S.; Li, S.; Huang, L.; Lin, X.; Yao, H. Polyvinyl butyral/graphene oxide nanocomposite modified electrode for the integrate determination of terminal metabolites of catecholamines in human urine. J. Electroanal. Chem. 2019, 848, 113267. [Google Scholar] [CrossRef]


| 423 K | 433 K | 443 K | 453 K | 463 K | 473 K | |
|---|---|---|---|---|---|---|
| 5 × 10−4 | 1 × 10−4 | 2 × 10−4 | 4 × 10−4 | 3 × 10−4 | 3 × 10−4 | |
| 0.304 | 0.303 | 0.333 | 0.317 | 0.295 | 0.274 | |
| (s) | 2.11 × 10−4 | 1.26 × 10−4 | 7.51 × 10−5 | 5.02 × 10−5 | 3.35 × 10−5 | 2.37 × 10−5 |
| 0.932 | 0.958 | 0.985 | 0.989 | 0.992 | 0.994 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puente-Córdova, J.G.; Rentería-Baltiérrez, F.Y.; López-Walle, B.; Aguilar-Garib, J.A. Dielectric and Viscoelastic Behavior of Polyvinyl Butyral Films. Polymers 2023, 15, 4725. https://doi.org/10.3390/polym15244725
Puente-Córdova JG, Rentería-Baltiérrez FY, López-Walle B, Aguilar-Garib JA. Dielectric and Viscoelastic Behavior of Polyvinyl Butyral Films. Polymers. 2023; 15(24):4725. https://doi.org/10.3390/polym15244725
Chicago/Turabian StylePuente-Córdova, Jesús G., Flor Y. Rentería-Baltiérrez, Beatriz López-Walle, and Juan A. Aguilar-Garib. 2023. "Dielectric and Viscoelastic Behavior of Polyvinyl Butyral Films" Polymers 15, no. 24: 4725. https://doi.org/10.3390/polym15244725
APA StylePuente-Córdova, J. G., Rentería-Baltiérrez, F. Y., López-Walle, B., & Aguilar-Garib, J. A. (2023). Dielectric and Viscoelastic Behavior of Polyvinyl Butyral Films. Polymers, 15(24), 4725. https://doi.org/10.3390/polym15244725








