Simulating Stress–Strain Behavior by Using Individual Chains: Uniaxial Deformation of Amorphous Cis- and Trans-1,4-Polybutadiene
Abstract
:1. Introduction
2. Methodology
2.1. Coarse Graining Steps
2.2. Elastic Free Energy
2.3. Force Derivatives of Free Energy
2.4. Orientation of Undeformed and Deformed Chains
2.5. Numerical Implementation
2.6. Gaussian Test Case
2.7. RIS Chains
2.8. Finite Strain
3. Results and Discussion
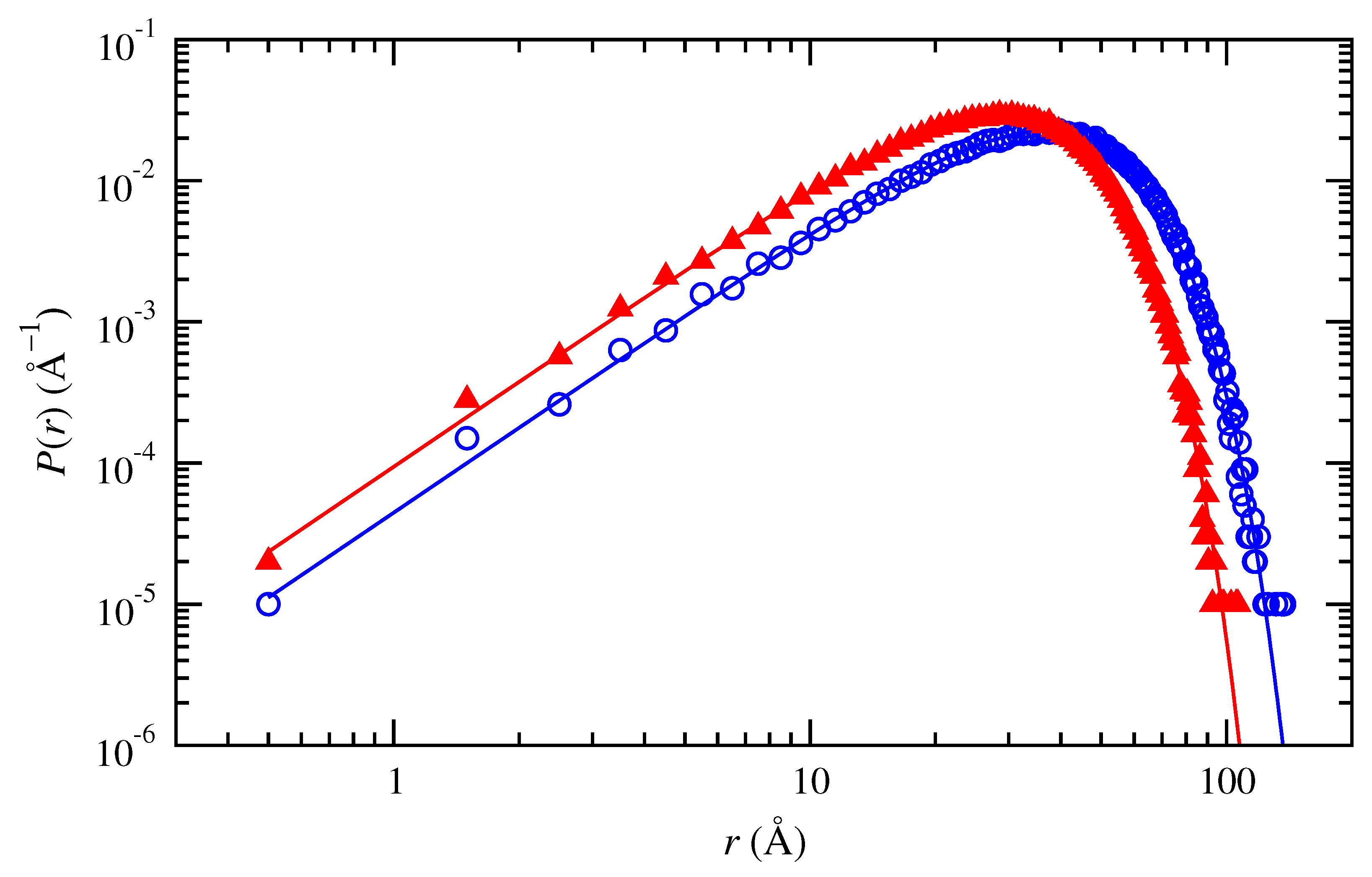
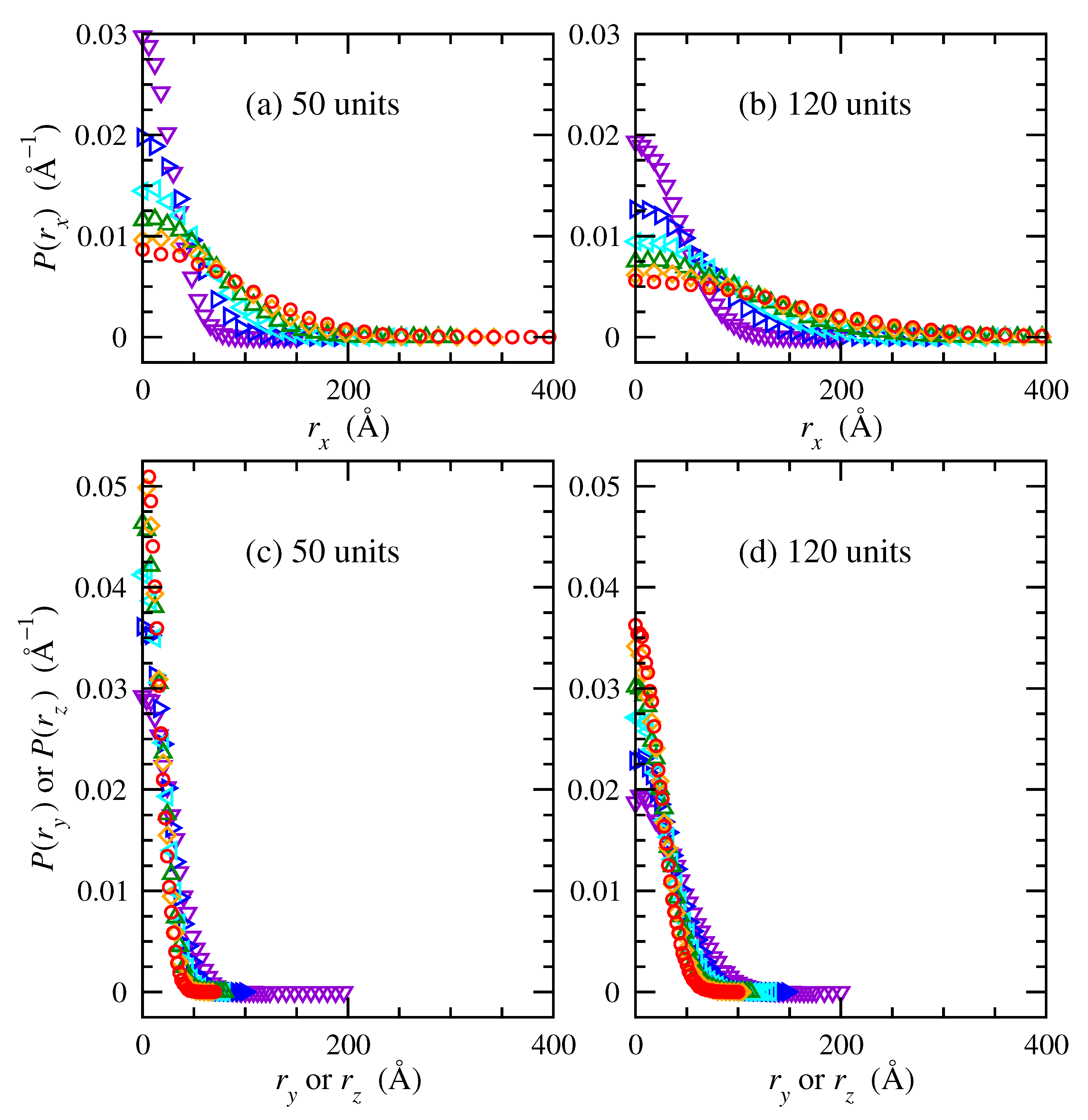
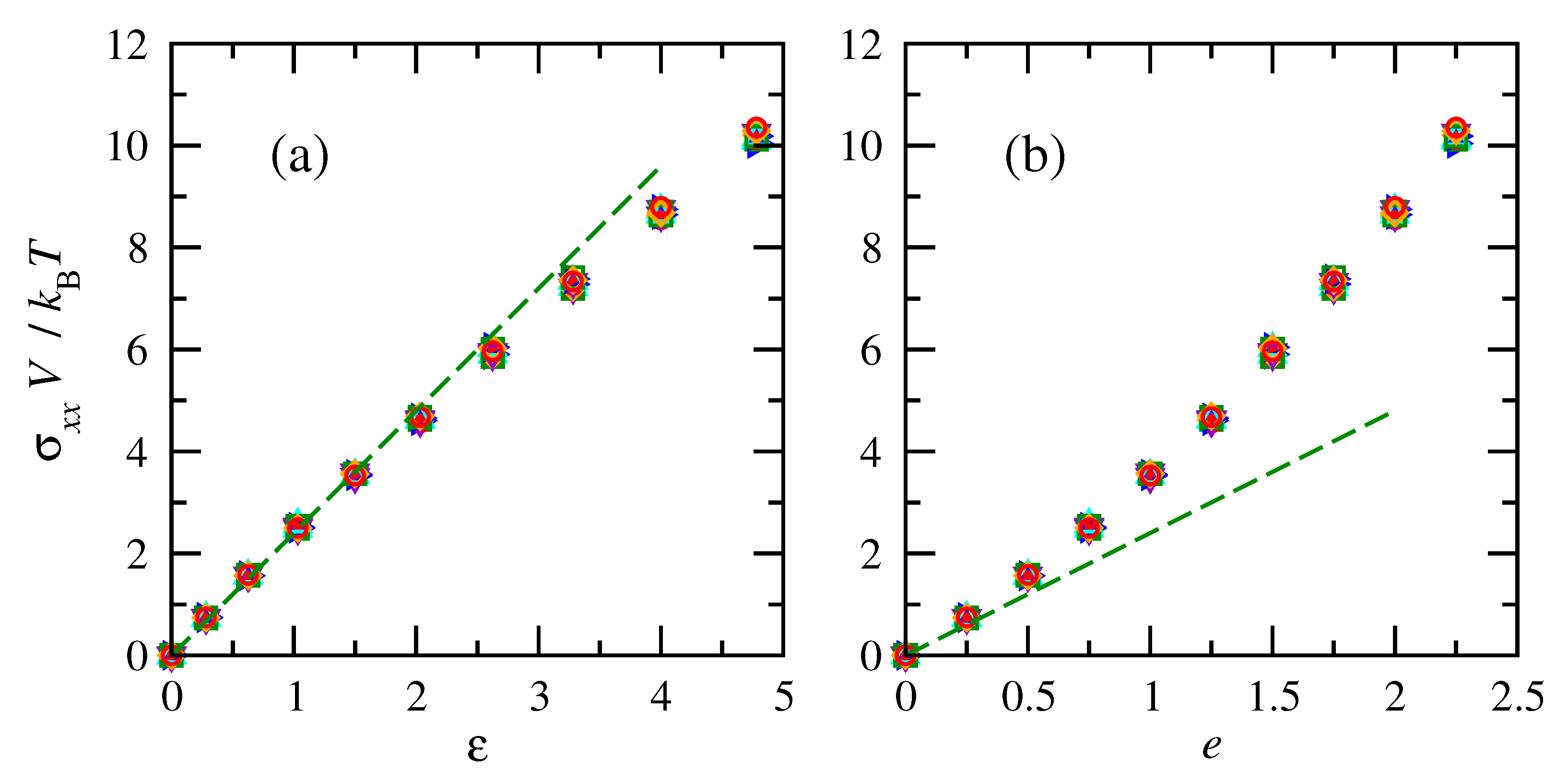
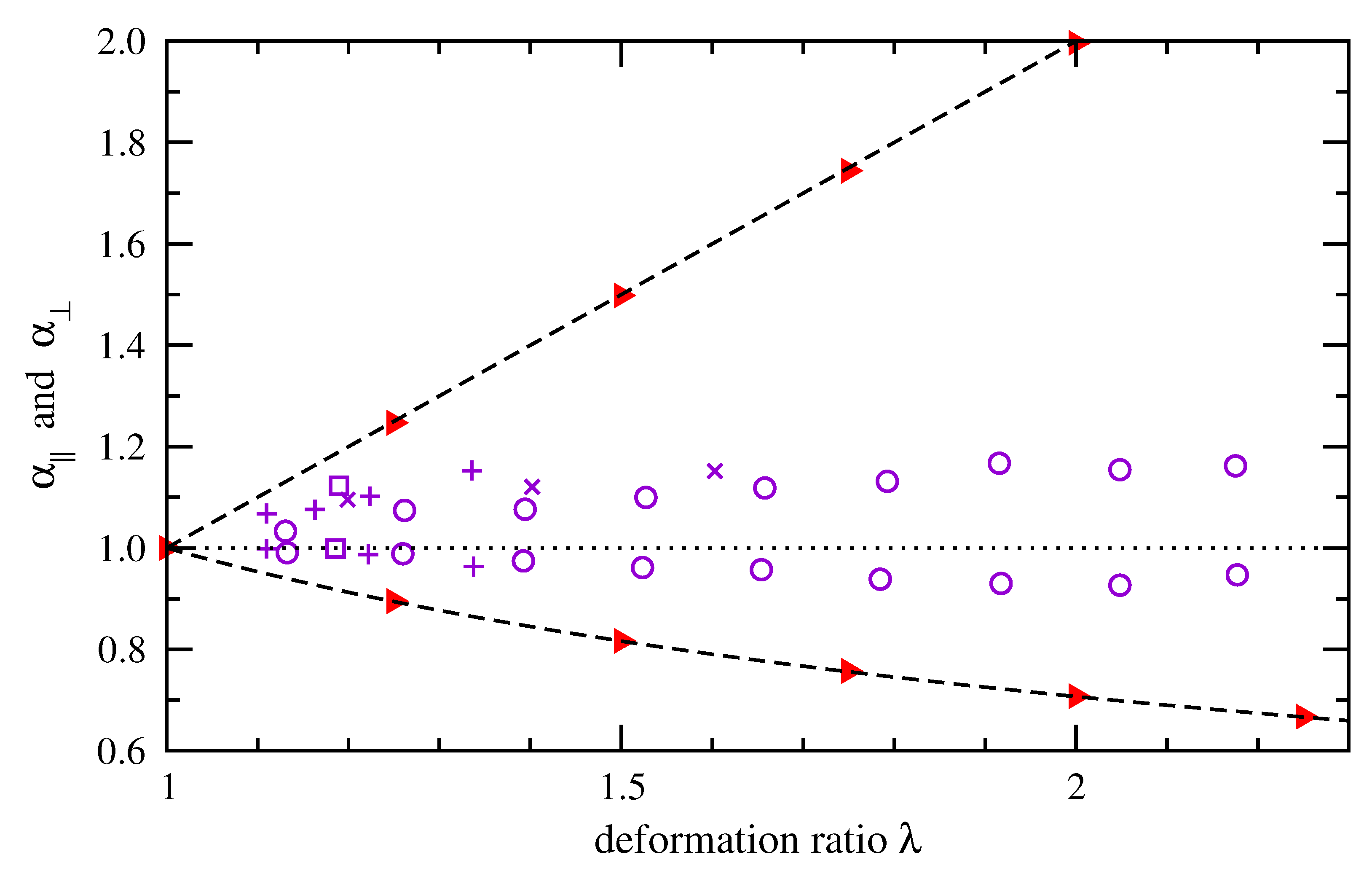
3.1. Gaussian Chains
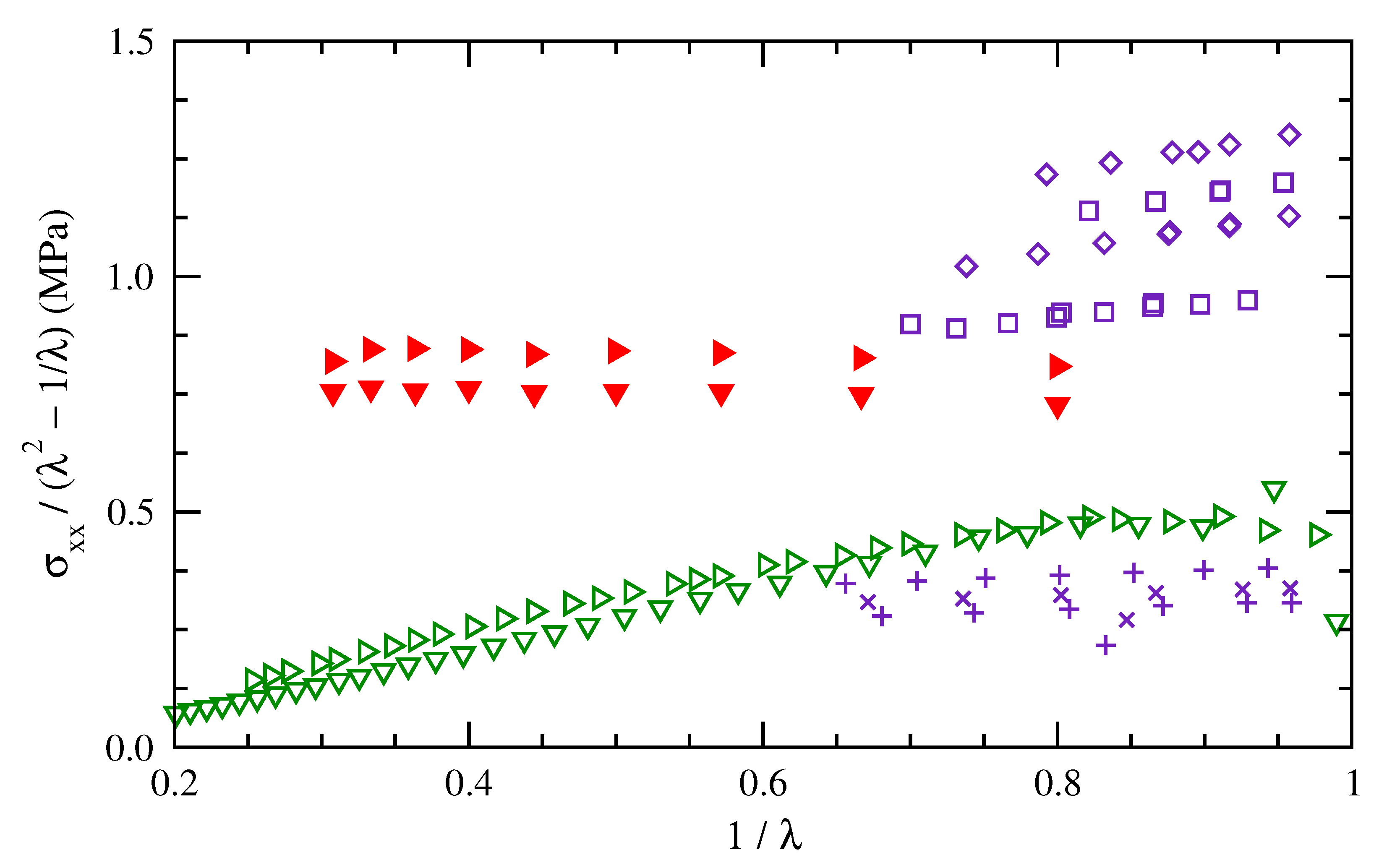
3.2. RIS Chains
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Blow, C.M.; Hepburn, C. Rubber Technology and Manufacture; Plastics and Rubber Institute: London, UK, 1982. [Google Scholar]
- White, J.L. Rubber Processing: Technology, Materials, and Principles; Hanser: Munich, Germany, 1995. [Google Scholar]
- Mark, J.E.; Erman, B. Rubberlike Elasticity: A Molecular Primer; John Wiley & Sons: New York, NY, USA, 1988. [Google Scholar]
- McCrum, N.G.; Buckley, C.P.; Bucknall, C.B. Principles of Polymer Engineering, 2nd ed.; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Tonelli, A.; Shen, J. Conformations; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Fetters, L.J.; Lohse, D.J.; Richter, D.; Witten, T.A.; Zirkel, A. Connection between Polymer Molecular Weight, Density, Chain Dimensions, and Melt Viscoelastic Properties. Macromolecules 1994, 27, 4639–4647. [Google Scholar] [CrossRef]
- ten Brinke, J.W.; Litvinov, V.M.; Wijnhoven, J.E.G.J.; Noordermeer, J.W.M. Interactions of Stober Silica with Natural Rubber under the Influence of Coupling Agents, Studied by 1H NMR T2 Relaxation Analysis. Macromolecules 2002, 35, 10026–10037. [Google Scholar] [CrossRef]
- Reuvekamp, L.A.E.M.; Debnath, S.C.; Brinke Ten, J.W.; Van Swaaij, J.P.; Noordermeer, J.W.M. Effect of Zinc Oxide on the Reaction of TESPT Silane Coupling Agent with Silica and Rubber. Rubber Chem. Tech. 2004, 77, 34–49. [Google Scholar] [CrossRef]
- Flanigan, C.M.; Beyer, L.; Klekamp, D.; Rohweder, D.; Stuck, B.; Terrill, E.R. Comparative study of silica, carbon black and novel fillers in tread compounds. Rubber World 2012, 245, 18–31. [Google Scholar]
- Veiga, V.D.; Rossignol, T.M.; Crespo, J.d.S.; Carli, L.N. Tire tread compounds with reduced rolling resistance and improved wet grip. J. Appl. Polym. Sci. 2017, 134, 45334. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Zheng, Z.J. Recent progress of elastomer–silica nanocomposites toward green tires: Simulation and experiment. Polym. Int. 2023; in press. [Google Scholar] [CrossRef]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Tao, H.; Lodge, T.P.; von Meerwall, E.D. Diffusivity and Viscosity of Concentrated Hydrogenated Polybutadiene Solutions. Macromolecules 2000, 33, 1747–1758. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Cohen Addad, J.P.; Guillermo, A. NMR and Entangled Chain Dynamics in Molten Polybutadiene. Molecular Weight Dependent Segmental Friction. Macromolecules 2003, 36, 1609–1615. [Google Scholar] [CrossRef]
- Danielsen, S.P.O.; Beech, H.K.; Wang, S.; El-Zaatari, B.M.; Wang, X.; Sapir, L.; Ouchi, T.; Wang, Z.; Johnson, P.N.; Hu, Y.; et al. Molecular Characterization of Polymer Networks. Chem. Rev. 2021, 121, 5042–5092. [Google Scholar] [CrossRef] [PubMed]
- Cohen Addad, J.P.; Thanh, B.P.; Montes, H. Evidence for a Linear NMR–Elasticity Interrelationship in Polymeric Gels. Macromolecules 1997, 30, 4374–4380. [Google Scholar] [CrossRef]
- Vieyres, A.; Pérez-Aparicio, R.; Albouy, P.A.; Sanseau, O.; Saalwächter, K.; Long, D.R.; Sotta, P. Sulfur-Cured Natural Rubber Elastomer Networks: Correlating Cross-Link Density, Chain Orientation, and Mechanical Response by Combined Techniques. Macromolecules 2013, 46, 889–899. [Google Scholar] [CrossRef]
- Kameda, T.; Asakura, T. Structure and dynamics in the amorphous region of natural rubber observed under uniaxial deformation monitored with solid-state 13C NMR. Polymer 2003, 44, 7539–7544. [Google Scholar] [CrossRef]
- Valić, S.; Judeinstein, P.; Deloche, B. Analysis of deuterium NMR spectra of probe chains diffusing in a stretched polybutadiene network. Polymer 2003, 44, 5263–5267. [Google Scholar] [CrossRef]
- Valić, S. Orientational motions of chain segments in natural rubber crosslinked under uniaxial deformation. Radiat. Phys. Chem. 2014, 97, 393–397. [Google Scholar] [CrossRef]
- Pérez-Aparicio, R.; Schiewek, M.; Valentín, J.L.; Schneider, H.; Long, D.R.; Saphiannikova, M.; Sotta, P.; Saalwächter, K.; Ott, M. Local Chain Deformation and Overstrain in Reinforced Elastomers: An NMR Study. Macromolecules 2013, 46, 5549–5560. [Google Scholar] [CrossRef]
- Schlögl, S.; Trutschel, M.L.; Chassé, W.; Riess, G.; Saalwächter, K. Entanglement Effects in Elastomers: Macroscopic vs Microscopic Properties. Macromolecules 2014, 47, 2759–2773. [Google Scholar] [CrossRef]
- Ott, M.; Pérez-Aparicio, R.; Schneider, H.; Sotta, P.; Saalwächter, K. Microscopic Study of Chain Deformation and Orientation in Uniaxially Strained Polymer Networks: NMR Results versus Different Network Models. Macromolecules 2014, 47, 7597–7611. [Google Scholar] [CrossRef]
- James, H.M.; Guth, E. Theory of the elasticity of rubber. J. Appl. Phys. 1944, 15, 294–303. [Google Scholar] [CrossRef]
- Heinrich, G.; Straube, E.; Helmis, G. Rubber Elasticity of Polymer Networks: Theories. Adv. Polym. Sci. 1988, 85, 33–87. [Google Scholar]
- Wagner, M. Analysis of Small-Angle Neutron Scattering Data on Poly (dimethylsiloxane) Network Unfolding. Macromolecules 1994, 27, 5223–5226. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Nonaffine Deformation and Elasticity of Polymer Networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- Naumova, A.; Agudelo, D.C.; Villar, M.A.; Vega, D.A.; Valentin, J.L.; Saalwächter, K. Microscopic State of Polymer Network Chains upon Swelling and Deformation. Macromolecules 2019, 52, 5042–5053. [Google Scholar] [CrossRef]
- Toki, S.; Sics, I.; Ran, S.; Liu, L.; Hsiao, B.S.; Murakami, S.; Senoo, K.; Kohjiya, S. New Insights into Structural Development in Natural Rubber during Uniaxial Deformation by In Situ Synchrotron X-ray Diffraction. Macromolecules 2002, 35, 6578–6584. [Google Scholar] [CrossRef]
- Neuefeind, J.; Skov, A.L.; Daniels, J.E.; Honkimaki, V.; Jakobsen, B.; Oddershede, J.; Poulsen, H.F. A multiple length scale description of the mechanism of elastomer stretching. RSC Adv. 2016, 6, 95910–95919. [Google Scholar] [CrossRef] [Green Version]
- Higgins, J.S.; Benoît, H.C. Polymers and Neutron Scattering; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Beltzung, M.; Picot, C.; Herz, J. Investigation of the Chain Conformation in Uniaxially Stretched Poly(dimethylsiloxane) Networks by Small-Angle Neutron Scattering. Macromolecules 1984, 17, 663–669. [Google Scholar] [CrossRef]
- Fernandez, A.M.; Sperling, L.H.; Wignall, G.D. Conformation of polybutadiene in the network state by small-angle neutron scattering. Macromolecules 1986, 19, 2572–2575. [Google Scholar] [CrossRef]
- Straube, E.; Urban, V.; Pyckhout-Hintzen, W.; Richter, D.; Glinka, C.J. Small-Angle Neutron Scattering Investigation of Topological Constraints and Tube Deformation in Networks. Phys. Rev. Lett. 1995, 74, 4464–4467. [Google Scholar] [CrossRef] [PubMed]
- Dossin, L.M.; Graessley, W.W. Rubber Elasticity of Well-Characterized Polybutadiene Networks. Macromolecules 1979, 12, 123–130. [Google Scholar] [CrossRef]
- Subhani, P.M.; Kumar, R.K. A New Stored Energy Function for Rubber Like Materials for Low Strains. Mech. Adv. Mater. Struct. 2009, 16, 402–416. [Google Scholar] [CrossRef]
- Starkova, O.; Aniskevich, A. Poisson’s ratio and the incompressibility relation for various strain measures with the example of a silica-filled SBR rubber in uniaxial tension tests. Polym. Test. 2010, 29, 310–318. [Google Scholar] [CrossRef]
- Tonelli, A.E.; Andrady, A. Molecular estimates of the moduli of tough, elastic networks formed through end-linking of poly(dimethyl siloxane) oligomers. Comput. Theor. Polym. Sci. 1996, 6, 103–108. [Google Scholar]
- Chen, P.; Lin, Y.; Zhao, J.; Meng, L.; Wang, D.; Chen, W.; Li, L. Reconstructing the mechanical response of polybutadiene rubber based on micro-structural evolution in strain-temperature space: Entropic elasticity and strain-induced crystallization as the bridges. Soft Matter 2020, 16, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Svaneborg, C.; Grest, G.S.; Everaers, R. Strain-Dependent Localization, Microscopic Deformations, and Macroscopic Normal Tensions in Model Polymer Networks. Phys. Rev. Lett. 2004, 93, 257801. [Google Scholar] [CrossRef] [PubMed]
- Hsu, H.P.; Kremer, K. Primitive Path Analysis and Stress Distribution in Highly Strained Macromolecules. ACS Macro. Lett. 2018, 7, 107–111. [Google Scholar] [CrossRef] [Green Version]
- Tsolou, G.; Mavrantzas, V.G.; Theodorou, D.N. Detailed Atomistic Molecular Dynamics Simulation of cis-1,4-Poly(butadiene). Macromolecules 2005, 38, 1478–1492. [Google Scholar] [CrossRef]
- Paul, D.R.; DiBenedetto, A.T. Diffusion in Amorphous Polymers. J. Polym. Sci. C Polym. Symp. 1965, 10, 17–44. [Google Scholar] [CrossRef]
- Gee, R.H.; Boyd, R.H. Conformational dynamics and relaxation in bulk polybutadienes: A molecular dynamics simulation study. J. Chem. Phys. 1994, 101, 8028–8038. [Google Scholar] [CrossRef]
- Behbahani, A.F.; Rissanou, A.; Kritikos, G.; Doxastakis, M.; Burkhart, C.; Polińska, P.; Harmandaris, V.A. Conformations and Dynamics of Polymer Chains in Cis and Trans Polybutadiene/Silica Nanocomposites through Atomistic Simulations: From the Unentangled to the Entangled Regime. Macromolecules 2020, 53, 6173–6189. [Google Scholar] [CrossRef]
- Pavlov, A.S.; Khalatur, P.G. Fully atomistic molecular dynamics simulation of nanosilica-filled crosslinked polybutadiene. Chem. Phys. Lett. 2016, 653, 90–95. [Google Scholar] [CrossRef]
- Kempfer, K.; Devémy, J.; Dequidt, A.; Couty, M.; Malfreyt, P. Realistic Coarse-Grain Model of cis-1,4-Polybutadiene: From Chemistry to Rheology. Macromolecules 2019, 52, 2736–2747. [Google Scholar] [CrossRef]
- Behbahani, A.F.; Schneider, L.; Rissanou, A.; Chazirakis, A.; Bačová, P.; Jana, P.K.; Li, W.; Doxastakis, M.; Polińska, P.; Burkhart, C.; et al. Dynamics and Rheology of Polymer Melts via Hierarchical Atomistic, Coarse-Grained, and Slip-Spring Simulations. Macromolecules 2021, 54, 2740–2762. [Google Scholar] [CrossRef]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Wiley Interscience: Hoboken, NJ, USA, 1969. [Google Scholar]
- Mark, J.E. Random-coil configurations of cis-l,4-polybutadiene and cis-1,4-polyisoprene. Theoretical interpretation. J. Am. Chem. Soc. 1966, 88, 4354–4359. [Google Scholar] [CrossRef]
- Mark, J.E. Interpretation of random-coil configurations of trans-1,4-polybutadiene and trans-1,4-polyisoprene. J. Am. Chem. Soc. 1967, 89, 6829–6835. [Google Scholar] [CrossRef]
- Abe, Y.; Flory, P.J. Configurational statistics of 1,4-polybutadiene chains. Macromolecules 1971, 4, 219–229. [Google Scholar] [CrossRef]
- Kajiwara, K.; Burchard, W. Rotational isomeric state calculations of the dynamic structure factor and related properties of some linear chains. 1. The ρ = 〈S2〉1/2〈RH−1〉 parameter. Macromolecules 1984, 17, 2669–2673. [Google Scholar] [CrossRef]
- Kajiwara, K.; Burchard, W. Rotational isomeric state calculations of the dynamic structure factor and related properties of some linear chains. 2. First cumulant of the dynamic structure factor. Macromolecules 1984, 17, 2674–2678. [Google Scholar] [CrossRef]
- Mark, J.E.; Abou-Hussein, R.; Sen, T.Z.; Kloczkowski, A. Some simulations on filler reinforcement in elastomers. Polymer 2005, 46, 8894–8904. [Google Scholar] [CrossRef] [Green Version]
- Kar, S.; Greenfield, M.L. Sizes and shapes of simulated amorphous cis- and trans-1,4-polybutadiene. Polymer 2015, 62, 129–138. [Google Scholar] [CrossRef]
- Kar, S.; Cuddigan, J.; Greenfield, M.L. Origin of Characteristic Ratio Temperature Dependence: Calculations for Polypropylene and Polystyrene. Macromolecules, 2023; in preparation. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Yi, Y.X.; Zoller, P. An experimental and theoretical study of the PVT equation of state of butadiene and isoprene elastomers to 200 °C and 200 MPa. J. Polym. Sci. Part B Polym. Phys. 1993, 31, 779–788. [Google Scholar] [CrossRef]
- Ward, I.M.; Sweeney, J. An Introduction to the Mechanical Properties of Solid Polymers; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Treloar, L.R.G. Stress-strain data for vulcanised rubber under various types of deformation. Trans. Faraday Soc. 1944, 40, 59–70. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity; Oxford University Press: Oxford, UK, 1975. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kar, S.; Cuddigan, J.L.; Greenfield, M.L. Simulating Stress–Strain Behavior by Using Individual Chains: Uniaxial Deformation of Amorphous Cis- and Trans-1,4-Polybutadiene. Polymers 2023, 15, 1441. https://doi.org/10.3390/polym15061441
Kar S, Cuddigan JL, Greenfield ML. Simulating Stress–Strain Behavior by Using Individual Chains: Uniaxial Deformation of Amorphous Cis- and Trans-1,4-Polybutadiene. Polymers. 2023; 15(6):1441. https://doi.org/10.3390/polym15061441
Chicago/Turabian StyleKar, Suvrajyoti, Julie L. Cuddigan, and Michael L. Greenfield. 2023. "Simulating Stress–Strain Behavior by Using Individual Chains: Uniaxial Deformation of Amorphous Cis- and Trans-1,4-Polybutadiene" Polymers 15, no. 6: 1441. https://doi.org/10.3390/polym15061441





