Describing and Modeling Rough Composites Surfaces by Using Topological Data Analysis and Fractional Brownian Motion
Abstract
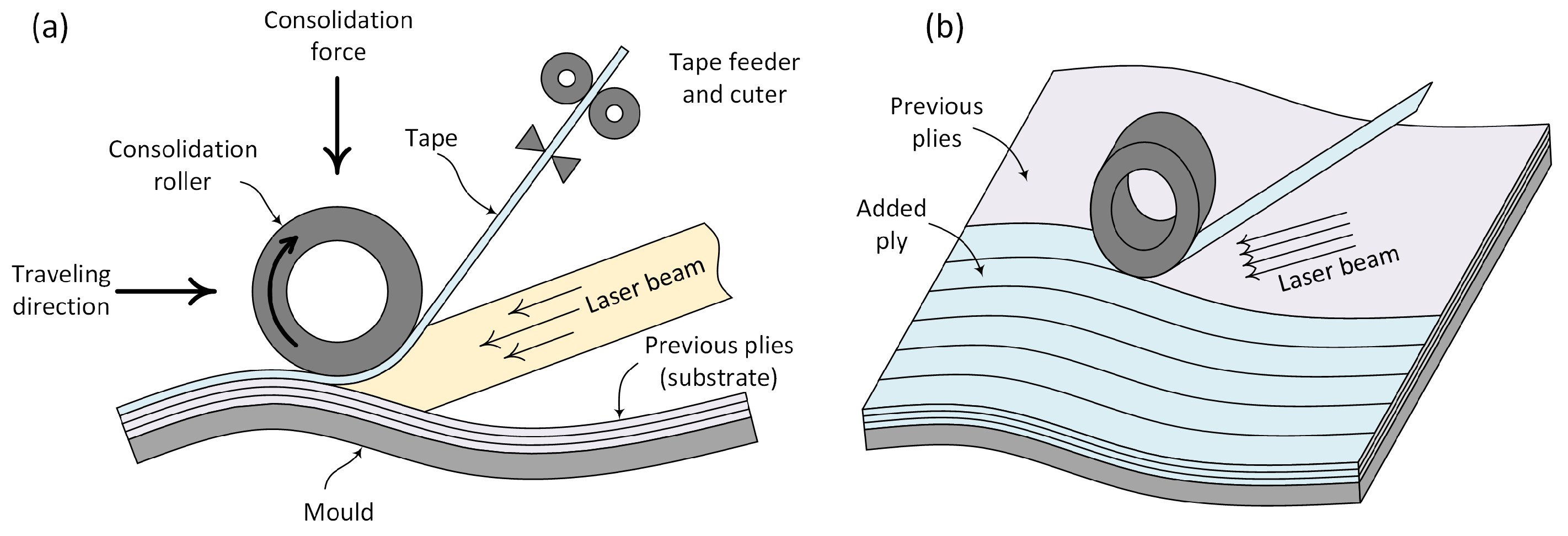
:1. Introduction
1.1. Rough Surface Representation
1.2. Original Contribution and Paper Outline
2. Methods
2.1. Topological Data Analysis
2.2. From Brownian Diffusion to Anomalous Diffusion
2.2.1. Brownian Diffusion
2.2.2. Brownian Motion
2.3. Fractional Brownian Motion
3. Numerical Tests
3.1. Topological Data Analysis
3.2. Fractional Brownian Surfaces
3.3. Hurst Index Evolution during the Surface Compression
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chinesta, F.; Leygue, A.; Bognet, B.; Ghnatios, C.; Poulhaon, F.; Bordeu, F.; Barasinski, A.; Poitou, A.; Chatel, S.; Maison-Le-Poec, S. First steps towards an advanced simulation of composites manufacturing by automated tape placement. Int. J. Mater. Form. 2014, 7, 81–92. [Google Scholar] [CrossRef]
- Boon, Y.D.; Joshi, S.C.; Bhudolia, S.K. Filament Winding and Automated Fiber Placement with In Situ Consolidation for Fiber Reinforced Thermoplastic Polymer Composites. Polymers 2021, 13, 1951. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Liu, W.; Chen, J.; Zhao, D.; Yi, C.; Liu, R.; Geng, Y.; Yang, Y.; Zheng, Y.; Yuan, Y. Research on Void Dynamics during In Situ Consolidation of CF/High-Performance Thermoplastic Composite. Polymers 2022, 14, 1401. [Google Scholar] [CrossRef]
- Pierik, E.R.; Grouve, W.J.B.; Wijskamp, S.; Akkerman, R. Prediction of the peak and steady-state ply-ply friction response for UDC/PAEK tapes. Compos. Part A 2022, 163, 107185. [Google Scholar] [CrossRef]
- Li, C.; Fei, J.; Zhang, T.; Zhao, S.; Qi, L. Relationship between surface characteristics and properties of fiber-reinforced resin-based composites. Compos. Part B Eng. 2023, 249, 110422. [Google Scholar] [CrossRef]
- Rajasekaran, T.; Palanikumar, K.; Latha, B. Investigation and analysis of surface roughness in machining carbon fiber reinforced polymer composites using artificial intelligence techniques. Carbon Lett. 2022, 32, 615–627. [Google Scholar] [CrossRef]
- Leon, A.; Argerich, C.; Barasinski, A.; Soccard, E.; Chinesta, F. Effects of material and process parameters on in-situ consolidation. Int. J. Mater. Form. 2019, 12, 491–503. [Google Scholar] [CrossRef]
- Lee, W.I.; Springer, G.S. A model of the manufacturing process of thermoplastic matrix composites. J. Compos. Mater. 1987, 21, 1057–1082. [Google Scholar]
- Levy, A.; Heider, D.; Tierney, J.; Gillespie, J. Inter-layer thermal contact resistance evolution with the degree of intimate contact in the processing of thermoplastic composite laminates. J. Compos. Mater. 2014, 48, 491–503. [Google Scholar] [CrossRef]
- Borodich, F.; Mosolov, A. Fractal roughness in contact problems. J. Appl. Math. Mech. 1992, 56, 786–795. [Google Scholar] [CrossRef]
- Ganti, S.; Bhushan, B. Generalized fractal analysis and its applications to engineering surfaces. Wear 1995, 180, 17–34. [Google Scholar] [CrossRef]
- Leon, A.; Barasinski, A.; Chinesta, F. Microstructural analysis of pre-impreganted tapes consolidation. Int. J. Mater. Form. 2017, 10, 369–378. [Google Scholar] [CrossRef]
- Majumdar, A.; Tien, C. Fractal Characterization and simulation of rough surfaces. Wear 1990, 136, 313–327. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Passoja, D.; Paullay, A. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Yang, F.; Pitchumani, R. A fractal Cantor set based description of interlaminar contact evolution during thermoplastic composites processing. J. Mater. Sci. 2001, 36, 4661–4671. [Google Scholar] [CrossRef]
- Senin, P. Dynamic Time Warping Algorithm Review; Technical Report; University of Hawaii at Manoa: Honolulu, HI, USA, 2008. [Google Scholar]
- Argerich, C.; Ibáñez, R.; León, A.; Abisset-Chavanne, E.; Chinesta, F. Tape surface characterization and classification in automated tape placement processability: Modeling and numerical analysis. AIMS Mater. Sci. 2018, 5, 870–888. [Google Scholar] [CrossRef]
- Longuet-Higgins, M. Statistical properties of an isotropic random surface. Ser. A-Math. Phys. Sci. 1957, 250, 157–174. [Google Scholar]
- Longuet-Higgins, M. The Statistical Analysis of a Random, moving surface. Ser. A-Math. Phys. Sci. 1957, 249, 321–387. [Google Scholar]
- Sayles, R.; Thomas, T. The spatial representation of surface roughness by means of the structure function: A practical alternative to correlation. Wear 1977, 42, 263–276. [Google Scholar] [CrossRef]
- Yaglom, A. Volume I—Basic Results. In Correlation Theory of Stationary and Related Random Function; Springer: New York, NY, USA, 1987. [Google Scholar]
- Torquato, S. Statistical Description of Microstructures. Annu. Rev. Mater. Res. 2002, 32, 77–111. [Google Scholar] [CrossRef]
- Argerich, C.; Ibanez, R.; Leon, A.; Barasinski, A.; Chinesta, F. Code2vect: An efficient heterogenous data classifier and nonlinear regression technique. C. R. Mécanique 2019, 347, 754–761. [Google Scholar] [CrossRef]
- Carlsson, G.; Zomorodian, A.; Colling, A.; Guibas, L. Persistence Barcodes for Shapes. In Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Nice, France, 8–10 July 2004. [Google Scholar]
- Carlsson, G. Topology and Data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef]
- Chazal, F.; Michel, B. An introduction to Topological Data Analysis: Fundamental and practical aspects for data scientists. arXiv 2017, arXiv:1710.04019. [Google Scholar] [CrossRef]
- Oudot, S.Y. Persistence Theory: From Quiver Representation to Data Analysis; Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2010; Volume 209. [Google Scholar]
- Rabadan, R.; Blumberg, A. Topological Data Analysis For Genomics And Evolution; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Saul, N.; Tralie, C. Scikit-TDA: Topological Data Analysis for Python. 2019. Available online: https://github.com/scikit-tda/scikit-tda (accessed on 12 March 2023).
- Venkatesan, R.; Li, B. Convolutional Neural Networks in Visual Computing: A Concise Guide; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Frahi, T.; Yun, M.; Argerich, C.; Falco, A.; Chinesta, F. Tape Surfaces Characterization with Persistence Images. AIMS Mater. Sci. 2020, 7, 364–380. [Google Scholar] [CrossRef]
- Lee, J.A.; Verleysen, M. Nonlinear Dimensionality Reduction; Springer: New York, NY, USA, 2007. [Google Scholar]
- Yun, M.; Argerich, C.; Cueto, E.; Duval, J.L.; Chinesta, F. Nonlinear regression operating on microstructures described from Topological Data Analysis for the real-time prediction of effective properties. Materials 2020, 13, 2335. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Zemel, R.S. Autoencoders, minimum description length and Helmholtz free energy. In Advances in Neural Information Processing Systems 6 (NISP 1993); Morgan-Kaufmann: Burlington, MA, USA, 1993; pp. 3–10. [Google Scholar]
- Chinesta, F.; Abisset, E. A Journey Around the Different Scales Involved in the Description of Matter and Complex Systems; SpringerBrief: Cham, Germany, 2017. [Google Scholar]
- Bardet, J.M.; Surgailis, D. Measuring the roughness of random paths by increment ratios. Bernoulli 2011, 17, 749–780. [Google Scholar] [CrossRef]
- Gelbaum, Z.; Titus, M. Simulation of Fractional Brownian Surfaces via Spectral Synthesis on Manifolds. arXiv 2013, arXiv:1303.6377v1. [Google Scholar] [CrossRef]
- Kroese, D.P.; Botev, Z.I. Spatial Process Generation. arXiv 2013, arXiv:1308.0399v1. [Google Scholar]
- Rabiei, H.; Coulon, O.; Lefevre, J.; Richard, F. Surface regularity via the estimation of fractional Brownian motion index. IEEE Trans. Image Process. 2020, 30, 1453–1460. [Google Scholar] [CrossRef]
- Stein, M.L. Fast and Exact Simulation of Fractional Brownian Surfaces. J. Comput. Graph. Stat. 2002, 11, 587–599. [Google Scholar] [CrossRef]
- Frahi, T.; Chinesta, F.; Falco, A.; Badias, A.; Cueto, E.; Choi, H.Y.; Han, M.; Duval, J.L. Empowering Advanced Driver-Assistance Systems from Topological Data Analysis. Mathematics 2021, 9, 634. [Google Scholar] [CrossRef]
















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Runacher, A.; Kazemzadeh-Parsi, M.-J.; Di Lorenzo, D.; Champaney, V.; Hascoet, N.; Ammar, A.; Chinesta, F. Describing and Modeling Rough Composites Surfaces by Using Topological Data Analysis and Fractional Brownian Motion. Polymers 2023, 15, 1449. https://doi.org/10.3390/polym15061449
Runacher A, Kazemzadeh-Parsi M-J, Di Lorenzo D, Champaney V, Hascoet N, Ammar A, Chinesta F. Describing and Modeling Rough Composites Surfaces by Using Topological Data Analysis and Fractional Brownian Motion. Polymers. 2023; 15(6):1449. https://doi.org/10.3390/polym15061449
Chicago/Turabian StyleRunacher, Antoine, Mohammad-Javad Kazemzadeh-Parsi, Daniele Di Lorenzo, Victor Champaney, Nicolas Hascoet, Amine Ammar, and Francisco Chinesta. 2023. "Describing and Modeling Rough Composites Surfaces by Using Topological Data Analysis and Fractional Brownian Motion" Polymers 15, no. 6: 1449. https://doi.org/10.3390/polym15061449
APA StyleRunacher, A., Kazemzadeh-Parsi, M.-J., Di Lorenzo, D., Champaney, V., Hascoet, N., Ammar, A., & Chinesta, F. (2023). Describing and Modeling Rough Composites Surfaces by Using Topological Data Analysis and Fractional Brownian Motion. Polymers, 15(6), 1449. https://doi.org/10.3390/polym15061449









