Prediction Accuracy of Hyperelastic Material Models for Rubber Bumper under Compressive Load
Abstract
:1. Introduction
2. Hyperelasticity
2.1. Hyperelastic Material Models
2.1.1. Mooney-Rivlin Model
2.1.2. Yeoh Model
2.1.3. Gent Model
2.1.4. Ogden Model
2.1.5. Arruda-Boyce Model
2.2. Modelling the Volumetric Strain Energy Density Function
2.3. Drucker’s Stability
3. Calibration of Hyperelastic Material Model
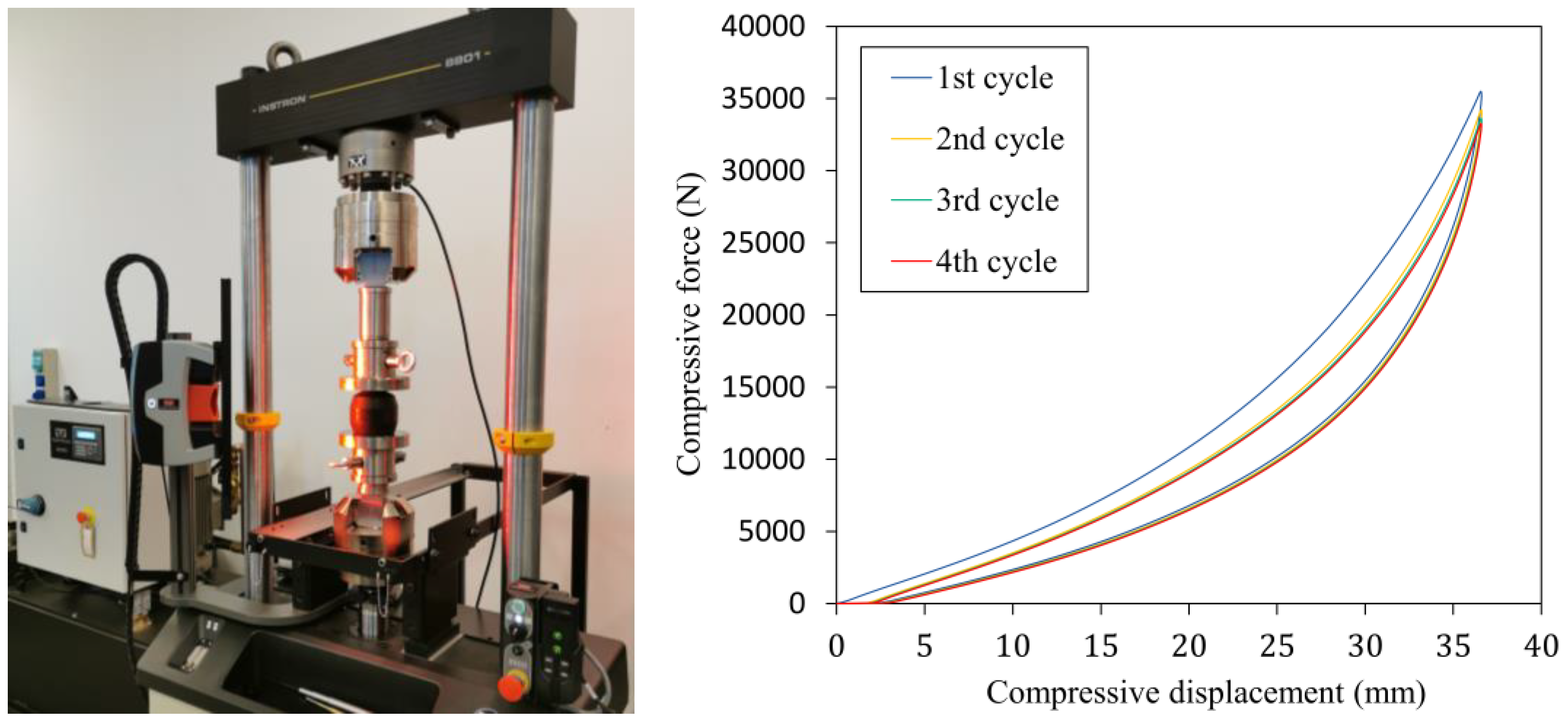
3.1. Compression Test of the Rubber Bumper
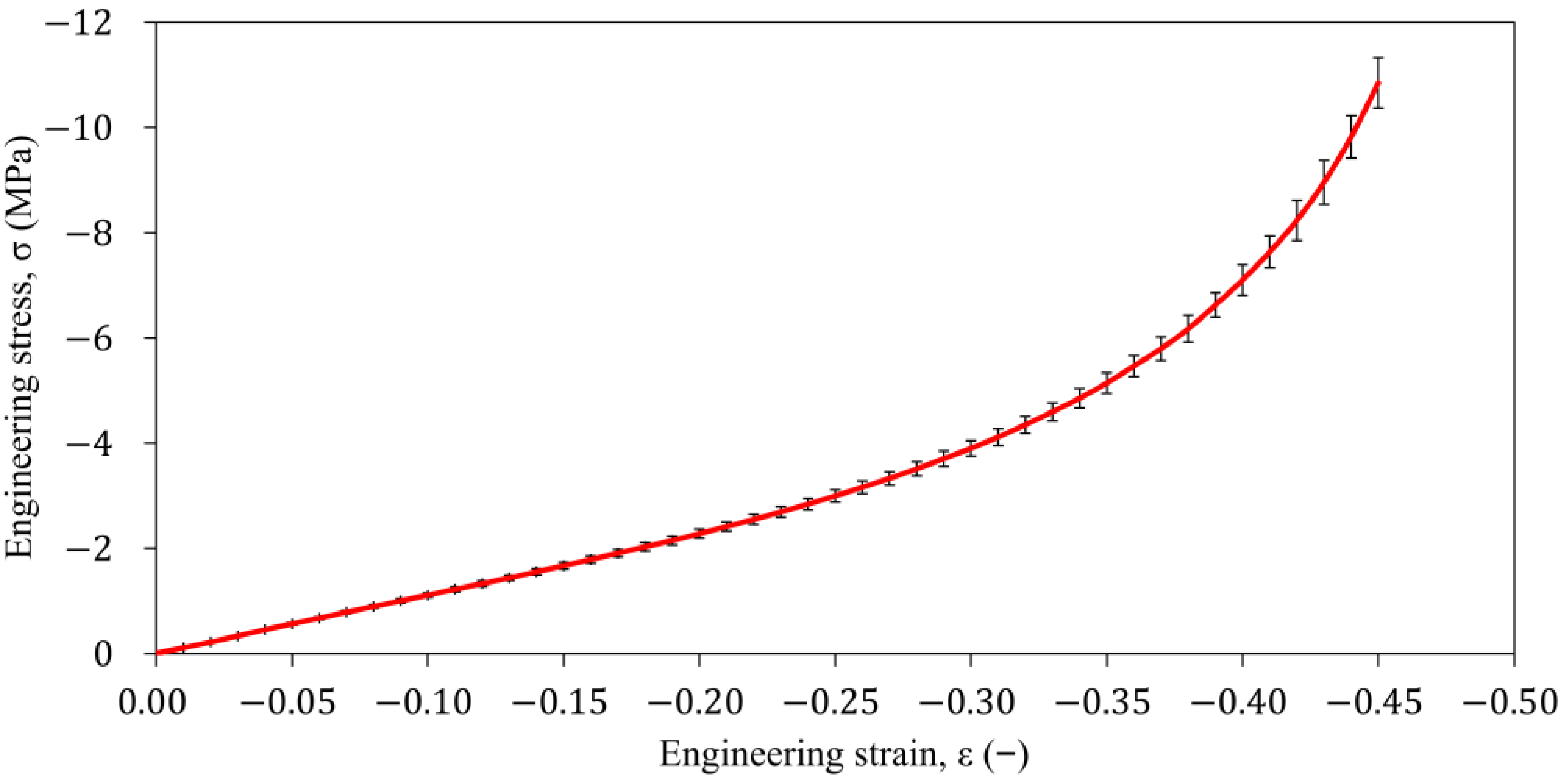
3.2. Compressive Stress-Strain Characteristics of the Rubber
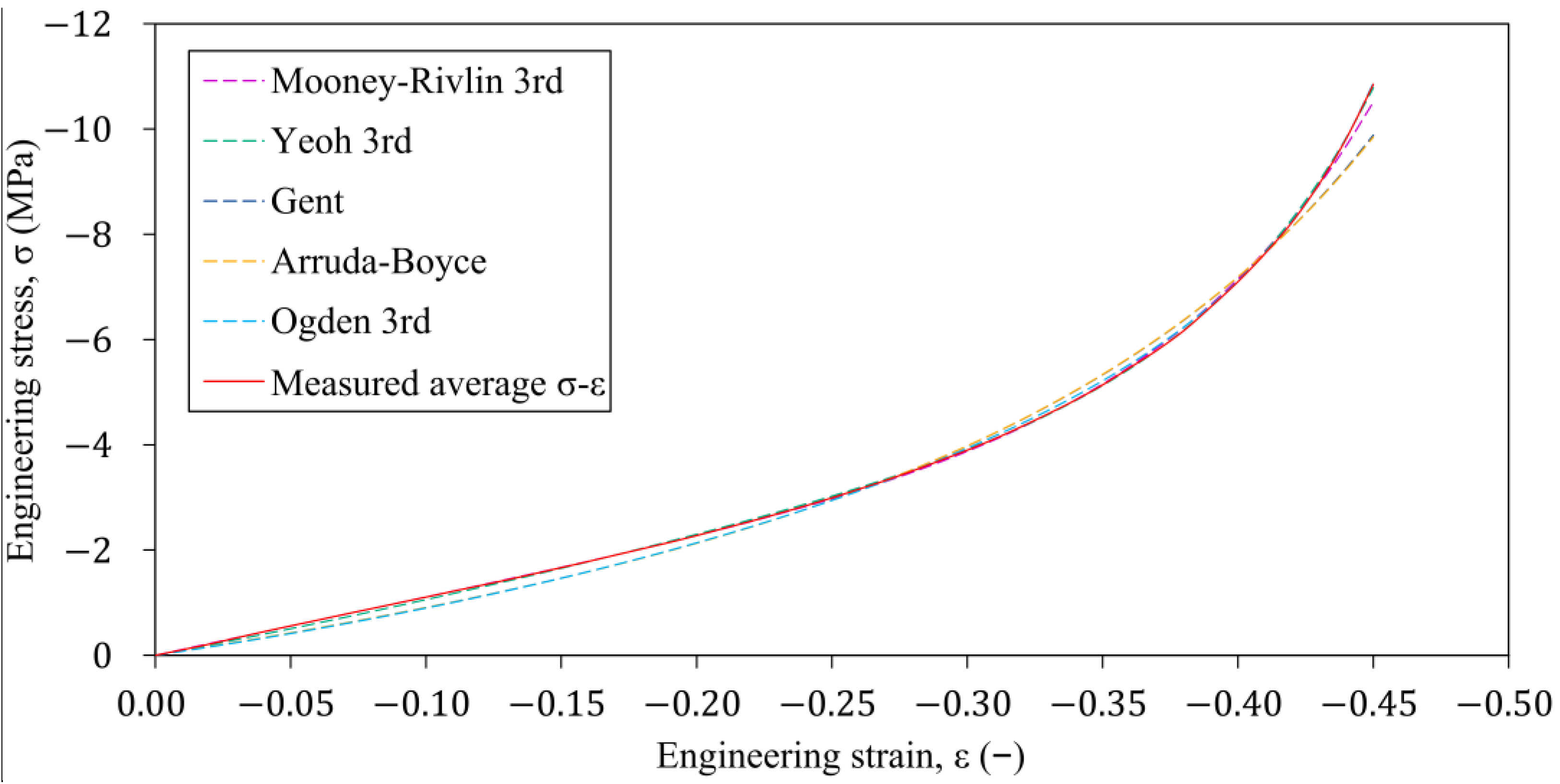
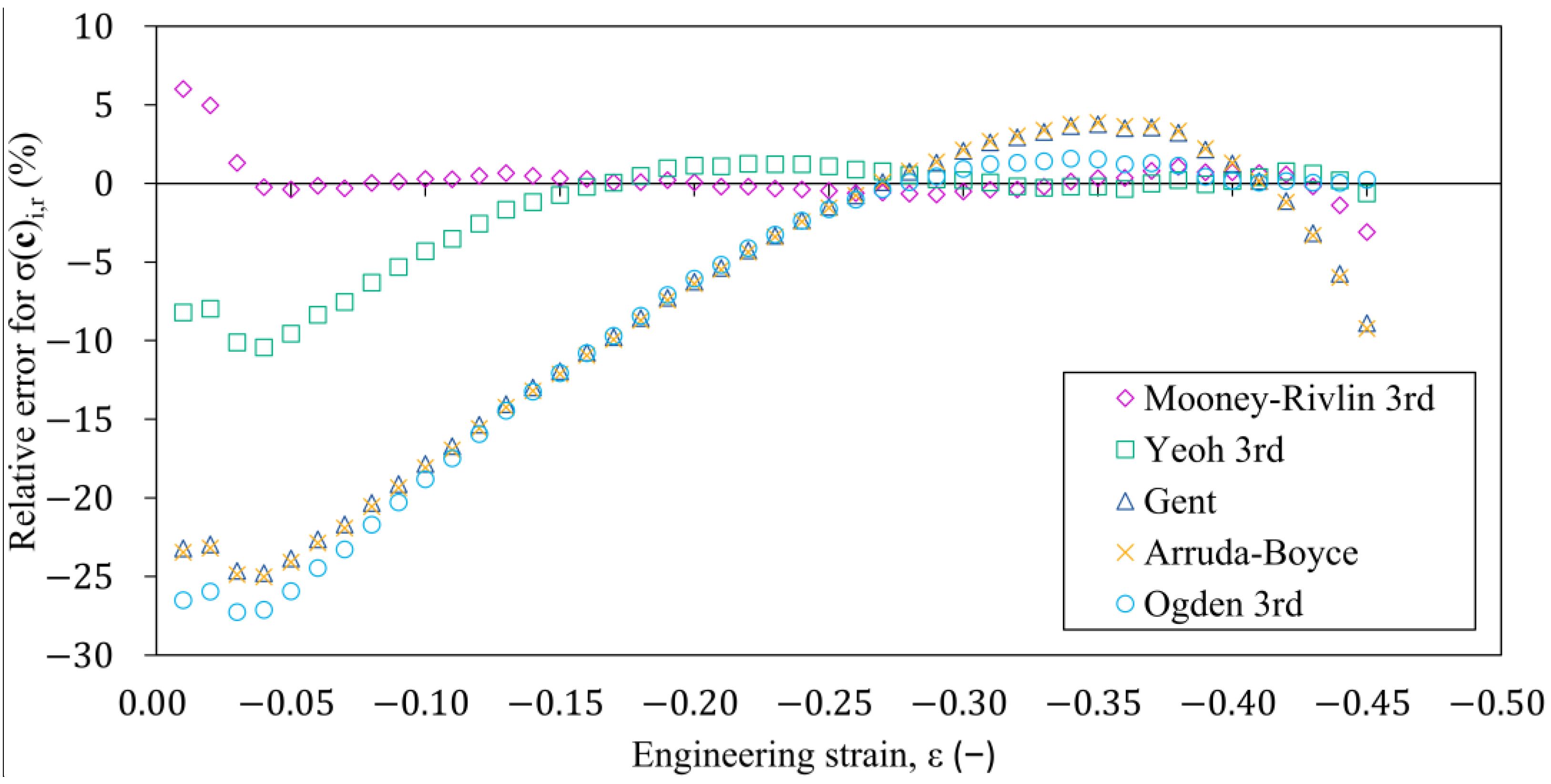
3.3. Fitting the Material Parameters of the Phenomenological Hyperelastic Models Describing the Deviatoric Strain Energy Density Function
3.4. Verification of Material Models Using the Finite Element Model of the Compression Test
4. Verification of Material Models Using the Finite Element Model of the Rubber Bumper Compression Test
5. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| No.1 | No.2 | No.3 | No.4 | Average | Median | Standard Deviation | |
|---|---|---|---|---|---|---|---|
| −0.01 | −0.11 | −0.10 | −0.11 | −0.11 | −0.106 | −0.107 | 0.004 |
| −0.02 | −0.22 | −0.21 | −0.22 | −0.21 | −0.214 | −0.214 | 0.006 |
| −0.03 | −0.35 | −0.33 | −0.32 | −0.32 | −0.332 | −0.329 | 0.013 |
| −0.04 | −0.47 | −0.45 | −0.44 | −0.43 | −0.448 | −0.443 | 0.018 |
| −0.05 | −0.59 | −0.56 | −0.55 | −0.54 | −0.560 | −0.556 | 0.023 |
| −0.06 | −0.71 | −0.67 | −0.66 | −0.64 | −0.670 | −0.665 | 0.030 |
| −0.07 | −0.82 | −0.78 | −0.77 | −0.75 | −0.781 | −0.775 | 0.030 |
| −0.08 | −0.94 | −0.89 | −0.87 | −0.86 | −0.889 | −0.881 | 0.036 |
| −0.09 | −1.05 | −1.01 | −0.98 | −0.96 | −0.998 | −0.992 | 0.041 |
| −0.10 | −1.17 | −1.11 | −1.08 | −1.07 | −1.107 | −1.096 | 0.044 |
| −0.11 | −1.29 | −1.22 | −1.19 | −1.17 | −1.218 | −1.205 | 0.051 |
| −0.12 | −1.40 | −1.33 | −1.30 | −1.27 | −1.326 | −1.313 | 0.056 |
| −0.13 | −1.51 | −1.44 | −1.41 | −1.39 | −1.435 | −1.423 | 0.052 |
| −0.14 | −1.63 | −1.56 | −1.52 | −1.50 | −1.550 | −1.539 | 0.059 |
| −0.15 | −1.76 | −1.67 | −1.64 | −1.60 | −1.667 | −1.653 | 0.067 |
| −0.16 | −1.87 | −1.80 | −1.75 | −1.72 | −1.784 | −1.773 | 0.069 |
| −0.17 | −2.00 | −1.91 | −1.88 | −1.83 | −1.906 | −1.893 | 0.071 |
| −0.18 | −2.14 | −2.03 | −1.99 | −1.95 | −2.026 | −2.008 | 0.081 |
| −0.19 | −2.26 | −2.15 | −2.12 | −2.06 | −2.147 | −2.134 | 0.083 |
| −0.20 | −2.39 | −2.28 | −2.23 | −2.20 | −2.276 | −2.258 | 0.085 |
| −0.21 | −2.53 | −2.42 | −2.37 | −2.33 | −2.412 | −2.396 | 0.088 |
| −0.22 | −2.68 | −2.55 | −2.50 | −2.45 | −2.547 | −2.528 | 0.098 |
| −0.23 | −2.82 | −2.70 | −2.65 | −2.59 | −2.691 | −2.675 | 0.099 |
| −0.24 | −2.98 | −2.85 | −2.79 | −2.73 | −2.838 | −2.822 | 0.108 |
| −0.25 | −3.15 | −3.00 | −2.95 | −2.88 | −2.994 | −2.976 | 0.115 |
| −0.26 | −3.32 | −3.18 | −3.10 | −3.03 | −3.159 | −3.140 | 0.122 |
| −0.27 | −3.50 | −3.33 | −3.29 | −3.19 | −3.327 | −3.309 | 0.128 |
| −0.28 | −3.68 | −3.53 | −3.46 | −3.36 | −3.509 | −3.495 | 0.135 |
| −0.29 | −3.89 | −3.72 | −3.66 | −3.54 | −3.703 | −3.689 | 0.145 |
| −0.30 | −4.09 | −3.91 | −3.86 | −3.74 | −3.899 | −3.882 | 0.147 |
| −0.31 | −4.33 | −4.13 | −4.06 | −3.94 | −4.113 | −4.091 | 0.163 |
| −0.32 | −4.56 | −4.37 | −4.29 | −4.17 | −4.347 | −4.329 | 0.162 |
| −0.33 | −4.81 | −4.62 | −4.53 | −4.41 | −4.593 | −4.577 | 0.170 |
| −0.34 | −5.09 | −4.88 | −4.78 | −4.65 | −4.852 | −4.834 | 0.184 |
| −0.35 | −5.38 | −5.17 | −5.09 | −4.92 | −5.140 | −5.130 | 0.194 |
| −0.36 | −5.72 | −5.50 | −5.41 | −5.23 | −5.464 | −5.453 | 0.200 |
| −0.37 | −6.09 | −5.82 | −5.72 | −5.54 | −5.795 | −5.773 | 0.227 |
| −0.38 | −6.48 | −6.23 | −6.11 | −5.87 | −6.171 | −6.169 | 0.255 |
| −0.39 | −6.89 | −6.68 | −6.59 | −6.33 | −6.624 | −6.635 | 0.234 |
| −0.40 | −7.43 | −7.18 | −7.07 | −6.73 | −7.101 | −7.126 | 0.291 |
| −0.41 | −7.95 | −7.75 | −7.61 | −7.24 | −7.635 | −7.679 | 0.301 |
| −0.42 | −8.66 | −8.37 | −8.15 | −7.76 | −8.234 | −8.258 | 0.382 |
| −0.43 | −9.39 | −9.17 | −8.85 | −8.43 | −8.959 | −9.007 | 0.419 |
| −0.44 | −10.17 | −10.08 | −9.76 | −9.27 | −9.820 | −9.920 | 0.402 |
| −0.45 | −11.19 | −11.21 | −10.82 | −10.18 | −10.851 | −11.006 | 0.480 |
Appendix B

References
- Palička, P.; Huňady, R.; Hagara, M.; Lengvarský, P. Optimization of Apex Shape for Mounting to the Bead Bundle Using FEM. Materials 2022, 16, 377. [Google Scholar] [CrossRef] [PubMed]
- Kudelin, D.V.; Nesiolovskaia, T.N. Application of the Finite Element Analysis in the Design of Rubber Membranes. AIP Conf. Proc. 2022; 2486, 030005. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; Cheng, Y.; Liu, J. A Time-Dependent Yeoh Model to Predict the Corrosion Effect of Supercritical CO2 on the HNBR Sealing Rubber. J. Mech. Sci. Technol. 2022, 36, 2461–2470. [Google Scholar] [CrossRef]
- Cernuda, C.; Llavori, I.; Zavoianu, A.-C.; Aguirre, A.; Zabala, A.; Plaza, J. Critical Analysis of the Suitability of Surrogate Models for Finite Element Method Application in Catalog-Based Suspension Bushing Design. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; pp. 829–836. [Google Scholar]
- Premarathna, W.A.A.S.; Jayasinghe, J.A.S.C.; Wijesundara, K.K.; Gamage, P.; Ranatunga, R.R.M.S.K.; Senanayake, C.D. Investigation of Design and Performance Improvements on Solid Resilient Tires through Numerical Simulation. Eng. Fail. Anal. 2021, 128, 105618. [Google Scholar] [CrossRef]
- Zheng, C.; Zheng, X.; Qin, J.; Liu, P.; Aibaibu, A.; Liu, Y. Nonlinear Finite Element Analysis on the Sealing Performance of Rubber Packer for Hydraulic Fracturing. J. Nat. Gas Sci. Eng. 2021, 85, 103711. [Google Scholar] [CrossRef]
- Dong, L.; Tang, Y.; Tang, G.; Li, H.; Wu, K.; Luo, W. Sealing Performance Analysis of Rubber Core of Annular BOP: FEM Simulation and Optimization to Prevent the SBZ. Petroleum 2021. [CrossRef]
- Szántó, A.; Hajdu, S.; Sziki, G.Á. Optimizing Parameters for an Electrical Car Employing Vehicle Dynamics Simulation Program. Appl. Sci. 2023, 13, 8897. [Google Scholar] [CrossRef]
- Wu, J.; He, Y.; Wu, K.; Dai, M.; Xia, C. The Performance Optimization of the Stripper Rubber for the Rotating Blowout Preventer Based on Experiments and Simulation. J. Pet. Sci. Eng. 2021, 204, 108623. [Google Scholar] [CrossRef]
- Hejazi, F.; Farahpour, H.; Ayyash, N.; Chong, T. Development of a Volumetric Compression Restrainer for Structures Subjected to Vibration. J. Build. Eng. 2022, 46, 103735. [Google Scholar] [CrossRef]
- Mankovits, T.; Szabo, T.; Kocsis, I.; Paczelt, I. Optimization of the Shape of Axi-Symmetric Rubber Bumpers. Stroj. Vestnik/Journal Mech. Eng. 2014, 60, 61–71. [Google Scholar] [CrossRef]
- Mankovits, T.; Szabó, T. Finite Element Analysis of Rubber Bumper Used in Air-Springs. Procedia Eng. 2012, 48, 388–395. [Google Scholar] [CrossRef]
- Mankovits, T.; Kocsis, I.; Portik, T.; Szabó, T.; Páczelt, I. Shape Design of Rubber Part Using FEM. Int. Rev. Appl. Sci. Eng. 2013, 4, 85–94. [Google Scholar] [CrossRef]
- Kaya, N. Shape Optimization of Rubber Bushing Using Differential Evolution Algorithm. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Somanath, S.; Marimuthu, R.; Krishnapillai, S.; Narayanan, S. Transient Vibration Response Study of Moulded and Pre-Stressed Silicone Elastomer Vibration Isolators. Int. J. Dyn. Control 2023. [CrossRef]
- Bonet, J.; Wood, R.D. Nonlinear Continuum Mechanics for Finite Element Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008; ISBN 978−0−511−39468−3. [Google Scholar]
- Kozák, I. Kontinuummechanika; Miskolci Egyetemi Kiadó: Miskolc, Hungary, 1995. [Google Scholar]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers; John Wiley & Sons, Ltd.: Chichester, UK, 2012; Volume 1, ISBN 9781119967125. [Google Scholar]
- Rivlin, R.S. Large Elastic Deformations of Isotropic Materials. I. Fundamental Concepts. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1948, 240, 459–490. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Ogden, R.W.; A, P.R.S.L. Large Deformation Isotropic Elasticity – on the Correlation of Theory and Experiment for Incompressible Rubberlike Solids. Proc. R. Soc. Lond. A. Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A Three-Dimensional Constitutive Model for the Large Stretch Behavior of Rubber Elastic Materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Gent, A.N. A New Constitutive Relation for Rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Bergström, J. Mechanics of Solid Polymers; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 9780323311502. [Google Scholar]
- El Yaagoubi, M.; Fulari, G.S.; Aloui, S.; Shetty, R.R. Influence of Permanent Deformation on the Fitting Quality and the Simulation Prediction of Filled Elastomers. Int. J. Non. Linear. Mech. 2021, 137, 103801. [Google Scholar] [CrossRef]
- Aloui, S.; El Yaagoubi, M. Determining the Compression-Equivalent Deformation of SBR-Based Rubber Material Measured in Tensile Mode Using the Finite Element Method. Appl. Mech. 2021, 2, 195–208. [Google Scholar] [CrossRef]
- Treloar, L.R.G. Stress-Strain Data for Vulcanized Rubber under Various Types of Deformation. Rubber Chem. Technol. 1944, 17, 813–825. [Google Scholar] [CrossRef]
- Steinmann, P.; Hossain, M.; Possart, G. Hyperelastic Models for Rubber-like Materials: Consistent Tangent Operators and Suitability for Treloar’s Data. Arch. Appl. Mech. 2012, 82, 1183–1217. [Google Scholar] [CrossRef]
- Hossain, M.; Steinmann, P. More Hyperelastic Models for Rubber-like Materials: Consistent Tangent Operators and Comparative Study. J. Mech. Behav. Mater. 2013, 22, 27–50. [Google Scholar] [CrossRef]
- Marckmann, G.; Verron, E. Comparison of Hyperelastic Models for Rubber-Like Materials. Rubber Chem. Technol. 2006, 79, 835–858. [Google Scholar] [CrossRef]
- Dal, H.; Açıkgöz, K.; Badienia, Y. On the Performance of Isotropic Hyperelastic Constitutive Models for Rubber-Like Materials: A State of the Art Review. Appl. Mech. Rev. 2021, 73. [Google Scholar] [CrossRef]
- Melly, S.K.; Liu, L.; Liu, Y.; Leng, J. A Review on Material Models for Isotropic Hyperelasticity. Int. J. Mech. Syst. Dyn. 2021, 1, 71–88. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Zhang, Y.; Chen, J.; Zhang, L.; Li, F. A Comparative Study of 85 Hyperelastic Constitutive Models for Both Unfilled Rubber and Highly Filled Rubber Nanocomposite Material. Nano Mater. Sci. 2022, 4, 64–82. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. New Numerical Stress Solutions to Calibrate Hyper-Visco-Pseudo-Elastic Material Models Effectively. Mater. Des. 2020, 194. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. Constitutive Modelling of Rubbers: Mullins Effect, Residual Strain, Time-Temperature Dependence. Int. J. Mech. Sci. 2021, 210, 106735. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. Closed-Form and Numerical Stress Solution-Based Parameter Identification for Incompressible Hyper-Viscoelastic Solids Subjected to Various Loading Modes. Int. J. Mech. Sci. 2019, 151, 650–660. [Google Scholar] [CrossRef]
- Fazekas, B.; Burkhart, C.; Staub, S.; Thielen, S.; Andrä, H.; Goda, T.J.; Sauer, B.; Koch, O. Radial Shaft Seals: How Ageing in Oil and Hyper-Viscoelasticity Affect the Radial Force and the Numerically Predicted Wear. Tribol. Int. 2023, 186, 108601. [Google Scholar] [CrossRef]
- Zhao, Z.; Mu, X.; Du, F. Modeling and Verification of a New Hyperelastic Model for Rubber-Like Materials. Math. Probl. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Guo, L.; Zeng, Y.; Huang, J.; Wang, Z.; Li, J.; Han, X.; Xia, C.; Qian, L. Fatigue Optimization of Rotary Control Head Rubber Core Based on Steady Sealing. Eng. Fail. Anal. 2022, 132, 105935. [Google Scholar] [CrossRef]
- Nguyen, H.-D.; Huang, S.-C. The Uniaxial Stress–Strain Relationship of Hyperelastic Material Models of Rubber Cracks in the Platens of Papermaking Machines Based on Nonlinear Strain and Stress Measurements with the Finite Element Method. Materials 2021, 14, 7534. [Google Scholar] [CrossRef]
- Íñiguez-Macedo, S.; Lostado-Lorza, R.; Escribano-García, R.; Martínez-Calvo, M. Finite Element Model Updating Combined with Multi-Response Optimization for Hyper-Elastic Materials Characterization. Materials 2019, 12, 1019. [Google Scholar] [CrossRef] [PubMed]
- Lei, G.; Chen, Q.; Liu, Y.; Jiang, J. An Inverse Method to Reconstruct Complete Stiffness Information of Rubber Bushing. Adv. Mater. Sci. Eng. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Yenigun, B.; Gkouti, E.; Barbaraci, G.; Czekanski, A. Identification of Hyperelastic Material Parameters of Elastomers by Reverse Engineering Approach. Materials 2022, 15, 8810. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. Numerical Stress Solutions for the Accurate Calibration of Hyper-Viscoelastic Material Models of Polymer Foams. Int. J. Solids Struct. 2020; 191–192, 390–400. [Google Scholar] [CrossRef]
- Fazekas, B.; Goda, T.J. Determination of the Hyper-Viscoelastic Model Parameters of Open-Cell Polymer Foams and Rubber-like Materials with High Accuracy. Mater. Des. 2018, 156, 596–608. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics, A Continuum Approach for Engineering; John Wiley and Sons Ltd.: Chichester, UK, 2000; ISBN 047182304X. [Google Scholar]
- Valanis, K.C.; Landel, R.F. The Strain-Energy Function of a Hyperelastic Material in Terms of the Extension Ratios. J. Appl. Phys. 1967, 38, 2997–3002. [Google Scholar] [CrossRef]
- Kaliske, M.; Rothert, H. On the Finite Element Implementation of Rubber-like Materials at Finite Strains. Eng. Comput. 1997, 14, 216–232. [Google Scholar] [CrossRef]
- Kawabata, S.; Yamashita, Y.; Ooyama, H.; Yoshida, S. Mechanism of Carbon-Black Reinforcement of Rubber Vulcanizate. Rubber Chem. Technol. 1995, 68, 311–329. [Google Scholar] [CrossRef]
- Horgan, C.O.; Murphy, J.G. On the Volumetric Part of Strain-Energy Functions Used in the Constitutive Modeling of Slightly Compressible Solid Rubbers. Int. J. Solids Struct. 2009, 46, 3078–3085. [Google Scholar] [CrossRef]
- Huri, D. Incompressibility and Mesh Sensitivity Analysis in Finite Element Simulation of Rubbers. Int. Rev. Appl. Sci. Eng. 2016, 7, 7–12. [Google Scholar] [CrossRef]
- Drucker, D.C. A Definition of a Stable Inelastic Material. J. Appl. Mech. 1959, 26, 101–195. [Google Scholar] [CrossRef]
- Hill, R. A General Theory of Uniqueness and Stability in Elastic-Plastic Solids. J. Mech. Phys. Solids 1958, 6, 236–249. [Google Scholar] [CrossRef]







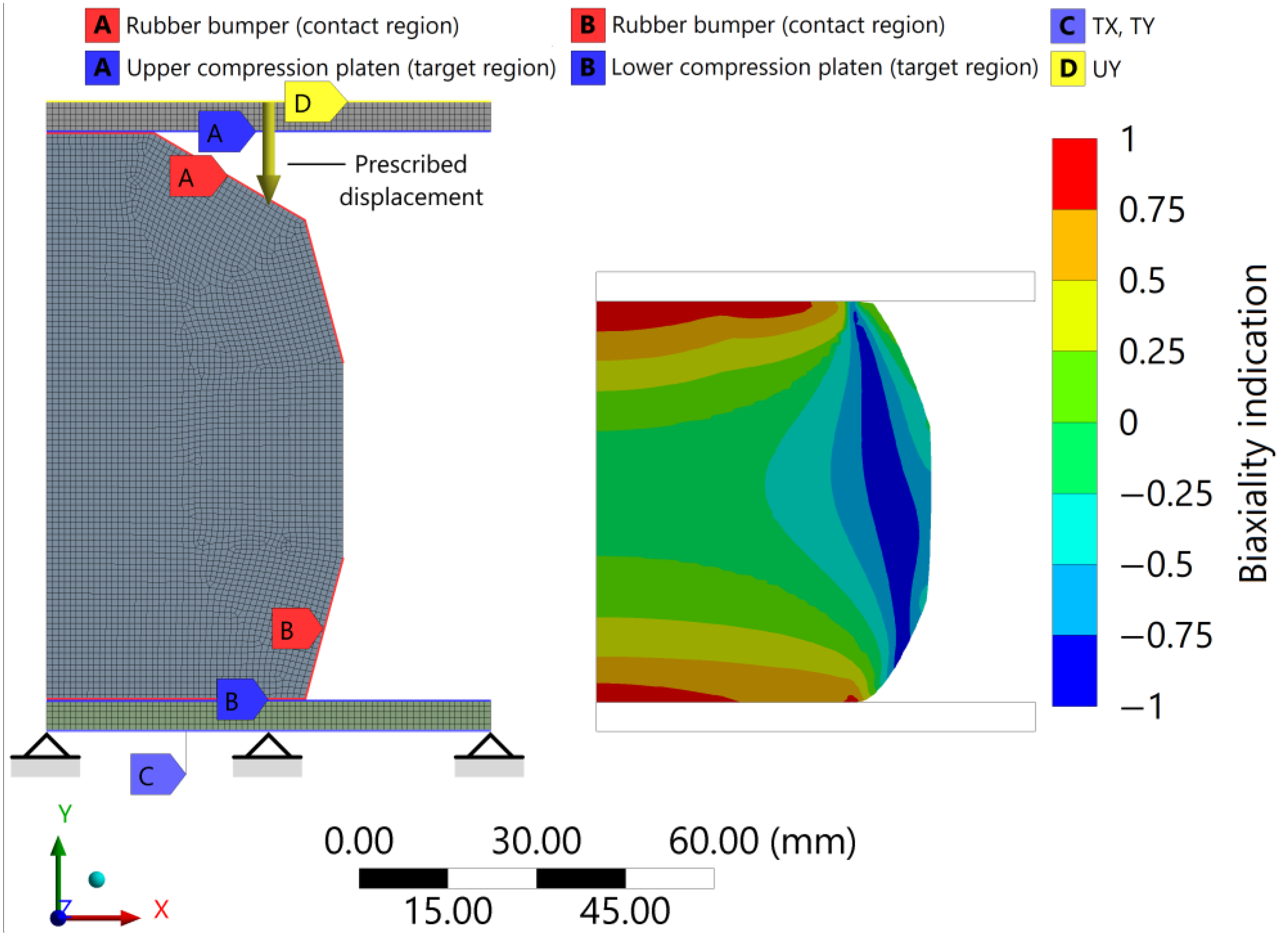
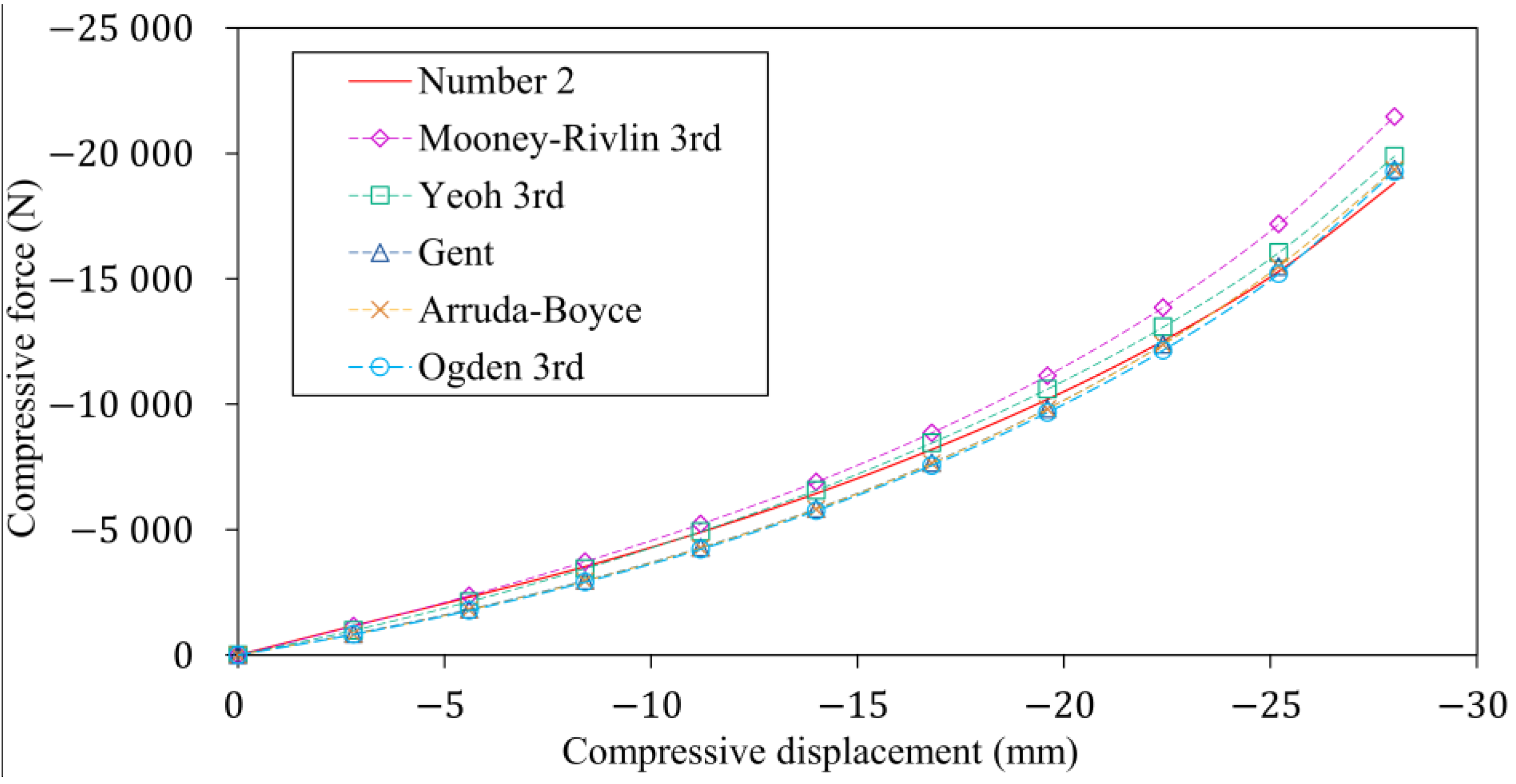
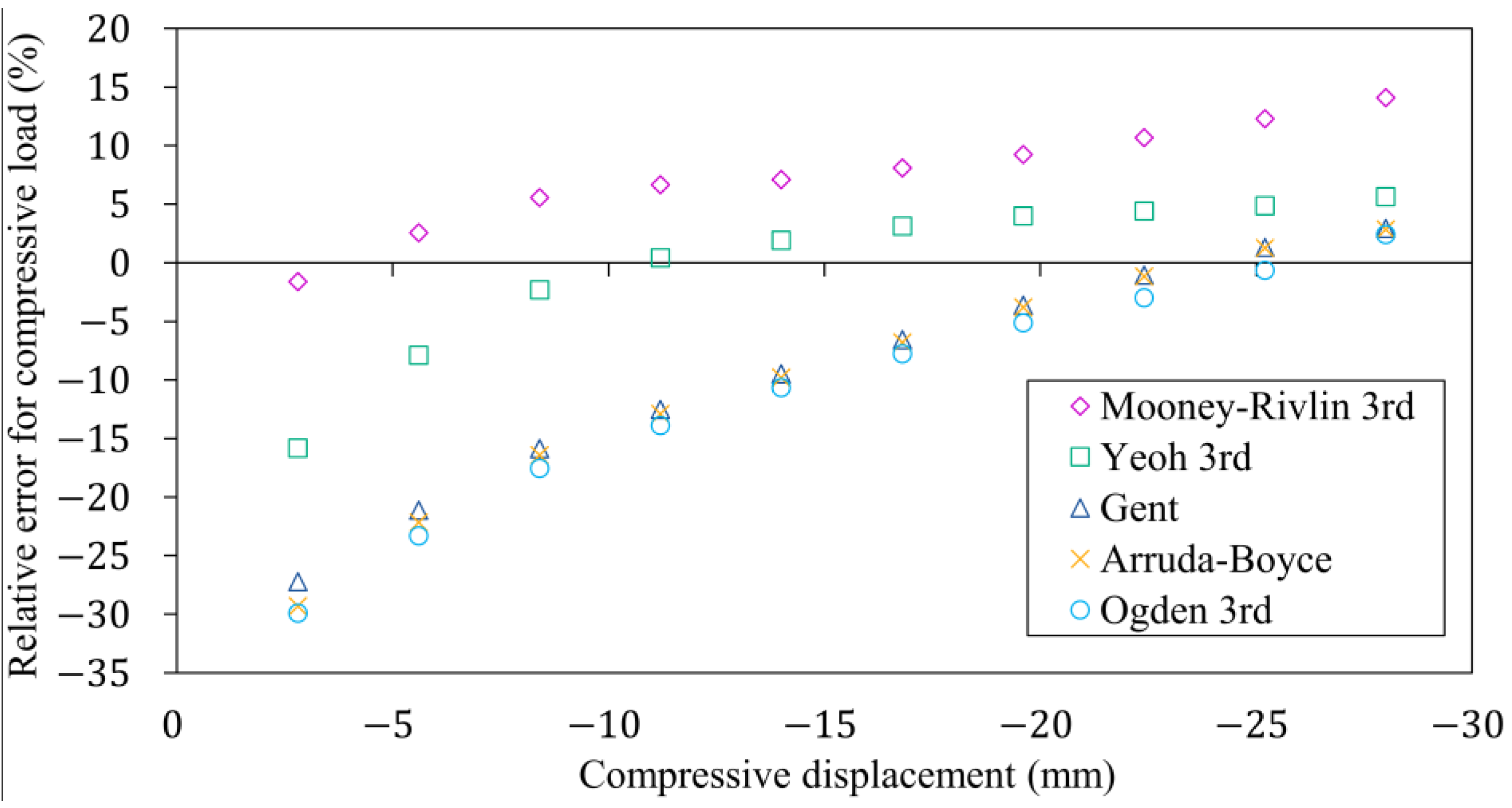
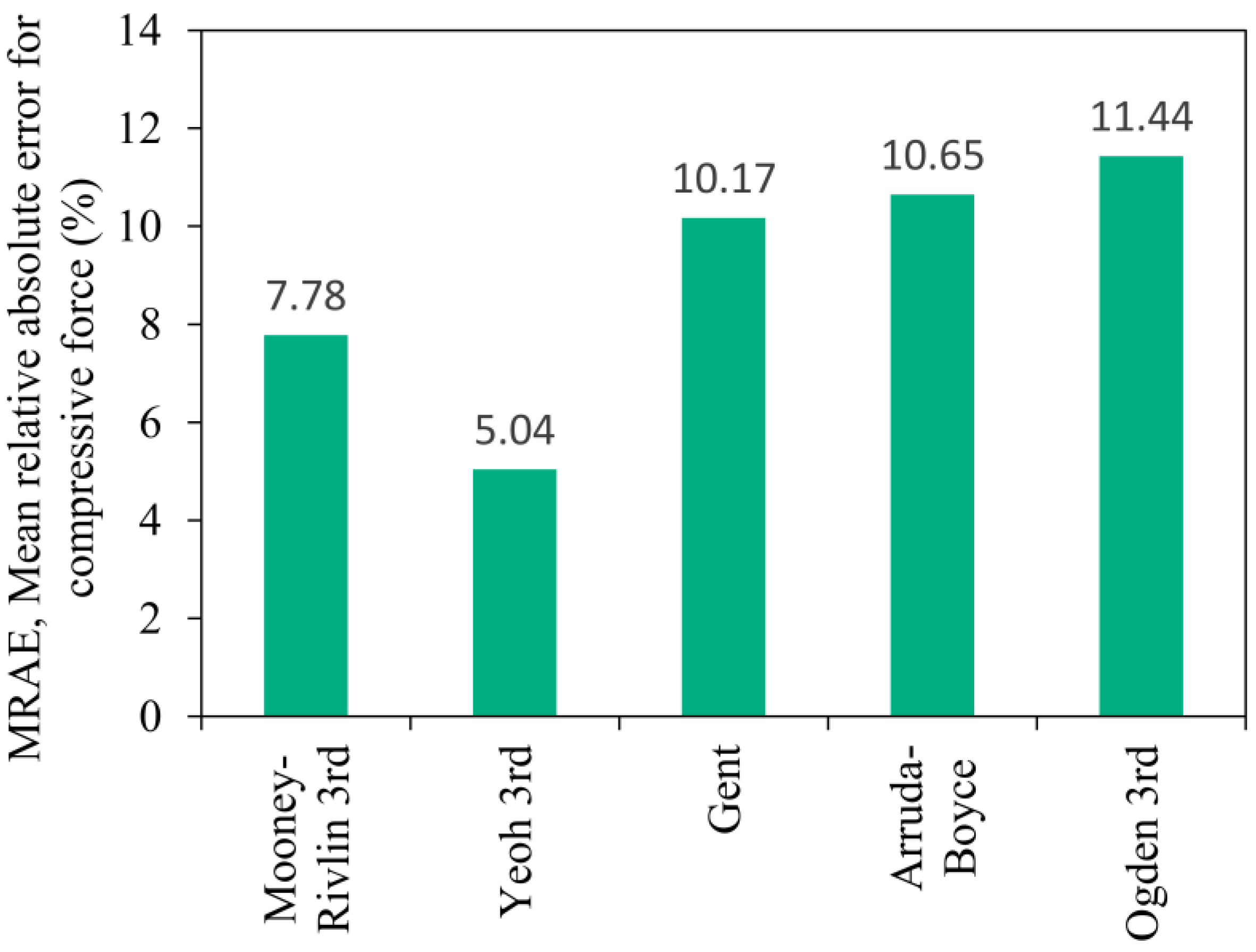
| Mode of Load | Range of Strain |
|---|---|
| Uniaxial compression-tension | |
| Pure shear | |
| Biaxial compression-tension | |
| Simple shear | |
| Volumetric compression-tension |
| Temperature and Relative Humidity of the Test | 25 (°C); 50% |
|---|---|
| The number, magnitude and speed of the preload cycles | 3 cycles; 35 mm; 50 (mm∙min−1) |
| The number, magnitude and speed of the measured cycle | 4th cycle; 35 (mm); 50 (mm∙min−1) |
| Test setup | Polished compression platen without lubrication |
| Temperature and Relative Humidity of the Test | 25 (°C); 50% |
|---|---|
| The number, magnitude and speed of the preload cycles | 3 cycles; 6.4 (mm); 6.76 (mm∙min−1) |
| The number, magnitude and speed of the measured cycle | 4th cycle; 6.4 (mm); 6.76 (mm∙min−1) |
| Test setup | Polished and lubricated compression platens |
| Hyperelastic Model | Material Parameters | Drucker’s Stability | |
|---|---|---|---|
| Mooney-Rivlin 3rd | stable | ||
| Yeoh 3rd | stable | ||
| Gent | stable | ||
| Arruda-Boyce | stable | ||
| Ogden 3rd | not stable for biaxial compression | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huri, D. Prediction Accuracy of Hyperelastic Material Models for Rubber Bumper under Compressive Load. Polymers 2024, 16, 2534. https://doi.org/10.3390/polym16172534
Huri D. Prediction Accuracy of Hyperelastic Material Models for Rubber Bumper under Compressive Load. Polymers. 2024; 16(17):2534. https://doi.org/10.3390/polym16172534
Chicago/Turabian StyleHuri, Dávid. 2024. "Prediction Accuracy of Hyperelastic Material Models for Rubber Bumper under Compressive Load" Polymers 16, no. 17: 2534. https://doi.org/10.3390/polym16172534
APA StyleHuri, D. (2024). Prediction Accuracy of Hyperelastic Material Models for Rubber Bumper under Compressive Load. Polymers, 16(17), 2534. https://doi.org/10.3390/polym16172534






