Evaluation of the Flexural Behavior of One-Way Slabs by the Amount of Carbon Grid Manufactured by Adhesive Bonding
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.1.1. Material Properties
2.1.2. Specimen Overview
2.2. Loading and Measurement Method
3. Results and Discussion
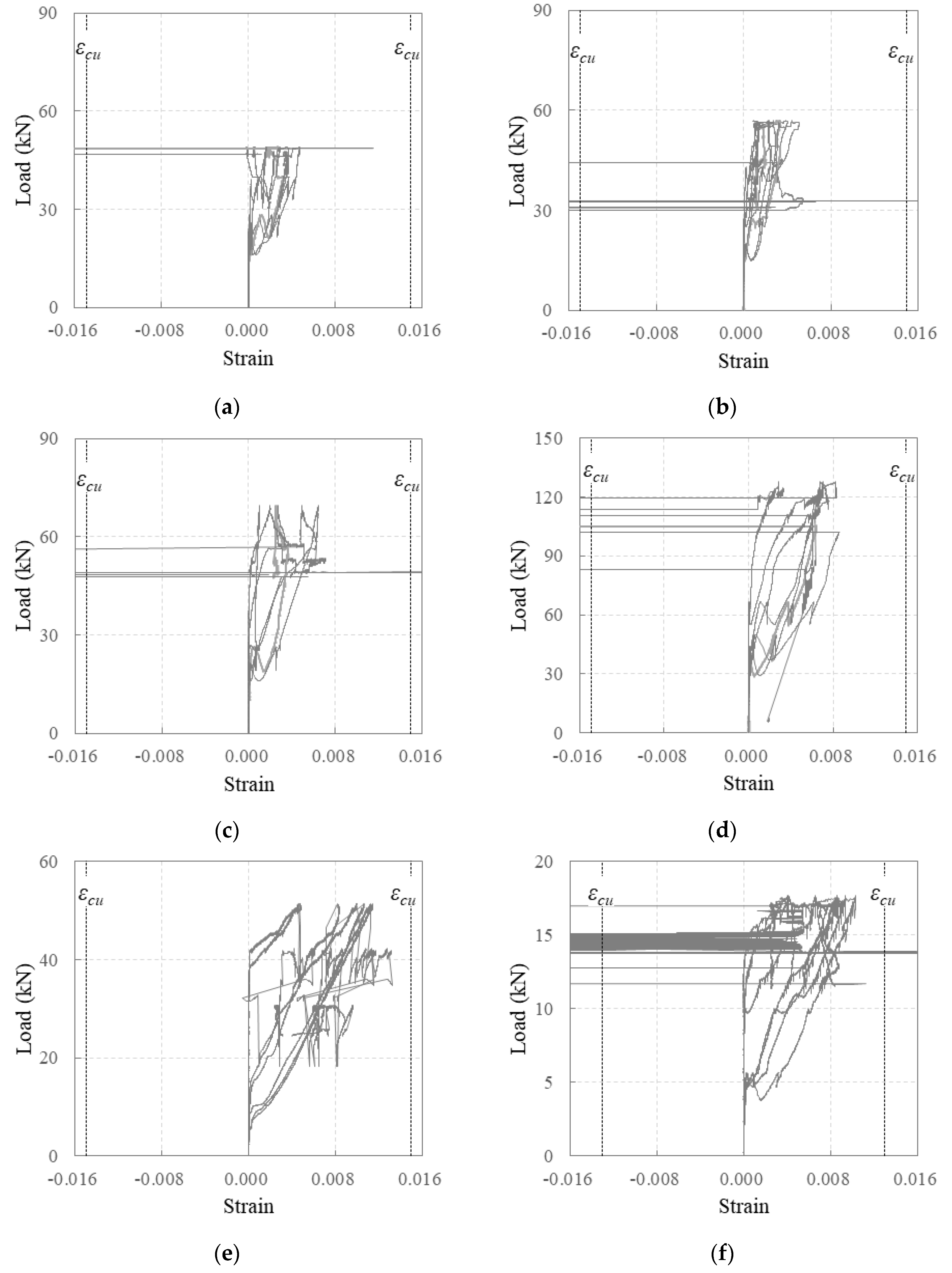
3.1. Crack and Failure Geometry
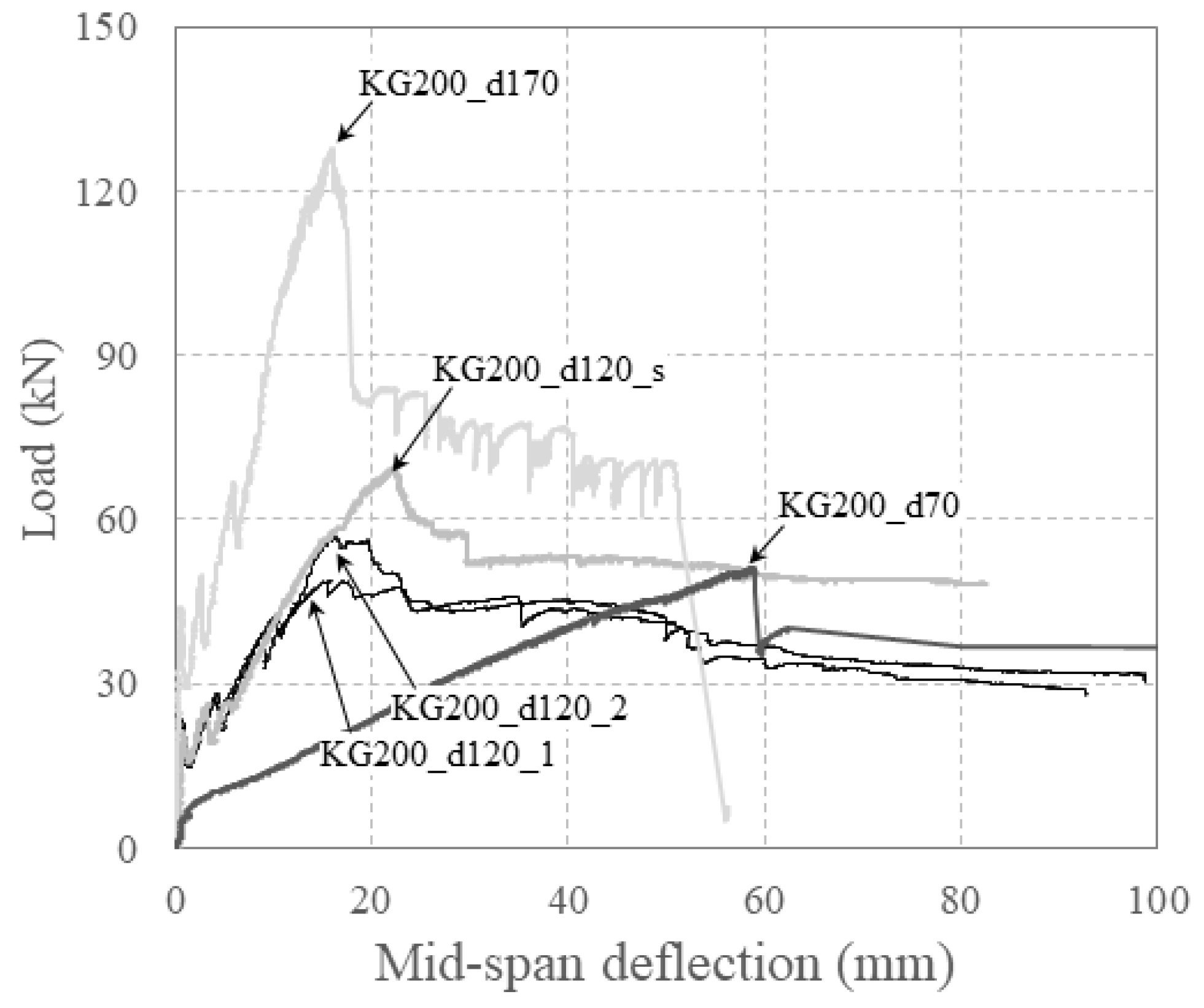
3.2. Load–Deflection Relationship
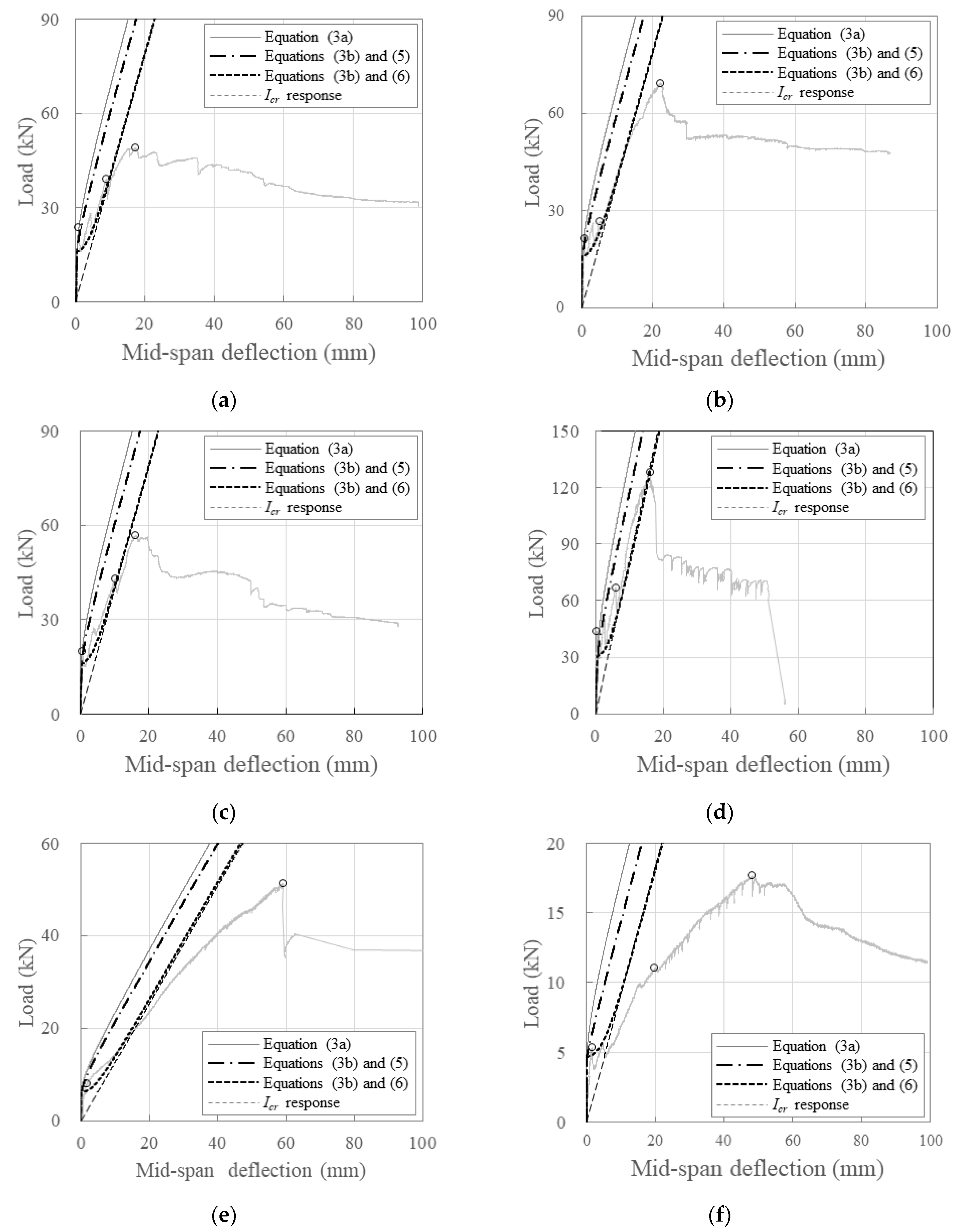
3.3. Flexural Behavior Evaluation
3.3.1. Crack and Maximum Load
3.3.2. Stiffness of Cracked Section
3.4. Comparison of Flexural Behaviors with RC
4. Conclusions
- The carbon-grid-reinforced specimens exhibited wide crack spaces and fewer cracks. Poor bond properties between the carbon grid and concrete, such as bonding cracks, were also observed on the surfaces. Ultimately, the specimens exhibited an increased crack width that penetrated the cross-section, leading to the slipping of the carbon grid and the separation of the specimens along the cracks. Despite the strain measurements indicating tensile strains exceeding those at the tensile strength in the longitudinal CFRP strands, the CFRP strand sections did not fracture. Instead, damage was observed in the form of interfacial failure between the fibers and resin, along with fiber rupture.
- The relationship between load and mid-span deflection varied with the amount of carbon grid reinforcement used. The specimen over-reinforced or reinforced close to the balanced reinforcement ratio exhibited ductile failure, but the specimen under-reinforced with the carbon grid exhibited brittle failure. In particular, for specimens with carbon grid reinforcement close to the balanced reinforcement ratio, the ratios of the experimental to the calculated maximum loads were found to be 0.43–0.61, which were similar to or lower than the strength reduction factor of 0.6 suggested by the design standard. This indicates that achieving the expected flexural strength using carbon grids is challenging.
- As the effective depth increased, the moment of inertia of the specimens also increased, resulting in a higher stiffness. This resulted in the specimens reaching maximum loads with smaller deflections. Because the experiment focused on one-way slab specimens, the transverse CFRP strands did not significantly influence the strength of the specimens. The specimens reinforced with a wider width of the CFRP strands also exhibited the 0.86~1.00 lower ratios of experimental to calculated maximum loads compared to the specimen reinforced with a narrower width of the CFRP strands.
- Based on the experimental results, this study proposes a formula to assess the impact of poor bonds between the carbon grid and concrete on the post-cracking stiffness degradation of carbon-grid-reinforced concrete members. The post-cracking stiffness calculated using the proposed formula closely matched the experimental results.
- Compared to the RC specimens, the carbon-grid-reinforced specimens exhibited a lower flexural strength, but they demonstrated ductile behavior regardless of the effective depth except for the specimens under-reinforced with carbon grids. The flexural behavior of one-way concrete slabs reinforced with carbon grids composed of thin-plate-shaped CFRP strands was still evaluated through a limited set of experiments. Therefore, further research is required to predict the flexural behavior of carbon-grid-reinforced concrete members, which is different from RC members.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maslehuddin, M.; Saricimen, H.; Al-Mana, A.I.; Shamin, M. Performance of concrete in a high-chloride sulfate environment. Spec. Publ. 1990, 122, 469–494. [Google Scholar]
- Jaffer, S.J.; Hansson, C.M. Chloride-induced corrosion products of steel in cracked-concrete subjected to different loading conditions. Cem. Constr. Res. 2009, 39, 116–125. [Google Scholar] [CrossRef]
- Cabrera, J.G. Deterioration of concrete due to reinforcement steel corrosion. Cem. Con. Compos. 1996, 18, 47–59. [Google Scholar] [CrossRef]
- Erdoğdu, Ş.; Bremner, T.; Kondratova, I. Accelerated testing of plain and epoxy-coated reinforcement in simulated seawater and chloride solutions. Cem. Concr. Res. 2001, 31, 861–867. [Google Scholar] [CrossRef]
- Pour-Ali, S.; Dehghanian, C.; Kosari, A. Corrosion protection of the reinforcing steels in chloride-laden concrete environment through epoxy/polyaniline-camphorsulfonate nanocomposite coating. Corros. Sci. 2015, 90, 239–247. [Google Scholar] [CrossRef]
- Almusallam, A.A.; Khan, F.M.; Dulaijan, S.U.; Al-Amoudi, O.S.B. Effectiveness of surface coatings in improving concrete durability. Cem. Con. Compos. 2003, 25, 473–481. [Google Scholar] [CrossRef]
- Jalili, M.; Moradian, S.; Hosseinpour, D. The use of inorganic conversion coatings to enhance the corrosion resistance of reinforcement and the bond strength at the rebar/concrete. Constr. Build. Mater. 2009, 23, 233–238. [Google Scholar] [CrossRef]
- ACI 440.1R-15; Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer(FRP) Bars. ACI: Farmington Hills, MI, USA, 2015.
- Nanni, A.; Luca, A.D.; Zadeh, H.J. Reinforced Concrete with FRP Bars; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Cheng, L. Steel-Free Bridge Decks Reinforced with FRP Composites. In Fiber Reinforced Polymer (FRP) Composites for Infrastructure Application; Springer: Dordrecht, The Netherlands, 2012; pp. 143–162. [Google Scholar]
- Naanam, A.E. Textile reinforced cement composites: Competitive status and research directions. In Proceedings of the International RILEM Conference on Materials Science (MatSci) I, Aachen, Germany, 6–10 September 2010; pp. 3–22. [Google Scholar]
- Peled, A.; Bentur, A.; Mobasher, B. Textile Reinforced Concrete; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Vautard, F.; Drzal, L.T. Carbon fiber—Vinyl ester interfacial adhesion improvement by the use of a reactive epoxy coating. In Proceedings of the ICCM17, 17th International Conference on Composite Materials, Edingburgh, UK, 27–31 July 2009. [Google Scholar]
- Portal, N.W.; Perez, I.F.; Thrane, L.N.; Lundgren, K. Pull-out of textile reinforcement in concrete. Constr. Build. Mater. 2014, 71, 63–71. [Google Scholar] [CrossRef]
- Portal, N.W. Usability of Textile Reinforced Concrete: Structural Performance, Durability and Sustainability. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2015. [Google Scholar]
- Mechtvherine, V.; Schneider, K.; Brameshuber, W. Mineral-based Matrix for Textile-reinforced Concrete. In Textile Fibre Composites in Civil Engineering; Woodhead Publishing: Sawston, UK, 2016; pp. 25–44. [Google Scholar]
- Gries, T.; Raina, M.; Quadflieg, T.; Stolyarov, O. Manufacturing of textiles for civil engineering applications. In Textile Fibre Composites in Civil Engineering; Woodhead Publishing: Sawston, UK, 2016; pp. 3–24. [Google Scholar] [CrossRef]
- Portal, N.W.; Thrane, L.N.; Lundgren, K. Flexural behaviour of textile reinforced concrete composites: Experimental and numerical evaluation. Mater. Struct. 2017, 50, 4. [Google Scholar] [CrossRef]
- Meng, W.; Khayat, K.H.; Bao, Y. Flexural behaviors of fiber-reinforced polymer fabric reinforced ul-tra-high-performance concrete panels. Cem. Concr. Compos. 2018, 93, 43–53. [Google Scholar] [CrossRef]
- Wagner, J.; Curbach, M. Bond Fatigue of TRC with Epoxy Impregnated Carbon Textiles. Appl. Sci. 2019, 9, 1980. [Google Scholar] [CrossRef]
- Rampini, M.C.; Zani, G.; Colombo, M.; di Prisco, M. Mechanical Behaviour of TRC Composites: Experimental and Analytical Approaches. Appl. Sci. 2019, 9, 1492. [Google Scholar] [CrossRef]
- Zeng, J.J.; Zeng, W.B.; Ye, Y.Y.; Liao, J.J.; Zhuge, Y.; Fan, T.H. Flexural behavior of FRP grid reinforced ultra-high-performance concrete composite plates with different types of fibers. Eng. Struct. 2022, 272, 115020. [Google Scholar] [CrossRef]
- Gao, J.; Xu, P.; Fan, L.; Li, J.; Terrasi, G.P.; Meier, U. Experimental Study of Fatigue and Fracture Behavior of Carbon Fiber-Reinforced Polymer (CFRP) Straps. Polymers 2022, 14, 2129. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.M.; Cheon, J.H. Flexural Behavior of One-Way Slab Reinforced with Grid-Type Carbon Fiber Reinforced Plastics of Various Geometric and Physical Properties. Appl. Sci. 2022, 12, 12491. [Google Scholar] [CrossRef]
- Schumann, A.; Michler, H.; Schladizt, F.; Curbach, M. Parking slabs made of carbon reinforced concrete. Struct. Concr. 2018, 19, 647–655. [Google Scholar] [CrossRef]
- Tietze, M.; Kirmse, S.; Kahnt, A.; Schladitz, F.; Curbach, M. The ecological and economic advantages of carbon reinforced concrete—Using the C3 result house CUBE especially the BOX value chain as an example. Civ. Eng. Des. 2022, 4, 79–88. [Google Scholar] [CrossRef]
- Michael, A.P. Using Carbon Fiber Reinforced Polymer Grids as Confinement Reinforcement for Concrete. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2006. [Google Scholar]
- Saleem, M.U.; Qureshi, H.J.; Amin, M.N.; Khan, K.; Khurshid, H. Cracking behavior of RC beams strengthened with different amounts and layouts of CFRP. Appl. Sci. 2019, 9, 1017. [Google Scholar] [CrossRef]
- Giese, A.C.H.; Giese, D.N.; Dutra, V.F.P.; Filho, L.C.P.D.S. Flexural behavior of reinforced concrete beams strengthened with textile reinforced mortar. J. Build. Eng. 2021, 33, 101873. [Google Scholar] [CrossRef]
- Almushaikeh, A.M.; Alaswad, S.O.; Alsuhybani, M.S.; Alotaibi, B.M.; Alarifi, I.M.; Alqahtani, N.B.; Aldosari, S.M.; Alsaleh, S.S.; Haidyrah, A.S.; Alolyan, A.A.; et al. Manufacturing of carbon fiber reinforced thermoplastics and its recovery of carbon fiber: A review. Polym. Test. 2003, 122, 108029. [Google Scholar] [CrossRef]
- Xian, G.; Bai, Y.; Zhou, P.; Wang, J.; Li, C.; Dong, S.; Guo, R.; Tian, J.; Li, J.; Zhong, J.; et al. Long-term properties evolution and life prediction of glass fiber reinforced thermoplastic bending bars exposed in concrete alkaline environment. J. Build. Eng. 2024, 91, 109641. [Google Scholar] [CrossRef]
- Xian, G.; Zhou, P.; Bai, Y.; Wang, J.; Li, C.; Dong, S.; Guo, R.; Li, J.; Du, H.; Zhong, J. Design, preparation and mechanical properties of novel glass fiber reinforced polypropylene bending bars. Constr. Build. Mater. 2024, 429, 136455. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete. ACI: Farmington Hills, MI, USA, 2022.
- Min, K.J.; Kim, K.M.; Song, B.K.; Park, S.W. Flexural behavior slabs reinforced with grid-type CFRP reinforcement manufactured using adhesion. J. Korea Concr. Inst. 2023, 2, 197–206. [Google Scholar] [CrossRef]
- Portal, N.W.; Flansbjer, M.; Zandi, K.; Wlasak, L.; Malaga, K. Bending behaviour of novel Textile Reinforced Concrete-foamed concrete (TRC-FC) sandwich elements. Compos. Struct. 2017, 177, 104–118. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, B.; Lu, X.; Guo, J. Flexural properties of textile-reinforced concrete with nonorthogonal grids. Polymers 2022, 14, 5185. [Google Scholar] [CrossRef]
- Zdanowica, K.; Marx, S. Flexural behaviour of thin textile reinforced concrete slabs enhanced by chemical prestressing. Eng. Struct. 2022, 256, 113946. [Google Scholar] [CrossRef]
- Chinnasamy, M.; Ajithkumar, R.; Singh, A.; Yandzom, D.; Parvati, T.S.; Joanna, P.S. Comparative study on the behaviour of textile reinforced concrete slab with engineered cementitious composite slab. Mater. Today Proc. 2020, 33, 1175–1180. [Google Scholar] [CrossRef]
- Goonewardena, J.; Ghabraie, K.; Subhani, M. Flexural performance of FRP-reinforced geopolymer concrete beam. J. Compos. Sci. 2020, 4, 187. [Google Scholar] [CrossRef]
- ASTM D7205/D7205M; Standard Test Method for Tensile Properties of Fiber Reinforced Polymer Matrix Composite Bars. ASTM International: West Conshohocken, PA, USA, 2016.
- CAN/CSA-S806-02; Design and Construction of Building Components with Fibre-Reinforced Polymers. Canadian Standards Association: Toronto, ON, Canada, 2009.
- ISO 6935-2:2019; Steel for the Reinforcement of Concrete—Part 2: Ribbed Bars. ISO: Geneva, Switzerland, 2020.
- KS F 2527:2022; Aggregates for Concrete. KATS: Chungcheongbuk-do, Republic of Korea, 2022.
- ISO 1920-4:2020; Strength of Hardened Concrete. ISO: Geneva, Switzerland, 2020.
- Hegger, J.; Voss, S. Investigations on the bearing behaviour and application potential of textile reinforced concrete. Eng. Struct. 2008, 30, 2050–2056. [Google Scholar] [CrossRef]
- Scheerer, S.; Chudoba, R.; Garobaldi, M.P.; Curbach, M. Shells made of textile reinforced concrete—Applications in Germany. J. IASS 2017, 58, 1175–1180. [Google Scholar] [CrossRef]
- Haji, T.K. Evaluating the Effects of Tunnel Construction on Buildings. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2017. [Google Scholar]
- Khuntia, M.; Ghosh, S.K. Flexural stiffness of reinforced concrete columns and beams: Analytical approach. ACI Struct. Struct. J. 2004, 101-S36, 351–363. [Google Scholar]
- Bischoff, P.H.; Scanlon, A. Effective moment of inertia for calculating deflections of concrete members containing steel reinforcement and fiber-reinforced polymer reinforcement. ACI Struct. J. 2007, 104, 68–75. [Google Scholar]



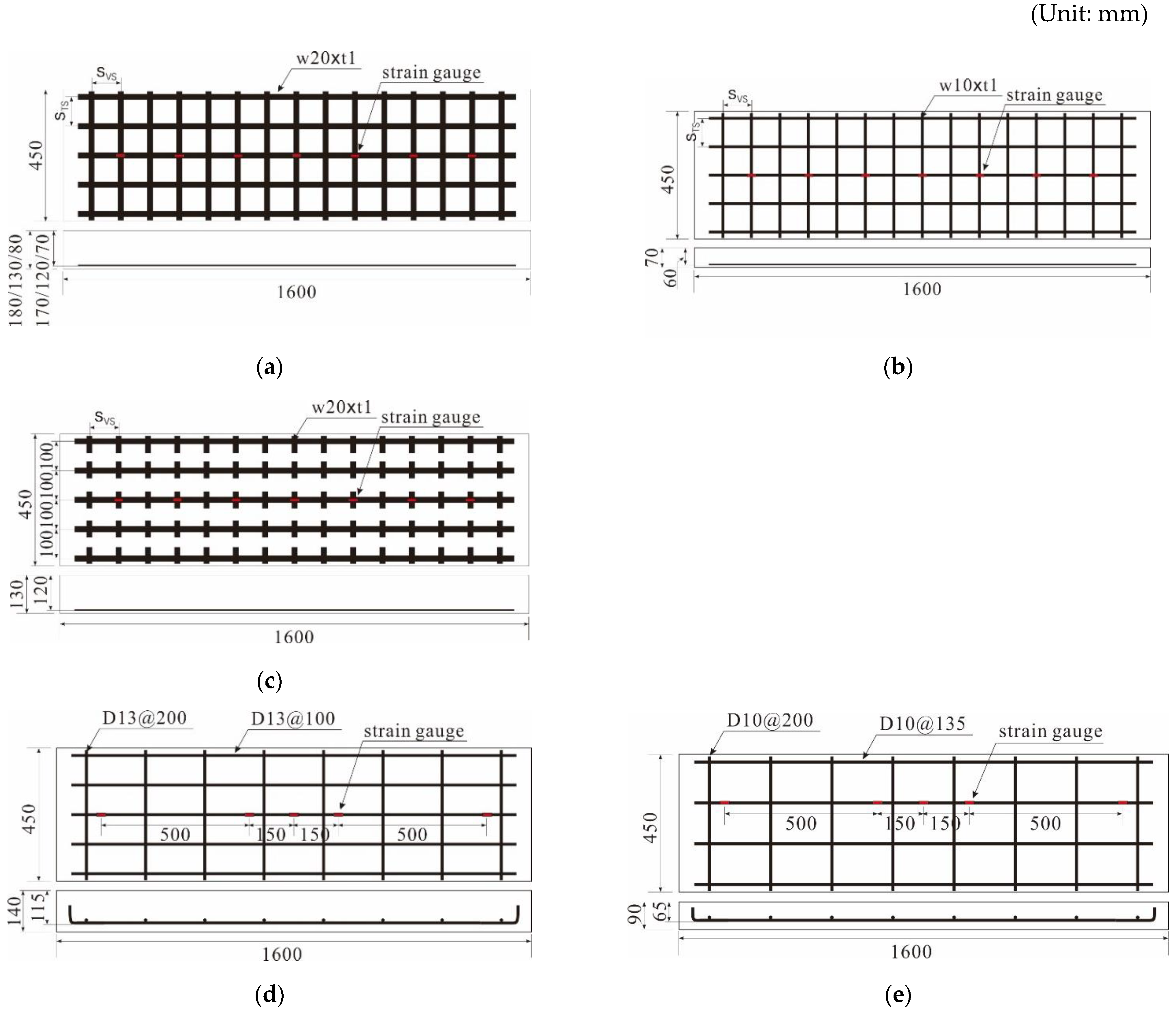







| Name | Strand | Grid Geometry (Longitudinal (G_VS) × Transverse (G_TS) Spacing, mm) | Tensile Strength (MPa) | Tensile Modulus of Elasticity (MPa) | ||
|---|---|---|---|---|---|---|
| Width (mm) | Thickness (mm) | Area (mm2) | ||||
| KC_w20 | 20 | 1 | 20 | 100 × 100 | 2271 | 151,994 |
| KC_w10 | 10 | 1 | 10 | 100 × 100 | 2327 | 179,000 |
| d13 | - | - | 126.7 | - | 637 (501) | 186,516 |
| d10 | - | - | 71.3 | - | 582 (469) | 216,657 |
| Cement (kg/m3) | Water (kg/m3) | W/C (%) | Fine Aggregate (kg/m3) | Coarse Aggregate (kg/m3) | Compressive Strength (MPa) |
|---|---|---|---|---|---|
| 455 | 159 | 35 | 765 | 900 | 42.7 |
| Specimen | Width (mm) | Depth/ Effective Depth (mm) | Length (mm) | Reinforcement | Reinforcement Ratio (%) |
|---|---|---|---|---|---|
| K200_d120_1 | 450 | 130/120 | 1600 | KC_w20 | 0.19 |
| K200_d120_2 | |||||
| K200_d120_s | |||||
| K200_d170 | 180/170 | 0.13 | |||
| K200_d70 | 80/70 | 0.32 | |||
| K100_d60 | 70/60 | KC_w10 | 0.19 | ||
| RC_d109 | 140/109 | d13@200 × d13@100 | 1.01 | ||
| RC_d60 | 90/60 | d10@200 × d10@135 | 0.70 |
| Specimen | Crack Strength | Flexural Strength | Failure Mode | |||
|---|---|---|---|---|---|---|
| Moment (kNm) | Load (kN) | Moment (kNm) | Load (kN) | |||
| K200_d120_i for i = 1, 2, s | 0.93 | 5175 | 23.0 | 25,549 | 113.6 | CFRP strand rupture |
| K200_d170 | 0.66 | 9943 | 44.2 | 36,195 | 160.9 | CFRP strand rupture |
| K200_d70 | 1.60 | 1950 | 8.7 | 11,420 | 50.8 | Concrete crushing |
| K100_d60 | 0.86 | 1512 | 6.7 | 6492 | 28.9 | CFRP strand rupture |
| RC_d109 | 0.45 | 6049 | 26.9 | 31,787 | 141.3 | Rebar yield |
| RC_d60 | 0.31 | 2500 | 11.1 | 7564 | 33.6 | Rebar yield |
| Specimen | Number of Cracks | Average Crack Space (mm) |
|---|---|---|
| K200_d120_1 | 4 | 176 |
| K200_d120_2 | 3 | 200 |
| K200_d120_s | 3 | 191 |
| K200_d170 | 3 | 219 |
| K200_d70 | 8 | 101 |
| K100_d60 | 4 | 147 |
| RC_d109 | 10 | 67 |
| RC_d60 | 10 | 74 |
| Specimen | Crack Formation Point (CF) | Crack Stabilization Point (CS) | Maximum Load Point | (1)/(3) | (2)/(3) | |||
|---|---|---|---|---|---|---|---|---|
| Load (1) (kN) | Deflection of Mid-Span (mm) | Load (2) (kN) | Deflection of Mid-Span (mm) | Load (3) (kN) | Deflection of Mid-Span (mm) | |||
| K200_d120_1 | 23.58 | 0.86 | 39.05 | 9.00 | 48.97 | 17.20 | 0.48 | 0.80 |
| K200_d120_2 | 19.72 | 0.67 | 42.85 | 10.37 | 56.80 | 16.17 | 0.35 | 0.75 |
| K200_d120_s | 21.30 | 0.90 | 26.84 | 5.28 | 69.37 | 22.12 | 0.31 | 0.39 |
| K200_d170 | 43.92 | 0.47 | 66.63 | 5.95 | 127.81 | 16.07 | 0.34 | 0.52 |
| K200_d70 | 7.99 | 1.85 | - | - | 51.33 | 59.03 | 0.16 | - |
| K100_d60 | 5.32 | 1.59 | 11.05 | 19.89 | 17.66 | 48.33 | 0.30 | 0.63 |
| RC_d109 | 35.92 | 1.20 | 113.48 | 5.46 | 179.91 | 38.64 | 0.20 | 0.63 |
| RC_d60 | 5.70 | 0.60 | 27.23 | 6.27 | 47.36 | 88.97 | 0.12 | 0.57 |
| Specimen | Stiffness (N/mm) | ||
|---|---|---|---|
| Before Crack Formation (Stage 1) | Crack Formation (Stage 2) | Crack Stabilization (Stage 3) | |
| K200_d120_1 | 27,453 | 1900 | 1209 |
| K200_d120_2 | 29,614 | 2383 | 2406 |
| K200_d120_s | 23,609 | 1265 | 2526 |
| K200_d170 | 92,933 | 4147 | 6048 |
| K200_d70 | 4326 | - | 758 |
| K100_d60 | 3345 | 313 | 232 |
| RC_d109 | 29,868 | 18,235 | 2002 |
| RC_d60 | 9482 | 3795 | 244 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.-M.; Park, S.-W.; Song, B.-K.; Yoon, S.-H. Evaluation of the Flexural Behavior of One-Way Slabs by the Amount of Carbon Grid Manufactured by Adhesive Bonding. Polymers 2024, 16, 2690. https://doi.org/10.3390/polym16192690
Kim K-M, Park S-W, Song B-K, Yoon S-H. Evaluation of the Flexural Behavior of One-Way Slabs by the Amount of Carbon Grid Manufactured by Adhesive Bonding. Polymers. 2024; 16(19):2690. https://doi.org/10.3390/polym16192690
Chicago/Turabian StyleKim, Kyung-Min, Sung-Woo Park, Bhum-Keun Song, and Seon-Hee Yoon. 2024. "Evaluation of the Flexural Behavior of One-Way Slabs by the Amount of Carbon Grid Manufactured by Adhesive Bonding" Polymers 16, no. 19: 2690. https://doi.org/10.3390/polym16192690
APA StyleKim, K.-M., Park, S.-W., Song, B.-K., & Yoon, S.-H. (2024). Evaluation of the Flexural Behavior of One-Way Slabs by the Amount of Carbon Grid Manufactured by Adhesive Bonding. Polymers, 16(19), 2690. https://doi.org/10.3390/polym16192690




