Computational Analysis of the Micromechanical Stress Field in Undamaged and Damaged Unidirectional Fiber-Reinforced Plastics Using a Modified Principal Component Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Preparation and Tensile Test
2.2. Computational Micromechanics Modeling
2.2.1. RVE for the Modified Mesh-Independent PCA Study
2.2.2. RVEs with Random Fiber Arrangements for the Micromechanical Stress Field Study
2.2.3. Micromechanical Damage Modeling Approaches
The Stiffness Degradation Model for the Matrix and Interface
Probabilistic Modeling of Fiber Breaks
2.3. Application of Principal Component Analysis for the Matrix Stress Field
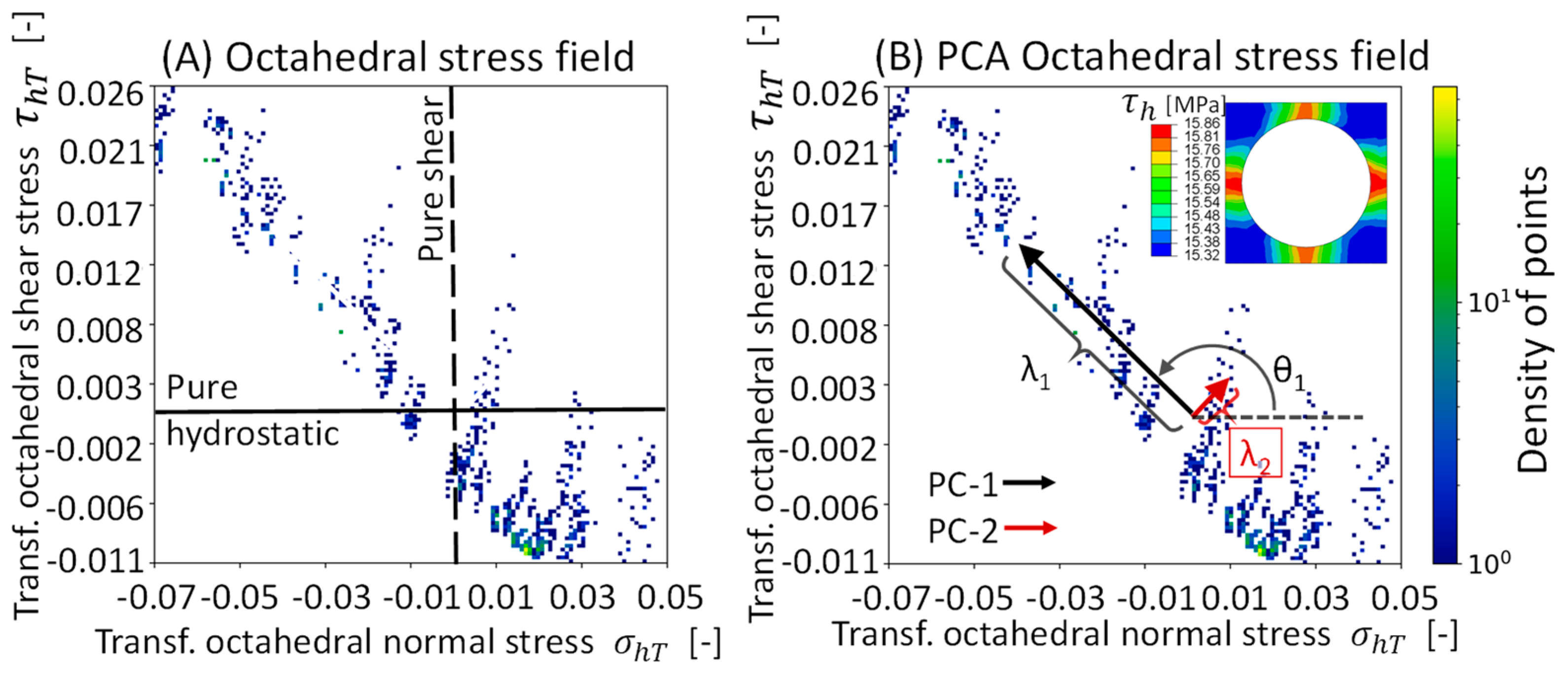
2.3.1. Octahedral Stress Field Within the Matrix
2.3.2. Implementation of Principal Component Analysis (PCA)
3. Results and Discussion
3.1. Development of a Modified Mesh-Independent PCA
3.2. Analysis of the Micromechanical Stress Field of RVE with Random Fiber Arrangements
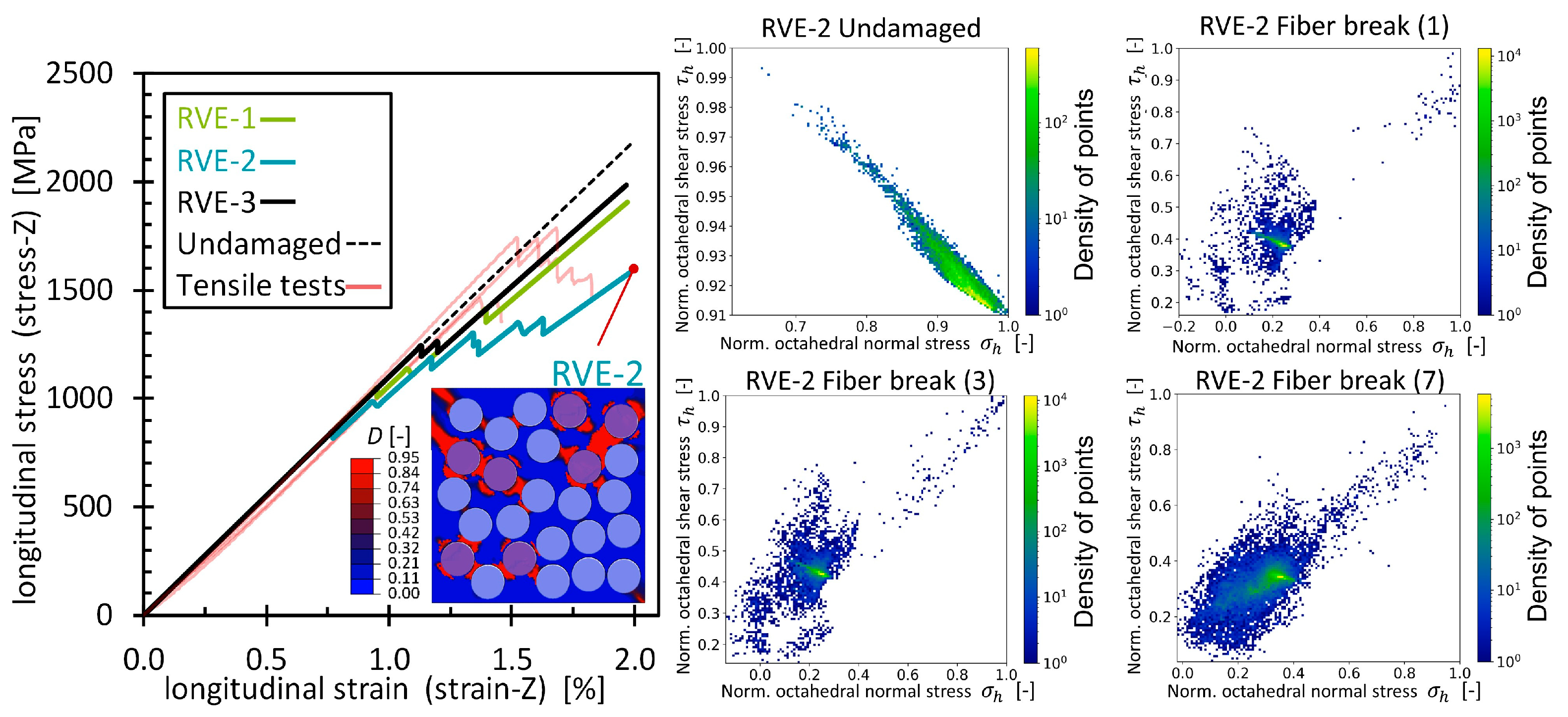
3.2.1. Validation of the RVE Models with Random Fiber Arrangements
3.2.2. Modified PCA of Transverse Tensile Strain Simulations (Matrix/Interface Damage)
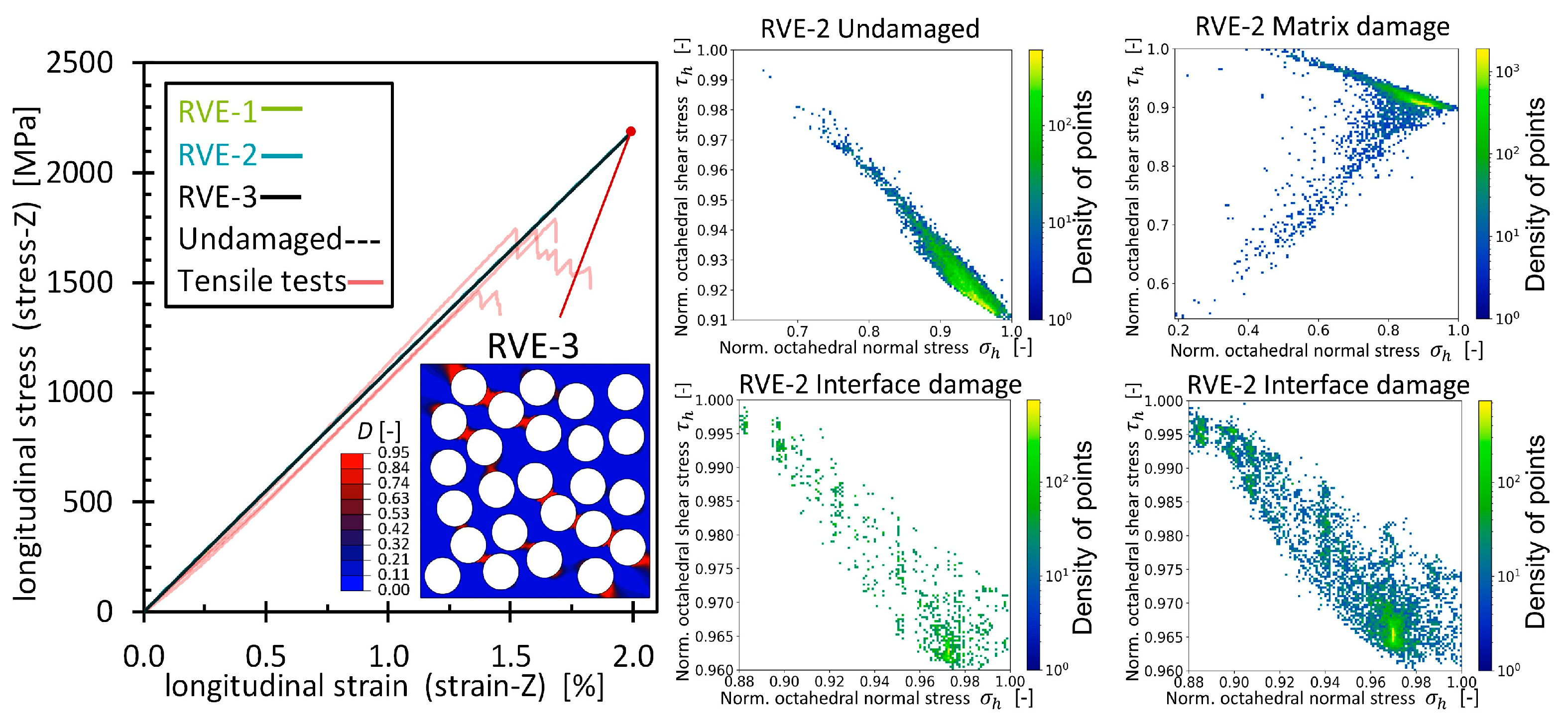
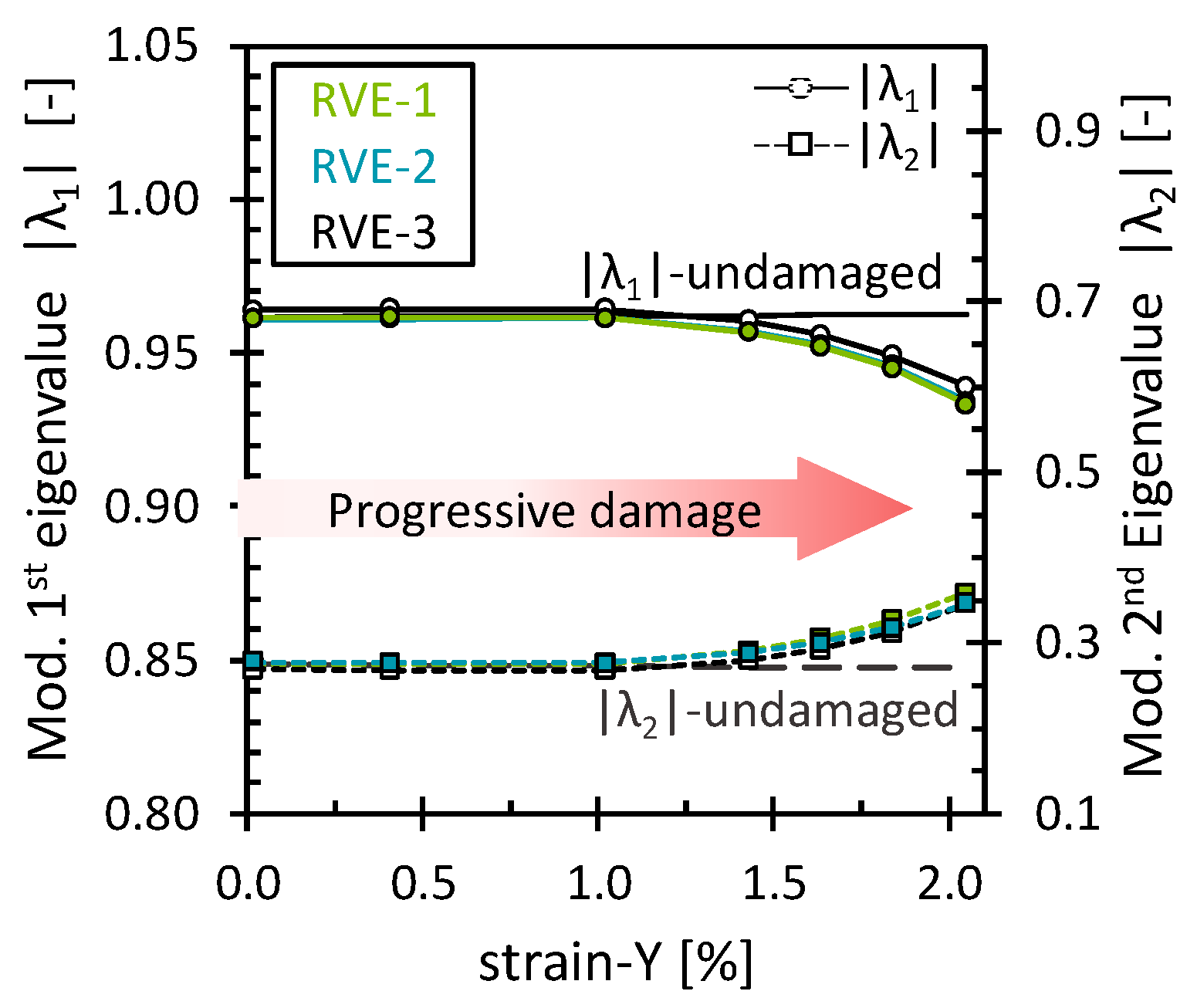
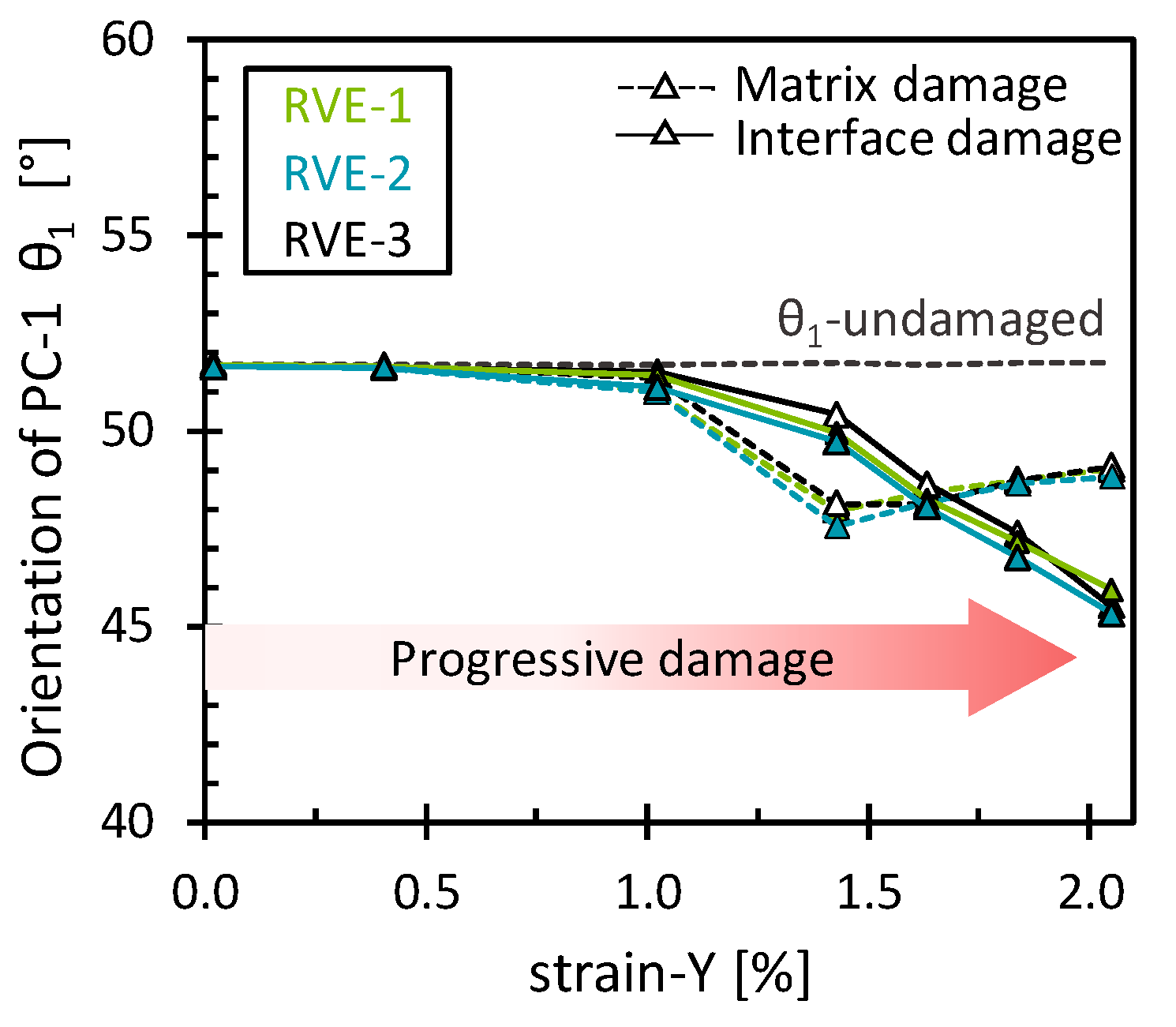
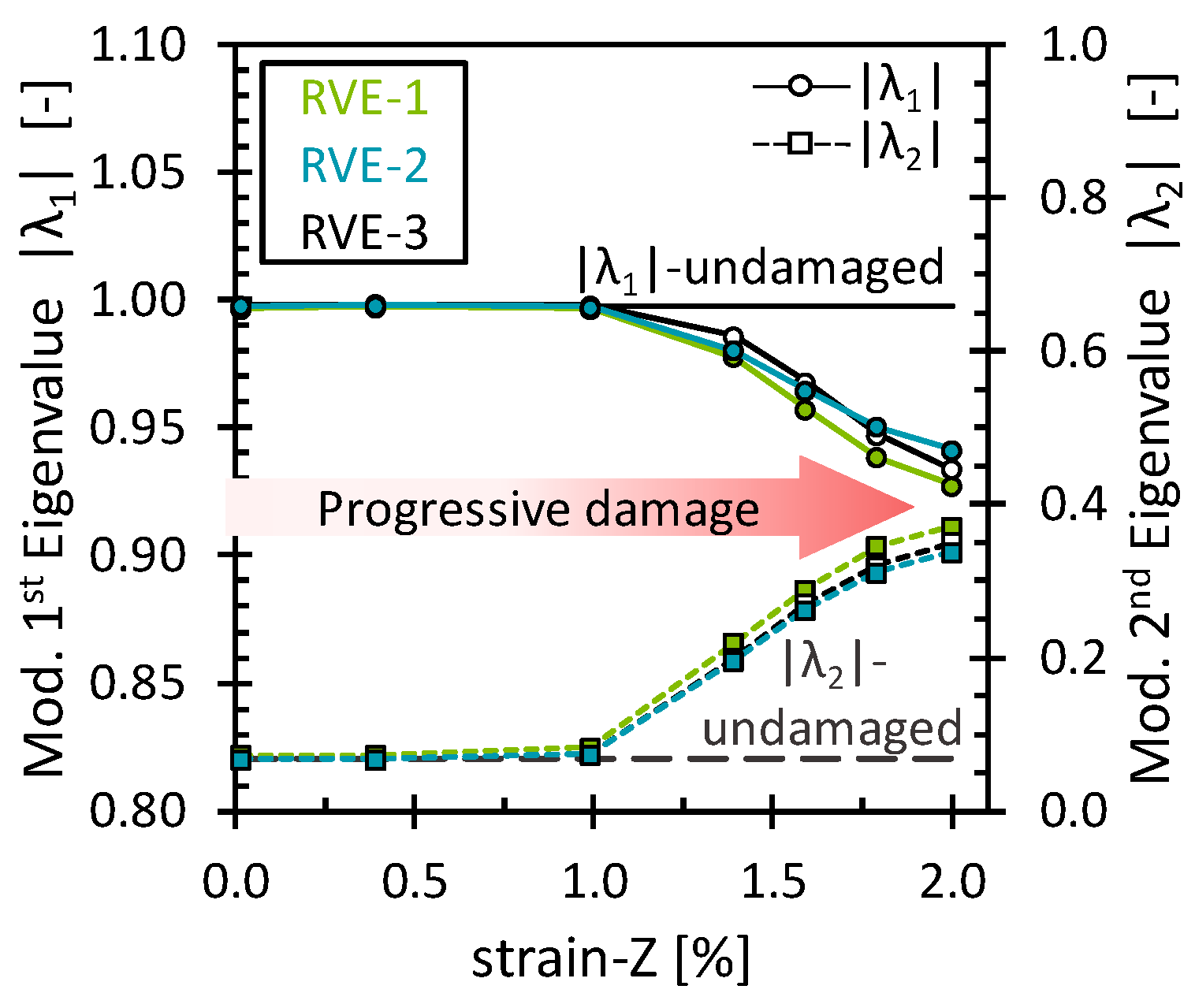
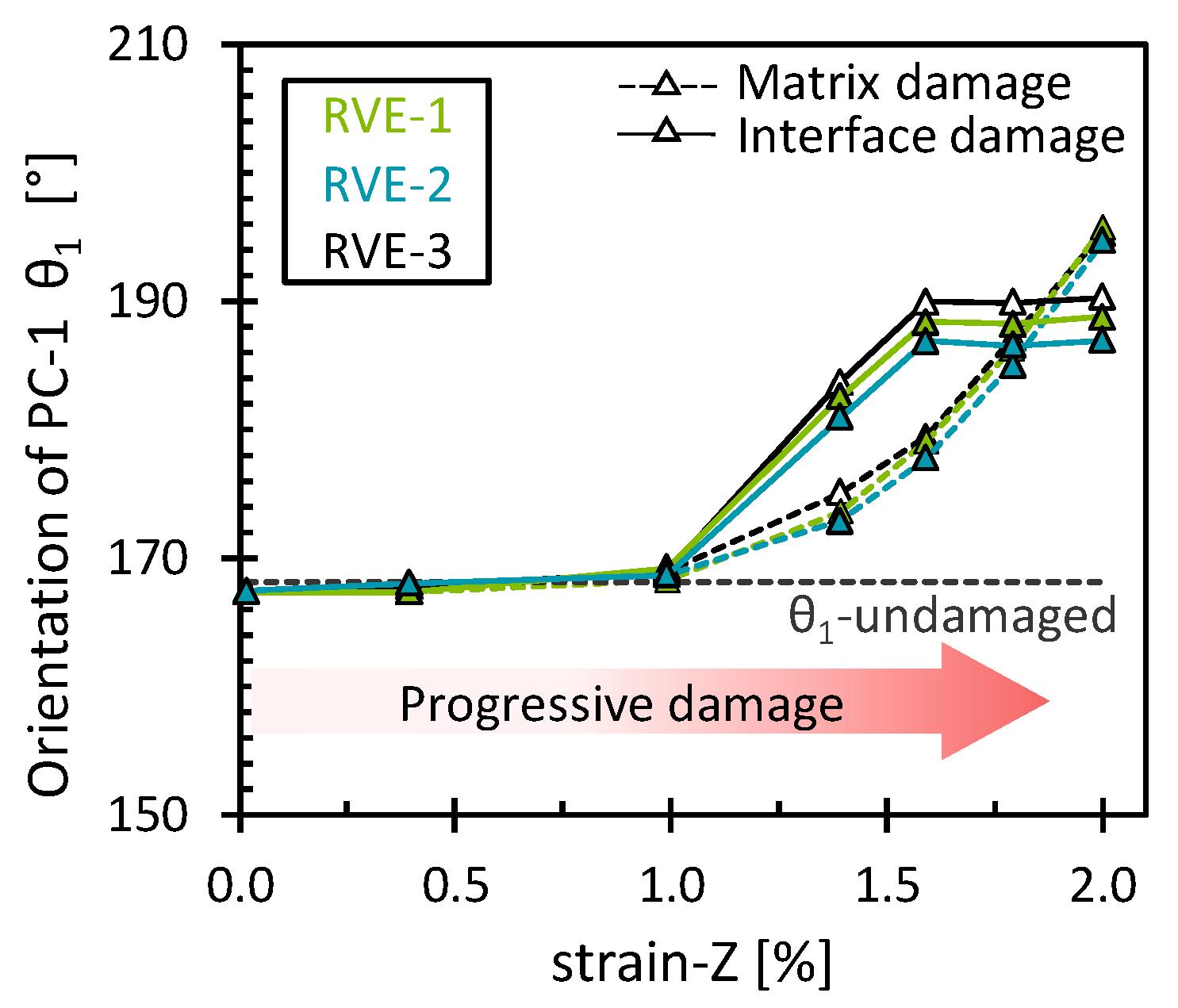
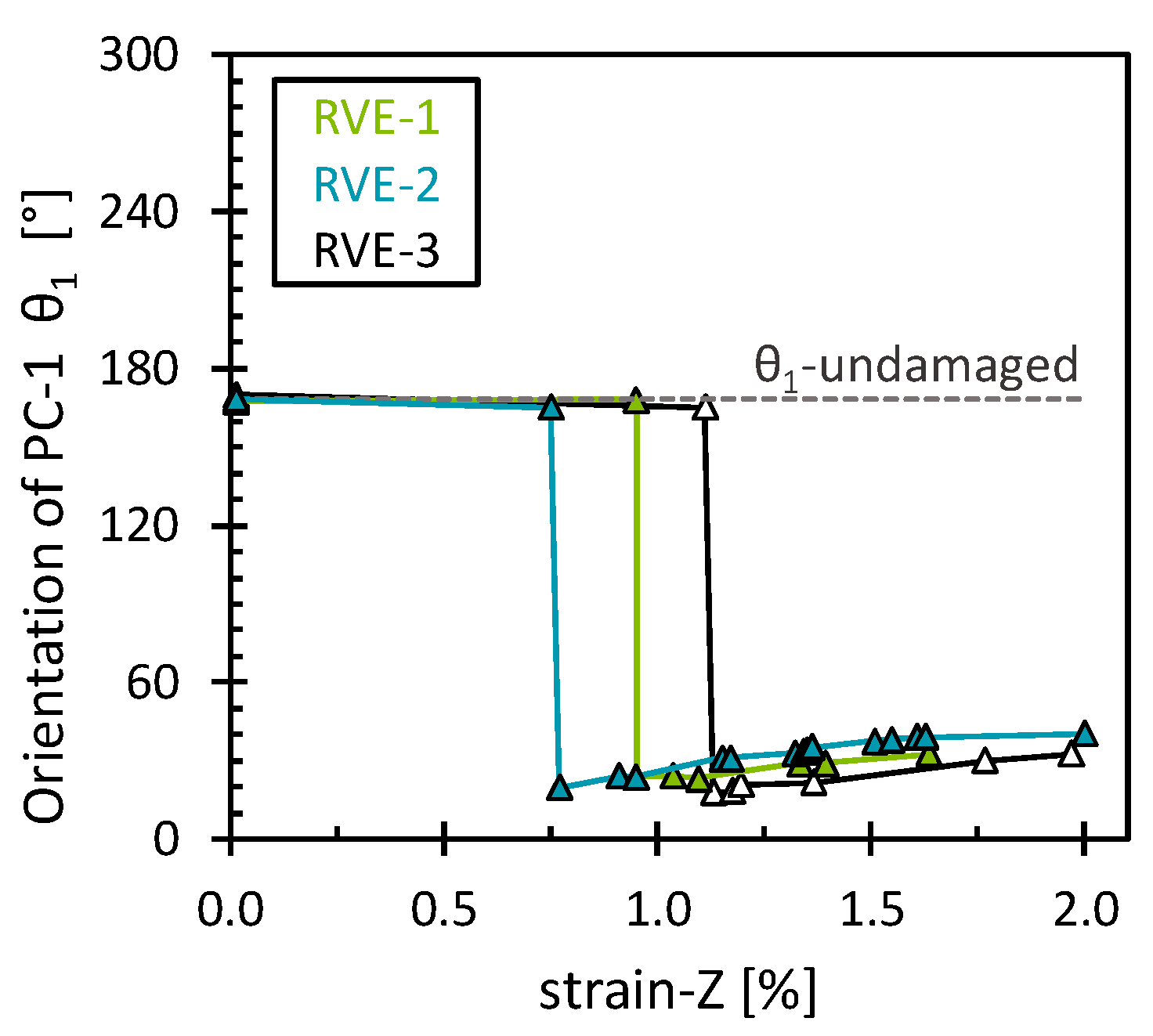
3.2.3. Modified PCA of the Longitudinal Tensile Strain Simulations (Matrix/Interface Damage)
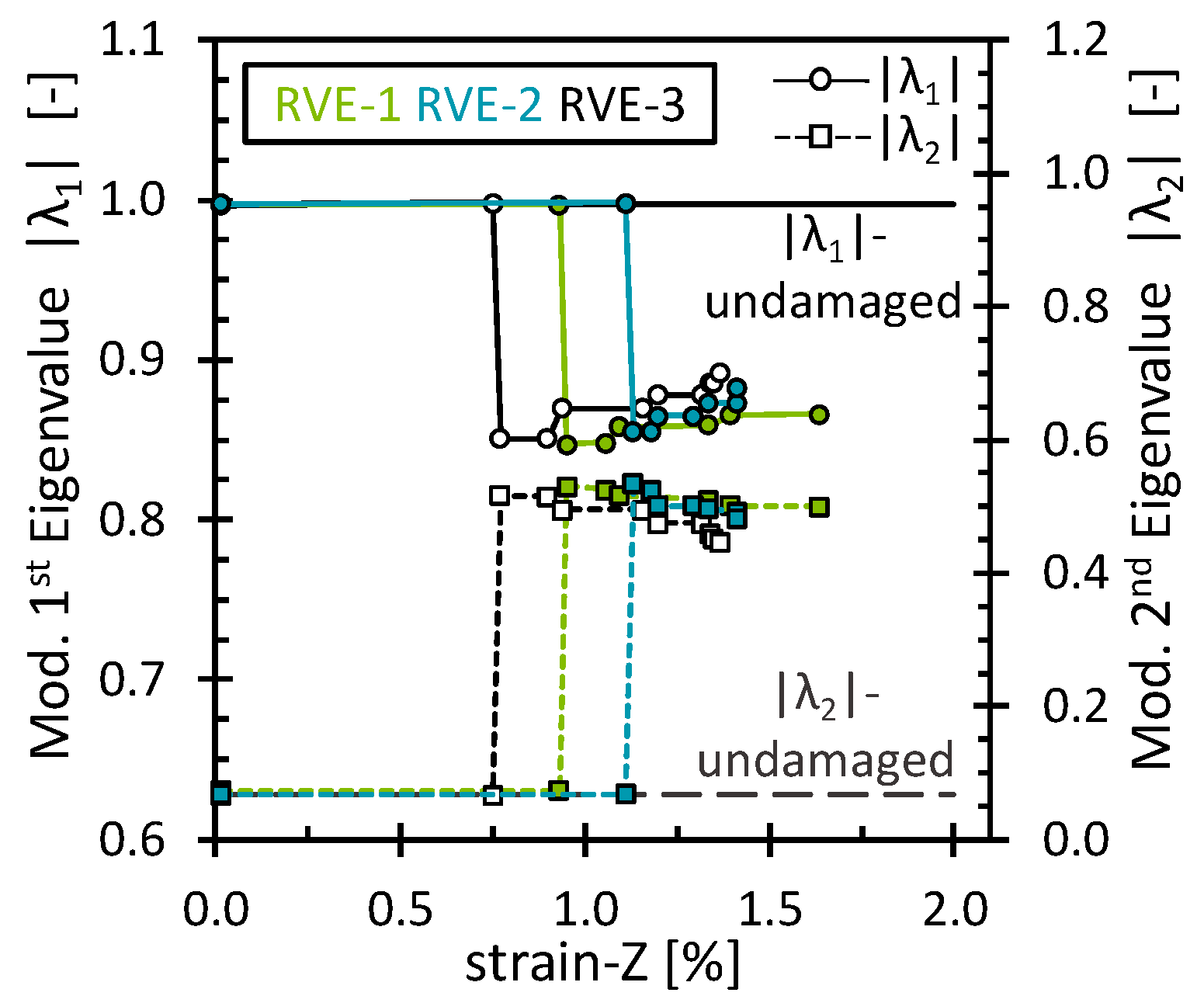
3.2.4. Modified PCA of the Longitudinal Tensile Strain Simulations (Fiber Breaks)
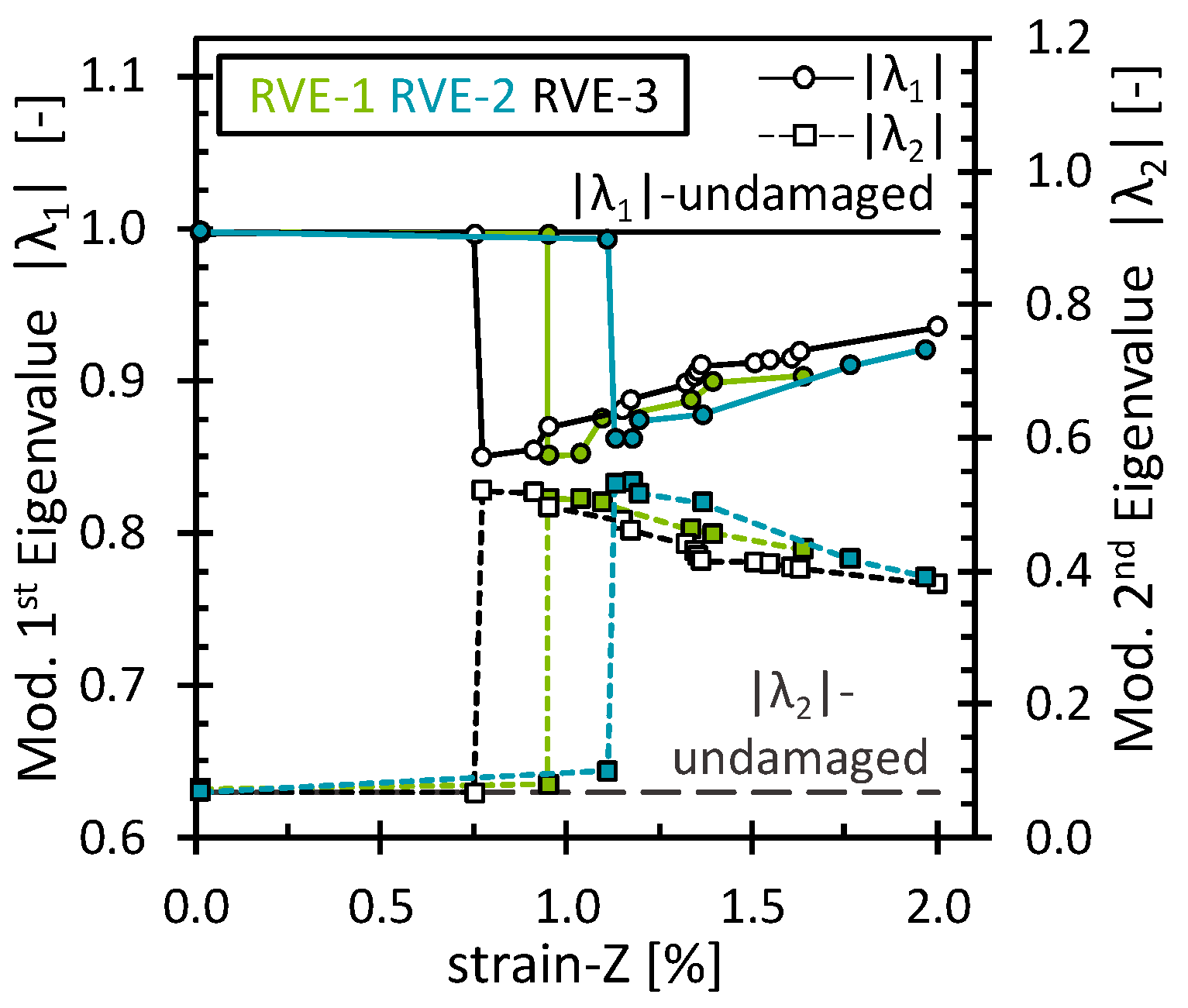
3.2.5. Modified PCA of the Longitudinal Tensile Strain Simulations (Matrix/Interface Damage and Fiber Breaks)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A


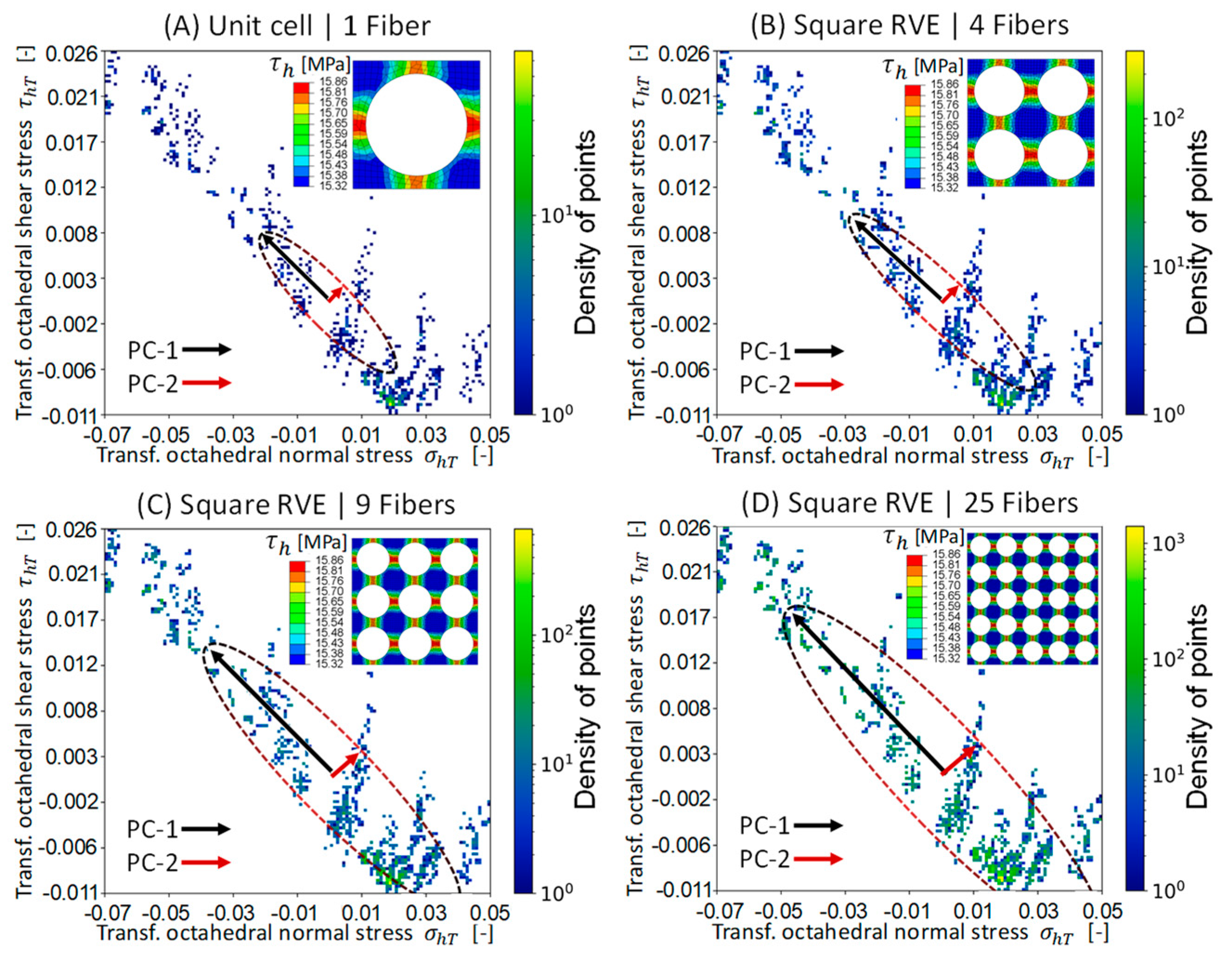
Appendix B
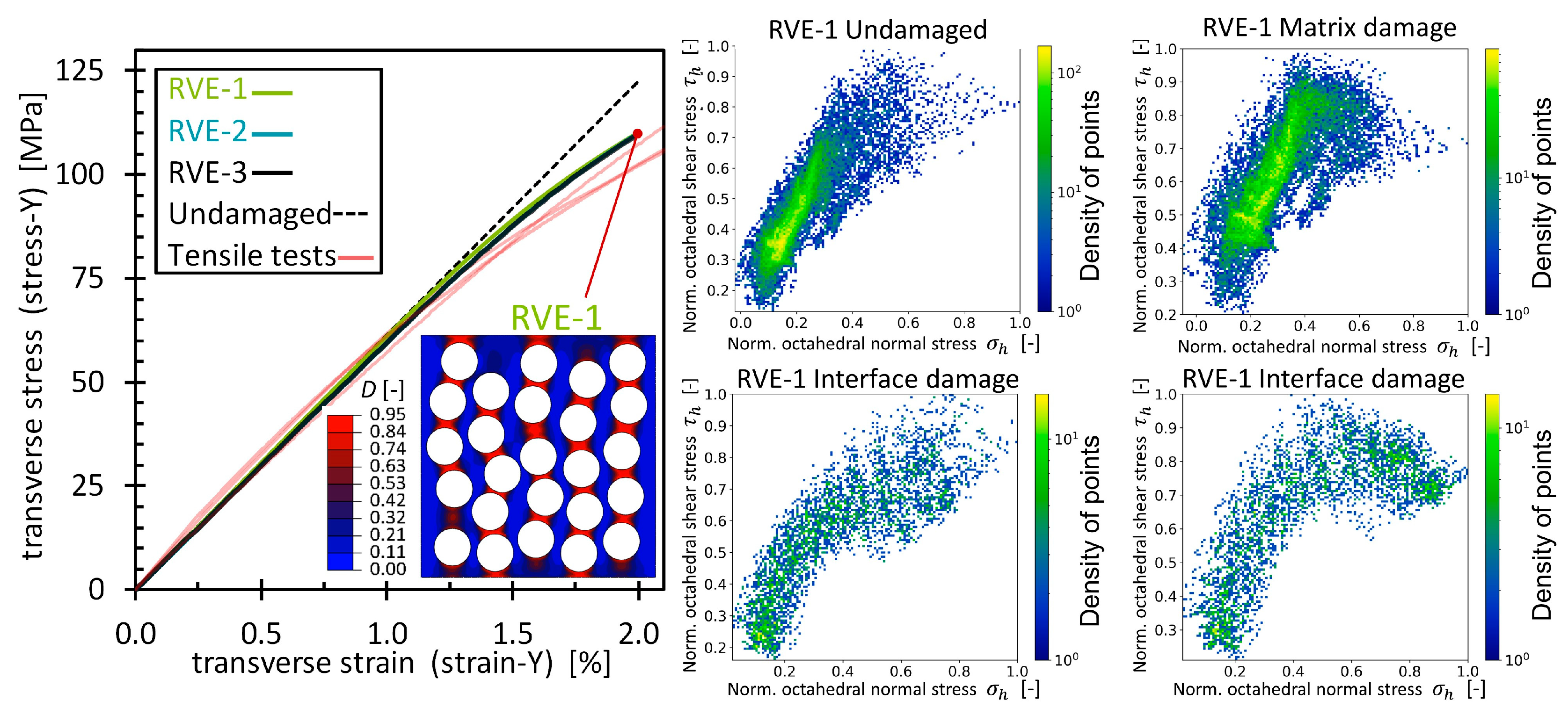
Appendix C
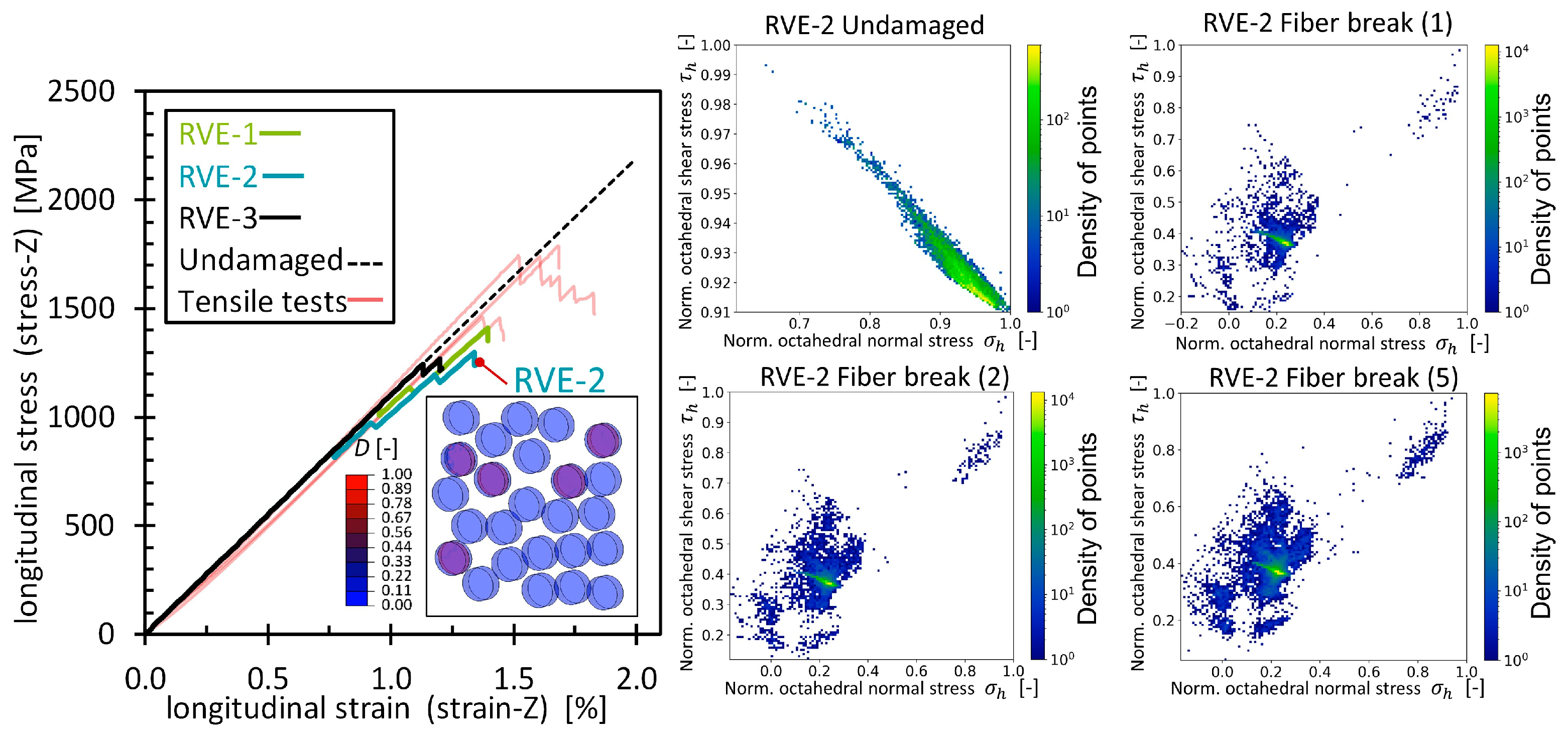
References
- Al-Lami, A.; Hilmer, P.; Sinapius, M. Eco-efficiency assessment of manufacturing carbon fiber reinforced polymers (CFRP) in aerospace industry. Aerosp. Sci. Technol. 2018, 79, 669–678. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P. The history of fiber-reinforced polymer composite laminate fatigue. Int. J. Fatigue 2020, 134, 105512. [Google Scholar] [CrossRef]
- Knops, M. Analysis of Failure in Fiber Polymer Laminates: The Theory of Alfred Puck; Springer: Berlin/Heidelberg, Germany, 2008; pp. 37–114. [Google Scholar]
- Sharma, H.; Kumar, A.; Rana, S.; Sahoo, N.G.; Jami, M.; Kumar, R.; Sharma, S.; Li, C.; Kumar, A.; Eldin, S.M.; et al. Critical review on advancements on the fiber-reinforced composites: Role of fiber/matrix modification on the performance of the fibrous composites. J. Mater. Res. Technol. 2023, 26, 2975–3002. [Google Scholar] [CrossRef]
- Gamstedt, K.; Andersen, S.I.S. Fatigue Degradation and Failure of Rotating Composite Structures—Materials Characterisation and Underlying Mechanisms; Report Risoe-R No. 1261; Risø National Laboratory: Roskilde, Denmark, 2001. [Google Scholar]
- Alam, P.; Mamalis, D.; Robert, C.; Floreani, C.; Bradaigh, C.M.O. The fatigue of carbon fibre reinforced plastics—A review. Compos. Part B 2019, 166, 555–579. [Google Scholar] [CrossRef]
- Awad, Z.K.; Aravinthan, T.; Zhunge, Y.; Gonzalez, F. A review of optimization techniques used in the design of fibre composite structures for civil engineering applications. Mater. Des. 2012, 33, 534–544. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Bahmani, A.; Geng, L.; Willet, T.L.; Montesano, J. Three-dimensional microscopic assessment of randomly distributed representative volume elements for high fiber volume fraction unidirectional composites. Compos. Struct. 2018, 192, 153–164. [Google Scholar] [CrossRef]
- Sengodan, G.A. Prediction of two-phase composite microstructure properties through deep learning of reduced dimensional structure-response data. Compos. Part B 2021, 225, 109282. [Google Scholar] [CrossRef]
- González, C.; LLorca, J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: Microscopic mechanisms and modeling. Compos. Sci. Technol. 2007, 67, 2795–2806. [Google Scholar] [CrossRef]
- Romanov, V.; Lomov, S.V.; Swolfs, Y.; Orlova, S.; Gorbatikh, L.; Verpoest, I. Statistical analysis of real and simulated fibre arrangements in unidirectional composites. Compos. Sci. Technol. 2013, 87, 126–134. [Google Scholar] [CrossRef]
- Pupurs, A.; Goutianos, S.; Brondsted, P.; Varna, J. Interface debond crack growth in tension–tension cyclic loading of single fiber polymer composites. Compos. A 2013, 44, 86–94. [Google Scholar] [CrossRef]
- Naghdinasab, M.; Farrokhabadi, A.; Madadi, H. A numerical method to evaluate the material properties degradation in composite RVEs due to fiber-matrix debonding and induced matrix cracking. Finite Elem. Anal. Des. 2018, 146, 84–95. [Google Scholar] [CrossRef]
- Babaei, R.; Farrokhadadi, A. Prediction of debonding growth in two-dimensional RVEs using an extended interface element based on continuum damage mechanics concept. Compos. Struct. 2020, 238, 111981. [Google Scholar] [CrossRef]
- Mueller, J.M.; Rozo Lopez, N.; Klein, E.A.; Hopmann, C. Predicting the damage development in epoxy resins using an anisotropic damage model. Polym. Eng. Sci. 2020, 60, 1324–1332. [Google Scholar] [CrossRef]
- Zhu, F.; Yu, D.; Tian, J.; Cheng, Y.; Zhang, S. Modelling on stress redistribution around broken fibers for fiber reinforced plastic with poor fiber distribution uniformity. Polym. Compos. 2022, 43, 8507–8516. [Google Scholar] [CrossRef]
- Sabuncuoglu, B.; Mutlu, C.; Kadioglu, F.S.; Swolfs, Y. Stress redistribution around fiber breaks in unidirectional steel fiber composites considering the nonlinear material behavior. Compos. Struct. 2020, 239, 111959. [Google Scholar] [CrossRef]
- Hopmann, C.; Rozo Lopez, N. Investigation of the correlation creep/fatigue in unidirectional fibre reinforced plastics. Int. Colloq. Plast. Technol. 2022, 31, 629–642. [Google Scholar]
- Koch, I.; Just, G.; Brod, M.; Chen, J.; Doblies, A.; Dean, A.; Gude, M.; Rolfes, R.; Hopmann, C.; Fiedler, B. Evaluation and Modeling of the Fatigue Damage Behavior of Polymer Composites at Reversed Cyclic Loading. Materials 2019, 12, 1727. [Google Scholar] [CrossRef]
- Rozo Lopez, N.; Hakan, Ç.; Hopmann, C. A numerical study on the fiber detachment affecting the complex stress state at microstructural level of unidirectional fiber reinforced plastics. In Proceedings of the Annual Technical Conference—ANTEC, Conference Proceedings 2023, Denver, CO, USA, 27–30 March 2023. [Google Scholar]
- Bian, L.; Chen, L.; Gao, M. Stress distribution analysis and interface influence on fiber reinforced composites. Mech. Mater. 2020, 146, 103400. [Google Scholar] [CrossRef]
- Zhu, J.; Lang, F.C.; Wang, S.Y.; Zhuo, L.; Xing, Y.M. Determination of the interfacial properties of carbon fiber reinforced polymers using nanoindentation. J. Reinf. Plast. Compos. 2021, 41, 509–516. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Jolliffe, I.; Cadima, J. Principal component analysis: A review and recent developments. Phil. Trans. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Gao, B.; Tian, G.Y.; Woo, W.L.; Berthiau, G. Impact Damage Detection and Identification Using Eddy Current Pulsed Thermography Through Integration of PCA and ICA. IEEE Sens. J. 2014, 14, 1655–1663. [Google Scholar] [CrossRef]
- Saeedifar, M.; Zarouchas, D. Damage characterization of laminated composites using acoustic emission: A review. Compos. Part B 2020, 195, 108039. [Google Scholar] [CrossRef]
- ISO 527-5; Plastics—Determination of Tensile Properties—Part 5: Test Conditions for Unidirectional Fibre-Reinforced Plastic Composites. International Organization for Standardization: Geneva, Switzerland, 2021.
- Rozo Lopez, N.; Chen, J.; Hopmann, C. A micromechanical model for loading and unloading behavior of fiber reinforced plastics under cyclic loading. Polym. Compos. 2020, 41, 3892–3902. [Google Scholar] [CrossRef]
- Huntsman Corporation, Technical Datasheet Araldite LY556/HY906/DY070. Available online: https://sigerom.ro/ro/epoxidice/3692-araldite-ly-556-bidon-25-kg.html (accessed on 22 October 2024).
- Wan, L.; Ismail, Y.; Zhu, C.; Zhu, P.; Sheng, Y.; Liu, J.; Yang, D. Computational micromechanics-based prediction of the failure of unidirectional composite lamina subjected to transverse and in-plane shear stress states. J. Compos. Mater. 2020, 54, 3637–3654. [Google Scholar] [CrossRef]
- Yang, L.; Yan, Y.; Ran, Z.; Liu, Y. A new method for generating random fibre distributions for fibre-reinforced composites. Compos. Sci. Technol. 2013, 76, 14–20. [Google Scholar] [CrossRef]
- Grigorovitch, M.; Gal, E.; Waisman, H. Embedded unit cell homogenization model for localized non-periodic elasto-plastic zones. Comput. Mech. 2021, 68, 1437–1456. [Google Scholar] [CrossRef]
- Grigorovitch, M.; Gal, E. The local response in structures using the Embedded Unit Cell Approach. Comput. Struct. 2015, 157, 189–200. [Google Scholar] [CrossRef]
- Fiedler, B.; Hojo, M.; Ochiai, S.; Ando, M. Failure behavior of an epoxy matrix under different kinds of static loading. Compos. Sci. Technol. 2001, 61, 1615–1624. [Google Scholar] [CrossRef]
- Seupel, A.; Hütter, G.; Kuna, M. An efficient FE-implementation of implicit gradient-enhanced damage models to simulate ductile failure. Eng. Fract. Mech. 2018, 199, 41–60. [Google Scholar] [CrossRef]
- Raghavan, P.; Gosh, S. A continuum damage mechanics model for unidirectional composites undergoing interfacial debonding. Mech. Mater. 2005, 37, 955–979. [Google Scholar] [CrossRef]
- Hohe, J.; Gall, M.; Fliegener, S.; Hamid, Z.M.A. A continuum damage mechanics model for fatigue and degradation of fiber reinforced materials. J. Compos. Mater. 2020, 54, 2837–2852. [Google Scholar] [CrossRef]
- Etcheverry, M.; Barbosa, S.E. Glass Fiber Reinforced Polypropylene Mechanical Properties Enhancement by Adhesion Improvement. Materials 2012, 5, 1084–1113. [Google Scholar] [CrossRef]
- Ballarini, R.; Pisano, G.; Royer-Garfagni, G. The Lower Bound for Glass Strength and Its Interpretation with Generalized Weibull Statistics for Structural Applications. J. Eng. Mech. 2016, 142, 04016100. [Google Scholar] [CrossRef]
- Hu, H.; Xia, Z.; Ellyin, F. The Failure behavior of an epoxy resin subject to multiaxial loading. In Proceedings of the ASCE 2006 Pipeline Conference, Chicago, IL, USA, 30 July–2 August 2006; pp. 1–8. [Google Scholar]
- Kody, R.S.; Lesser, A.J. Deformation and yield of epoxy networks in constrained states of stress. J. Mater. Sci. 1997, 32, 5637–5643. [Google Scholar] [CrossRef]
- Elnekhaily, S.A.; Zhuang, L.; Talreja, R. Formation of transverse cracks in cross ply laminates in an environment of nonuniformly distributed fibers. Compos. Sci. Technol. 2024, 253, 110651. [Google Scholar] [CrossRef]
- Andersons, J.; Joffe, R.; Hojo, M.; Ochinai, S. Fibre fragemnt distribution in a sinlge-fibre composite tension test. Compos. Part B 2001, 32, 323–332. [Google Scholar] [CrossRef]




| Mechanical Properties | Toray T700 Carbon Fibers [29] | LY556/H917 Epoxy Matrix [30] | |
|---|---|---|---|
| Longitudinal modulus [GPa] | E∥ | 230 | 3.15 |
| Transverse modulus [GPa] | E⊥ | 15 | - |
| Longitudinal shear modulus [GPa] | G⊥∥ | 15 | 1.17 |
| Transverse shear modulus [GPa] | G⊥⊥ | 7 | - |
| Longitudinal Poisson’s ration [–] | ν⊥∥ | 0.2 | 0.35 |
| Transverse Poisson’s ration [–] | ν⊥⊥ | 0.5 | - |
| Tensile strength [MPa] | σf | 4900 | 93 |
| Model Parameter | Matrix | Interface | |
|---|---|---|---|
| A | [–] | 1.0−6 | 5.0−19 |
| n | [–] | 10.0 | 8.0 |
| b | [–] | 0.5 | 0.5 |
| [–] | 75.0 | 55.0 | |
| [–] | 10.0 | 10.0 | |
| [–] | 0.1 | 0.25 | |
| [–] | 0.5 | 0.75 |
| RVE Size | Longitudinal Strain 2% | Transverse Strain 2% | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fibers | Integration Points | λ1 | λ2 | |λ1| | |λ2| | θ1 [°] | λ1 | λ2 | |λ1| | |λ2| | θ1 [°] |
| 1 | 2305 | 1.019 | 0.345 | 0.993 | 0.116 | 161.2 | 0.937 | 0.419 | 0.913 | 0.408 | 30.3 |
| 4 | 9220 | 1.441 | 0.489 | 0.993 | 0.116 | 161.2 | 1.325 | 0.592 | 0.913 | 0.408 | 30.3 |
| 9 | 20,745 | 1.765 | 0.599 | 0.993 | 0.116 | 161.2 | 1.622 | 0.725 | 0.913 | 0.408 | 30.3 |
| 25 | 57,625 | 2.278 | 0.773 | 0.993 | 0.116 | 161.2 | 2.094 | 0.936 | 0.913 | 0.408 | 30.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez, N.R.; Çelik, H.; Hopmann, C. Computational Analysis of the Micromechanical Stress Field in Undamaged and Damaged Unidirectional Fiber-Reinforced Plastics Using a Modified Principal Component Analysis. Polymers 2024, 16, 3000. https://doi.org/10.3390/polym16213000
Lopez NR, Çelik H, Hopmann C. Computational Analysis of the Micromechanical Stress Field in Undamaged and Damaged Unidirectional Fiber-Reinforced Plastics Using a Modified Principal Component Analysis. Polymers. 2024; 16(21):3000. https://doi.org/10.3390/polym16213000
Chicago/Turabian StyleLopez, Nicolas Rozo, Hakan Çelik, and Christian Hopmann. 2024. "Computational Analysis of the Micromechanical Stress Field in Undamaged and Damaged Unidirectional Fiber-Reinforced Plastics Using a Modified Principal Component Analysis" Polymers 16, no. 21: 3000. https://doi.org/10.3390/polym16213000
APA StyleLopez, N. R., Çelik, H., & Hopmann, C. (2024). Computational Analysis of the Micromechanical Stress Field in Undamaged and Damaged Unidirectional Fiber-Reinforced Plastics Using a Modified Principal Component Analysis. Polymers, 16(21), 3000. https://doi.org/10.3390/polym16213000







