Review on Damage and Failure in Adhesively Bonded Composite Joints: A Microscopic Aspect
Abstract
:1. Introduction
2. Stress Triaxiality-Dependent Behavior of Polymeric Materials
3. Experimental Characterization
4. Modeling and Numerical Simulation
5. Concluding Remarks and Future Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Sugita, Y.; Winkelmann, C.; La Saponara, V. Environmental and chemical degradation of carbon/epoxy lap joints for aerospace applications, and effects on their mechanical performance. Compos. Sci. Technol. 2010, 70, 829–839. [Google Scholar] [CrossRef]
- Li, Y.; Deng, H.; Takamura, M.; Koyanagi, J. Durability analysis of CFRP adhesive joints: A study based on entropy damage modeling using FEM. Materials 2023, 16, 6821. [Google Scholar] [CrossRef] [PubMed]
- Federal Aviation Administration. Advisory Circular 20-107A, Composite Aircraft Structure; Federal Aviation Administration: Washington, DC, USA, 2009.
- Federal Aviation Administration. 14 CFR 23.573—Damage Tolerance and Fatigue Evaluation of Structure; Federal Aviation Administration: Washington, DC, USA, 2011.
- Kruse, T.; Körwien, T.; Geistbeck, M.; Schmid Fuertes, T. Bonding of CFRP primary aerospace structures–discussion of the certification boundary conditions and related technology fields addressing the needs for development. In Proceedings of the 16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014. [Google Scholar]
- Chowdhury, N.; Wang, J.; Chiu, W.; Chang, P. Experimental and finite element studies of thin bonded and hybrid carbon fibre double lap joints used in aircraft structures. Compos. Part B Eng. 2016, 85, 233–242. [Google Scholar] [CrossRef]
- Kelly, G. Quasi-static strength and fatigue life of hybrid (bonded/bolted) composite single-lap joints. Compos. Struct. 2006, 72, 119–129. [Google Scholar] [CrossRef]
- Kawashita, L.; Kinloch, A.; Moore, D.; Williams, J. The influence of bond line thickness and peel arm thickness on adhesive fracture toughness of rubber toughened epoxy–aluminium alloy laminates. Int. J. Adhes. Adhes. 2008, 28, 199–210. [Google Scholar] [CrossRef]
- Manterola, J.; Cabello, M.; Zurbitu, J.; Renart, J.; Turon, A.; Jumel, J.; Urresti, I. Effect of the width-to-thickness ratio on the mode I fracture toughness of flexible bonded joints. Eng. Frac. Mech. 2019, 218, 106584. [Google Scholar] [CrossRef]
- General Services Administration. Federal Specifications: MMM-A-132B: Adhesives, Heat Resistant, Airframe Structural, Metal To-Met; General Services Administration: Washington, DC, USA, 2011.
- Mishnaevsky, L., Jr.; Branner, K.; Petersen, H.; Beauson, J.; McGugan, M.; Sørensen, B. Materials for wind turbine blades: An overview. Materials 2017, 10, 1285. [Google Scholar] [CrossRef]
- Amraei, J.; Katunin, A. Recent advances in limiting fatigue damage accumulation induced by self-heating in polymer–matrix composites. Polymers 2022, 14, 5384. [Google Scholar] [CrossRef]
- Lahuerta, F.; Nijssen, R.; Van Der Meer, F.; Sluys, L. Experimental–computational study towards heat generation in thick laminates under fatigue loading. Int. J. Fatigue 2015, 80, 121–127. [Google Scholar] [CrossRef]
- Griffith, A. The Phenomena of Rupture and Flow in Solids. Philos. Trans. R Soc. A Math. Phys. Eng. Sci. 1921, 221, 163–198. [Google Scholar]
- Anderson, T. Fracture Mechanics Fundamentals and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Gleich, D.; Van Tooren, M.; Beukers, A. Analysis and evaluation of bondline thickness effects on failure load in adhesively bonded structures. J. Adhes. Sci. Technol. 2001, 15, 1091–1101. [Google Scholar] [CrossRef]
- Jø rgensen, J. Adhesive Joints in Wind Turbine Blades. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2017. [Google Scholar]
- Lahuerta, F.; Koorn, N.; Smissaert, D. Wind turbine blade trailing edge failure assessment with sub-component test on static and fatigue load conditions. Compos. Struct. 2018, 204, 755–766. [Google Scholar] [CrossRef]
- Fernandes, R.; Budzik, M.; Benedictus, R.; de Freitas, S. Multi-material adhesive joints with thick bond-lines: Crack onset and crack deflection. Compos. Struct. 2021, 266, 113687. [Google Scholar] [CrossRef]
- Cassano, A.; Dev, S.; Maiaru, M.; Hansen, C.; Stapleton, S. Cure simulations of thick adhesive bondlines for wind energy applications. J. Appl. Polym. Sci. 2021, 138, 49989. [Google Scholar] [CrossRef]
- Srinivasan, D.; Vassilopoulos, A. Manufacturing and toughening effects on the material properties of wind turbine blade adhesives. Polym. Test. 2022, 116, 107770. [Google Scholar] [CrossRef]
- Asp, L.; Berglund, L.; Gudmundson, P. Effects of a composite-like stress state on the fracture of epoxies. Compos. Sci. Technol. 1995, 53, 27–37. [Google Scholar] [CrossRef]
- Asp, L.; Berglund, L.; Talreja, R. A criterion for crack initiation in glassy polymers subjected to a composite-like stress state. Compos. Sci. Technol. 1996, 56, 1291–1301. [Google Scholar] [CrossRef]
- Fiedler, B.; Hojo, M.; Ochiai, S.; Schulte, K.; Ando, M. Failure behavior of an epoxy matrix under different kinds of static loading. Compos. Sci. Technol. 2001, 61, 1615–1624. [Google Scholar] [CrossRef]
- Hobbiebrunken, T.; Fiedler, B.; Hojo, M.; Tanaka, M. Experimental determination of the true epoxy resin strength using micro-scaled specimens. Compos. Part A Appl. Sci. Manuf. 2007, 38, 814–818. [Google Scholar] [CrossRef]
- Misumi, J.; Ganesh, R.; Sockalingam, S.; Gillespie, J., Jr. Experimental characterization of tensile properties of epoxy resin by using micro-fiber specimens. J. Reinf. Plast. Compos. 2016, 35, 1792–1801. [Google Scholar] [CrossRef]
- Qiao, Y.; Salviato, M. Strength and cohesive behavior of thermoset polymers at the microscale: A size-effect study. Eng. Fract. Mech. 2019, 213, 100–117. [Google Scholar] [CrossRef]
- Oshima, S.; Kobayashi, S. Experimental and numerical investigation of mesoscopic damage accumulation in adhesively bonded composite scarf joints. Compos. Part A Appl. Sci. Manuf. 2024, 179, 108036. [Google Scholar] [CrossRef]
- Oshima, S.; Mikami, T.; Yoshimura, A.; Hirano, Y.; Ogasawara, T. In situ optical observation of damage and failure process in adhesively bonded CFRP joints under mixed-mode loading. Compos. Struct. 2023, 305, 116453. [Google Scholar] [CrossRef]
- Oshima, S.; Higuchi, R.; Kato, M.; Minakuchi, S.; Yokozeki, T.; Aoki, T. Cooling rate-dependent mechanical properties of polyphenylene sulfide (PPS) and carbon fiber reinforced PPS (CF/PPS). Compos. Part A Appl. Sci. Manuf. 2023, 164, 107250. [Google Scholar] [CrossRef]
- Yamanaka, K.; Inoue, T. Structure development in epoxy resin modified with poly (ether sulphone). Polymer 1989, 30, 662–667. [Google Scholar] [CrossRef]
- Cho, J.; Hwang, J.; Cho, K.; An, J.; Park, C. Effects of morphology on toughening of tetrafunctional epoxy resins with poly (ether imide). Polymer 1993, 34, 4832–4836. [Google Scholar] [CrossRef]
- Mimura, K.; Ito, H.; Fujioka, H. Toughening of epoxy resin modified with in situ polymerized thermoplastic polymers. Polymer 2001, 42, 9223–9233. [Google Scholar] [CrossRef]
- Kinloch, A.J. Toughening epoxy adhesives to meet today’s challenges. MRS Bull. 2003, 28, 445–448. [Google Scholar] [CrossRef]
- Bagheri, R.; Pearson, R. Role of particle cavitation in rubber-toughened epoxies: 1. Microvoid toughening. Polymer 1996, 37, 4529–4538. [Google Scholar] [CrossRef]
- Sue, H.; Garcia-Meitin, I.; Pickelman, D. Fracture behavior of rubber-modified high-performance epoxies. In Polymer Toughening; Arends, C., Ed.; Marcel Dekker Inc.: New York, NY, USA, 1996; pp. 131–174. [Google Scholar]
- Taylor, A. Adhesives with Nanoparticles. In Handbook of Adhesion Technology; da Silva, L., Öchsner, A., Adams, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1437–1460. [Google Scholar]
- Shaffer, O.; Bagheri, R.; Qian, J.; Dimonie, V.; Pearson, R.; El-Aasser, M. Characterization of the particle–matrix interface in rubber-modified epoxy by atomic force microscopy. J. Appl. Polym. Sci. 1995, 58, 465–484. [Google Scholar] [CrossRef]
- Manzione, L.; Gillham, J.; McPherson, C. Rubber-modified epoxies. II. Morphology and mechanical properties. J. Appl. Polym. Sci. 1981, 26, 907–919. [Google Scholar] [CrossRef]
- Kishi, H.; Matsuda, S.; Imade, J.; Shimoda, Y.; Nakagawa, T.; Furukawa, Y. The effects of the toughening mechanism and the molecular weights between cross-links on the fatigue resistance of epoxy polymer blends. Polymer 2021, 223, 123712. [Google Scholar] [CrossRef]
- Sue, H. Craze-like damage in a core-shell rubber-modified epoxy system. J. Mater. Sci. 1992, 27, 3098–3107. [Google Scholar] [CrossRef]
- Gam, K.; Miyamoto, M.; Nishimura, R.; Sue, H. Fracture behavior of core-shell rubber–modified clay-epoxy nanocomposites. Polym. Eng. Sci. 2003, 43, 1635–1645. [Google Scholar] [CrossRef]
- Lee, D.; Ikeda, T.; Miyazaki, N.; Choi, N. Fracture behavior around a crack tip in rubber-modified epoxy adhesive joint with various bond thicknesses. J. Mater. Sci. Lett. 2003, 22, 229–233. [Google Scholar] [CrossRef]
- Oshima, S.; Higuchi, R.; Kobayashi, S. Experimental characterization of cracking behavior initiating from microdefects in cross-ply CFRP laminates. Eng. Fract. Mech. 2023, 281, 109116. [Google Scholar] [CrossRef]
- O’Dwyer, D.; O’Dowd, N.; McCarthy, C.T. In-situ SEM mechanical testing of miniature bonded joints. Int. J. Adhes. Adhes. 2014, 50, 57–64. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, R.; Lv, Z.; Chen, W.; Li, X. Acoustic emission behaviors and damage mechanisms of adhesively bonded single-lap composite joints with adhesive defects. J. Reinf. Plast. Compos. 2015, 34, 84–92. [Google Scholar] [CrossRef]
- Xu, D.; Liu, P.; Li, J.; Chen, Z. Damage mode identification of adhesive composite joints under hygrothermal environment using acoustic emission and machine learning. Compos. Struct. 2019, 211, 351–363. [Google Scholar] [CrossRef]
- Manterola, J.; Aguirre, M.; Zurbitu, J.; Renart, J.; Turon, A.; Urresti, I. Using acoustic emissions (AE) to monitor mode I crack growth in bonded joints. Eng. Fract. Mech. 2020, 224, 106778. [Google Scholar] [CrossRef]
- Williams, J. The fracture mechanics of delamination tests. J. Strain Anal. Eng. Des. 1989, 24, 207–214. [Google Scholar] [CrossRef]
- Hojo, M.; Kageyama, K.; Tanaka, K. Prestandardization study on mode I interlaminar fracture toughness test for CFRP in Japan. Composites 1995, 26, 243–255. [Google Scholar] [CrossRef]
- ASTM D7905/D7905M-14; Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D5528/D5528M-21; Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites. ASTM International: West Conshohocken, PA, USA, 2021.
- Oshima, S.; Mamishin, A.; Hojo, M.; Nishikawa, M.; Matsuda, N.; Kanesaki, M. High-resolution in situ characterization of micromechanisms in CFRP laminates under mode II loading. Eng. Fract. Mech. 2022, 260, 108189. [Google Scholar] [CrossRef]
- Blackman, B.; Kinloch, A.; Paraschi, M. The determination of the mode II adhesive fracture resistance, GIIC, of structural adhesive joints: An effective crack length approach. Eng. Fract. Mech. 2005, 72, 877–897. [Google Scholar] [CrossRef]
- Morimoto, T.; Katoh, H.; Ishida, Y.; Hara, E.; Kusano, M.; Naito, K.; Watanabe, M.; Takagi, K.; Arai, K.; Hasegawa, K. Modified double cantilever beam test method for mode-I energy release rate of elastic adhesive layers. Eng. Fract. Mech. 2024, 307, 110320. [Google Scholar] [CrossRef]
- Lahuerta, F.; Westphal, T.; Nijssen, R.; Van Der Meer, F.; Sluys, L. Measuring the delamination length in static and fatigue mode I tests using video image processing. Compos. Part B Eng. 2014, 63, 1–7. [Google Scholar] [CrossRef]
- Oshima, S.; Ishida, H.; Kusaka, T.; Takeda, T. Experimental characterization of dynamic crack growth behavior in CFRP adhesive interface. Adv. Compos. Mater. 2018, 27, 397–411. [Google Scholar] [CrossRef]
- Chai, H. Shear fracture. Int. J. Fract. 1988, 37, 137–159. [Google Scholar] [CrossRef]
- Chai, H.; Chiang, M. A crack propagation criterion based on local shear strain in adhesive bonds subjected to shear. J. Mech. Phys. Solids 1996, 44, 1669–1689. [Google Scholar] [CrossRef]
- Leffler, K.; Alfredsson, K.; Stigh, U. Shear behaviour of adhesive layers. Int. J. Solids Struct. 2007, 44, 530–545. [Google Scholar] [CrossRef]
- Leffler, K. Shear Fracture of Adhesive Layers. Licentiate Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2005. [Google Scholar]
- Oshima, S.; Yoshimura, A.; Hirano, Y.; Ogasawara, T.; Tan, K.T. In-situ observation of microscopic damage in adhesively bonded CFRP joints under mode I and mode II loading. Compos. Struct. 2019, 227, 111330. [Google Scholar] [CrossRef]
- Bradley, W. Relationship of matrix toughness to interlaminar fracture toughness. In Composite Materials Series, 6: Application of Fracture Mechanics to Composite Materials; Friedrich, K., Ed.; Elsevier Science Publishers: Amsterdam, The Netherland, 1989; pp. 159–187. [Google Scholar]
- Lee, S. Mode II delamination failure mechanisms of polymer matrix composites. J. Mater. Sci. 1997, 32, 1287–1295. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Guo, W.; Deng, H.; Tong, J.; Aymerich, F. An investigation on strain/stress distribution around the overlap end of laminated composite single-lap joints. Compos. Struct. 2009, 89, 589–595. [Google Scholar] [CrossRef]
- Sun, G.; Liu, X.; Zheng, G.; Gong, Z.; Li, Q. On fracture characteristics of adhesive joints with dissimilar materials—An experimental study using digital image correlation (DIC) technique. Compos. Struct. 2018, 201, 1056–1075. [Google Scholar] [CrossRef]
- Moutrille, M.P.; Derrien, K.; Baptiste, D.; Balandraud, X.; Grédiac, M. Through-thickness strain field measurement in a composite/aluminium adhesive joint. Compos. Part A Appl. Sci. Manuf. 2009, 40, 985–996. [Google Scholar] [CrossRef]
- Kashfuddoja, M.; Ramji, M. Assessment of local strain field in adhesive layer of an unsymmetrically repaired CFRP panel using digital image correlation. Int. J. Adhes. Adhes. 2015, 57, 57–69. [Google Scholar] [CrossRef]
- Comer, A.; Katnam, K.; Stanley, W.; Young, T. Characterising the behaviour of composite single lap bonded joints using digital image correlation. Int. J. Adhes. Adhes. 2013, 40, 215–223. [Google Scholar] [CrossRef]
- Guo, B.; Xie, H.; Zhu, J.; Wang, H.; Chen, P.; Zhang, Q. Study on the mechanical behavior of adhesive interface by digital image correlation. Sci. China-Phys. Mech. Astron. 2011, 54, 574–580. [Google Scholar] [CrossRef]
- Tsai, M.; Morton, J.; Matthews, F. Experimental and numerical studies of a laminated composite single-lap adhesive joint. J. Compos. Mater. 1995, 29, 1254–1275. [Google Scholar] [CrossRef]
- Ruiz, P.; Jumbo, F.; Huntley, J.; Ashcroft, I.; Swallowe, G. Experimental and numerical investigation of strain distributions within the adhesive layer in bonded joints. Strain 2011, 47, 88–104. [Google Scholar] [CrossRef]
- Fikry, M.; Wang, Q.; Irita, M.; Ri, S.; Toyama, N.; Vinogradov, V.; Ogihara, S. Measurement of microscopic strain distributions of CFRP laminates with fiber discontinuities by sampling moiré method. Adv. Compos. Mater. 2022, 31, 273–288. [Google Scholar] [CrossRef]
- Oshima, S.; Yoshimura, A.; Hirano, Y.; Ogasawara, T. Experimental method for mode I fracture toughness of composite laminates using wedge loaded double cantilever beam specimens. Compos. Part A Appl. Sci. Manuf. 2018, 112, 119–125. [Google Scholar] [CrossRef]
- Ding, J.; Xu, W. Determination of mode I interlaminar fracture toughness of composite by a wedge-insert double cantilever beam and the nonlinear J integral. Compos. Sci. Technol. 2021, 206, 108674. [Google Scholar] [CrossRef]
- Oshima, S.; Yoshimura, A.; Yashiro, S.; Hirano, Y.; Ogasawara, T. Experimental and analytical validation of mode II fracture toughness tests for a type of double-lap joint. Compos. Struct. 2020, 234, 111757. [Google Scholar] [CrossRef]
- Yashiro, S.; Agata, T.; Yoshimura, A. A new approach for evaluating crack growth resistance curve of mode II delamination by doubly end-notched tension tests. Adv. Compos. Mater. 2018, 27, 119–133. [Google Scholar] [CrossRef]
- Oshima, S.; Ishida, H.; Choo, Y.; Kusaka, T.; Takeda, T. Effects of loading rate on the crack growth behavior of adhesively bonded CFRP joints with a structural film adhesive. J. Soc. Mater. Sci. Jpn. 2018, 67, 438–444. (In Japanese) [Google Scholar] [CrossRef]
- Álvarez, D.; Guild, F.; Kinloch, A.; Blackman, B. Partitioning of mixed-mode fracture in adhesively-bonded joints: Experimental studies. Eng. Fract. Mech. 2018, 203, 224–239. [Google Scholar] [CrossRef]
- Huang, Y.; Kinloch, A. Modelling of the toughening mechanisms in rubber-modified epoxy polymers: Part I Finite element analysis studies. J. Mater. Sci. 1992, 27, 2753–2762. [Google Scholar] [CrossRef]
- Pearson, R.; Yee, A. Toughening mechanisms in elastomer-modified epoxies: Part 2 Microscopy studies. J. Mater. Sci. 1986, 21, 2475–2488. [Google Scholar] [CrossRef]
- Pearson, R.; Yee, A. Influence of particle size and particle size distribution on toughening mechanisms in rubber-modified epoxies. J. Mater. Sci. 1991, 26, 3828–3844. [Google Scholar] [CrossRef]
- Terasaki, N.; Fujio, Y.; Horiuchi, S.; Akiyama, H. Mechanoluminescent studies of failure line on double cantilever beam (DCB) and tapered-DCB (TDCB) test with similar and dissimilar material joints. Int. J. Adhes. Adhes. 2019, 93, 102328. [Google Scholar] [CrossRef]
- Terasaki, N.; Fujio, Y.; Horiuchi, S.; Akiyama, H.; Itabashi, M. Mechanoluminescent study for optimization of joint design on cross tension test. J. Adhes. 2022, 98, 637–646. [Google Scholar] [CrossRef]
- Terasaki, N.; Fujio, Y.; Shimamoto, K.; Akiyama, H.; Horiuchi, S. Mechanoluminescent visualization for considering effect of bondline thickness and overlap length on single lap joint. Int. J. Adhes. Adhes. 2024, 134, 103786. [Google Scholar] [CrossRef]
- Terasaki, N.; Fujio, Y.; Sakata, Y.; Houjou, K.; Shimamoto, K.; Akiyama, H.; Yase, K.; Horiuchi, A.; Hartwig, S.; Steinberg, J.; et al. Effect of laser pre-treatment on adhesive joint performance and evaluation of interfacial strain distribution using mechanoluminescence. J. Adhes. 2025, 101, 191–208. [Google Scholar] [CrossRef]
- Haj-Ali, R.; Elhajjar, R. An infrared thermoelastic stress analysis investigation of single lap shear joints in continuous and woven carbon/fiber epoxy composites. Int. J. Adhes. Adhes. 2014, 48, 210–216. [Google Scholar] [CrossRef]
- Palumbo, D.; De Finis, R.; Galietti, U. Thermoelastic stress analysis as a method for the quantitative non-destructive evaluation of bonded CFRP T-joints. NDT E Int. 2021, 124, 102526. [Google Scholar] [CrossRef]
- Kimura, M.; Watanabe, T.; Oshima, S.; Takeichi, Y.; Niwa, Y.; Seryo, Y.; Hojo, M. Nanoscale in situ observation of damage formation in carbon fiber/epoxy composites under mixed-mode loading using synchrotron radiation X-ray computed tomography. Compos. Sci. Technol. 2022, 230, 109332. [Google Scholar] [CrossRef]
- Watanabe, T.; Takeichi, Y.; Niwa, Y.; Hojo, M.; Kimura, M. Nanoscale in situ observations of crack initiation and propagation in carbon fiber/epoxy composites using synchrotron radiation X-ray computed tomography. Compos. Sci. Technol. 2020, 197, 108244. [Google Scholar] [CrossRef]
- Takahashi, K.; Shoya, R.; Matsuo, T.; Sato, W.; Nakamura, T.; Takeuchi, A.; Uesugi, M.; Uesugi, K. X-ray nanoimaging of a transversely embedded carbon fiber in epoxy matrix under static and cyclic loads. Sci. Rep. 2022, 12, 8843. [Google Scholar] [CrossRef]
- Borstnar, G.; Gillard, F.; Mavrogordato, M.; Sinclair, I.; Spearing, S. Three-dimensional deformation mapping of Mode I interlaminar crack extension in particle-toughened interlayers. Acta Mater. 2016, 103, 63–70. [Google Scholar] [CrossRef]
- Schöberl, E.; Breite, C.; Melnikov, A.; Swolfs, Y.; Mavrogordato, M.; Sinclair, I.; Spearing, S. Fibre-direction strain measurement in a composite ply under quasi-static tensile loading using Digital Volume Correlation and in situ Synchrotron Radiation Computed Tomography. Compos. Part A Appl. Sci. Manuf. 2020, 137, 105935. [Google Scholar] [CrossRef]
- Drucker, D.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Naya, F.; Herráez, M.; Lopes, C.; González, C.; Van der Veen, S.; Pons, F. Computational micromechanics of fiber kinking in unidirectional FRP under different environmental conditions. Compos. Sci. Technol. 2017, 144, 26–35. [Google Scholar] [CrossRef]
- Naya, F.; González, C.; Lopes, C.; Van der Veen, S.; Pons, F. Computational micromechanics of the transverse and shear behavior of unidirectional fiber reinforced polymers including environmental effects. Compos. Part A Appl. Sci. Manuf. 2017, 92, 146–157. [Google Scholar] [CrossRef]
- Canal, L.; González, C.; Segurado, J.; LLorca, J. Intraply fracture of fiber-reinforced composites: Microscopic mechanisms and modeling. Compos. Sci. Technol. 2012, 72, 1223–1232. [Google Scholar] [CrossRef]
- Chevalier, J.; Camanho, P.; Lani, F.; Pardoen, T. Multi-scale characterization and modelling of the transverse compression response of unidirectional carbon fiber reinforced epoxy. Compos. Struct. 2019, 209, 160–176. [Google Scholar] [CrossRef]
- Herráez, M.; Mora, D.; Naya, F.; Lopes, C.; González, C.; LLorca, J. Transverse cracking of cross-ply laminates: A computational micromechanics perspective. Compos. Sci. Technol. 2015, 110, 196–204. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, X.; Li, W.; Yang, J.; Guan, Z. Compressive strength determined for ultrahigh modulus fiber reinforced composites by [90/0]ns laminates. Compos. Struct. 2018, 191, 24–35. [Google Scholar] [CrossRef]
- Kohler, S.; Cugnoni, J.; Amacher, R.; Botsis, J. Transverse cracking in the bulk and at the free edge of thin-ply composites: Experiments and multiscale modelling. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105468. [Google Scholar] [CrossRef]
- Oshima, S.; Seryo, Y.; Kimura, M.; Hojo, M. Mesoscale mechanism of damage in fracture process zone of CFRP laminates simulated with triaxial stress state-dependent constitutive equation of matrix resin. Compos. Sci. Technol. 2024, 257, 110837. [Google Scholar] [CrossRef]
- Fiedler, B.; Hojo, M.; Ochiai, S. The influence of thermal residual stresses on the transverse strength of CFRP using FEM. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1323–1326. [Google Scholar] [CrossRef]
- Fiedler, B.; Hojo, M.; Ochiai, S.; Schulte, K.; Ochi, M. Finite-element modeling of initial matrix failure in CFRP under static transverse tensile load. Compos. Sci. Technol. 2001, 61, 95–105. [Google Scholar] [CrossRef]
- González, C.; LLorca, J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: Microscopic mechanisms and modeling. Compos. Sci. Technol. 2007, 67, 2795–2806. [Google Scholar] [CrossRef]
- Vaughan, T.; McCarthy, C. Micromechanical modelling of the transverse damage behaviour in fibre reinforced composites. Compos. Sci. Technol. 2011, 71, 388–396. [Google Scholar] [CrossRef]
- Gurson, A. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol 1977, 99, 2–15. [Google Scholar] [CrossRef]
- Needleman, A.; Tvergaard, V. An analysis of ductile rupture in notched bars. J. Mech. Phys. Solids 1984, 32, 461–490. [Google Scholar] [CrossRef]
- Canal, L.; Segurado, J.; LLorca, J. Failure surface of epoxy-modified fiber-reinforced composites under transverse tension and out-of-plane shear. Int. J. Solids Struct. 2009, 46, 2265–2274. [Google Scholar] [CrossRef]
- Imanaka, M.; Orita, R.; Nakamura, Y.; Kimoto, M. Comparison of failure mechanisms between rubber-modified and unmodified epoxy adhesives under mode II loading condition. J. Mater. Sci. 2008, 43, 3223–3233. [Google Scholar] [CrossRef]
- Lee, C.; Chun, M.; Kim, M.; Lee, J. Numerical evaluation for debonding failure phenomenon of adhesively bonded joints at cryogenic temperatures. Compos. Sci. Technol. 2011, 71, 1921–1929. [Google Scholar] [CrossRef]
- Hoshikawa, Y.; Kawagoe, Y.; Ryuzono, K.; Okabe, T. Finite element modeling for cohesive/adhesive failure of adhesive structures with a thermosetting resin. Eng. Fract. Mech. 2024, 311, 110552. [Google Scholar] [CrossRef]
- Dassault Systémes. Abaqus User Manual; Dassault Systémes: Vélizy-Villacoublay, France, 2020. [Google Scholar]
- Koyanagi, J.; Nakakura, A.; Takamura, M.; Takeda, S.; Morimoto, T. Numerical simulation for enhancing joint strength of CFRP single-wrap bonds through post-processing. J. Jpn. Soc. Compos. Mater. 2024, 50, 171–176. (In Japanese) [Google Scholar] [CrossRef]
- Schwarzkopf, G.; Bobbert, M.; Teutenberg, D.; Meschut, G.; Matzenmiller, A. Tolerance analysis of adhesive bonds in crash simulation. Procedia CIRP 2016, 43, 321–326. [Google Scholar] [CrossRef]
- Schmelzle, L.; Striewe, M.; Mergheim, J.; Meschut, G.; Possart, G.; Teutenberg, D.; Hein, D.; Steinmann, P. Testing, modelling, and parameter identification for adhesively bonded joints under the influence of temperature. J. Adhes. Sci. Technol. 2023, 37, 2285–2316. [Google Scholar] [CrossRef]
- Campilho, R.; Banea, M.; Neto, J.; da Silva, L. Modelling adhesive joints with cohesive zone models: Effect of the cohesive law shape of the adhesive layer. Int. J. Adhes. Adhes. 2013, 44, 48–56. [Google Scholar] [CrossRef]
- Alfano, M.; Furgiuele, F.; Leonardi, A.; Maletta, C.; Paulino, G. Mode I fracture of adhesive joints using tailored cohesive zone models. Int. J. Fatigue 2009, 157, 193–204. [Google Scholar] [CrossRef]
- Khoramishad, H.; Crocombe, A.; Katnam, K.; Ashcroft, I. Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. Int. J. Fatigue 2010, 32, 1146–1158. [Google Scholar] [CrossRef]
- Takamura, M.; Isozaki, M.; Takeda, S.; Oya, Y.; Koyanagi, J. Evaluation of true bonding strength for adhesive bonded carbon fiber-reinforced plastics. Materials 2024, 17, 394. [Google Scholar] [CrossRef] [PubMed]
- Marques, E.; da Silva, L. Joint strength optimization of adhesively bonded patches. J. Adhes. 2008, 84, 915–934. [Google Scholar] [CrossRef]
- Monteiro, J.; Akhavan-Safar, A.; Carbas, R.; Marques, E.; Goyal, R.; El-Zein, M.; Da Silva, L. Mode II modeling of adhesive materials degraded by fatigue loading using cohesive zone elements. Theor. Appl. Fract. Mech. 2019, 103, 102253. [Google Scholar] [CrossRef]
- Eghbalpoor, R.; Akhavan-Safar, A.; Jalali, S.; Ayatollahi, M.; Da Silva, L. A progressive damage model to predict the shear and mixed-mode low-cycle impact fatigue life of adhesive joints using cohesive elements. Finite Elem. Anal. Des. 2023, 216, 103894. [Google Scholar] [CrossRef]
- Shenoy, V.; Ashcroft, I.; Critchlow, G.; Crocombe, A. Fracture mechanics and damage mechanics based fatigue lifetime prediction of adhesively bonded joints subjected to variable amplitude fatigue. Eng. Fract. Mech. 2010, 77, 1073–1090. [Google Scholar] [CrossRef]
- Imanaka, M.; Hamano, T.; Morimoto, A.; Ashino, R.; Kimoto, M. Fatigue damage evaluation of adhesively bonded butt joints with a rubber-modified epoxy adhesive. J. Adhes. Sci. Technol. 2003, 17, 981–994. [Google Scholar] [CrossRef]
- Imanaka, M.; Taniguchi, M.; Hamano, T.; Kimoto, M. Fatigue life estimation of adhesively bonded scarf joints based on a continuum damage mechanics model. Polym. Polym. Compos. 2005, 13, 359–370. [Google Scholar] [CrossRef]
- Wahab, M.; Ashcroft, I.; Crocombe, A.; Shaw, S. Prediction of fatigue thresholds in adhesively bonded joints using damage mechanics and fracture mechanics. J. Adhes. Sci. Technol. 2001, 15, 763–781. [Google Scholar] [CrossRef]
- Li, Y.; Fikry, M.; Koyanagi, J. Numerical simulation for durability of a viscoelastic polymer material subjected to variable loadings fatigue based on entropy damage criterion. Polymers 2024, 16, 2857. [Google Scholar] [CrossRef] [PubMed]
- Liljedahl, C.; Crocombe, A.; Wahab, M.; Ashcroft, I. The effect of residual strains on the progressive damage modelling of environmentally degraded adhesive joints. J. Adhes. Sci. Technol. 2005, 19, 525–547. [Google Scholar] [CrossRef]
- Doyle, G.; Pethrick, R. Environmental effects on the ageing of epoxy adhesive joints. Int. J. Adhes. Adhes. 2009, 29, 77–90. [Google Scholar] [CrossRef]
- Oshima, S.; Kitagawa, K.; Takeda, T.; Kumazawa, H.; Kitazono, K. Effects of freeze–thaw cycles on mode I fracture toughness of adhesively bonded CFRP joints. Adv. Compos. Mater. 2024, 33, 90–104. [Google Scholar] [CrossRef]
- Heshmati, M.; Haghani, R.; Al-Emrani, M. Dependency of cohesive laws of a structural adhesive in Mode-I and Mode-II loading on moisture, freeze-thaw cycling, and their synergy. Mater. Des. 2017, 122, 433–447. [Google Scholar] [CrossRef]
- Hua, Y.; Crocombe, A.; Wahab, M.; Ashcroft, I. Continuum damage modelling of environmental degradation in joints bonded with EA9321 epoxy adhesive. Int. J. Adhes. Adhes. 2008, 28, 302–313. [Google Scholar] [CrossRef]
- Leger, R.; Roy, A.; Grandidier, J. A study of the impact of humid aging on the strength of industrial adhesive joints. Int. J. Adhes. Adhes. 2013, 44, 66–77. [Google Scholar] [CrossRef]
- Heshmati, M.; Haghani, R.; Al-Emrani, M. Durability of CFRP/steel joints under cyclic wet-dry and freeze-thaw conditions. Compos. Part B Eng. 2017, 126, 211–226. [Google Scholar] [CrossRef]


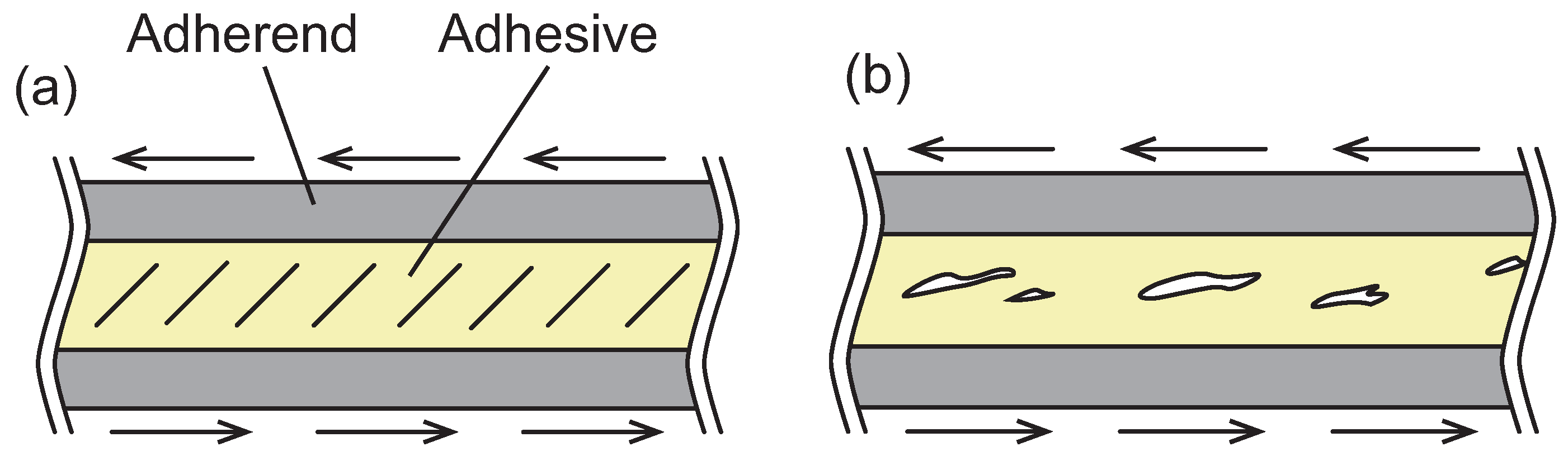

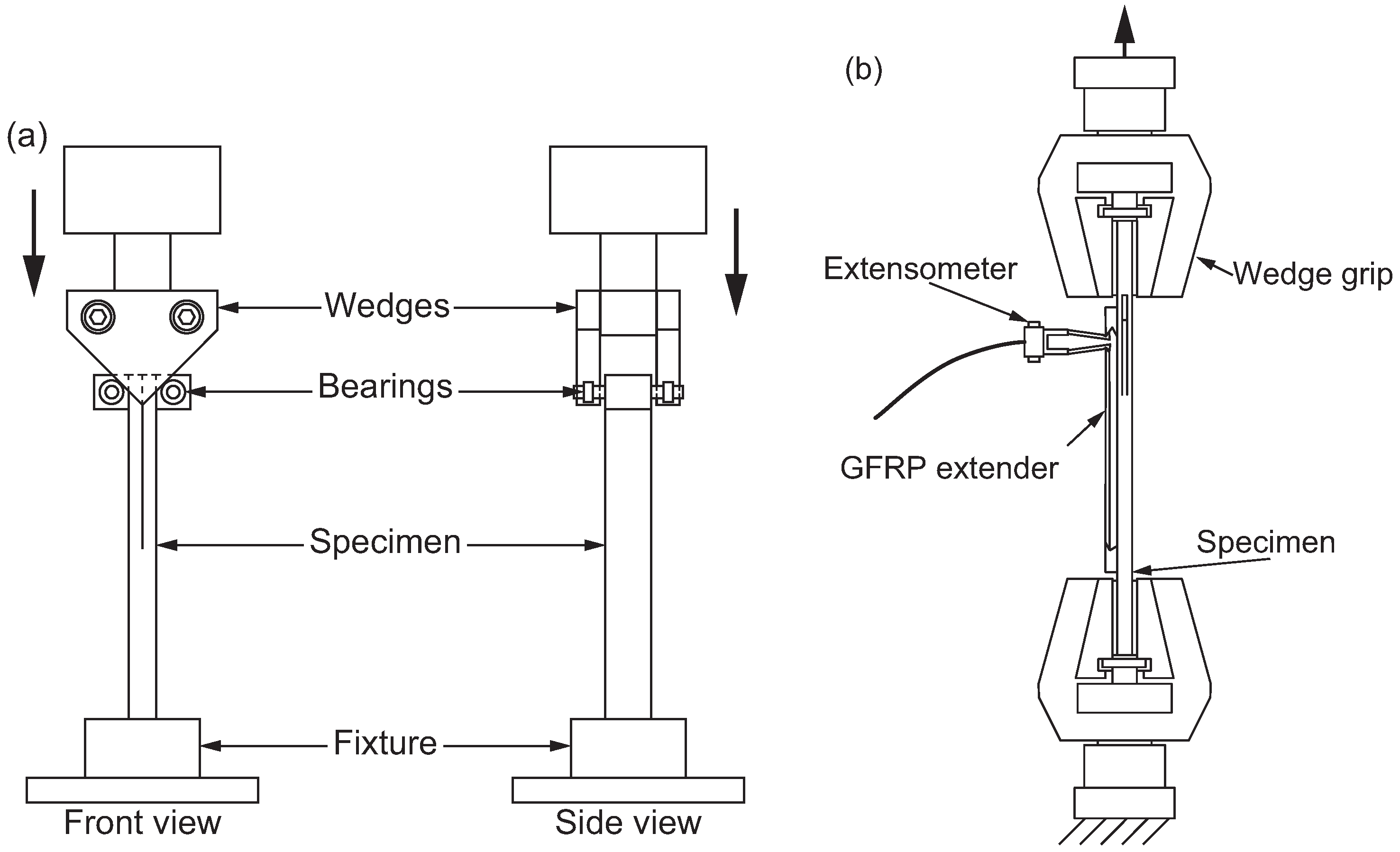
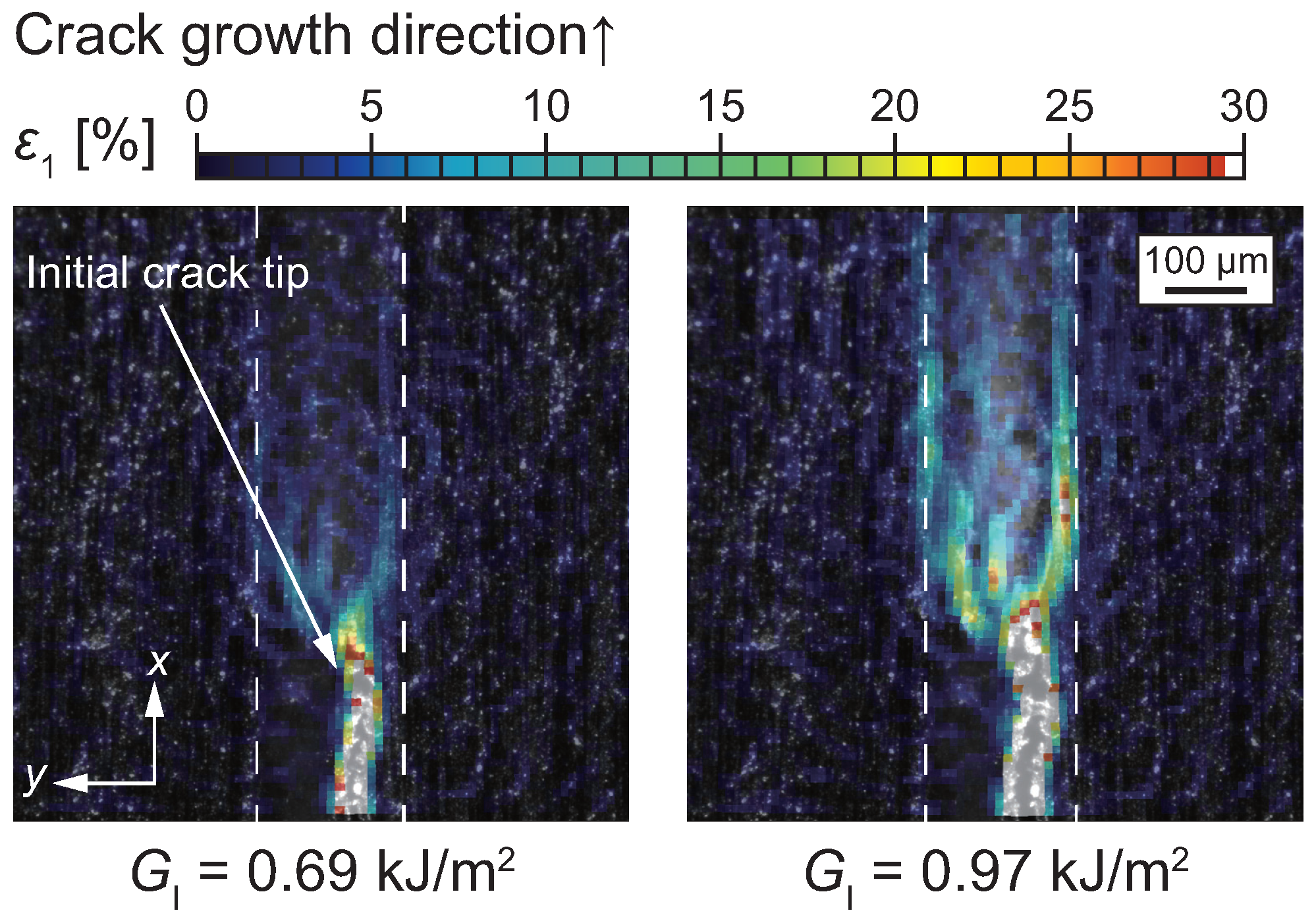
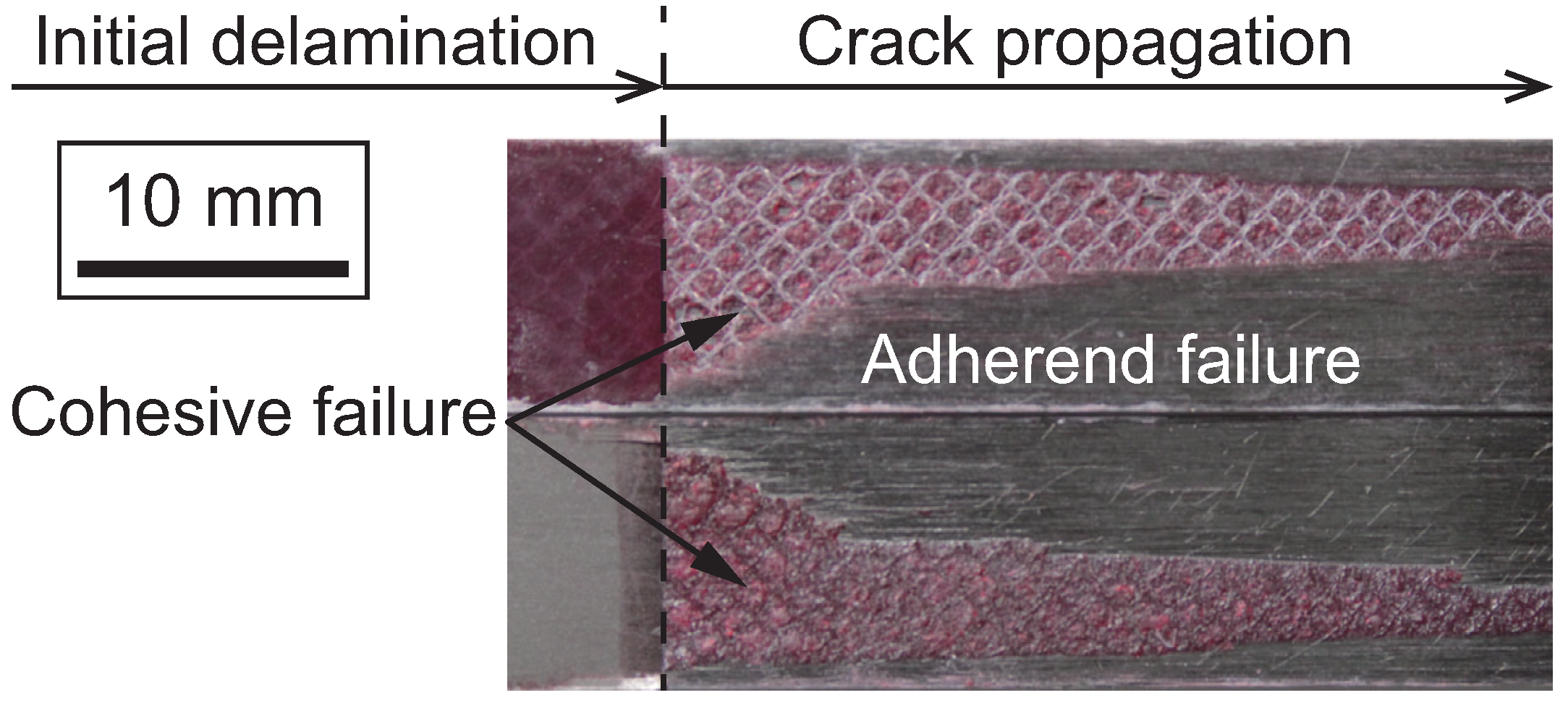
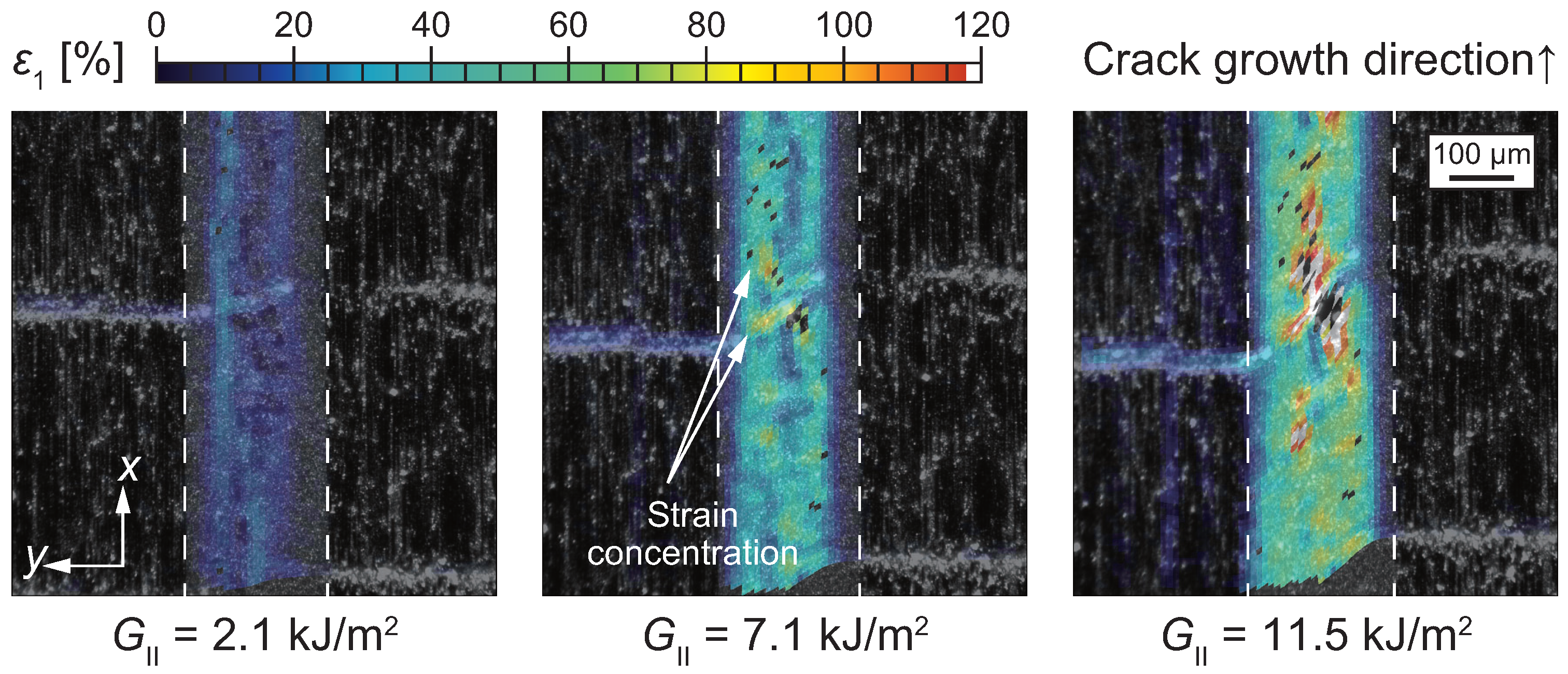
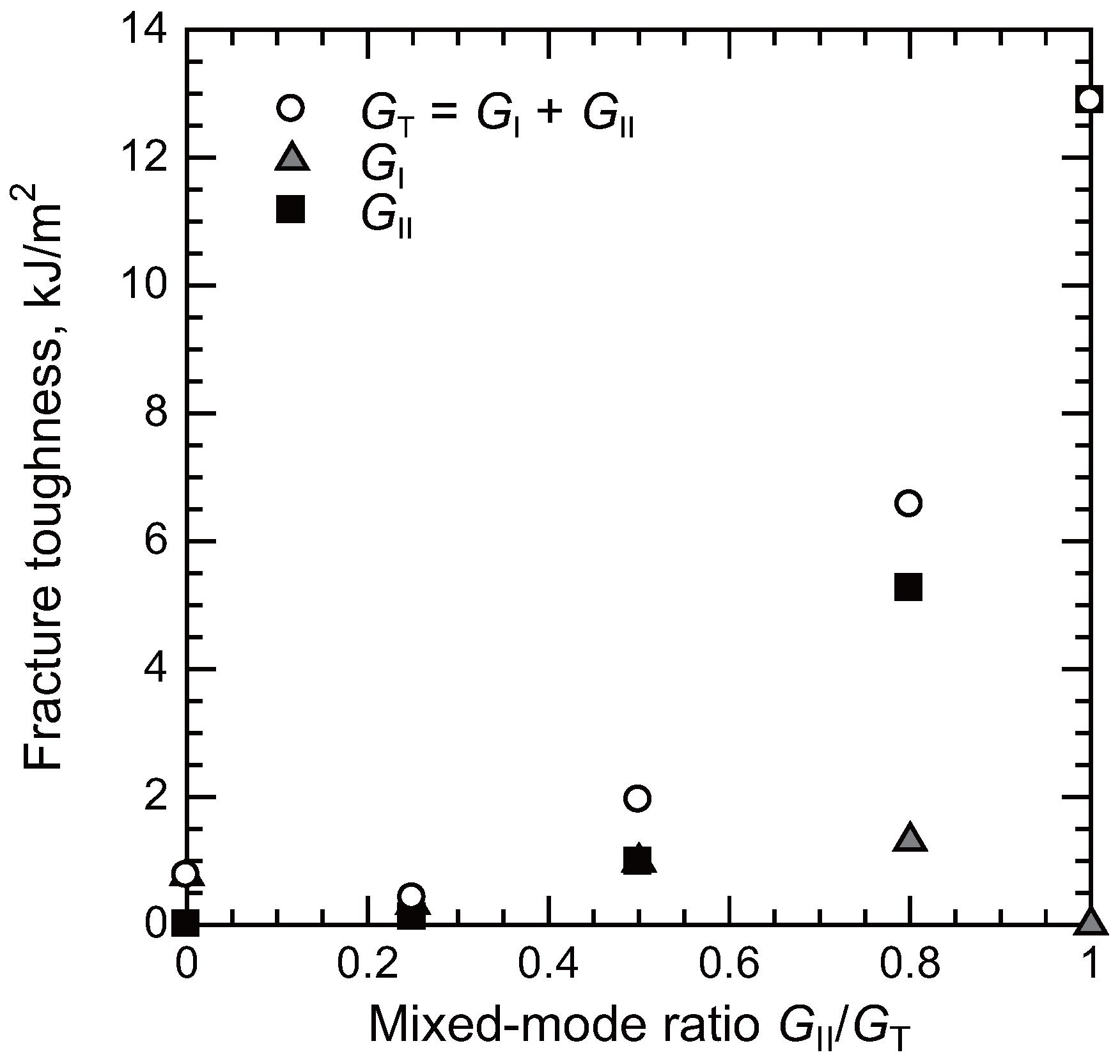

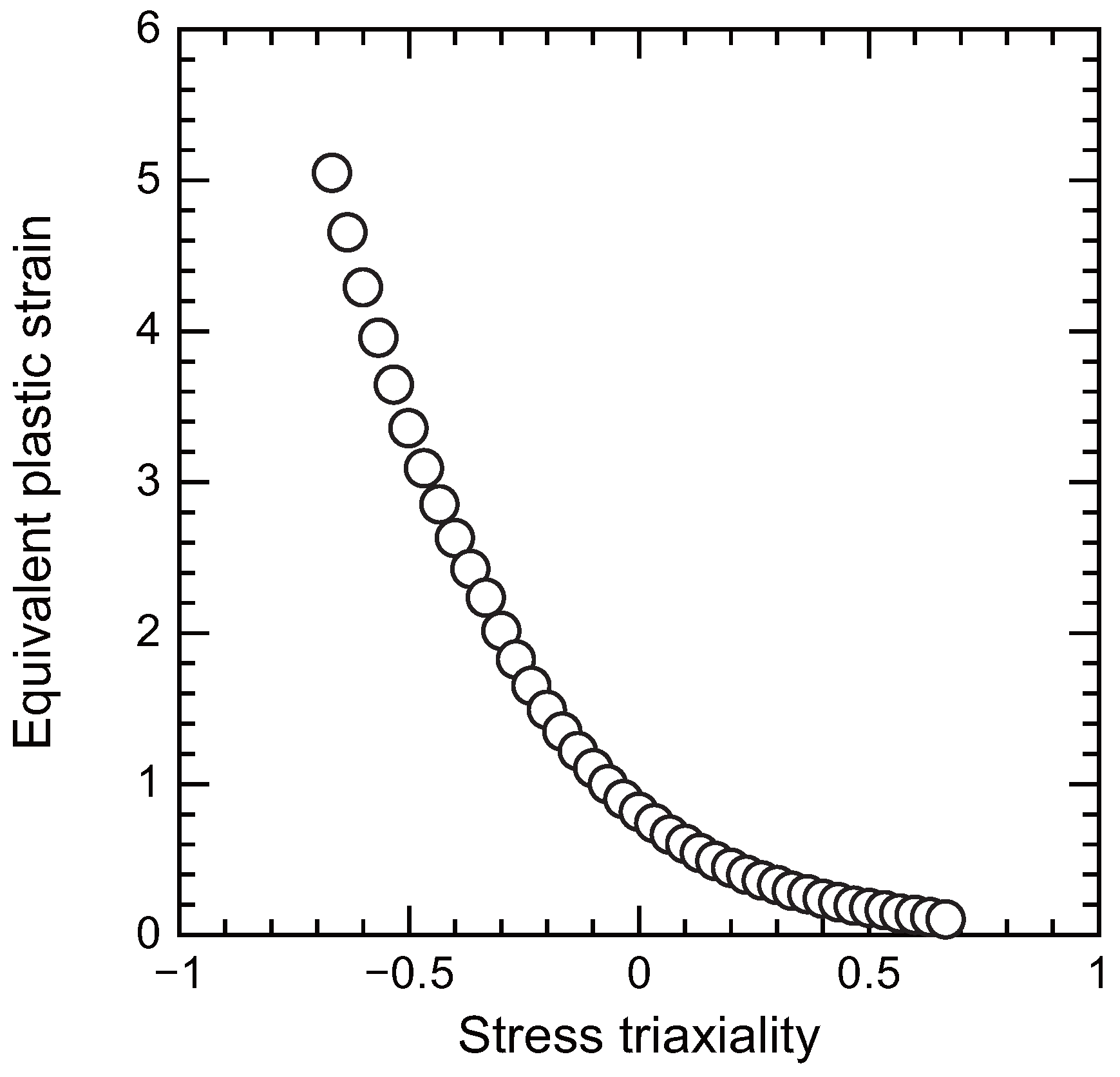
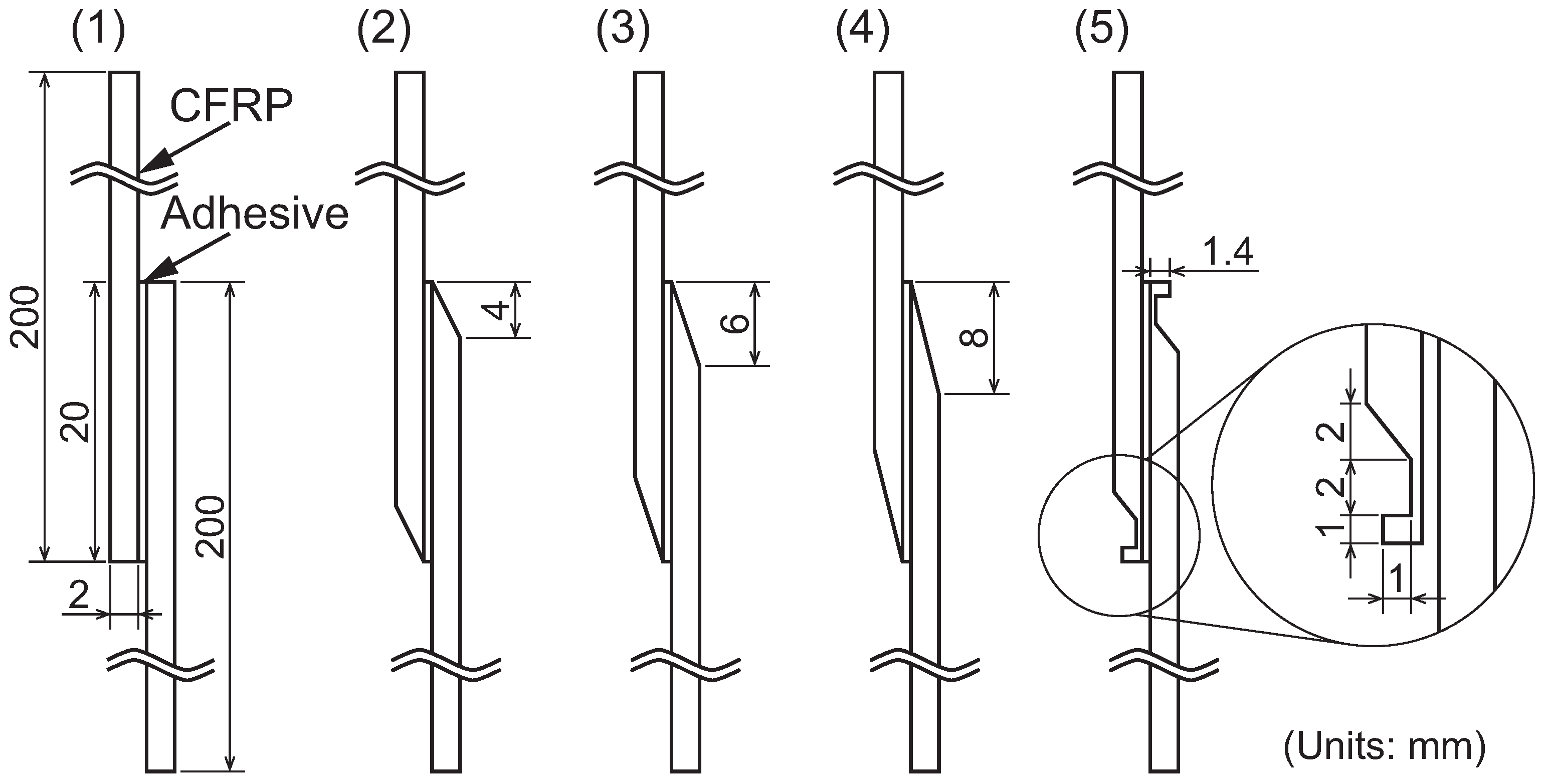

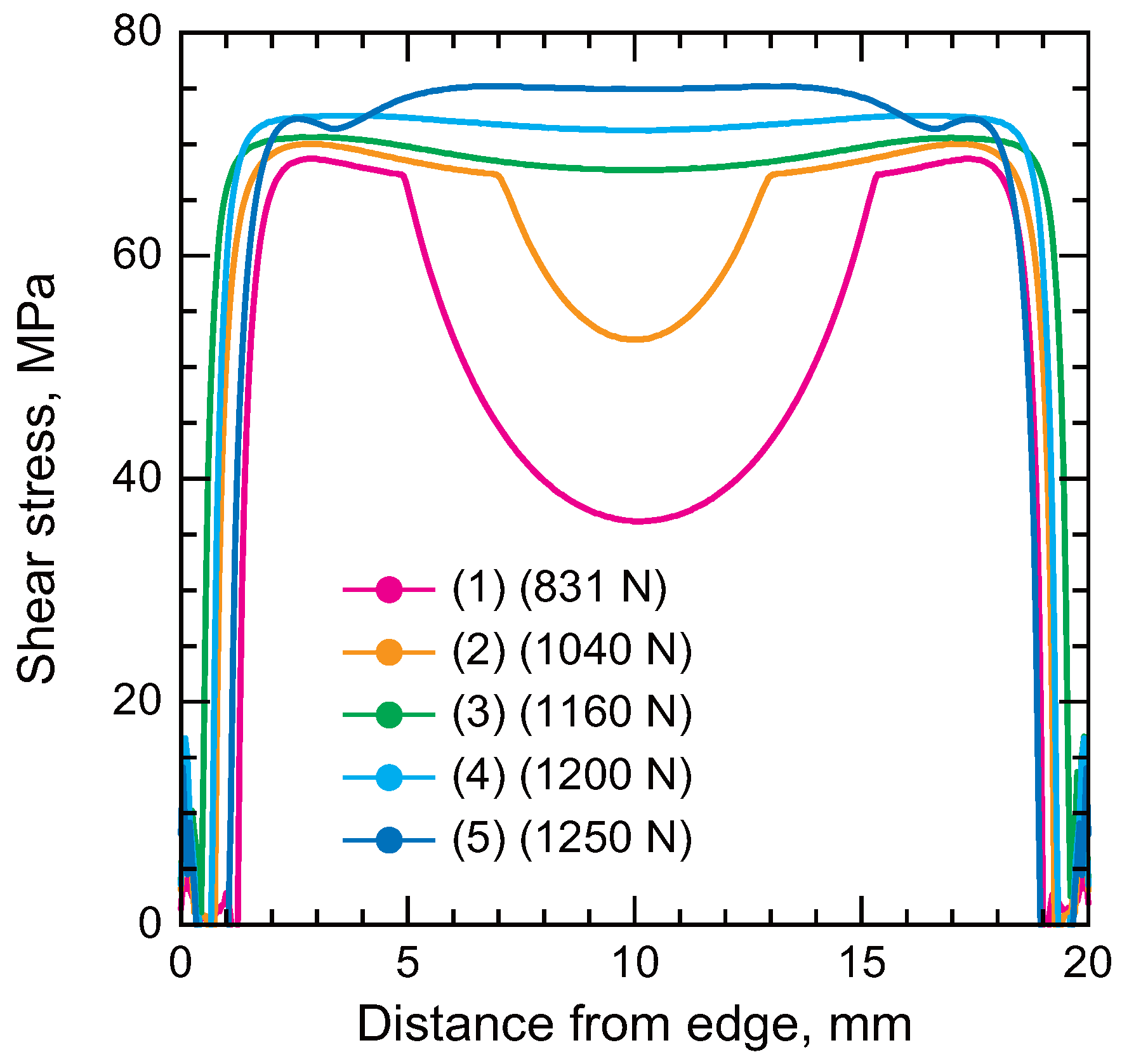
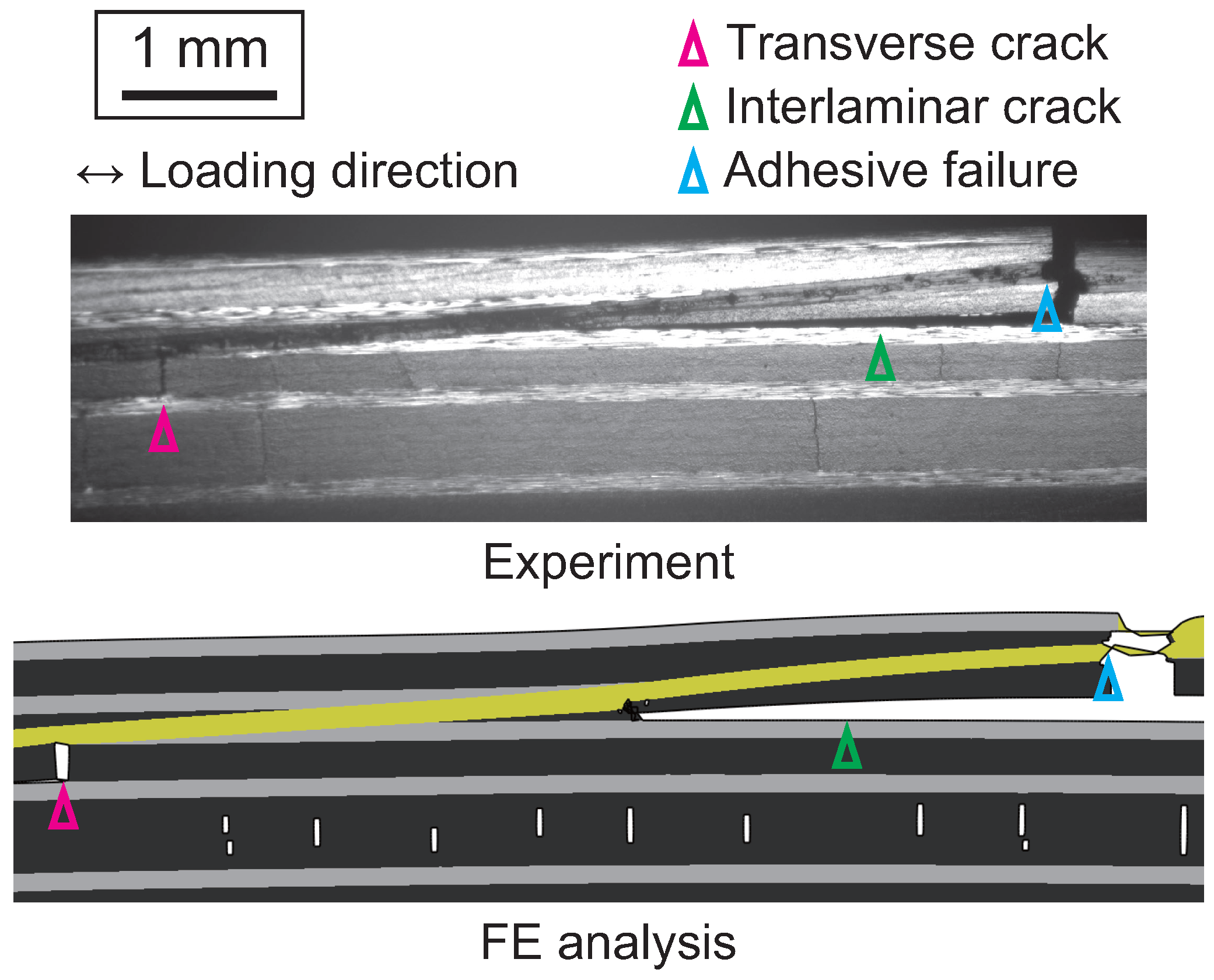
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oshima, S.; Koyanagi, J. Review on Damage and Failure in Adhesively Bonded Composite Joints: A Microscopic Aspect. Polymers 2025, 17, 377. https://doi.org/10.3390/polym17030377
Oshima S, Koyanagi J. Review on Damage and Failure in Adhesively Bonded Composite Joints: A Microscopic Aspect. Polymers. 2025; 17(3):377. https://doi.org/10.3390/polym17030377
Chicago/Turabian StyleOshima, Sota, and Jun Koyanagi. 2025. "Review on Damage and Failure in Adhesively Bonded Composite Joints: A Microscopic Aspect" Polymers 17, no. 3: 377. https://doi.org/10.3390/polym17030377
APA StyleOshima, S., & Koyanagi, J. (2025). Review on Damage and Failure in Adhesively Bonded Composite Joints: A Microscopic Aspect. Polymers, 17(3), 377. https://doi.org/10.3390/polym17030377





