Optimizing the Synthesis of CO2-Responsive Polymers: A Kinetic Model Approach for Scaling Up
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
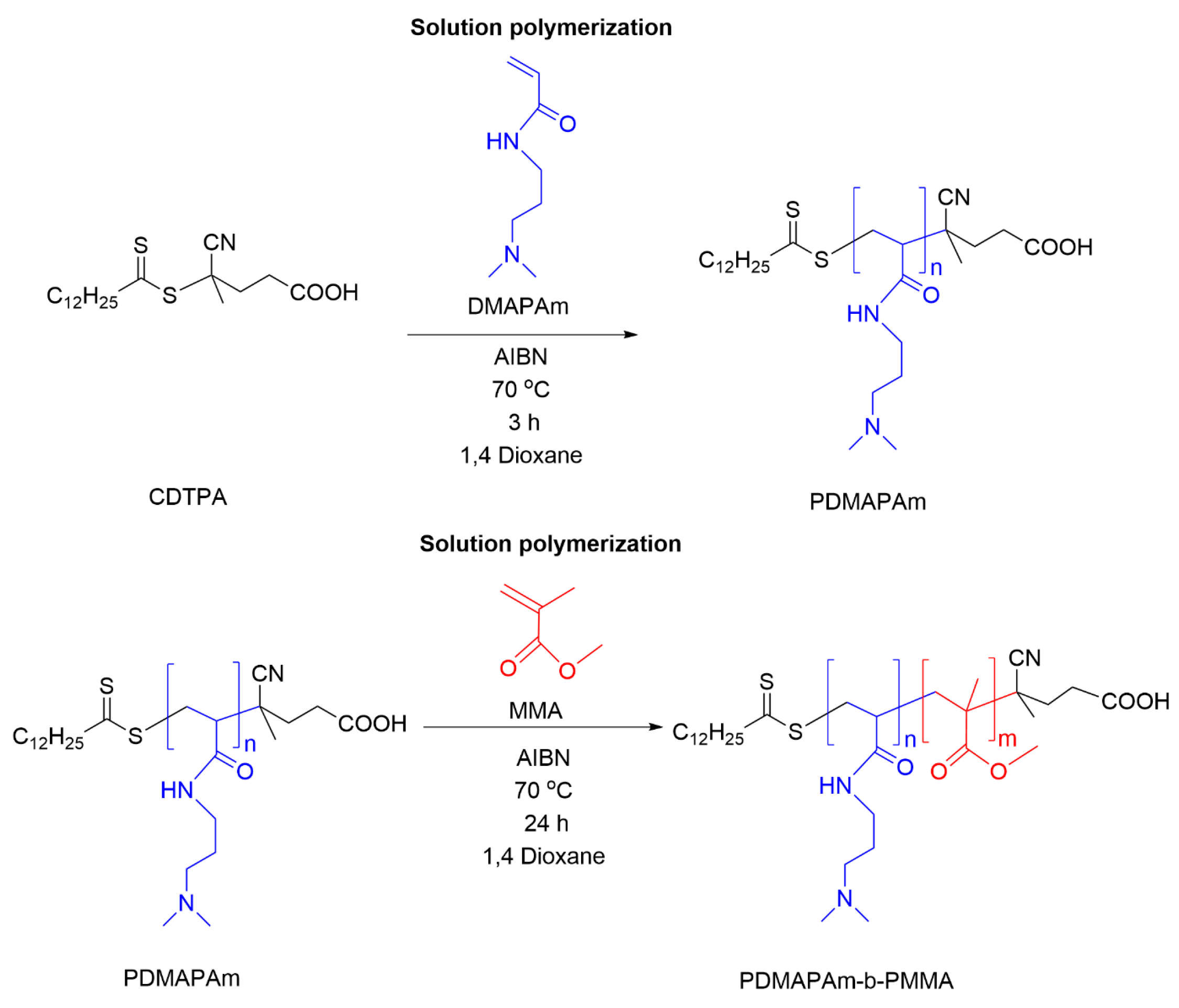
2.1.1. Synthesis of PDMAPAm via RAFT Polymerization
2.1.2. Synthesis of PDMAPAm-b-PMMA via RAFT Polymerization
2.2. Analytics
2.2.1. Proton Nuclear Magnetic Resonance Spectroscopy (1H NMR)
2.2.2. Gel Permeation Chromatography (GPC)
3. Results
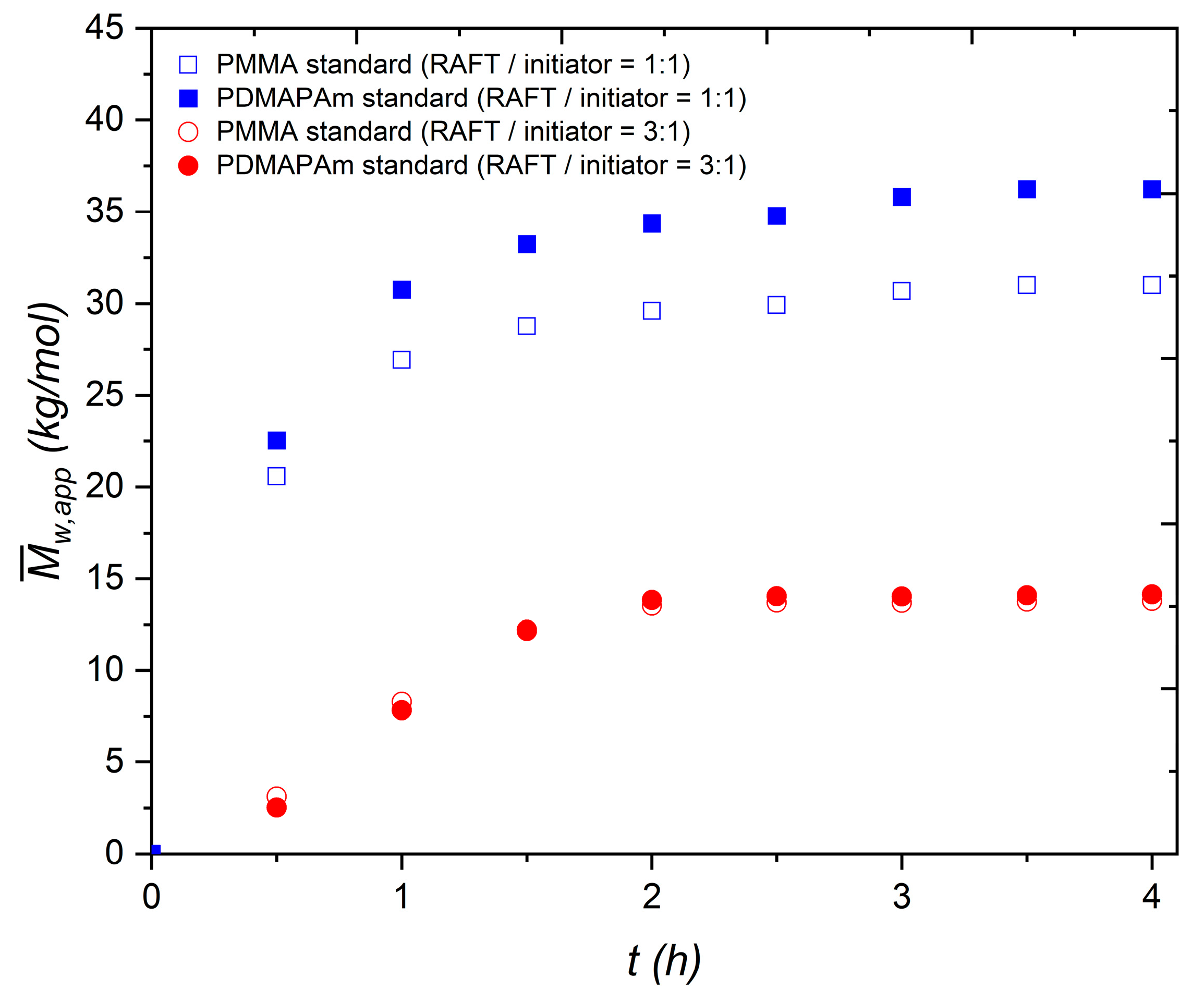
3.1. Preliminary Remarks on Kinetic Experiments and Polymer Synthesis
3.2. Mark–Houwink–Sakurada Parameters
3.3. Model Description
3.3.1. Structure of Model
3.3.2. Reaction Rates
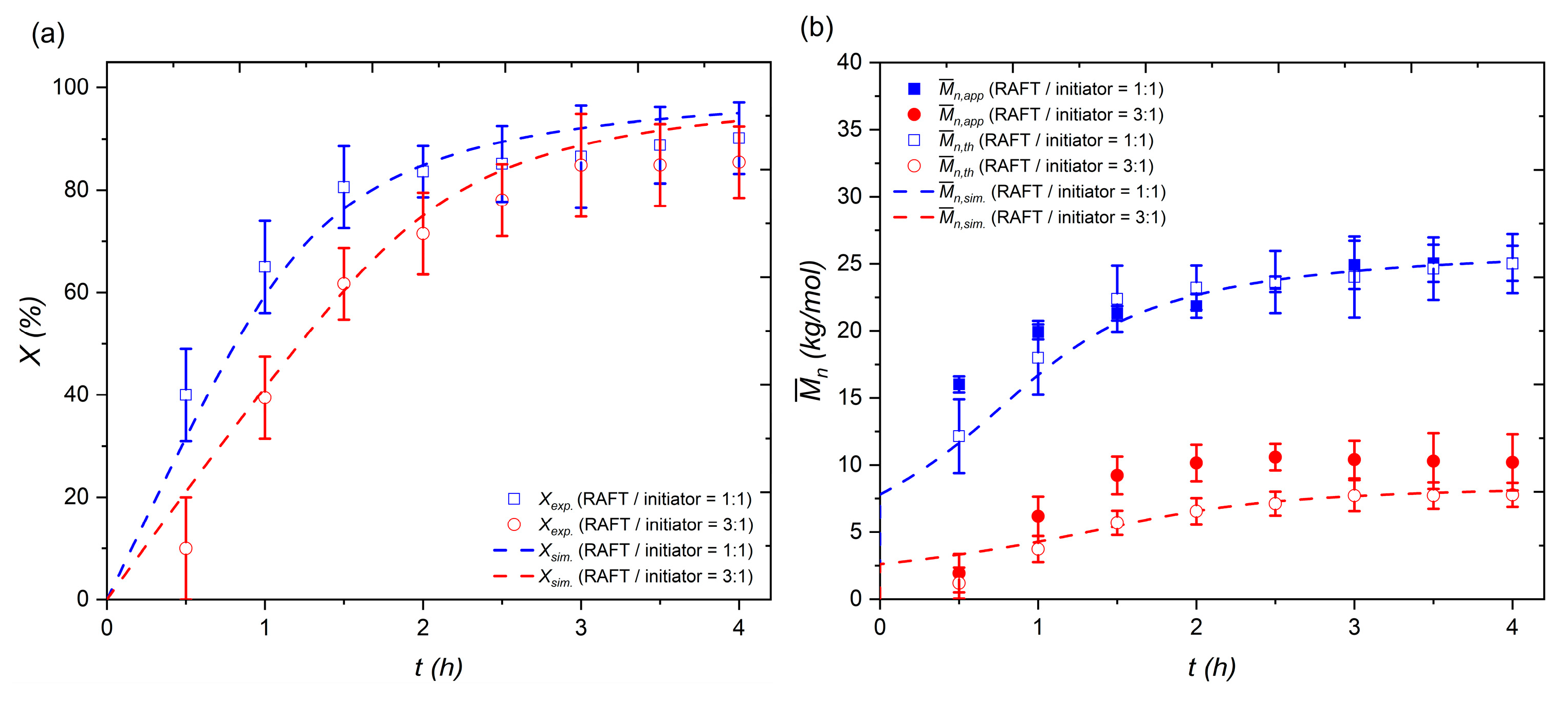
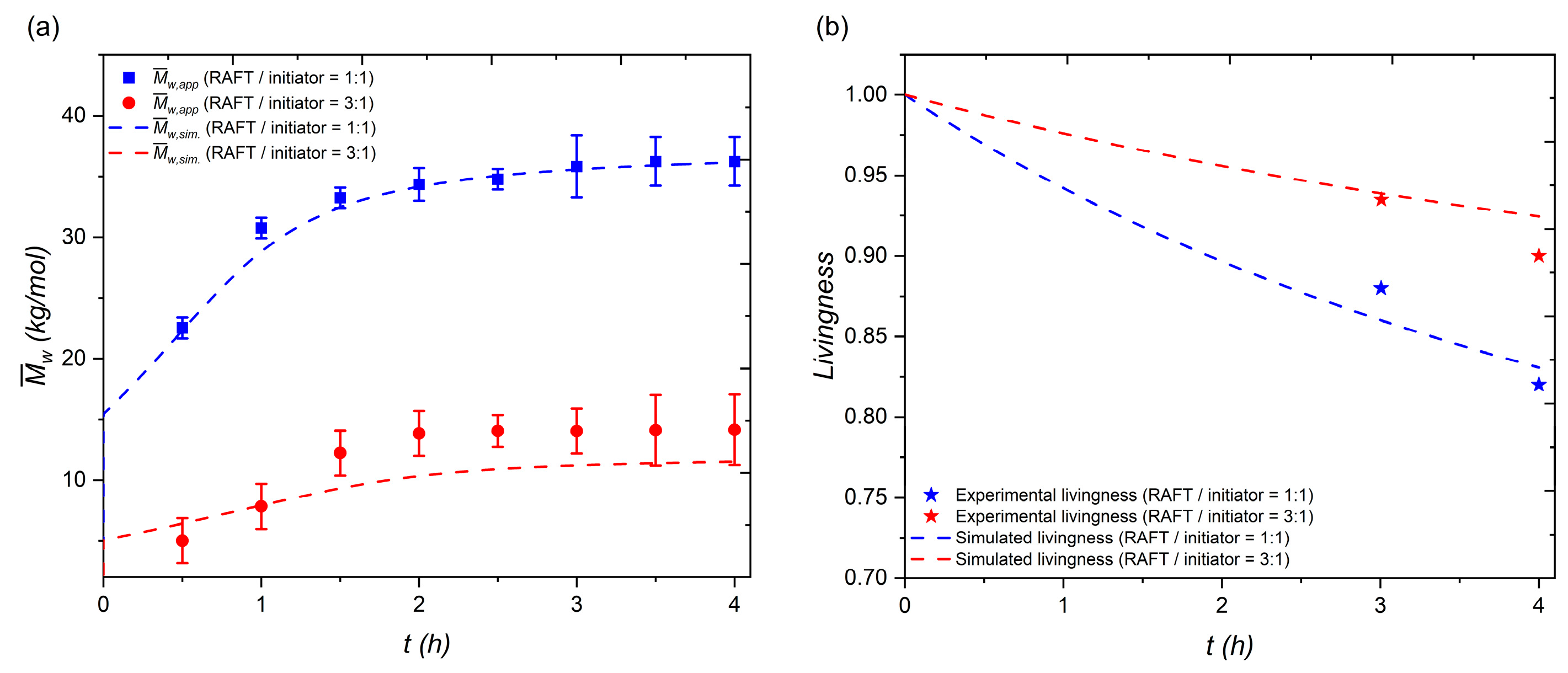
3.3.3. Model Validation
3.4. Model Prediction and Application for Scaling Up
3.5. Preliminary Results of CO2-Responsiveness of Polymer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DMAPAm | N-[3-(dimethylamino)propyl]-acrylamide |
| MMA | Methyl methacrylate |
| PDMAPAm-b-PMMA | Poly(N-[3-(dimethylamino)propyl]-acrylamide)-b-poly(methyl methacrylate) |
| RAFT | Reversible Addition−Fragmentation Chain-Transfer |
| CDTPA | 4-cyano-4-[(dodecylsulfanylthiocarbonyl)-sufanyl]pentanoic acid |
| AIBN | 2,2′-Azobis(2-methylpropionitrile) |
| CDCl3 | Deuterated chloroform |
| THF | Tetrahydrofuran |
| 4VP | 4-Vinylpyridine |
| 1H NMR | Proton Nuclear Magnetic Resonance Spectroscopy |
| GPC | Gel permeation chromatography |
References
- Bui, M.; Adjiman, C.S.; Bardow, A.; Anthony, E.J.; Boston, A.; Brown, S.; Fennell, P.S.; Fuss, S.; Galindo, A.; Hackett, L.A. Carbon capture and storage (CCS): The way forward. Energy Environ. Sci. 2018, 11, 1062–1176. [Google Scholar] [CrossRef]
- Ozkan, M.; Nayak, S.P.; Ruiz, A.D.; Jiang, W. Current status and pillars of direct air capture technologies. Iscience 2022, 25, 103990. [Google Scholar] [CrossRef] [PubMed]
- Erans, M.; Sanz-Pérez, E.S.; Hanak, D.P.; Clulow, Z.; Reiner, D.M.; Mutch, G.A. Direct air capture: Process technology, techno-economic and socio-political challenges. Energy Environ. Sci. 2022, 15, 1360–1405. [Google Scholar] [CrossRef]
- Breyer, C.; Fasihi, M.; Bajamundi, C.; Creutzig, F. Direct air capture of CO2: A key technology for ambitious climate change mitigation. Joule 2019, 3, 2053–2057. [Google Scholar] [CrossRef]
- Murdock, C.R.; Didas, S.; Jones, C.W. Direct capture of CO2 from ambient air. Chem. Rev. 2016, 116, 11840–11876. [Google Scholar]
- Zhou, Z.; Liu, T.; Khan, A.U.; Liu, G. Block copolymer–based porous carbon fibers. Sci. Adv. 2019, 5, eaau6852. [Google Scholar] [CrossRef] [PubMed]
- Nieswandt, K.; Georgopanos, P.; Abetz, V. Well-defined polyvinylpyridine-block-polystyrene diblock copolymers via RAFT aqueous-alcoholic dispersion polymerization: Synthesis and isoporous thin film morphology. Polym. Chem. 2021, 12, 2210–2221. [Google Scholar] [CrossRef]
- Shevate, R.; Kumar, M.; Karunakaran, M.; Canlas, C.; Peinemann, K.-V. Surprising transformation of a block copolymer into a high performance polystyrene ultrafiltration membrane with a hierarchically organized pore structure. J. Mater. Chem. A 2018, 6, 4337–4345. [Google Scholar] [CrossRef]
- Kandelhard, F.; Pashayev, E.; Schymura, J.; Georgopanos, P. Kinetic Modeling of the Synthesis of Poly (4-vinylpyridine) Macro-Reversible Addition-Fragmentation Chain Transfer Agents for the Preparation of Block Copolymers. Ind. Eng. Chem. Res. 2023, 62, 8696–8708. [Google Scholar] [CrossRef]
- Pashayev, E.; Kandelhard, F.; Georgopanos, P. Experimental & Modelling Digital Twin Approach for Polymer Synthesis via Re-initiated Oxygen inhibited RAFT Polymerization. Macromol. React. Eng. 2023, 17, 2200068. [Google Scholar]
- Kandelhard, F.; Schuldt, K.; Schymura, J.; Georgopanos, P.; Abetz, V. Model-Assisted Optimization of RAFT Polymerization in Micro-Scale Reactors—A Fast Screening Approach. Macromol. React. Eng. 2021, 15, 2000058. [Google Scholar] [CrossRef]
- Pashayev, E.; Kandelhard, F.; Georgopanos, P. Sauerstoffempfindlichkeit der RAFT-Polymerisation–Eine Modellierungsstudie. Chem.-Ing.-Tech. 2024, 96, 805–812. [Google Scholar] [CrossRef]
- Shieh, Y.-T.; Lin, Y.-T.; Cheng, C.-C. CO2-switchable behavior of chitosan-g-poly [(2-dimethylamino) ethyl methacrylate] as an emulsifier. Carbohydr. Polym. 2017, 170, 281–288. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhou, J.; Ye, X.; Li, Z.; Wang, Y. CO2-responsive membranes prepared by selective swelling of block copolymers and their behaviors in protein ultrafiltration. J. Membr. Sci. 2022, 641, 119928. [Google Scholar] [CrossRef]
- Cunningham, M.F.; Jessop, P.G. An introduction to the principles and fundamentals of CO2-switchable polymers and polymer colloids. Eur. Polym. J. 2016, 76, 208–215. [Google Scholar] [CrossRef]
- Riabtseva, A.; Ellis, S.N.; Champagne, P.; Jessop, P.G.; Cunningham, M.F. CO2-responsive branched polymers for forward osmosis applications: The effect of branching on draw solute properties. Ind. Eng. Chem. Res. 2021, 60, 9807–9816. [Google Scholar] [CrossRef]
- Demirci, S.; Sutekin, S.D.; Guven, O.; Sahiner, N. Poly (2-aminoethyl methacrylate) based microgels catalyst system to be used in hydrolysis and methanolysis of NaBH4 for H2 generation. Int. J. Hydrog. Energy 2023, 48, 23002–23012. [Google Scholar] [CrossRef]
- Ji, W.; Panus, D.; Palumbo, R.N.; Tang, R.; Wang, C. Poly (2-aminoethyl methacrylate) with well-defined chain length for DNA vaccine delivery to dendritic cells. Biomacromolecules 2011, 12, 4373–4385. [Google Scholar] [CrossRef]
- Pashayev, E.; Georgopanos, P. CO2-Responsive Copolymers for Membrane Applications, Synthesis, and Performance Evaluation. Macromol. Mater. Eng. 2025, 310, 2400290. [Google Scholar] [CrossRef]
- Nieswandt, K.; Georgopanos, P.; Abetz, C.; Filiz, V.; Abetz, V. Synthesis of poly (3-vinylpyridine)-block-polystyrene diblock copolymers via surfactant-free RAFT emulsion polymerization. Materials 2019, 12, 3145. [Google Scholar] [CrossRef]
- Nieswandt, K.; Georgopanos, P.; Held, M.; Sperling, E.; Abetz, V. RAFT Emulsion Polymerization of Styrene Using a Poly ((N, N-dimethyl acrylamide)-co-(N-isopropyl acrylamide)) mCTA: Synthesis and Thermosensitivity. Polymers 2021, 14, 62. [Google Scholar] [CrossRef]
- Abetz, V. Isoporous block copolymer membranes. Macromol. Rapid Commun. 2015, 36, 10–22. [Google Scholar] [CrossRef] [PubMed]
- Barner-Kowollik, C.; Quinn, J.F.; Morsley, D.R.; Davis, T.P. Modeling the reversible addition–fragmentation chain transfer process in cumyl dithiobenzoate-mediated styrene homopolymerizations: Assessing rate coefficients for the addition–fragmentation equilibrium. J. Polym. Sci. Part A Polym. Chem. 2001, 39, 1353–1365. [Google Scholar] [CrossRef]
- Ribelli, T.G.; Konkolewicz, D.; Bernhard, S.; Matyjaszewski, K. How are radicals (re) generated in photochemical ATRP? J. Am. Chem. Soc. 2014, 136, 13303–13312. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Hong, C.-Y.; Pan, C.-Y. Polymerization techniques in polymerization-induced self-assembly (PISA). Polym. Chem. 2020, 11, 3673–3689. [Google Scholar] [CrossRef]
- Delplace, V.; Guégain, E.; Harrisson, S.; Gigmes, D.; Guillaneuf, Y.; Nicolas, J. A ring to rule them all: A cyclic ketene acetal comonomer controls the nitroxide-mediated polymerization of methacrylates and confers tunable degradability. Chem. Commun. 2015, 51, 12847–12850. [Google Scholar] [CrossRef]
- Konkolewicz, D.; Hawkett, B.S.; Gray-Weale, A.; Perrier, S. RAFT polymerization kinetics: Combination of apparently conflicting models. Macromolecules 2008, 41, 6400–6412. [Google Scholar] [CrossRef]
- Antonopoulou, M.-N.; Whitfield, R.; Truong, N.P.; Wyers, D.; Harrisson, S.; Junkers, T.; Anastasaki, A. Concurrent control over sequence and dispersity in multiblock copolymers. Nat. Chem. 2022, 14, 304–312. [Google Scholar] [CrossRef]
- Shimizu, T.; Whitfield, R.; Jones, G.R.; Raji, I.O.; Konkolewicz, D.; Truong, N.P.; Anastasaki, A. Controlling primary chain dispersity in network polymers: Elucidating the effect of dispersity on degradation. Chem. Sci. 2023, 14, 13419–13428. [Google Scholar] [CrossRef]
- Mishima, E.; Yamago, S. Controlled random and alternating copolymerization of (meth) acrylates, acrylonitrile, and (meth) acrylamides with vinyl ethers by organotellurium-, organostibine-, and organobismuthine-mediated living radical polymerization reactions. J. Polym. Sci. Part A Polym. Chem. 2012, 50, 2254–2264. [Google Scholar] [CrossRef]
- Breulmann, M. Synthesis, Properties and Applications of Acrylonitrile ± Styrene ± Acrylate Polymers; John Wiley & Sons: Hoboken, NJ, USA, 2003; p. 341. [Google Scholar]
- Saunders, K.; Saunders, K. Acrylic Polymers; Springer Science & Business Media: Berlin, Germany, 1988; pp. 125–148. [Google Scholar]
- Peinemann, K.-V.; Abetz, V.; Simon, P.F. Asymmetric superstructure formed in a block copolymer via phase separation. Nat. Mater. 2007, 6, 992–996. [Google Scholar] [CrossRef] [PubMed]
- Desmet, G.B.; De Rybel, N.; Van Steenberge, P.H.; D’hooge, D.R.; Reyniers, M.F.; Marin, G.B. Ab-Initio-Based Kinetic Modeling to Understand RAFT Exchange: The Case of 2-Cyano-2-Propyl Dodecyl Trithiocarbonate and Styrene. Macromol. Rapid communications 2018, 39, 1700403. [Google Scholar] [CrossRef] [PubMed]
- De Rybel, N. Deterministic Modeling of the Interplay Between Molecular Diffusion and Chemical Kinetics of Bulk RAFT Polymerization. Doctoral Dissertation, Ghent University, Ghent, Belgium, 2019. [Google Scholar]
- Chiefari, J.; Chong, Y.; Ercole, F.; Krstina, J.; Jeffery, J.; Le, T.P.; Mayadunne, R.T.; Meijs, G.F.; Moad, C.L.; Moad, G. Living free-radical polymerization by reversible addition-fragmentation chain transfer: The RAFT process. Macromolecules 1998, 31, 5559. [Google Scholar] [CrossRef]
- Moad, G.; Rizzardo, E.; Thang, S.H. Living radical polymerization by the RAFT process. Aust. J. Chem. 2005, 58, 379–410. [Google Scholar] [CrossRef]
- Hernández-Ortiz, J.C.; Jaramillo-Soto, G.; Palacios-Alquisira, J.; Vivaldo-Lima, E. Modeling of Polymerization Kinetics and Molecular Weight Development in the Microwave-Activated RAFT Polymerization of Styrene. Macromol. React. Eng. 2010, 4, 210–221. [Google Scholar] [CrossRef]
- Smulders, W.; Gilbert, R.G.; Monteiro, M.J. A Kinetic Investigation of Seeded Emulsion Polymerization of Styrene Using Reversible Addition− Fragmentation Chain Transfer (RAFT) Agents with a Low Transfer Constant. Macromolecules 2003, 36, 4309–4318. [Google Scholar] [CrossRef]
- Goto, A.; Sato, K.; Tsujii, Y.; Fukuda, T.; Moad, G.; Rizzardo, E.; Thang, S.H. Mechanism and kinetics of RAFT-based living radical polymerizations of styrene and methyl methacrylate. Macromolecules 2001, 34, 402–408. [Google Scholar] [CrossRef]
- De Rybel, N.; Van Steenberge, P.H.; Reyniers, M.F.; Barner-Kowollik, C.; D’hooge, D.R.; Marin, G.B. An update on the pivotal role of kinetic modeling for the mechanistic understanding and design of bulk and solution raft polymerization. Macromol. Theory Simul. 2017, 26, 1600048. [Google Scholar] [CrossRef]
- De Rybel, N.; Van Steenberge, P.H.; Reyniers, M.-F.; D’hooge, D.R.; Marin, G.B. How chain length dependencies interfere with the bulk RAFT polymerization rate and microstructural control. Chem. Eng. Sci. 2018, 177, 163–179. [Google Scholar] [CrossRef]
- López-Domínguez, P.; Rivera-Peláez, J.E.; Jaramillo-Soto, G.; Barragán-Aroche, J.F.; Vivaldo-Lima, E. Modeling of RAFT polymerization of MMA in supercritical carbon dioxide using the PC-SAFT equation of state. React. Chem. Eng. 2020, 5, 547–560. [Google Scholar] [CrossRef]
- López-Domínguez, P.; Zapata-González, I.; Saldívar-Guerra, E.; Vivaldo-Lima, E. Mathematical modelling of RAFT polymerization. RAFT Polym. Methods Synth. Appl. 2021, 1, 187–221. [Google Scholar]
- Devlaminck, D.J.; Van Steenberge, P.H.; Reyniers, M.-F.; D’hooge, D.R. Deterministic modeling of degenerative RAFT miniemulsion polymerization rate and average polymer characteristics: Invalidity of zero–one nature at higher monomer conversions. Macromolecules 2018, 51, 9442–9461. [Google Scholar] [CrossRef]
- Tou, J.C.; Whiting, L.F. The thermokinetic performance of an accelerating rate calorimeter. Thermochim. Acta 1981, 48, 21–42. [Google Scholar] [CrossRef]
- Luan, B.; Li, C.e.; Moad, G.; Muir, B.W.; Zhu, J.; Patel, J.; Lim, S.; Hao, X. Kinetic modelling of the reversible addition–fragmentation chain transfer polymerisation of N-isopropylacrylamide. Eur. Polym. J. 2019, 120, 109193. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, P.; Qing, A.; Lan, Y.; Lu, M. Poly (N-isopropylacrylamide) hydrogels with improved shrinking kinetics by RAFT polymerization. Polymer 2006, 47, 2330–2336. [Google Scholar] [CrossRef]
- Quiñonez-Angulo, P.; Ruiz-Villegas, J.; Licea-Claveríe, Á.; Ramirez-Jiménez, A.; Miranda-Soto, V.; Zapata-González, I. A kinetic study, thermal analysis and kinetic modeling on homo and copolymerization of 2-(N, N-diethylamino) ethyl methacrylate and PEGMA. Eur. Polym. J. 2018, 109, 347–359. [Google Scholar] [CrossRef]
- Krasia, T.C.; Patrickios, C.S. Amphiphilic polymethacrylate model co-networks: Synthesis by RAFT radical polymerization and characterization of the swelling behavior. Macromolecules 2006, 39, 2467–2473. [Google Scholar] [CrossRef]
- Ajogbeje, O.J.; Lacík, I.; Hutchinson, R.A. The influence of monomer ionization and hydrolysis on the radical polymerization kinetics of 2-(dimethylamino) ethyl methacrylate in aqueous solution. Polym. Chem. 2023, 14, 2624–2639. [Google Scholar] [CrossRef]
- Masuelli, M.A. Mark-Houwink parameters for aqueous-soluble polymers and biopolymers at various temperatures. J. Polym. Biopolym. Phys. Chem. 2014, 2, 37–43. [Google Scholar]
- Masuelli, M.A. Dextrans in aqueous solution. Experimental review on intrinsic viscosity measurements and temperature effect. J. Polym. Biopolym. Phys. Chem. 2014, 1, 13–21. [Google Scholar]
- Kockler, K.B.; Fleischhaker, F.; Barner-Kowollik, C. Free radical propagation rate coefficients of N-containing methacrylates: Are we family? Macromolecules 2016, 49, 8572–8580. [Google Scholar] [CrossRef]
- Sakellariou, G.; Siakali-Kioulafa, A.; Hadjichristidis, N. Synthesis, chain flexibility, and glass-transition temperature of poly (2, 2-diphenylethyl methacrylate). Int. J. Polym. Anal. Charact. 2003, 8, 269–277. [Google Scholar] [CrossRef]
- Kockler, K.B.; Fleischhaker, F.; Barner-Kowollik, C. Investigating the propagation kinetics of a novel class of nitrogen-containing methacrylates via PLP-SEC. Polym. Chem. 2016, 7, 4342–4351. [Google Scholar] [CrossRef]
- Wagner, H.L. The Mark–Houwink–Sakurada relation for poly (methyl methacrylate). J. Phys. Chem. Ref. Data 1987, 16, 165–173. [Google Scholar] [CrossRef]
- Janča, J.; Vlček, P.; Trekoval, J.; Kolínský, M. Universal calibration in gel permeation chromatography for poly (methyl methacrylate) and poly (2-methoxyethyl methacrylate). J. Polym. Sci. Polym. Chem. Ed. 1975, 13, 1471–1473. [Google Scholar] [CrossRef]
- Gruendling, T.; Junkers, T.; Guilhaus, M.; Barner-Kowollik, C. Mark–Houwink Parameters for the Universal Calibration of Acrylate, Methacrylate and Vinyl Acetate Polymers Determined by Online Size-Exclusion Chromatography—Mass Spectrometry. Macromol. Chem. Phys. 2010, 211, 520–528. [Google Scholar] [CrossRef]
- Monteiro, M.J.; de Brouwer, H. Intermediate radical termination as the mechanism for retardation in reversible addition−fragmentation chain transfer polymerization. Macromolecules 2001, 34, 349–352. [Google Scholar] [CrossRef]
- Konkolewicz, D.; Hawkett, B.S.; Gray-Weale, A.; Perrier, S. RAFT polymerization kinetics: How long are the cross-terminating oligomers? J. Polym. Sci. Part A Polym. Chem. 2009, 47, 3455–3466. [Google Scholar] [CrossRef]
- Magri, G.; Barter, M.; Fletcher-Charles, J.; Choi, H.; Slocombe, D.; Richards, E.; Folli, A.; Porch, A.; Murphy, D.M. An in situ study of the thermal decomposition of 2, 2′-azobis (2-methylpropionitrile) radical chemistry using a dual-mode EPR resonator. Res. Chem. Intermed. 2023, 49, 289–305. [Google Scholar] [CrossRef]
- Magri, G.; Barter, M.; Fletcher-Charles, J.; Choi, H.; Slocombe, D.; Richards, E.; Folli, A.; Porch, A.; Murphy, D.M. An in-situ study of the thermal decomposition of AIBN radical chemistry using a dual mode EPR resonator. Preprint 2022. [Google Scholar] [CrossRef]
- Chernikova, E.; Zaitsev, S.; Plutalova, A.; Mineeva, K.; Zotova, O.; Vishnevetsky, D. Control over the relative reactivities of monomers in RAFT copolymerization of styrene and acrylic acid. RSC Adv. 2018, 8, 14300–14310. [Google Scholar] [CrossRef]
- Barner-Kowollik, C. Handbook of RAFT Polymerization; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Moad, G. RAFT polymerization to form stimuli-responsive polymers. Polym. Chem. 2017, 8, 177–219. [Google Scholar] [CrossRef]
- Moad, G.; Rizzardo, E.; Thang, S.H. End-functional polymers, thiocarbonylthio group removal/transformation and reversible addition–fragmentation–chain transfer (RAFT) polymerization. Polym. Int. 2011, 60, 9–25. [Google Scholar] [CrossRef]
- Moad, G. RAFT polymerization–then and now. In Controlled Radical Polymerization: Mechanisms; ACS Publications: Washington, DC, USA, 2015; pp. 211–246. [Google Scholar]
- Perrier, S. 50th Anniversary Perspective: RAFT Polymerization—A User Guide. Macromolecules 2017, 50, 7433–7447. [Google Scholar] [CrossRef]
- Crooks, J.E.; Donnellan, J.P. Kinetics of the reaction between carbon dioxide and tertiary amines. J. Org. Chem. 1990, 55, 1372–1374. [Google Scholar] [CrossRef]
- Chowdhury, F.A.; Yamada, H.; Higashii, T.; Goto, K.; Onoda, M. CO2 Capture by Tertiary Amine Absorbents: A Performance Comparison Study. Ind. Eng. Chem. Res. 2013, 52, 8323–8331. [Google Scholar] [CrossRef]
- Lai, N.; Zhu, Q.; Qiao, D.; Chen, K.; Tang, L.; Wang, D.; He, W.; Chen, Y.; Yu, T. CO2 capture with absorbents of tertiary amine functionalized nano–SiO2. Front. Chem. 2020, 8, 146. [Google Scholar] [CrossRef]
- Chen, M.; Luo, Q.; Lin, H.; Sun, Q.; Gao, H.; Liu, S.; Li, Y.; Liang, Z. A study on reaction mechanism and kinetics of CO2 and MEA/DEA-tertiary amines in non-aqueous and water-lean solutions. Chem. Eng. Sci. 2023, 269, 118431. [Google Scholar] [CrossRef]





| 1.29 × 10−4 | 6.25 × 10−1 |
| Coefficient | A [Variable Unit] | [K] | k (at 70 °C) [Variable Unit] | Reference |
|---|---|---|---|---|
| 1.58 × 1015 [s−1] | 1.55 × 104 | 3.64 × 10−5 [s−1] | [9] | |
| - | - | 0.6 | [9] | |
| 2.44 × 106 [L mol−1 s−1] | 2.36 × 103 | 2.5 × 103 [L mol−1 s−1] | [54] | |
| [9] | ||||
| Estimated in this work | ||||
| - | - | 1.00 × 104 [s−1] | [9] | |
| - | - | 2.00 × 104 [L mol−1 s−1] | [9] | |
| 8.00 × 109 [L mol–1 s–1] | 4.00 × 106 [L mol−1 s−1] | 1.00 × 104 [L mol−1 s−1] |
| Polymer | |||
|---|---|---|---|
| PDMAPAm165 | 19 | 26 | 1.4 |
| PDMAPAm163-b-PMMA130 | 26 | 39 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pashayev, E.; Georgopanos, P. Optimizing the Synthesis of CO2-Responsive Polymers: A Kinetic Model Approach for Scaling Up. Polymers 2025, 17, 1115. https://doi.org/10.3390/polym17081115
Pashayev E, Georgopanos P. Optimizing the Synthesis of CO2-Responsive Polymers: A Kinetic Model Approach for Scaling Up. Polymers. 2025; 17(8):1115. https://doi.org/10.3390/polym17081115
Chicago/Turabian StylePashayev, Emil, and Prokopios Georgopanos. 2025. "Optimizing the Synthesis of CO2-Responsive Polymers: A Kinetic Model Approach for Scaling Up" Polymers 17, no. 8: 1115. https://doi.org/10.3390/polym17081115
APA StylePashayev, E., & Georgopanos, P. (2025). Optimizing the Synthesis of CO2-Responsive Polymers: A Kinetic Model Approach for Scaling Up. Polymers, 17(8), 1115. https://doi.org/10.3390/polym17081115








