Generation of Polymer Nanocomposites through Shear-Driven Aggregation of Binary Colloids
Abstract
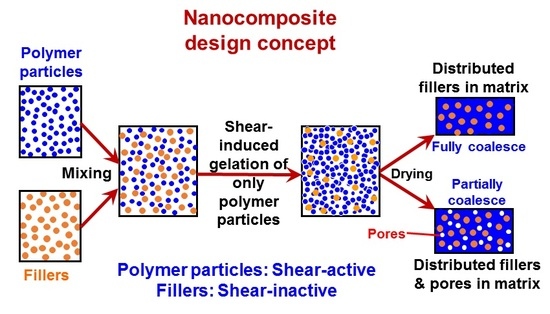
:1. Introduction
2. Intense Shear-Driven Aggregation
2.1. Main Phenomena Observed Experimentally
2.2. Theoretical Background of the Intense Shear-Driven Aggregation
3. Applications of the Shear-Driven Aggregation to Binary Colloids
- (1)
- It starts with two colloids: fillers (A) NP dispersion and polymer (B) NP dispersion, both of which have the same sign of charges;
- (2)
- When the two colloids mix, a stable binary colloid is formed, where A and B NPs are homogeneously distributed at nanoscales;
- (3)
- The polymer (B) is the dominant colloid, and the volume fraction of the fillers (A) is smaller;
- (4)
- The colloidal interactions are controlled such that the B (polymer) NPs are unstable under the used shear rate (referred to as shear active) and can aggregate to form clusters or gels. Instead, the A (fillers) NPs are very stable under the same shear rate and the shear-driven aggregation does not occur, referred to as shear-inactive.
3.1. Distribution of PMMA Particles into PS NP Matrix
3.2. Distribution of GO Sheets into PVDF NP Matrix
4. Concluding Remarks and Perspectives
Acknowledgments
Conflicts of Interest
References
- Schadler, L.S. Polymer-based and polymer-filled nanocomposites. In Nanocomposite Science and Technology; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2003; pp. 77–153. [Google Scholar]
- Chan, W.C.W.; Nie, S. Quantum dot bioconjugates for ultrasensitive nonisotopic detection. Science 1998, 281, 2016–2018. [Google Scholar] [CrossRef] [PubMed]
- Chang, M.C.; Ko, C.-C.; Douglas, W.H. Preparation of hydroxyapatite-gelatin nanocomposite. Biomaterials 2003, 24, 2853–2862. [Google Scholar] [CrossRef]
- Sershen, S.R.; Westcott, S.L.; Halas, N.J.; West, J.L. Temperature-sensitive polymer-nanoshell composites for photothermally modulated drug delivery. J. Biomed. Mater. Res. 2000, 51, 293–298. [Google Scholar] [CrossRef]
- Misra, S.K.; Valappil, S.P.; Roy, I.; Boccaccini, A.R. Polyhydroxyalkanoate (pha)/inorganic phase composites for tissue engineering applications. Biomacromolecules 2006, 7, 2249–2258. [Google Scholar] [CrossRef] [PubMed]
- Elimelech, M.; Phillip, W.A. The future of seawater desalination: Energy, technology, and the environment. Science 2011, 333, 712–717. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Mahendra, S.; Lyon, D.Y.; Brunet, L.; Liga, M.V.; Li, D.; Alvarez, P.J.J. Antimicrobial nanomaterials for water disinfection and microbial control: Potential applications and implications. Water Res. 2008, 42, 4591–4602. [Google Scholar] [CrossRef] [PubMed]
- Francis, R.; Joy, N.; Aparna, E.P.; Vijayan, R. Polymer grafted inorganic nanoparticles, preparation, properties, and applications: A review. Polym. Rev. 2014, 54, 268–347. [Google Scholar] [CrossRef]
- Chattopadhyay, D.K.; Raju, K.V.S.N. Structural engineering of polyurethane coatings for high performance applications. Prog. Polym. Sci. 2007, 32, 352–418. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Xu, X.; Zhu, X.; Men, X.; Zhou, X. Superhydrophilic-superoleophobic coatings. J. Mater. Chem. 2012, 22, 2834–2837. [Google Scholar] [CrossRef]
- Jhaveri, J.H.; Murthy, Z.V.P. A comprehensive review on anti-fouling nanocomposite membranes for pressure driven membrane separation processes. Desalination 2016, 379, 137–154. [Google Scholar] [CrossRef]
- McDonald, S.A.; Konstantatos, G.; Zhang, S.; Cyr, P.W.; Klem, E.J.D.; Levina, L.; Sargent, E.H. Solution-processed pbs quantum dot infrared photodetectors and photovoltaics. Nat. Mater. 2005, 4, 138–142. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, S.; Schaefer, J.L.; Yang, Z.; Tu, Z.; Archer, L.A. 25th anniversary article: Polymer-particle composites: Phase stability and applications in electrochemical energy storage. Adv. Mater. 2014, 26, 201–234. [Google Scholar] [CrossRef] [PubMed]
- Althues, H.; Henle, J.; Kaskel, S. Functional inorganic nanofillers for transparent polymers. Chem. Soc. Rev. 2007, 36, 1454–1465. [Google Scholar] [CrossRef] [PubMed]
- Bishop, K.J.M.; Wilmer, C.E.; Soh, S.; Grzybowski, B.A. Nanoscale forces and their uses in self-assembly. Small 2009, 5, 1600–1630. [Google Scholar] [CrossRef] [PubMed]
- Ke, K.; Wang, Y.; Liu, X.-Q.; Cao, J.; Luo, Y.; Yang, W.; Xie, B.-H.; Yang, M.-B. A comparison of melt and solution mixing on the dispersion of carbon nanotubes in a poly(vinylidene fluoride) matrix. Compos. Part B 2012, 43, 1425–1432. [Google Scholar] [CrossRef]
- Yousefi, N.; Gudarzi, M.M.; Zheng, Q.; Aboutalebi, S.H.; Sharif, F.; Kim, J.-K. Self-alignment and high electrical conductivity of ultralarge graphene oxide-polyurethane nanocomposites. J. Mater. Chem. 2012, 22, 12709–12717. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Q.; Chen, D.; Lu, P. Enhanced mechanical properties of graphene-based poly(vinyl alcohol) composites. Macromolecules 2010, 43, 2357–2363. [Google Scholar] [CrossRef]
- Kim, H.; Miura, Y.; Macosko, C.W. Graphene/polyurethane nanocomposites for improved gas barrier and electrical conductivity. Chem. Mater. 2010, 22, 3441–3450. [Google Scholar] [CrossRef]
- Cavallaro, G.; Lazzara, G.; Milioto, S. Dispersions of nanoclays of different shapes into aqueous and solid biopolymeric matrices. Extended physicochemical study. Langmuir 2011, 27, 1158–1167. [Google Scholar] [CrossRef] [PubMed]
- Makaremi, M.; Pasbakhsh, P.; Cavallaro, G.; Lazzara, G.; Aw, Y.K.; Lee, S.M.; Milioto, S. Effect of morphology and size of halloysite nanotubes on functional pectin bionanocomposites for food packaging applications. ACS Appl. Mater. Interfaces 2017, 9, 17476–17488. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Huang, J.; Yang, L.; Zhang, N.; Jin, G.; Qu, J. In-situ thermal reduction and effective reinforcement of graphene nanosheet/poly (ethylene glycol)/poly(lactic acid) nanocomposites. Polym. Adv. Technol. 2014, 25, 1515–1522. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Z.; Wang, S.; Zhang, Y. Preparation and properties of octadecylamine modified graphene oxide/styrene-butadiene rubber composites through an improved melt compounding method. J. Appl. Polym. Sci. 2016, 133, 42907. [Google Scholar] [CrossRef]
- Mofokeng, J.P.; Luyt, A.S. Morphology and thermal degradation studies of melt-mixed pla/phbv biodegradable polymer blend nanocomposites with tio2 as filler. J. Appl. Polym. Sci. 2015, 132, 42138. [Google Scholar] [CrossRef]
- El Achaby, M.; Arrakhiz, F.-E.; Vaudreuil, S.; el Kacem Qaiss, A.; Bousmina, M.; Fassi-Fehri, O. Mechanical, thermal, and rheological properties of graphene-based polypropylene nanocomposites prepared by melt mixing. Polym. Compos. 2012, 33, 733–744. [Google Scholar] [CrossRef]
- Tripathi, S.; Saini, P.; Gupta, D.; Choudhary, V. Electrical and mechanical properties of pmma/reduced graphene oxide nanocomposites prepared via in situ polymerization. J. Mater. Sci. 2013, 48, 6223–6232. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C.; Hu, H.; Wan, L.; Chen, R.; Zheng, H.; Liu, F.; Zhang, M.; Shang, X.; Wang, X. Synthesis, mechanical, and barrier properties of ldpe/graphene nanocomposites using vinyl triethoxysilane as a coupling agent. J. Nanopart. Res. 2011, 13, 869–878. [Google Scholar] [CrossRef]
- Wang, J.; Hu, H.; Wang, X.; Xu, C.; Zhang, M.; Shang, X. Preparation and mechanical and electrical properties of graphene nanosheets–poly(methyl methacrylate) nanocomposites via in situ suspension polymerization. J. Appl. Polym. Sci. 2011, 122, 1866–1871. [Google Scholar] [CrossRef]
- Jin, L.; Wu, H.; Morbidelli, M. Synthesis of water-based dispersions of polymer/TiO2 hybrid nanospheres. Nanomaterials 2015, 5, 1454. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Bai, L.; Feng, G.; Yang, X.Y.; Lv, M.J.; Zhang, C.A.; Hu, H.; Wang, X.B. Thermal reduced graphene based poly(ethylene vinyl alcohol) nanocomposites: Enhanced mechanical properties, gas barrier, water resistance, and thermal stability. Ind. Eng. Chem. Res. 2013, 52, 16745–16754. [Google Scholar] [CrossRef]
- Mittal, G.; Dhand, V.; Rhee, K.Y.; Park, S.-J.; Lee, W.R. A review on carbon nanotubes and graphene as fillers in reinforced polymer nanocomposites. J. Ind. Eng. Chem. 2015, 21, 11–25. [Google Scholar] [CrossRef]
- Taguet, A.; Cassagnau, P.; Lopez-Cuesta, J.M. Structuration, selective dispersion and compatibilizing effect of (nano)fillers in polymer blends. Prog. Polym. Sci. 2014, 39, 1526–1563. [Google Scholar] [CrossRef]
- Istrate, O.M.; Paton, K.R.; Khan, U.; O’Neill, A.; Bell, A.P.; Coleman, J.N. Reinforcement in melt-processed polymer-graphene composites at extremely low graphene loading level. Carbon 2014, 78, 243–249. [Google Scholar] [CrossRef]
- Sheng, X.; Xie, D.; Wang, C.; Zhang, X.; Zhong, L. Synthesis and characterization of core/shell titanium dioxide nanoparticle/polyacrylate nanocomposite colloidal microspheres. Colloid Polym. Sci. 2015, 294, 463–469. [Google Scholar] [CrossRef]
- Sheng, X.; Xie, D.; Cai, W.; Zhang, X.; Zhong, L.; Zhang, H. In situ thermal reduction of graphene nanosheets based poly(methyl methacrylate) nanocomposites with effective reinforcements. Ind. Eng. Chem. Res. 2015, 54, 649–658. [Google Scholar] [CrossRef]
- Liu, H.T.; Zeng, X.F.; Zhao, H.; Chen, J.F. Highly transparent and multifunctional polymer nanohybrid film with superhigh zno content synthesized by a bulk polymerization method. Ind. Eng. Chem. Res. 2012, 51, 6753–6759. [Google Scholar] [CrossRef]
- Meng, X.; Wu, H.; Storti, G.; Morbidelli, M. Effect of dispersed polymeric nanoparticles on the bulk polymerization of methyl methacrylate. Macromolecules 2016, 49, 7758–7766. [Google Scholar] [CrossRef]
- Wang, H.; Dong, Y.-N.; Zhu, M.; Li, X.; Keller, A.A.; Wang, T.; Li, F. Heteroaggregation of engineered nanoparticles and kaolin clays in aqueous environments. Water Res. 2015, 80, 130–138. [Google Scholar] [CrossRef] [PubMed]
- Labille, J.; Harns, C.; Bottero, J.-Y.; Brant, J. Heteroaggregation of titanium dioxide nanoparticles with natural clay colloids. Environ. Sci. Technol. 2015, 49, 6608–6616. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Liu, F.; Wang, Z.; Cao, X.; Xing, B. Heteroaggregation of graphene oxide with minerals in aqueous phase. Environ. Sci. Technol. 2015, 49, 2849–2857. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Phenrat, T.; Tilton, R.D.; Lowry, G.V. Effect of kaolinite, silica fines and ph on transport of polymer-modified zero valent iron nano-particles in heterogeneous porous media. J. Colloid. Interface Sci. 2012, 370, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Huynh, K.A.; McCaffery, J.M.; Chen, K.L. Heteroaggregation of multiwalled carbon nanotubes and hematite nanoparticles: Rates and mechanisms. Environ. Sci. Technol. 2012, 46, 5912–5920. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Silva, M.; Uribe-Salas, A.; Waters, K.E.; Finch, J.A. Zeta potential study of pentlandite in the presence of serpentine and dissolved mineral species. Miner. Eng. 2016, 85, 66–71. [Google Scholar] [CrossRef]
- Armstrong, R.; Friedrich, V.L.; Holmes, K.V.; Dubois-Dalcq, M. In vitro analysis of the oligodendrocyte lineage in mice during demyelination and remyelination. J. Cell Biol. 1990, 111, 1183–1195. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.-S.; Davis, L.M.; Shows, T.B. Mapping small DNA sequences by fluorescence in situ hybridization directly on banded metaphase chromosomes. Proc. Natl. Acad. Sci. USA 1990, 87, 6223–6227. [Google Scholar] [CrossRef] [PubMed]
- Di Michele, L.; Zaccone, A.; Eiser, E. Analytical theory of polymer-network-mediated interaction between colloidal particles. Proc. Natl. Acad. Sci. USA 2012, 109, 10187–10192. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Pedrero, F.; Alousque, F.; de Gaudemaris, B.; Berriot, J.; Gaboriaud, F.; Bremond, N.; Bibette, J. Making an elastomeric composite material via the heteroaggregation of a binary colloidal dispersion. Soft Matter 2012, 8, 8752–8757. [Google Scholar] [CrossRef]
- Meng, X.; Wu, H.; Morbidelli, M. Shear-driven aggregation of binary colloids for randomly distributing nanoparticles in a matrix. Soft Matter 2016, 12, 3696–3702. [Google Scholar] [CrossRef] [PubMed]
- Pandey, R.; Conrad, J.C. Dynamics of confined depletion mixtures of polymers and bidispersed colloids. Soft Matter 2013, 9, 10617–10626. [Google Scholar] [CrossRef]
- Sheng, X.; Xie, D.; Zhang, X.; Zhong, L.; Wu, H.; Morbidelli, M. Uniform distribution of graphene oxide sheets into a poly-vinylidene fluoride nanoparticle matrix through shear-driven aggregation. Soft Matter 2016, 12, 5876–5882. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Zuo, K.; Wang, Z.; Zhang, L.; Liu, L.; Guo, B. Using a green method to develop graphene oxide/elastomers nanocomposites with combination of high barrier and mechanical performance. Compos. Sci. Technol. 2014, 92, 1–8. [Google Scholar] [CrossRef]
- Kim, A.Y.; Berg, J.C. Fractal heteroaggregation of oppositely charged colloids. J. Colloid Interface Sci. 2000, 229, 607–614. [Google Scholar] [CrossRef] [PubMed]
- Islam, A.M.; Chowdhry, B.Z.; Snowden, M.J. Heteroaggregation in colloidal dispersions. Adv. Colloid Interface Sci. 1995, 62, 109–136. [Google Scholar] [CrossRef]
- Lopez-Lopez, J.M.; Schmitt, A.; Moncho-Jorda, A.; Hidalgo-Alvarez, R. Stability of binary colloids: Kinetic and structural aspects of heteroaggregation processes. Soft Matter 2006, 2, 1025–1042. [Google Scholar] [CrossRef]
- Furusawa, K.; Anzai, C. Heterocoagulation behaviour of polymer latices with spherical silica. Colloids Surf. 1992, 63, 103–111. [Google Scholar] [CrossRef]
- Ottewill, R.H.; Schofield, A.B.; Waters, J.A.; Williams, N.S.J. Preparation of core-shell polymer colloid particles by encapsulation. Colloid Polym. Sci. 1997, 275, 274–283. [Google Scholar] [CrossRef]
- Grossiord, N.; Loos, J.; Regev, O.; Koning, C.E. Toolbox for dispersing carbon nanotubes into polymers to get conductive nanocomposites. Chem. Mater. 2006, 18, 1089–1099. [Google Scholar] [CrossRef]
- Thomassin, J.-M.; Trifkovic, M.; Alkarmo, W.; Detrembleur, C.; Jérôme, C.; Macosko, C. Poly(methyl methacrylate)/graphene oxide nanocomposites by a precipitation polymerization process and their dielectric and rheological characterization. Macromolecules 2014, 47, 2149–2155. [Google Scholar] [CrossRef]
- Hui, D.; Nawaz, M.; Morris, D.P.; Edwards, M.R.; Saunders, B.R. Study of ph-triggered heteroaggregation and gel formation within mixed dispersions. J. Colloid Interface Sci. 2008, 324, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Kobayashi, M.; Skarba, M.; Mu, C.; Galletto, P.; Borkovec, M. Heteroaggregation in binary mixtures of oppositely charged colloidal particles. Langmuir 2006, 22, 1038–1047. [Google Scholar] [CrossRef] [PubMed]
- Chan, A.J.; Steenkeste, K.; Canette, A.; Eloy, M.; Brosson, D.; Gaboriaud, F.; Fontaine-Aupart, M.-P. Natural rubber–filler interactions: What are the parameters? Langmuir 2015, 31, 12437–12446. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Zaccone, A.; Tsoutsoura, A.; Lattuada, M.; Morbidelli, M. High shear-induced gelation of charge-stabilized colloids in a microchannel without adding electrolytes. Langmuir 2009, 25, 4715–4723. [Google Scholar] [CrossRef] [PubMed]
- Zaccone, A.; Wu, H.; Gentili, D.; Morbidelli, M. Theory of activated-rate processes under shear with application to shear-induced aggregation of colloids. Phys. Rev. E 2009, 80, 051404. [Google Scholar] [CrossRef] [PubMed]
- Arosio, P.; Xie, D.L.; Wu, H.; Braun, L.; Morbidelli, M. Effect of primary particle morphology on the structure of gels formed in intense turbulent shear. Langmuir 2010, 26, 6643–6649. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Tsoutsoura, A.; Lattuada, M.; Zaccone, A.; Morbidelli, M. Effect of temperature on high shear-induced gelation of charge-stabilized colloids without adding electrolytes. Langmuir 2010, 26, 2761–2768. [Google Scholar] [CrossRef] [PubMed]
- Xie, D.L.; Wu, H.; Zaccone, A.; Braun, L.; Chen, H.Q.; Morbidelli, M. Criticality for shear-induced gelation of charge-stabilized colloids. Soft Matter 2010, 6, 2692–2698. [Google Scholar] [CrossRef]
- Zaccone, A.; Gentili, D.; Wu, H.; Morbidelli, M. Shear-induced reaction-limited aggregation kinetics of brownian particles at arbitrary concentrations. J. Chem. Phys. 2010, 132, 134903. [Google Scholar] [CrossRef] [PubMed]
- Xie, D.L.; Arosio, P.; Wu, H.; Morbidelli, M. Effect of surfactants on shear-induced gelation and gel morphology of soft strawberry-like particles. Langmuir 2011, 27, 7168–7175. [Google Scholar] [CrossRef] [PubMed]
- Zaccone, A.; Gentili, D.; Wu, H.; Morbidelli, M.; Del Gado, E. Shear-driven solidification of dilute colloidal suspensions. Phys. Rev. Lett. 2011, 106, 138301. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Wu, H.; Morbidelli, M. Snapshotted glass and gel transitions of stable colloidal dispersions after shear-driven aggregation in a microchannel. Soft Matter 2015, 11, 981–986. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Wu, H.; Morbidelli, M. Kinetics and cluster morphology evolution of shear-driven aggregation of well-stabilized colloids. Langmuir 2015, 31, 1113–1119. [Google Scholar] [CrossRef] [PubMed]
- Zaccone, A.; Wu, H.; Lattuada, M.; Morbidelli, M. Charged molecular films on brownian particles: Structure, interactions, and relation to stability. J. Phys. Chem. B 2008, 112, 6793–6802. [Google Scholar] [CrossRef] [PubMed]
- Zaccone, A.; Wu, H.; Lattuada, M.; Morbidelli, M. Correlation between colloidal stability and surfactant adsorption/association phenomena studied by light scattering. J. Phys. Chem. B 2008, 112, 1976–1986. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Morbidelli, M. Gelation of polymeric nanoparticles. Particuology 2014, 14, 1–11. [Google Scholar] [CrossRef]
- Parsegian, V.A.; Zemb, T. Hydration forces: Observations, explanations, expectations, questions. Curr. Opin. Colloid Interface Sci. 2011, 16, 618–624. [Google Scholar] [CrossRef]
- Li, Y.; Hu, J.; He, J.; Gao, L. The graphene oxide polymer composites with high breakdown field strength and energy storage ability. In Proceedings of the International Congress on Energy Efficiency and Energy Related Materials (ENEFM 2013), Antalya, Turkey, 9–12 October 2013; Oral, A.Y., Bahsi, Z.B., Ozer, M., Eds.; Springer International Publishing: New York, NY, USA, 2014; Volume 155, pp. 431–438. [Google Scholar]
- El Achaby, M.; Arrakhiz, F.Z.; Vaudreuil, S.; Essassi, E.M.; Qaiss, A. Piezoelectric β-polymorph formation and properties enhancement in graphene oxide—Pvdf nanocomposite films. Appl. Surf. Sci. 2012, 258, 7668–7677. [Google Scholar] [CrossRef]







© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, X.; Zhang, L.; Wu, H. Generation of Polymer Nanocomposites through Shear-Driven Aggregation of Binary Colloids. Polymers 2017, 9, 619. https://doi.org/10.3390/polym9110619
Sheng X, Zhang L, Wu H. Generation of Polymer Nanocomposites through Shear-Driven Aggregation of Binary Colloids. Polymers. 2017; 9(11):619. https://doi.org/10.3390/polym9110619
Chicago/Turabian StyleSheng, Xinxin, Li Zhang, and Hua Wu. 2017. "Generation of Polymer Nanocomposites through Shear-Driven Aggregation of Binary Colloids" Polymers 9, no. 11: 619. https://doi.org/10.3390/polym9110619
APA StyleSheng, X., Zhang, L., & Wu, H. (2017). Generation of Polymer Nanocomposites through Shear-Driven Aggregation of Binary Colloids. Polymers, 9(11), 619. https://doi.org/10.3390/polym9110619