Abstract
Greenhouse technology has advanced over the past few decades in terms of environmental control (e.g., indoor temperature, relative humidity, and CO2 concentration). Ventilation is an effective way to adjust the indoor climate. Natural ventilation has gained significant research attention recently because of its low energy requirement. To evaluate the ventilation effectiveness, the ventilation rate is often used. This review summarizes the published review papers related to greenhouse ventilation. Ventilation models are reported under different conditions, including wind-induced, buoyancy-induced, and combined effects-induced ventilation in greenhouses. The influencing factors are described, such as the wind and buoyancy strength and distribution, greenhouse geometry, and vent arrangement. Various methods assessing natural ventilation in greenhouses are introduced, consisting of tracer gas techniques, the pressure difference method, the energy balance method, the emptying fluid-filling box method, and numerical simulation. The values of the key coefficients deduced and used in the literature are listed. This paper reports what has been done in the world and where we can start to develop dynamic ventilation models for solar and tunnel-type greenhouses in China. Further valuable investigations are discussed. The pressure distribution function in greenhouses with horizontal openings, a model for cross-ventilation induced by combined wind and buoyancy force, and an analytical plant-considered ventilation model with higher applicability are described. To ensure the accuracy of the ventilation models, other environmental variables, especially geography-dependent ones, can be added. More criteria are suggested to evaluate the ventilation performance rather than the ventilation rate to provide a comprehensive assessment.
1. Introduction
As of 2018, 577,455 and 1,335,663 hectares of land were occupied by small greenhouses, namely Chinese solar greenhouses (CSG) and Chinese plastic greenhouses (CPG), respectively [1] (Figure 1f,g).
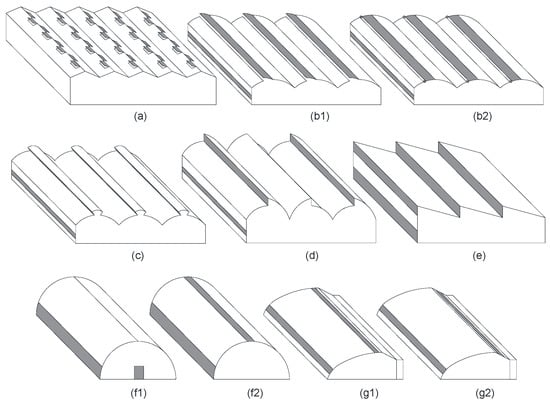
Figure 1.
The structures of mixing ventilation (a), (b1,b2,e) with closed side wall vents, cross-ventilation (f1), (b1–e) with closed roof vents, and displacement ventilation (b1–e,f2–g2).
CSGs provide a suitable environment for planting in cold regions due to the thick back wall and the thermal insulation quilt. Therefore, CSGs are usually built in the northern plains and western plateau areas in China. A typical CSG has a lower opening toward the south and an upper opening parallel to the ground. In order to improve the ventilation efficiency and thus the production performance, researchers have studied the flow field characteristics, the effects of vent heights on indoor climate, and the structural renovation of vents. However, few theoretical models describe the correct behavior of natural ventilation in typical CSGs (Figure 1(g1)).
There are two forms of CPGs, which are also called tunnel-type greenhouses, with side vents only (Figure 1(f1)) or with both side and roof vents (Figure 1(f2)). Because of the vast area of China, the operating conditions of greenhouses are dramatically different. In the southern rainy regions of China, from plains to plateau areas, CPGs without roof vents are commonly constructed. This kind of tunnel greenhouse (CPG-f1) has been well studied with respect to wind-induced ventilation, while few studies have focused on the buoyancy-induced ventilation performance and its theoretical models.
This paper surveys what has been done, how to understand the ventilation mechanism, and how we might develop ventilation models for small greenhouses in China.
The sensible heat released in greenhouses is mainly induced by the absorbed solar radiation contributed by the cover, the structural elements, the soil, and the crop absorption [2]. The purpose of ventilation in greenhouses is to bring in carbon dioxide and remove excess heat and humidity, and to provide a comfortable environment for plants [3,4]. A sustainable and healthy indoor environment is important for both humans and plants, and natural ventilation is one basic element.
The concept of natural ventilation received increasing attention from scholars starting in the 1990s. Boulard [5] surveyed the approaches to natural ventilation in greenhouses. Sethi and Sharma [6] summarized natural ventilation studies as one of the cooling technologies in greenhouses. Norton et al. [7] performed modeling of the computational fluid dynamics (CFD) applications of ventilation systems and designs in the field of agriculture. Bournet and Boulard [8] summarized the effects of ventilator configurations on greenhouse indoor climate distribution, including greenhouse geometry and opening arrangements. Khanal and Lei [9] discussed solar chimneys as a passive strategy to enhance natural ventilation with respect to the buoyancy effect [10]. Rong et al. [11] discussed natural ventilation mechanisms in livestock buildings and the ventilation coefficients used in the literature. Akrami et al. [12] reported on the methods and technologies used for natural ventilation in greenhouses. Sakiyama et al. [13] provided an overview of natural ventilation investigations with respect to thermal comfort, the efficiency of energy usage, and indoor air quality. Wang et al. [14] summarized the wind pressure coefficients on the surface of different greenhouse types. Zhong et al. [15] discussed papers relevant to single-sided natural ventilation.
Natural ventilation is induced by the wind effect, buoyancy effect, and combined wind and stack effect [16]. The wind action results in a pressure field surrounding the openings, and the buoyancy effect is relevant to the gradient of air density between the indoor and outdoor environments [17]. Ventilation rate is a widely used and well-developed concept in ventilation assessment, namely the frequency of exchanged air volume between the inside and outside per unit of time [18]. Models have been established with the driving forces and influencing factors (Figure 2) for different greenhouses (Figure 1), but not for Chinese greenhouses in particular.
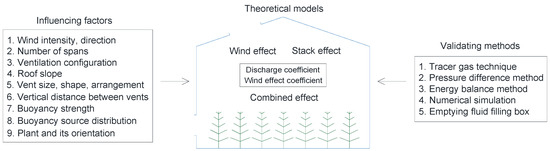
Figure 2.
The factors involved in natural ventilation in greenhouses, considered from the past to present.
2. Current Models of Wind-Induced Ventilation
2.1. Theoretical Models
The wind action results in a pressure field surrounding the openings [17]. The pressure field is different in various application scenarios, including greenhouse structures and ventilation categories. In addition, the wind-induced ventilation rate is affected by the vent size and arrangement, insect screens, roof geometry, plant characteristics, and wind direction.
According to Bernoulli’s equation, the pressure difference (Δp) decides the mean flow velocity through the opening (V), with a known resistance coefficient (ξ) and air density (ρ) (Equation (1)). The function of ξ for rectangular openings was introduced by Bot [19], with different forms including for the ratio between the length and height of vents L/H > 1 (Equation (2)) and for a hinged flap (Equation (3)), which was also used in later studies [20,21,22].
Δp = 1/2 ξρV2
ξ = 1.75 + 0.7exp(−L/(32.5H))
ξ = 1.75 + 0.7exp(−L/(32.5Hsinα))
When a window is used, covering the vent, the window function f(α) with a value between 1 at full and 0 at closed opening, is applied (Equation (4)) based on the opening angle (α) [19], where ϕv is the ventilation rate and Ao the opening effective area.
Δp = 1/2 (ξ/f(α)) ρ(ϕv/Ao)2
The discharge coefficient is often used as a function of resistance coefficient (Cd = 1/ξ0.5) [17,20,23]. The mean velocity at the opening can be calculated via Equation (5). Gong, et al. [24] estimated the discharge coefficient in different types of greenhouses, with a specific ratio between the height and length of openings and different opening angles, considering the ventilation as the outflow through thin-walled orifices:
V = Cd (2/ρ ∆p)0.5.
2.2. Application Scenarios
2.2.1. Mixing Ventilation
The wind turbulence significantly influences the mixing ventilation [19,20,25,26,27,28,29]. When there are only roof vents facing the same direction (Figure 1 (mixing ventilation)), the ventilation is induced by two factors: the static and turbulent wind effect.
At the windward side of the building with external wind speed Vw, the static pressure (pu) is higher than the barometric pressure, whereas the static pressure is lower at the leeward side [30]. Dimensionless static pressure coefficient (Kp) is positive at the windward side and negative in the contrast. In this case, ventilation is formed only when there are vents on both sides of the construction [25].
pu = 1/2 KpρVw2
As wind has the nature of fluctuation related to the wind turbulence interacting with the building structure, the momentary pressure (pu′) outside the openings was considered the driving force [19], with a dimensionless pressure fluctuation coefficient (Kf) defined. Both Kp and Kf can be obtained by experiments only [31,32,33].
pu′ = 1/2 Kf ρV2
The wind effect coefficient (Cw) was proposed and clarified as a whole, covering both the static and turbulent effect to compute the ventilation rate caused by wind (Equation (8)) [17,19,29,31,32,34]:
ϕ = Cd A/2 (Cw Vw2)0.5.
Differently, Hellickson et al. [35] and Albright [36] gave the ventilation rate in Equation (9), where E is the opening effectiveness, recommended as 0.35 for agricultural buildings. An algorithm was proposed to calculate the opening effectiveness of natural ventilation by Nääs et al. [37]:
ϕ = AEVw/2.
2.2.2. Displacement Ventilation
The wind-induced ventilation rate of greenhouses with side and roof vents (Figure 1 (displacement ventilation)) can be estimated according to Equation (10) [38]. Researchers [3,16,17,19,20,23,27,32,33,34,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] have deduced and applied the discharge coefficient and the wind effect coefficient in greenhouses with vertical openings (see Table 1).
ϕ = Cd AiAo/√(Ai2 + Ao2) [(Cwi−Cwo) Vw2]0.5

Table 1.
The wind effect coefficient given by various greenhouses. Note: “global” means the global wind effect coefficient in the form of CdCw0.5.
Typical Chinese solar greenhouses (CSG) have horizontal roof openings. However, the measured wind pressure coefficients of CSG were only used to evaluate the wind load of the greenhouses [14] and to deduce the critical wind speed for wind disasters in various areas of the facility [62,63,64]. The wind pressure coefficient of CSG is often calculated using a scale model with the vents completely closed in the wind tunnel. Studies showed that the wind pressure coefficient decreased with opened vents compared to closed vents [65].
The natural ventilation of typical Chinese solar greenhouses (CSG) has been studied since 2000. With the rapid development of computational fluid dynamics during that time, researchers started to investigate the air flow characteristics of CSG via CFD simulations [66,67] and energy balance models [68] instead of theoretical models. According to the CFD simulations, the functions of the wind pressure coefficient (Equation (11)) and discharge coefficient (Equation (12)) of CSG were proposed according to the angle θ between the vent and the wind direction and the area ratio (R) between the inlet and outlet, respectively [69].
Cw = 0.7486sinθ + 0.0237sin2θ
Cd = e(−0.67403R)
2.2.3. Cross-Ventilation
Cross-ventilation (Figure 1 (cross-ventilation)) leads to better cooling and dehumidification uniformity in greenhouses [70], and has often been investigated via CFD simulations [71]. Chu et al. [72] indicated that the discharge coefficient is a function of the Reynolds number, the incident angle of external wind, and the opening positions (Equation (13)). Rec is the critical Reynolds number, 18,000, leading to the critical discharge coefficient (Cdc) 0.66. The power n is different with inlet, outlet, and wind direction.
Cd/Cdc = (Re/Rec)n
To have effective wind driven cross-ventilation, the rule of thumb is that the length of the building (the horizontal distance between the two openings) should be smaller than five times the ceiling height [73,74]. The internal friction should be considered when the greenhouse length is six-times greater than the height [75].
2.3. Factors Influencing Ventilation Rates
2.3.1. Vent Size, Shape, and Arrangement
When the outdoor wind speed is low, the cooling effect of ventilation with combined roof vents and side vents is better than with roof vents alone [33]. However, when the wind speed exceeds a certain value, the cooling effect of roof vents alone is better [76,77]. With a larger opening area on the roof, the reduction of the temperature and humidity ratio (ventilation effect) increases [46].
A vortex can be produced in greenhouses with the bottom vent or bottom and roof vents, while the air circulation is not strong with the opened roof vent [78]. The most homogeneous distribution of indoor environment was achieved with roof vents only [79], leading to decreased air temperature–humidity ratios over time [46]. The combined roof and side vents caused increased the spatial heterogeneity of the microclimate, increased the air speed, and decreased the temperature inside the greenhouse [70,79,80]. Hence, roof vent ventilation was recommended under cold weather to keep the inside warm and meet the requirements of dehumidifying [70].
The increased vertical distance between the vents [81] resulted in greater ventilation flux. However, Shen et al. [82] found that the ventilation rate is dependent on the ratio between the inlet and outlet sizes, whereas the positions have little impact. Larger side vents resulted in a lower indoor temperature [83]. The indoor air velocity increased with larger side vents, while the effect decreased when the vent width exceeded 1 m [84]. Various outlets did not affect indoor velocities, but inlets influenced the outlet velocities [82].
Increasing the number of roof vents (roof vent area) resulted in a higher overall ventilation rate but weaker air movement at the crop level [85,86]. Yan [87] compared the ventilation performance in CSG with rear slope integral vents, rear slope interval vents, and top end vents (Figure 3a–c). The rear slope vents resulted in a higher daily average wind speed.
The optimal range of area ratio between vents and a greenhouse was recommended as 18–25% in CSG [88]. However, Tian [69] determined that the best area ratio was 11.6% in CSG with wind-induced ventilation, producing the highest air velocity in the crop zone. He also indicated that the best vent area ratio between the inlet and outlet to reach the greatest ventilation rate is 1.
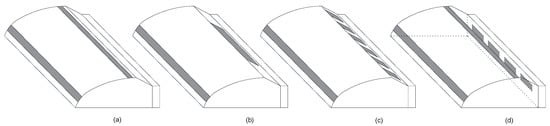
Figure 3.
Chinese solar greenhouses with top end vents (a), rear slope integral vents (b), and rear slope interval vents (c) [87], and vents on the back wall (d) [89].
The backwall vents in CSG (Figure 3d) could not improve the ventilation effectiveness, which leads to two low-speed eddy currents at the upper and lower sides of the backwall vents [89].
2.3.2. Insect Screens
Insect screens are often installed over vents, which is of great importance for reducing insect pests and diseases in greenhouses, but results in resistance to the ventilation.
Miguel et al. [90] analyzed the effects of different screen materials on ventilation rate with respect to the porosity of the screen and the pressure drop through it. Based on the motion equation [42,90], Muñoz et al. [43] determined the ventilation rate of greenhouses with insect-proof screens over different types of vents. The discharge coefficient of the screened vent (Cdsv) can be computed with the discharge coefficients of the vent (Cdv) and the screen (Cds) (Equation (14)) [91]:
1/Cdsv2 = 1/Cd2 +1/Cds2.
The total screened vent resistance coefficient is equal to the sum of the resistance coefficients of the vent and the screen (Equation (15)). The screen resistance is higher, with lower wind speed, related to the smaller Re value [92]. The total resistance is also influenced by the incidence angle (θ) of wind (16) [93]. Parra et al. [49] indicated that the ratio between the ventilation rate with and without a screen (Equation (17)) can be represented by the screen porosity (ε).
ξtotal = ξvent + ξscreen
ξθ = ξ0 cos2θ
Gscreen/G = ε (2 − ε)
The ventilation rate was reduced by 77–87% with a screened roof and side vents in the buoyancy-ventilated greenhouse, where the reduction depended on the greenhouse size [55]. However, the ventilation rate reduction was much smaller in the wind-driven ventilation.
Reduced spatial heterogeneity was observed in greenhouses with screened roof and side openings [79,94]. The air temperature at the crop level was lower than outside due to the absence of screens, but higher with screens because of the lower ventilation rate and weaker turbulence [79].
2.3.3. Plants and Their Orientation
The fluid loses some momentum due to collisions during the movement through the plant zone, leading to a decreased ventilation rate compared to with no plants. The estimation of air speed profiles in greenhouses was recommended to divide the section area into a crop part and a void part [95].
Researchers [96,97,98,99] have quantified the drag effect of plants by combining Equation (18) [100], corresponding to the pressure gradients term in the Navier–Stokes equation and the porous medium approach. The drag coefficients (CD) can be measured in wind tunnels, with 0.32 for tomato plants [101], 0.30 for forest trees [102], and 0.2 for plants in general [103]. According to the plant cover characteristics (leaf area density l, CD), the inertial factor (Cf) and the permeability (K) can be deduced (Equation (19)).
∇P = l CD ρu2
Cf/K0.5 = l CD
It was indicated that the plant drag coefficient was not affected by the ranges of pressure drop and crop canopy geometry, but by leaf area density [104]. A taller canopy with greater leaf area density resulted in lower temperature and stronger temperature stratification [105].
The energy model of natural ventilation was modified (Equation (20)) based on crops of different growth heights (x) using crop height coefficient k (Equation (21)) [106].
Q = kϕρC (Tin − Tout)
k = −0.02667x4 + 0.1467x3 − 0.2333x2 + 0.02333x + 1
Chu et al. [89] determined the effects of plants, insect screens, and internal friction on ventilation rates using a resistance model (Equation (22)) [107,108]:
ϕ* = ϕ/(VwA*) = 1/A* [(Cpw-CpL)/(ζw + ζi + ζL)]0.5.
Although plants are mostly cultivated in the north–south ridge direction in CSGs due to the good lighting conditions, the ridge length in this direction is short [109]. During actual production operations, farmers need to go in and out of the ridges in a cyclical manner, resulting in low work efficiency. Because of the suitability of the east–west crop rows orientation for machine operations in CSGs, it has been favored by researchers in China recently [110]. However, the growth of north–south-oriented tomatoes was indicated to be higher than in east–west rows [111]. Based on data collected from December 2016 to April 2017, no dramatic difference in tomato yield was found between the east–west ridges and the north–south ones [112].
Majdoubi et al. [113] analyzed the influence of plant orientation alone on ventilation performance according to the additive property of the resistance coefficients. The crop rows oriented perpendicular to the direction of indoor air movement resulted in a 50% reduction in the ventilation rate [113].
2.3.4. Roof Geometry and Slope
The geometry and roof slope can influence the natural ventilation efficiency [114,115,116]. The ventilation flow rate of a convex roof was 8.8% higher than that of a concave roof and 3.5% higher than that of a straight roof (Figure 4) [117]. A curved and gothic roof resulted in a 3.4-fold higher ventilation rate than the traditional greenhouse used in Colombia and more homogeneous thermal distribution, with the mean temperature reduced by 2.8 °C [61].
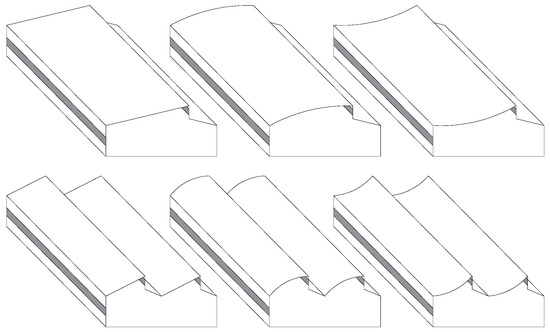
Figure 4.
The different roof geometries, including straight, concave, and convex roof geometries, and number of spans, studied by Perén et al. [117].
The height and number of spans has dramatic consequences in terms of the climate performance [117,118]. As the greenhouse height and number of spans increase, the ventilation performance increases [118]. However, this does not mean that we can increase them indefinitely, because there is a greater heating requirement [118] and a discrepancy between different roof slopes, with a double-span roof performing better than a straight or concave roof but worse than a convex roof (Figure 4) [117].
2.3.5. Wind Direction
Different wind directions with respect to the lengthwise axis of the tunnel greenhouse result in a clear effect on the inner temperature, humidity, and velocity distributions [119,120,121]. Chu et al. [122] investigated the wind-induced ventilation for buildings with two vents on the same wall. They found that when the wind direction was 22.5–45°, the mean pressure difference across the vent dominated the air entering the room, while the fluctuating pressure entrained the air across the vents when the wind direction was 0° and 67.5–180°.
The discharge coefficient and wind effect coefficient are significantly influenced by the surrounding of the greenhouse and the wind direction close to the openings [123,124]. To take full advantage of the wind, a multispan monoslope greenhouse (Figure 1e) was suggested to use prevailing windward ridge vents [60].
3. Current Models of Buoyancy-Induced Ventilation
3.1. Theoretical Models
The stack effect is caused by the uneven temperature field of the fluid, resulting in an uneven density field, leading to the driving force of the fluid movement [125]. In the case of buoyancy-driven ventilation, the spatial distribution and intensity of sensible heat sources decide the air flow.
The pressure difference at the opening can be calculated via Equation (23), with constant values of interior and exterior air density [19]. According to the Boussinesq approximation, the density difference was expressed as a temperature difference with a thermal expansion coefficient (Equation (24)), where g is the gravitational acceleration.
∆p = pi − pe = (ρe − ρi) gz
ρβ (Ti − Te) gz = ξ 1/2 ρVz2
The similarity between the scaled model and the full-scale greenhouse ventilated by buoyancy was often defined by the Rayleigh number (Ra) and Archimedes number (Ar) [2]. Hou and Ma [126] reviewed it and concluded that the Ra number of the airflow field in the greenhouse is 2 × 107–6 × 1011. The buoyancy effect was found to be more important as the Rayleigh number increased [127]. Foster and Down [128] summarized the methods of computing the buoyancy-induced ventilation rate [129,130,131,132,133].
3.2. Application Scenarios
3.2.1. Vertical Openings
To simplify the problem, the temperature field was assumed to be homogeneous in greenhouses with one-side vents. The neutral plane determines the direction of air flow, in or out, which can be determined according to the mass balance between the intake air and exhaust air [134]. The positions of neutral planes of rooms with a single vertical opening and with two equal vertical openings follow the symmetrical distribution of the hydrostatic pressure, but are closer to the bigger vent in the case of two unequally sized vertical openings [19,23].
Scholars define the pressure and velocity distribution in three ways: first-order distribution, second-order distribution, and third-order distribution (Figure 5) [17,123]. The first-order distribution has the pressure staying constant at each half of the vent, the second-order distribution integrates it by height, and the third-order distribution introduces a linear change in temperature along the height of the window.
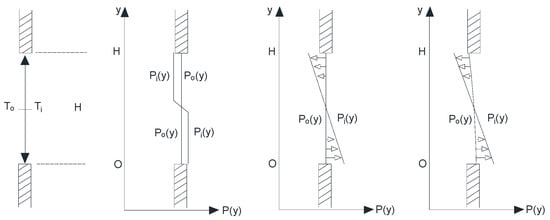
Figure 5.
Scheme of the pressure distribution at the opening, with (left to right) first-order, second-order, and third-order distributions, adapted from Boulard and Baille [17] and Roy et al. [123].
The first-order assumption was verified via experiments by Boulard and Baille [17], leading to the ventilation rate function (Equation (25)):
ϕ = S/2Cd [g∆Th/(2T)]1⁄2.
The second-order pressure distribution has been the most popular assumption in natural ventilation studies [17,19], resulting in the ventilation rate function (Equation (26)):
ϕ = L/3 [gβ∆T/ξ] 1/2 h 3/2.
As for the third-order assumption, the function of interior temperature distribution (Equation (27)) was introduced to compute the interior air density (Equation (28)) and pressure (Equation (29)) along the height of the vent [135]. Similarly, the exterior variables were obtained in the same way. Then, the pressure difference could be deduced and applied to Equation (5), resulting in a function of velocity along the opening height (Equation (30)).
Ti (z) = T0i + biz
ρi(z) = ρ0 − ρβ (Ti(z) − T0)
Pi(z) = P0i − ∫ ρi(z)gdz
V(z) = Cd {2/ρ (P0i − P0e) + 2βg[(T0i − T0e)y + (bi − be)y2/2]}0.5
3.2.2. Horizontal Openings
The horizontal openings (Figure 6) were considered in the study of De Jong [20], while there were not conclusive results here because of the rather complicated and unstable flow conditions at the opening. The heavier air moves downward and the hot air upward, where a release of potential energy forms, providing kinetic energy for the motion. Thus, the pressure and flow distribution cannot be assumed in a steady way; instead, the ventilation flow rate can be quantified in an unbalanced way, considering the growth of perturbations [136].
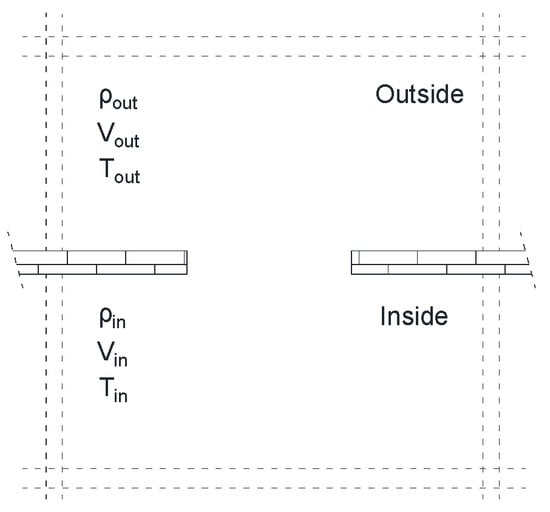
Figure 6.
The horizontal opening investigated by De Jong [20].
A typical CSG has a bottom vent and a top vent, which are vertical and horizontal, respectively. The cold air mixes with the hot air at the horizontal roof vent, resulting in a smaller thermal pressure difference than with a vertical opening under the same temperature difference. The interior temperature and air velocity were observed to decrease dramatically near the roof vent in CSG, while the specific humidity increased [137]. The first-order assumption was applied to the ventilation model of CSG with a roof vent only (Figure 7) [58]. The deduced discharge coefficients were 0.78, 0.60, and 0.44 for different widths (3, 5, and 7 cm, respectively) of roof vents, which decreased as the vent width increased [58].
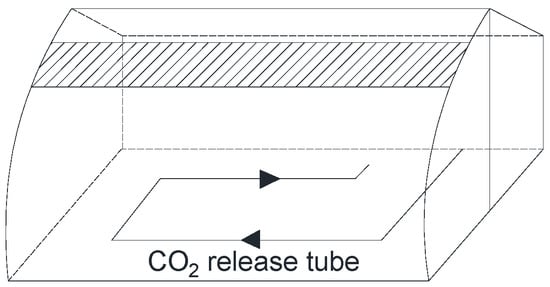
Figure 7.
Chinese solar greenhouse model used in the study of Fang et al. [58], with a roof opening only.
3.3. Factors Influencing Ventilation Rates
3.3.1. Buoyancy Source Strength and Distribution
The flow pattern of natural convection is influenced by the buoyancy strength and position. The normalized temperature gradient increased with mature plants compared to young plants [138]. The Prandtl number (Pr) was found to be a critical variable for thermal convection patterns. When Pr << 1, the heat is mainly transported through large-scale circulation; when Pr >> 1, the heat transport is mainly caused by plumes [139].
The vertical stratification is stable with different entrainments in the displacement ventilation (Figure 8) [3,140,141], while it is weak in the mixing ventilation [3]. The position of interfaces was found to be a function of the effective area of the openings, the height of the enclosure, and the ratio between the buoyancy sources [142,143].
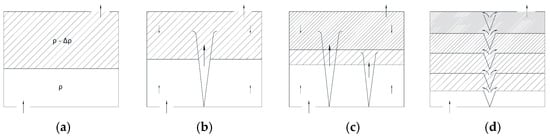
Figure 8.
Vertical stratification with different buoyancy sources, including (a) the discontinuous buoyancy, (b) single buoyancy source, (c) two buoyancy sources with different strengths, and (d) buoyancy sources at different positions, adapted from Linden et al. [3].
As the heat source in greenhouses is usually areal instead of separate, researchers used a floor with holes (Figure 9a) and a heated floor (Figure 9b) to simulate the real situation. The viscosity and thermal diffusivity can be ignored with a high enough Re (>900) and Pe [45]. Taking the heat loss through the cover into account, the ventilation flux decreased by 25%. Compared to the single buoyancy source, the areal heat source produced warm air with a lower temperature but a greater air flux circulating through the room [48].
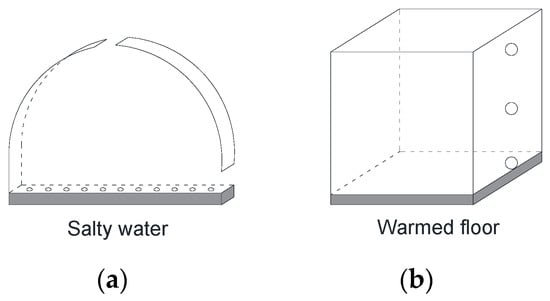
Figure 9.
(a) The greenhouse model used in the study of Oca et al. [45], (b) the ventilation model applied by Gladstone and Woods [48].
3.3.2. Vent Size, Shape, and Arrangement
Boulard et al. [144] investigated the natural ventilation driven by thermal gradients in a greenhouse with a single-sided roof opening and two symmetrical roof vents, respectively. The experimental greenhouse was set according to the Rayleigh–Bénard convection pattern. Different vent arrangements did not influence the convective loop of the incoming air streams.
Baeza et al. [55] tested a multispan greenhouse CFD model with buoyancy-driven ventilation according to the obtained data [130], and concluded that double the ventilation rate could be achieved with combined roof and sidewall vents rather than only roof vents. The combined roof and sidewall ventilation rate was higher with a smaller number of spans. Miao [86] found that increasing the roof opening area enhances the ventilation caused by heat pressure.
4. Current Natural Ventilation Models and Methods of Measurements
4.1. Theoretical Models
The combined force of wind and buoyancy affects the ventilation rate in two ways [17,19,20,35,36,44,145,146], assuming that the wind pressure and thermal pressure ventilation are dependent on each other (Equations (31) and (32)). Ventilation rate models of greenhouses under different ventilation configurations have been proposed in the literature (Equations (33) and (34)) [17,23,38]. The parameters applied in the ventilation models under various conditions are summarized in Table 2.
ϕ = √ (ϕw2 + ϕb2)
ϕ = ϕw + ϕb
Mixing ventilation [16,22]:
ϕ = CdA/2 [2gΔT/To h/4 + CwVw2]0.5.
Displacement ventilation [37]:
Φ = Cd (AiAo)/√(Ai2 + Ao2) [2gΔT/Toh + (Cwi − Cwo)Vw2]0.5.
A simplified model (Equation (35)) was proposed with only two variables: the wind speed and temperature difference between the inside and outside [147,148]:
ϕ = A √(fV2V2 + fT2∆T).
Air change rate parameters a, b, and c were used (Equations (36)–(38)) to determine the relationships between the buoyancy force, the building heat loss, and the wind force, respectively [149,150]. The ventilation rate drops dramatically when the building heat loss b increases from 0, and drops slowly when b increases further [151].
a = (CdA*)2⁄3 (Egh/(ρCpTo))1⁄3
b = ∑UwallAwall/(3ρCp)
c = 1/√3 (CdA*) √(2∆Pw)
In the case of wind-assisted natural ventilation, Heiselberg et al. [152] determined a hysteresis phenomenon to describe the abrupt switch that happened in the wind-dominated ventilation with continuously increasing buoyancy strength. The mode became buoyancy-driven ventilation with a certain strength of buoyancy, while the decreased buoyancy flux did not return the flow to the mode of wind-dominated ventilation. The driving force of ventilation with opposing wind and buoyancy effects can shift when there is sufficient perturbation [153,154].
4.2. Methods of Measuring Ventilation Rates
4.2.1. Tracer Gas Technique
The ventilation rate can be computed according to the measured tracer gas concentration and the volume of the greenhouse (Equation (39)) [19,20,43]. Accordingly, the wind and temperature factors of the simplified ventilation function [27,148,155,156] and the discharge coefficient were estimated [157,158].
c(t) = c(t0) e −[(t−t0)ϕ/V]
Katsoulas et al. [52] used the N2O gas tracing method to study the effect of window size and insect screens on ventilation. By comparing the ventilation rate computed via the tracer gas method and energy balance, a correlation was developed (Equation (40)):
ϕtracer = 0.81ϕenergy.
4.2.2. Pressure Difference Method
The pressure difference method (Figure 10) [159] is usually applied together with tracer gas tracking technology [42] to obtain the discharge coefficient and wind effect coefficient. Researchers have estimated the static pressure coefficient and the turbulent pressure coefficient of a greenhouse with a continuous roof vent [32,33].
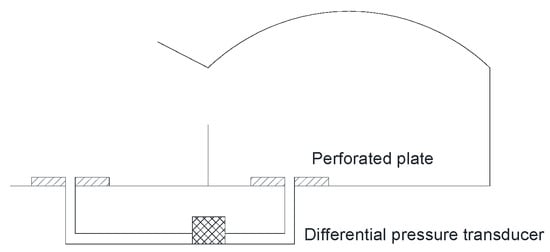
Figure 10.
The setup of the experiments measuring the pressure difference between the inside and outside of a greenhouse, adapted from Boulard et al. [34].
4.2.3. Energy Balance Simulation Method
The energy and mass balance was chosen to determine the ventilation rate because of its wide applicability [160]. The measurements of the ventilation rate in the greenhouse using a tracer gas consisting of CO2 and N2O showed good agreement with those obtained from the mass balance between the air humidity and tomato transpiration [41]. However, the tracer gas technique has numerous disadvantages, especially the large test space and low ventilation rate in the greenhouse [161], resulting in a low accuracy of around 30% [162].
The ventilation rate deduced from greenhouse energy balance (Equations (41)–(43)) was used to identify the discharge coefficient and wind effect coefficient [163] based on the ventilation model (Equation (44)) [164], with the computed convective heat transfer coefficient Ch [161] and sensible heat loss coefficient Ck [165].
Rnet = qSi,e + qSi,c + qSi,w + qLi,e + Fs
qSi,e = (ρairCp∆Ti,eϕ)/Asoil, qSi,c = Ch∆Ti,c
qLi,e = (ρairL∆HAϕ)/Asoil, qSi,w = Ck∆Ti,w
ϕ = Cd ((Ai + Ao)/2) (2gε2∆T/Te h/2 + CwVw2)0.5
4.2.4. Numerical Simulation Method
The greenhouse climate can be assessed via various numerical models [25] that have an error as high as 25% [166,167]. A temperature gradient was clearly observed in the vertical direction in the simulated CSG [168] and Venlo-type greenhouse [169] using the DO radiation model. Fatnassi et al. [170] applied the ventilation rate model [171] in a greenhouse CFD simulation, with successful verification via experiments. The plant resistance can be considered using a drag coefficient in the source term of the porous media [172]. According to the target ventilation rate, the required wind speed outside the inlet was estimated using two-dimensional numerical simulation [173].
The major difference between energy balance simulation (ES) and CFD is that it is difficult for ES to consider the detailed flow pattern and heat transfer fluxes, while CFD is not able to provide fluid dynamics information over a long period due to the limited computational resources [174]. It has been indicated by several studies that coupled CFD and ES enhanced the accuracy by taking advantage of each simulation method and reducing their drawbacks [175,176,177,178].
4.2.5. Emptying Fluid-Filling Box Method
The emptying water-filling box method uses water of different densities to simulate the natural ventilation [179,180] with the absence [181] or presence [47] of a continuous buoyancy source (Figure 11). The contribution to total velocity of the effects of buoyance and wind forces were measured by a Froude number Fr [44]: When Fr > 1, wind force dominates the ventilation, while buoyancy dominates when Fr < 1. Considering the surface thermal radiation, the emptying water-filling box model was modified to an emptying air-filling box model [182,183] by applying the node model [140].
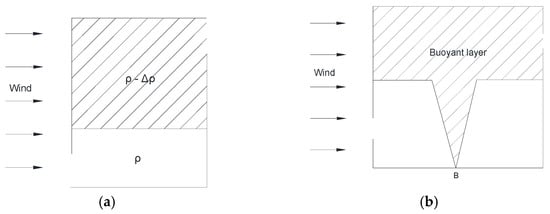
Figure 11.
Displacement flow in naturally ventilated enclosure. Adapted from Hunt and Linden [44] and Hunt and Linden [47], with the absence (a) and presence (b) of a continuous buoyant source.
4.3. Critical Wind Speed Determining Driving Forces of Natural Ventilation
The dominant driver of natural ventilation is the critical wind speed. The critical wind speed is relevant to the shape and size of the greenhouse, the position and shape of the ventilation openings, and the initial temperature difference between indoors and outdoors. Researchers have defined the critical wind speed under different conditions (Table 2).

Table 2.
The critical wind speed defining the dominant drivers of natural ventilation.
Table 2.
The critical wind speed defining the dominant drivers of natural ventilation.
| References | Ventilation Configuration | Opening Geometry | Driving Force | Critical Wind Speed (m/s) |
|---|---|---|---|---|
| Meneses and Raposo [184] | Displacement | Continuous | Buoyancy | 0.5–1.5 |
| Meneses and Raposo [184] | Displacement | Continuous | Wind | >1.5 |
| Boulard and Baille [17] | Mixing | Continuous | Combined | 0.5–2 |
| Boulard and Baille [17] | Mixing | Continuous | Buoyancy | 0–0.5 |
| Boulard, et al. [34] | Mixing | Continuous | Wind | >1.2 |
| Kittas, et al. [32] | Mixing | Continuous | Wind | >1.5 |
| Baptista, et al. [16] | Mixing | Discontinuous | Buoyancy | 0–1 |
5. Discussion
5.1. Further Research on Ventilation Models of Greenhouses with Horizontal Openings (CSG)
The material of the opening of CSG is mostly plastic, unlike the glass openings of Venlo-type greenhouses. Since the resistance coefficient of the opening is related to the Reynolds number and roughness, the existing resistance coefficient models (Equations (2) and (3)) for rectangular openings are not suitable for CSG. In addition, more studies are needed to investigate wind pressure coefficients at the CSG openings under various conditions. It seems that the ventilation model in CSG can follow the logic of Equation (34), but the buoyancy term needs to be further established.
Compared with the vertical opening in most studies, the air exchange at the horizontal vent in CSG is more complicated. The dense air moves down and the hot air moves up, where the thermal pressure difference under the same temperature difference between inside and outside is smaller than that of the vertical vent. Therefore, the existing first-order, second-order, and third-order hypotheses cannot correctly describe the thermal pressure distribution around horizontal openings. Establishing a buoyancy-induced ventilation model in CSG might require a new function of temperature distribution for horizontal openings.
5.2. Further Research on Cross-Ventilation Models (CPG)
Most cross-ventilation studies have investigated wind force only [185,186,187] or considered buoyancy force via CFD simulations. No analytical model has yet been found to describe the stack effect in cross-ventilation. The cross-ventilated greenhouse climate cannot be well simulated and controlled without such an analytical model.
A hypothesis is proposed for the cross-ventilation model. When the wind force drives it, the air stream goes into the greenhouse via the windward vents and out via the leeward vents, where the ventilation rate might be calculated according to the wind term of Equation (34). If the buoyancy force dominates, there might be two symmetrical vertexes between the two vents, and the air flows in through the lower half vents and out through the upper half. The buoyancy-induced ventilation could be calculated as twice the result of Equation (33), neglecting the wind term. When the air flow is driven by the combined forces, the air flows in via the windward vent, then upward along the tunnel cover, and out via the leeward vent. Different flow patterns result in a change in the ventilation effect—for instance, the age of air for the crop zone and heat accumulation in the zone above plants. The critical wind speeds determining the flow patterns can be classified by the strength ratio between the wind force and the stack force.
5.3. Influence of the Porosity and Height of Plants on Ventilation Models
A plant ventilation model with higher accuracy must be developed. Practically, the fluid loses momentum due to collisions during movement, leading to a changed flow direction. The method considering the leaf area density is able to involve a sink of momentum, but is not yet included in the analytical ventilation models. The sink of momentum was considered in the 2D image processing method; however, the remaining kinetic energy after the collision was ignored because of the underestimated porosity of the plants.
In general, the rows of crops in CSG are parallel to the direction of incoming air, with aisles between rows where the trajectory of air is greatly affected by the wind speed and plant characteristics. When the wind speed is relatively high, the aerodynamic force is strong: The fresh air can pass through the crop area, then up to the roof vent. Accordingly, the plant resistance model in greenhouses with side and roof openings should be investigated according to the porosity and height of plants, the orientation of plant rows, and the wind speed.
5.4. More Variables Considered in Ventilation Models
Other variables should be considered in further ventilation models [188]. This is because the vent size and wind speed were indicated to be the most important variables in air exchange rage, explaining over 50% of variance, whereas the other considered variables explained a further 30% [188].
The geographical variables might have effects on the process of ventilation. Stronger solar radiation resulted in higher buoyancy [21] and a decreased ventilation effect (reduction in temperature and humidity ratio) [46] inside the greenhouse. Under the same indoor temperature, stronger radiation resulted in a higher ventilation rate [189], which may influence the critical wind speed. In addition, with lower air density, the amount of convective heat could be different under the same ventilation rate, leading to a poor ventilation effect.
The physical properties of air change as the altitude increases, leading to lower air pressure, density, temperature, humidity, and heat transfer coefficient, and a higher radiation [190,191,192,193,194]. Greenhouses are considered a tool to provide enough vegetables in high-altitude areas, but there are limited relevant studies [195,196,197], and further investigations are necessary.
5.5. Application of Ventilation Model in Greenhouse Climate Prediction
The purpose of ventilation models involves application in greenhouse climate models as sub-models to analyze and control the indoor climate and control. Greenhouses are intensively coupled Multi-Input, Multi-Output systems that are highly nonlinear and influenced by the outdoor weather and practical limitations [198]. Energy balance models have been widely used to predict the indoor climate of greenhouses [199,200,201,202]. However, these models are limited by the requirement of empirical expressions for convective heat transfer coefficients and the known wind pressure coefficients [178].
By introducing the established ventilation models [17], a dynamic model predicting the indoor environment with insect screen was developed [203]. Wang and Boulard [204] improved the calculations of the Gembloux Greenhouse Dynamic Model [205,206,207,208,209,210,211]. According to the ventilation model proposed by Kittas et al. [38], Singh et al. [212] established a dynamic model to simulate the microclimate in a greenhouse. The simulation results of GGDM fitted well with the measurements [213].
More criteria have been suggested to evaluate the ventilation performance in addition to the ventilation rate, since it is only estimated through the opening surfaces, which might overestimate the real ventilation performance [214,215]. The air speed at the crop level, the crop aerodynamic resistance, the efficiency of ventilation rate, and the temperature difference between the interior and exterior are recommended variables for consideration in further investigations. In addition, the ventilation efficiency is usually computed by the local mean age of air [216,217,218,219].
6. Conclusions
This paper provides a review of the literature on natural ventilation in greenhouses. The wind-induced ventilation models are classified by application scenarios, including mixing ventilation, displacement ventilation, and cross-ventilation. Horizontal vents and vertical vents are considered as application scenarios for buoyancy-induced ventilation models.
The wind-induced ventilation rate of greenhouses is influenced by wind direction, roof geometry, vent size, insect screens, plant properties, and plant row orientation. Buoyancy strengths and distributions, and vent sizes and arrangements, affect the temperature-induced ventilation rate. Key parameters of the ventilation models, including the discharge coefficient, wind pressure coefficient, and opening effectiveness, are summarized according to the driving force and influencing factors.
Methods of measuring ventilation rates that can be used to validate the theoretical models are described, including the tracer gas technique, pressure difference method, energy balance method, emptying water-filling box method, and numerical simulation method. Moreover, the critical wind speeds are summarized, which can determine the driving force simply.
Regarding the development of ventilation models for typical Chinese greenhouses, further investigations are recommended in Section 5. First, for Chinese solar greenhouses (CSG), the pressure distribution function is recommended in greenhouses with horizontal openings. Second, for Chinese plastic greenhouses (CPG), a cross-ventilated model should be established with combined wind and buoyancy force. A hypothesis is proposed for natural ventilation in CPGs. Third, a more accurate plant-considering ventilation model is needed. Fourth, for greenhouses at high altitudes, other environmental variables, especially geography-dependent ones, can be added to ventilation models, including solar radiation and air density. Finally, more criteria are suggested to evaluate the ventilation performance rather than the ventilation rate only. These recommendations offer a development path for ventilation models for Chinese greenhouses.
Author Contributions
Writing—original draft preparation, J.Z.; writing—review and editing, T.D.; supervision, S.Z.; project administration, A.D.; data curation, P.W., Z.L. and B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of China (U20A2020) and the Beijing Vegetable Facility Industry System.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qi, F.; Ding, X.; Lu, S.; Yin, Y.; Lian, Q.; Wei, X.; Li, K. National Greenhouse Data System; Institute of Facility Agriculture, Planning and Design Institute, Ministry of Agriculture: Beijing, China, 2014.
- Mistriotis, A.; Arcidiacono, C.; Picuno, P.; Bot, G.P.A.; Scarascia Mugnozza, G. Computational analysis of ventilation in greenhouses at zero-and low-wind-speeds. Agric. For. Meteorol. 1997, 88, 121–135. [Google Scholar] [CrossRef]
- Linden, P.F.; Lane-Serff, G.F.; Smeed, D.A. Emptying filling boxes: The fluid mechanics of natural ventilation. J. Fluid Mech. 1990, 212, 309–335. [Google Scholar] [CrossRef]
- von Zabeltitz, C. Energy Conservation and Renewable Energies for Greenhouse Heating. CNRE Guideline, No. 2; REUR Technical Series No. 3; FAO: Rome, Italy, 1989. [Google Scholar]
- Boulard, T. Greenhouse natural ventilation modelling: A survey of the different approaches. In Proceedings of the International Symposium on Greenhouse Cooling 719, Almeria, Spain, 24–27 April 2006; pp. 29–30. [Google Scholar]
- Sethi, V.P.; Sharma, S.K. Survey of cooling technologies for worldwide agricultural greenhouse applications. Sol. Energy 2007, 81, 1447–1459. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W.; Grant, J.; Fallon, R.; Dodd, V. Applications of computational fluid dynamics (CFD) in the modelling and design of ventilation systems in the agricultural industry: A review. Bioresour. Technol. 2007, 98, 2386–2414. [Google Scholar] [CrossRef] [PubMed]
- Bournet, P.E.; Boulard, T. Effect of ventilator configuration on the distributed climate of greenhouses: A review of experimental and CFD studies. Comput. Electron. Agric. 2010, 74, 195–217. [Google Scholar] [CrossRef]
- Khanal, R.; Lei, C. Solar chimney—A passive strategy for natural ventilation. Energy Build. 2011, 43, 1811–1819. [Google Scholar] [CrossRef]
- Sandberg, M.; Moshfegh, B. Ventilated-solar roof air flow and heat transfer investigation. Renew. Energy 1998, 15, 287–292. [Google Scholar] [CrossRef]
- Rong, L.; Bjerg, B.; Batzanas, T.; Zhang, G. Mechanisms of natural ventilation in livestock buildings: Perspectives on past achievements and future challenges. Biosyst. Eng. 2016, 151, 200–217. [Google Scholar] [CrossRef]
- Akrami, M.; Salah, A.H.; Javadi, A.A.; Fath, H.E.S.; Hassanein, M.J.; Farmani, R.; Dibaj, M.; Negm, A. Towards a sustainable greenhouse: Review of trends and emerging practices in analysing greenhouse ventilation requirements to sustain maximum agricultural yield. Sustainability 2020, 12, 2794. [Google Scholar] [CrossRef]
- Sakiyama, N.R.M.; Carlo, J.C.; Frick, J.; Garrecht, H. Perspectives of naturally ventilated buildings: A review. Renew. Sustain. Energy Rev. 2020, 130, 109933. [Google Scholar] [CrossRef]
- Wang, C.; Nan, B.; Wang, T.; Bai, Y.; Li, Y. Wind pressure acting on greenhouses: A review. Int. J. Agric. Biol. Eng. 2021, 14, 1–8. [Google Scholar] [CrossRef]
- Zhong, H.-Y.; Sun, Y.; Shang, J.; Qian, F.-P.; Zhao, F.-Y.; Kikumoto, H.; Jimenez-Bescos, C.; Liu, X. Single-sided natural ventilation in buildings: A critical literature review. Build. Environ. 2022, 212, 108797. [Google Scholar] [CrossRef]
- Baptista, F.J.; Bailey, B.J.; Randall, J.M.; Meneses, J.F. Greenhouse ventilation rate: Theory and measurement with tracer gas techniques. J. Agric. Eng. Res. 1999, 72, 363–374. [Google Scholar] [CrossRef]
- Boulard, T.; Baille, A. Modelling of air exchange rate in a greenhouse equipped with continuous roof vents. J. Agric. Eng. Res. 1995, 61, 37–47. [Google Scholar] [CrossRef]
- Kwon, K.S.; Lee, I.B.; Han, H.T.; Shin, C.Y.; Hwang, H.S.; Hong, S.W.; Bitog, J.P.; Seo, I.H.; Han, C.P. Analysing ventilation efficiency in a test chamber using age-of-air concept and CFD technology. Biosyst. Eng. 2011, 110, 421–433. [Google Scholar] [CrossRef]
- Bot, G.P.A. Greenhouse Climate: From Physical Processes to a Dynamic Model. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 1983. [Google Scholar]
- De Jong, T. Natural Ventilation of Large Multi-Span Greenhouses. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 1990. [Google Scholar]
- Fernandez, J.E.; Bailey, B.J. Predicting greenhouse ventilation rates. In Proceedings of the International Workshop on Greenhouse Crop Models 328, Saumane, France, 25–29 August 1991; pp. 107–114. [Google Scholar]
- Boulard, T.; Baille, A.; Draoui, B. Greenhouse Natural Ventilation Measurements and Modelling; International Workshop Agritech, Agriculture Research Organisation: Sophia Antipolis, France, 1993. [Google Scholar]
- Bruce, J.M. Natural convection through openings and its application to cattle building ventilation. J. Agric. Eng. Res. 1978, 23, 151–167. [Google Scholar] [CrossRef]
- Gong, B.; Ma, C.; Li, Z. Confirmation the Flow Coefficient of Greenhouse Ventilation by Computational Fluid Dynamics Technique. J. Agric. Mech. Res. 2010, 32, 11–15+74. [Google Scholar]
- Kozai, T.; Sase, S.; Nara, M. A modeling approach to greenhouse environmental control by ventilation. Acta Hort 1980, 106, 125–136. [Google Scholar] [CrossRef]
- Sase, S.; Takakura, T.; Nara, M. Wind tunnel testing on airflow and temperature distribution of a naturally ventilated greenhouse. In Proceedings of the III International Symposium on Energy in Protected Cultivation 148, Columbus, OH, USA, 21–26 August 1983; pp. 329–336. [Google Scholar]
- Fernandez, J.E.; Bailey, B.J. Measurement and prediction of greenhouse ventilation rates. Agric. For. Meteorol. 1992, 58, 229–245. [Google Scholar] [CrossRef]
- Bruce, J.M. Ventilation of a model livestock building by thermal buoyancy. Trans. ASAE 1982, 25, 1724–1726. [Google Scholar] [CrossRef]
- Van Der Maas, J. Air Flow through Large Openings in Buildings; International Energy Agency: Bern, Switzerland, 1992. [Google Scholar]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics, 2nd ed.; Edward Arnold: London, UK, 1990. [Google Scholar]
- Gandemer, J.; Bietry, J. Cours dáérodynamique REEF, Vol. 2. In Sciences du Bâtiment; CSTB Nantes: Paris, France, 1989. [Google Scholar]
- Kittas, C.; Boulard, T.; Mermier, M.; Papadakis, G. Wind induced air exchange rates in a greenhouse tunnel with continuous side openings. J. Agric. Eng. Res. 1996, 65, 37–49. [Google Scholar] [CrossRef]
- Papadakis, G.; Mermier, M.; Meneses, J.F.; Boulard, T. Measurement and analysis of air exchange rates in a greenhouse with continuous roof and side openings. Agric. Eng. Res. 1996, 63, 219–227. [Google Scholar] [CrossRef]
- Boulard, T.; Meneses, J.F.; Mermier, M.; Papadakis, G. The mechanisms involved in the natural ventilation of greenhouses. Agric. For. Meteorol. 1996, 79, 61–77. [Google Scholar] [CrossRef]
- Hellickson, M.A.; Hinkle, C.N.; Jedele, D.G. Natural ventilation. In Ventilation of Agricultural Structures; ASAE: St. Joseph, MI, USA, 1983. [Google Scholar]
- Albright, L.D. Environment Control for Animals and Plants; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1990. [Google Scholar]
- Nääs, I.A.; Moura, D.J.; Bucklin, R.A.; Fialho, F.B. An algorithm for determining opening effectiveness in natural ventilation by wind. Trans. ASAE 1998, 41, 767. [Google Scholar] [CrossRef]
- Kittas, C.; Boulard, T.; Papadakis, G. Natural ventilation of a greenhouse with ridge and side openings: Sensitivity to temperature and wind effects. Trans. ASAE 1997, 40, 415–425. [Google Scholar] [CrossRef]
- Zhang, J.S.; Janni, K.A.; Jacobson, L.D. Modeling natural ventilation induced by combined thermal buoyancy and wind. Trans. ASAE 1989, 32, 2165–2174. [Google Scholar] [CrossRef]
- Kittas, C.; Draoui, B.; Boulard, T. Quantification du taux d’aération d’une serre à ouvrant continu en toiture. Agric. For. Meteorol. 1995, 77, 95–111. [Google Scholar] [CrossRef]
- Boulard, T.; Draoui, B. Natural ventilation of a greenhouse with continuous roof vents: Measurements and data analysis. J. Agric. Eng. Res. 1995, 61, 27–35. [Google Scholar] [CrossRef]
- Miguel, A.A.F. Transport Phenomena through Porous Screens and Openings: From Theory to Greenhouse Practice; Wageningen University and Research: Wageningen, The Netherlands, 1998. [Google Scholar]
- Muñoz, P.; Montero, J.I.; Antón, A.; Giuffrida, F. Effect of insect-proof screens and roof openings on greenhouse ventilation. J. Agric. Eng. Res. 1999, 73, 171–178. [Google Scholar] [CrossRef]
- Hunt, G.R.; Linden, P.F. The fluid mechanics of natural ventilation—displacement ventilation by buoyancy-driven flows assisted by wind. Build. Environ. 1999, 34, 707–720. [Google Scholar] [CrossRef]
- Oca, J.; Montero, J.I.; Anton, A.; Crespo, D. A method for studying natural ventilation by thermal effects in a tunnel greenhouse using laboratory-scale models. J. Agric. Eng. Res. 1999, 72, 93–104. [Google Scholar] [CrossRef]
- Teitel, M.; Tanny, J. Natural ventilation of greenhouses: Experiments and model. Agric. For. Meteorol. 1999, 96, 59–70. [Google Scholar] [CrossRef]
- Hunt, G.R.; Linden, P.F. Steady-state flows in an enclosure ventilated by buoyancy forces assisted by wind. J. Fluid Mech. 2001, 426, 355–386. [Google Scholar] [CrossRef]
- Gladstone, C.; Woods, A.W. On buoyancy-driven natural ventilation of a room with a heated floor. J. Fluid Mech. 2001, 441, 293–314. [Google Scholar] [CrossRef]
- Parra, J.P.; Baeza, E.; Montero, J.I.; Bailey, B.J. Natural ventilation of parral greenhouses. Biosyst. Eng. 2004, 87, 355–366. [Google Scholar] [CrossRef]
- Si, H.; Miao, X. Opening model of natural vent ilation windows for East-China Multi-span Plast ic Greenhouse and studies on it. J. Zhejiang Univ. 2005, 31, 113–118. [Google Scholar]
- Liu, S.; He, Y.; Zhang, Y.; Miao, X. Prediction and analysis model of temperature and its application to a natural ventilation multi-span plastic greenhouse equipped with insect-proof screen. J. Zhejiang Univ. Sci. B 2005, 6, 523. [Google Scholar] [CrossRef]
- Katsoulas, N.; Bartzanas, T.; Boulard, T.; Mermier, M.; Kittas, C. Effect of vent openings and insect screens on greenhouse ventilation. Biosyst. Eng. 2006, 93, 427–436. [Google Scholar] [CrossRef]
- Teitel, M.; Ziskind, G.; Liran, O.; Dubovsky, V.; Letan, R. Effect of wind direction on greenhouse ventilation rate, airflow patterns and temperature distributions. Biosyst. Eng. 2008, 101, 351–369. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X. Ventilation rate of various vents in plastic covered multi-span greenhouse. Trans. Chin. Soc. Agric. Eng. 2009, 25, 248–252. [Google Scholar]
- Baeza, E.J.; Pérez-Parra, J.J.; Montero, J.I.; Bailey, B.J.; López, J.C.; Gázquez, J.C. Analysis of the role of sidewall vents on buoyancy-driven natural ventilation in parral-type greenhouses with and without insect screens using computational fluid dynamics. Biosyst. Eng. 2009, 104, 86–96. [Google Scholar] [CrossRef]
- Mashonjowa, E.; Ronsse, F.; Milford, J.R.; Lemeur, R.; Pieters, J.G. Measurement and simulation of the ventilation rates in a naturally ventilated Azrom-type greenhouse in Zimbabwe. Appl. Eng. Agric. 2010, 26, 475–488. [Google Scholar] [CrossRef]
- Teitel, M.; Wenger, E. Air exchange and ventilation efficiencies of a monospan greenhouse with one inflow and one outflow through longitudinal side openings. Biosyst. Eng. 2014, 119, 98–107. [Google Scholar] [CrossRef]
- Fang, H.; Yang, Q.; Zhang, Y.; Cheng, R.; Zhang, F.; Lu, W. Simulation on Ventilation Flux of Solar Greenhouse Based on the Coupling between Stack and Wind Effects. Chin. J. Agrometeorol. 2016, 37, 531–537. [Google Scholar]
- Chu, C.R.; Lan, T.W.; Tasi, R.K.; Wu, T.R.; Yang, C.K. Wind-driven natural ventilation of greenhouses with vegetation. Biosyst. Eng. 2017, 164, 221–234. [Google Scholar] [CrossRef]
- Chu, C.R.; Lan, T.W. Effectiveness of ridge vent to wind-driven natural ventilation in monoslope multi-span greenhouses. Biosyst. Eng. 2019, 186, 279–292. [Google Scholar] [CrossRef]
- Villagran, E.A.; Romero, E.J.B.; Bojacá, C.R. Transient CFD analysis of the natural ventilation of three types of greenhouses used for agricultural production in a tropical mountain climate. Biosyst. Eng. 2019, 188, 288–304. [Google Scholar] [CrossRef]
- Li, N.; Xue, X.; Li, H. The risk assessment of wind disaster of greenhouse in Shandong province based on information dissemination theory. J. Meteorol. Environ. 2018, 34, 149–155. [Google Scholar]
- Yang, Z.; Zhang, B.; Xue, X.; Huang, C.; Zhu, K. The wind tunnel test of plastic greenhouse and its surface wind pressure patterns. Acta Ecol. Sin. 2012, 32, 7730–7737. [Google Scholar] [CrossRef][Green Version]
- Yang, Z.Q.; Li, Y.X.; Xue, X.P.; Huang, C.R.; Zhang, B. Wind loads on single-span plastic greenhouses and solar greenhouses. HortTechnology 2013, 23, 622–628. [Google Scholar] [CrossRef]
- Wang, J.; Ding, W.; Wu, Y. Wind tunnel test of wind pressure distribution on mutual insert multi-greenhouse roof. Trans. CSAE 2008, 24, 230–234. [Google Scholar]
- Zhang, Q.; Yu, H.; Zhang, Z.; Dong, L.; Zhang, Q.; Shao, C.; Yang, K.; Wang, X. Airflow simulation in solar greenhouse using CFD model. Trans. Chin. Soc. Agric. Eng. 2012, 28, 166–171. [Google Scholar]
- Su, W. CFD Numerical Simulation about Effect of Natural Ventilation on Microclimate in Greenhouse. Master’s Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2016. [Google Scholar]
- Tong, G.; Christopher, D.M.; Li, B. Numerical modelling of temperature variations in a Chinese solar greenhouse. Comput. Electron. Agric. 2009, 68, 129–139. [Google Scholar] [CrossRef]
- Tian, Y. Study on Natural Ventilation and Enhancement in Single-Slope Solar Greenhouse. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2021. [Google Scholar]
- Zhao, R. Influence of Different Ventilation Conditions on Air Flow and Temperature and Humidity in Plastic Greenhouse. Master’s Thesis, Northwest A&F University, Xianyang, China, 2021. [Google Scholar]
- Nebbali, R.; Roy, J.C.; Boulard, T. Dynamic simulation of the distributed radiative and convective climate within a cropped greenhouse. Renew. Energy 2012, 43, 111–129. [Google Scholar] [CrossRef]
- Chu, C.R.; Chiu, Y.H.; Chen, Y.J.; Wang, Y.W.; Chou, C.P. Turbulence effects on the discharge coefficient and mean flow rate of wind-driven cross-ventilation. Build. Environ. 2009, 44, 2064–2072. [Google Scholar] [CrossRef]
- CIBSE. Natural Ventilation in Non-Domestic Buildings: Applications Manual AM10; Chartered Institution of Building Services Engineers (CIBSE): London, UK, 1997. [Google Scholar]
- Mumovic, D.; Santamouris, M. A Handbook of Sustainable Building Design and Engineering: An Integrated Approach to Energy, Health and Operational Performance; Routledge: London, UK, 2013. [Google Scholar]
- Chu, C.R.; Chiang, B.F. Wind-driven cross ventilation in long buildings. Build. Environ. 2014, 80, 150–158. [Google Scholar] [CrossRef]
- Bartzanas, T.; Katsoulas, N.; Kittas, C. Effect of vent configuration and insect screen on greenhouse microclimate. Int. J. Vent. 2005, 4, 193–202. [Google Scholar] [CrossRef]
- He, K.; Chen, D.; Sun, L.; Liu, Z. Effects of Wind Regime and Vent Configuration on Microclimate in Tunnel Greenhouses in Summer. Trans. Chin. Soc. Agric. Mach. 2017, 48, 311–318+339. [Google Scholar]
- Zhao, P. Simulation and Experimental Research on Indoor Environment of Solar Greenhouse under Natural Ventilation. Master’s Thesis, Shandong Jianzhu University, Jinan, China, 2021. [Google Scholar]
- Kittas, C.; Katsoulas, N.; Bartzanas, T.; Mermier, M.; Boulard, T. The impact of insect screens and ventilation openings on the greenhouse microclimate. Trans. ASABE 2008, 51, 2151–2165. [Google Scholar] [CrossRef]
- Majdoubi, H.; Fatnassi, H.; Boulard, T.; Senhaji, A.; Demrati, H.; Mouqallid, M.; Bouirden, L. Computational study of thermal performance of an unheated canarian-Type greenhouse: Influence of the opening configurations on airflow and climate patterns at the crop level. Acta Hortic. 2017, 1182, 87–94. [Google Scholar] [CrossRef]
- Luan, T. Numerieal Simulation and PIV Test Research on Natural Ventilation of Coupling Thermal Pressure and Wind Pressure. Master’s Thesis, Chang’an University, Xi’an, China, 2010. [Google Scholar]
- Shen, X.; Su, R.; Ntinas, G.K.; Zhang, G. Influence of sidewall openings on air change rate and airflow conditions inside and outside low-rise naturally ventilated buildings. Energy Build. 2016, 130, 453–464. [Google Scholar] [CrossRef]
- Fu, W.; You, S. The influence of intake size of strawberry solar greenhouse on the microclimate in natural ventilation: An experimental study. J. Hebei Univ. Technol. 2013, 42, 52–56. [Google Scholar]
- Bai, Z.; Xia, L.; Lv, X.; Zhang, M.; Tao, J. Simulations of greenhouse window settings with natural ventilation Based on CFD. Jiangsu Agric. Sci. 2016, 44, 379–382. [Google Scholar]
- Espinoza, K.; Lopez, A.; Valera, D.L.; Molina-Aiz, F.D.; Torres, J.A.; Pena, A. Effects of ventilator configuration on the flow pattern of a naturally-ventilated three-span Mediterranean greenhouse. Biosyst. Eng. 2017, 164, 13–30. [Google Scholar] [CrossRef]
- Miao, Z. Numerical Simulation and Optimization of Vent Configuration for Natural Ventilation of The Large Space Exhibition Greenhouse. Refrig. Air Cond. 2020, 34, 29–38. [Google Scholar]
- Yan, L. Effects of Different Natural Ventilation Methods on Solar Greenhouse Environment and Tomato Growth. Master’s Thesis, Northwest A&F University, Xianyang, China, 2020. [Google Scholar]
- Yang, Z.; Zou, Z.; Chen, S.; Wang, J. Distribution law of inside wind speed and relationship between wind speed inside and outside and ventilation area ratio in northwest type sunlight greenhouse. J. Northwest AF Univ. 2006, 34, 36–40. [Google Scholar]
- Yang, Z. Optimal Wind Speed and CFD Simulation in Sunlight Greenhouse. Ph.D. Thesis, Northwest A&F University, Xianyang, China, 2006. [Google Scholar]
- Miguel, A.F.; Van de Braak, N.J.; Bot, G.P.A. Analysis of the airflow characteristics of greenhouse screening materials. J. Agric. Eng. Res. 1997, 67, 105–112. [Google Scholar] [CrossRef]
- Teitel, M. The effect of insect-proof screens in roof openings on greenhouse microclimate. Agric. For. Meteorol. 2001, 110, 13–25. [Google Scholar] [CrossRef]
- Bailey, B.J.; Montero, J.I.; Parra, J.P.; Robertson, A.P.; Baeza, E.; Kamaruddin, R. Airflow resistance of greenhouse ventilators with and without insect screens. Biosyst. Eng. 2003, 86, 217–229. [Google Scholar] [CrossRef]
- Laws, E.M.; Livesey, J.L. Flow through screens. Annu. Rev. Fluid Mech. 1978, 10, 247–266. [Google Scholar] [CrossRef]
- Santolini, E.; Pulvirenti, B.; Benni, S.; Barbaresi, L.; Torreggiani, D.; Tassinari, P. Numerical study of wind-driven natural ventilation in a greenhouse with screens. Comput. Electron. Agric. 2018, 149, 41–53. [Google Scholar] [CrossRef]
- Wang, S.; Boulard, T.; Haxaire, R. Air speed profiles in a naturally ventilated greenhouse with a tomato crop. Agric. For. Meteorol. 1999, 96, 181–188. [Google Scholar] [CrossRef]
- Roy, J.C.; Boulard, T.; Kittas, C.; Wang, S. Convective and ventilation transfers in greenhouses, Part 1: The greenhouse considered as a perfectly stirred tank. Biosyst. Eng. 2002, 83, 1–20. [Google Scholar] [CrossRef]
- Boulard, T.; Wang, S. Experimental and numerical studies on the heterogeneity of crop transpiration in a plastic tunnel. Comput. Electron. Agric. 2002, 34, 173–190. [Google Scholar] [CrossRef]
- Majdoubi, H.; Boulard, T.; Fatnassi, H.; Bouirden, L. Airflow and microclimate patterns in a one-hectare Canary type greenhouse: An experimental and CFD assisted study. Agric. For. Meteorol. 2009, 149, 1050–1062. [Google Scholar] [CrossRef]
- Fatnassi, H.; Boulard, T.; Roy, J.C.; Suay, R.; Poncet, C. CFD coupled modeling of distributed plant activity and climate in greenhouse. Acta Hortic. 2017, 57–64. [Google Scholar] [CrossRef]
- Thom, A.S. Momentum absorption by vegetation. Q. J. R. Meteorol. Soc. 1971, 97, 414–428. [Google Scholar] [CrossRef]
- Haxaire, R. Caractérisation et Modélisation des écoulements d’air Dans une Serre. [Characterisation and Modelling of Air Flow in a Greenhouse]. Ph.D. Thesis, l’Université de Nice Sophia Antipolis, Nice, France, 1999. [Google Scholar]
- Green, S.R. Modeling turbulent air flow in a stand of widely spaced trees. PHOENICS J. Comput. Fluid Dyn. Its Appl. 1992, 5, 294–312. [Google Scholar]
- Bruse, M. Development of a Micro-Scale Model for the Calculation of Surface Temperature in Structured Terrain. Ph.D. Thesis, University of Bochum, Institute for Geography, Bochum, Germany, 1995. [Google Scholar]
- Sase, S.; Kacira, M.; Boulard, T.; Okushima, L. Wind tunnel measurement of aerodynamic properties of a tomato canopy. Trans. ASABE 2012, 55, 1921–1927. [Google Scholar] [CrossRef]
- Boulard, T.; Roy, J.C.; Pouillard, J.B.; Fatnassi, H.; Grisey, A. Modelling of micrometeorology, canopy transpiration and photosynthesis in a closed greenhouse using computational fluid dynamics. Biosyst. Eng. 2017, 158, 110–133. [Google Scholar] [CrossRef]
- Zheng, M.; Mao, H. CFD Analysis about Effect of Plant Height on Natural Ventilation in Greenhouse. J. Agric. Mech. Res. 2016, 38, 20–23+27. [Google Scholar]
- Chu, C.R.; Wang, Y.W. The loss factors of building openings for wind-driven ventilation. Build. Environ. 2010, 45, 2273–2279. [Google Scholar] [CrossRef]
- Chu, C.R.; Chiang, B.F. Wind-driven cross ventilation with internal obstacles. Energy Build. 2013, 67, 201–209. [Google Scholar] [CrossRef]
- Liang, Z. Study on the Effect of Applying the Cultivation Pattern of Overwintering Tomatoes from the East-West Ridge of Solar Greenhouse. Master’s Thesis, Shenyang Agricultrual University, Shenyang, China, 2018. [Google Scholar]
- Yang, Y. Tomato Yield Formation and Influencing Factors under East-West Cultivation Pattern in Slide Cover Type Solar Greenhouse. Master’s Thesis, Shenyang Agricultrual University, Shenyang, China, 2017. [Google Scholar]
- Zhiguo, L.; Zishuang, Y.; Liguo, Y.; Chuanyou, L.; Zongxu, L.; Xiaoming, L. Experimental study on tomato cultivation mode in solar greenhouse based on integration of agricultural machinery and agronomy. J. Chin. Agric. Mech. 2021, 42, 55–59. [Google Scholar]
- Song, W.; Li, C.; Sun, X.; Wang, P.; Zhao, S. Effects of ridge direction on growth and yield of tomato in solar greenhouse with diffuse film. Trans. Chin. Soc. Agric. Eng. 2017, 33, 242–248. [Google Scholar]
- Majdoubi, H.; Boulard, T.; Hanafi, A.; Bekkaoui, A.; Fatnassi, H.; Demrati, H.; Nya, M.B.; Bouirden, L. Natural Ventilation Performance of a Large Greenhouse Equipped with Insect Screens. Trans. ASABE 2007, 50, 641–650. [Google Scholar] [CrossRef]
- Perén, J.I.; Van Hooff, T.; Leite, B.C.C.; Blocken, B. CFD analysis of cross-ventilation of a generic isolated building with asymmetric opening positions: Impact of roof angle and opening location. Build. Environ. 2015, 85, 263–276. [Google Scholar] [CrossRef]
- Baeza, E.J. Optimización del Diseño de los Sistemas de Ventilación en Invernaderos Tipo Parral. Ph.D. Thesis, Universidad de Almería, Almería, Spain, 2007. [Google Scholar]
- Peren, J.I.; Van Hooff, T.; Ramponi, R.; Blocken, B.; Leite, B.C.C. Impact of roof geometry of an isolated leeward sawtooth roof building on cross-ventilation: Straight, concave, hybrid or convex? J. Wind. Eng. Ind. Aerodyn. 2015, 145, 102–114. [Google Scholar] [CrossRef]
- Perén, J.I.; van Hooff, T.; Leite, B.C.C.; Blocken, B. CFD simulation of wind-driven upward cross ventilation and its enhancement in long buildings: Impact of single-span versus double-span leeward sawtooth roof and opening ratio. Build. Environ. 2016, 96, 142–156. [Google Scholar] [CrossRef]
- Fatnassi, H.; Boulard, T.; Benamara, H.; Roy, J.C.; Suay, R.; Poncet, C. Increasing the height and multiplying the number of spans of greenhouse: How far can we go. Acta Hortic. 2017, 1170, 137–144. [Google Scholar] [CrossRef]
- Roy, J.C.; Boulard, T. CFD prediction of the natural ventilation in a tunnel-type greenhouse: Influence of wind direction and sensibility to turbulence models. Acta Hortic. 2004, 691, 457–464. [Google Scholar] [CrossRef]
- Pontikakos, C.; Ferentinos, K.P.; Tsiligiridis, T.A.; Sideridis, A.B. Natural ventilation efficiency in a twin-span greenhouse using 3D computational fluid dynamics. In Proceedings of the 3rd International Conference on Information and Communication Technologies in Agriculture, Volos, Greece, 20–23 September 2006. [Google Scholar]
- He, K.; Chen, D.; Liu, Z. Effects of vent configuration and wind regime on the microclimate in the tunnel greenhouse. In Proceedings of the 2017 6th International Conference on Agro-Geoinformatics, Fairfax, VA, USA, 7–10 August 2017; pp. 1–6. [Google Scholar]
- Chu, C.R.; Chiu, Y.H.; Tsai, Y.T.; Wu, S.L. Wind-driven natural ventilation for buildings with two openings on the same external wall. Energy Build. 2015, 108, 365–372. [Google Scholar] [CrossRef]
- Boulard, T.; Kittas, C.; Roy, J.C.; Wang, S. Convective and ventilation transfers in greenhouses, part 2: Determination of the distributed greenhouse climate. Biosyst. Eng. 2002, 83, 129–147. [Google Scholar] [CrossRef]
- Bailey, B.J. Constraints, limitations and achievements in greenhouse natural ventilation. Acta Hortic. 2000, 534, 21–30. [Google Scholar] [CrossRef]
- Tao, W. Heat Transfer; Higher Education Press: Beijing, China, 2019. [Google Scholar]
- Hou, C.; Ma, C. Study Applying Fluent in Greenhouse Ventilation. J. Agric. Mech. Res. 2007, 29, 5–9. [Google Scholar]
- Mezrhab, A.; Elfarh, L.; Naji, H.; Lemonnier, D. Computation of surface radiation and natural convection in a heated horticultural greenhouse. Appl. Energy 2010, 87, 894–900. [Google Scholar] [CrossRef]
- Foster, M.P.; Down, M.J. Ventilation of livestock buildings by natural convection. J. Agric. Eng. Res. 1987, 37, 1–13. [Google Scholar] [CrossRef]
- Handbook, A. Fundamentals, 1981; American Society of Heating, Refrigerating and Air-conditioning Engineers: Atlanta, GA, USA, 1981. [Google Scholar]
- IHVE. Guide; The Institution of Heating and Ventilating Engineers: London, UK, 1970; p. 64. [Google Scholar]
- Daly, B.B. Woods Practical Guide to Fan Engineering; Woods of Colchester Limited: Colchester, UK, 1978. [Google Scholar]
- Hellickson, M.A.; Walker, J.N. Ventilation of Agricultural Structures; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1983. [Google Scholar]
- Sainsbury, D.; Sainsbury, P. Livestock Health and Housing; Baillière Tindall: London, UK, 1988. [Google Scholar]
- Liu, H.; Xu, Z. Determination of Hot Pressing Neutral Plane Position of High Building. China Saf. Sci. J. 2001, 11, 17–19. [Google Scholar]
- Kirkpatrick, A.T.; Hill, D.D. Mixed convection heat transfer in a passive solar building. Sol. Energy 1988, 40, 25–34. [Google Scholar] [CrossRef]
- Wise, N.H.; Hunt, G.R. Buoyancy-driven unbalanced exchange flow through a horizontal opening. J. Fluid Mech. 2020, 888, A22. [Google Scholar] [CrossRef]
- Wang, X.; Luo, J.; Li, X. CFD based study of heterogeneous microclimate in a typical chinese greenhouse in central China. J. Integr. Agric. 2013, 12, 914–923. [Google Scholar] [CrossRef]
- Zhao, Y.; Teitel, M.; Barak, M. SE—Structures and Environment: Vertical temperature and humidity gradients in a naturally ventilated greenhouse. J. Agric. Eng. Res. 2001, 78, 431–436. [Google Scholar] [CrossRef]
- Breuer, M.; Wessling, S.; Schmalzl, J.; Hansen, U. Effect of inertia in Rayleigh-Bénard convection. Phys. Rev. E 2004, 69, 026302. [Google Scholar] [CrossRef]
- Li, Y.; Sandberg, M.; Fuchs, L. Vertical temperature profiles in rooms ventilated by displacement: Full-scale measurement and nodal modelling. Indoor Air 1992, 2, 225–243. [Google Scholar] [CrossRef]
- Li, Y.; Delsante, A.E.; Symons, J.G.; Eng, B. Simulation tools for analysing natural ventilation of large enclosures with large openings. AIRAH J. 1997, 51, 21–28. [Google Scholar]
- Cooper, P.; Linden, P.F. Natural ventilation of an enclosure containing two buoyancy sources. J. Fluid Mech. 1996, 311, 153–176. [Google Scholar] [CrossRef]
- Linden, P.F.; Cooper, P. Multiple sources of buoyancy in a naturally ventilated enclosure. J. Fluid Mech. 1996, 311, 177–192. [Google Scholar] [CrossRef]
- Boulard, T.; Haxaire, R.; Lamrani, M.A.; Roy, J.C.; Jaffrin, A. Characterization and modelling of the air fluxes induced by natural ventilation in a greenhouse. J. Agric. Eng. Res. 1999, 74, 135–144. [Google Scholar] [CrossRef]
- Sherman, M.H. Superposition in infiltration modeling. Indoor Air 1992, 2, 101–114. [Google Scholar] [CrossRef]
- Walker, I.S.; Wilson, D.J. Evaluating models for superposition of wind and stack effect in air infiltration. Build. Environ. 1993, 28, 201–210. [Google Scholar] [CrossRef]
- Sherman, M.H.; Grimsrud, D.T. Infiltration-pressurization correlation: Simplified physical modeling. Am. Soc. Heat. Refrig. Air-Cond. Eng. 1980, 86, 778–807. [Google Scholar]
- Okada, M.; Takakura, T. Guide and Data for Greenhouse Air Conditioning 3. Heat loss due to air infiltration of heated greenhouse. J. Agric. Meteorol. 1973, 28, 223–230. [Google Scholar] [CrossRef]
- Li, Y.; Delsante, A. On natural ventilation of a building with two openings. In Proceedings of the Document-Air Infiltration Centre AIC Proc, Oslo, Norway, 28–30 September 1998; pp. 188–196. [Google Scholar]
- Li, Y.; Delsante, A. Natural ventilation induced by combined wind and thermal forces. Build. Environ. 2001, 36, 59–71. [Google Scholar] [CrossRef]
- Li, Y.; Delsante, A.; Chen, Z.; Sandberg, M.; Andersen, A.; Bjerre, M.; Heiselberg, P. Some examples of solution multiplicity in natural ventilation. Build. Environ. 2001, 36, 851–858. [Google Scholar] [CrossRef]
- Heiselberg, P.; Li, Y.; Andersen, A.; Bjerre, M.; Chen, Z. Experimental and CFD evidence of multiple solutions in a naturally ventilated building. Indoor Air 2004, 14, 43–54. [Google Scholar] [CrossRef]
- Andersen, A.; Bjerre, M.; Chen, Z.D.; Heiselberg, P.; Li, Y. Experimental Study of Wind-Opposed Buoyancy-Driven Natural Ventilation; Department of Building Technology and Structural Engineering, Aalborg University: Aalborg, Copenhagen, 2000. [Google Scholar]
- Hunt, G.R.; Linden, P.F. Displacement and mixing ventilation driven by opposing wind and buoyancy. J. Fluid Mech. 2005, 527, 27–55. [Google Scholar] [CrossRef]
- Whittle, R.M.; Lawrence, W.J.C. The climatology of glasshouses. II. Ventilation. J. Agric. Eng. Res. 1960, 5, 36–41. [Google Scholar]
- Nederhoff, E.M.; Van de Vooren, J.; Ten Cate, A.J.U. A practical tracer gas method to determine ventilation in greenhouses. J. Agric. Eng. Res. 1985, 31, 309–319. [Google Scholar] [CrossRef]
- Florentzou, F. Experiments in natural ventilation for passive cooling. In Proceedings of the 17th AIVC Conference, Gothenburg, Sweden, 17–20 September 1996; Volume1, pp. 121–134. [Google Scholar]
- Flourentzou, F.; Van der Maas, J.; Roulet, C.A. Natural ventilation for passive cooling: Measurement of discharge coefficients. Energy Build. 1998, 27, 283–292. [Google Scholar] [CrossRef]
- Liddament, M.W. Air Infiltration Calculation Techniques: An Applications Guide; Air Infiltration and Ventilation Centre: Berkshire, UK, 1986. [Google Scholar]
- Chalabi, Z.S.; Bailey, B.J. Simulation of the Energy Balance in a Greenhouse; Divisional Note; AFRC Institute of Engineering Research: Glasgow, UK, 1989. [Google Scholar]
- Wang, S. Measurement and Modelling of Natural Ventilation in a Large Venlo-Type Greenhouse. Ph.D. Thesis, Faculté Universitaire des Sciences Agronomiques de Gembloux, Gembloux, Belgium, 1998. [Google Scholar]
- Ducarme, D.; Vandaele, L.; Wouters, P. Single sided ventilation: A comparison of the measured air change rates with tracer gas and with the heat balance approach. In Proceedings of the 15. AIVC Conference on the Role of Ventilation, Buxton, UK, 27–30 September 1994; pp. 26–35. [Google Scholar]
- Demrati, H.; Boulard, T.; Bekkaoui, A.; Bouirden, L. SE—Structures and Environment: Natural ventilation and microclimatic performance of a large-scale banana greenhouse. J. Agric. Eng. Res. 2001, 80, 261–271. [Google Scholar] [CrossRef]
- Kittas, C.; Giaglaras, P.; Papadakis, G. Heat and mass transfer processes in the greenhouse ecosystem. In Proceedings of the AgEng Oslo 98, International Conference on Agricultural Engineering, Oslo, Norway, 24–27 August 1998; Norges Landbrukshoegskole: Oslo, Norway, 1998. [Google Scholar]
- Baille, M.; Laury, J.C.; Baille, A.; Sappe, G. Influence du matériau de couverture sur les échanges énergétiques d’une serre: Étude comparative verre normal-verre à faible émissivité. I. Influence sur les déperditions thermiques. Agronomie 1983, 3, 197–202. [Google Scholar] [CrossRef]
- Choab, N.; Allouhi, A.; El Maakoul, A.; Kousksou, T.; Saadeddine, S.; Jamil, A. Review on greenhouse microclimate and application: Design parameters, thermal modeling and simulation, climate controlling technologies. Sol. Energy 2019, 191, 109–137. [Google Scholar] [CrossRef]
- Piscia, D.; Montero, J.I.; Bailey, B.; Muñoz, P.; Oliva, A. A new optimisation methodology used to study the effect of cover properties on night-time greenhouse climate. Biosyst. Eng. 2013, 116, 130–143. [Google Scholar] [CrossRef]
- Zhang, T. Numerical Simulation and Experimental Research on Microclimate Environment in Greenhouse-Take Greenhouses of Shandong Shouguang as Examples. Master’s Thesis, Xi’an University of Architecture & Technology, Xi’an, China, 2006. [Google Scholar]
- Cheng, X.; Mao, H.; Wu, D.; Li, B. Numerical Simulation of Thermal Profiles in Spatial and Temporal Field for Natural Ventilated Glasshouse. Trans. Chin. Soc. Agric. Mach. 2009, 40, 179–183. [Google Scholar]
- Fatnassi, H.; Boulard, T.; Bouirden, L. Simulation of climatic conditions in full-scale greenhouse fitted with insect-proof screens. Agric. For. Meteorol. 2003, 118, 97–111. [Google Scholar] [CrossRef]
- Jones, P.J.; Whittle, G.E. Computational fluid dynamics for building air flow prediction—current status and capabilities. Build. Environ. 1992, 27, 321–338. [Google Scholar] [CrossRef]
- Roy, J.C.; Boulard, T. CFD predictions of natural ventilation and climate in a tunnel-type greenhouse using a transpiration active crop model. Acta Hortic. 2004, 205–212. [Google Scholar] [CrossRef]
- Lee, I.B.; Short, T.H. Two-dimensional numerical simulation of natural ventilation in a multi-span greenhouse. Trans. ASAE 2000, 43, 757. [Google Scholar]
- Piscia, D.; Muñoz, P.; Panadès, C.; Montero, J.I. A method of coupling CFD and energy balance simulations to study humidity control in unheated greenhouses. Comput. Electron. Agric. 2015, 115, 129–141. [Google Scholar] [CrossRef]
- Zhai, Z.; Chen, Q.; Haves, P.; Klems, J.H. On approaches to couple energy simulation and computational fluid dynamics programs. Build. Environ. 2002, 37, 857–864. [Google Scholar] [CrossRef]
- Zhai, Z.; Chen, Q.Y. Solution characters of iterative coupling between energy simulation and CFD programs. Energy Build. 2003, 35, 493–505. [Google Scholar] [CrossRef]
- Zhai, Z.J.; Chen, Q.Y. Performance of coupled building energy and CFD simulations. Energy Build. 2005, 37, 333–344. [Google Scholar] [CrossRef]
- Zhang, R.; Lam, K.P.; Yao, S.-C.; Zhang, Y. Coupled EnergyPlus and computational fluid dynamics simulation for natural ventilation. Build. Environ. 2013, 68, 100–113. [Google Scholar] [CrossRef]
- Baines, W.D.; Turner, J.S. Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 1969, 37, 51–80. [Google Scholar] [CrossRef]
- Worster, M.G.; Huppert, H.E. Time-dependent density profiles in a filling box. J. Fluid Mech. 1983, 132, 457–466. [Google Scholar] [CrossRef]
- Hunt, G.R.; Linden, P.F. Natural ventilation by the combined effects of buoyancy and wind. In Proceedings of the ROOMVENT 96 the 5th Annual Conference on Air Distribution in Rooms, Yokohama, Japan, 17–19 July 1996; pp. 239–246. [Google Scholar]
- Li, Y. Buoyancy-driven natural ventilation in a thermally stratified one-zone building. Build. Environ. 2000, 35, 207–214. [Google Scholar] [CrossRef]
- Andersen, K.T. Theoretical considerations on natural ventilation by thermal buoyancy. ASHRAE Trans. 1995, 101, 1–15. [Google Scholar]
- Meneses, J.F.; Raposo, J.R. Ventilação natural de instalações agrícolas: Teoria e métodos de cálculo (Natural ventilation of animal housings: Theory and methods of calculation). An. Inst. Super. Agron. 1987, 42, 249. [Google Scholar]
- Kurabuchi, T.; Ohba, M.; Endo, T.; Akamine, Y.; Nakayama, F. Local dynamic similarity model of cross-ventilation part 1-theoretical framework. Int. J. Vent. 2004, 2, 371–382. [Google Scholar] [CrossRef]
- Kurabuchi, T.; Ohba, M.; Goto, T.; Akamine, Y.; Endo, T.; Kamata, M. Local dynamic similarity concept as applied to evaluation of discharge coefficients of cross-ventilated buildings—part 1 basic idea and underlying wind tunnel tests; part 2 applicability of local dynamic similarity concept; part 3 simplified method for estimating dynamic pressure tangential to openings of cross-ventilated buildings. Int. J. Vent. 2005, 4, 285–300. [Google Scholar]
- Ohba, M.; Kurabuchi, T.; Tomoyuki, E.; Akamine, Y.; Kamata, M.; Kurahashi, A. Local dynamic similarity model of cross-ventilation Part 2-Application of local dynamic similarity model. Int. J. Vent. 2004, 2, 383–394. [Google Scholar] [CrossRef]
- Boulard, T.; Feuilloley, P.; Kittas, C. Natural ventilation performance of six greenhouse and tunnel types. J. Agric. Eng. Res. 1997, 67, 249–266. [Google Scholar] [CrossRef]
- Critten, D.L.; Bailey, B.J. A review of greenhouse engineering developments during the 1990s. Agric. For. Meteorol. 2002, 112, 1–22. [Google Scholar] [CrossRef]
- Levine, B.D.; Stray Gundersen, J.; Mehta, R.D. Effect of altitude on football performance. Scand. J. Med. Sci. Sports 2008, 18, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol. Climatol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Liu, W.; Wang, J.; Li, Y.; Zhu, Z.; Qie, D.; Ding, L. Natural convection heat transfer at reduced pressures. Exp. Heat Transf. 2019, 32, 14–24. [Google Scholar] [CrossRef]
- Marty, C. Surface Radiation, Cloud Forcing and Greenhouse Effect in the Alps; ETH Zurich: Zurich, Switzerland, 2000. [Google Scholar]
- Saidi, M.; Abardeh, R.H. Air pressure dependence of natural-convection heat transfer. In Proceedings of the World Congress on Engineering, London, UK, 30 June–2 July 2010; pp. 1–5. [Google Scholar]
- Pandey, D. Solar Greenhouse as an Energy Alternative Solution for Growing Vegetable in High Altitude Region: A Case of Baragaon, Mustang. J. Inst. Eng. 2019, 15, 234–244. [Google Scholar] [CrossRef]
- Candy, S.; Moore, G.; Freere, P. Design and modeling of a greenhouse for a remote region in Nepal. Procedia Eng. 2012, 49, 152–160. [Google Scholar] [CrossRef]
- Fuller, R.J.; Aye, L.; Zahnd, A.; Thakuri, S. Thermal evaluation of a greenhouse in a remote high altitude area of Nepal. Int. Energy J. 2009, 10, 71–80. [Google Scholar]
- Zeng, S.; Hu, H.; Xu, L.; Li, G. Nonlinear adaptive PID control for greenhouse environment based on RBF network. Sensors 2012, 12, 5328–5348. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, H.; Zhang, S.; Wang, Y.; Chow, D. Modeling and optimization of environment in agricultural greenhouses for improving cleaner and sustainable crop production. J. Clean. Prod. 2021, 285, 124843. [Google Scholar] [CrossRef]
- Iddio, E.; Wang, L.; Thomas, Y.; McMorrow, G.; Denzer, A. Energy efficient operation and modeling for greenhouses: A literature review. Renew. Sustain. Energy Rev. 2020, 117, 109480. [Google Scholar] [CrossRef]
- Katzin, D.; van Henten, E.J.; van Mourik, S. Process-based greenhouse climate models: Genealogy, current status, and future directions. Agric. Syst. 2022, 198, 103388. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.; Zhao, H.; Wang, Y.; Chow, D.; Fang, Y. Methodologies of control strategies for improving energy efficiency in agricultural greenhouses. J. Clean. Prod. 2020, 274, 122695. [Google Scholar] [CrossRef]
- Fatnassi, H.; Boulard, T.; Bouirden, L. Development, validation and use of a dynamic model for simulate the climate conditions in a large scale greenhouse equipped with insect-proof nets. Comput. Electron. Agric. 2013, 98, 54–61. [Google Scholar] [CrossRef]
- Wang, S.; Boulard, T. Predicting the microclimate in a naturally ventilated plastic house in a Mediterranean climate. J. Agric. Eng. Res. 2000, 75, 27–38. [Google Scholar] [CrossRef]
- De Halleux, D.; Deltour, J.; Nijskens, J.; Nisen, A.; Coutisse, S. Dynamic simulation of heat fluxes and temperatures in horticultural and low emissivity glass-covered greenhouses. Greenh. Constr. Cover. Mater. 1984, 170, 91–96. [Google Scholar] [CrossRef]
- Deltour, J.; De Halleux, D.; Nijskens, J.; Coutisse, S.; Nisen, A. Dynamic modelling of heat and mass transfer in greenhouses. In Proceedings of the Symposium Greenhouse Climate and its Control, Wageningen, The Netherlands, 19–24 May 1985; International Society for Horticultural Science (ISHS): Leuven, Belgium, 1985; pp. 119–126. [Google Scholar]
- Nijskens, J.; Deltour, J.; Halleux, D.D. Sensitivity Study of a Greenhouse Climate Dynamic Model; Bulletin des Recherches Agronomiques de Gembloux: Gembloux, Belguim, 1991. [Google Scholar]
- Pieters, J.G.; Deltour, J.M. Performances of greenhouses with the presence of condensation on cladding materials. J. Agric. Eng. Res. 1997, 68, 125–137. [Google Scholar] [CrossRef]
- Pieters, J.G.; Deltour, J.M.; Debruyckere, M.J. Condensation and dynamic heat transfer in greenhouses, Part I: Theoretical model. Int. Agric. Eng. J. 1996, 5, 119–133. [Google Scholar]
- Pieters, J.G.; Deltour, J.M.; Debruyckere, M.J. Condensation and dynamic heat transfer in greenhouses, Part II: Results for a standard glasshouse. Int. Agric. Eng. J. 1996, 5, 135–148. [Google Scholar]
- Zhu, S.; Deltour, J.; Wang, S. Modeling the thermal characteristics of greenhouse pond systems. Aquac. Eng. 1998, 18, 201–217. [Google Scholar] [CrossRef]
- Singh, M.C.; Singh, J.P.; Singh, K.G. Development of a microclimate model for prediction of temperatures inside a naturally ventilated greenhouse under cucumber crop in soilless media. Comput. Electron. Agric. 2018, 154, 227–238. [Google Scholar] [CrossRef]
- Mashonjowa, E.; Ronsse, F.; Milford, J.R.; Pieters, J.G. Modelling the thermal performance of a naturally ventilated greenhouse in Zimbabwe using a dynamic greenhouse climate model. Sol. Energy 2013, 91, 381–393. [Google Scholar] [CrossRef]
- Bartzanas, T.; Boulard, T.; Kittas, C. Effect of vent arrangement on windward ventilation of a tunnel greenhouse. Biosyst. Eng. 2004, 88, 479–490. [Google Scholar] [CrossRef]
- Park, J.; Rhee, G.H. Comparison of volume flow rate and volume-averaged local mean age of air for evaluating ventilation performance in natural ventilation. J. Mech. Sci. Technol. 2017, 31, 5801–5812. [Google Scholar] [CrossRef]
- Li, X.; Li, D.; Yang, X.; Yang, J. Total air age: An extension of the air age concept. Build. Environ. 2003, 38, 1263–1269. [Google Scholar] [CrossRef]
- Park, S.; Lee, I.-B.; Hong, S. New development of a straightforward method of estimating age-of-air using CFD. Acta Hortic. 2014, 1037, 963–969. [Google Scholar] [CrossRef]
- Zhou, J.; Hua, Y.; Xiao, Y.; Ye, C.; Yang, W. Analysis of Ventilation Efficiency and Effective Ventilation Flow Rate for Wind-driven Single-sided Ventilation Buildings. Aerosol Air Qual. Res. 2021, 21, 200383. [Google Scholar] [CrossRef]
- Sandberg, M. What is ventilation efficiency? Build. Environ. 1981, 16, 123–135. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).