Abstract
Greenhouses are employed worldwide to protect crops from meteorological conditions as well as to control some plant production variables. As multi-tunnel structures are amongst the most used, in this article, we focus on cost optimization of both the steel structure and the concrete foundation of this greenhouse typology. Firstly, three structural alternatives composed of three tunnels and differentiated portal frames were dimensioned conforming to the European design of steel structures, namely, Eurocode 3; meanwhile, the foundation was calculated through a previously validated matrix method. Then, genetic algorithms were employed to optimize for cost each proposed design and to evaluate the relative weight of each element in the overall steel consumption. Moreover, the influence of the greenhouse design on the final cost was also assessed, and it was found that the most cost-effective solution corresponded to the optimized greenhouse alternative exhibiting a 3.5 m separation between portal frames and the combination of a steel profile and plastic gutter (i.e., M3OPT at 15.14 €/m2). Finally, from the study on the influence of the portal frame separation, a further cost per square meter reduction was found for a design with the so-called structural gutter (i.e., steel profile and plastic water collection system) as support for the arches and a 4.5 m separation at 14.21 €/m2.
1. Introduction
For more than a century, greenhouse structures have been employed to protect crops from meteorological conditions. Worldwide, China represents the largest greenhouse production area [1], whereas, at the European level, Spain is the leading country with 73.12 × 103 ha [2].
Contrary to the climatic requirements imposed in the northern regions of Europe, greenhouses located in the Mediterranean Basin have to be adapted to mild winter conditions, but intensive hot summers. Hence, film cladding systems and arch structures are preferred, among which multi-tunnel greenhouses are the most common typology.
From a structural point of view, greenhouses can be rather traditional, such as the Parral-type greenhouse, which is typical from Almeria (Spain), or a greenhouse that has an engineered structural design. The latter is denoted as a commercial greenhouse by the standard EN 13031 [3], which establishes the requirements for the design and construction of commercial production greenhouses. The aforementioned EN standard sets the basis for the estimation of actions on the structure as well as the necessary structural calculation conditions. In addition, the European design of steel structures, namely Eurocode 3 [4], also includes the structural verifications to be considered for vaulted, tunnel, and multi-tunnel greenhouses.
The scientific works focused on the study of greenhouse structures approach the subject from different perspectives. The topic was pioneered by Roux and Motro [5] and Roux et al. [6,7]. In this regard, it is worth noting that the research carried out by the aforementioned researchers set the basis for the buckling study of greenhouse arches, as it was included as a regulatory annex for the stability check of greenhouse arches in EN 13031-1 [3].
Nonetheless, more recent approaches to the study of greenhouse structures can be found in the literature. For instance, Briassoulis et al. [8] analyzed numerically the collapse of a multi-tunnel greenhouse through 2D and 3D model simulations. The failure was attributed to a sum of factors (unfavorable combination of snow and wind actions, improper heating conditions, and the absence of some structural elements). The authors reported that, for a buckling eigenvalue of 2.68 (i.e., lower than the one established for a first-order calculation λcr < 3.60), the failure occurred for a nonlinear elastic critical load factor (αcr) of 1.12.
Similarly, a finite element analysis of a large-span plastic greenhouse was carried out by Ren et al. [1] to evaluate the causes leading to its collapse. Once again, the nonlinear elastic critical load factor was slightly greater than the unit for a λcr < 3.60. Although studies focused on greenhouses of large dimensions are limited, the research carried out by both Ren et al. [1] and Xu et al. [9] evaluated multi-tunnel greenhouses with spans greater than 20 m.
Maraveas and Tsavdaridis [10], who employed the SOFiSTiK software to simulate a vaulted and a Venlo greenhouse, stated that pre-engineered structures (i.e., based on empirical calculations) were often insufficiently designed according to the Eurocode requirements [4] and, thus, called for structural upgrades.
The approach followed in the research carried out by Moghaddam et al. [11] was based on the development of a method for designing greenhouse structures based on topology optimization to improve structure strength. However, it was noticed that the penalty numbers had a significant effect on the optimization results.
Recently, there has been a proliferation of scientific works [12,13,14,15,16] that have evaluated wind action, and even its specific influence, in both multi-tunnel and Venlo-type greenhouse structures.
For example, the authors of [17] reported on the influence of wind action in a multi-tunnel greenhouse by comparing the load stipulated by EN 13031 [3] with the load obtained through a computational fluid dynamics (CFD) simulation. Moreover, the foundation was studied by using a finite element method (FEM) as well as a matrix method based on the Wrinkler model. On this subject, the work carried out by Peña et al. [18] was the only other paper that addressed the study of greenhouse footings by evaluating their tensile resistance.
Although the norm for a greenhouse stability investigation is a static structural analysis, Hur and Kwon [19] carried out a fatigue assessment on a typical Korean Venlo greenhouse to consider the effect of the dynamic wind loads. Capacity ratios of the cross-sections and bars were determined under a combination of self-weight and wind loads. For boundary conditions similar to those set in [20] and rigid nodes, Li et al. [21] assessed a 10 m span steel frame solar greenhouse under wind loads. The authors compared both the dynamic and static structural responses of the structure and proposed a 2.02 wind-induced vibration coefficient to convert between the dynamic and static load, and thus to improve the efficiency of calculation and design.
Finally, even though outside of the scope of this manuscript, it is also worth mentioning the study carried out by Lee et al. [22], who conducted a structural analysis model and a structural safety review on a greenhouse installed without a foundation.
Albeit there is some knowledge on the structure of greenhouses, further research is still needed. Especially, in those aspects concerning the greenhouse foundation and the overall optimization of the greenhouse structure, for instance, in regards to the cost.
Therefore, in this paper, we aim to study possible alternatives for the structural optimization of multi-tunnel greenhouse structures and foundations by means of genetic algorithms, which have been successfully employed in other construction fields [23,24,25,26,27,28]. Hence, software programed in Matlab R2022a (Natick, MA, USA) was employed for both the calculations and optimization of several structural alternatives. Finally, a comparison in terms of cost per square meter was employed to compare the alternatives and determine the more economical approach to the construction of multi-tunnel greenhouses.
2. Materials and Methods
2.1. Multi-Tunnel Greenhouse
The greenhouse used as the basis for this research work was a type B10 [3] multi-span metal frame covered with a single sheet of low-density polyethylene. As the greenhouse has been previously studied by the authors, more comprehensive information regarding the geometry, dimensions, boundary conditions, actions on the structure, and load combinations can be found elsewhere [17].
For this investigation, three structural alternatives (M1, M2, and M3) were initially proposed and optimized later on, in order to evaluate the influence of the greenhouse design on the overall cost of the structure.
All the structures were composed of three tunnels and two differentiated portal frame types (Figure 1). The separation between the primary portal frame (i.e., the symmetry plane with intermediate columns) and secondary portal frame (i.e., the symmetry plane without intermediate columns), which is defined as S, also conditioned the three original design alternatives.
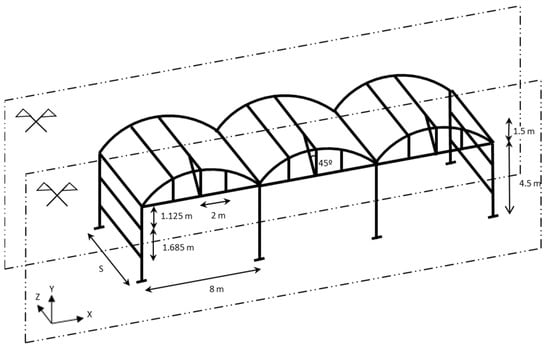
Figure 1.
Symmetry planes and dimensions of the studied greenhouse (M1 and M3 structural design alternatives) [17].
Three structural alternatives, as well as the resulting optimizations, were contemplated to evaluate the influence of the greenhouse design on the overall cost of the structure:
- Model 1 (M1) Figure 1 illustrates the multi-tunnel greenhouse studied in this model. A 2.50 m separation (S) between the primary and secondary portal frames was considered, and both the design and the steel profiles represent those commonly employed in the construction practice. The so-called steel gutter was also based on a commercial element typically employed for greenhouses and exhibited the same geometry as the one employed in this paper (i.e., 400 mm development length); thus, ensuring the compliance with all the necessary structural checks.
- Model 2 (M2) Although based on the previous model, the secondary portal frames were removed in M2 (Figure 2). Therefore, the primary portal frame was connected to the rest of the structure by the purlins and gutter in the same manner as M1, as defined by the boundary conditions. In this structural alternative, the separation between portal frames was 5 m and the gutter was subjected to the structural verifications described in Section 3. Similar to M1, the existence of two planes of symmetry, which were maintained at a 2.50 m distance, simplified the matrix calculation.
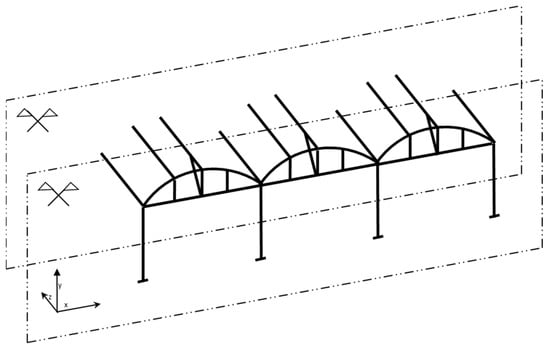 Figure 2. M2 structural design.
Figure 2. M2 structural design.
- Model 3 (M3) The geometry and connections both employed in this model were based on those set forth in M1, as shown in Figure 1. Nonetheless, some changes were proposed. On the one hand, the separation S between the primary and secondary portal frames was 3.50 m. On the other hand, the original steel gutter was replaced by a tubular steel profile (i.e., the so-called structural gutter) that served as a support for the arches and a plastic water collection element.
The approaches both intended to lower the overall cost per square meter by reducing the number of frames and concrete footings and the needed labor in M2, or by increasing the constructed area with a higher separation between frames in M3.
Regarding the materials employed, all structural elements were made of structural galvanized steel grade S275. Cold-formed welded profiles with a circular, rectangular, and square hollow cross-section were employed according to EN 10305-3 [29] and EN 10305-5 [30]. The dimensions and technical properties were obtained both from structural engineering compendiums and manufacturers’ catalogs in the greenhouse field. Nonetheless, only those profiles classified as Class 1, Class 2, or Class 3 according to Eurocode 3 [4] were considered. Therefore, the following steel profiles were employed in the present research work:
- Steel profiles with a circular cross-section, ranging from 21.40 mm diameter and 1.50 mm thickness to 200 mm diameter and 8 mm thickness.
- Steel profiles with a quadrangular cross-section, ranging from 40 mm height/width and 2 mm thickness to 140 mm height/width and 8 mm thickness.
- Steel profiles with a rectangular cross-section, ranging from 60 mm height, 40 mm width and 2 mm thickness to 140 mm height and 80 mm width and 4 mm thickness.
For the foundation, all structural design alternatives featured concrete cylindrical footings. Indeed, this solution is the typical construction practice for a greenhouse with footings of 0.50 m in diameter and a depth that ranges from 1 to 2 times the diameter. In this research, the developed model (see Section 3.4) adjusted both diameter and depth, taking into consideration the reactions of each design alternative.
2.2. Structural Calculation
A 3D matrix analysis programed in Matlab R2022a (Natick, MA, USA) was employed to calculate the greenhouse structure both in first- and second-order calculations. Since the use of Method 1 in Annex A of Eurocode 3 [4] has been reported as more precise than Method 2 in Annex B of the aforementioned standard [31], the former was employed in this investigation. For the first-order calculation, the resulting displacements, as well as the bending moments, were stored for each load combination (LC). In this regard, the same convention for member axes as Eurocode 3 [4] has been followed in this paper (i.e., x-x is the axe along the member, y-y is the axis perpendicular to the structural or symmetry plane, z-z is the section axis in the plane of the frame or symmetry plane). Nonetheless, caution should be taken as the global axes X, Y, and Z are the ones displayed in Figure 1 and Figure 2.
According to Eurocode 3 [4] and EN 13031-1 [3], both global and local imperfections were considered. On the one hand, the effect of the local imperfections was contemplated in the bar verifications by means of the buckling coefficient. On the other hand, global imperfections were applied to the initial geometry for the second-order calculation as established in Annex D of EN 13031-1 [3].
Cross-section and bar verifications were both calculated and the results (i.e., utilization ratios (UR)) were stored for each verification.
2.2.1. Cross-Section Verifications
The analysis of the cross-section of the different structural elements was carried out by assessing the stresses on each node of the structure for the following verifications:
- Resistance of the cross-section subjected to tension (Section 6.2.3. in Eurocode 3 [4]);
- Resistance of the cross-section subjected to compression (Section 6.2.4. in Eurocode 3 [4]);
- Resistance of the cross-section subjected to bending and shear (Section 6.2.8. in Eurocode 3 [4]);
- Resistance of the cross-section subjected to bending and axial force (Section 6.2.9. in Eurocode 3 [4]);
- Resistance of the cross-section subjected to bending, shear and axial force (Section 6.2.10. in Eurocode 3 [4]).
2.2.2. Bar Verifications
Bar checks were conducted according to Section 6.3.3. and Method 1 in Annex A of Eurocode 3 [4]. Nevertheless, the verifications were only applied to members subjected to bending and compression axial force. Since only Class 1, Class 2, or Class 3 cross-section were considered and no bending occurred outside the plane of the structure (i.e., Mz,Ed = 0), the members had to satisfy Equations (1) and (2):
Note that:
- NEd is the design value of the axial force;
- My,Ed is the design bending moment in the y-y axis;
- and are the interaction factors established by Method 1 in Annex A of Eurocode 3 [4];
- and are the reduction factors due to flexural buckling;
- is the partial factor for resistance of member to instability assessed by member checks;
- is the reduction factor due to lateral torsional buckling ( = 1 since no lateral buckling occurred as all elements were closed sections);
- NRk is the characteristic resistance to normal force of the critical cross-section (NRk = fy … A);
- My,Rk is the characteristic moment resistance of the critical cross-section (My,Rk = fy … Wy).
where:
fy is the yield strength (275 N/mm2); A is the cross-section area;
Wy is either the elastic (Wel,y) or plastic (Wpl,y) section modulus as indicated in Section 6.3.3 of Eurocode 3 [4] (Table 1).

Table 1.
Codification of the different cross-section classes.
Table 2 shows the buckling lengths, both in the plane of the structure and the plane perpendicular to the structure, employed for the verification of the different bars on the multi-tunnel greenhouse. Figure 3 illustrates the reference numbers used to identify each structural element. It should be noted that the brace connecting the purlins to the horizontal beam, which was dimensioned for the same cross-section as the vertical tie, exhibited a buckling length of 2.14 m (i.e., the actual length of the element).

Table 2.
Buckling lengths for the different bars in the multi-tunnel greenhouse.
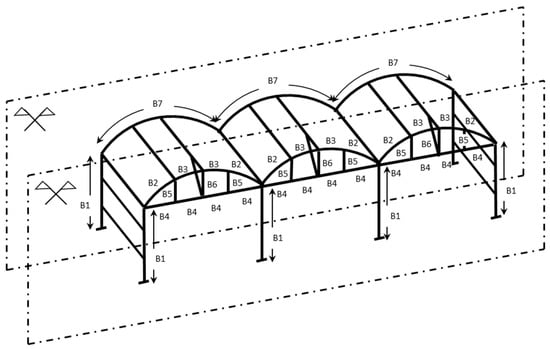
Figure 3.
Codification of the different bars in the greenhouse structure.
2.2.3. Purlins
As the loads were directly transmitted to the arch, the purlins used in the matrix model only accounted for their self-weight. Moreover, in the calculation, the purlins were considered to be a continuous beam with 3 or more spans. In any case, the cross-section of the purlin had to satisfy Equation (3):
where Wy is the section modulus as indicated in Table 1, fy is the yield strength (275 N/mm2), p is the load applied to the purlin according the load combinations [17], l is the length of the purlin.
It should be noted that, as the first portal frame endures the horizontal wind loads, the purlin was not subjected to axial force since the member connected two planes of symmetry. Thus, the numerator in Equation (3) (i.e., ) is the maximum bending moment of a continuous beam with 3 or more spans.
Finally, it is also worth mentioning that the lateral purlins employed the same cross-section as the ones connecting the arches.
2.2.4. Foundation
In this research, the method employed to calculate the foundation was built on the matrix method proposed in a previous work [17] but also included the ultimate limit state (ULS) verifications. The matrix model of 3D articulated bars based on the Winkler model programed with Matlab is considered to be a more suitable procedure to assess the typical stress distribution displayed by greenhouse footing. Whereas analytical methods hardly detect the bending moment between the walls and the base of the footing, the proposed method allows part of the stresses received from the column to be distributed to the ground, both from the lateral walls and the base.
The foundation was calculated from the reaction values registered on the base of the columns for each load combination. All footings comprising the greenhouse foundation were designed with the same diameter and depth (i.e., the dimensions resulting from the most unfavorable footing were employed for all foundation elements). Note that the ultimate aim of this paper was to assess the depth of the footing, for a fixed diameter value, on the overall cost of the foundation.
The algorithm was programed to accept the dimensioning of the footing when the stresses transmitted to the soil were lower than the bearing capacity (padm), both in the vertical and horizontal directions. In addition, the requirement to limit the rotation of the footing to 1/500 set in Eurocode 7 [32] was also fulfilled.
A bearing capacity of 200 kN m−2 and an internal friction angle ρ of 23° were selected to describe the properties of the soil, which was considered to be sandy. The subgrade reaction modulus (K) used to described the elastic behavior of the soil was calculated based on the equations proposed by Jiménez-Salas et al. [33] for cylindrical footings. In Equations (4) and (5), Kv and Kh are the vertical and horizontal subgrade reaction modulus, respectively, required to assign the spring coefficients in the Wrinkler model:
where D is the diameter of the footing and Eo is the deformation modulus, and according to Jiménez-Salas et al. [33], Eo is equal to 1.53 times the depth of the footing for a medium sandy soil type.
Note that the obtained outputs were in line with those established in the current Spanish legislation, namely the Spanish Technical Building Code and, specifically, the Basic Document for Structural Safety/Foundations (CTE-DB-C) [34].
Lastly, the footing geometry should carry a sufficient self-weight in order to resist a possible uplift taking into account a 1.50 safety coefficient (i.e., the maximum tensile reaction (Ftmax) must reach a value greater than 1.50 times the uplift action). According to Peña et al. [18], Ftmax can be determined by Equation (6) through the weight of the footing and the lateral friction, which depends on the pressure exerted by the concrete in a fluid state and the internal friction angle of the soil (ρ).
where Wc is the footing weight, H is the depth of the footing, Af is the friction footing area (Af = π … D … H), γh is the concrete unit weight (24 kN m−3), ρ is the internal friction angle of the soil.
2.3. Optimization Procedure with Genetic Algorithms
The structural optimization work seeks to minimize the cost of the construction by means of genetic algorithms (GAs), which is an adaptive heuristic search approach based upon Charles Darwin’s theory of survival of the fittest. In this regard, a reduction in the weights of both the structure and the foundation of the multi-tunnel greenhouses were sought. Since structural optimization with GA has been described by the authors and other researchers in previous works [28,35,36,37,38], this section only addresses the adaptation to the present research.
Two interrelated GAs were performed. First, the structure was optimized based on a GA that employed the cross-section of the different structural elements as variables. Subsequently, the optimization of the foundation was carried out by using the reaction values to determine the height and diameter of the footing (i.e., the optimization variables).
2.3.1. Individuals
Each individual represented one of the solutions to the problem posed. Thus, in this work, individuals for the structure and the foundation were studied. The union of genes (i.e., consisting of bit strings that encode a variable) formed the chromosome that represents the individual. Chromosomes determined the genotype of the individual, whereas, the phenotype expressed the cross-sections of the structural elements and the footing dimensions by decoding the genome for each case.
For the structure, the genes encoded the cross-section used in each type of structural element: arch, vertical tie, horizontal beam, purlin, and column. Nonetheless, note that genes for the M3 alternative also included the structural gutter cross-section.
For the foundation, discrete values of depth and diameter were considered and each dimension was encoded in the foundation genes. The range examined for both parameters oscillated between 50 cm and 200 cm in 5 cm increments.
2.3.2. Population
The population is the set of individuals evaluated during a generation. Small populations may not completely cover the search space, but large populations would cause excessive computational costs [39]. In the literature, the number of individuals is highly variable. Nonetheless, the common range oscillates from 20 to 250 individuals [28,35,36,40,41]. In this research work, after a sensitivity study, 60 individuals were selected for the optimization of the greenhouse structure and 15 individuals for the foundation.
2.3.3. Objective Function
The measure of the effectiveness of each individual was determined by the objective function. In this research, the fitness was based on the minimum weight of the structure and the foundation. Since some individuals were not valid as they did not meet the constraints of the structural calculation rules, a modified objective function was necessary to penalize the lack of compliance [39].
In order to meet the restrictions and originate valid individuals, the value of the utilization ratios (UR) was limited to the unit. In addition, a coefficient much lower than 1 would indicate that the element was oversized. The penalty assigned a greater weight to those elements (i.e., did not meet the constraints or were oversized). Nevertheless, the penalty was kept as low as possible, i.e., above the limit from which the infeasible solutions are optimal. Equation (7) shows the modified objective functions employed for the structure and the foundation. The modified functions were similar to those used in other structural optimization works [28,38,40]; and, thus, their validity has previously been demonstrated:
where x is the individual of the study population; F(x) is the modified objective function, j is the number of variables studied; f(x) is the objective function regarding the structure or foundation weight, assumed in kilograms; Pj is the penalization according to the restrictions imposed on each of the elements; the penalty parameter of imposed restrictions is (Gj(x)) with the same order of magnitude as the objective function, Gj(x) is defined according to the maximum utilization ratio noticed in each structural element.
For the steel structure:
- 0 > Gj(x) > 1, then Pj(Gj(x)) = 10(2−Gj(x));
- Gj(x) = 1, then Pj(Gj(x)) = 0;
- Gj(x) = 0, then Pj(Gj(x)) = 2000;
- Gj(x) > 1, then Pj(Gj(x)) = Gj(x) × 1000.
For the concrete footing:
- 0 > Gj(x) > 1, then Pj(Gj(x)) = 103+(1−Gj(x));
- Gj(x) = 1, then Pj(Gj(x)) = 0;
- Gj(x) = 0, then Pj(Gj(x)) = 200,000;
- Gj(x) > 1, then Pj(Gj(x)) = Gj(x) × 10,000,000.
2.3.4. The AG Operators
The Selection Operator
In this paper, the roulette-wheel selection operator was employed, in which the individuals that are going to be part of the reproduction are selected, and the fittest individuals are given more opportunities to reproduce. Therefore, each individual was associated with a probability of reproduction that was inversely proportional to its value in the modified objective function. This method have been proved effective by the authors’ previous work [28,38] as well as other researchers [36,40].
The Crossover Operator
A different approach was followed for the GA applied to the structure and the foundation.
In the structure, a “double crossover by phenotype” [28,35,38] was employed. First, two random points were randomly selected on the parents’ phenotypes. Then, the offspring was created by alternating sections between those points originating from each ascendant. Those parts not previously chosen formed the second descendant.
In the foundation, a “crossing by a point per phenotype” was employed since only two phenotypes (i.e., diameter and depth) were considered. Hence, from a selected position on the parents’ chromosomes, the sections were exchanged to get the children.
The number of individuals crossed is given by the probability of crossover (Figure 4). Depending on the problem to be optimized, different operators were used to fine tune the power of the method. Thus, a sensitivity analysis, in which the population size was a fixed value, was carried out to select the crossover operator. Then, a percentage of crossover of 80% was employed, which was in line with those found in the literature [28,35,36,38,40,42].
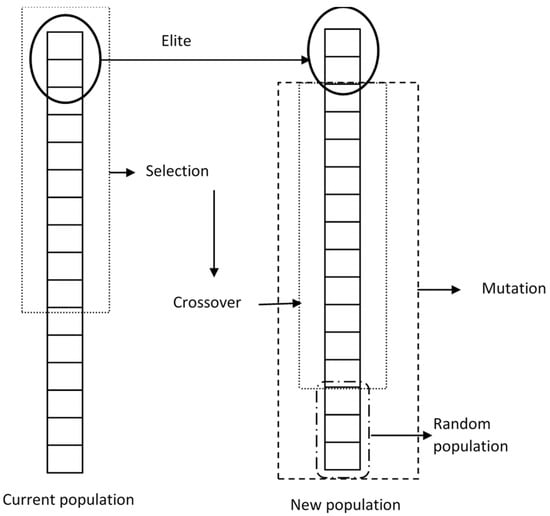
Figure 4.
New population generated with the elitist GA.
The Elitism Operator
To ensure that the best individuals in each population are not lost between generations, an elitist strategy was followed. The individuals with the lowest value for the modified objective function were directly incorporated into the next generation (Figure 4), which turned the GA elitist. As per the sensitivity analysis, the percentage of elitism was 5% of total individuals, similar to that used by other authors [28,35,36,37,38].
The Mutation Operator
The mutation operator allows the evolution when the population is stagnant around a local minimum. Thus, it provides variability by continuing to prospect for the global minimum as bits of a few members of the population are altered (Figure 4). In any case, both the individuals and the position of the genome to be mutated are chosen randomly. Based on the sensitivity analysis carried out, a mutation probability percentage of 0.10% was considered, which has previously showed its fitness in other structural optimizations [28,42,43].
2.3.5. New Population, Reassessment, and Stopping Condition
Figure 4 illustrates the composition of the new population in the next generation. The new population was comprised of some of the individuals from the initial population as well as new individuals due to the implementation of the elitist GA.
The re-evaluation of the new population was carried out by determining the value of the modified objective function for each individual. The optimization ended after a number of iterations, i.e., 300 generations. In addition, the process also ended when no improvement was obtained for the optimum individual after a fixed number of successive generations, which was established at 50. The values were both selected based on the convergence tests on the algorithm as well as the previous works’ carried out by the authors.
The procedure followed is schematically illustrated in Figure 5.
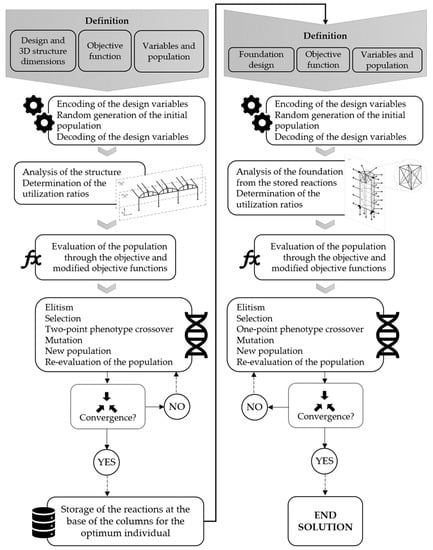
Figure 5.
Elitist GA flow.
3. Results and Discussion
For all structural alternatives (both the original and the optimization models), the first-order buckling eigenvalue (λcr) was analyzed and resulted in a value greater than 3.60. Thus, conforming to EN 13031-1 [3], a first-order calculation could suffice, but also serves as a validation of the second-order calculation developed in this research work.
3.1. Structural Analysis
The structural results obtained from the M1, M2, and M3 models are presented in this section. For the M1 model, the commercially available profiles commonly used (as per the analysis of different companies) were employed. After the dimensioning of M1, each bar element of the M2 and M3 models was determined using the M1 profile as a starting point of the calculation.
Steel profiles with a circular cross-section are identified by the Ø symbol followed by the values of diameter and thickness expressed in mm. Quadrangular or rectangular steel profiles are identified by the # symbol followed by the width, height, and thickness expressed in mm.
3.1.1. Steel Analysis of Original Structures
Table 3 illustrates the selected steel profiles for the different elements in the M1 greenhouse structure, the maximum utilization ratio (UR) as well as the load combination (LC) responsible. As it could be observed, LC1, LC11, and LC13 are the most relevant in the structural calculation.

Table 3.
Utilization ratio for the most unfavorable load combination of each member in M1, both for the cross-section and bar verification.
A maximum UR of 0.63 was reached in the arch for the cross-section verification (i.e., the cross-section resistance of elements exposed to an axial force and bending moment) and bar verification (i.e., due to buckling of members subjected to axial force and bending moment in the plane of the structure as indicated in Eurocode 3 [4]).
The vertical tie exhibited a relatively low UR as compared with the other structural elements. A maximum value of 0.04 occurred in the cross-section verification for LC1.
LC1 was also responsible for the maximum UR of the column. The buckling due to axial force and bending moment in the y-y axis (i.e., in the plane of the structure) resulted in a maximum UR of 0.79. It is worth mentioning that, for LC1, the vertical load transmitted by the primary portal frames to the ground was 88.71%. This finding evidences that the secondary portal frames are strongly supported by the steel gutter, which is responsible for the vertical load transmittal to the primary portal frames.
In the bar verification, the horizontal beam exhibited a UR of 0.98 in the z-z axis for LC13. It was the second largest UR of the structure due to the greatest buckling length in the z-z axis (i.e., a distance of 4 m between the column-horizontal beam connection and the stay as compared with the 2 m buckling length that existed in the plane of the structure between the vertical ties). In addition, the horizontal beam at the windward arch was subjected to greater compression axial forces than the remaining horizontal beams, which justified the higher UR value.
Except for the horizontal beam, there are no significant differences between the UR arising from the cross-section or bar verifications, which either indicates that the structural elements worked in tension or did not suffer failures due to compression and buckling; thus, presenting a margin of utilization. The influence of the horizontal beam on the failure of the structure was consistent with the findings established in [17], in which the buckling instability of this type of greenhouse was analyzed. The higher UR values are due to the suction effect of the wind, which causes compression in the horizontal beam, combined with the important slenderness of this bar.
Among all the structural elements, the purlin exhibited the most unfavorable situation. A maximum UR of 0.99 was observed in the cross-section plastification check for LC11.
In addition to LC1, LC11, and LC13, the M2 model also highlighted the relative importance of LC19 as it was responsible for the maximum UR of the arch in the bar verification. Nonetheless, as in the previous model, the greater UR values resulted when the column, purlin, and horizontal beam were considered for LC1, LC11, and LC13, respectively (Table 4).

Table 4.
Utilization ratio for the most unfavorable load combination of each member in M2, both for the cross-section and bar verification.
The arch exhibited a UR of 0.44 in the bar buckling verification for LC19. However, LC1 was responsible for a higher UR (0.64) in the cross-section check of the element, which was subjected to tensile and shear loads and a bending moment.
The maximum UR displayed by the vertical tie also occurred in the cross-section verification for LC1. Nevertheless, the value was almost zero (0.04) due to the tensile performance of the element.
In addition, for LC1, the bar verification considering the compression force and bending moment in the y-y axis resulted in the most unfavorable UR (0.69) for the column.
Regarding the horizontal beam, the UR obtained in the bar verification for LC13 was greater (0.97) than in the cross-section check. As explained in the previous model, this result was due to the larger buckling length considered in the perpendicular plane to the structure or z-z-axis.
Similar to the previous model, the purlin displayed the maximum UR for LC11 in the cross-section plastification check. However, in this case, the purlin did not exhibit the greatest UR of the structure.
As it already occurred in M2, the most significant load combinations in the M3 design were LC1, LC11, LC13, and LC19 (Table 5). Among them, LC13 was the most unfavorable and resulted in the greatest UR of the structure, which occurred in the horizontal beam for the bar verification.

Table 5.
Utilization ratio for the most unfavorable load combination of each member in M3, both for the cross-section and bar verification, as well as the von Mises verification for the gutter.
For both the cross-section and bar verifications, the arch presented a maximum UR of 0.69 for both LC1 and LC19.
The horizontal beam exhibited the greatest UR of the structure. A value of 0.99 was observed for LC13 in the bar check. The verification was carried out through the analysis of the buckling due to the compression and bending moment in the perpendicular axis to the bar, as in previous models.
The maximum UR of the vertical tie reached 0.17 and it was found for the LC1 as the buckling due to compression was checked.
LC1 was also responsible for the most unfavorable performance of the column. Although the UR is similar in both the cross-section and bar verification, the latter value (0.59) was due to the buckling by compression and bending moment. As compared with M1, the vertical load transmission in the primary portal frames only reached 71.31%, which indicated a more even distribution.
The structural gutter was not subjected to the bar verification since it was not exposed to any axial force. According to Eurocode 3 [4], the von Mises verification was performed to assess the cross-section resistance. The most unfavorable load combination was LC11, which was responsible for a 0.69 UR.
The purlins, which were calculated as a continuous beam, displayed maximum URs for LC11 as in previous models. Nevertheless, the 0.78 value observed in this model was lower than those reported in M1 and M2.
From the comparison among M1, M2, and M3 (Table 3, Table 4 and Table 5), some patterns regarding the most unfavorable load combinations for each structural element were noticeable. The determination of the cross-section of the arch was always based on the LC1, whereas, as a bar, LC19 was the main factor in its calculation. Although LC1 was the most limiting combination for the vertical tie, LC13 and LC19 also represented a significant influence in the determination of this structural element. Except for the cross-section verification in M1, the horizontal beam was mostly influenced by LC13. The purlin displayed LC11 as the most unfavorable combination. Finally, LC1 was found to be the limiting combination for the column.
3.1.2. Foundation
Table 6 shows the dimensions of the concrete footings for each original design. For the M1 model, the dimensions are in line with those of the common practice [44]. Whereas, for the M2 and M3 models, the height of the footing was dimensioned under the restriction of the same value diameter as in M1.

Table 6.
Dimensions of the cylindrical concrete footings.
For all designs, LC2 was the most unfavorable regarding the sliding and bearing capacity verifications; whereas, the uplift check presented the maximum utilization ratio values for LC13 (Table 7).

Table 7.
Utilization ratio for the most unfavorable load combination in the original foundation models.
The verification of the bearing capacity resulted in the maximum utilization ratios for the LC2 on both M2 and M3 (i.e., 0.94 and 0.93, respectively). However, M1 displayed the maximum utilization ratio value (0.96) on the uplift verification for the LC13. This finding was consistent with the distribution of the vertical loads transmitted by each frame, since some footings presented tensile forces which prevented their own uplift.
3.2. Optimization of the Models
The optimized solutions of M1, M2, and M3 were defined as M1OPT, M2OPT, and M3OPT. Table 8 illustrates the results arising from the optimization of the M1 structure. Despite the relative influence of LC1 and LC13, the most unfavorable utilization ratio arose from LC19. Due to buckling, a value of 0.96 in the perpendicular plane to the structure was observed for the arch.

Table 8.
Utilization ratio for the most unfavorable load combination of each member in M1OPT, both for the cross-section and bar verification.
The gravitational actions (such as permanent, crop, and snow load) were the most detrimental actions for the arch. However, permanent and wind loads were found to be the most damaging for the rest of the structure.
As in the original structure design, the vertical tie exhibited an almost zero utilization ratio in both the cross-section and bar verifications (0.04 and 0.06 for LC1 and LC13, respectively).
LC13 was responsible for the maximum utilization ratio in the horizontal beam. A value of 0.91 was noticed in the plane of the structure in the buckling verification. Nonetheless, a value of 0.66 was reported in the cross-section (axial, shear, and moment) verification.
The column exhibited a greater utilization ratio (0.83) resulting from the buckling check in the parallel plane to the structure. For both the cross-section and bar verification, the most unfavorable situation was produced by LC1.
As compared with M1, the GA focused on a reduction in the cost of the structure by achieving higher UR values in the bar verification for structural elements that previously showed a maximum UR in the cross-section check (mainly due to the lack of compression loads).
The GA was responsible for a reduction in the arch cross-section at the expense of an increased horizontal beam cross-section. Nonetheless, the utilization ratio achieved by the two structural elements was similar in both the cross-section and bar verification.
Regarding the purlin, the GA also found high utilization ratios for the structural elements, but not the maximum of the structure.
Table 9 shows the percentages of steel employed for each structural member as compared with the total material usage in the original and optimized model. In this regard, an overall 7.75% reduction in steel usage was noticed between M1 and M1OPT. Moreover, the element-by-element comparison between models revealed the operation followed by the GA in the material cost reduction. The arch and column both reduced the initial required mass of steel at the expense of a higher utilization ratio; whereas, the purlin achieved a mass reduction but also exhibited a decrease in the UR. Conversely, although to a minor extent, the amount of steel required for the horizontal beam and vertical tie increased, which was in line with the authors’ previous findings [17] that showed the horizontal beam to be the structural element with greater buckling. Therefore, the GA exhibited a coherent behavior by reinforcing the most critical element as well as those directly connected (i.e., the vertical tie and the stay).

Table 9.
Influence of the M1 optimization in the percentage of steel employed for each member.
Moreover, there is another noteworthy aspect of the GA operation as it is capable of affecting the cross-section of the perpendicular structural element in order to adjust the load distribution to the secondary portal frame. For instance, the secondary portal frame supports 17.46% of the load as compared with the initial 11.29% in LC1. Thus, the overall mass of steel was reduced as the primary portal frame was unloaded by the optimization of the purlin cross-section (since the steel gutter presented a fixed cross-section).
In the optimization of the M2 model (Table 10), it was noticed that the largest utilization ratios corresponded to the same structural elements and load combinations as in M1OPT.

Table 10.
Utilization ratio for the most unfavorable load combination of each member in M2OPT, both for the cross-section and bar verification.
The arch displayed the higher utilization ratio for LC19. A 0.87 was noticed in the z-z axis due to the buckling caused by the compression load and bending moment. The UR determined in the cross-section (axial, shear, and moment) check reached a maximum of 0.59 for LC1.
The vertical tie displayed a 0.13 utilization ratio for LC13 in the bar check and a 0.05 utilization ratio for LC19 in the cross-section verification as it was subjected to a tensile load.
The maximum UR values in the horizontal beam were found for LC13. The cross-section (compression and bending moment) and bar (buckling due to bending moment) verifications both produced similar results, 0.79 and 0.74, respectively.
The largest UR of the structure was observed in the column. LC1 was responsible for the maximum UR in both the cross-section (buckling in the plane of the structure, i.e., in the y-y axis) and bar (axial, shear, and moment) verification with values of 0.88 and 0.78, respectively.
Once again, the strategy followed by the GA consisted of reductions in the cross-sections of the arch and the column at the expense of greater steel consumption in the horizontal beam and vertical tie. Nonetheless, the GA selected steel profiles with a better overall performance than those initially established. Therefore, M2OPT resulted in a structure with more restrictive bar verifications as compared with the original M2 model.
The UR exhibited by the purlin evidenced the high performance of the GA that optimized the steel profile for the same load combination as in M1 and with a similar mass of steel requirement.
According to Table 11, the GA operated in a manner that resulted in an increase in the mass of steel employed in the horizontal beam as well as the vertical tie, whereas the arch, purlin, and column decreased their steel usage. Therefore, the previous behavior was maintained as the horizontal beam was strengthened and the cost of the remaining elements was reduced by using the optimal profiles. Nevertheless, in this optimization, the GA only affected the portal frame plane.

Table 11.
Influence of the M2 optimization in the percentage of steel employed for each member.
Table 12 illustrates the optimization results of M3. In addition to the previously highlighted load combinations (i.e., LC1, LC11, LC13, and LC19), the vertical tie reached its maximum UR for LC14.

Table 12.
Utilization ratio for the most unfavorable load combination of each member in M3OPT, both for the cross-section and bar verification, as well as the von Mises verification for the gutter.
The arch exhibited a utilization ratio of 0.37 for LC13 in the cross-section check due to tensile stresses. The greatest value (0.56) was observed for LC19 in the bar verification (i.e., buckling due to compression and bending moment in the z-z axis).
The vertical tie displayed a 0.08 utilization ratio for LC14 in the check of the buckling due to compression and bending moment and a 0.05 utilization ratio for LC19 in the cross-section verification as it was subjected to a compression load.
In the horizontal beam, a similar UR was observed for both verifications (i.e., 0.70 and 0.72 for the cross-section and bar checks, respectively).
The column exhibited a greater UR (0.79) in the cross-section verification as compared with that in the bar verification (0.71). Nonetheless, LC1 was responsible for the maximum values of both verifications.
The von Mises verification performed on the structural gutter showed a utilization ratio of 0.82 as a result of the LC13, which was the most unfavorable for the type of verification and structural element.
Similar to previous models, the purlins were optimized to a maximum UR of 0.97 for LC11.
As in M2, the GA strategy was to maintain the material consumption for the arch, vertical tie, and horizontal beam; whereas, a significant material reduction was observed for the column, gutter and purlin.
The assessment of the steel savings achieved by the GA is illustrated in Table 13. The optimization approach focused on maintaining the steel employed in the truss. The mass of steel required by the purlin also decreased significantly (19.77%). Since in this structural alternative the section of the structural gutter was not fixed, the GA opted for the adjustment of its cross-section and achieved a 5.15% reduction in the steel usage of the element. Moreover, a 4.48% mass decrease was obtained for the column. As occurred in M1OPT, the overall reduction was due to the load redistribution between portal frames and the greater contribution of the secondary frame. For instance, in LC1, the primary portal frame supported 55.11% of the total load and the remaining 44.89% was held by the secondary portal frame. Meanwhile, in the optimization of M1, the only adjustment to distribute loads to the frame was to the purlin; the optimization of M3 was possible in both perpendicular structural elements, the structural gutter, and purlins.

Table 13.
Influence of the M3 optimization in the percentage of steel employed for each member.
Analogous to the previous section, the comparisons among M1OPT, M2OPT, and M3OPT (Table 8, Table 10 and Table 12) showed some patterns regarding the most unfavorable load combinations influencing each structural element. Once again, LC1 and LC19 were the limiting combinations for the cross-section and bar verifications of the arch, respectively. LC1 was also found as the most unfavorable combination for the cross-section of the vertical tie; meanwhile, LC13 stood out as the limiting one in the bar verification. As in the original models, except for the cross-section verification in M1OPT, the horizontal beam was mostly influenced by LC13. Similarly, LC11 and LC19 remained as the most unfavorable combinations for the purlin and column, respectively.
Table 14 shows the optimized dimensions of the concrete footings of each design according to the actions transmitted by the optimized steel profiles.

Table 14.
Dimensions of the cylindrical concrete footings in the optimized foundation models.
For M1OPT and M3OPT, the maximum UR values occurred for the same load combinations as in the original designs: LC2 for sliding and bearing capacity verifications and LC13 for uplift check (Table 15). Moreover, in both cases, the maximum UR value resulted from the uplift analysis of the interior footings in the primary portal frames (0.94 and 0.95 for M1OPT and M3OPT, respectively).

Table 15.
Utilization ratio for the most unfavorable load combination in the optimized foundation models.
For M2OPT, the bearing capacity verification exhibited the most unfavorable results, with a 0.95 utilization ratio for the LC1 (Table 15).
It was noticed that LC1, LC2, LC12, and LC13 were the most unfavorable combinations for both the original and optimized foundations.
In the optimization, the GA always pursued the minimum allowed diameter (i.e., 0.50 m) due to the equipment used in the common construction practice. Nonetheless, if no limitation was imposed, an alternative optimal section with a smaller diameter could be possible, which would make the ideal footing closer to a small pile rather than a shallow foundation. Such a configuration would allow for a better overcome of the uplift tendency as well as a better tensile behavior in the vertical plane. Moreover, it is worth noting that for M1, in which the uplift represented the most unfavorable condition, a non-cylindrical geometry, such as the frustum of a cone, could also pose a better solution.
3.3. Cost Analysis of the Proposed and Optimized Greenhouses
An economic assessment was carried out to identify the cost per square meter of each original and optimized (Mi/MiOPT) design. Average cost values of both materials and labor were obtained from cost databases as well as provided by construction companies (Table 16). Note that the steel cost included the fabrication cost as well as the auxiliary connection elements.

Table 16.
Economic assessment of the original and optimized models.
For each model, the area corresponding to the influence of two portal frames was considered (i.e., 5 m in M1/M1OPT and M2/M2OPT as the separation between frames is 2.50 m, and 7 m in M3/M3OPT due to the larger separation between frames, i.e., 3.5 m- exhibited by this design). Thus, the studied areas were 120 m2 and 168 m2 (Table 16).
Table 16 illustrates the resulting total cost as well as the material and labor costs.
Amongst the three original designs, the M1 structure had the lowest material cost per square meter since it exhibited the minimum requirement for steel and an intermediate amount of concrete as compared with M2 and M3. In contrast, M1 displayed an important labor cost per square meter due to its assembly demands.
M2 represented the lowest option in terms of labor costs per square meter; whereas, the material consumption was the greatest among the three original designs, which resulted in the greatest total costs per square meter. The comparison between the M2 and M1 designs also resulted in time savings as the M2 design did not include secondary portal frames and required a smaller amount of concrete footings; thus, lower assembly demands. Nevertheless, the M2 design resulted in a greater total cost per square meter (16.55%).
Although the M3 design had the greatest labor cost per square meter, the addition of the material’s cost resulted in an alternative with a cost close to M2. It should be noted that before optimization, the maximum differences in labor costs (€1.2/m2) and material costs (€3.78/m2) were important enough to optimize these alternatives.
M1OPT presented an intermediate material cost per square meter and important labor costs (close to M2OPT). In terms of the foundation, an intermediate volume of concrete was needed (i.e., greater than M2OPT but lower than M3OPT)
M2OPT exhibited a higher cost per square meter (17.38 €/m2) than M1OPT (15.21 €/m2). However, the time requirements for the assembly of both the structure and foundation were significantly lower, since no secondary portal frames were incorporated in the design, which resulted in fewer concrete footings. For the structure, labor costs per square meter of M2OPT were lower than M1OPT and M3OPT but with the higher cost of material did not compensate for the labor costs. For the foundation, the cost of concrete was the lowest among all optimized designs. In any case, M2OPT exhibited the greatest material and total costs per square meter.
M3OPT resulted in the greatest demands of labor for assembly. Moreover, it was the more economical alternative, with a total cost per square meter of 15.14 €/m2. The greater separation between portal frames (i.e., 3.50 m as compared with the 2.50 m of M1OPT) and the reinforcement exerted by the structural gutter both allowed for better cost as compared with M1OPT. This shows that the incorporation of a plastic gutter and a bar to reinforce the interior arches is a correct optimization approach.
Therefore, the comparison between the original and optimized models evidenced the correct performance of the GA employed as reductions in cost per square meter were observed in all optimized designs.
Cost savings were catalyzed by the optimization achieved in steel consumption: 7.67% (M1/M1OPT), 8.64% (M2/M2OPT), and 27.52% (M3/M3OPT). On the one hand, M1OPT required footings of greater dimensions than the original M1 design (i.e., a 6.49% increase in the concrete consumption). On the other hand, M2OPT and M3OPT maintained the same footing dimensions as in their respective original designs, but both optimized models were subjected to greater stresses. In any case, the effects of the GA optimization on the structure-foundation binomial resulted in more economical alternatives: 4.97% (M1/M1OPT), 6.86% (M2/M2OPT), and 18.70% (M3/M3OPT). It should be noted that M3OPT displayed the best result in terms of cost per square meter (15.14 €/m2), which was 0.45% and 12.87% lower than that of M1OPT and M2OPT, respectively.
3.4. Influence of the Portal Frame Separation
Based on the previous findings, further studies were conducted solely on the M3-M3OPT design alternative as it was decidedly better than the M2-M2OPT design. Since the advantage of M3OPT relied on the greater portal frame separation as compared with M1OPT, the influence of the portal frame separation on the cost per square meter was assessed in this section. Thus, different optimizations were carried out under the same criteria as in the previous analyses for separations from 2.50 m to 5 m in varying intervals of 0.50 m. The costs and dimensioning results for the different portal frame separations are shown in Table 17.

Table 17.
Dimensioning and overall cost per square meter for the different portal frame separations.
In general, up to a 4 m separation, profiles with a circular cross-section represented the optimal solution for all structural elements. Nonetheless, some quadrangular profiles were occasionally selected for greater separations (i.e., 4.50 and 5 m).
As expected, the overall cost per square meter was reduced with an increase in the separation between portal frames, and the lowest cost was registered for 4.50 m, which goes beyond the alternative proposed in M3OPT.
In this regard, the GA’s strategy consisted of finding the optimum solution based on the combined work of the structural gutter and purling in the support of the vertical loads. For the 3.50 m spacing, the purlin showed lower resistance than the structural gutter, but, as the separation between portal frames increased, the dimensioned purlin became more resistant, which reduced the need for higher steel consumption in the structural gutter.
Table 18 illustrates the percentage of steel employed for each member. The arch cross-section implies around 18% of the total steel consumption, whereas, the vertical tie only represents 4%. Average values of around 10% were found for both the structural gutter and the horizontal beam. Nonetheless, the latter exhibited a lineal reduction (y = −2.816x + 19.838; R² = 0.9982) from 11.36% at 3 m to almost half the percentage at 5 m. Higher steel consumption values were noticed for both the purlin and column cross-sections at around 33% and 26%, respectively. As a generalization, these values could be used as a simplified near-optimal dimensioning procedure since the sum of both percentages were quite stable as compared with the individual variations. For instance, a combined 42% steel consumption could be set as the objective in the dimensioning of the structural gutter and purlin. Otherwise, for a known portal frame separation, the values presented in Table 18 could also be employed as a particular simplified near-optimal dimensioning procedure.

Table 18.
Influence of the portal frame separation in the percentage of steel employed for each member.
Regarding the foundation, Table 17 shows the influence of the portal frame separation on the optimum height values of the concrete footing. The optimal solution was again found for the minimum allowed diameter. An almost linear relationship was noticed with an optimum of 0.70 m for a 2.50 separation and an optimum of 1.05 m for a 5 m separation.
4. Conclusions
For the greenhouses analyzed, several conclusions were drawn as follows:
- All greenhouses studied in this research exhibited a λcr greater than 3.60 that allowed for a first-order calculation, which could have resulted in a lower computational cost. The calculation of columns and purlins was driven by the same load combination regardless of the structural design, i.e., LC1 and LC11, respectively. Except in M1, LC13 was the most unfavorable load combination for the cross-section verification of the horizontal beam. For the arch, LC1 and LC19 were the most significant load combinations. Nevertheless, the latter was responsible for the higher utilization ratios. Conversely, depending on the structural design, several load combinations (LC1, LC13, LC14, and LC19) were responsible for the dimensioning of the vertical tie.
- In terms of the foundation, LC13 was the most unfavorable situation in the dimensioning of the concrete footing. Moreover, the optimized diameter coincided with the minimum diameter employed in the current construction practice, which suggested that a margin for optimization could still be achieved by further reducing the allowed diameter to be used in the GA.
- To reduce the overall cost, the most common approach relied on an increase in the section of the horizontal beam in the portal frame as well as the load redistribution between primary and secondary portal frames by adjusting the cross-section of the purlins and the gutter. Therefore, the use of a gutter with a fixed cross-section in the structural alternative M1 limited the optimization reach of the GA. In any case, elimination of the secondary portal frames (i.e., structural design M2) was not advisable from an economic point of view as they contributed to the reduction in the cost per square meter. Regarding the concrete footings, for the minimum diameter of 0.5 m, the optimum height values ranged from 0.70 m to 1.05 m due to the uplift.
- In general, the genetic algorithm found similar percentages of steel consumption for similar types of sections, which could serve as the basis of a simplified near-optimal dimensioning procedure. Moreover, for the alternatives studied, optimal solutions were generally found among circular cross-section profiles instead of rectangular or square profiles.
- For both the original and optimized models, the structural design number 3 (i.e., M3 and M3OPT) displayed the lower overall costs per square meter. M3OPT was the most cost-effective solution (15.14 €/m2) and a 4.50 m portal frame separation was found to be the best alternative for a reduction in the cost per square meter, at 14.21 €/m2, despite the higher steel consumption for the purlins.
Author Contributions
Conceptualization, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; methodology, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; validation, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; formal analysis, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; investigation, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; resources, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; writing—original draft preparation, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; writing—review and editing, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; supervision, M.S.F.-G., P.V.-L., D.R.-R. and J.R.V.-G.; funding acquisition, P.V.-L., D.R.-R. and J.R.V.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This publication has been made possible thanks to funding granted by the Consejería de Economía, Ciencia y Agenda Digital of the Junta de Extremadura and by the European Regional Development Fund of the European Union through grants GR21163 and GR21091.
Data Availability Statement
Not applicable.
Acknowledgments
Administrative and technical support of the Forest Research Group and the Mechanical and Fluid Engineering Research Group, University of Extremadura, is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ren, J.; Wang, J.; Guo, S.; Li, X.; Zheng, K.; Zhao, Z. Finite element analysis of the static properties and stability of a large-span plastic greenhouse. Comput. Electron. Agric. 2019, 165, 104957. [Google Scholar] [CrossRef]
- Spanish Ministry of Agriculture, Fisheries and Food. Survey on Crops Surfaces and Yields [Encuesta sobre Superficies y Rendimientos Cultivos (ESYRCE)]; Spanish Ministry of Agriculture, Fisheries and Food: Madrid, Spain, 2021. (In Spanish)
- EN 13031-1; Greenhouses—Design and Construction—Part 1: Commercial Production Greenhouses. CEN: Belgium, Brussels, 2019.
- EN 1993-1-1; Eurocode 3: Design of Steel Structures. Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2014.
- Roux, P.; Motro, R. Study of the global behavior of monotubular arches: Pathology of tunnel greenhouses under the effect of snow. [Etude du comportement global d’arcs monotubulaires: Pathologie des serres tunnels sous l’effet de la neige]. Rev. Constr. Métallique 1993, 1, 23–39. (In French) [Google Scholar]
- Roux, P.; Robertson, A.; Motro, R. The design of slender monotubular steel arches. Struct. Eng. 1997, 75, 143–151. [Google Scholar]
- Roux, P.; Lezeau, S.; Motro, R. Evaluation of the resistance of an arch in a tunnel greenhouse: Impact of the tube behavior model. [Evaluation de la résistance d’un arceau de serre tunnel: Incidence du modèle de comportement des tubes]. Rev. Constr. Métallique 1995, 4, 53–62. (In French) [Google Scholar]
- Briassoulis, D.; Dougka, G.; Dimakogianni, D.; Vayas, I. Analysis of the collapse of a greenhouse with vaulted roof. Biosyst. Eng. 2016, 151, 495–509. [Google Scholar] [CrossRef]
- Xu, J.; Fang, C.; Wang, W.; Chen, G. Structural design of irregular curved lattice shells in China. Proc. Inst. Civ. Eng.-Civ. Eng. 2019, 172, 37–47. [Google Scholar] [CrossRef]
- Maraveas, C.; Tsavdaridis, K.D. Strengthening Techniques for Greenhouses. AgriEngineering 2020, 2, 37–54. [Google Scholar] [CrossRef]
- Javadi Moghaddam, J.; Momeni, D.; Zarei, G. Application of topology optimization method for the gothic greenhouse design. World J. Eng. 2021. [Google Scholar] [CrossRef]
- Maraveas, C. Wind Pressure Coefficients on Greenhouse Structures. Agriculture 2020, 10, 149. [Google Scholar] [CrossRef]
- Vieira Neto, J.G.; Soriano, J. Computational modelling applied to predict the pressure coefficients in deformed single arch-shape greenhouses. Biosyst. Eng. 2020, 200, 231–245. [Google Scholar] [CrossRef]
- Wang, C.; Nan, B.; Wang, T.; Bai, Y.; Li, Y. Wind pressure acting on greenhouses: A review. Int. J. Agric. Biol. Eng. 2021, 14, 1–8. [Google Scholar] [CrossRef]
- Hur, D.-J.; Noh, J.-H.; Lee, H.J.; Song, H.W. Evaluation of stress distribution with wind speed in a greenhouse structure. Wind Struct. 2018, 27, 347–356. [Google Scholar] [CrossRef]
- Kim, R.; Lee, I.; Yeo, U.; Lee, S. Estimating the wind pressure coefficient for single-span greenhouses using an large eddy simulation turbulence model. Biosyst. Eng. 2019, 188, 114–135. [Google Scholar] [CrossRef]
- Fernández-García, M.S.; Vidal-López, P.; Rodríguez-Robles, D.; Villar-García, J.R.; Agujetas, R. Numerical simulation of multi-span greenhouse structures. Agriculture 2020, 10, 499. [Google Scholar] [CrossRef]
- Peña, A.; Pérez, F.; Valera, D.L.; Ayuso, J.; Pérez, J. Assessment of response of greenhouse foundations to traction, and their simulation using finite elements. Inf. Constr. 2002, 53, 47–57. [Google Scholar] [CrossRef][Green Version]
- Hur, D.-J.; Kwon, S. Fatigue Analysis of Greenhouse Structure under Wind Load and Self-Weight. Appl. Sci. 2017, 7, 1274. [Google Scholar] [CrossRef]
- Kim, R.; Lee, I.; Yeo, U.; Lee, S. Evaluation of various national greenhouse design standards for wind loading. Biosyst. Eng. 2019, 188, 136–154. [Google Scholar] [CrossRef]
- Li, X.; Wang, C.; Jiang, Y.; Bai, Y. Dynamic response analysis of a whole steel frame solar greenhouse under wind loads. Sci. Rep. 2022, 12, 5200. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Jeong, Y.; Choi, W. Development of a structural analysis model for pipe structures to reflect ground conditions. Biosyst. Eng. 2020, 197, 231–244. [Google Scholar] [CrossRef]
- Di Trapani, F.; Malavisi, M.; Marano, G.C.; Sberna, A.P.; Greco, R. Optimal seismic retrofitting of reinforced concrete buildings by steel-jacketing using a genetic algorithm-based framework. Eng. Struct. 2020, 219, 110864. [Google Scholar] [CrossRef]
- Dias, Y.; Mahendran, M. Shape optimisation of cold-formed steel framed wall studs with sheathing restraints. Thin-Walled Struct. 2021, 158, 107135. [Google Scholar] [CrossRef]
- Shahnewaz, M.; Alam, M.S. Genetic algorithm for predicting shear strength of steel fiber reinforced concrete beam with parameter identification and sensitivity analysis. J. Build. Eng. 2020, 29, 101205. [Google Scholar] [CrossRef]
- Sistla, S.; Kalyana Rama, J.S. Evaluating the performance of nature inspired algorithms using 52-bar steel truss subjected to dynamic load. Mater. Today Proc. 2020, 38, 2464–2470. [Google Scholar] [CrossRef]
- Skoglund, O.; Leander, J.; Karoumi, R. Optimizing the steel girders in a high strength steel composite bridge. Eng. Struct. 2020, 221, 110981. [Google Scholar] [CrossRef]
- Villar-García, J.R.; Vidal-López, P.; Rodríguez-Robles, D.; Guaita, M. Cost optimisation of glued laminated timber roof structures using genetic algorithms. Biosyst. Eng. 2019, 187, 258–277. [Google Scholar] [CrossRef]
- EN 10305-3; Steel Tubes for Precision Applications—Technical Delivery Conditions—Part 3: Welded Cold Sized Tubes. CEN: Belgium, Brussels, 2016.
- EN 10305-5; Steel Tubes for Precision Applications—Technical Delivery Conditions—Part 5: Welded Cold Sized Square and Rectangular Tubes. CEN: Belgium, Brussels, 2016.
- Maquoi, R.; Boissonnade, N.; Muzeau, J.P.; Jaspart, J.-P.; Villette, M. The interaction formulae for beam-columns: A new step of yet long story. In Proceedings of the SSRC Annual Technical Session and Meeting, Fort Lauderdale, FL, USA, 9–12 May 2001; pp. 63–88. [Google Scholar]
- EN 1997-1; Eurocode 7: Geotechnical Design. Part 1: General Rules. CEN: Brussels, Belgium, 2013.
- Jiménez-Salas, J.A.; Cañizo, L.; Escario, B. Geotecnia y Cimientos III. Cimentaciones, Excavaciones Y Aplicaciones de la Geotecnia; Rueda: Madrid, Spain, 1980; Volume 2. [Google Scholar]
- Spanish Ministry of Public Works. Spanish Technical Building Code. Basic Document for Structural Safety-Foundations. [Código Técnico de la Edificación. Documento Básico de Seguridad Estructural-Cimientos]; Spanish Ministry of Public Works: Madrid, Spain, 2019. (In Spanish)
- Cazacu, R.; Grama, L. Steel Truss Optimization Using Genetic Algorithms and FEA. Procedia Technol. 2014, 12, 339–346. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, K.; Wang, X. Parameter study of framed-tube structures with outriggers using genetic algorithm. Struct. Des. Tall Spec. Build. 2018, 27, e1499. [Google Scholar] [CrossRef]
- McKinstray, R.; Lim, J.B.P.; Tanyimboh, T.T.; Phan, D.T.; Sha, W. Optimal design of long-span steel portal frames using fabricated beams. J. Constr. Steel Res. 2015, 104, 104–114. [Google Scholar] [CrossRef]
- Villar, J.R.; Vidal, P.; Fernández, M.S.; Guaita, M. Genetic algorithm optimisation of heavy timber trusses with dowel joints according to Eurocode 5. Biosyst. Eng. 2016, 144, 115–132. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 978-0-12-416743-8. [Google Scholar]
- Prendes-Gero, M.-B.; Bello-García, A.; del Coz-Díaz, J.-J.; Suárez-Domínguez, F.-J.; García Nieto, P.-J. Optimization of steel structures with one genetic algorithm according to three international building codes. Rev. Constr. 2018, 17, 47–59. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.; Jia, H.; Zhang, M.; Wang, D. Application of multi-objective genetic algorithm to optimize energy efficiency and thermal comfort in building design. Energy Build. 2015, 88, 135–143. [Google Scholar] [CrossRef]
- Ebrahimi, E.; Abdollahzadeh, G.; Jahani, E. Assessment of axial load effect on nonlinear modeling and seismic response of reinforced concrete-structures based on fuzzy set theory using genetic algorithm. Struct. Concr. 2019, 20, 614–627. [Google Scholar] [CrossRef]
- Villar, J.; Crespo, J.; Lorenzana, J.; Guaita, M. Experimental and finite element analysis of the stress state at single and double step front notched traditional joint in timber structures. [Análisis experimental y por elementos finitos del estado tensional de uniones tradicionales por embarbillado simple y doble en madera estructural]. In Proceedings of the VIII Congreso Ibérico de Agroingeniería. Retos de la Nueva Agricultura Mediterránea, Orihuela-Algorfa, Spain, 1–3 June 2015. (In Spanish). [Google Scholar]
- Fernández-García, M.S. Optimization of Greenhouse Structures by Genetic Algorithms [Optimización de Estructuras de Invernadero por Algoritmos Genéticos]. Master’s Thesis, Universidad de Extremadura, Extremadura, Spain, 2014. (In Spanish). [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).