Monitoring of Wheat Stripe Rust Using Red SIF Modified by Pseudokurtosis

Abstract

Red solar-induced chlorophyll fluorescence (SIF_B) is closely related to the photosynthetically active radiation absorbed by chlorophyll. The scattering and reabsorption of SIF_B by the vegetation canopy significantly change the spectral intensity and shape of SIF, which affects the relationship between SIF and crop stress. To address this, we propose a method of modifying SIF_B using SIF spectral shape characteristic parameters to reduce this influence. A red pseudokurtosis (PK_B) parameter that can characterize spectral shape features was calculated using full-spectrum SIF data. On this basis, we analyzed the photosynthetic physiological mechanism of PK_B and found that it significantly correlates with both the fraction of photosynthetically active radiation absorbed by chlorophyll(fPAR_chl) and the red SIF escape rate (fesc680); thus, it is closely related to the scattering and reabsorption of SIF_B by the vegetation canopy. Consequently, we constructed an expression of PK_B to modify SIF_B. To evaluate the modified SIF_B (MSIF_B) in monitoring the severity of wheat stripe rust, we analyzed the correlations between SIF_B, MSIF_B, SIF_B-VIs (a fusion of the vegetation index and SIF_B), and MSIF_B-VIs (a fusion of the vegetation index and MSIF_B) with the severity level (SL), respectively. The results show that the correlation between MSIF_B and the severity of wheat stripe rust increased by an average of 25.6% and at least 16.95% compared with that for SIF_B. In addition, we constructed remote sensing monitoring models for wheat stripe rust using linear regression methods, with SIF_B, MSIF_B, SIF_B-VIs, and MSIF_B-VIs as independent variables. PK_B significantly improves the accuracy and robustness of models based on SIF_B and its fusion index SIF_B-VIs in the constructed testing set. The R-value between the predicted SL and the measured SL of the remote sensing monitoring model for wheat stripe rust was established using MSIF_B-VIs as the independent variable, and it was improved by an average of 39.49% compared with the model using SIF_B-VIs. The RMSE was reduced by an average of 18.22%. Therefore, the SIF_B modified by PK_B can weaken the effects of chlorophyll reabsorption and canopy architecture on SIF_B and improve the ability of SIF_B to detect stress information.

1. Introduction

Wheat is the most important food product in the world, and its yield is crucial for the livelihood of nations. Yellow rust (stripe rust), caused by Puccinia striiformis f. sp. tritici (Pst), is a serious constraint to global wheat production. The optimal conditions for rust disease development involve warm days, mild nights, moisture, and humidity [1]. With global climate change, wheat yellow rust has increasingly become a problem. Approximately 70% of the world’s wheat area is susceptible to yellow rust, leading to recurrent epidemics and substantial economic losses [2]. To combat this threat, extensive international endeavors are being conducted to meticulously track the development and spread of virulent wheat rust species.

After stripe rust infection, the internal cell tissues of wheat leaves are destroyed, changing the biochemical composition of the wheat and the open ratio of chloroplast photoreaction centers, which leads to a decreased net photosynthetic rate, and the transfer and output of photosynthetic products are inhibited and disturbed [3]. The reflectance spectrum can be directly correlated with the biochemical and biophysical parameters of vegetation, including chlorophyll content and biomass, but it primarily represents “potential photosynthesis” rather than the actual physiological state [4]. Consequently, it is challenging to directly assess the physiological state of vegetation photosynthesis using the reflectance spectrum and to capture early photosynthetic responses to disease stress [5].

Solar-induced chlorophyll fluorescence (SIF) is the fluorescence emitted within the 640–800 nm wavelength range by chlorophyll in vegetation leaves when it returns to its ground state after being excited by sunlight [6]. SIF can reflect the inherent connection between vegetation and photosynthesis and is a direct detection method for “actual photosynthesis” [7,8]. It can be detected through remote sensing and is a direct and non-invasive indicator for measuring photosynthetic status. It is becoming an important tool for monitoring crop physiological conditions through remote sensing [9] and detecting stress information before changes occur in biochemical vegetation components and canopy structures [10]. The SIF spectrum emitted by vegetation has two peaks: red (approximately 685 nm, O₂-B) and far-red (approximately 740 nm, O₂-A). Far-red SIF (SIF_A) originates from chlorophyll associated with photosystem I (PSI) and photosystem II (PSII), and it is significantly influenced by the structural characteristics of vegetation [11]. Red SIF (SIF_B) is derived from chlorophyll associated with PSII and is closely related to chlorophyll reabsorption by vegetation. It can sensitively reflect the photosynthetic status of vegetation [12] and holds significant importance in monitoring crop stresses, such as diseases [13]. However, red SIF is significantly impacted by the absorption of chlorophyll within leaves [14], and its Fraunhofer absorption lines are narrower and shallower than those of far-red SIF [15]. Consequently, its inversion accuracy is less robust than that of far-red SIF. As a result, few studies are related to using red SIF [9,10,16]. The scattering and reabsorption effects of vegetation on SIF lead to the biochemical components and structural characteristics of vegetation having a significant impact on the spectral intensity and shape of SIF [11]. Therefore, the spectral features of full-spectrum SIF not only change with physiological regulation through energy dissipation pathways but also differ with variations in plant biochemical components [17]. These factors significantly impact the shape and intensity of SIF spectral curves. Full-spectrum SIF provides not only intensity information at peaks but also shape information near peaks, enabling a more comprehensive and accurate reflection of crop physiological changes induced by disease and stress [18]. However, current research has mainly focused on monitoring crop stress conditions based on single-band SIF intensity, without considering the shape information of full-band SIF spectra, missing out on valuable information contained in unused spectral bands. Based on this, we extracted the full-spectrum SIF spectrum using the F-SFM algorithm to fully utilize its shape and intensity information. Furthermore, the standardized fourth central moment was extracted from the red SIF spectrum and was used to calculate pseudokurtosis (PK_B) under different disease severity levels. Based on the analysis of the physiological mechanism of PK_B, we used PK_B to modify SIF_B (MSIF_B) to eliminate the influence of reabsorption and scattering effects on SIF_B. Finally, we analyzed the correlation between MSIF_B and the severity of wheat stripe rust and evaluated the effectiveness of MSIF_B in estimating wheat stripe rust severity. The findings of this study are significant for improving wheat stripe rust monitoring accuracy and provide an important reference value for the remote sensing monitoring of other crop stresses.

2. Materials and Methods

The data used in this study primarily consisted of measured data from plot control experiments, natural disease field experiments on stripe rust, and model simulation data. The measured data mainly comprised field canopy spectra and wheat stripe rust disease severity levels. The model simulation data were divided into two parts: the Fluspect model simulates absorption spectra and analyzes the influence of vegetation reabsorption effects on the shape of the SIF spectrum; the SCOPE model simulates SIF spectral curves and photosynthesis-related parameters to analyze the photosynthetic physiological mechanisms underlying shape parameters.

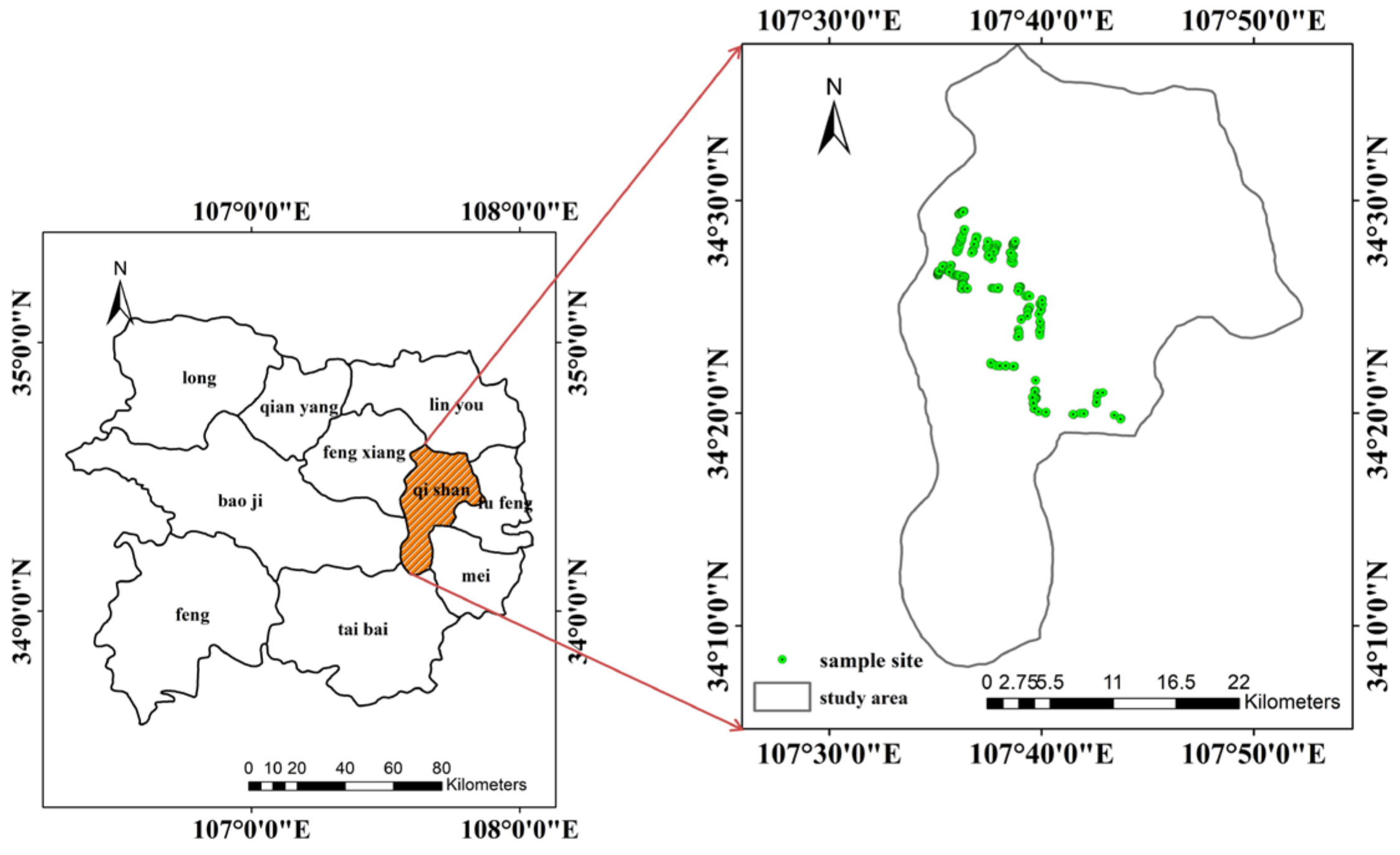
2.1. Overview of the Study Area and Data Acquisition

2.1.1. Plot Disease Field Experiment

A plot disease field experiment was conducted at the experimental station of the Chinese Academy of Agricultural Sciences in Langfang, Hebei Province (located between a latitude of 38°28′ N and 40°15′ N and longitude of 114°47′ E and 117°14′ E). The wheat variety Mingxian 169 was used, as it is highly susceptible to stripe rust. The seeding density was set at 113 grains per square meter. On 9 April 2018, a spore solution with a concentration of 9 mg/100 mL was used to inoculate the wheat with stripe rust. Each experimental group covered 220 square meters and was divided into 8 quadrats.

2.1.2. Natural Disease Field Experiment

The natural disease field experimental area was located in Qishan County, Baoji City, Shaanxi Province, China (39°30′ N, 116°36′ E) (Figure 1). This area is situated close to the over-summering region of stripe rust in Longnan and belongs to the warm temperate semi-humid climate zone. The annual precipitation ranges from 590 to 1000 mm. These climatic and geographical factors provide suitable conditions for stripe rust outbreaks. The soil types in the natural disease field area were mainly semialfisol and primary soil, and the wheat variety used was Xinong 822. The planting time and management practices for wheat varied between farmers in the survey area.

2.1.3. Disease Severity and Field Canopy Spectral Measurement

The measurement times for the plot disease field experiment were 15, 18, 24, and 30 May 2018, with 7 quadrats measured each day. Each plot was 3 m × 7 m, and each quadrat was 40 cm × 40 cm. For the field natural disease experiment, the measurement times were 16, 17, 28, 29, and 30 April and 12 and 13 May 2021, with 30 quadrats measured daily. The sample plot size was also 40 cm × 40 cm.

The canopy spectrum was measured using a QE-pro spectrometer (Ocean Optics, Inc., Dunedin, FL, USA) [19]. The measurement height was 0.9 m above the wheat canopy, with a probe view optical field of 25° and an observed area of 0.13 m². Observations were made perpendicular to the canopy. For each quadrat, spectral data for the sampling point were derived by averaging 10 consecutive observations [20]. Figure 1 illustrates the measurement area for each period.

The five-point sampling method was adopted to investigate the severity level (SL) of wheat stripe rust. Firstly, five symmetrical points were selected within each quadrat. Then, two wheat plants were randomly selected at each point to investigate their disease severity. Disease severity was quantified referring to the “Technical Specifications for Wheat Stripe Rust Forecasting” national standard (GB/T15795-2011) [21].

In addition, the chlorophyll content (C_ab) and the leaf area index (LAI) were measured as supporting data. C_ab was measured using Dualex, a new multi-function blade-measuring instrument developed by Force-A, France. The LAI was obtained through digital hemispherical photography measurements [22]. All observed targets and timings corresponded to the disease experiment.

2.2. Simulation Data

2.2.1. Fluspect Model

We used the Fluspect-B model to simulate absorption spectra and analyze the impact of vegetation reabsorption effects on the shape of SIF spectra. The Fluspect-B model is based on the PROSPECT model and incorporates the concept of dense leaf layers [23]. Under incident light, the Fluspect-B model simulates leaf spectra by inputting various parameters, including chlorophyll and carotenoid content, leaf water content, dry matter and senescent matter (brown pigments) content, leaf structure parameters, and fluorescence quantum yield. The input parameters are presented in the

Table 1. Main input parameters for Fluspect-B simulations.

Parameter	Unit	Values	Unit Description
Cab	ug cm−2	5–80 interval 5	Chlorophyll AB content
Cdm	g cm−2	0.002, 0.01, 0.02	Dry matter content
Cw	cm	0.005, 0.01, 0.02, 0.04	Leaf water equivalent layer
N	-	1, 2	Leaf thickness parameters
qLs	-	1, 0.5	Fraction of functional reaction centers
Stressfactor	-	1, 3, 5	Stress factor to reduce Vcmax
LAI	m2 m−2	1, 2, 4, 6	Leaf area index
SZA	Degree	20, 60	Solar zenith angle
VZA	Degree	0, 30, 60	Observation zenith angle
RAA	Degree	90	Relative azimuth angle
Vcmax25	umol m−2 s−1	60	Maximum carboxylation capacity

below.

2.2.2. SCOPE 2.0 Model

SCOPE (Soil-Canopy-Observation of Photosynthesis and Energy) is a widely used radiative transfer model that simulates the interaction between solar radiation and vegetation canopies [24]. Based on the SCOPE 2.0 model, we simulated datasets for the wheat canopy, including the SIF escape rate (fesc), the chlorophyll ab absorption of photosynthetically active radiation (aPAR_chl), photosynthetic active radiation (PAR), the fraction of absorbed photosynthetically active radiation by chlorophyll (fPAR_chl), canopy net photosynthesis (CNP), electron transport rate (ETR), and nonphotochemical quenching (NPQ). PAR is calculated by integrating solar irradiance from 400 to 700 nm, while calculating fPAR_chl follows a specific methodology. Referring to the results of [25], and considering the measured chlorophyll content under different stripe rust severities, the C_ab parameter input range shown in

Table 2. Main input parameters for SCOPE simulations.

Parameter	Unit	Values	Unit Description
Cab	ug cm−2	5, 20, 40, 60, 80	Chlorophyll AB content
Cdm	g cm−2	0.002,0.01, 0.02	Dry matter content
Cw	cm	0.005, 0.01, 0.02, 0.04	Leaf water equivalent layer
N	-	1, 2	Leaf thickness parameters
qLs	-	1, 0.5	Fraction of functional reaction centers
stressfactor	-	1, 3, 5	Stress factor to reduce Vcmax
LAI	m2 m−2	1, 2, 4, 6	Leaf area index
SZA	Degree	20, 60	Solar zenith angle
VZA	Degree	0, 30, 60	Oobservation zenith angle
RAA	Degree	90	Relative azimuth angle
FQE	-	0.04	Fluorescence quantum yield Efficiency at photosystem level
Vcmax25	umol m−2 s−1	60	Maximum carboxylation capacity

was set. The parameter ranges for dry matter content (C_dm) and equivalent water thickness (C_w) were determined based on parameters set by [25]. Changing the thickness of the leaf blades (N) affects internal radiation transmission within the leaves. Under stress conditions, the proportion of the functional reaction center of the vegetation (qLs) and the maximum carboxylation rate (Vcmax) are altered [26]. In the SCOPE model, these quantity changes can be achieved by adjusting the qLs and stress factor parameters. Based on previous research results, the wheat leaf inclination angle was set as spherical [25]. By changing the LAI to express differences in the canopy’s geometric structure, we could set the solar zenith angle (SZA) according to the solar position from 10:00 to 16:00 in the experimental area. The observation zenith angle (VZA) was set perpendicular to the canopy direction. The SCOPE model results were validated using the measured data ranges.

2.3. Canopy Spectral Processing

2.3.1. Full-Spectrum SIF Spectral Retrieval

Full-spectrum SIF spectral retrieval uses the SIF full-spectrum spectral fitting method (F-SFM) proposed in [27]. This method models the full-spectrum reflectance and SIF within the 650–800 nm region using PCA, based on a training dataset simulated by the SCOPE model. The weighting coefficients of the principal components are then estimated using the least-squares fitting method.

The total upwelling radiance at the top of the canopy can be expressed as follows [27]:

$$\mathrm{L}={\displaystyle \frac{\mathrm{E}}{\pi }}\mathrm{R}+\mathrm{S}\mathrm{I}\mathrm{F}$$

(1)

where R is the canopy reflectance, and E is the downwelling irradiance.

PCA was used to extract features from the SCOPE simulation data and accurately estimate the reflectance and SIF spectrum:

$$\mathrm{\Phi }=\mathrm{X}\mathrm{W}$$

(2)

where X is the matrix representing the training dataset, Φ is the matrix representing the full set of reflectance PCs (or SIF), and W is a matrix whose columns are the eigenvectors of X^TX.

The reflectance and SIF can then be reconstructed using a linear combination of the first few PCs in Φ:

$${\mathrm{R}}^{\prime }(\lambda )={\displaystyle \sum _{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{r}}}{\mathrm{k}}_{\mathrm{i}}{\varphi }_{\mathrm{i}}(\lambda )}$$

(3)

$$\mathrm{S}\mathrm{I}{\mathrm{F}}^{\prime }(\lambda )={\displaystyle \sum _{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{F}}}{\mathrm{j}}_{\mathrm{i}}{\phi }_{\mathrm{i}}(\lambda )}$$

(4)

where ${\mathrm{R}}^{\prime }(\lambda )$ and $\mathrm{S}\mathrm{I}{\mathrm{F}}^{\prime }(\lambda )$ are the reconstructed spectra of the reflectance and SIF, respectively; ${\varphi }_i(\lambda )$ and ${\phi }_i(\lambda )$ are the i-th PC of the reflectance and SIF, respectively; k_i and j_i are the weight coefficients of the i-th PC; and n_r and n_F are the numbers of reflectance and SIF PCs that were used, respectively. The training set used by [27] for their F-SFM algorithm was derived from data simulated by the SCOPE model, which inherently cannot directly simulate spectral data under stripe rust stress. As a result, Liu et al.‘s findings could not be directly applied to extracting full-band SIF spectra in this study. Given that the stress factor can describe variation in Vcmax in vegetation under stress and that qLs can characterize the impact of stress on the photosynthetic reaction centers of vegetation, we incorporated variations in both stress factors and qLs into our SCOPE simulations. The resulting simulated data were then used as the training set for the F-SFM algorithm. This modification to the training set enabled us to calculate full-spectrum SIF under different disease severity levels.

2.3.2. Full-Spectrum SIF Spectral Preprocessing

The instantaneous SIF intensity signal of the canopy detected by the QE Pro spectrometer is susceptible to incident solar radiation. Normalizing SIF using PAR can reduce the influence of incident radiation intensity and angle on the SIF intensity of the canopy [28,29]:

$$\mathrm{S}\mathrm{I}\mathrm{F}=\mathrm{S}\mathrm{I}{\mathrm{F}}_{\lambda }/\mathrm{P}\mathrm{A}\mathrm{R}$$

(5)

where SIF is the normalized SIF at the λ wavelength, SIF_λ is the SIF at the λ wavelength, and PAR is photosynthetically active radiation measured by solar irradiance integration.

2.4. The Influence of Canopy on the Shape of SIF Spectrum

The impact of the vegetation canopy on SIF_B encompasses both scattering and absorption, with chlorophyll reabsorption being particularly severe [16,25]. Assuming there is a non-reflective surface beneath the canopy (the “black soil” condition), the SIF from the leaves to the canopy can be expressed as follows:

$$\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{c}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{p}\mathrm{y}}(\lambda )=\mathrm{f}\mathrm{e}\mathrm{s}\mathrm{c}(\lambda )\times \mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}(\lambda )=(1-\gamma (\lambda )-\mathrm{t}(\lambda ))\times \mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}(\lambda )$$

(6)

where $\lambda$ is the wavelength, SIF_canopy is the canopy-level SIF; SIF_leaf is the leaf-level SIF; $\gamma$ and $t$ are the scattering rate and absorption rate, respectively; and $1-\gamma (\lambda )-t(\lambda )$ represents the probability of SIF escaping from the leaves to the canopy. For the entire SIF_B emission peak, the canopy’s effect on SIF varies across different bands, changing the SIF shape from the leaf level to the canopy level. Extracting the SIF emission peak in the red band is crucial. In taking the minimum value between the two fluorescence peaks (near 700 nm) as the dividing point, the shorter wavelength SIF value greater than this point is designated as the left peak (Figure 2).

Vegetation exhibits high absorption rates for photons in the 600–700 nm range, peaking around 680 nm, with lower absorption rates closer to 640 nm and 700 nm [30]. The chlorophyll content in vegetation is closely linked to chlorophyll reabsorption, and as the chlorophyll content increases, the rate of decrease in relative absorption at 680 nm is higher than in other bands [30] (Figure 3). This subsequently affects the shape of the SIF in the red spectrum within the canopy, necessitating the use of kurtosis to reflect the flatness of the curve. Kurtosis is defined as the standardized fourth-order central moment of a sample, essentially expressing the fourth-order statistic of the data distribution [31]. When a large amount of data are distributed closely around the mean, the curve’s distribution is relatively narrow, resulting in positive kurtosis. Conversely, when few data are distributed around the mean, the curve’s distribution is relatively wide, resulting in negative kurtosis.

$$\mathrm{K}={\displaystyle \sum _{\mathrm{t}=1}^{\mathrm{n}}{({\mathrm{x}}_{\mathrm{t}}-\mu )}^4/}\mathrm{n}{\sigma }^4-3$$

(7)

where K is kurtosis; n is the number of bands, which represents the emission peak width; x_i is the fluorescence value of the i-th band; and μ and σ are the mean and standard deviation of the data, respectively.

In summary, the higher absorption of SIF_B by the canopy results in a smaller K for the red canopy SIF curve. The following relationship between fesc (680) and K can be obtained:

$$\mathrm{K}\propto -\mathrm{f}\mathrm{e}\mathrm{s}\mathrm{c}(680)$$

(8)

Reflectance can effectively describe the directional reflection information of vegetation at a specific band (i.e., scattering in multiple directions). However, vegetation has low scattering properties in SIF_B, meaning that canopy scattering has minimal impact on the shape of the SIF_B spectrum [25]. Notably, reflectivity increases near 700 nm, which could result in a more pronounced SIF_B canopy signature shape. In this study, we can consider the scattering within the 640–690 nm range a relatively constant factor, namely,

$$\gamma (\lambda )=\mathrm{a},\lambda \in [640,690]$$

(9)

The width of the red-band SIF emission peak is not constant, and it becomes relatively narrow as the emission peak becomes sharper. Therefore, we introduce the emission peak width (n) as a factor and construct a pseudokurtosis metric. This metric compensates for the scattering effects in this spectral region and more accurately represents the SIF signature.

$$\mathrm{P}\mathrm{K}={\displaystyle \sum _{\mathrm{t}=1}^{\mathrm{n}}{({\mathrm{x}}_{\mathrm{t}}-\mu )}^4/}{\sigma }^4-3$$

(10)

The fesc is the probability of fluorescence photons escaping from the photosystem level to the canopy level, negatively correlating with absorption and scattering. At this time, the relationship between the PK_B and the red SIF escape rate (fesc680) can be approximately obtained:

$$\mathrm{f}\mathrm{e}\mathrm{s}\mathrm{c}680=1-\gamma (680)-\mathrm{f}\mathrm{e}\mathrm{s}\mathrm{c}(680)\propto \mathrm{P}{\mathrm{K}}_{\mathrm{B}}$$

(11)

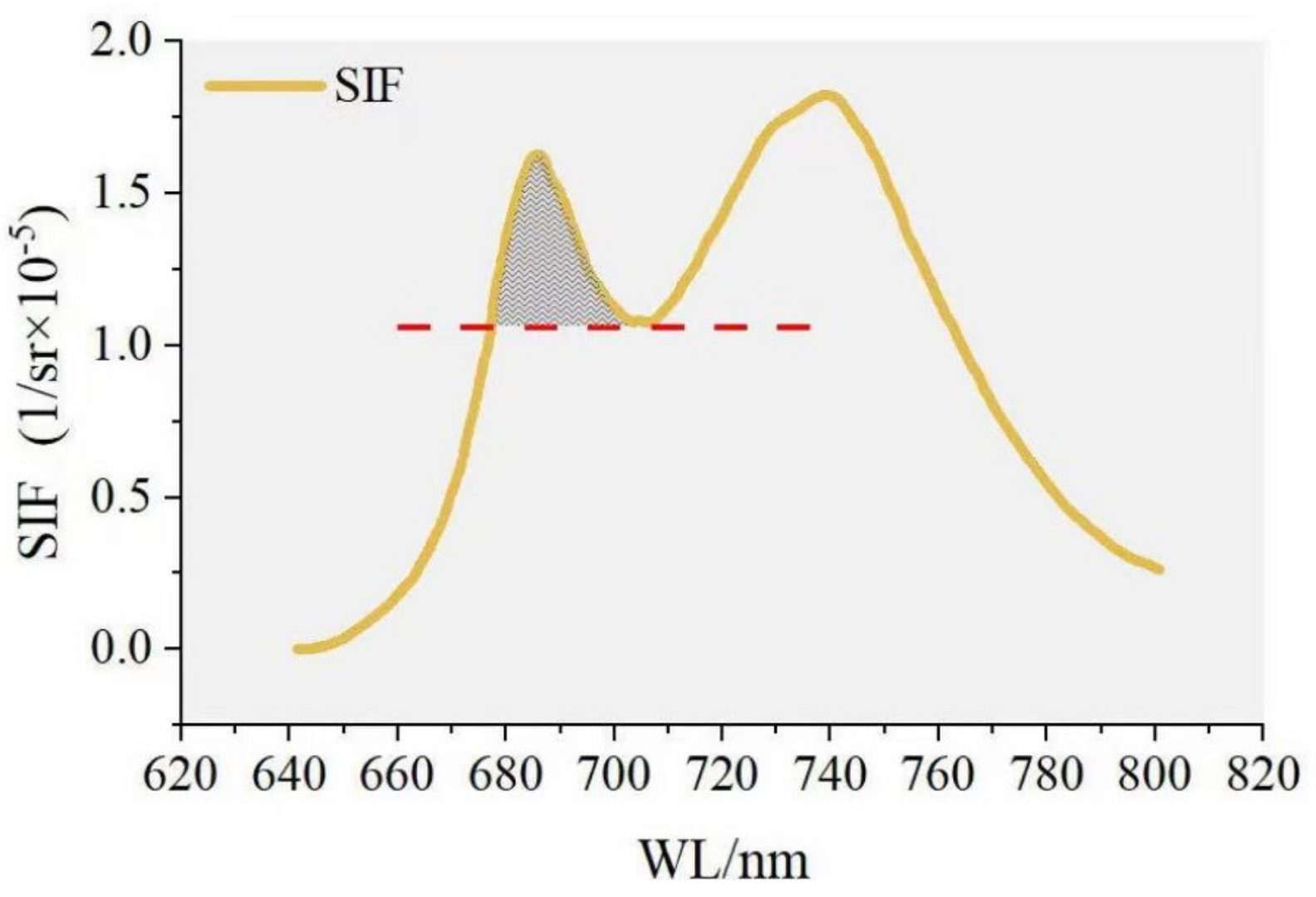
2.5. Modification of SIF_B

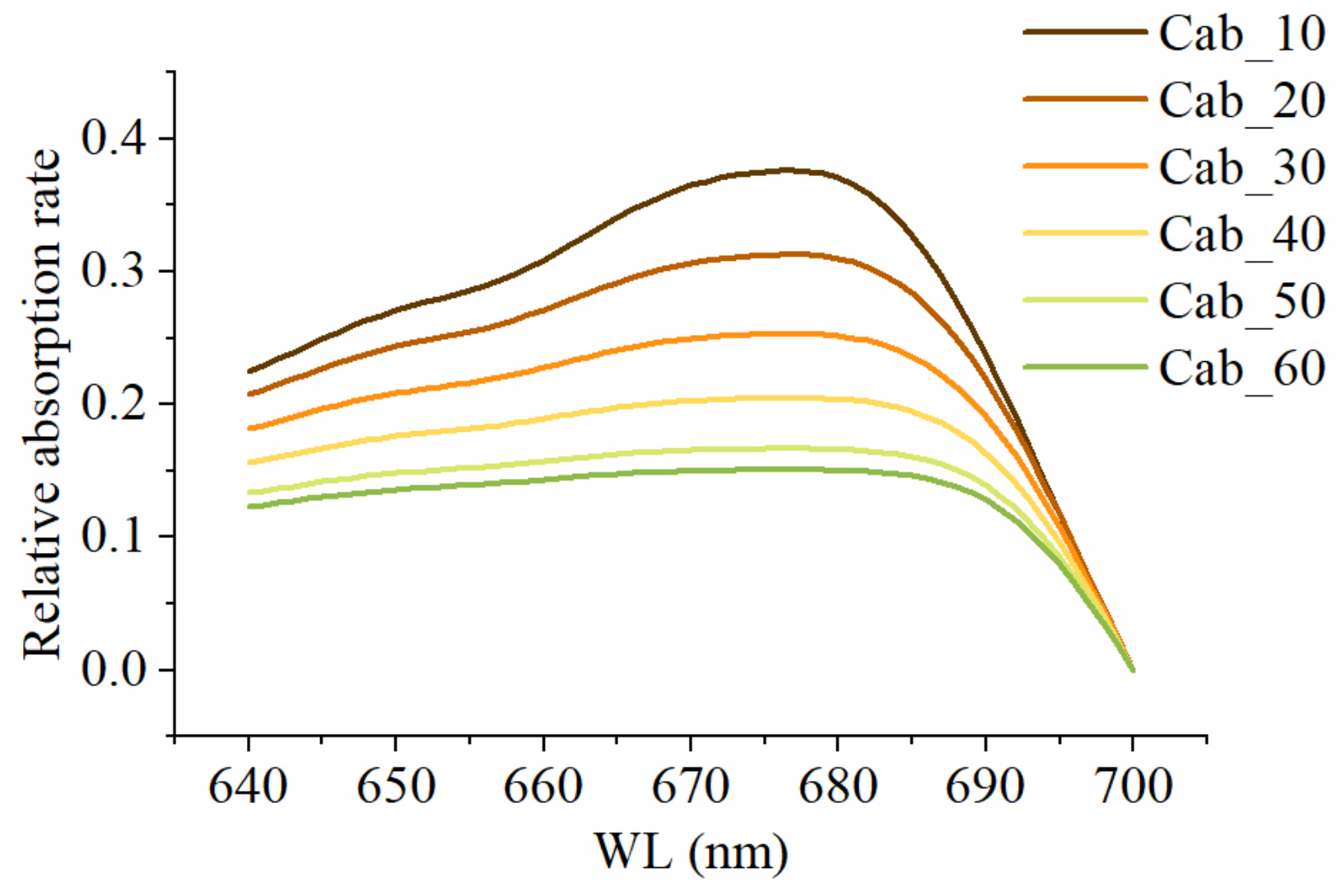
2.5.1. Photosynthetic Physiological Basis of PK_B

To quantitatively investigate the relationship between PK_B and the photosynthetic physiological status of wheat, we employed the SCOPE model to simulate various parameters pertinent to photosynthesis, including PAR, fPAR_chl, CNP, ETR, and NPQ, as well as fesc680. Based on these simulations, we conducted a correlation analysis between PK_B and the aforementioned characteristic parameters (Figure 4) to gain further insight into the physical significance of PK_B.

Figure 4 demonstrates a significant correlation (p < 0.001) between PK_B and key photosynthetic process parameters, including the fraction of PAR absorbed by chlorophyll and the canopy structure parameter, fesc680. Notably, the correlation between PK_B and fPAR_chl was the strongest, with a correlation coefficient of R = −0.83, closely followed by the correlation between PK_B and the ETR at R = −0.74. These findings suggest that the shape feature parameter of PK_B can effectively capture and characterize vegetation photosynthetic information. Additionally, the correlation between PK_B and fesc680 yields a correlation coefficient of R = 0.67, consistent with the theoretical derivation presented in Section 2.4. In summary, PK_B can simultaneously represent photosynthetic capacity (via fPAR_chl) and canopy structure (via fesc680), highlighting its potential as a comprehensive indicator of vegetation photosynthetic status.

2.5.2. Modifying SIF_B by Means of PK_B

Compared with the canopy SIF detected by a sensor, the fluorescence quantum yield (SIF_y)—a parameter closely associated with the physiological status of plants—has been found to provide higher monitoring accuracy for detecting wheat stripe rust severity [10]. The relationship between SIF and SIF_y can be mathematically expressed as follows [32]:

$$\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{y}}=\mathrm{S}\mathrm{I}\mathrm{F}/(\mathrm{f}\mathrm{P}\mathrm{A}\mathrm{R}\times \mathrm{f}\mathrm{e}\mathrm{s}\mathrm{c})$$

(12)

In practical applications, it is difficult to estimate the fesc680 of SIF in the red band under stress conditions [16].

PK_B also has a good correlation with fPAR_chl when characterizing fesc680. Therefore, using PK_B to modify SIF_B can not only reduce the effect of canopy reabsorption and scattering on SIF_B but also weaken the effect of fPAR_chl on SIF_B. Based on this rationale, we propose modifying the canopy directionality SIF_B detected by the sensor, leveraging the expression of fluorescence quantum yield to derive a modified SIF_B (MSIF_B):

$$\mathrm{M}\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}=\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}/\mathrm{P}{\mathrm{K}}_{\mathrm{B}}$$

(13)

2.5.3. Fusing MSIF_B with Vegetation Indices (VIs)

To comprehensively assess the efficacy of MSIF_B in monitoring wheat stripe rust severity, we conducted a detailed analysis of the correlation between MSIF_B, MSIF_B fused with vegetation indices (MSIF_B-VIs), and wheat stripe rust severity. Furthermore, the remote sensing monitoring accuracy for wheat stripe rust was also evaluated.

The normalized difference vegetation index (NDVI) is a valuable tool for characterizing vegetation population biomass [9] and monitoring changes in canopy structure [25]. Widely employed in vegetation area extraction and crop physiological state monitoring, fusing NDVI with MSIF_B (MSIF_B-N) has the potential to mitigate the impact of canopy geometry to a certain extent, enhancing the accuracy of wheat stripe rust monitoring. The expression of this fusion is as follows:

$$\mathrm{M}\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}-\mathrm{N}=\mathrm{M}\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}\times \mathrm{N}\mathrm{D}\mathrm{V}\mathrm{I}$$

(14)

Stripe rust infections significantly alter chlorophyll content in wheat mesophyll cells. Incorporating chlorophyll content parameters can further enhance the monitoring accuracy of SIF_B for stripe rust [9]. The MERIS Terrestrial Chlorophyll Index (MTCI) is highly sensitive to chlorophyll content [33] and is frequently used as an index to estimate chlorophyll content. Fusing MTCI and MSIF_B (MSIF_B-M) can potentially mitigate the effects of chlorophyll reabsorption to some extent [9]. The fused expression is as follows:

$$\mathrm{M}\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}-\mathrm{M}=\mathrm{M}\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}\times \mathrm{M}\mathrm{T}\mathrm{C}\mathrm{I}$$

(15)

Furthermore, we attempted to enhance the correlation between MSIF_B and stripe rust severity after fusing the NDVI and MTCI indices. The resulting expression for the fused index is as follows:

$$\mathrm{M}\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}-\mathrm{N}\mathrm{M}=\mathrm{M}\mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{B}}\times \mathrm{N}\mathrm{D}\mathrm{V}\mathrm{I}\times \mathrm{M}\mathrm{T}\mathrm{C}\mathrm{I}$$

(16)

3. Results

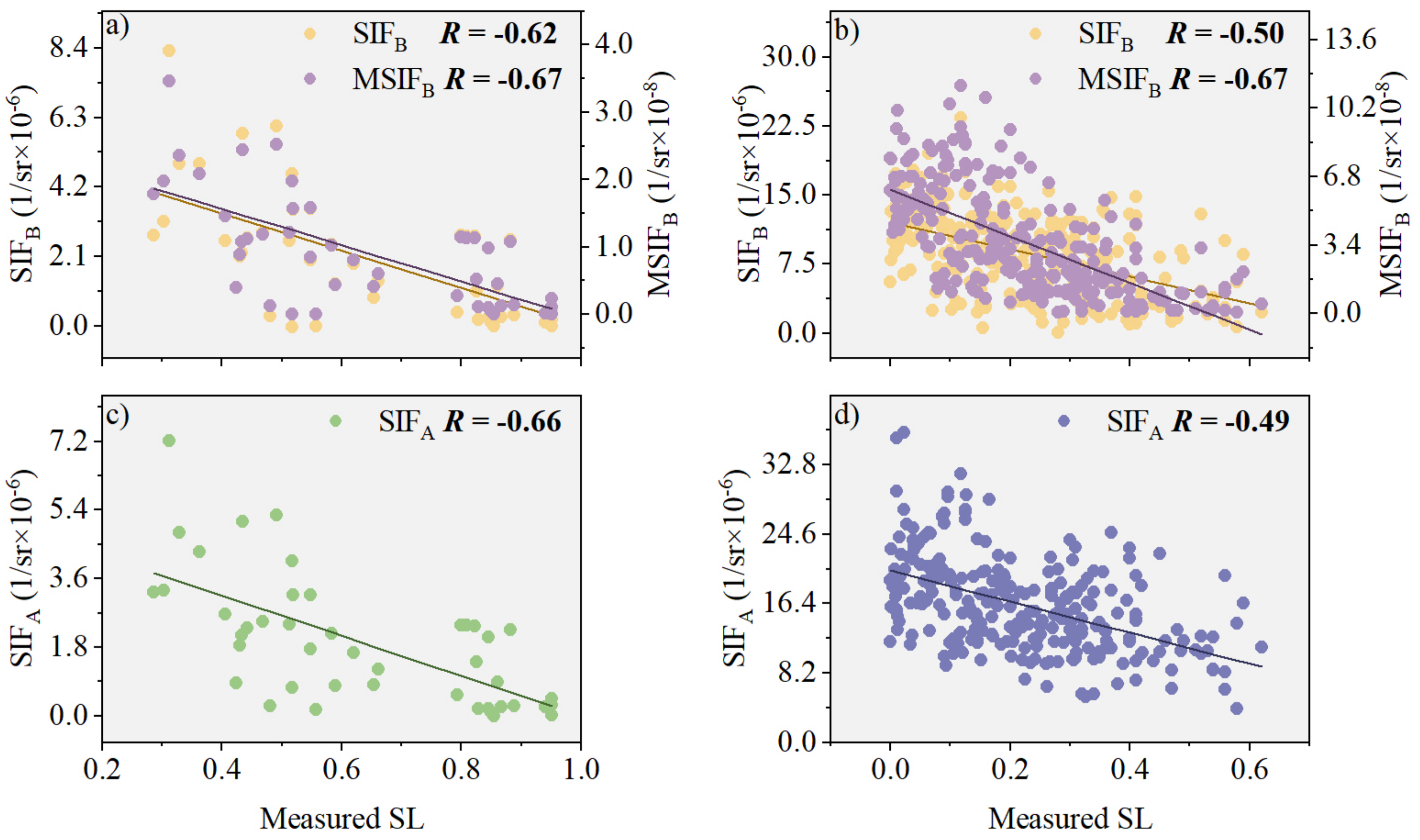
3.1. Performance Evaluation of PK_B Modifying SIF_B

To assess the enhancement effect of the characteristic parameter (PK_B) on canopy SIF_B, we analyzed the correlations between SIF_B and SL, as well as those between MSIF_B and SL, using field-measured data (Figure 5). In the natural disease field experiment, our results indicate that the correlation between MSIF_B and SL increased by 34.00% compared with SIF_B (Figure 5b), which is closely tied to the correlation between PK_B and another factor (assuming that “fesc” is a placeholder for another variable that was not explicitly defined in this context). In contrast to SIF_A, the correlation coefficient (R) for MSIF_B was notably higher, 36.73% above that of SIF_A (Figure 5d). However, in the plot disease field experiment, we observed that the improved correlation between MSIF_B and SL was not significant compared with SIF_B and SIF_A. Specifically, the correlation between MSIF_B and SL increased by only 8.06% compared with SIF_B (Figure 5a) and by a mere 1.52% compared with SIF_A (Figure 5c).

3.2. Performance Evaluation of PK_B Modifying SIF_B-VIs

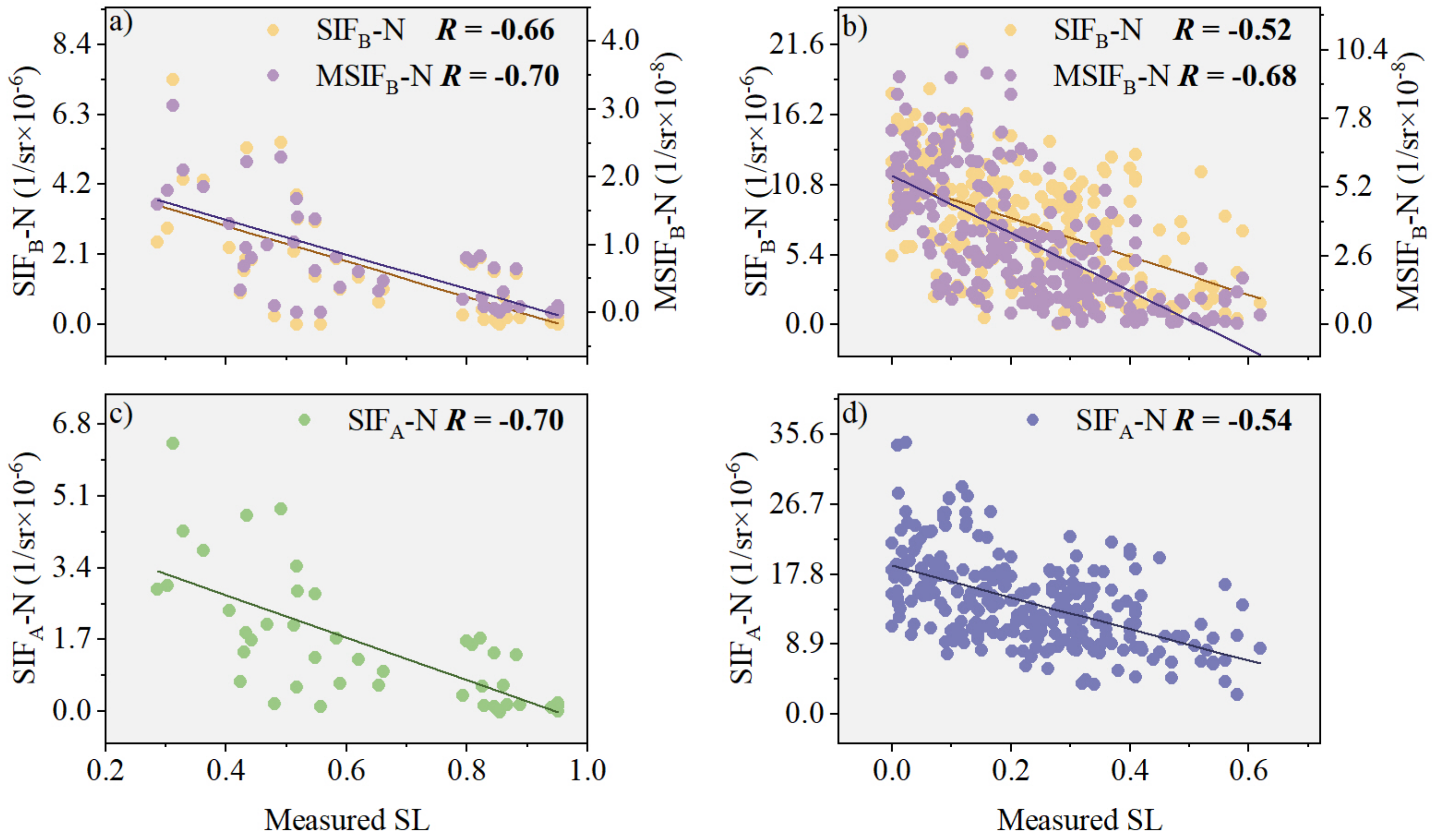
3.2.1. Performance Analysis of MSIF_B-N in Monitoring Wheat Stripe Rust SL

Based on field measurements, we analyzed the correlations between SIF_B-N and stripe rust severity and between MSIF_B-N and SL (Figure 6). Figure 6 demonstrates that the correlation between MSIF_B-N and SL improved to varying degrees in both the natural disease field experiment and the plot disease field experiment. Specifically, in the natural disease field experiment, the correlation between MSIF_B-N and SL increased by 30.77% compared with SIF_B-N (Figure 6a) and by 25.93% compared with SIF_A-N fused with NDVI (Figure 6d). In the plot disease field experiment, the correlation between MSIF_B-N and SL improved by 6.06% compared with SIF_B-N (Figure 6b).

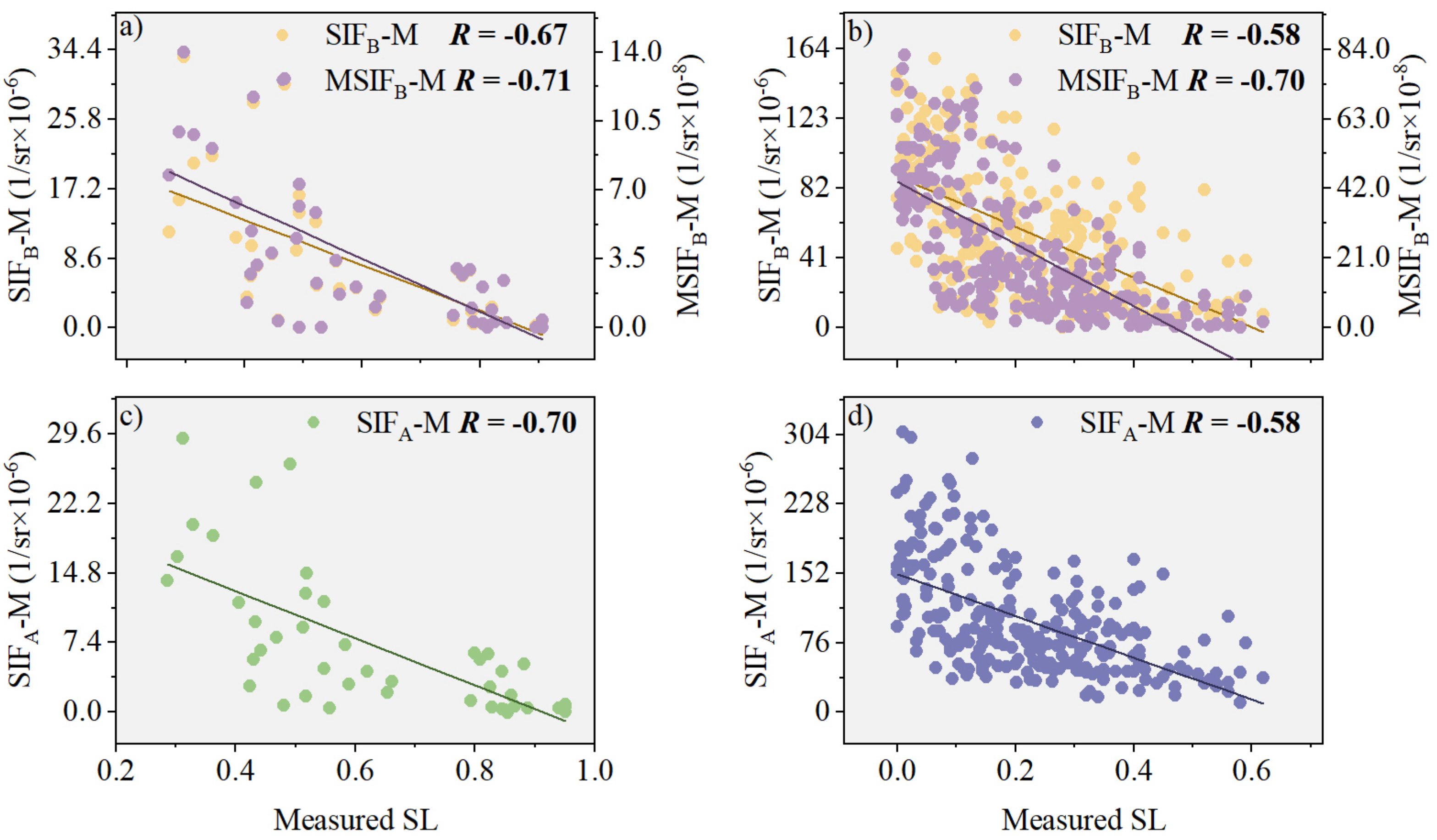
3.2.2. Performance Analysis of MSIF_B-M in Monitoring Wheat Stripe Rust SL

Based on field measurements, we analyzed the correlations between SIF_B-M and stripe rust severity and between MSIF_B-M and SL (Figure 7). Figure 7 shows that in both the natural disease field experiment and the plot disease field experiment, there was a varying degree of improvement in the correlation between MSIF_B-M and SL compared with SIF_B-M. Specifically, in the natural disease field experiment focused on wheat stripe rust, the R between MSIF_B-M and SL increased by 20.69% compared with SIF_B-M and by 20.69% compared with SIF_A-M fused with MTCI (Figure 7b,d). In the plot disease field experiment, the correlation between MSIF_B-M and SL improved by 13.48% compared with SIF_B-M (Figure 7a) and by a relatively modest 1.43% compared with SIF_A-M (Figure 7c).

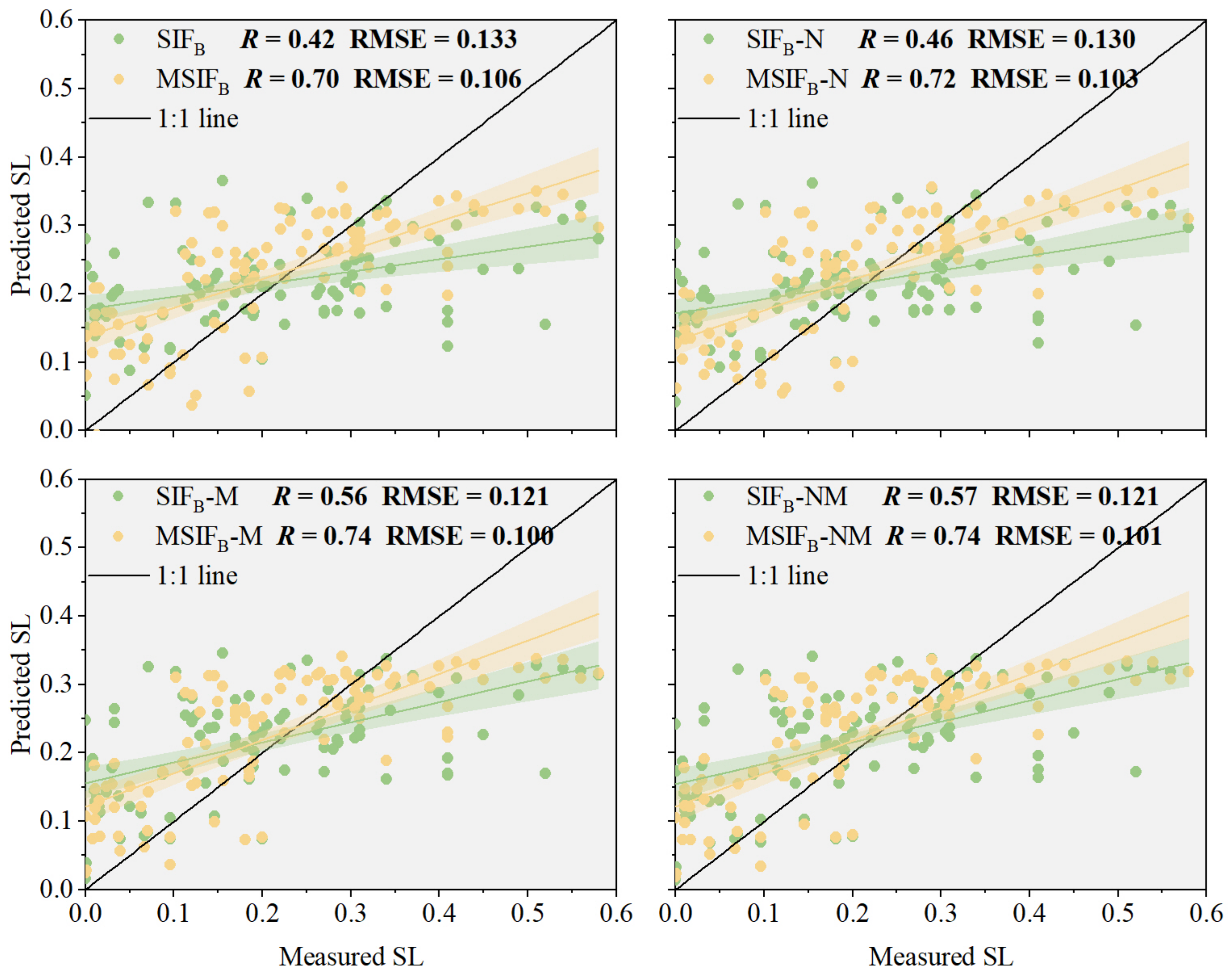
3.2.3. Performance Analysis of MSIF_B-NM in the Monitoring of the Wheat Stripe Rust SL

PK_B shows promising performance in enhancing the efficacy of SIF_B-N and SIF_B-M for monitoring stripe rust severity. We now delve further into improving the correlation between MSIF_B and SL, specifically after fusing the NDVI and MTCI indices. Based on field-measured data, we separately analyzed the correlations of SIF_B-NM and MSIF_B-NM with SL (Figure 8). Figure 8 shows that in both the natural disease field experiment and the plot disease field experiment, there was a varying degree of improvement in the correlation between MSIF_B-NM and SL compared with that for SIF_B-NM. Specifically, in the natural disease field experiment, the correlation between MSIF_B-NM and SL increased by 16.95% compared with those for both SIF_B-NM and SIF_A-NM (Figure 8b). In the plot disease field experiment, we observed that the correlation between MSIF_B-NM and SL improved by 13.48% compared with that for SIF_B-NM (Figure 8a) and by a more modest 1.43% compared with that for SIF_A-NM (Figure 8c).

3.3. Model Evaluation of PK_B for Improved Performance of SIF_B

PK_B can improve the correlation between SIF_B and wheat stripe rust severity. To further assess whether MSIF_B can enhance the accuracy of wheat stripe rust SL monitoring, we compared and analyzed changes in the performance of SIF_B within the wheat stripe rust remote sensing monitoring model before and after applying PK_B.

In the construction and accuracy evaluation of the wheat stripe rust SL model, 253 sample data points were used. These data were divided into a training group of 152 samples and a verification group of 101 samples, adhering to a ratio of 6:4. Subsequently, SIF_B indices, MSIF_B, and MSIF_B-VIs were employed as independent variables to develop the SL estimation model. The performance of this model, as measured by determining the R and RMSE values, is presented in

Table 3. Evaluation of model accuracy.

Independent Variable	R	RMSE
SIFB	0.536	0.133
MSIFB	0.650	0.121
SIFB-N	0.554	0.131
MSIFB-N	0.664	0.118
SIFB-M	0.594	0.128
MSIFB-M	0.671	0.117
SIFB-NM	0.597	0.128
MSIFB-NM	0.667	0.117

.

Table 3 shows that using MSIF_B or MSIF_B-VIs as independent variables results in varying degrees of improvement in model accuracy compared with SIF_B or SIF_B-VIs. Specifically, the wheat stripe rust remote sensing monitoring model constructed with MSIF_B as the independent variable increased by 21.27% in the R between the predicted and measured SL, accompanied by a 9.02% RMSE decrease compared with SIF_B. When fused with NDVI, the model using MSIF_B-N as the independent variable exhibited a 19.86% R increase and a 9.92% RMSE decrease compared with SIF_B-N. Similarly, in the training sample set fused with MTCI, the model with MSIF_B-M as the independent variable showed a 12.69% R increase and an 8.59% RMSE decrease compared with SIF_B-M. Lastly, when fused with both NDVI and MTCI (NDVI*MTCI), the model using MSIF_B-NM as the independent variable demonstrated an R increase of 11.73% and an RMSE decrease of 8.59% compared with SIF_B-NM. There are varying degrees of improvement in model accuracy when using MSIF_B or MSIF_B-VIs as independent variables compared with unrevised SIF_B or SIF_B-VIs.

Using the remaining 101 data points from the modeling as verification samples, we evaluated the ability of PK_B to improve SIF_B in the wheat stripe rust SL monitoring model, and the wheat stripe rust SL prediction model constructed with the MSIF_B method was tested (Figure 9). Figure 9 shows that PK_B significantly enhances the accuracy and robustness of models based on SIF_B and its fusion indices (SIF_B-VIs) in the constructed testing set. Compared with SIF_B, the model established with MSIF_B as the independent variable shows a 66.67% R increase and a 20.30% RMSE decrease when predicting SL. In the testing set fused with NDVI, the model with MSIF_B-N as the independent variable exhibits a 56.52% R increase and a 20.77% RMSE decrease compared with SIF_B-N. Similarly, in the testing set fused with MTCI, the model using MSIF_B-M as the independent variable demonstrates a 32.14% R increase and a 17.36% RMSE decrease compared with SIF_B-M. Lastly, in the testing set fused with both NDVI and MTCI, the model employing MSIF_B-NM as the independent variable shows a 29.82% R increase and a 16.53% RMSE decrease compared with SIF_B-NM when predicting SL. Notably, the increased accuracy of the wheat stripe rust severity estimation model over SIF_B-NM when using MSIF_B-NM as the independent variable is the smallest compared with other MSIF_B-VIs. This can be attributed to the fact that NDVI represents vegetation biomass, which is inherently linked to chlorophyll content; conversely, MTCI is a vegetation index specifically tailored to quantifying chlorophyll content. The combination of these two indices may result in information redundancy, contributing to the relatively modest enhancement in model accuracy.

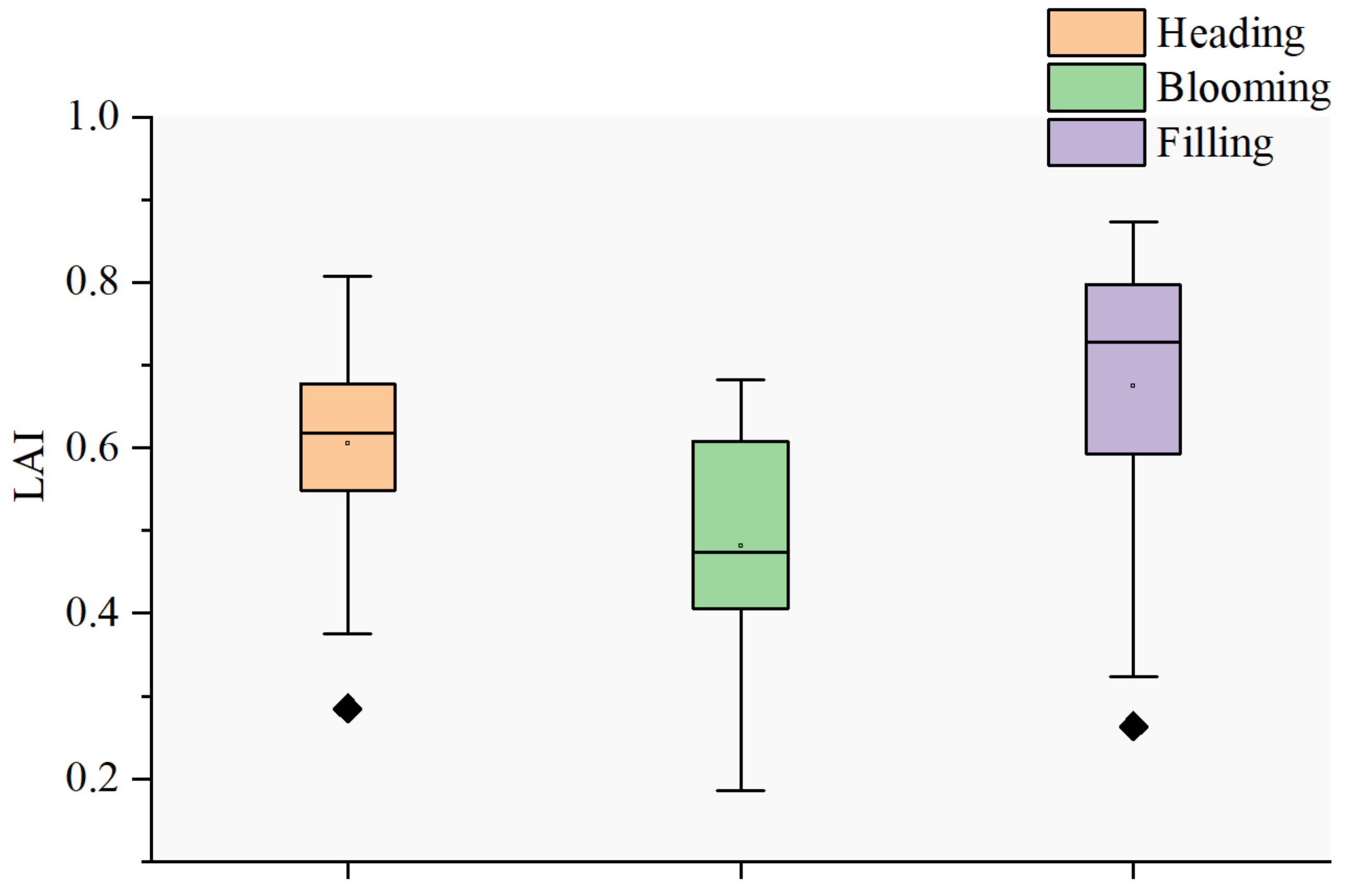
3.4. Changes in SL, SIF_B, MSIF_B, and C_ab with Growth Period

Clarifying the influence of the wheat growth period on SIF_B is crucial for tracking the degree of disease stress using MSIF_B [34]. Figure 10 illustrates the changes in SIF_B (Figure 10b), MSIF_B (Figure 10c), and C_ab (Figure 10d) under both healthy (Figure 10a) and diseased conditions from the heading to filling stages. As the wheat plant develops, the specific leaf area increases, and the rate of increase becomes more pronounced (Figure 10a). Under healthy conditions, the SIF_B of wheat generally increases with development, whereas the SIF_B of wheat affected by stripe rust remains relatively unchanged throughout the growth period (Figure 10b). Similarly, the C_ab of healthy wheat modestly increases over time, whereas the C_ab of stripe rust-infected wheat exhibits an insignificant decrease overall (Figure 10d). In contrast to SIF_B and C_ab, MSIF_B does not significantly vary with wheat development under healthy conditions, and under the influence of stripe rust, it further decreases with growth (Figure 10c). This suggests that the physiological changes in vegetation associated with the growth period are not readily reflected in MSIF_B, making it a potentially useful indicator for distinguishing between healthy and disease-stressed wheat plants.

4. Discussion

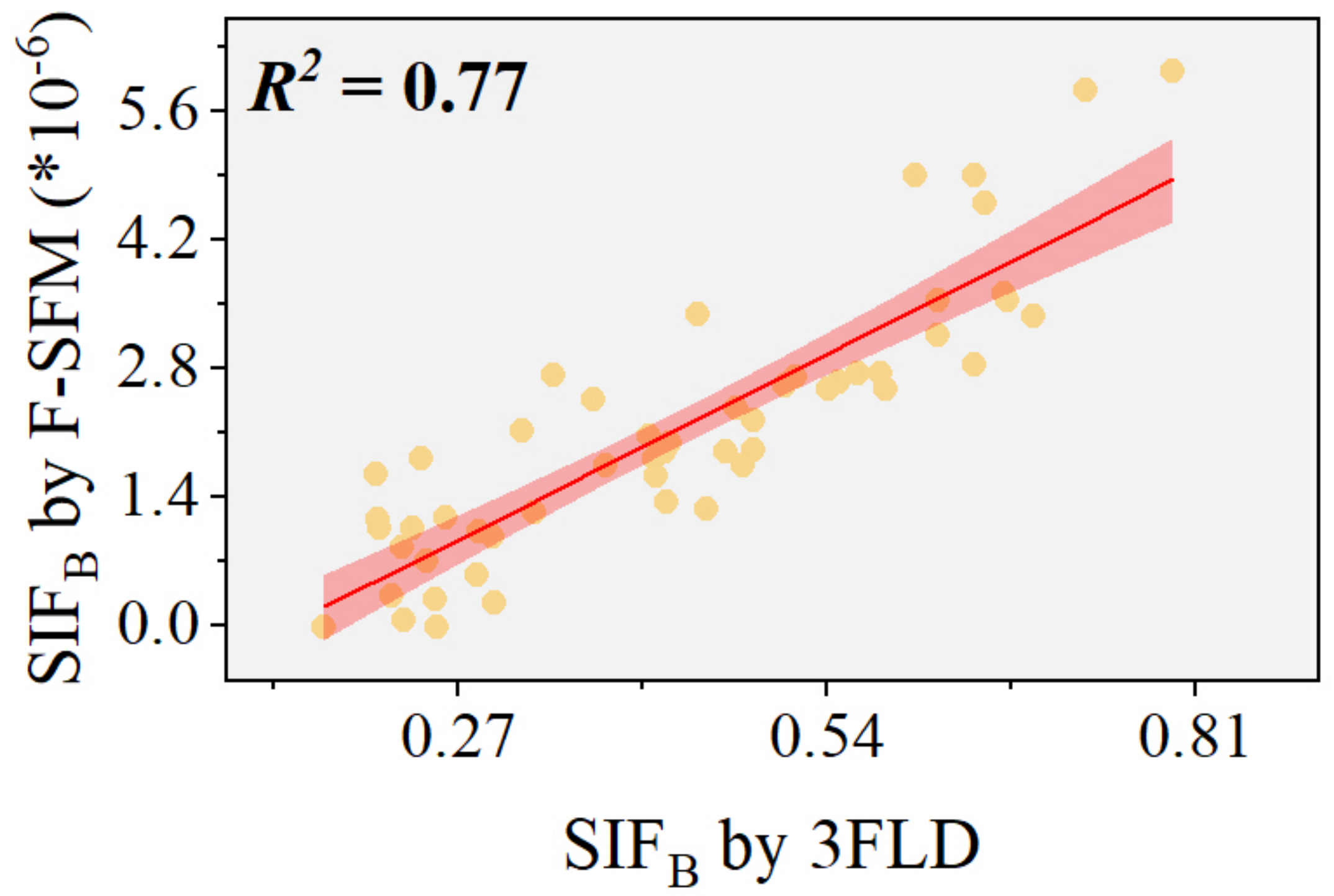
4.1. The Accuracy of F-SFM in Calculating PK_B

The accuracy of the modified SIF_B based on PK_B significantly relies on the precision of extracting full-band SIF values. The F-SFM algorithm has demonstrated exceptional retrieval accuracy within the 650–770 nm range, which encompasses the peak emission band of the red spectrum [27,35]. In the presence of atmospheric effects, the F-SFM algorithm continues to outperform other bands within this spectral range [35]. When operating under conditions with a high signal-to-noise ratio (SNR) of 1000:1 and a spectral resolution (SR) of 0.30 nm, the F-SFM algorithm typically exhibits a low root mean square error, which is sufficient for instruments like the QE-Pro spectrometer [27]. Additionally, except for a slightly decreased accuracy at a VZA of 25°, the F-SFM algorithm maintains a high retrieval accuracy across various VZAs, making it suitable for standard remote sensing observations. However, the overall full-spectrum retrieval accuracy of SIF is contingent upon the representativeness of the training dataset used. Consequently, we modified the training set for the F-SFM algorithm to better suit the retrieval of SIF under stress conditions. In general, this algorithm is well suited for our study. Furthermore, recent advancements in full-spectrum SIF inversion algorithms [35,36] have laid a foundation for the high-precision extraction of PK_B, further enhancing the potential of this research approach.

Research has shown that the 3FLD algorithm can effectively retrieve SIF_B measured by the QE-pro spectrometer [27]. To further validate the accuracy of the F-SFM algorithm after refining its training set, we conducted an analysis using experimental data from controlled wheat rust plots. We employed red SIF retrieved by the 3FLD algorithm as a benchmark reference (Figure 11). We found an R² value of 0.77 between the SIF_B values obtained by the F-SFM algorithm and those from the 3FLD algorithm, indicating a robust correlation and confirming the precision of the adjusted F-SFM algorithm in extracting SIF_B from experimental data.

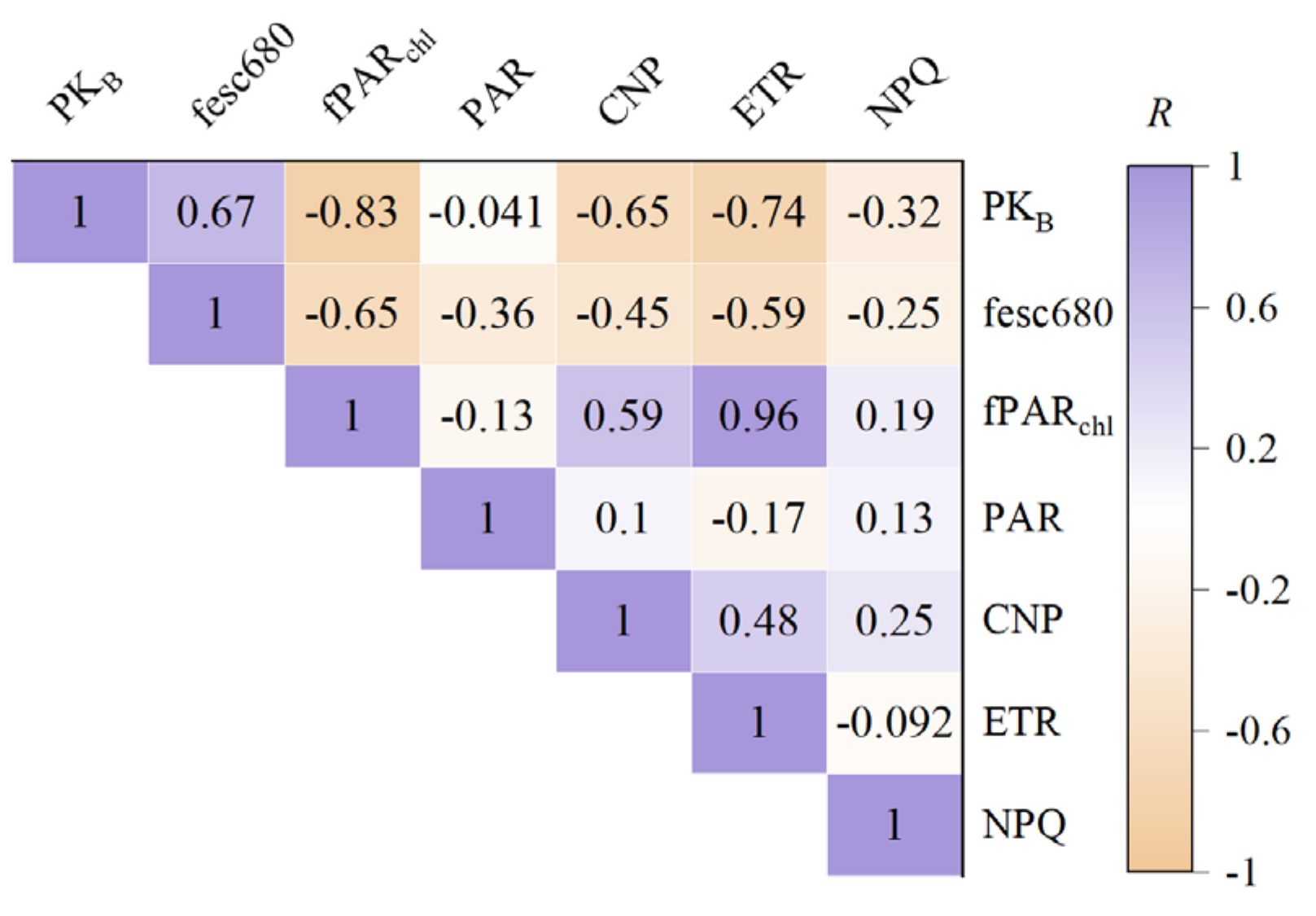
4.2. Physiological Mechanism of MSIF_B Improving Remote Sensing Monitoring of Wheat Stripe Rust

The experimental data show that PK_B, as an improved canopy SIF_B parameter, can effectively improve the correlation between SIF_B and SL and the estimation accuracy of wheat stripe rust. The observed SIF can be divided into three influencing factors: absorbed PAR (aPAR), fesc, and SIF_y (Equation (17)). Stripe rust mainly affects the biochemical components of vegetation, causing changes in SIF_y, and it is thus more closely related to SIF_y. PK_B can simultaneously weaken the effects of canopy reabsorption and scattering on SIF_B, characterizing SL to a greater extent.

$$\mathrm{S}\mathrm{I}\mathrm{F}=\mathrm{a}\mathrm{P}\mathrm{A}\mathrm{R}\times \mathrm{S}\mathrm{I}{\mathrm{F}}_{\mathrm{y}}\times \mathrm{f}\mathrm{e}\mathrm{s}\mathrm{c}$$

(17)

As a source of energy in photochemical reactions, aPAR_chl has a strong effect on SIF_B. Studies have shown that the effective light use efficiency of canopy fluorescence (LUE_f) can more accurately capture the dynamic response of vegetation under stress conditions [37], explaining both the fluorescence quantum yield and proportion of emitted photons that escape from the canopy [17]. LUE_f is defined as

$$\mathrm{L}\mathrm{U}{\mathrm{E}}_{\mathrm{f}}=\mathrm{S}\mathrm{I}\mathrm{F}/(\mathrm{f}\mathrm{P}\mathrm{A}\mathrm{R}\times \mathrm{P}\mathrm{A}\mathrm{R})$$

(18)

The analysis in Section 3.2 showed that the relationship between fPAR_chl and PK_B can be obtained as follows:

$$\mathrm{P}{\mathrm{K}}_{\mathrm{B}}\sim \mathrm{f}{\mathrm{PAR}}_{\mathrm{chl}}$$

(19)

The results of [28] showed that fPAR_chl can be expressed as a linear function of fPAR:

$$\mathrm{f}\mathrm{P}\mathrm{A}{\mathrm{R}}_{\mathrm{chl}}=\mathrm{k}\times \mathrm{f}\mathrm{P}\mathrm{AR}$$

(20)

Therefore, PK_B has an approximate relationship with fPAR:

$$\mathrm{P}{\mathrm{K}}_{\mathrm{B}}\sim \mathrm{f}\mathrm{P}\mathrm{A}\mathrm{R}$$

(21)

When using PK_B to improve SIF_B, MSIF_B is similar to LUE_f, which can more accurately capture the dynamic response of vegetation under stress conditions [37].

Fluorescence emission intensity is jointly determined by PSI and PSII. PSII is the photoreaction stage, absorbing light energy to split water and generate energy, which is subsequently utilized by PSI for the dark reaction. Notably, the fluorescence emitted by PSII is usually the dominant signal [25], with an emission wavelength range of 640 nm to 800 nm. By contrast, the fluorescence energy emitted by PSI is lower, and its emission is primarily concentrated at 700 nm to 750 nm [38]. Therefore, changes in SIF_B can be attributed to PSII alone. In other words, only the fluorescence of PSII varies with photochemical changes [13]. The strong correlation between PK_B and fesc680 brings MSIF_B closer to the PS-level SIF. This allows the SIF emitted by PSII to be better expressed, which is more closely associated with photochemical changes and can more accurately reflect the SL.

The above analyses indicate that PK_B, an indicator highly correlated with fPAR_chl and fesc680, can simultaneously reduce the impact of canopy radiative transfer and fPAR_chl on SIF_B, resulting in MSIF_B being closer to SIF_y.

4.3. Analysis of the Correlation between MSIF_B and the SL Improved by VIs

VIs can effectively complement the incomplete weakening of canopy structure and chlorophyll reabsorption caused by MSIF_B (Figure 12). Therefore, incorporating NDVI—which sensitively reflects changes in canopy structure—and the MTCI—closely related to chlorophyll content [9,25]—with MSIF_B can further mitigate the impact of the canopy structure and chlorophyll reabsorption on SIF_B. In our natural disease field experiment on wheat stripe rust disease, adding VIs improved the correlation between MSIF_B and SL to some extent (Figure 7). The MTCI significantly enhanced the correlation between MSIF_B and SL. The R-value between MSIF_B-M and SL increased by 4.48% compared with MSIF_B alone, indicating that the MTCI can better complement the incomplete effect of PK_B in mitigating the canopy chlorophyll reabsorption on SIF_B. However, compared with the individual MTCI, the combination of NDVI and MTCI showed a lower correlation enhancement between MSIF_B and SL because both NDVI and MTCI can represent chlorophyll content to a certain extent. They may provide similar or overlapping information and introduce errors. These results indirectly demonstrate that the primary factor influencing SIF_B is the chlorophyll reabsorption effect of vegetation.

4.4. Effect of Growth Period

If not prevented and controlled, rust disease severity will worsen with the development of wheat [39], as evident in Figure 10a. In healthy wheat, C_ab, SIF_B, and MSIF_B exhibit similar changes alongside wheat development (Figure 10b–d), consistent with temporal changes in chlorophyll content and aPAR observed in numerous studies [40,41]. However, under rust stress, the consistency of SIF_B changes that come with wheat development is disrupted (Figure 10b,d), attributable to the rust pathogen altering the open ratio of PSII reaction centers. Reactive oxygen species (ROS) play a pivotal role in regulating plant immune defense [42]. Low ROS concentrations can activate immune-related gene expression [43], whereas high ROS concentrations can inactivate pathogens [44]. Producing ROS decreases the expression of genes related to photosynthesis [45], explaining the reduction in C_ab observed under rust infection.

When infected by stripe rust, MSIF_B changes more regularly with the growth period under the influence of PK_B, showing an opposite trend from SL and the same trend as C_ab (Figure 10b–d). Therefore, PK_B can eliminate the growth period effects on SIF_B in wheat stripe rust monitoring.

Our results indicate that the PK_B’s performance in modifying SIF_B varied across field experiments. Specifically, PK_B exhibited higher performance in natural disease field experiments than in plot disease field experiments. The measurement times for the plot disease field experiment were 15, 18, 24, and 30 May 2018, when wheat was in the filling stage. However, the measurement times for the natural disease field experiment were 16, 17, 28, 29, and 30 April and 12 and 13 May 2021, covering the wheat heading, blooming, and filling stages. The canopy structure of crops changes with their development [46], and there are significant differences in the LAI at different growth stages (Figure 13). The natural disease field experiment encompassed more changes in canopy structure than the plot disease field experiment. Therefore, the ability of PK_B to attenuate the effects of canopy reabsorption and scattering on SIF_B is more pronounced in natural disease field experiments.

4.5. Prospect

Because the stripe rust pathogen primarily affects the photosynthetic ability of wheat, the close relationship between SIF_B and vegetation photosynthetic physiology, as well as canopy structure, renders it a valuable tool for detecting diseases that impact wheat photosynthesis. Therefore, the ability of PK_B to improve the correlation between SIF_B and SL is expected to apply to monitoring a wider range of disease stresses. Furthermore, based on the physiological mechanism analysis of PK_B presented in this study, we anticipate that the ability of PK_B to modify SIF_B will further enhance the relationship between SIF_B and GPP, although this hypothesis requires validation with actual data.

5. Conclusions

Based on the F-SFM full-spectrum SIF inversion algorithm, we extracted the shape feature parameter (PK_B) associated with SIF_B. By analyzing the correlation between PK_B and parameters such as photosynthetic physiology and canopy structure, we could utilize PK_B to refine SIF_B. We evaluated the performance of the MSIF_B in monitoring wheat stripe rust using field experiment data. The results show that, whether single-band SIF_B or SIF_B-VIs, PK_B can improve the correlation between SIF_B and SL and enhance the accuracy of wheat stripe rust remote sensing monitoring. Its effectiveness and robustness were validated through field experiments with natural disease conditions and plot-based disease field experiments.