Characteristics of Rain and Sea Spray Droplet Size Distribution at a Marine Tower
Abstract
:1. Introduction
2. Methods
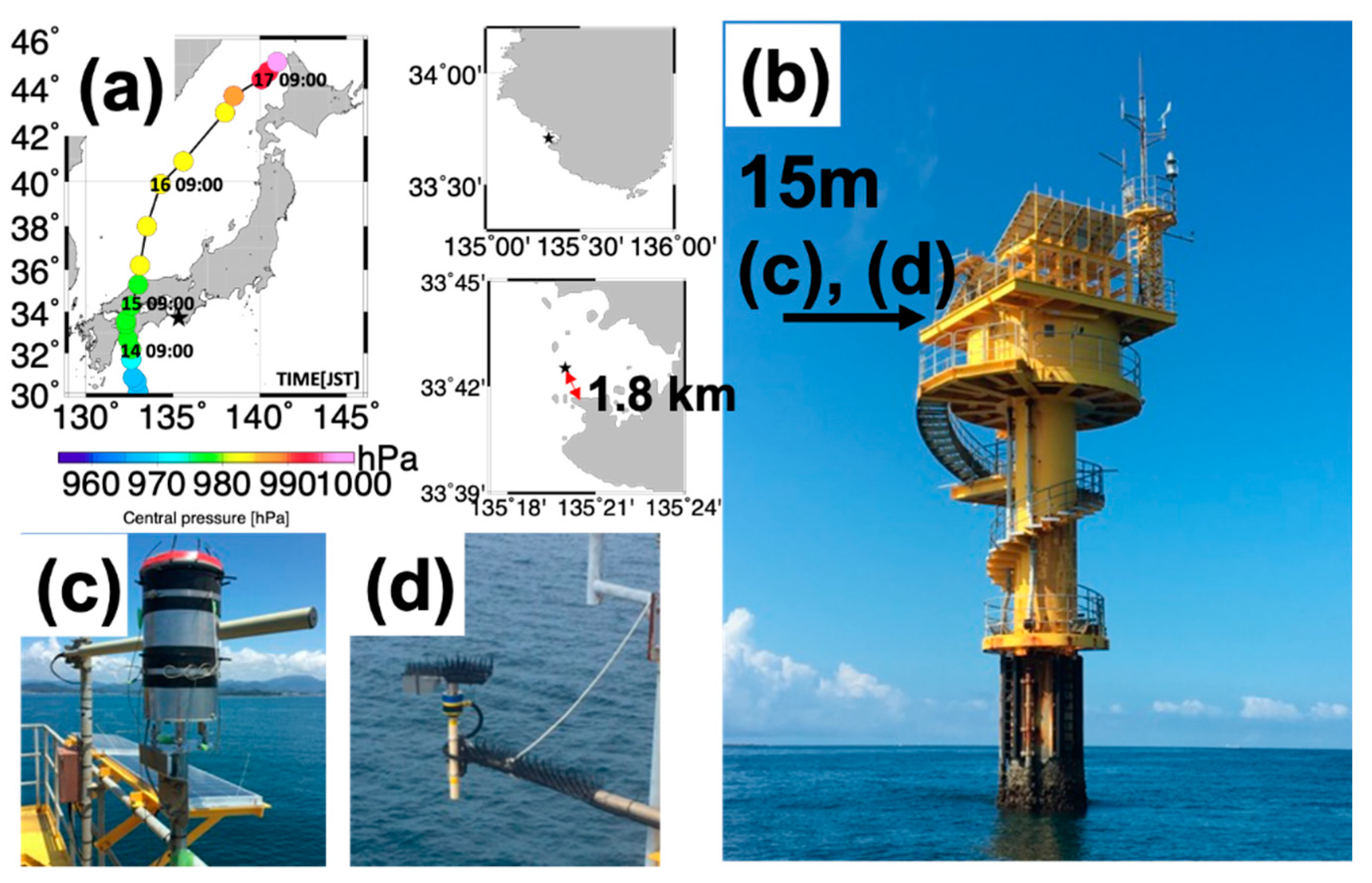
2.1. Site and Data Collection
2.2. Disdrometer
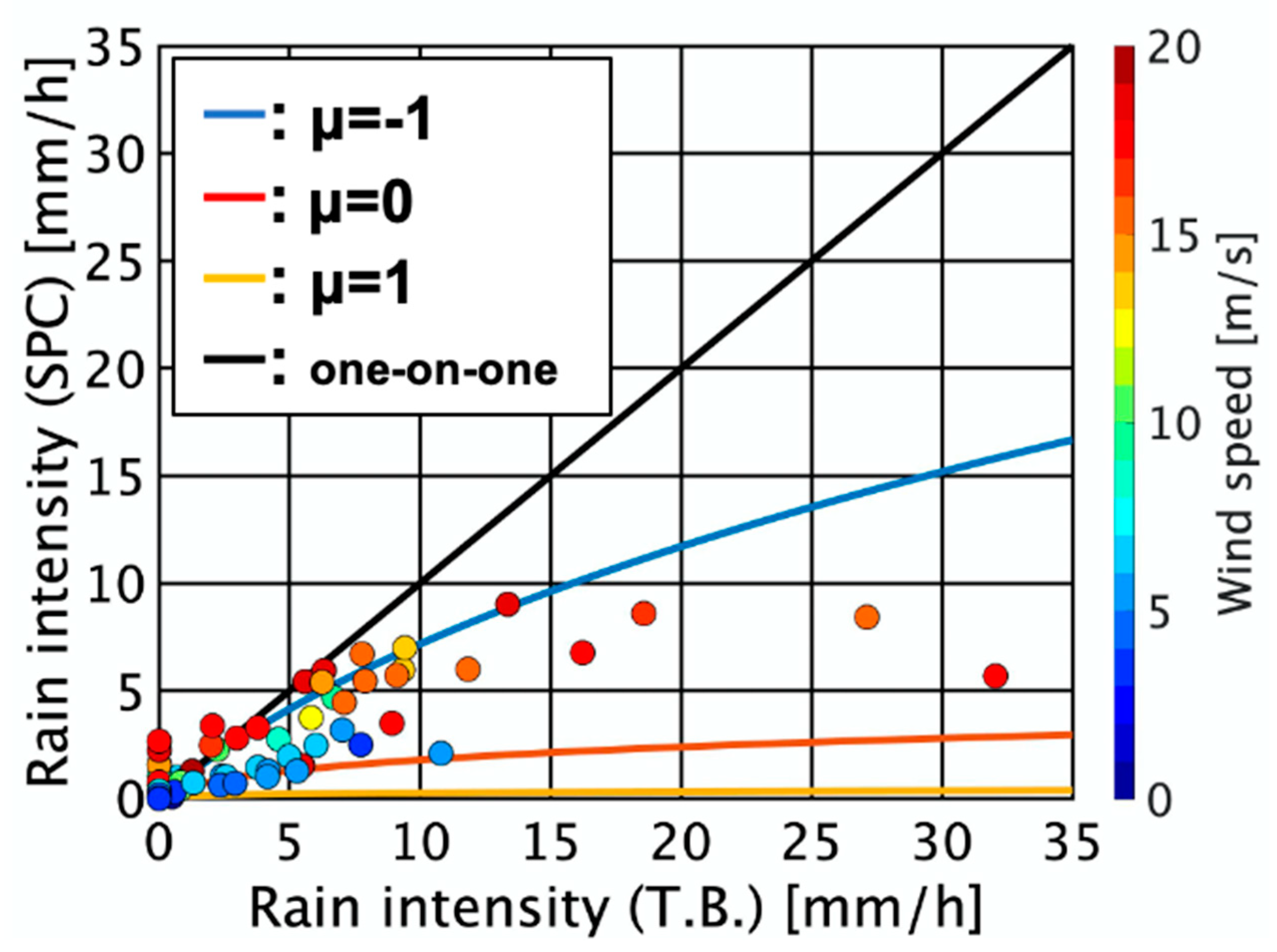
2.3. Data Correction for Tipping Bucket
2.4. Estimation Methods
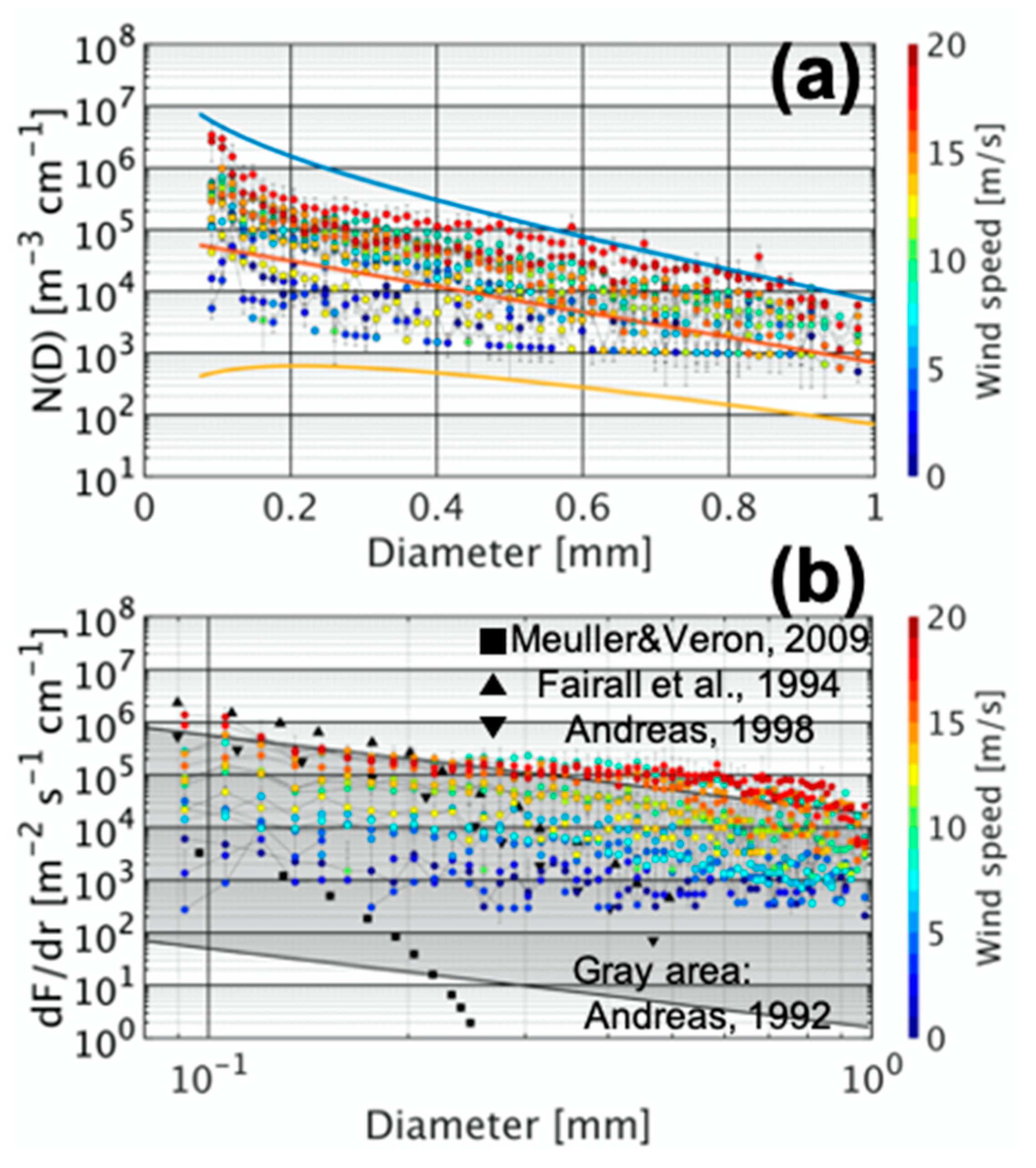
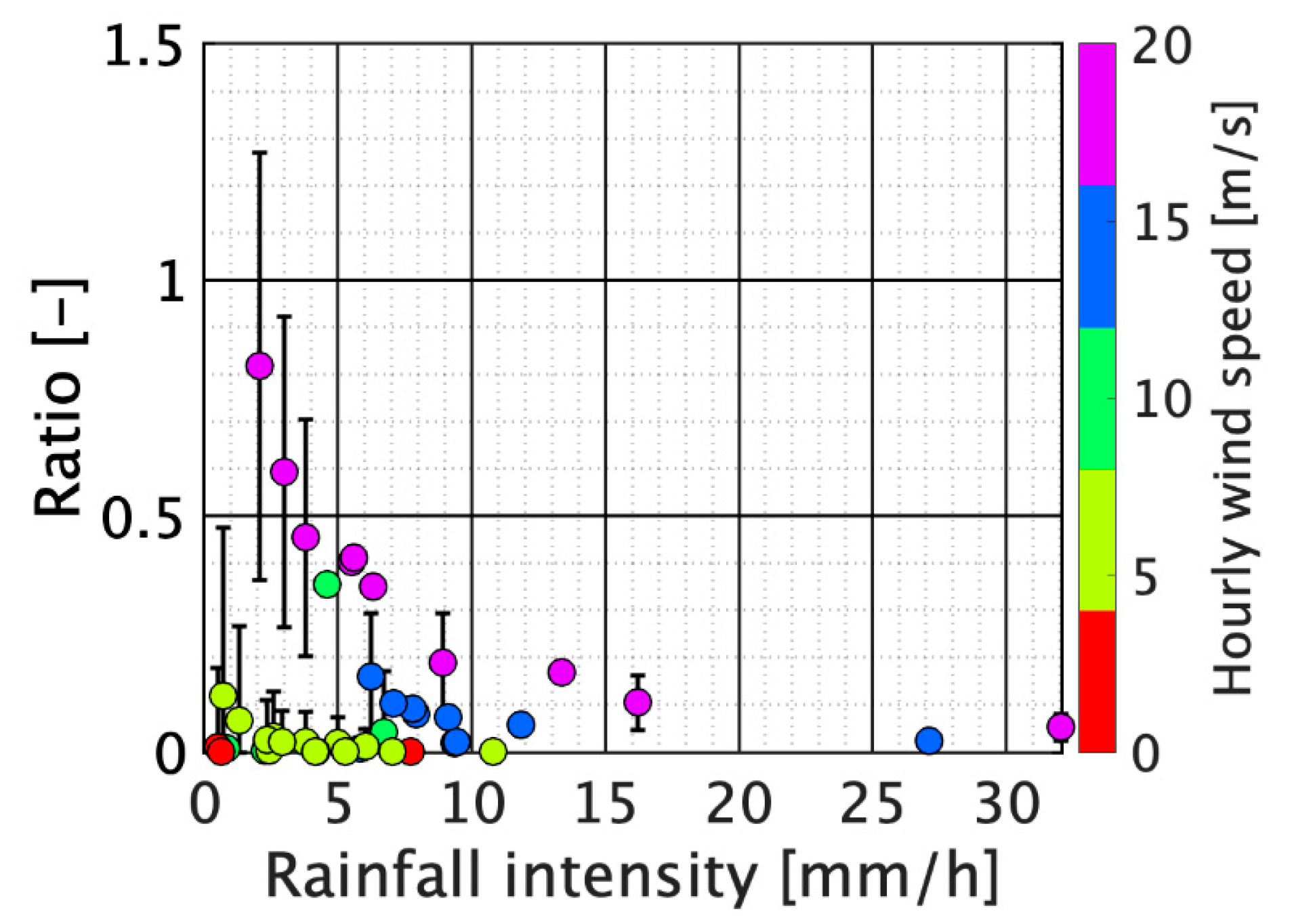
3. Results and Discussion
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yuter, S.E.; Parker, W.S. Rainfall measurement on ship revisited: The 1997 PACS TEPPS cruise. J. Appl. Meteorol. 2001, 40, 1003–1018. [Google Scholar] [CrossRef]
- Yuter, S.E.; Houze, R.A., Jr. The 1997 pan American climate studies tropical Eastern Pacific process study. Part I: ITCZ region. Bull. Am. Meteorol. Soc. 2000, 81, 451–481. [Google Scholar] [CrossRef]
- Bumke, K.; Fenning, K.; Strehz, A.; Mecking, R.; Schröder, M. HOAPS precipitation validation with ship-borne rain gauge measurements over the Baltic Sea. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 18486. [Google Scholar] [CrossRef]
- Hasse, L.; Grosskalaus, M.; Uhlig, K.; Timm, P. A ship rain gauge for use in high wind speeds. J. Atmos. Ocean. Technol. 1998, 15, 380–386. [Google Scholar] [CrossRef] [Green Version]
- Skaar, J. On the measurement of precipitation at sea. Geophys. Publ. 1955, 19, 1–32. [Google Scholar]
- Yamamoto, H.; Sakamoto, K.; Iwaya, K.; Kawamoto, E.; Nasu, M.; Watanabe, Y. Characteristics of meteorological and salt damage by Typhoon No.24 in 2018 (Trami). J. JSNDS 2019, 37, 365–382. (In Japanese) [Google Scholar]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef]
- Andreas, E.L. Spray stress revisited. J. Phys. Oceanogr. 2004, 34, 1429–1440. [Google Scholar] [CrossRef]
- Andreas, E.L.; Mahrt, L.; Vickers, D. An improved bulk air–sea surface flux algorithm, including spray-mediated transfer. Quart. J. R. Meteor. Soc. 2015, 141, 642–654. [Google Scholar] [CrossRef]
- Caldwell, D.R.; Elliot, W.P. Surface stresses produced by rainfall. J. Phys. Ocenogr. 1971, 1, 145–148. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, D.R.; Elliot, W.P. The effect of rainfall on the wind in the surface layer. Bound.-Layer Meteor. 1972, 3, 146–151. [Google Scholar] [CrossRef]
- Doviak, R.; Zrnić, D.S. Doppler Radar and Weather Observations; Courier Corporation: North Chelmsford, MA, USA, 2006; pp. 219–235. [Google Scholar]
- Marshall, J.S.; McK, P.W. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Auf der Maur, A.N. Statistical tools for drop size distribution: Moments and generalized gamma. J. Atmos. Sci. 2001, 58, 407–418. [Google Scholar] [CrossRef]
- Lee, G.; Zawadzki, I.; Szyrmer, W.; Sempere-Torres, D.; Uijlenhoet, R. A general approach to double-moment normalization of drop size distributions. J. Appl. Meteorol. 2004, 43, 264–281. [Google Scholar] [CrossRef] [Green Version]
- Thurai, M.; Bringi, V.N. Application of the generalized gamma model to represent the full rain drop size distribution spectra. J. Appl. Meteorol. Climatol. 2018, 57, 1197–1210. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variation in the analytical form of the raindrop size distribution. J. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef] [Green Version]
- Serio, M.A.; Carollo, F.G.; Ferro, V. Raindrop size distribution and terminal velocity for rainfall erosivity studies. A review. J. Hydrol. 2019, 276, 210–228. [Google Scholar] [CrossRef]
- Adetan, O.; Afullo, T.J. Raindrop size distribution and rainfall attenuation modeling in equatorial and subtropical Africa: The critical diameters. Ann. Telecommun. 2014, 69, 607–619. [Google Scholar] [CrossRef]
- Blanchard, D.C. Raindrop size-distribution in Hawaiian rains. J. Meteor. 1953, 10, 457–473. [Google Scholar] [CrossRef] [Green Version]
- Hachani, S.; Boudevillain, B.; Delrieu, G.; Bargaoui, Z. Drop size distribution climatology in Cévennes-Vivarais region, France. Atmosphere 2017, 8, 233. [Google Scholar] [CrossRef] [Green Version]
- Monahan, C.M. Sea spray as a function of low elevation wind speed. J. Geophys. Res. 1968, 73, 1127–1137. [Google Scholar] [CrossRef]
- Marks, R. Preliminary investigations on the influence of rain on the production, concentration, and vertical distribution of sea salt aerosol. J. Geophys. Res. Oceans 1990, 95, 22299–22304. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bertotti, L.; Bidlot, J.-R. Waving in the rain. J. Geophys. Res. Oceans 2015, 120, 3248–3260. [Google Scholar] [CrossRef]
- Lewis, E.R.; Schwartz, S.E. Sea Salt Aerosol Production Mechanisms, Methods, Measurements and Models, a Critical Review. Geophys. Monogr. 2004, 152, 71–74. [Google Scholar]
- Callaghan, A.H. An improved whitecap timescale for sea spray aerosol production flux modeling using the discrete whitecap method. J. Geophys. Res. Atmos. 2013, 118, 9997–10010. [Google Scholar] [CrossRef]
- Norris, S.J.; Brooks, I.M.; Hill, M.K.; Brooks, B.J.; Smith, M.H.; Sproson, D.A. Eddy covariance measurements of the sea spray aerosol flux over the open ocean. J. Geophys. Res. Atmos. 2012, 117, D07210. [Google Scholar] [CrossRef]
- Salter, M.E.; Nilsson, E.D.; Butcher, A.; Bilde, M. On the seawater temperature dependence of the sea spray aerosol generated by a continuous plunging jet. J. Geophys. Res. Atmos. 2014, 119, 9052–9072. [Google Scholar] [CrossRef] [Green Version]
- Markuszewski, P.; Klusek, Z.; Nilsson, E.D.; Petelski, T. Observations on relations between marine aerosol fluxes and surface-generated noise in the southern Baltic Sea. Oceanologia 2020, 62, 413–427. [Google Scholar] [CrossRef]
- Veron, F. Ocean spray. Annu. Rev. Fluid Mech. 2015, 47, 507–538. [Google Scholar] [CrossRef]
- Andreas, E.L. The temperature of evaporating sea spray droplets. J. Atmos. Sci. 1995, 52, 852–862. [Google Scholar] [CrossRef] [Green Version]
- Gelfand, B.E. Droplet breakup phenomena in flows with velocity lag. Energy Combust. Sci. 1996, 22, 201. [Google Scholar] [CrossRef]
- Andreas, E.L. Sea spray and the turbulent air-sea heat fluxes. J. Geophys. Res. 1992, 97, 11429–11441. [Google Scholar] [CrossRef]
- Ortiz-Suslow, D.G.; Haus, B.K.; Mehta, S.; Laxague, N.J. Sea spray generation in very high winds. J. Atmos. Sci. 2016, 73, 3975–3995. [Google Scholar] [CrossRef]
- Mueller, J.A.; Veron, F. A sea state–dependent spume generation function. J. Phys. Oceanogr. 2009, 39, 2363–2372. [Google Scholar] [CrossRef]
- Fairall, C.W.; Kepert, J.D.; Holland, G.J. The effect of sea spray on surface energy transports over the ocean. Glob. Atmos. Ocean. Syst. 1994, 2, 121–142. [Google Scholar]
- Andreas, E.L. A new sea spray generation function for wind speeds up to 32 m s−1. J. Phys. Oceanogr. 1998, 28, 2175–2184. [Google Scholar] [CrossRef] [Green Version]
- Kimura, T.; Maruyama, T.; Ishimaru, T. SPC-III no sekkei to seisaku. Proc. Cold Reg. Technol. Conf. 1993, 665–670. (In Japanese) [Google Scholar]
- Japan Meteorological Agency (JMA). Available online: http://www.jma.go.jp/en/amedas (accessed on 5 November 2020).
- Schmidt, R.A. A system that measures blowing snow. USDA For. Serv. Res. Paper 1977, 194, 1–80. [Google Scholar]
- Nishimura, K. Measurement of blowing snow. J. Fluid Mech. 2009, 28, 455–460. (In Japanese) [Google Scholar]
- Sugiura, K.; Nishimura, K.; Maeno, N.; Kimura, T. Measurements of snow mass flux and transport rate at different particle diameters in drifting snow. Cold Reg. Sci. Technol. 1998, 27, 83–89. [Google Scholar] [CrossRef]
- Sato, A. Calculation of size-effect of blowing snow particles on the snow particle counter (first report). Tech. Rep. Natl. Cent. Disaster Prev. 1987, 40, 93–101. [Google Scholar]
- Mikami, M.; Yamada, Y.; Ishizuka, M.; Ishimaru, T.; Gao, W.; Zeng, F. Measurement of saltation process over Gobi and sand dunes in the Taklimakan desert, China, with newly developed sand particle counter. J. Geophys. Res. 2005, 110, D18S02. [Google Scholar] [CrossRef] [Green Version]
- Ozeki, T.; Toda, S.; Yamaguchi, H. Field investigation of impinging seawater spray on the R/V Mirai using spray particle counter type sea spray meter. In Proceedings of the 33rd International Symposium on Okhotsk Sea and Polar Oceans, Hokkaido, Japan, 18–21 February 2018; Volume D-5, pp. 93–96. [Google Scholar]
- Ozeki, T.; Shiga, T.; Sawamura, J.; Yashiro, Y.; Adachi, S.; Yamaguchi, H. Development of sea spray meters and an analysis of sea spray characteristics in large vessel. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016; Volume 1, pp. 1335–1340. [Google Scholar]
- Schmidt, R.A.; Meister, R.; Gubler, H. Comparison of snow drifting measurements at an alpine ridge crest. Cold Reg. Sci. Technol. 1984, 9, 131–141. [Google Scholar] [CrossRef]
- Sato, T.; Kimura, T.; Ishimaru, T.; Maruyama, T. Field test of a new snow-particle counter (SPC) system. Ann. Glaciol. 1993, 18, 149–154. [Google Scholar] [CrossRef] [Green Version]
- World Meteorological Organization. Guide to Hydrological Practices (WMO-No. 168); WMO: Geneva, Switzerland, 2008; Volume 1, pp. I.3–I.8. [Google Scholar]
- World Meteorological Organization. Methods of Correction for Systematic Error in Point Precipitation Measurement for Operational Use; Operational Hydrology Report No. 21 (WO-No. 589); WMO: Genova, Switzerland, 1982. [Google Scholar]
- Førland, E.J.; Hanssen-Bauer, I. Increased precipitation in the Norwegian Arctic: True or false? Clim. Chang. 2000, 46, 385–509. [Google Scholar] [CrossRef]



| Hourly Wind Speed [m s−1] | a | b |
|---|---|---|
| 0−5 | 4.05 | −11.7 |
| 5−10 | 0.22 | −0.89 |
| 10−15 | 0.050 | 0.16 |
| 15−20 | 0.16 | −0.099 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okachi, H.; Yamada, T.J.; Baba, Y.; Kubo, T. Characteristics of Rain and Sea Spray Droplet Size Distribution at a Marine Tower. Atmosphere 2020, 11, 1210. https://doi.org/10.3390/atmos11111210
Okachi H, Yamada TJ, Baba Y, Kubo T. Characteristics of Rain and Sea Spray Droplet Size Distribution at a Marine Tower. Atmosphere. 2020; 11(11):1210. https://doi.org/10.3390/atmos11111210
Chicago/Turabian StyleOkachi, Hiroki, Tomohito J. Yamada, Yasuyuki Baba, and Teruhiro Kubo. 2020. "Characteristics of Rain and Sea Spray Droplet Size Distribution at a Marine Tower" Atmosphere 11, no. 11: 1210. https://doi.org/10.3390/atmos11111210
APA StyleOkachi, H., Yamada, T. J., Baba, Y., & Kubo, T. (2020). Characteristics of Rain and Sea Spray Droplet Size Distribution at a Marine Tower. Atmosphere, 11(11), 1210. https://doi.org/10.3390/atmos11111210





